Предметный тур. Информатика. 3 этап

Информатика. 8–11 классы

Задача 1.1.(10 баллов)

Экономный палиндром

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

У Вениамина есть три различные маленькие буквы латинского алфавита. Вениамин хочет, чтобы из них можно было составить палиндром. Напомним, что строка называется палиндромом, если она читается одинаково как слева направо, так и справа налево. Например, строки zzz, bob являются палиндромами, а abc — не является. Очевидно, что из трех различных букв, как их ни переставляй, палиндром не получится.

Вениамин может удалить из своего набора одну любую букву и добавить в свой набор также любую букву. При этом как за удаление, так и за добавление он должен будет доплатить.

Для того чтобы узнать цену удаления или добавления буквы, пронумеруем их от \(0\) до \(25\): (буква \(a\) имеет номер \(0\), буква \(b\) имеет номер \(1\), …, буква \(z\) имеет номер \(25\)). Пусть изначально у Вениамина есть три буквы, которые обозначим \(\alpha,~\beta,~\gamma\), а сумму их номеров как \(S\). Зафиксируем число \(S\), оно в дальнейшем изменяться не будет ни при каких условиях.

Для любой буквы \(\lambda\) определим ее показатель \(P(\lambda)\) как остаток от деления суммы номера этой буквы \(\lambda\) и числа \(S\) на \(26\).

Например, пусть у Вениамина есть три буквы \(d,~e,~z\), (порядковые номера \(3\), \(4\) и \(25\)). Тогда \(S = 3 + 4 + 25 = 32\), а показатели, соответственно, следующие: \[P(d) = (3 + 32) \% 26 = 9,~ P(e) = (4 + 32) \% 26 = 10,~ P(z) = (25 + 32) \% 26 = 5.\]

Тогда для того чтобы добавить букву \(\lambda\), нужно заплатить \(P(\lambda)\), а для того чтобы удалить эту букву, нужно заплатить \(26 - P(\lambda)\). Еще раз заметим, что показатель буквы вычисляется перед началом всех операций, и затем уже не изменяется.

Требуется вывести палиндром, который сможет в этих условиях построить Вениамин, заплатив за это минимальную возможную сумму.

Формат входных данных

В трех строках подаются три различных символа. Все они являются строчными буквами из интервала от \(a\) до \(z\).

Формат выходных данных

Вывести в одну строку без пробелов палиндром из трех символов, который может быть получен из исходных букв путем удаления одной из них и добавления новой с наименьшими затратами. Можно показать, что при этих условиях решение единственно.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	d e z	zdz
2	b a y	byb

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> vi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;

int P(char a, int S){
    int res = (a - 'a' + S) % 26;
    return res;
}

int cost(char a, char b, int S){
    return P(a, S) + 26 - P(b, S);
}

signed main(){
       ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    char a, b, c;
    cin >> a >> b >> c;
    int S = a + b + c - 3 * 'a';
    char ta = a, tb = b;
    int tcost = cost(a, b, S);
    if(cost(b, a, S) < tcost){
        ta = b, tb = a;
        tcost = cost(b, a, S);
    }
    if(cost(a, c, S) < tcost){
        ta = a, tb = c;
        tcost = cost(a, c, S);
    }
    if(cost(c, a, S) < tcost){
        ta = c, tb = a;
        tcost = cost(c, a, S);
    }
    if(cost(b, c, S) < tcost){
        ta = b, tb = c;
        tcost = cost(b, c, S);
    }
    if(cost(c, b, S) < tcost){
        ta = c, tb = b;
        tcost = cost(c, b, S);
    }
    char o = a + b + c - ta - tb;
    cout << ta << o << ta;
}

Задача 1.2.(15 баллов)

Былинная история

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 128 Мбайт.

Условие

Не все знают, но кроме короля Артура, круглый стол был и у великого былинного князя Владимира Красно Солнышко. За этим столом он любил собираться и пировать со своей многочисленной дружиной. Каждое место за этим столом имело свой номер, номера начинались с 1 и шли по часовой стрелке. Всего было \(n\) мест, и, так как стол был круглым, за последним \(n\)-м местом снова шло первое. Все члены дружины, включая князя, были упорядочены по старшинству, князь имел самый первый номер.

Рассадка производилась следующим образом: сначала рассаживались самые почетные члены дружины — первые \(k\) человек. Они выбирали случайные места по своему настроению и садились, как хотели. Далее возможность выбора места предоставлялась остальным \((n - k)\) членам дружины. Все они выбирали места по очереди в порядке старшинства. Каждый из них при выборе места действовал так: среди всех пустых оставшихся на данный момент мест выбиралось то, рядом с которым сидел самый почетный дружинник (то есть человек с самым маленьким номером), и садился на это место. Если у самого почетного, на текущий момент, оба места вокруг него были свободны, предпочтение отдавалось правому месту (выбиравший предпочитал сесть справа от выбранного почетного дружинника, это называлось «одесную»). С точки зрения нумерации мест это значило сесть на меньшее по номеру место (кроме случая, когда выбранный почетный дружинник сидел на первом месте).

Былины сохранили порядок в дружине князя и рассадку первых \(k\) ее членов. Нужно восстановить полную рассадку дружины, это важная историческая деталь.

Формат входных данных

В первой строке находится два целых числа \(n\) и \(k\) через пробел — общее количество человек в дружине, включая князя и количество самых почетных дружинников, которые могли выбирать места как хотят, \(1 \leqslant k < n \leqslant 3 \cdot 10^5\).

Во второй строке через пробел указаны \(k\) чисел \(a_i\) — номера мест за столом, на которые сели эти \(k\) самых важных дружинников. Число \(a_i\) в этом наборе означает, что \(i\)-й дружинник сел на место с номером \(a_i\), \(1 \leqslant a_i \leqslant n\). Все \(a_i\) на входе попарно различны.

Формат выходных данных

Вывести \((n - k)\) чисел через пробел — номера мест, на которые сядут оставшиеся члены дружины. Номера выводятся в том порядке, в котором они выбирались, то есть первым выводится место, на которое сел \((k + 1)\)-й дружинник, вторым — место, на которое сел \((k + 2)\)-й и т. д.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	10 3 5 4 1	6 3 10 2 7 9 8

Примечания

Рис. 1.1.

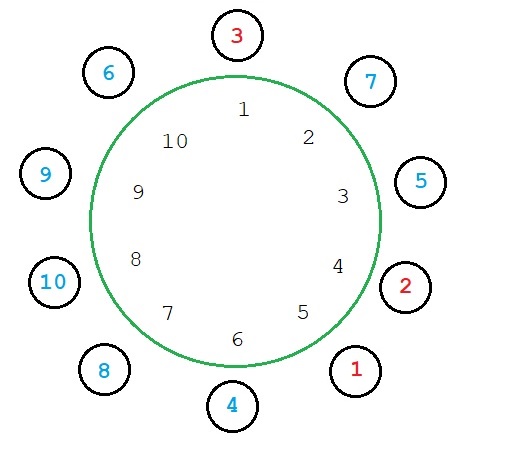
На рисунке 1.1 представлена рассадка для примера из условия. Красными номерами указаны первые трое дружинников, которые выбирали места самостоятельно, синими номерами — остальные семеро, которые рассаживались по указанному в условии методу.

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> vi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;
signed main(){
       ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, k;
    cin >> n >> k;
    vi to(n, -1), pos(n, -1);
    for0(i, k){
        int a;
        cin >> a;
        a--;
        to[a] = i;
        pos[i] = a;
    }
    int t = 0;
    for(int i = k; i < n; i++){
        while(1){
            if(to[(pos[t] + n - 1) % n] == -1){
                cout << (pos[t] + n - 1) % n + 1 <<' ';
                to[(pos[t] + n - 1) % n] = i;
                pos[i] = (pos[t] + n - 1) % n;
                break;
            }
            if(to[(pos[t] + 1) % n] == -1){
                cout << (pos[t] + 1) % n + 1 <<' ';
                to[(pos[t] + 1) % n] = i;
                pos[i] = (pos[t] + 1) % n;
                break;
            }
            t++;
        }
    }
    cout << endl;
}

Задача 1.3.( баллов)

Плюс-минус

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

Возьмем некоторое натуральное число \(n\) и заведем \((n + 1)\) ячейку. Пронумеруем ячейки от \(0\) до \(n\). Изначально в каждой ячейке находится число \(0\). Мы находимся в ячейке с индексом \(0\) и начинаем двигаться в сторону увеличения индексов.

На каждом шаге перемещаемся в следующую по номеру ячейку и смотрим, какое число там стоит. Если это \(0\) или отрицательное число, тогда в ячейку с этим номером и во все кратные этому номеру ячейки прибавляется индекс этих ячеек. Если в ячейке с этим номером число больше \(0\), то из этой и всех кратных этому номеру ячеек вычитается их индекс. После этого пересчета переходим в следующую по номеру ячейку и повторяем набор описанных операций.

По числу \(n\) найти сумму всех чисел, оказавшихся в ячейках с номерами от \(0\) до \(n\).

Например, \(n = 8\).

Сначала находимся в \(0\), и все ячейки равны \(0\): \(0,~0,~0,~0,~0,~0,~0,~0,~0\).

Делаем шаг на ячейку номер \(1\). Там стоит \(0\). Тогда в нее и все кратные \(1\) (то есть вообще во все ячейки) добавим их индекс. Получим: \(0,~1,~2,~3,~4,~5,~6,~7,~8\).

Делаем шаг в ячейку номер \(2\). Там стоит \(2\), то есть число, большее \(0\). Вычитаем из нее и всех кратных \(2\) ячеек их индекс. Получим \(0,~1,~0,~3,~0,~5,~0,~7,~0\).

Делаем шаг в ячейку номер \(3\). Там стоит \(3\), то есть число, большее \(0\). Вычитаем из нее и всех кратных \(3\) ячеек их индекс. Получим \(0,~1,~0,~0,~0,~5,~-6,~7,~0\).

Делаем шаг на ячейку номер \(4\). Там стоит \(0\). Тогда в нее и все кратные \(4\) добавим их индекс. Получим \(0,~1,~0,~0,~4,~5,~-6,~7,~8\).

Делаем шаг в ячейку номер \(5\). Там стоит \(5\), то есть число, большее \(0\). Вычитаем из нее и всех кратных \(5\) ячеек их индекс. Получим \(0,~1,~0,~0,~4,~0,~-6,~7,~8\).

Делаем шаг в ячейку номер \(6\). Там стоит \(-6\), то есть число, меньшее \(0\). Прибавим к ней и во все кратные \(6\) ячейки их индекс. Получим \(0,~1,~0,~0,~0,~5,~0,~7,~8\).

Делаем шаг в ячейку номер \(7\). Там стоит \(7\), то есть число, большее \(0\). Вычитаем из нее и всех кратных \(7\) ячеек их индекс. Получим \(0,~1,~0,~0,~4,~0,~0,~0,~8\).

Делаем шаг в ячейку номер \(8\). Там стоит \(8\), то есть число, большее \(0\). Вычитаем из нее и всех кратных \(8\) ячеек их индекс. Получим \(0,~1,~0,~0,~4,~0,~0,~0,~0\).

Просуммируем получившиеся значения во всех ячейках и получим число \(5\). Это и будет ответом.

Формат входных данных

На вход подается единственное число \(n\), \(1 \leqslant n \leqslant 10^{13}\).

Формат выходных данных

Вывести одно число — итоговую сумму после того, как пройдем по всем \(n\) ячейкам.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	8	5

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    int L = sqrt(n);
    long double ans = 0;
    for(long double i = 1; i <= L; i++){
        ans += i * i;
    }
    cout.precision(0);
    cout << fixed<< ans;
}

Задача 1.4.(25 баллов)

Варианты эксперимента на БЛК

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 256 Мбайт.

Условие

Исследователи, работающие на БЛК (Большом линейном коллайдере), задумали новый эксперимент. На равных расстояниях в БЛК будет сгенерирован утвержденный набор частиц двух разных знаков. После старта эксперимента частицы полетят с одинаковой скоростью каждая в своем направлении (отрицательные влево, положительные — вправо). Если две частицы, летящие навстречу друг другу, сталкиваются, они взаимно уничтожаются. Эксперимент будет успешным, если в итоге взаимно уничтожатся все сгенерированные частицы.

Один из исследователей пишет диссертацию, в которой рассматривает все успешные варианты эксперимента. Вариантом эксперимента он называет некоторый непустой набор частиц, полученный из исходного путем удаления нескольких (возможно, ни одной) частиц из начала утвержденного набора и нескольких (возможно, ни одной) частиц из его конца. Вариант будет успешным, если эти частицы после старта снова все взаимно уничтожатся.

Для понимания объема своей диссертации ее автор хочет знать, сколько успешных вариантов эксперимента ему придется рассмотреть.

Формат входных данных

В единственной строке ввода содержится описание утвержденного набора частиц. Набор непустой. Каждая частица задается одной буквой L или R. Те, что помечены L после старта полетят влево, те что помечены R — вправо. Буквы в наборе заданы без пробелов между ними. Считаем, что соседние частицы расположены на равных расстояниях друг от друга. Гарантируется, что заданный на входе набор описывает успешный эксперимент (все частицы взаимно уничтожатся). Длина набора не превосходит \(10^6\).

Формат выходных данных

Вывести одно число — количество всех непустых успешных вариантов эксперимента для утвержденного набора частиц, заданного во входных данных.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	RRLRRLRRLLLLRLRRLRLRRLLL	20

Примечание

Для примера из условия будет ровно 20 следующих успешных вариантов (числа указывают номер первой и последней частицы варианта): 2–3, 5–6, 8–9, 7–10, 5–10, 4–11, 2–11, 1–12, 13–14, 1–14, 16–17, 18–19, 16–19, 21–22, 20–23, 18–23, 16–23, 15–24, 13–24, 1–24.

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define int long long
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> vi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;

signed main(){
       ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    string s;
    cin >> s;
    int ans = 0;
    vi st, dp(sz(s), 0);
    for0(i, sz(s)){
        if(s[i] == 'R'){
            st.pb(i);
        }
        if(s[i] == 'L'){
            dp[i]++;
            if(st.back() > 0 && s[st.back() - 1] == 'L'){
                dp[i] += dp[st.back() - 1];
            }
            st.pop_back();
        }
    }
    for0(i, sz(s)){
        ans += dp[i];
    }
    cout << ans << endl;
}

Задача 1.5.(30 баллов)

Пробка

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 128 Мбайт.

Условие

Предлагаем вам сыграть в увлекательную игру-головоломку «Пробка». Правила следующие: дано квадратное поле, разбитое на клетки, размер поля \(6 \times 6\). Строки поля пронумеруем от 1 до 6 сверху вниз, столбцы от 1 до 6 слева направо. Поле ограничено по своему периметру ограждением. В этом ограждении, на его правой границе, напротив третьей строки есть свободный выход (выезд). Других выходов (выездов) в периметре нет.

На поверхности поля находятся несколько автомобилей. Каждый автомобиль занимает либо две, либо три рядом стоящие клетки в одном горизонтальном или вертикальном ряду. Таким образом, для автомобиля можно сказать, что он расположен горизонтально или вертикально. Автомобиль может передвигаться на свободную клетку, расположенную рядом с ним в его ряду (спереди или сзади от него). Автомобиль не может передвигаться вбок. В зависимости от вида автомобиля, будем называть его горизонтальным или вертикальным. Разумеется, никакие два автомобиля не могут одновременно находиться в одной клетке.

На поле имеется как минимум один горизонтальный автомобиль, назовем его автомобилем A или целевым автомобилем. Этот автомобиль всегда расположен в третьей строке. Кроме него в третьей строке нет ни одного горизонтального автомобиля. Остальные автомобили могут располагаться произвольно, в том числе и по несколько в одном ряду.

Задача головоломки заключается в том, чтобы вывести из пробки автомобиль A, поставив его правую клетку на поле с координатами \((3, 6)\). Этому могут мешать другие автомобили. Их можно передвигать в пределах поля на свободные клетки в соответствии с их ориентацией. Одно передвижение одного любого автомобиля будем называть одним ходом.

Требуется за минимальное число ходов вывести A-автомобиль из пробки.

Формат входных данных

На вход в шести строках по шесть символов в каждой подается описание пробки. В этом описании пустому пространству соответствуют клетки, помеченные символом «.». Каждый автомобиль задается своей большой буквой латинского алфавита. Целевой автомобиль, который нужно вывести из пробки, всегда располагается в двух или трех рядом стоящих клетках третьего горизонтального ряда и обозначен буквой A. Остальные автомобили (если они есть) задаются своими большими буквами, отличными от буквы A. Буквы могут быть произвольными от B до Z. Каждый автомобиль занимает две или три рядом стоящие клетки в одном горизонтальном или вертикальном ряду.

Гарантируется, что всегда существует решение для заданной в тесте пробки.

Формат выходных данных

Требуется вывести одно число — минимальное количество ходов, требующихся для того, чтобы правая клетка автомобиля A оказалась в клетке с координатами \((3, 6)\).

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	...... ...... AAB..W ..B..W Q.B..W QZZXXX	10

Примечание

На рисунках 1.2–1.4 показан ход решения головоломки из примера. На первом рисунке показан начальный вид пробки. Далее по шагам показан кратчайший путь ее решения (кратчайших решений может быть несколько). Целевой автомобиль имеет красный цвет, в этом примере состоит из двух клеток и расположен в третьей строке. Видно, что за 10 ходов правая клетка целевого автомобиля попадает в клетку с координатой \((3, 6)\). Последний рисунок демонстрирует, что целевой автомобиль выехал из пробки. Этот ход не нужно учитывать в ответе.

Рис. 1.2.

Рис. 1.3.

Рис. 1.4.

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;

bool inside(int x, int y){
    return (x >= 0 && y >= 0 && x < 6 && y < 6);
}

void step_left(vector<string> &P, int x, int y){
    int t = y + 1;
    char c = P[x][y + 1];
    while(t < 6 && P[x][t] == c){
        t++;
    }
    t--;
    P[x][t] = '.';
    P[x][y] = c;
}

void step_right(vector<string> &P, int x, int y){
    int t = y - 1;
    char c = P[x][y - 1];
    while(t >= 0 && P[x][t] == c){
        t--;
    }
    t++;
    P[x][t] = '.';
    P[x][y] = c;
}

void step_up(vector<string> &P, int x, int y){
    int t = x + 1;
    char c = P[x + 1][y];
    while(t < 6 && P[t][y] == c){
        t++;
    }
    t--;
    P[t][y] = '.';
    P[x][y] = c;
}

void step_down(vector<string> &P, int x, int y){
    int t = x - 1;
    char c = P[x - 1][y];
    while(t >= 0 && P[t][y] == c){
        t--;
    }
    t++;
    P[t][y] = '.';
    P[x][y] = c;
}

signed main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    deque<vector<string> > D;
    map<vector<string>, int> used;
    map<vector<string>, vector<string> >par;
    vector<string> P(6);
    for0(i, 6){
        cin >> P[i];
    }
    par[P] = P;
    par[P][0][0] = '*';
    used[P] = 1;
    D.pb(P);
    while(sz(D) > 0)
    {
      vector<string> T = D[0], Z;
        if(T[2][5] == 'A'){
            vector<vector<string> > ans;
            vector<string> TT = T;
            while(TT[0][0] != '*'){
                ans.pb(TT);
                TT = par[TT];
            }
            reverse(all(ans));
            int cnt = 0;
            for(auto el : ans){
                cnt++;
            }
            cout << sz(ans) - 1 << endl;
            break;
        }
        D.pop_front();
        for0(i, 6){
            for0(j, 6){
                if(T[i][j] == '.'){
               if(inside(i, j + 1) && inside(i, j + 2) && T[i][j + 1] == T[i][j + 2]){
                        Z = T;
                        step_left(Z, i, j);
                        if(!used[Z]){
                            used[Z] = used[T] + 1;
                            D.pb(Z);
                            par[Z] = T;
                        }
                   }
                }

                if(T[i][j] == '.'){
               if(inside(i, j - 1) && inside(i, j - 2) && T[i][j - 1] == T[i][j - 2]){
                        Z = T;
                        step_right(Z, i, j);
                        if(!used[Z]){
                            used[Z] = used[T] + 1;
                            D.pb(Z);
                            par[Z] = T;
                        }
                   }
                }
                if(T[i][j] == '.'){
               if(inside(i + 1, j) && inside(i + 2, j) && T[i + 1][j] == T[i + 2][j]){
                        Z = T;
                        step_up(Z, i, j);
                        if(!used[Z]){
                            used[Z] = used[T] + 1;
                            D.pb(Z);
                            par[Z] = T;
                        }
                   }
                }
                if(T[i][j] == '.'){
               if(inside(i - 1, j) && inside(i - 2, j) && T[i - 1][j] == T[i - 2][j]){
                        Z = T;
                        step_down(Z, i, j);
                        if(!used[Z]){
                            used[Z] = used[T] + 1;
                            D.pb(Z);
                            par[Z] = T;
                        }
                   }
                }
            }
        }
    }
}