Предметный тур. Физика. 3 этап
Для нужд микроэлектроники был изготовлен элемент, представляющий собой куб со стороной \(a = 2\textrm{\,мкм}\) из \(n = 32\) тонко напыленных слоев металла и \(m = 31\) слоя слабопроводящего полупроводника, параллельных одной из пар граней куба. Удельное сопротивление полупроводника \(r = 210\) Ом\(\cdot\)м, удельное сопротивление металла ничтожно мало по сравнению с этой величиной. Плотность полупроводника \(\rho_1 = 2000\) кг/м\(^3\), плотность металла \(\rho_2 = 8000\) кг/м\(^3\). Определите сопротивление такого элемента в направлении поперек слоев, если его средняя плотность составила \(\rho = 4000\) кг/м\(^3\).
При измерении сопротивления слоистой структуры поперек слоев она включается в цепь как набор отдельных слоев, соединенных последовательно. Следовательно, ее общее сопротивление \(R\) может быть найдено по формуле \[R = \sum_{i=1}^{n+m} R_i = \sum_{i=1}^{n+m}\frac{r_id_i}{a^2},\] где \(R_i\) — сопротивление \(i\)-го слоя, \(r_i\) — удельное сопротивление его материала, \(d_i\) — толщина этого слоя, а суммирование осуществляется по всем слоям структуры. Учитывая при этом, что сопротивление металлических слоев пренебрежимо мало по сравнению с сопротивлением полупроводниковых, можем суммировать только последние: \[R = \sum_{i=1}^n R_i = \sum_{i=1}^n\frac{r d_i}{a^2} = \frac{r}{a^2} \sum_{i=1}^n d_i.\] В этом случае удельное сопротивление \(r\) и площадь одного слоя \(a^2\) выносятся за знак суммы, а оставшееся внутри него выражение представляет собой не что иное, как суммарную толщину всех полупроводниковых слоев, независимо от числа слоев. Обозначим ее \(b\): \[R = \frac{rb}{a^2}.\]
Чтобы найти эту суммарную толщину, выразим массу элемента через его среднюю плотность и через плотности отдельных его составляющих: \[\rho a^3 = \rho_1 a^2 b + \rho_2 a^2(a-b).\] Сокращая \(a^2\), получим линейное уравнение на \(b\): \[\rho a = \rho_1 b + \rho_2(a-b) \Rightarrow b = \frac{\rho_2 - \rho}{\rho_2 - \rho_1} a,\] откуда окончательно \[R = \frac{r (\rho_2 - \rho)}{a (\rho_2 - \rho_1)} = 70\textrm{\,МОм}.\]
\[R = \frac{r (\rho_2 - \rho)}{a (\rho_2 - \rho_1)} = 70\textrm{\,МОм}.\]
| Указано, что слои можно считать соединенными последовательно или записано демонстрирующее это выражение для сопротивлений или напряжений и токов | 3 балла |
| Показано, что сопротивление элемента определяется общей толщиной полупроводниковых слоев и не зависит от их числа и распределения | 3 балла |
| Верно записано соотношение для средней плотности или общей массы, позволяющее найти общую толщину полупроводниковых слоев | 4 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 16 баллов |
При проведении ядерного эксперимента радиоактивный образец был окружен оболочкой поглотителей продуктов распада, представляющей собой сферический слой, имеющей внутренний радиус \(R\) и внешний радиус \(4R\), в центре которого находился экспериментальный образец. Начальная температура всей оболочки \(t_0 = 25~°\)C.
После инициации в образце цепной реакции слой материала, находившийся от центра установки на расстоянии меньше \(3R\), быстро поглотил большую энергию излучения и практически мгновенно достиг температуры \(t_1 = 340~°\)C, а материал, находившийся от центра установки на большем расстоянии, практически не изменил своей температуры. Определите, какая температура \(t_2\) установилась в поглощающей оболочке через \(20\) мин, если известно, что за это время температура всей оболочки выровнялась, а внешней среде было передано \(\eta = 20\%\) изначально поглощенной теплоты. Объем шара радиуса \(R\) задается выражением \(4\pi R^3/3\).
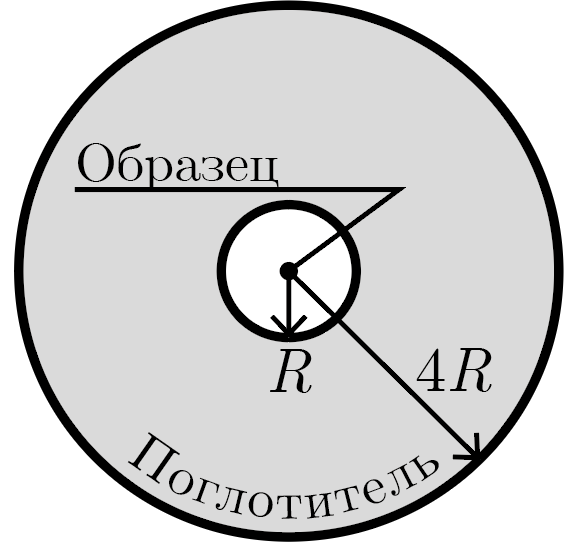
Поглотитель представляет собой сферический слой, который можно представить как разность двух шаров, обладающих радиусами \(4R\) и \(R\).
Тогда общий объем \(V_0\) поглотителя равен \[V_0 = \frac{4\pi}{3} (4R)^3 - \frac{4\pi}{3} R^3 = 63 \frac{4\pi}{3} R^3,\] а объем \(V_1\) нагревшейся части этого поглотителя \[V_1 = \frac{4\pi}{3} (3R)^3 - \frac{4\pi}{3} R^3 = 26 \frac{4\pi}{3} R^3.\] Обозначив плотность поглотителя \(\rho\), а его удельную теплоемкость \(c\), легко найдем, что изначально веществом было поглощено количество теплоты \[Q = c\rho V_1(t_1 -t_0) = 26 \frac{4\pi}{3} c\rho R^3 (t_1 -t_0).\] По условиям задачи доля \(\eta\) этого тепла рассеивается во внешней среде, а остальная теплота перераспределяется равномерно по всему объему поглотителя: \[Q(1-\eta) = c\rho V_0 = 63 \frac{4\pi}{3} c\rho R^3 (t_2 - t_0).\] Подставляя эти два выражения друг в друга, получим \[(1-\eta) 26\cancel{\frac{4\pi}{3} c \rho R^3} (t_1 - t_0) = 63\cancel{\frac{4\pi}{3} c \rho R^3} (t_2 - t_0) \Rightarrow t_2 = t_0 + (1-\eta)\frac{26}{63}(t_1 - t_0) = 129~°\text{C}.\]
\[t_2 = t_0 + (1-\eta)\frac{26}{63}(t_1 - t_0) = 129~°\text{C}.\]
| Верно найден общий объем поглотителя (в том числе через неизвестный коэффициент пропорциональности) | 3 балла |
| Верно найден объем нагревшейся части поглотителя (в том числе через неизвестный коэффициент пропорциональности) | 2 балла |
| Записано правильное уравнение теплового баланса с учетом тепловых потерь | 5 баллов |
| Получен правильный ответ | 6 баллов |
| Всего | 16 баллов |
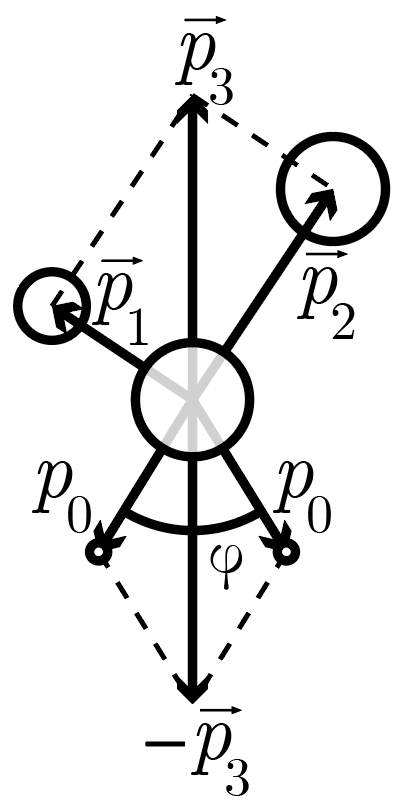
Покоящееся ядро нестабильного элемента, находящееся вдали от других заряженных частиц, претерпевает деление, в результате которого образуются два крупных осколка и два нейтрона. Первый осколок имеет массу \(m_1 = 55\) а. е. м. и получает \(\eta_1 = 0{,}8\%\) энергии, выделившейся в результате деления ядра, второй — массу \(m_2 = 198\) а. е. м. и получает \(\eta_2 = 0{,}5\%\) энергии, выделившейся в результате деления. Остальная энергия деления поровну распределилась между нейтронами. Вся энергия осколков чисто кинетическая. Под каким углом друг к другу разлетаются два нейтрона, если крупные осколки разлетелись под прямым углом друг к другу? Масса нейтрона \(m_0 = 1\) а. е. м.
Импульс \(\vec{p}\) частицы определяется выражением \(\vec{p} = m \vec{v}\), где \(m\) — масса частицы, а \(\vec{v}\) — ее скорость. Кинетическая энергия \(K\) частицы определяется выражением \(K = mv^2/2\). Подставляя эти два выражения друг в друга, получим \(p = \sqrt{2mK}.\) Обозначим \(E\) общую энергию, выделившуюся в результате распада. Тогда \[p_1 = \sqrt{2m_1\eta_1E};\quad p_2 = \sqrt{2m_2\eta_2E}.\] Суммарный импульс \(p_3\) этих двух осколков легко найти, сложив \(\vec{p}_1 + \vec{p}_2\). Суммирование, разумеется, следует проводить геометрически, а значит, его модуль определяется по теореме Пифагора: \[p_3 = \sqrt{p_1^2 + p_2^2} = \sqrt{2E(m_1 \eta_1 + m_2 \eta_2)}.\] Импульс \(p_0\) каждого из нейтронов легко выразить из той же логики, учитывая, что каждому из них достается половина остальной энергии: \[p_0 = \sqrt{m_0E(1-\eta_1-\eta_2)}.\]
Систему отсчета ядра можно считать инерциальной, поскольку по условиям ядро находится вдали от других заряженных частиц. Следовательно, геометрическая сумма импульсов всех четырех его осколков должна равняться нулю, а отдельно взятых двух нейтронов — составлять, соответственно, \(-\vec{p_3}\). Из рис. 1.2 легко видеть, что модуль этой суммы равен \[p_3 = 2p_0\cos\frac{\phi}{2},\] откуда получим \[\cos\frac{\phi}{2} = \frac{p_3}{2p_0} = \frac{\sqrt{2\cancel{E}(m_1 \eta_1 + m_2 \eta_2)}}{2\sqrt{m_0\cancel{E}(1-\eta_1-\eta_2)}} \Rightarrow \phi = 2 \operatorname{arccos}\sqrt{\frac{m_1 \eta_1 + m_2 \eta_2}{2m_0(1-\eta_1-\eta_2)}} \approx 63°.\]
Вообще говоря, шесть векторов на рис. 1.2 могут и не лежать в одной плоскости. Угол между импульсами нейтронов и тяжелых осколков установить невозможно, но внутри этих пар углы должны оставаться такими, какими они вычислены и изображены.
\[\phi = 2 \operatorname{arccos}\sqrt{\frac{m_1 \eta_1 + m_2 \eta_2}{m_0(1-\eta_1-\eta_2)}} \approx 63°.\]
| Продемонстрировано понимание того, что импульс системы в рассматриваемом взаимодействии сохраняется | 3 балла |
| Изображен рисунок или словами описана процедура векторного сложения импульсов | 3 балла |
| Верно найдено выражение, связывающее импульс, массу и кинетическую энергию | 4 балла |
| Грамотно применена теорема Пифагора к сложению импульсов тяжелых осколков | 3 балла |
| Записано верное соотношение между импульсом одного нейтрона, суммарным импульсом двух и искомым углом | 3 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 22 балла |
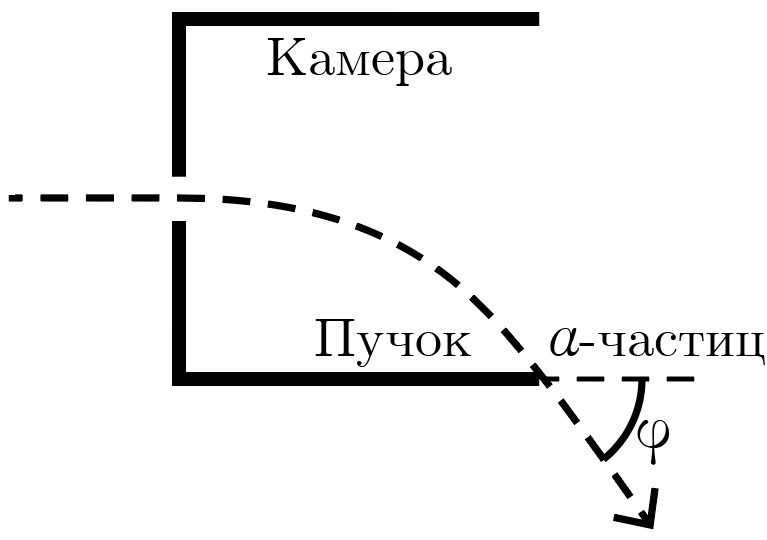
В ядерной лаборатории тестируются два различных устройства, предназначенных для управления пучком \(\alpha\)-частиц. Оба устройства представляют собой кубические камеры одинаковых размеров со стороной \(l\), в которые пучок \(\alpha\)-частиц, испущенных радионуклидом, попадает через окошко в центре одной из граней параллельно оси симметрии камеры и должен выйти через противоположную стенку. Внутри камеры создано однородное поле, отклоняющее частицу, при этом интенсивность поля достаточна, чтобы ограничение на максимальный угол отклонения пучка частиц \(\phi\) было обусловлено только геометрией камеры (см. рис. 1.3).
Первое использует для поворота частицы электрическое поле, которое оказывает на частицу постоянную по величине и направлению силу, перпендикулярную вектору начальной скорости частицы. Второе — магнитное поле, оказывающее на частицу постоянную по величине силу, всегда направленную перпендикулярно вектору мгновенной скорости частицы На какую величину отличаются максимальные углы \(\phi\), на которые способны отклонить пучок в плоскости рис. 1.3 эти два устройства, если силы, создаваемые ими, существуют только в пределах кубической камеры?
Обозначим максимальные углы отклонения пучка \(\phi_E\) и \(\phi_M\) для электрической и магнитной камер соответственно. При движении в электрической камере под воздействием постоянной по модулю и направлению силы \(\vec{F}\) закон движения частицы удобно записать в проекции на две оси: \(0x\), сонаправленную с вектором ее начальной скорости и \(0y\), сонаправленную с вектором \(\vec{F}\) и создаваемым ей ускорением \(\vec{a}\). Движение в первой проекции является равномерным, во второй — равноускоренным. При максимальном отклонении частица проходит у самого ребра кубической камеры, через точку с координатами \((l;l/2)\). Тогда для момента вылета частицы из камеры получим \[\left\{\begin{aligned} &vt = l,\\ &\frac{at^2}{2} = \frac{l}{2}. \end{aligned}\right.\] Решая эту систему, получим \(t = v/a\). Тогда вертикальная компонента скорости \(v_y = a t\), набранная частицей, равна \(v_y = a t = v\) ее изначальной горизонтальной компоненте скорости, а значит, угол \(\phi_E\) максимального отклонения частицы составляет \(45°\).
При движении в магнитной камере под действием силы, постоянно направленной перпендикулярно к вектору мгновенной скорости, созданное этой силой ускорение является чисто центростремительным, а значит, частица движется по дуге окружности. Найти радиус этой окружности можно при помощи геометрии.
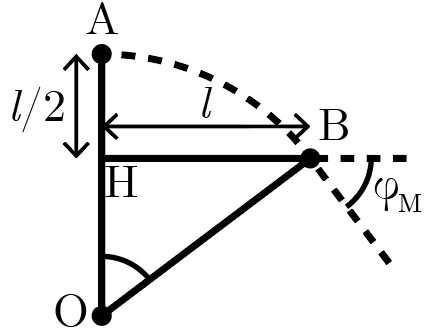
Обозначим точку попадания частицы в камеру \(\textrm{A}\), точку выхода частицы \(\textrm{B}\), а центр кривизны ее траектории \(\textrm{O}\). Также обозначим \(\textrm{H}\) угол в сечении камеры плоскостью рис. 1.4, лежащий на отрезке \(\textrm{OA}\). Отрезки \(\textrm{OA}\) и \(\textrm{OB}\) равны как радиусы, обозначим их длины \(R\). Тогда из геометрии камеры и теоремы Пифагора легко получить
\[(R - l/2)^2 + l^2 = R^2 \Rightarrow \frac{5}{4}l^2 - R l = 0 \Rightarrow R = \frac{5l}{4},\] откуда угол \[\angle \textrm{AOB} = \operatorname{arcsin}\frac{4}{5},\] но так как \(\angle \textrm{OHB}\) прямой, \(\angle \textrm{AOB} = 90°-\angle \textrm{HBO} = \varphi_M\) (так как касательная к окружности перпендикулярна ее радиусу).
Тогда окончательно \[\phi_M - \phi_E = \operatorname{arcsin}\frac{4}{5} - 45° \approx 8{,}1°.\]
\[\phi_M - \phi_E = \operatorname{arcsin}\frac{4}{5} - 45° \approx 8{,}1°.\]
| Продемонстрировано понимание того, что траектория \(\alpha\)-частицы в электрической камере представляет собой дугу параболы | 2 балла |
| Верно записаны законы движения частицы в этом случае | 3 балла |
| Верно найдена вертикальная проекция скорости частицы на выходе из камеры | 2 балла |
| Верно найден максимальный угол отклонения частицы в электрической камере | 4 балла |
| Продемонстрировано понимание того, что траектория \(\alpha\)-частицы в магнитной камере представляет собой дугу окружности | 3 балла |
| Верно сделан чертеж, позволяющий найти угол отклонения в этом случае и/или записаны эквивалентные этому чертежу геометрические соотношения между отрезками | 3 балла |
| Верно найден максимальный угол отклонения частицы в магнитной камере | 5 баллов |
| Получен правильный ответ | 4 балла |
| Всего | 26 баллов |
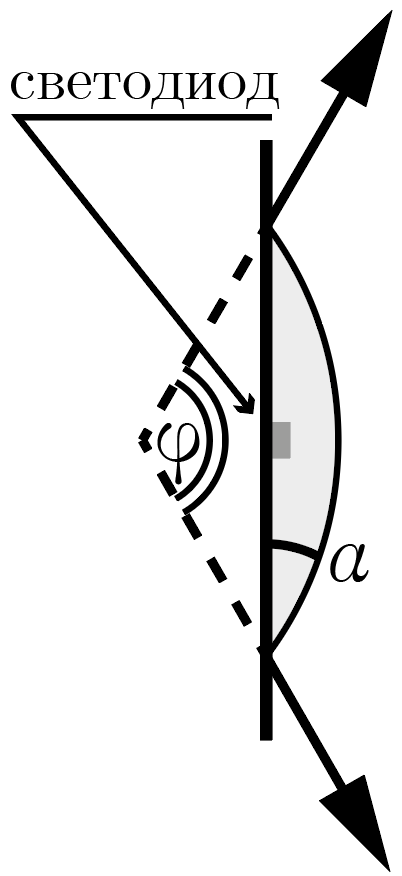
Для медицинских нужд изготавливается микроскопический осветительный прибор, работающий внутри биологических тканей, окружающая среда в которых может иметь достаточно высокий показатель преломления. Его испытания проводятся в специальном растворе с показателем преломления \(n_0 = 1{,}5\). Прибор представляет собой крошечный светодиод, напаянный на плоскую плату и окруженный «капелькой» из оптической смолы с низким показателем преломления \(n < n_0\). Капелька имеет форму сегмента сферы, сходящегося с плоскостью платы под углом \(\alpha = 15°\), как изображено на рис. 1.5. Определите значение \(n\), если известно, что устроенный таким образом фонарик внутри раствора дает конус света, угол между крайними лучами которого \(\phi = 120°\).
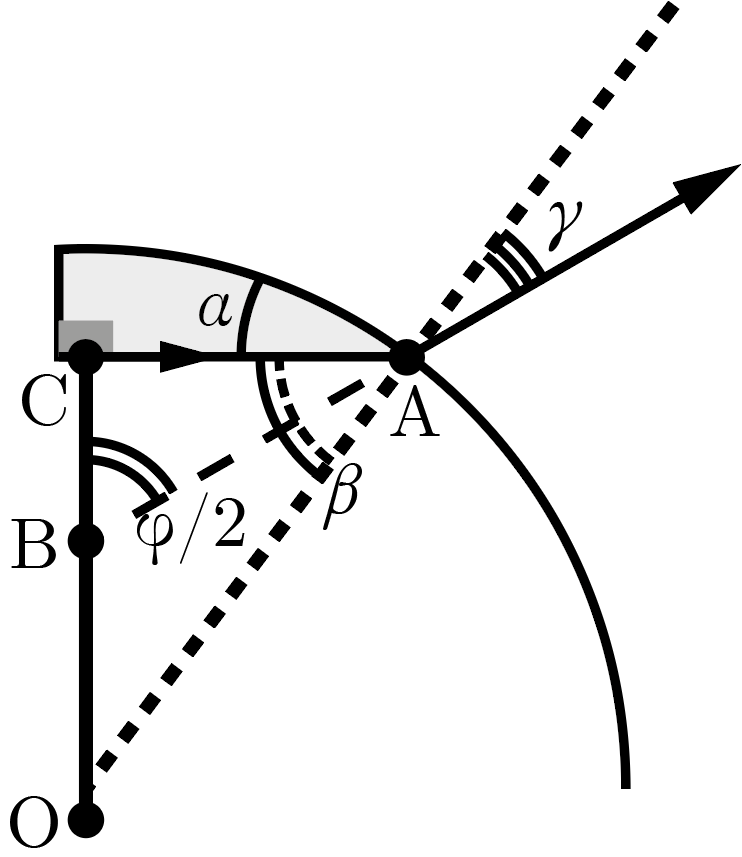
Чем ближе к полюсу капельки падает луч, тем меньше будет угол его падения, а значит, по закону Снеллиуса, меньше будет и угол преломления. Поэтому угол \(\phi\) раствора светового конуса будет определяться преломлением крайних лучей, изображенных на рис. 1.6. До преломления эти лучи распространяются практически параллельно плате, поэтому их угол падения \(\beta\) на границу капельки и крови равен \(\beta = 90°-\alpha\). Изобразим ход этих лучей на чертеже вблизи. На чертеже \(\textrm{O}\) — центр кривизны капельки, \(\textrm{A}\) — точка преломления луча, \(\textrm{B}\) — вершина светового конуса, \(\textrm{C}\) — светодиод.
Тогда, в соответствии с законом Снеллиуса, угол преломления \(\gamma\) этих лучей связан с углом падения выражением \[n_0 \sin \gamma = n \sin \beta = n \cos \alpha \Rightarrow n = \frac{\sin \gamma}{\cos\alpha}n_0.\] В треугольнике \(\textrm{ABC}\) угол при вершине \(\textrm{A}\) равен \(\beta - \gamma\). Тогда из суммы углов этого треугольника легко получить \[\beta -\gamma + 90° + \phi/2 = 180° \Rightarrow \gamma = \beta + \phi/2 - 90° = \phi/2 - \alpha.\] Подставляя этот результат в закон Снеллиуса, получим \[n = \frac{\sin (\phi/2 - \alpha)}{\cos\alpha}n_0 \approx 1{,}1.\]
\[n = \frac{\sin (\phi/2 - \alpha)}{\cos\alpha}n_0 \approx 1{,}1.\]
| Изображен ход крайнего луча с отметкой углов его падения и преломления | 3 балла |
| Верно записан закон Снеллиуса | 4 балла |
| Верно найдено соотношение между углом \(\alpha\) и углом падения луча | 2 балла |
| Верно найдено соотношение между углами \(\alpha\), \(\phi\) и углом преломления луча | 5 баллов |
| Получен правильный ответ | 6 баллов |
| Всего | 20 баллов |
Электрический диполь, представляющий собой пару равных по модулю разноименных зарядов, которые соединены жесткой связью на некотором расстоянии \(l\) друг от друга, влетает со скоростью \(v = 200\) м/с в скрещенные под прямым углом друг к другу электрическое и магнитное поля. При этом скорость диполя сонаправлена с силовыми линиями электрического поля, а вектор \(\vec{l}\), соединяющий два заряда диполя, перпендикулярен линиям индукции магнитного (см. рис. 2.1).
Под каким углом к силовым линиям электрического поля должен быть ориентирован диполь, чтобы его движение оставалось чисто поступательным? Напряженность электрического поля \(E = 400\textrm{\,В/м}\), индукция магнитного \(B = 0{,}5\textrm{\,Тл}\).
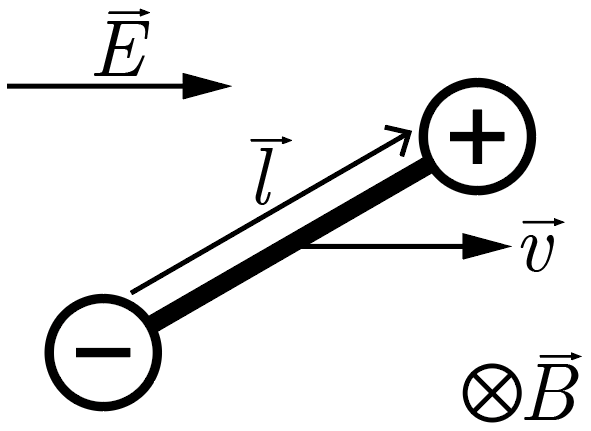
В электрическом поле на положительный заряд действует сила Кулона \(\vec{F}_E = \vec{E}q\), направленная вправо на рис. 2.1, а на отрицательный — строго противоположная ей. В магнитном поле на положительный заряд действует сила \(F_M = q v B\), направленная (по правилу левой руки) вверх на рис. 2.1, а на отрицательный — строго противоположная ей.
Поскольку обе эти силы возникают равными по модулю и противоположными по направлению парами, ускорение диполя в любом случае равно нулю, и он представляет собой инерциальную систему отсчета. Чтобы его движение было чисто поступательным, нулю также должна равняться сумма моментов этих сил относительно любой оси.
Проще всего записать соответствующие условия относительно оси, проходящей перпендикулярно плоскости рис. 2.1 через отрицательный заряд. В этом случае момент силы \(F_E\) равен \[M_E = F_E l \sin \alpha,\] где \(\alpha\) — искомый угол между векторами \(\vec{l}\) и скорости диполя, а момент силы \(F_M\) аналогично равен \[M_M = F_M l \cos \alpha.\] Приравнивая эти два момента, получим \[q E l \sin \alpha = q v B l \cos \alpha \Rightarrow \operatorname{tg} \alpha = \frac{vB}{E} \Rightarrow \alpha = \operatorname{arctg} \frac{vB}{E} \approx 14°.\]
\[\alpha = \operatorname{arctg} \frac{vB}{E} \approx 14°.\]
| Верно записано выражение для силы Кулона, действующей на заряды и определено направление этой силы | 2 балла |
| Верно записано выражение для силы Лоренца, действующей на заряды и определено направление этой силы | 4 балла |
| Верно записано уравнение моментов | 5 баллов |
| Получен правильный ответ | 4 балла |
| Всего | 15 баллов |
В лаборатории исследуется возможность передачи электрического разряда на большие расстояния по плазменному каналу в атмосфере. Для этого мощный пучок параллельных рентгеновских лучей «прожигает» по ходу своего следования воздух, в среднем отрывая от каждой молекулы газа по одному электрону, после чего высоковольтный источник создает в полученном таким образом канале однородное электрическое поле с напряженностью. Найдите удельное сопротивление полученного таким образом плазменного канала, если известно, что скорость \(\vec{v}\) дрейфа электронов в ионизированном воздухе прямо пропорциональна напряженности \(\vec{E}\) электрического поля \(v = -\mu \vec{E}\) с коэффициентом \(\mu = 0{,}15\) Кл\(\cdot\)с/кг (называемым подвижностью), а подвижность положительных ионов пренебрежимо мала. Концентрация молекул воздуха в условиях эксперимента \(n = 2{,}6\cdot 10^{25}\) м\(^{-3}\).
Удельное сопротивление вещества \(\rho\) может быть найдено по формуле \[\rho = \frac{RS}{l},\] где \(R\) — электрическое сопротивление рассматриваемого объема вещества, \(S\) — площадь его поперечного сечения, \(l\) — длина. Дополняя эту формулу определением электрического сопротивления \(R = U/I\), где \(U\) — напряжение на концах элемента, а \(I\) — сила тока в нем, получим \[\rho = \frac{US}{Il}.\] Сила тока \(I\), равная отношению переносимого через поперечное сечение проводника заряда \(q\) ко времени \(t\), может быть выражена через скорость движения заряженных частиц \(v\), заряд \(e\) одной из них и их концентрацию \(n\) как \[I = \frac{q}{t} = \frac{e n V}{t} = \frac{e n S l}{t} = e n S v.\] Здесь учитываем, что вклад ионов в общую проводимость плазменного канала пренебрежимо мал по сравнению со вкладом электронов, поскольку по условиям задачи пренебрежимо мала их подвижность и, следовательно, дрейфовая скорость. Тогда \[\rho = \frac{U\cancel{S}}{e n \cancel{S} v l} = \frac{E}{e n v} = \frac{1}{e n \mu} \approx 1{,}6\textrm{\,мкОм$\cdot$м},\] где \(E\) — напряженность электрического поля, связанная в однородном поле с напряжением соотношением \(U = El\).
\[\rho = \frac{1}{e n \mu} \approx 1{,}6\textrm{\,мкОм$\cdot$м}.\]
| Верно записано выражение связи удельного сопротивления с обычным | 3 балла |
| Верно записан закон Ома | 3 балла |
| Верно записана связь силы тока со скоростью, зарядом и концентрацией зарядов в проводнике | 6 баллов |
| Получен правильный ответ | 5 баллов |
| Всего | 17 баллов |
Первые два пункта критериев также могут быть заменены записью закона Ома в дифференциальной форме, если он известен участникам.
Наноантенны представляют собой миниатюрные электронные устройства, структурированные в наномасштабе комбинации различных материалов. Зачастую они имеют причудливые формы, сконструированные для взаимодействия со строго определенными типами излучения.
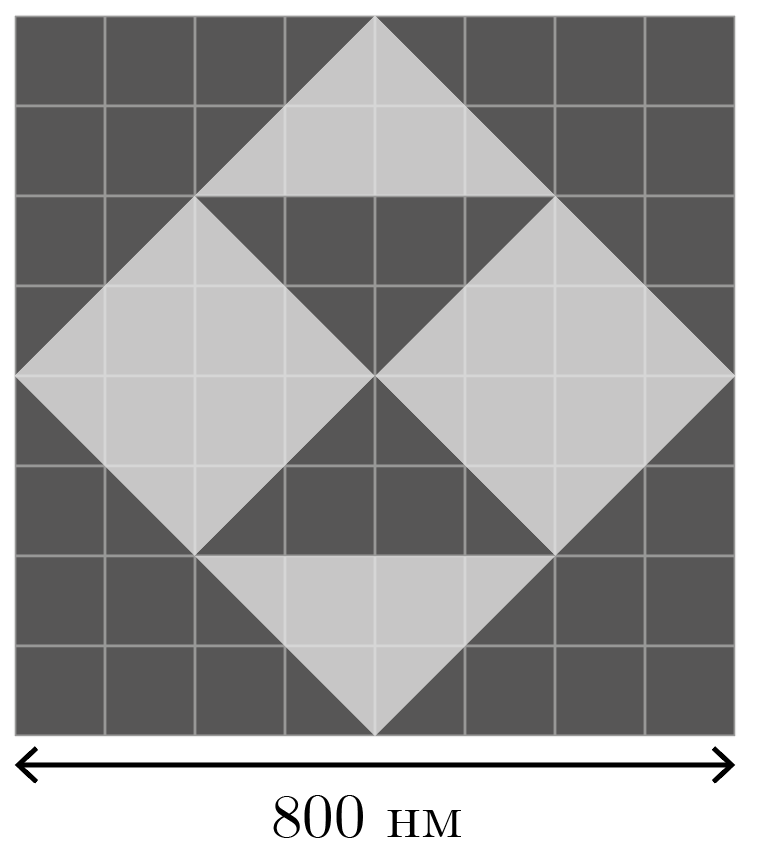
В лаборатории была изготовлена антенна, форма которой изображена на рис. 2.2: более темные участки представляют собой диэлектрик с проницаемостью \(\varepsilon_1 = 6\), более светлые — диэлектрик с проницаемостью \(\varepsilon_2 = 2\). Клетчатый узор представляет собой исключительно масштабную линейку, каждая клетка которой имеет сторону \(a = 100\textrm{\,нм}\). Изображенная структура изготовлена в виде плоского элемента с толщиной \(d = 20\textrm{\,нм}\) (в направлении, перпендикулярном плоскости рис. 2.2), зажатого между двумя такими же тонкими слоями металла. Оцените электроемкость полученного таким образом элемента. Электрическая постоянная \(\varepsilon_0 = 8{,}85\cdot 10^{-12}\textrm{\,Ф/м}\).
Из условий легко видеть, что толщина \(d\) диэлектрического слоя между двумя металлическими много меньше всех продольных характерных размеров узора антенны, наименьший из которых составляет порядка \(10d\).
В этом случае систему из двух тонких металлических слоев, между которыми зажат диэлектрический, можно рассматривать как плоский конденсатор. Причем каждую фигуру на изображенном рисунке антенны можно рассматривать как отдельный конденсатор, емкость которого задается формулой \[C = \frac{S\varepsilon\varepsilon_0}{d},\] где \(S\) — площадь этого участка, \(\varepsilon\) — диэлектрическая проницаемость образующего его диэлектрика.
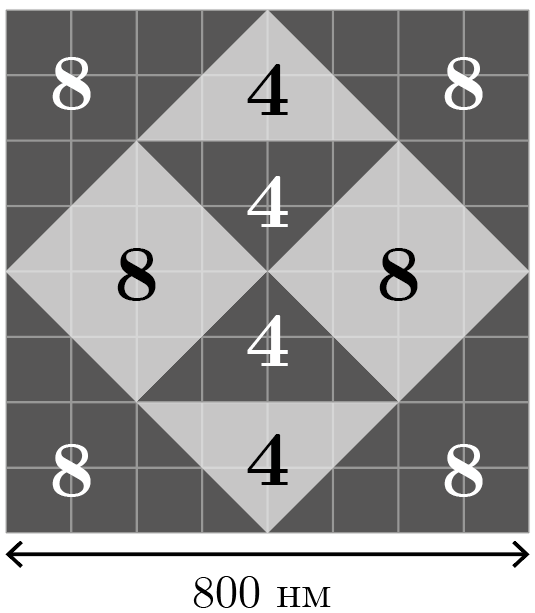
Площадь каждого элемента узора легко найти «по клеточкам». На рис. 2.3 она подписана в единицах \(a^2 = 10^{-14}\textrm{м}^2\) (площадь одной клетки). Все эти независимые конденсаторы соединены параллельно, поэтому общая емкость антенны может быть найдена как сумма их емкостей: \[C = \frac{\varepsilon_0}{d}{}\sum_{i=1}^{10} S_i \varepsilon_i,\] где \(i\) — номер участка на рис. 2.3 антенны, \(S_i\) — его площадь, а \(\varepsilon_i\) — его диэлектрическая проницаемость.
Подставляя в это выражение площади, отмеченные на рис. 2.3, и проницаемости, данные в условиях, получим окончательно \[C = \frac{a^2\varepsilon_0}{d}(40 \varepsilon_1 + 24 \varepsilon_2) \approx 1{,}27\cdot 10^{-15}\textrm{\,Ф}.\]
\[C = \frac{a^2\varepsilon_0}{d}(40 \varepsilon_1 + 24 \varepsilon_2) \approx 1{,}27\cdot 10^{-15}\textrm{\,Ф}.\]
| Верно записано выражение для электроемкости плоского конденсатора | 4 балла |
| Обоснована его применимость в связи с соотношением геометрических размеров системы | 3 балла |
| Замечено, что емкости отдельных фигур антенны выступают как соединенные параллельно | 4 балла |
| Верно найдены площади всех необходимых участков антенны | 3 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 20 баллов |
Радиоизотоп \(X\) делится с периодом полураспада \(T_1 = 20\textrm{\,сут.}\), в результате чего образуется ядро аргона \(^{40}_{18}\textrm{Ar}\) и стабильное металлическое ядро. Радиоизотоп \(Y\) с периодом полураспада \(T_2 = 8\textrm{\,сут.}\) претерпевает \(\alpha\)-распад, в ходе которого образуется еще один \(\alpha\)-радиоактивный изотоп \(Z\), период полураспада которого составляет несколько микросекунд. В результате распада изотопа \(Z\) также образуется стабильное металлическое ядро. Одинаковые количества вещества изотопов \(X\) и \(Y\) помещают в камеру, из которой откачан газ. По прошествии \(t = 40\textrm{\,сут.}\) оказывается, что в этой камере образовалась смесь благородных газов, при температуре \(\theta = 25~°\)C и давлении \(p = 12\textrm{\,кПа}\). Найдите плотность этой смеси. Универсальная газовая постоянная \(R \approx 8{,}31\) Дж/(моль\(\cdot\)К), абсолютный ноль температур \(0\textrm{\,К} = -273~°\text{C}\). \(\alpha\)-частица представляет собой ядро \(^{4}_{2}\textrm{He}\).
В результате одного деления ядра изотопа \(X\) образуется один атом аргона, следовательно, количество вещества \(\nu_{Ar}\) этого газа связано с числом \(N_1\) произошедших делений соотношением \[\nu_{Ar} = N_1/N_A,\] где \(N_A\) — число Авогадро.
В результате одного \(\alpha\)-распада ядра изотопа \(Y\) образуется один атом гелия, а также сильно нестабильный изотоп, который практически сразу (в течение микросекунд) претерпевает еще один \(\alpha\)-распад, также с образованием одного атома гелия. Поэтому количество \(\nu_{He}\) этого газа связано с числом \(N_2\) произошедших первичных \(\alpha\)-распадов соотношением \[\nu_{He} = 2 N_2/N_A.\] Согласно закону радиоактивного распада, при распаде с периодом полураспада \(T\) число \(n\) нераспавшихся ядер по прошествии времени \(t\) задается выражением \(n = n_02^{-t/T},\) где \(n_0\) — изначальное число этих ядер. Следовательно, число \(N\) распадов, произошедших за это время, задается выражением \[N = n_0 - n = n_0(1-2^{-t/T}).\] Используя это выражение, легко выразим количества вещества обоих образовавшихся газов: \[\nu_{Ar} = \frac{n_0}{N_A}(1-2^{-t/T_1}) = \frac{3n_0}{4N_A};\quad\nu_{He} = 2\frac{n_0}{N_A}(1-2^{-t/T_2}) = \frac{31n_0}{16N_A}.\] Для смеси газов, образовавшихся в камере, справедлив закон Дальтона \[p = p_{Ar} + p_{He},\] где \(p_{Ar}, p_{He}\) — парциальные давления аргона и гелия соответственно. Каждый из этих газов подчиняется уравнению Менделеева – Клапейрона, принимающему вид \[p V = (\nu_{Ar} + \nu_{He})R\theta,\] где \(V\) — объем камеры. Выразим его через молярные массы газов и искомую плотность смеси: \[V = \frac{\mu_{Ar} \nu_{Ar} + \mu_{He} \nu_{He}}{\rho} \Rightarrow \frac{p}{\rho} (\mu_{Ar} \nu_{Ar} + \mu_{He} \nu_{He}) = (\nu_{Ar} + \nu_{He})R\theta.\] Выражая из этого уравнения \(\rho\), получим \[\rho = \frac{p(\mu_{Ar}\nu_{Ar} + \mu_{He}\nu_{He})}{(\nu_{Ar} +\nu_{He})R\theta} = \frac{p \left(\mu_{Ar}\left(\frac{3n_0}{4N_A}\right)+\mu_{He}\left(\frac{31n_0}{16N_A}\right)\right)}{\left(\frac{3n_0}{4N_A} + \frac{31n_0}{16N_A}\right)R\theta}.\] Сокращая дробь на \(n_0/N_A\) и приводя все отношения к общему знаменателю, получим окончательно \[\rho = \frac{p(12\mu_{Ar} + 31\mu_{He})}{43R\theta} \approx 68\textrm{\,г/м}^3.\] Молярные массы аргона и гелия учащиеся должны понять из символов \(^{40}_{18}\textrm{Ar}\), \(^{4}_{2}\textrm{He}\), данных в условиях.
\[\rho = \frac{p(12\mu_{Ar} + 31\mu_{He})}{43R\theta} \approx 68\textrm{\,г/м}^3.\]
| Верно записан хотя бы один закон радиоактивного распада | 3 балла |
| Замечено и обосновано, что количество ядер гелия вдвое превосходит число первичных \(\alpha\)-распадов | 3 балла |
| Верно найдены количества образовавшихся газов или их отношение | 5 баллов |
| Верно записан закон Дальтона | 3 балла |
| Верно записано уравнение Менделеева – Клапейрона или основное уравнение МКТ в любой форме | 3 балла |
| Уравнение Менделеева – Клапейрона или основное уравнение МКТ преобразовано к (или сразу записано в) форме, содержащей искомую плотность | 3 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 26 баллов |
Согласно законам электродинамики, заряженные частицы, движущиеся с ускорением, испытывают взаимодействие со своими собственными электромагнитными полями, называемое радиационным трением. В общем случае описание этого взаимодействия весьма трудоемко, но для относительно медленных частиц сила радиационного трения может быть найдена по формуле \(\displaystyle \vec{F} = \frac{q^2}{6\pi \varepsilon_0 c^3} \frac{\Delta \vec{a}}{\Delta t}\), где \(q\) — электрический заряд частицы, \(c\) — скорость света в вакууме, \(\varepsilon_0\) — электрическая постоянная, \(\Delta \vec{a} / \Delta t\) — мгновенная скорость изменения мгновенного ускорения \(\vec{a}\)-частицы. В эксперименте, действуя на частицу с зарядом \(q < 0\) и массой \(m\) внешним электромагнитным полем, требуется поддерживать ее равномерное движение по окружности радиуса \(R\). При какой угловой скорости частицы сила, действующая на нее со стороны этого внешнего поля для обеспечения такого движения, должна быть направлена под углом \(45°\) к скорости частицы?
В приведенном выражении для силы радиационного трения затруднения может вызвать только дробь \(\Delta \vec{a} / \Delta t\). Эта величина — «мгновенная скорость» изменения ускорения — находится с мгновенным ускорением в том же соотношении, в котором само ускорение находится с мгновенной скоростью, а мгновенная скорость — с радиус-вектором.
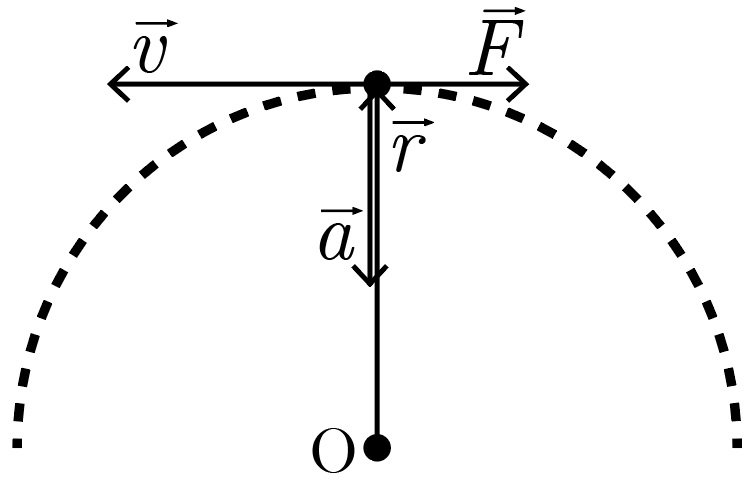
При равномерном движении по окружности радиус-вектор \(\vec{r}\), проведенный в точку из центра траектории, имеет постоянный модуль \(R\) и вращается вокруг своего начала с некоторой постоянной угловой скоростью \(\omega\). Из школьной кинематики известно, что вектор мгновенной скорости \(\vec{v}\) при таком движении имеет модуль \(v = \omega R\) и также вращается с угловой скоростью \(\omega\), «опережая» радиус-вектор на \(90°\) в направлении вращения, поскольку направлен по касательной к траектории. Аналогично вектор мгновенного (центростремительного) ускорения \(\vec{a}\) имеет модуль \(a = \omega v = \omega^2 R\) и вращается с угловой скоростью \(\omega\), «опережая» вектор мгновенной скорости на \(90°\) в направлении вращения, поскольку направлен к центру траектории.
Следовательно, используя те же математические инструменты, что доказывают предыдущие две связи, можно показать, что вектор \(\Delta \vec{a} / \Delta t\) имеет модуль \(\omega a = \omega^3 R\) и вращается с угловой скоростью \(\omega\), «опережая» вектор центростремительного ускорения на \(90°\) в направлении вращения. Поскольку вне зависимости от знака заряда выражение \(q^2\) в числителе формулы для радиационного трения больше нуля, как больше нуля и все входящие в выражение физические константы, вектор \(\vec{F}\) силы радиационного трения направлен так же, как и \(\Delta \vec{a} / \Delta t\) — строго против вектора мгновенной скорости, по касательной к траектории (см. рис. 2.4).
Чтобы ответить на вопрос задачи, заметим, что для поддержания равномерного движения заряженной частицы по окружности внешняя сила \(\vec{F}_\textrm{вн}\) должна
- создавать центростремительное ускорение,
- компенсировать радиационное трение.
Составляющая \(F_{\textrm{вн}\parallel}\) этой силы, параллельная скорости, должна быть равна по модулю силе радиационного трения: \[F_{\textrm{вн}\parallel} = \frac{q^2}{6\pi \varepsilon_0 c^3}\omega^3 R,\] в то время как составляющая \(F_{\textrm{вн}\perp}\) этой силы, перпендикулярная скорости, должна создавать центростремительное ускорение и, следовательно, равна \[F_{\textrm{вн}\perp} = m\omega^2R.\]
Поскольку по условиям сила \(\vec{F}_\textrm{вн}\) направлена к скорости под углом \(45°\), составляющие \(F_{\textrm{вн}\parallel}\) и \(F_{\textrm{вн}\perp}\) этой силы равны:
\[\frac{q^2}{6\pi \varepsilon_0 c^3} \omega^3 r = m \omega^2 r \Rightarrow \omega = \frac{6\pi \varepsilon_0 mc^3}{q^2}.\]
\[\omega = \frac{6\pi \varepsilon_0 mc^3}{q^2}.\]
| Продемонстрировано понимание того, что вектор \(\Delta \vec{a}/\Delta t\) относится к центростремительному ускорению так же, как оно само относится к мгновенной скорости, а та — к радиус-вектору | 4 балла |
| Верно найдено выражение для модуля этого вектора через любой набор более стандартных величин кинематики: линейную и/или угловую скорость или центростремительное ускорение, радиус | 3 балла |
| Верно найдено направление этого вектора | 3 балла |
| Продемонстрировано понимание того, что знак заряда в условиях не играет роли для ответа | 2 балла |
| Продемонстрировано понимание того, что направление внешней силы под углом \(45°\) к скорости означает равенство сил, необходимых для преодоления радиационного трения и для создания центростремительного ускорения | 4 балла |
| Верно найден ответ на вопрос задачи | 6 баллов |
| Всего | 22 балла |
Задача, разумеется, также имеет решение через производные. В этом случае запись верного определения вектора \(\dot{\vec{a}}\) как производную ускорения по времени является частным случаем выполнения первого критерия, а правильное вычисление этой производной по координатам — второго.