Предметный тур. Физика. 1 этап
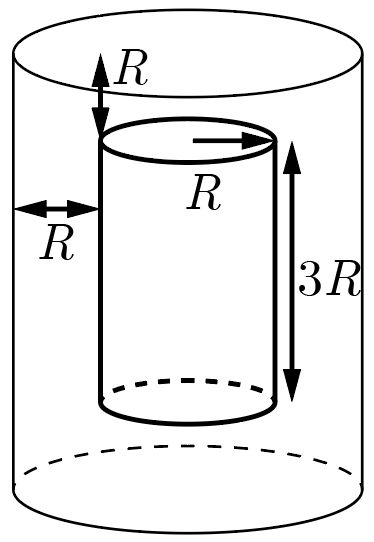
Внутренний стакан калориметра представляет собой цилиндр с радиусом \(R = 8\textrm{\,см}\) и высотой \(3R\). Внешний стакан также имеет форму цилиндра, стенки которого (как боковые, так и торцы) отстоят от стенок внутреннего на расстояние \(R\). Какая масса теплоизоляционного материала с плотностью \(\rho = 25\textrm{\,кг/м}^3\) необходима, чтобы полностью заполнить пространство между стаканами?
Чтобы найти массу \(m\) теплоизоляционного материала, необходимо его плотность умножить на занимаемый им объем \(V\): \[m = \rho V. \label{mass}\]
Объем области, заполняемой теплоизоляцией, удобнее всего найти, вычтя из объема \(V_1\) большого внешнего стакана объем \(V_2\) маленького внутреннего. Для любого кругового цилиндра с высотой \(h\) и радиусом \(r\) объем может быть найден по формуле \(V = \pi r^2 h\). В случае большого цилиндра \(r = 2R\) и \(h = 5R\), следовательно, \[V_1 = 5R \cdot \pi (2R)^2 = 20 \pi R^3. \label{volume1}\]
Аналогично, для маленького \(r = R\), \(h = 3R\) и, следовательно, \[V_2 = 3\pi R^3. \label{volume2}\]
Подставляя \eqref{volume1}, \eqref{volume2} в \eqref{mass}, получим, что искомая масса составляет: \[m = \rho (V_1 - V_2) = 17\pi R^3 \rho \approx 0{,}68\textrm{\,кг.}\]
Погрешность \(0{,}01\textrm{\,кг}.\)
\(\displaystyle m = 17\pi R^3 \rho = (0{,}68\pm0{,}01)\textrm{\,кг}\).
Нити накала ламп изготавливают из вольфрама, удельное сопротивление которого сильно зависит от температуры. По мере прогрева нити оно возрастает от \(\rho_0 = 5{,}5\cdot 10^{-8}\textrm{\,Ом}\cdot\text{м}\) до \(\rho_1 = 1{,}1\cdot 10^{-6}\textrm{\,Ом}\cdot\text{м}\). Определите электрическую мощность, потребляемую лампой в первый момент после ее включения, если в рабочем режиме (полностью прогревшись) лампа потребляет от той же сети мощность \(P_1 = 30\textrm{\,Вт}\).
Электрическая мощность \(P\), потребляемая нитью накала, может быть вычислена по закону Джоуля – Ленца, который для фиксированного напряжения \(U\) в сети удобно записать как \[P = U^2/R. \label{power}\]
При этом сопротивление \(R\) нити легко выразить через ее удельное сопротивление \(\rho\), длину \(l\) и площадь поперечного сечения \(S\) \[R = \frac{\rho l}{S}. \label{eq:resistance}\]
Подставляя \eqref{eq:resistance} в \eqref{power}, получим \[P = \frac{U^2 S}{\rho l},\] где только \(\rho\) зависит от температуры. В результате придем к выводу, что выделяющаяся в лампе мощность обратно пропорциональна ее удельному сопротивлению, откуда окончательно следует \[P_0 = P_1 \frac{\rho_1}{\rho_0} \approx 600\textrm{\,Вт}.\]
Погрешность \(1\textrm{\,Вт}.\)
\(\displaystyle P_0 = (600\pm1)\textrm{\,Вт}\).
Бетонная свая высотой \(h = 1{,}4\textrm{\,м}\) и массой \(m = 160\textrm{\,кг}\) полностью погружена в грунт так, что ее верхний торец совпадает с уровнем почвы. К сожалению, сваю понадобилось извлечь. Определите, какую работу для этого необходимо совершить, если сила трения со стороны грунта, действующая на сваю, прямо пропорциональна площади соприкосновения ее боковой стороны с землей и в начальный момент ее извлечения равна \(F = 4\textrm{\,кН}\). Ускорение свободного падения \(g \approx 9{,}8\textrm{\,м/с}^2\).
Работа \(A\), необходимая для извлечения сваи, складывается из увеличения потенциальной энергии сваи на величину \(mgh\) и работы по преодолению силы трения \(A_\textrm{тр}\). Последняя должна быть найдена с учетом постепенного уменьшения силы трения \(F_\textrm{тр}\) от максимального значения \(F\) до нуля. Поскольку это уменьшение происходит линейно, общая работа оказывается строго вдвое меньше, чем при постоянном значении \(F_\textrm{тр} = F\) (аналогично тому, как вычисляется значение работы сил упругости пружины). В результате \[A = mgh + \frac{Fh}{2} \approx 5\textrm{\,кДж}.\]
Погрешность \(0{,}1\textrm{\,кДж}.\)
\((5{,}0 \pm 0{,}1)\textrm{\,кДж}\).
Два дрона одновременно вылетают с общей пусковой станции и движутся по прямолинейным траекториям. Первый дрон на начальном этапе движения перемещается с постоянной скоростью \(v_1 = 15\textrm{\,м/с}\), а через время \(\tau = 40\textrm{\,с}\) быстро переключается на движение с постоянной скоростью \(v_2 = 20\textrm{\,м/с}\). Второй дрон — наоборот, сначала движется со скоростью \(v_2\), а через время \(\tau\) переключается на скорость \(v_1\). Наконец, дроны одновременно заканчивают полет. Определите, как долго длился этот полет, если по его итогам средняя путевая скорость первого дрона оказалась на \(\Delta v = 1\textrm{\,м/с}\) выше, чем средняя путевая скорость второго.
По определению средняя путевая скорость — это отношение общего пройденного пути \(S\) к общему времени движения \(t\): \[v = \frac{S}{t}.\]
Для первого дрона это уравнение принимает вид \[v_a = \frac{v_1 \tau + v_2(t-\tau)}{t}, \label{velocity_a}\] а для второго, соответственно, \[v_b = \frac{v_2 \tau + v_1(t-\tau)}{t}. \label{velocity_b}\]
Из условий задачи известно, что \(v_a - v_b = \Delta v\). Подставляя в это уравнение формулы \eqref{velocity_a} и \eqref{velocity_b}, а также домножая его на \(t\), получим \[v_1 \tau + v_2(t-\tau) -v_2 \tau - v_1(t-\tau) = \Delta v t.\]
Перегруппировав слагаемые, получим \[v_2 t - 2v_2 \tau - v_1 t + 2 v_1 \tau = \Delta v t,\] откуда окончательно \[t = \frac{2(v_2 - v_1)\tau}{v_2 - v_1 - \Delta v} = 100\textrm{\,с.}\]
Погрешность \(1\textrm{\,с}.\)
\((100 \pm 1)\textrm{\,с}\).
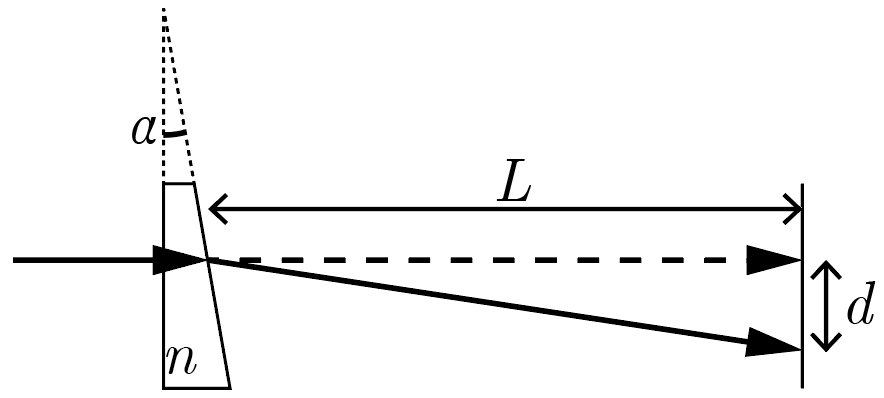
Для тонкого контроля параметров призмы используется следующая установка: отмечается точка, в которую падает лазерный луч, направленный на экран строго под прямым углом (пунктирный на рисунке). Затем на пути луча устанавливается исследуемая призма так, что задняя (первая по ходу распространения луча) ее грань оказывается строго перпендикулярна лучу, и измеряется расстояние \(d\), на которое в результате этого смещается пятно лазера.
Определите показатель преломления стекла, из которого изготовлена призма, если расстояние от передней грани призмы до экрана \(L = 3\textrm{\,м}\), смещение пятна при установке призмы \(d = 12\textrm{\,см}\), а угол между передней и задней поверхностями призмы \(\alpha = 3°\). Используйте приближение малых углов.
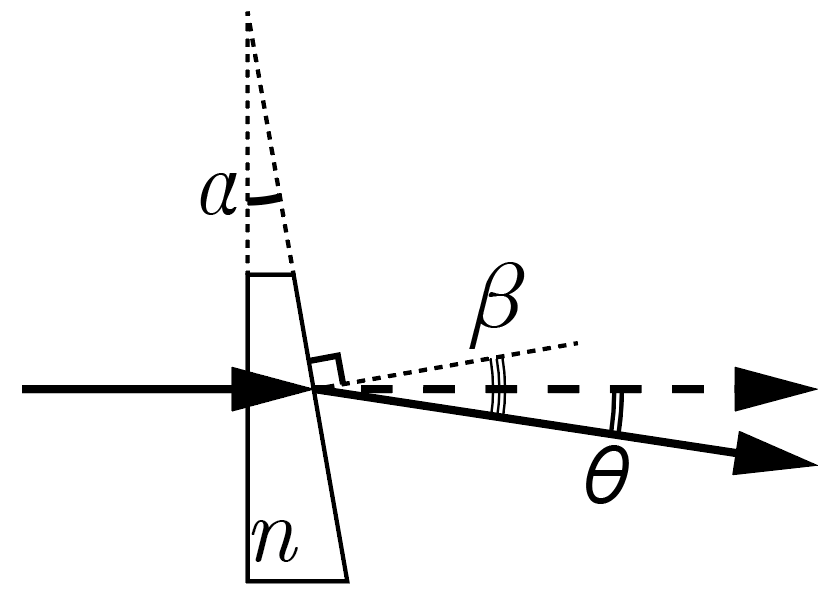
На первой по ходу распространения луча грани призмы свет не преломляется, поскольку падает на нее под прямым углом. Следовательно, угол падения луча на переднюю грань призмы равен \(\alpha\). Тогда по закону Снеллиуса \[n = \frac{\sin \beta}{\sin \alpha},\] где \(\beta\) — угол преломления луча, что с учетом приближения малых углов \(\sin \alpha \approx \alpha \approx \operatorname{tg} \alpha\) (в радианах) принимает форму \[n \approx \frac{\beta} {\alpha}.\]
Из геометрии рисунка легко видеть, что \(\beta = \alpha + \theta\), где \(\theta\) — угол, который преломленный луч составляет с направлением своего распространения до установки призмы. При этом \(\operatorname{tg} \theta = \frac{d}{L}\), откуда \[n \alpha \approx \beta = \alpha + \operatorname{arctg} \frac{d}{L} \Rightarrow n \approx 1 + \frac{d}{\alpha L} \approx 1{,}76.\]
Погрешность \(0{,}02\).
\(1{,}76 \pm 0{,}02\).
Для печи отопления требуется разработать аккумулятор тепла, представляющий собой емкость фиксированного объема, заполненную тем или иным минералом. Используя таблицу 1.1 плотностей \(\rho\) и удельных теплоемкостей \(c_\textrm{уд}\) различных подходящих для этого пород, расположите их в порядке увеличения количества теплоты, которое может быть запасено в таком аккумуляторе при его нагреве до одной и той же температуры \(\theta\). Считайте, что \(\theta\) заведомо меньше температур, при которых любой из этих минералов начнет плавиться или химически разрушаться, а тепловое расширение этих минералов при нагреве до \(\theta\) пренебрежимо мало.
| Минерал | \(\rho, \textrm{\,г/см}^3\) | \(c_\textrm{уд},\text{~кДж}/(\text{кг}\cdot°\text{C})\) | |
|---|---|---|---|
| A | Кварц | 2,6 | 0,75 |
| B | Базальт | 2,8 | 0,85 |
| C | Талькохлорит | 2,75 | 0,98 |
| D | Нефрит | 3 | 1,1 |
| E | Порфирит | 1,45 | 0,83 |
Введите в поле ответа последовательность букв, соответствующих выбранным минералам, без пробелов, от наименьшего к наибольшему количеству запасаемой теплоты.
Количество тепла \(Q\), которое может быть запасено в тепловом аккумуляторе фиксированного объема \(V\), удобно выразить через массу \(m\) материала этого аккумулятора \[Q = c_\text{уд} m (\theta - t_0),\] где \(t_0\) — начальная температура теплоаккумулятора. В свою очередь, масса \(m\) элементарно выражается через плотность вещества и объем \(V\) \[m = \rho V,\] откуда \[Q = c_\text{уд} \rho V (\theta - t_0).\] Поскольку величины \(V, \theta, t_0\) независимы от выбранного вещества, задача сводится к расположению в порядке возрастания произведений \(c_\text{уд}\rho\). Найдем эти произведения для всей таблицы 1.1.
| Минерал | \(\rho, \textrm{\,г/см}^3\) | \(c_\text{уд},\text{~кДж}/(\text{кг}\cdot°\text{C})\) | \(c_\text{уд} \rho,\text{~кДж}/(\text{м}^3\cdot°\text{C})\) | |
|---|---|---|---|---|
| A | Кварц | 2,6 | 0,75 | 1950 |
| B | Базальт | 2,8 | 0,85 | 2380 |
| C | Талькохлорит | 2,75 | 0,98 | 2695 |
| D | Нефрит | 3 | 1,1 | 3300 |
| E | Порфирит | 1,45 | 0,83 | 1204 |
EABCD.
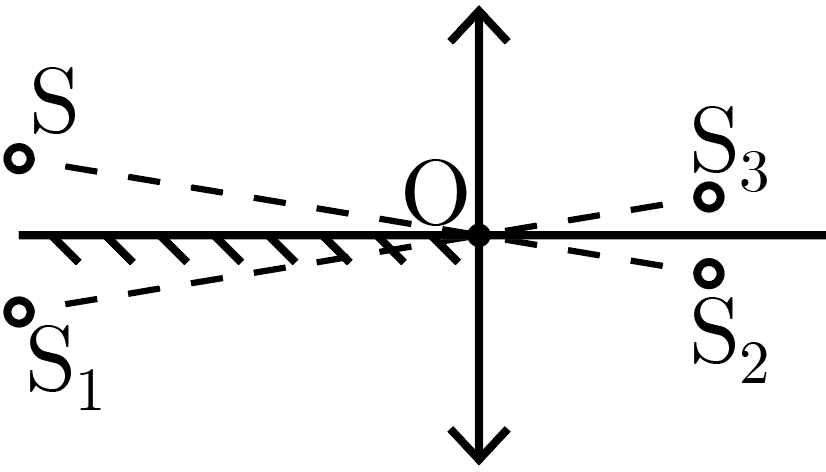
Тонкая собирающая линза имеет фокусное расстояние \(F = 20\textrm{\,см}\). Вдоль ее оптической оси перед линзой расположено плоское зеркало, на расстоянии \(h = 2\textrm{\,см}\) от которого и \(d = 60\textrm{\,см}\) от линзы размещен светодиод \(S\) (рис. 2.1). Найдите расстояние между двумя действительными изображениями светодиода, формируемыми этой оптической системой.
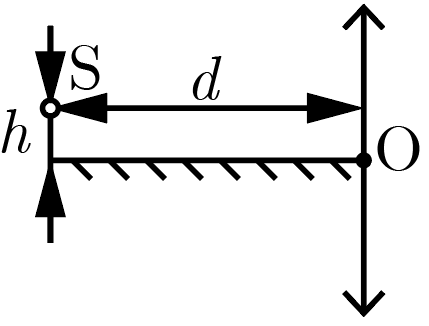
Зеркало формирует мнимое изображение \(S_1\) источника, расположенное в противоположном от него полупространстве на таком же расстоянии от зеркала, как и сам источник. В силу перпендикулярности зеркала и линзы, это мнимое изображение также окажется на расстоянии \(d\) от плоскости линзы. Далее линза формирует два действительных изображения: одно непосредственно от источника \(S\) (на рис. 2.2 оно обозначено \(S_2\)) и другое — от его мнимого изображения \(S_1\) (\(S_3\) на рисунке).
Расстояние \(f\), на котором находятся оба действительных изображения от плоскости линзы, легко найти по формуле тонкой линзы \[\frac{1}{f} + \frac{1}{d} = \frac{1}{F} \Rightarrow f = \frac{Fd}{d-F}.\] Искомое расстояние \(l\) между изображениями \(S_2\) и \(S_3\), благодаря подобию треугольников \(\triangle \mathrm{OSS_1}\) и \(\triangle \mathrm{OS_2S_3}\), относится к расстоянию \(2h\) между источником и его мнимым изображением \(S_1\) так же, как расстояния от соответствующих изображений и источников до плоскости линзы, являющиеся высотами указанных треугольников \[\frac{l}{2h} = \frac{f}{d} = \frac{F}{d-F}.\]
Отсюда окончательно находим \[l = 2h\frac{F}{d-F} = 2\textrm{\,см}.\]
Погрешность \(0{,}1\textrm{\,см}.\)
\(\displaystyle l = (2{,}0\pm0{,}1)\textrm{\,см}\).
Циркулярная пила представляет собой пильный диск диаметром \(D = 19\textrm{\,см}\), вращающийся с частотой \(4500\textrm{\,об/мин}\). Определите среднюю силу сопротивления заготовки вращению полотна пилы, если за один пропил, длившийся \(t = 3\textrm{\,с}\), выделилось \(Q = 5\textrm{\,кДж}\) тепла, а пила соприкасалась с заготовкой только узкой полоской своей внешней кромки.
При вращении пилы диссипативные силы (трения различных типов) переводят механическую энергию пильного диска в тепловую. При этом количество выделяющегося тепла равно по модулю работе \(A\) этих сил. Последнюю легко найти из ее определения \[A = FS = Fvt, \label{work}\] где \(S\) — путь точек соприкосновения диска с заготовкой, \(v\) — скорость этих точек. При вращении диска скорость точек его кромки удобно выразить через период вращения \(T\) этого диска \[v = \frac{\pi D}{T} = \pi D \nu, \label{velocity}\] где \(\nu\) — частота вращения диска в оборотах в секунду. Подставляя \eqref{velocity} в \eqref{work} и учитывая \(Q = A\), получим окончательно \[Q = \pi F D \nu t \Rightarrow F = \frac{Q}{\pi D \nu t} \approx 37\textrm{\,Н.}\]
Погрешность \(1\textrm{\,Н}.\)
\(\displaystyle F = (37\pm 1)\textrm{\,Н}\).
Транспортный робот перемещается из города \(A\) в город \(B\), двигаясь практически все время с некоторой постоянной скоростью \(v\). Однако один раз за маршрут ему необходима остановка для заправки и краткого технического обслуживания. Инженеры установили, что при уменьшении длительности этой остановки вдвое скорость движения робота на остальной части маршрута можно будет снизить на \(\delta = 10\%\), сохранив при этом его среднюю путевую скорость, что поможет повысить безопасность и экономичность движения. Определите, на сколько процентов (от исходного значения) удалось бы снизить скорость \(v\) без изменения средней путевой, если бы от технической остановки удалось полностью отказаться?
Средняя путевая скорость определяется как отношение всего пути ко всему времени, которое этот путь занимает. Поскольку расстояние между городами неизменно, сохранение средней путевой скорости означает и сохранение общего времени в пути (включая остановку). Следовательно, уменьшение длительности остановки на \(\Delta t\) эквивалентно увеличению времени непосредственного движения на ту же величину. Обозначим общее время робота в пути \(t\), исходную длительность его остановки \(\tau\), а исходную скорость движения \(v_0\). Тогда путь робота может быть выражен до и после снижения времени остановки как \[S = v_0 (t - \tau) = v_0(1 - \delta)\left(t - \frac{\tau}{2}\right).\]
Сократив \(v_0\) и перегруппировав слагаемые, получим \[\delta t = \tau \left(1 - \frac{1}{2} + \frac{\delta}{2}\right) = \tau \frac{\delta +1}{2}.\]
Полностью избавившись от остановки, таким образом, робот будет двигаться в течение времени \[t = \tau \frac{\delta +1}{2\delta}.\]
Аналогично, время движения \(t - \tau\) при наличии остановки удобно записать как \[t - \tau = \tau \left(\frac{\delta +1}{2\delta} - 1\right) = \tau \frac{1 - \delta}{2\delta}.\]
Обозначив \(v_1\) скорость, которой можно добиться, исключив остановку, запишем через эти выражения путь и приравняем его в случаях с остановкой и без \[v_1 t = v_0(t - \tau) \Rightarrow v_1 \tau \frac{\delta +1}{2\delta } = v_0 \tau\frac{1 - \delta}{2\delta}.\]
Отсюда окончательно \[\frac{v_1}{v_0} = \frac{1 - \delta}{1 + \delta} \approx 0{,}818.\]
Итого скорость движения без остановки может составлять приблизительно \(81{,}8\%\) от исходной скорости, то есть ниже ее на \(18{,}2\%\).
Погрешность \(0{,}5\%.\)
\((18{,}2 \pm 0{,}5)%\).
Два абсолютно одинаковых ползунковых реостата, сопротивления которых могут изменяться в пределах от \(0\) до \(R_0 = 2\textrm{\,кОм}\), размещены параллельно на печатной плате и соединены как изображено на рис. 2.4. Из-за ошибки в процессе пайки изоляция их ползунков слиплась таким образом, что ползунки всегда занимают одно и то же положение на обоих реостатах, но электрический контакт между ними отсутствует (это соединение обозначено на рисунке пунктиром). Найдите разницу между максимальным и минимальным сопротивлениями полученной батареи.
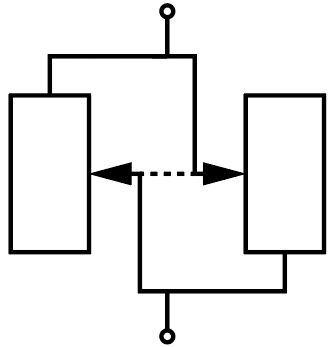
Реостаты на схеме соединены параллельно, поэтому общее сопротивление схемы \(R\) может быть выражено через сопротивления \(R_{1{,}2}\) каждого из реостатов по формуле \[R = \frac{R_1 R_2}{R_1 + R_2}. \label{resistance}\]
Несложно видеть из схемы, что когда ползунок находится в крайнем верхнем положении, левый реостат имеет нулевое сопротивление, а правый — сопротивление \(R_0\) и наоборот. Величина сопротивления находится в линейной зависимости от длины провода. Из этого можно заключить, что при любом положении ползунка
\[R_2 = R_0 - R_1.\]
Подставляя этот результат в \eqref{resistance}, получим \[R = \frac{R_1 (R_0 - R_1)}{R_0} = R_1 - \frac{R_1^2}{R_0}.\]
График полученной функции является параболой. Его минимумы и максимумы могут лежать либо на границах диапазона изменения \(R_1\), либо в вершине соответствующей параболы. Поскольку коэффициент перед квадратным слагаемым отрицательный, парабола «повернута» ветвями вниз, то есть на границах диапазона (при \(R_1 = 0\) или \(R_1 = R_0\)) сопротивления батареи минимальны и равны \(0\), а в ее вершине (которая, как легко видеть из симметрии или непосредственно по формуле \(x_{max} = -b/(2a)\), лежит в центре диапазона, при \(R_1 = R_2 = \dfrac{R_0}2\)) сопротивление батареи равно \(\dfrac{R_0}4\).
Таким образом, \[R_{max} - R_{min} = \frac{R_0}{4} - 0 = \frac{R_0}{4} = 0{,}5\textrm{\,кОм}.\]
Погрешность \(0{,}01\textrm{\,кОм}.\)
\(\displaystyle l = (0{,}50\pm0{,}01)\textrm{\,кОм}\).
В гидравлической системе используется башня, заполненная минеральным маслом с плотностью \(\rho = 900\textrm{\,кг/м}^3\). Верхний уровень масла расположен на \(h = 60\textrm{\,м}\) выше, чем смотровое окно в трубе с маслом, закрепленное на ней при помощи \(n = 16\) одинаковых болтов. Определите, какую нагрузку должен выдерживать каждый из этих болтов на разрыв, чтобы обеспечить трехкратный запас прочности? Площадь смотрового окна \(S = 0{,}1\textrm{\,м}^2\). Ускорение свободного падения \(g = 9{,}8\textrm{\,м/с}^2\).
Давление \(p\) масла на уровне окна элементарно вычисляется по формуле гидростатического давления \[p = \rho g h.\] Исходя из определения всякого давления \(p\) как отношения силы \(F\) к площади \(S\), на которую действует эта сила, найдем силу со стороны жидкости, «пытающуюся выдавить» смотровое окно \[F = pS = \rho g h S.\]
Искомая рассчетная нагрузка \(f\) каждого из болтов может быть получена домножением этой силы на \(3\) (требуемый запас прочности) и делением на число болтов \(n\), по которым распределяется нагрузка \[f = \frac{3F}{16} = \frac{3\rho g h S}{16} \approx 9{,}9\textrm{\,кН}.\]
Погрешность \(0{,}1\textrm{\,кН}.\)
\((9{,}9 \pm 0{,}1)\textrm{\,кН}\).
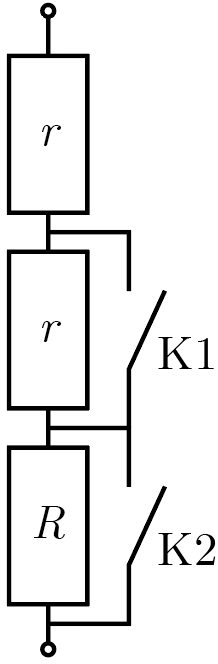
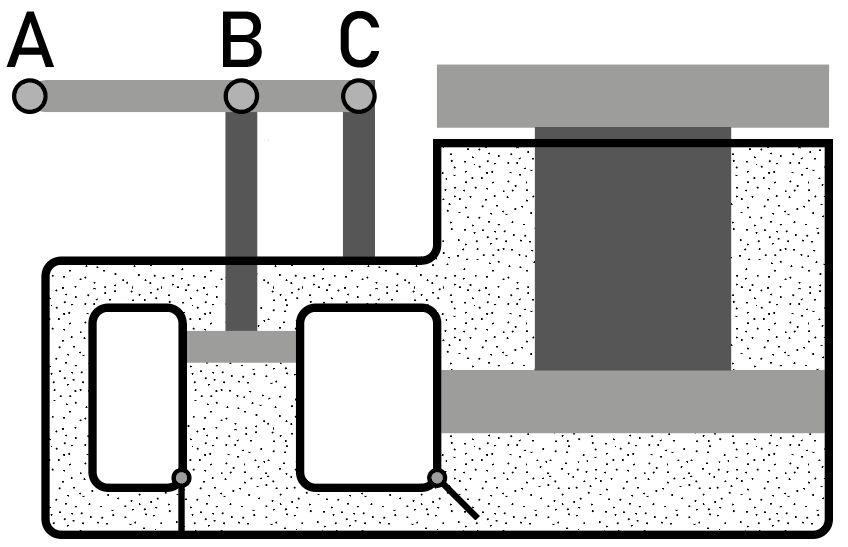
Имея в своем распоряжении резисторы только двух различных номиналов, начинающий радиолюбитель изготовил ступенчатый реостат оригинальной конструкции, позволяющий, переключая ключи, получить четыре различных значения сопротивления. Увы, на приложенной к прибору схеме он забыл указать сопротивления отдельных резисторов, указав только, какие из них совпадают. В техническом паспорте устройства остались данные о том, что при замыкании ключа \(K_1\) и размыкании ключа \(K_2\) оно имеет сопротивление \(R_1 = 2\) кОм, а напротив, при замыкании ключа \(K_2\) и размыкании ключа \(K_1\) — сопротивление \(R_2 = 3\) кОм. Найдите максимальное сопротивление, которое можно получить, используя этот реостат.
Когда параллельно резистору коротко замыкается цепь, этот резистор фактически перестает работать, поскольку сопротивление провода пренебрежимо мало. Следовательно, замыкание ключа К1 фактически эквивалентно замене среднего резистора на отрезок провода, а ключа К2 — такой же замене нижнего. Учитывая это и применяя формулу эквивалентного сопротивления последовательно соединенных резисторов, легко получим \[\left\{ \begin{aligned} &R_1 = r + R, \\ &R_2 = 2r. \end{aligned} \right.\]
Решая эту систему, находим \(r = \frac{R_2}2\) и \(R = R_1 - \frac{R_2}2\). Теперь точно так же составим выражения для оставшихся двух конфигураций реостата: \(R_3\) с обоими замкнутыми ключами и \(R_4\) с обоими разомкнутыми \[\left\{ \begin{aligned} &R_3 = r = \frac{R_2}{2} = 1{,}5\textrm{\,кОм}, \\ &R_4 = 2r + R = R_1 + \frac{R_2}{2} = 3{,}5\textrm{\,кОм}. \end{aligned} \right.\]
Погрешность \(0{,}01\textrm{\,кОм}.\)
\((3{,}50 \pm 0{,}1)\textrm{\,кОм}\).
В некоторых типах ядерных реакторов в качестве теплоносителя используются жидкие металлы. Определите, сколько теплоты за 1 с забирает у реактора жидкий свинец с удельной теплоемкостью \(c = 155\) Дж/(кг\(\cdot°\)С) и средней плотностью \(\rho = 10^4\) кг/м\(^3\), если, двигаясь в трубе диаметром \(d = 10\) см со скоростью \(v = 20\) м/с, он нагревается от \(t_1 = 400\,°\text{С}\) до \(t_2 = 900\,°\text{С}\).
Обозначим рассматриваемый промежуток времени (1 с) \(\tau\). Двигаясь со скоростью \(v\), свинец успевает за это время пройти в трубе дистанцию \(l = v \tau\). Учитывая площадь сечения трубы \(S = \pi d^2/4\), можно заключить из этого, что за время \(\tau\) в реактор поступает и из реактора уходит объем \[V = Sl = \frac{\pi}{4} d^2 v \tau\] расплавленного свинца. Количество теплоты \(Q\), которое этот свинец забирает у реактора, задается выражением \[Q = c m (t_2 - t_1) = c \rho V (t_2 - t_1) = \frac{\pi}{4} c \rho d^2 v \tau (t_2 - t_1) \approx 122\textrm{\,МДж},\] где \(m\) — масса поступившей и ушедшей порции свинца.
Погрешность \(2\textrm{\,МДж}.\)
\((122 \pm 2)~\text{МДж}\).
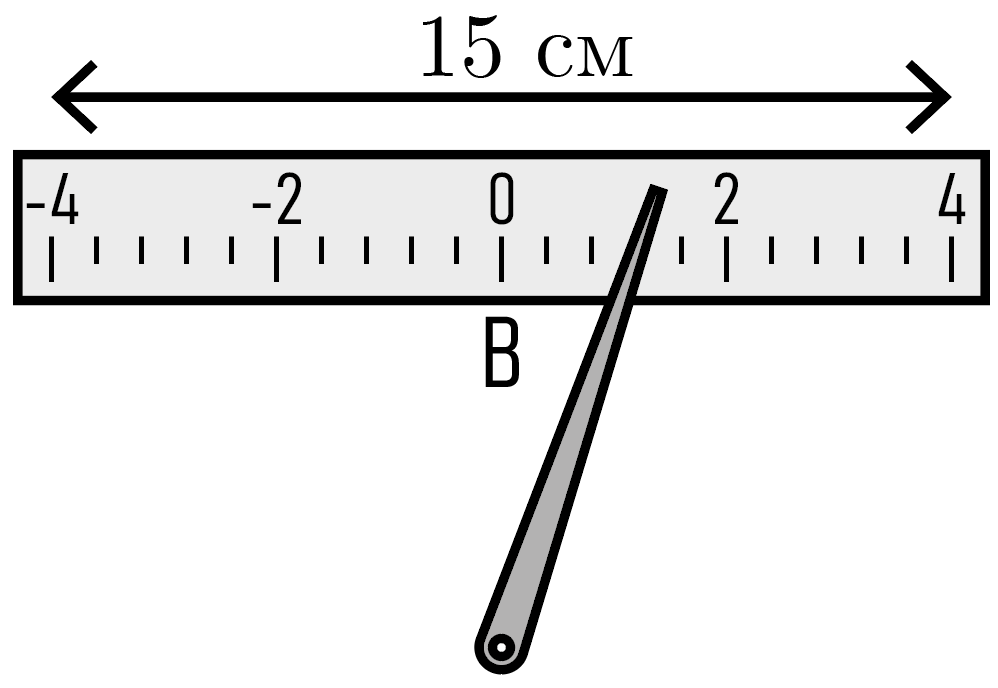
Шкала вольтметра, используемого в эксперименте, имеет вид, представленный на рис. 3.2, и общую длину \(l = 15\) см (от минимальной до максимальной отметки). Экспериментатор, глядя на прибор под углом \(45°\) к плоскости шкалы, считал показания вольтметра как \(U_1 = 1{,}2\) В ровно, однако на самом деле стрелка прибора находилась напротив отметки \(U_2 = 0{,}8\) В. Определите, на какое расстояние отстоит стрелка от шкалы, если известно, что глаза экспериментатора находились со шкалой строго на одном уровне высоты, а деления расположены на шкале равномерно.
Согласно условиям, глаза экспериментатора находятся на одной высоте со шкалой, поэтому удобно изобразить систему в горизонтальной плоскости (вид сверху), см. рис. 3.3. Поскольку угол \(\alpha\), под которым наблюдатель смотрит на стрелку, равен \(45°\), искомое расстояние \(x\) в точности равно расстоянию \(y\) между точкой \(A\) действительных показаний прибора и точкой \(B\) считанных экспериментатором показаний (треугольник \(ABC\), где \(C\) — стрелка — прямоугольный и равнобедренный).
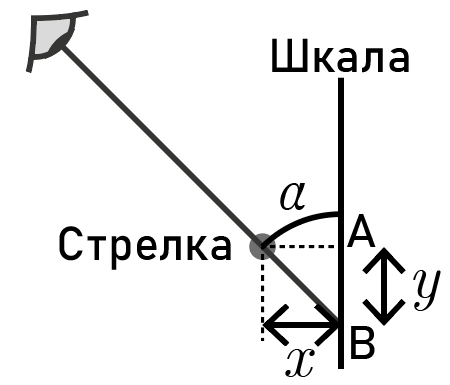
Тогда остается вычислить расстояние \(y\) между отметками шкалы, соответствующими значениям \(U_1\) и \(U_2\). Поскольку шкала равномерная, это расстояние относится к полной длине шкалы так же, как величина абсолютной ошибки к ее разнице между ее верхним \(U_{max}\) и нижним \(U_{min}\) пределами измерений \[\frac{y}{l} = \frac{U_2-U_1}{U_{max}-U_{min}}.\]
Отсюда окончательно \[x = y = l \frac{U_2-U_1}{U_{max}-U_{min}} = 7{,}5~\text{мм.}\] Погрешность \(0{,}1~\text{мм.}\)
\((7{,}5 \pm 0{,}1)\textrm{\,мм}\).
Три робота одновременно стартуют в углу А прямоугольной площадки ABCD. Все они движутся с постоянными по модулю скоростями и все заканчивают движение в точке D одновременно. Но первый робот движется по прямой вдоль стороны AD, второй — по трехзвенной ломаной ABCD, а третий — по двузвенной: сначала вдоль диагонали AC, а затем — по стороне CD. Во сколько раз средняя путевая скорость третьего робота выше, чем первого, если средняя путевая скорость второго робота выше, чем первого, в 2,5 раза? Временем на разгон, остановку и развороты роботов можно пренебречь.
Обозначив длину стороны AB (и, соответственно, CD) прямоугольника \(a\), а длину стороны BC (и, соответственно, DA) — \(b\), можно легко выразить через эти стороны пути \(S_{1{,}2,3}\) всех трех роботов
\[\left\{ \begin{aligned} &S_1 = b, \\ &S_2 = 2a + b, \\ &S_3 = \sqrt{a^2 + b^2} + a. \end{aligned} \right.\]
Поскольку время движения всех роботов совпадало, отношения их путей точно такие же, как и средних путевых скоростей: \[\frac{v_2}{v_1} = \frac{S_2}{S_1} = \frac{2a}{b} + 1 = 2{,}5,\] откуда легко найти \[\frac{2a}{b} = 1{,}5 \Rightarrow b = \frac{4}{3}a.\]
Теперь, пользуясь той же логикой, найдем ответ на вопрос задачи как отношение путей третьего и первого роботов \[\frac{v_3}{v_1} = \frac{S_3}{S_1} = \frac{\sqrt{a^2 + b^2} + a}{b} = \frac{\sqrt{\displaystyle\frac{25a^2}9} + a}{\displaystyle\frac{4a}3} = \frac{\displaystyle\frac{8a}3}{\displaystyle\frac{4a}3} = 2.\]
Погрешность \(0{,}01.\)
\(2{,}00 \pm 0{,}01\).
Расплавленная соль предлагается как эффективный аккумулятор тепла для некоторых типов теплоцентралей. Удельная теплота плавления и кристаллизации соли \(\lambda = 28{,}7\textrm{\,кДж/кг}\), ее теплоемкость в твердой форме \(c_1 = 0{,}92\textrm{\,кДж/(кг°C)}\), а в жидкой — \(c_2 = 1{,}5\textrm{\,кДж/(кг°C)}\), температура ее плавления \(\theta = 800\,°\text{C}\). Определите, какую массу соли необходимо взять, чтобы при ее нагреве от \(t_0 = 20\,°\text{C}\) до \(t_1 = 1200\,°\text{C}\) запасти \(Q = 1\textrm{\,МДж}\) тепла.
Количество теплоты, требуемое на нагрев твердой соли до температуры плавления, задается выражением \[Q_1 = c_1 m (\theta - t_0),\] где \(m\) — масса нагреваемой соли.
Количество теплоты, уходящее непосредственно на плавление \[Q_2 = \lambda m.\]
Наконец, количество теплоты, уходящее на нагрев расплава соли, \[Q_3 = c_2 m (t_1 - \theta).\]
Складывая все эти порции тепла, получим, что общая запасаемая теплота \[Q = Q_1 + Q_2 + Q_3 = m (c_1 (\theta - t_0) + \lambda + c_2 (t_1 - \theta)),\] откуда окончательно \[m = \frac{Q}{(c_1 (\theta - t_0) + \lambda + c_2 (t_1 - \theta))} \approx 743\textrm{\,г.}\]
Погрешность \(1\textrm{\,г}.\)
(\(743 \pm 1)\textrm{\,г}\).
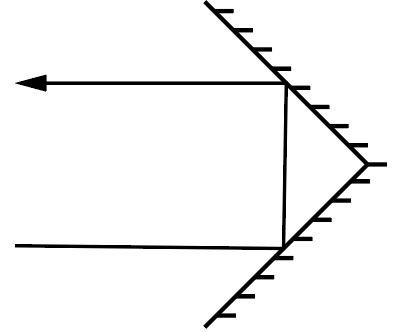
Катафот представляет собой два одинаковых квадратных зеркала, соединенных общей гранью под прямым углом друг к другу. При падении на него видимого света каждое зеркало поглощает \(\eta = 20\%\) достигающей его световой энергии, а остальную — отражает. Параллельно биссектрисе образованного зеркалами угла в плоскости, перпендикулярной к их общему ребру, на середину одного из зеркал падает узкий лазерный луч, переносящий мощность \(P = 5\textrm{\,мВт}\). Какое количество световой энергии поглотит второе зеркало за \(\tau = 10\textrm{\,с}\)?
Прежде всего отметим, что любой луч, падающий на катафот параллельно его биссектрисе, отразится последовательно от обоих зеркал катафота, как изображено на рис 4.1. При этом после первого отражения мощность луча снизится в \((1-\eta)\) раз, и доля \(\eta\) от этой оставшейся мощности будет поглощена вторым зеркалом. В результате связь между изначальной \(P\) и поглощаемой \(P_1\) мощностями имеет следующий вид:
\[P_1 = (1-\eta)\eta P.\]
Теперь остается лишь вспомнить определение мощности, как отношения энергии (в данном случае переносимой лазерным лучом или поглощаемой зеркалом) ко времени, чтобы получить окончательный ответ \[Q = P_1 \tau = (1-\eta)\eta P \tau \approx 8\textrm{\,мДж}.\]
Погрешность \(0{,}1\textrm{\,мДж}.\)
\((8{,}0 \pm 0{,}1)\textrm{\,мДж}\).
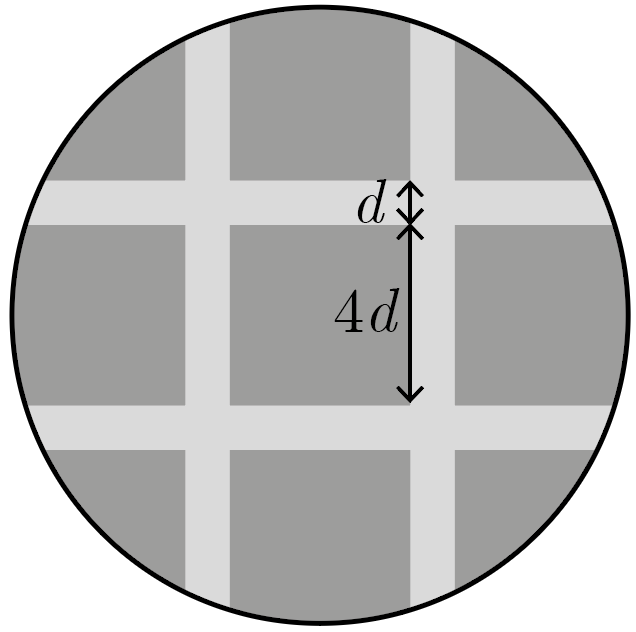
Композитный материал изготавливают, вырезая из алюминия (плотность \(\rho_1 = 2{,}7\textrm{\,г/см}^3\)) строго периодическую вдоль двух взаимно перпендикулярных осей квадратную сетку с толщиной стенки \(d\) и длиной внутренней стороны ячейки \(4d\), фрагмент которой изображен на рис. 4.2. Затем полости заполняют смолой, после затвердевания имеющей плотность \(\rho_2 = 1{,}2\textrm{\,г/см}^3\). Найдите среднюю плотность большого листа из такого материала.
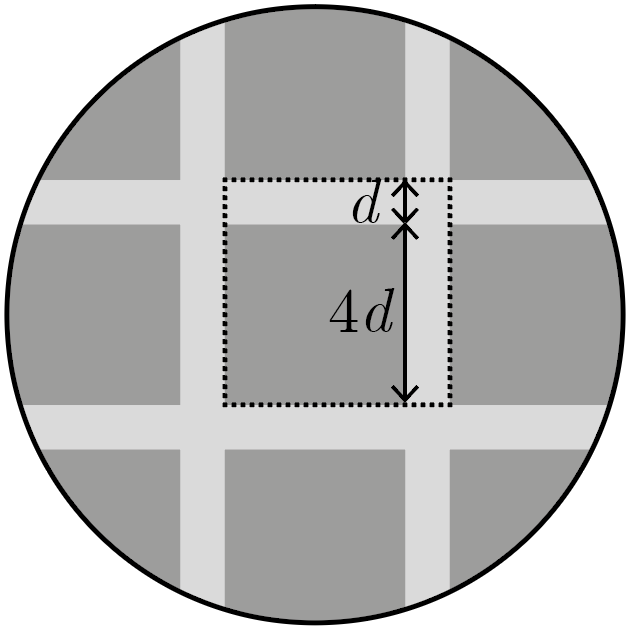
По мере увеличения размеров листа материала роль его краев в общей плотности постепенно снижается, поэтому среднюю плотность большого листа следует вычислять как среднюю плотность одного элемента периодичности, границы которого изображены пунктиром на рис. 4.3. Объем \(V\) этого элемента равен \(25dh\), где \(h\) — толщина листа материала.
Массу элемента найдем, сложив массы алюминия (индексы \(1\)) и смолы (индексы \(2\)) \[m = m_1 + m_2 = \rho_1 V_1 + \rho_2 V_2 = \rho_1 9 dh + \rho_2 16 dh.\]
Тогда искомая плотность окончательно равна \[\rho = \frac{m}{V} = \frac{\rho_1 9 \cancel{dh} + \rho_2 16 \cancel{dh}}{25 \cancel{dh}} \approx 1{,}74 \textrm{\,г/см}^3.\]
Погрешность \(0{,}01 \textrm{\,г/см}^3.\)
\((1{,}74 \pm 0{,}01) \textrm{\,г/см}^3\).
На рис. 4.4 приведена схема устройства гидравлического домкрата. Его поршни представляют собой цилиндры с радиусами \(R = 21\textrm{\,см}\) и \(r = 3\textrm{\,см}\). Чтобы поднимать при помощи этого домкрата груз \(m = 1{,}4\textrm{\,т}\), установленный на платформе большого цилиндра, к точке \(A\) рычага необходимо приложить силу не менее \(F = 87{,}5~\text{Н}\). Определите отношение \(AB:BC\). Ускорение свободного падения \(g = 9{,}8\textrm{\,м/с}^2\). На рисунке точный масштаб не сохранен.
Изображенный домкрат дает выигрыш в силе благодаря двум механизмам: рычагу и гидравлическому прессу. Выигрыш в силе, обеспечиваемый прессом, равен отношению площадей его цилиндров \[\frac{mg}{F_1} = \frac{\cancel{\pi} R^2}{\cancel{\pi} r^2} \Rightarrow F_1 = mg\frac{r^2}{R^2},\] где \(F_1\) — сила давления малого поршня.
В свою очередь, выигрыш в силе, обеспечиваемый рычагом, равен отношению его плеч, но так как рычаг закреплен в точке \(C\), нужно сравнивать плечи \(AC\) и \(BC\) \[\frac{F_1}{F} = \frac{AC}{BC} = \frac{AB + BC}{BC} = 1 + \frac{AB}{BC}.\]
Совместив эти уравнения, получим окончательно \[\frac{AB}{BC} = \frac{F_1}{F} - 1 = \frac{mg r^2}{F R^2} - 1 = 2{,}2.\]
Погрешность \(0{,}1.\)
\(2{,}2 \pm 0{,}1\).
Изучая электронагреватель прямого действия, ученик заметил, что увеличение подаваемой на него силы тока на \(\Delta I = 0{,}1\textrm{\,А}\) над номинальным значением приводит к увеличению тепловой мощности, выделяемой прибором, на \(\Delta P_1 = 44\textrm{\,Вт}\), а уменьшение силы тока на ту же величину от номинальной, приводит к уменьшению мощности на \(\Delta P_2 = 36\textrm{\,Вт}\). Найдите номинальную мощность прибора, считая его сопротивление независимым от температуры.
Согласно закону Джоуля – Ленца, тепловая мощность электронагревателя равна \[P = I^2 R,\] где \(I\) — сила пропускаемого через него тока, а \(R\) — сопротивление прибора. Последнее по условиям задачи можно считать неизменным, поэтому, введя обозначения \(I_0\) для номинальной силы тока и \(P_0\) для номинальной мощности прибора, можно составить пропорции \[\left\{ \begin{aligned} \frac{P_0 + \Delta P_1}{P_0} &= \left(\frac{I_0 + \Delta I}{I_0}\right)^2, \\ \frac{P_0 - \Delta P_2}{P_0} &= \left(\frac{I_0 - \Delta I}{I_0}\right)^2. \end{aligned} \right.\]
Обозначив \(\frac{\Delta I}{I_0}\) буквой \(x\) и частично сократив дроби, приведем их к виду \[\left\{ \begin{aligned} 1 + \frac{\Delta P_1}{P_0} &= (1 + x)^2, \\ 1 - \frac{\Delta P_2}{P_0} &= (1 - x)^2. \end{aligned} \right. \label{alpha}\]
Эту систему можно решить, вычитая второе уравнение из первого \[\frac{\Delta P_1 + \Delta P_2}{P_0} = 4x \Rightarrow x = \frac{\Delta P_1 + \Delta P_2}{4P_0}\]
и подставляя результат в любое уравнение системы \eqref{alpha} \[\cancel{1} +\frac{\Delta P_1}{P_0} = \cancel{1} + \frac{\Delta P_1 + \Delta P_2}{2P_0} + \frac{(\Delta P_1 + \Delta P_2)^2}{16P_0^2}.\]
Домножим на \(16 P_0^2\) \[16 \Delta P_1 P_0 = 8P_0 (\Delta P_1 + \Delta P_2) + (\Delta P_1 + \Delta P_2)^2.\] и выразим окончательно \[P_0 = \frac{(\Delta P_1 +\Delta P_2)^2}{8(\Delta P_1 - \Delta P_2)} = 100\textrm{\,Вт.}\]
Погрешность \(1\textrm{\,Вт}.\)
\(100 \pm 1\) Вт.
Беспилотник, двигаясь равномерно и прямолинейно и обладая при этом импульсом \(p_0 = 10^4\text{ кг}\cdot\text{м/с}\), преодолевает дистанцию \(L = 20\) км ровно за 1,5 мин. За какое время преодолеет ее этот же беспилотник, двигаясь также равномерно и прямолинейно, но обладая на \(\Delta p = 10^3\text{ кг}\cdot\text{м/с}\) меньшим импульсом?
Импульс \(p\) тела — это произведение его массы на его скорость, поэтому скорость беспилотника легко может быть вычислена как \[p_0 = \frac{m L}{t_0}, \label{init_momentum}\] где \(t_0\) — время в пути с импульсом \(p_0\). Искомое время \(t\) можно аналогично выразить через скорость \(v\) беспилотника во второй рассмотренной ситуации как \[t = \frac{L}{v} = \frac{Lm}{p_0 - \Delta p}. \label{final_momenum}\]
Выражая массу беспилотника из \eqref{init_momentum} и подставляя ее в \eqref{final_momenum}, получим: \[t = \frac{\cancel{L} p_0 t_0}{\cancel{L} (p_0 - \Delta p)} = 100\textrm{\,с}.\]
Погрешность \(1\textrm{\,c.}\)
\((100 \pm 1)\textrm{\,с}\).
На плоское горизонтальное дно кузова транспортного грузовика погрузили большой грузовой контейнер и забыли его закрепить. Благодаря силе трения контейнер оставался в покое относительно грузовика до тех пор, пока ускорение последнего не превосходило \(a_0 = 2{,}0\textrm{\,м/с}^2\), и начинал скользить при превышении этого значения. Совершая маневр, грузовик приобрел ускорение \(a = 2{,}12\textrm{\,м/с}^2\), направленное по ходу движения. Какое время длился маневр, если в результате контейнер сдвинулся на \(l = 1{,}5\textrm{\,м}\) относительно грузовика?
Исходя из того, что контейнер остается на месте при ускорении грузовика до \(a_0\), можно, по второму закону Ньютона, заключить, что сила трения покоя, обеспечивающая это ускорение для контейнера, не превышает значения \[F = m a_0, \label{friction}\] где \(m\) — масса контейнера. При любом маневре, при котором контейнер начинает скользить, на него действует сила трения скольжения, равная \(F\) и, следовательно, его ускорение относительно дороги оказывается равно \(a_0\).
Во время маневра ускорение контейнера относительно грузовика равно (по модулю) \(a - a_0\), а пройденное контейнером относительно грузовика расстояние может быть выражено по законам кинематики как \[l = \frac{(a - a_0) t^2}{2},\] где \(t\) — искомое в задаче время. Преобразуя эту формулу, получим \[t = \sqrt{\frac{2l}{a-a_0}} = 5\textrm{\,с.}\]
Погрешность \(0{,}1\textrm{\,с}.\)
\((5{,}0 \pm 0{,}1)\textrm{\,с}\).
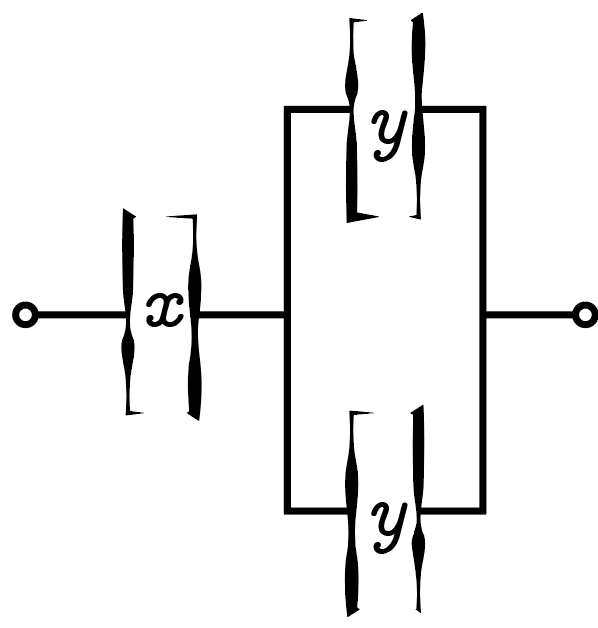
На лабораторной работе по физике в распоряжении школьников оказались резисторы двух номиналов: с сопротивлениями \(x\) и \(y\) кОм, а также конденсаторы двух номиналов: с емкостями \(x\) и \(y\) мкФ, при этом \(x > y\). В старой методичке, посвященной этой лабораторной работе, была изображена схема, приведенная на рисунке, чернила на которой сильно затерлись. В результате Витя решил, что изображенные элементы являются резисторами, и, соединив их согласно схеме, получил элемент с эквивалентным сопротивлением \(R = 5\textrm{\,кОм}\). Таня же решила, что это конденсаторы и, соединив их, получила элемент с эквивалентной емкостью \(C = 2\textrm{\,мкФ}\). Определите, чему равнялось число \(y\).
При последовательном соединении резисторов их сопротивления складываются, а при параллельном — складываются обратные сопротивлениям величины. Поэтому сопротивление \(R\) схемы Вити через числа \(x\) и \(y\) в килоомах (кОм) может быть выражено по формуле \[R = x + \frac y2. \label{resistance2}\]
Для конденсаторов правила поиска эквивалентной емкости при их последовательном и параллельном соединениях в точности обратные, поэтому емкость схемы Тани может быть выражена в микрофарадах (мкФ) по формуле \[C = \frac{2 xy}{x + 2y}. \label{capacitance}\]
Выразим \(x\) из уравнения \eqref{resistance2} и подставим в \eqref{capacitance}: \[C = \frac{2 (R-y/2)y}{R + 3y/2}. \label{capacitance22}\]
Домножив полученное уравнение на знаменатель дроби и раскрыв скобки, получим \[RC + \frac{3Cy}{2} = 2Ry - y^2.\]
Поскольку величины \(x\) и \(y\) имеют разную размерность в разных частях задачи, имеет смысл сразу перейти к численным значениям \[10 + 3 y = 10y - y^2.\]
Это квадратное уравнение, которое легко привести к канонической форме \[y^2 - 7y + 10 = 0\] и решить с помощью дискриминанта \[y_{1{,}2} = \frac{7 \pm \sqrt{49 - 40}}{2} = \frac{7 \pm 3}{2}.\]
Снова воспользовавшись уравнением \eqref{resistance2}, легко определить, что при \(y = 5\) (корень квадратного уравнения с плюсом) \(x = 2{,}5\), что не удовлетворяет условию \(x > y\). В то же время, при \(y = 2\) (корень с минусом) \(x = 4\), что удовлетворяет этому условию. Стало быть, верный корень — \(y = 2\).
Погрешность \(0{,}1.\)
\(2{,}0 \pm 0{,}1\).
Морозильная установка работает по циклу Карно, обходимому в обратном направлении. Какую работу должна потребить такая установка, чтобы заморозить \(m = 0{,}4\textrm{\,кг}\) воды, взятой при ее температуре замерзания, передав полученную от нее теплоту в помещение, температура \(\theta\) которого равна \(30\) °C? Удельная теплота плавления и кристаллизации воды \(\lambda = 333\textrm{\,кДж/кг}\), абсолютный ноль температур \(T_0 = -273\) °C.
Идеальный тепловой двигатель (машина Карно) работает, как известно, по циклу, состоящему из двух изотерм и двух адиабат, и имеет КПД \[\eta = \frac{T_2 - T_1}{T_2},\] где \(T_1\) — минимальная, а \(T_2\) — максимальная температуры в цикле. По определению КПД тепловой машины он равен отношению работы \(A\), совершаемой газом за цикл, к теплоте \(Q_2\), получаемой им от нагревателя \[\frac{T_2 - T_1}{T_2} = \eta = \frac{A}{Q_2}.\]
Отсюда \(Q_2\) может быть выражено как \[Q_2 = \frac{AT_2}{T_2 - T_1}.\]
Поскольку за полный цикл внутренняя энергия не изменяется, количество теплоты \(Q_1\), которую газ отдает холодильнику такой машины, равна разнице \[Q_1 = Q_2 - A = \frac{AT_1}{T_2 - T_1}. \label{carnot}\]
В рассматриваемой задаче тепловой двигатель заменен холодильной машиной, для чего его цикл необходимо обходить в обратном направлении. При этом тепловой резервуар с температурой \(T_2\) начинает получать тепло, а с температурой \(T_1\) — отдавать, но по модулю количества теплоты, которыми газ обменивается с этими тепловыми резервуарами, не изменяются. Остается заметить, что в описанной в условиях холодильной машине \(T_1 = 0\,°\)C \(= 273\textrm{\,К}\), \(T_2 = \theta\), \(Q_1 = \lambda m\), поскольку забираемая у теплового резервуара с меньшей температурой теплота идет на замораживание в нем воды. Подставив эти данные в \eqref{carnot}, получим \[\lambda m =\frac{AT_1}{\theta - T_1},\] откуда окончательно выразим ответ \[A = \frac{\lambda m(\theta - T_1)}{T_1} \approx 14{,}6\textrm{\,Дж.}\]
Погрешность: \(0{,}5\textrm{\,Дж}.\)
\((14{,}6 \pm 0{,}5)\textrm{\,Дж}\).
Для большого промышленного электромагнита критически важной стала проблема охлаждения. Было установлено, что при пропускании через электромагнит тока \(I_1 = 10\text{ А}\) он нагревается до температуры \(t_1 = 70\,°\text{C}\), после чего перестает увеличивать свою температуру, а при пропускании через него тока \(I_2 = 20\text{ A}\) — до температуры \(t_2 = 205\,°\text{C}\).
Определите температуру \(\theta\) в помещении цеха, в котором используется электромагнит, если известно, что основным механизмом, отвечающим за охлаждение магнита, выступает теплопроводность, мощность которой прямо пропорциональна разнице температур между телами, обменивающимися теплом.
Как указано в условиях, мощность теплопроводности прямо пропорциональна разнице температур между магнитом и окружающим его воздухом в помещении цеха. Обозначим коэффциент этой пропорциональности \(\kappa\) \[\left\{\begin{aligned} &P_1 = \kappa (\theta - t_1),\\ &P_2 = \kappa (\theta - t_2). \end{aligned}\right. \label{heat_transfer}\]
Повышение температуры останавливается, когда мощность производимого катушкой тепла и мощность тепла, уходящего от катушки, благодаря теплообмену, оказываются равны. Первую можно выразить из закона Джоуля – Ленца \[\left\{\begin{aligned} &P_1 = I_1^2 R,\\ &P_2 = I_2^2 R, \end{aligned}\right. \label{joule_heat}\] где \(R\) — сопротивление катушки.
Разделим друг на друга уравнения системы \eqref{heat_transfer} и уравнения системы \eqref{joule_heat}, а затем приравняем эти отношения:
\[\frac{P_1}{P_2} = \frac{\theta - t_1}{\theta - t_2} = \frac{I_1^2}{I_2^2}.\] Тривиальными алгебраическими преобразованиями выразим \(\theta\) \[(\theta - t_1)I_2^2 = (\theta - t_2)I_1^2 \Rightarrow \theta = \frac{t_1 I_2^2 - t_2 I_1^2}{I_2^2 - I_1^2} = 25\,°\text{С}.\]
Погрешность: \(0{,}1\,°\text{С.}\)
\((25{,}0 \pm 0{,}1)\textrm{\,}\).
Для увеличения ресурса аккумулятора его зарядка происходит по специальной программе, учитывающей внешние условия, интенсивность использования прибора и другие факторы. Рассчитав оптимальный режим, зарядное устройство в течении \(\tau = 10\textrm{\,мин}\) подавало на аккумулятор ток, линейно возраставший со временем от нуля до максимального значения \(I_0 = 3\textrm{\,А}\), затем в течение \(2{,}5\tau\) поддерживало постоянное значение этого тока и, наконец, на протяжении \(\tau/2\), также линейно опускало ток от максимального значения до нуля. Какой общий заряд поступил на положительную клемму аккумулятора за все это время?
Один из способов решения задачи состоит в обнаружении аналогии между током и движением. Подобно тому, как скорость описывает темп изменения координаты, сила тока описывает темп поступления заряда на аккумулятор. Из кинематики известно, что при равномерном увеличении этого темпа (равноускоренном движении) от нуля, либо при равномерном снижении этого темпа (равнозамедленном движении) до нуля тело проходит вдвое меньшее расстояние, чем при движении с постоянной скоростью, равной максимальной на рассматриваемом участке. Применяя этот результат к току, заметим, что за время \(2{,}5\tau\) постоянного тока зарядки на аккумулятор поступил заряд \[q_1 = 2{,}5\tau I_0,\] а за общее время \(1{,}5 \tau\) увеличения и уменьшения силы тока — заряд \[q_2 = \frac{1{,}5 \tau I_0}{2} = 0{,}75 \tau I_0.\]
Складывая эти заряды, получим окончательно \[q = 3{,}25 \tau I_0 = 5850\textrm{\,Кл}.\]
Задача также может быть решена графически, изображением зависимости \(I(t)\) и вычислением площади под ней. Фактически такое решение также является применением аналогии, но геометрической, а не кинематической.
Погрешность \(50\textrm{\,Кл}.\)
\((5850 \pm 50) \textrm{\,Кл}\).
Печатающая головка 3D-принтера может перемещаться вдоль направляющей (координата \(x\)), которая также может смещаться в перпендикулярном направлении (координата \(y\)) под действием двух сервоприводов. Для изготовления детали на принтер была передана программа, согласно которой сервоприводы должны перемещать головку по законам \(x(t) = 0{,}2 \sin(t/10); \; y(t) = 0{,}1+0{,}2\cos(t/10)\), где \(t\) — время, а все величины даны в основных единицах СИ. Найдите величину ускорения печатающей головки при выполнении этой программы.
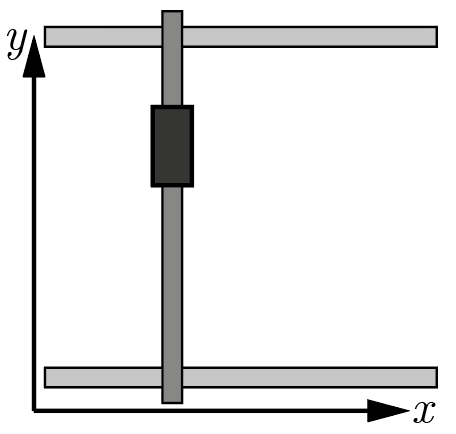
Прежде всего заметим, что уравнения приведенного типа параметрически задают окружность. Это следует из самого определения синуса и косинуса. Радиус \(R\) этой окружности равен множителю перед синусом и косинусом (т. к. в математическом определении тригонометрических функций используется единичная окружность), то есть \(R = 0{,}2\textrm{\,м}\). Здесь было учтено, что основными единицами СИ для измерения длины являются метры.
Поскольку зависимость угла на окружности (аргумента синуса и косинуса) от времени линейна, модуль скорости \(v\) печатающей головки постоянен. Чтобы найти его, определим период обращения. Печатающая головка описывает полную окружность, когда аргумент синуса и косинуса меняется на \(2\pi\), что происходит при достижении \(t\) значения \(T = 20\pi \textrm{\,с}\). Тогда \[v = \frac{2\pi R}{T}.\]
Окончательно заметим, что при неизменной по модулю скорости головки единственное ее ускорение — центростремительное, которое может быть найдено как \[a = \frac{v^2}{R} = \frac{4 \pi^2 R}{T^2} = \frac{4 \cancel{\pi^2} \cdot 0{,}2}{400 \cancel{\pi^2}} \approx 2\textrm{\,мм/с}^2.\]
Погрешность \(0{,}1\textrm{\,мм/с}^2.\)
\((2{,}0 \pm 0{,}1)\textrm{\,мм/с}^2\).
Квадратная плита ABCD со стороной \(a = 40\textrm{\,см}\) шарнирно закреплена в одной точке и вращается вокруг оси, перпендикулярной ее плоскости с постоянной угловой скоростью. При этом в некоторый момент времени скорость вершины C этой плиты направлена строго на вершину D, а ускорение вершины A — строго на вершину B (см. рис. 6.2). На каком расстоянии от центра пластины находится шарнир?
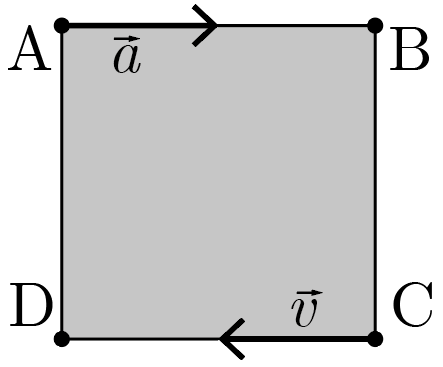
При плоском вращении скорость каждой точки тела направлена перпендикулярно направлению из этой точки на ось вращения, а ускорение (центростремительное) — непосредственно на эту ось. Поэтому, проведя одну прямую через точку C перпендикулярно ее скорости, а другую — через точку A вдоль ее ускорения, можно найти ось вращения как точку пересечения этих прямых. Такой точкой будет, разумеется, вершина B, а расстояние от нее до центра пластины равно \[l = \frac{\sqrt{2}}{2} a \approx 28{,}3\textrm{\,см}.\]
Погрешность \(0{,}5\textrm{\,см}.\)
\((28{,}3\pm 0{,}5)\textrm{\,см}\).
К проекту модельного теплового двигателя, рабочим телом которого является идеальный одноатомный газ, прилагается \(pV\)-диаграмма его рабочего цикла, представляющая собой прямоугольник 1234. К сожалению, автор не указал ни давления, ни объемы характерных точек, а ограничился «площадями» (в энергетических единицах) некоторых прямоугольников на данной диаграмме, которые указаны на рис. 6.2. Да к тому же самая важная площадь — площадь внутри цикла 1234, стерлась. Тем не менее определите КПД данного двигателя.
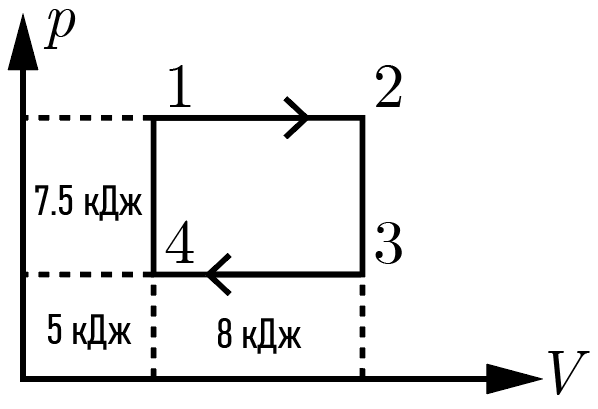
КПД \(\eta\) теплового двигателя определяется как отношение работы \(A\) газа за один цикл этого двигателя к количеству теплоты \(Q\), получаемой газом за этот цикл от нагревателя: \[\eta = \frac{A}{Q}. \label{ece}\]
Первая — есть площадь прямоугольника \(1234\). Найти ее просто, если заметить, что поскольку высота (вдоль оси \(p\)) у верхних двух прямоугольников одинакова, их площади относятся так же, как и их ширины (вдоль оси \(V\)), и то же верно для нижней пары прямоугольников \[A = 7{,}5\frac{8}{5} = 12\textrm{\,кДж}.\]
Чтобы найти теплоту \(Q\), воспользуемся первым началом термодинамики \(Q = A + \Delta U\) и заметим, что газ получает теплоту на процессах \(41\) и \(12\). Работа за эти два процесса равна полной площади под отрезком \(12\) \[A_{412} = 12 + 8 = 20\textrm{\,кДж},\] а внутренняя энергия может быть удобно вычислена по формуле \[U = \frac{3}{2}PV,\] из которой следует, что внутренняя энергия \(U_4\) газа в состоянии \(4\) равна \[U_4 = \frac{3}{2}5 = 7{,}5\textrm{\,кДж},\] поскольку произведение \(PV\) для этого состояния есть площадь одного соответствующего прямоугольника. Аналогично, внутренняя энергия \(U_2\) газа в состоянии \(2\) равна \[U_2 = \frac{3}{2}(7{,}5 + 12 + 5 +8) = 48{,}75\textrm{\,кДж},\] поскольку в этом состоянии соответствующее произведение \(PV\) равно общей площади всех прямоугольников на диаграмме.
Подставляя все найденные величины в исходное уравнение \eqref{ece}, получим окончательно \[\eta = \frac{A}{A_{412} + U_2 - U_4} = \frac{12}{20 + 48{,}75 - 7{,}5} \approx 19{,}6\%.\]
Погрешность \(1\%.\)
\((19{,}6 \pm 1{,}0)%\)
Трюм грузового судна представляет собой призму с основанием в виде равностороннего треугольника вершиной вниз. Длина внешней стороны треугольника \(a = 15\textrm{\,м}\), толщина его стенок \(d = 1{,}5\textrm{\,м}\), длина киля судна (высота призмы) \(l = 40\textrm{\,м}\). Инженерами было рассчитано, что для сохранения устойчивости судна центр тяжести сыпучего груза, перевозимого в трюме, должен быть хотя бы на \(h = 2\textrm{\,м}\) ниже центра тяжести вытесняемой трюмом воды при его полном погружении. Какой максимальный объем груза можно разместить в трюме, если при насыпании его центр тяжести занимает самое низкое доступное положение?
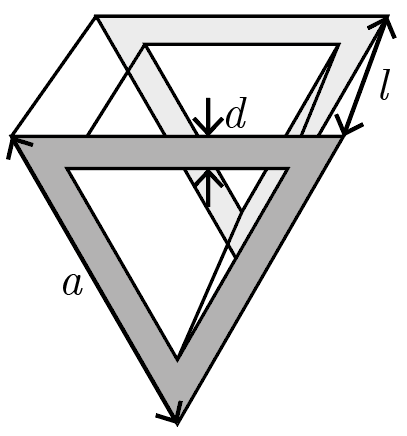
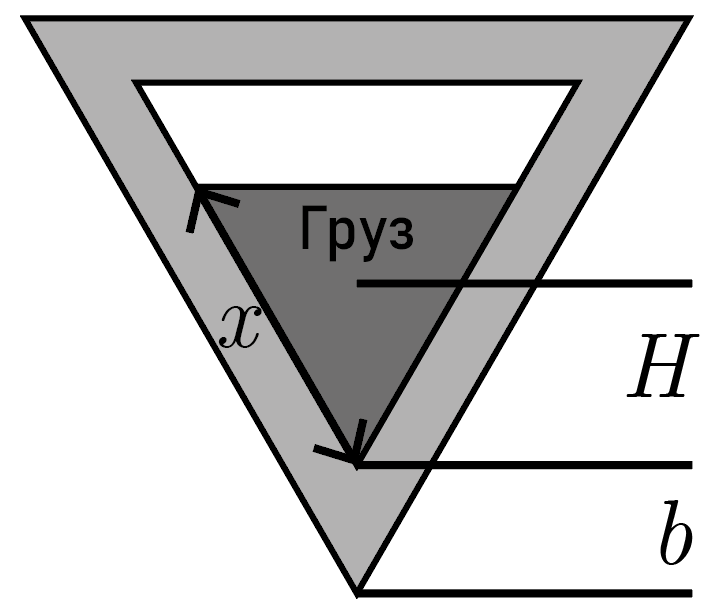
Сыпучий груз занимает объем, форма которого также является призмой с основанием в виде равностороннего треугольника, во всяком случае, при необходимости понизить центр тяжести. В силу симметрии, центр тяжести равностороннего треугольника находится в его геометрическом центре. Поскольку центр тяжести груза должен быть на \(h\) ниже, чем центр тяжести вытесненной воды, центр треугольника, формируемого сечением насыпанного груза (темный на рис. 6.5), на \(h\) ниже центра трюма.
Отсчитывая от киля (нижней вершины треугольника) высоту \(y_\textrm{в}\), на которой находится центр тяжести вытесненной воды, легко выразить как \[y_\textrm{в} = \frac{\sqrt{3}}{3}a,\] поскольку радиус описанной окружности для равностороннего треугольника в \(\sqrt{3}/3\) раз меньше его стороны.
Высота \(y_\textrm{г}\) центра тяжести груза может быть найдена как \[y_\textrm{г} = b + H,\] где \(b\) — толщина стенки вдоль соответствующего направления (см. рис. 6.5), а \(H\) — высота центра тяжести груза от нижней внутренней точки трюма. Обе эти величины вычисляются из тригонометрии \[b = 2d; \quad H = \frac{\sqrt{3}}{3}x,\] где \(x\) — сторона треугольника, являющегося поперечным сечением груза.
Учитывая \(y_\textrm{г} + h = y_\textrm{в}\), получим \[\frac{\sqrt{3}}{3}x + 2d + h = \frac{\sqrt{3}}{3}a,\] откуда \[x = a - \sqrt{3}(2d + h) \approx 6{,}34\textrm{\,м}.\]
Объем, занимаемый грузом при такой длине его стороны, находится как произведение площади равностороннего треугольника на длину киля \[V = \frac{\sqrt{3}}{4} x^2 l \approx 696\textrm{\,м$^3.$}\]
Погрешность 10 м\(^3\).
\((696 \pm 10)\) м\(^3\).
На конференции, посвященной освоению труднодоступных северных регионов, был представлен проект теплового двигателя, для работы которого используются два тепловых резервуара. Их можно собрать «на коленке»: в качестве холодильника выступает емкость с мокрым снегом, а в качестве нагревателя — котелок с кипящей водой. При этом, по заверениям авторов проекта, КПД двигателя только в \(\alpha = 1{,}6\) раз уступает КПД идеальной тепловой машины с такими же холодильником и нагревателем. Найдите этот КПД. Абсолютный ноль температур \(T_0 = -273\,°\text{C}\). Двигатель используется при нормальном атмосферном давлении на уровне моря.
Мокрый снег представляет собой смесь льда и воды, поэтому может существовать только при температуре плавления льда, \(t_\textrm{х} = 0\,°\text{C}\). Аналогично, при атмосферном давлении температура кипящей воды может быть равна только \(t_\textrm{н} = 100\,°\text{C}\). КПД идеальной тепловой машины (машины Карно) с известными абсолютными термодинамическими температурами \(T_\textrm{н}\) и \(T_\textrm{х}\) холодильника задается выражением \[\eta_0 = \frac{T_\textrm{н} - T_\textrm{х}}{T_\textrm{н}}.\]
Чтобы дать ответ на вопрос задачи, таким образом, остается разделить этот КПД на \(\alpha\) и перевести температуры в шкалу Кельвина \[\eta = \frac{\eta_0}{\alpha} = \frac{t_\textrm{н} - t_\textrm{х}}{\alpha(t_\textrm{н} - T_0)} \approx 16{,}8\%.\]
Погрешность: \(0{,}2\%\).
\((16{,}8 \pm 0{,}2)%\).
Корабль береговой охраны движется с постоянной скоростью \(v = 12\textrm{\,м/с}\) относительно поверхности воды. Наблюдательный дрон запрограммирован летать на постоянной высоте по траектории, в системе отсчета корабля представляющей собой окружность с радиусом \(R = 2\textrm{\,км}\) и центром на этом корабле, двигаясь в этой системе отсчета равномерно и совершая полный оборот за время \(T = 10\textrm{\,мин}\). Во сколько раз максимальная скорость дрона относительно поверхности воды выше его минимальной скорости относительно нее же?
Согласно правилу сложения скоростей, скорость \(\vec{v}_\textrm{дв}\) дрона относительно воды равна (векторной) сумме его скорости \(\vec{v}_\textrm{дк}\) относительно корабля и скорости \(\vec{v}_\textrm{кв}\) корабля относительно воды. Поскольку направление вектора \(\vec{v}_\textrm{кв}\) неизменно, а вектор \(\vec{v}_\textrm{дк}\) в ходе движения дрона принимает все возможные в горизонтальной плоскости направления, обязательно найдутся такие моменты времени, когда эти два вектора сонаправлены и такие, когда они противонаправлены. Эти два случая и будут соответствовать максимальному и минимальному значениям модуля суммы этих векторов, равным \(v_{max} = |\vec{v}_\textrm{дк}| + |\vec{v}_\textrm{кв}|\) и \(v_{min} = \left||\vec{v}_\textrm{дк}| - |\vec{v}_\textrm{кв}|\right|\) соответственно.
Модуль вектора \(\vec{v}_\textrm{кв}\) дан напрямую: он равен \(v\). Модуль вектора \(\vec{v}_\textrm{дк}\) легко получить, разделив путь дрона в СО корабля на период его обращения в этой СО \[v_\textrm{дк} = \frac{2\pi R}{T}.\]
Отсюда получим окончательно \[\frac{v_{max}}{v_{min}} = \frac{v T + 2\pi R}{|v T - 2\pi R|} \approx 3{,}68.\]
Погрешность \(0{,}02\).
\(3{,}68 \pm 0{,}02.\)
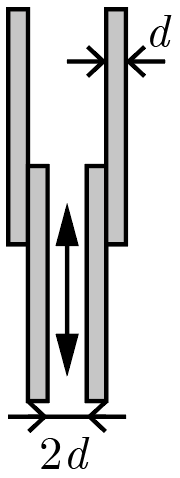
Переменный конденсатор состоит из двух пар металлических пластинок толщиной \(d\) и площадью \(S \gg d^2\), разделенных воздушными зазорами. При этом одна из пар (внутренняя) может частично или полностью входить в зазор другой (внешней), плотно прилегая к ней так, что электрический контакт между соответствующими пластинами никогда не нарушается, но при полном выдвижении площадь этого контакта пренебрежимо мала в сравнении с \(S\).
Определите, во сколько раз максимальная емкость такого конденсатора превосходит минимальную, если зазор между пластинами внутренней пары имеет ширину \(2d\).
Рассматриваемый конденсатор может быть представлен как батарея из двух параллельно соединенных конденсаторов, один из которых (внутренняя пара пластин) всегда имеет зазор \(2d\) и площадь обкладок \(S\), а другой (внешняя пара) имеет зазор \(4d\) и площадь обкладок, которая может изменяться в пределах от \(0\) до \(S\). Поскольку эти конденсаторы соединены параллельно, эквивалентная емкость батареи равна сумме их емкостей, а значит, максимальна, когда пары пластин максимально раздвинуты и минимальна, когда они полностью вдвинуты одна в другую. Используя формулу емкости плоского конденсатора, найдем, что емкость внутренней пары пластин (она же минимальная емкость всей батареи) равна \[C_1 = \frac{S \varepsilon_0}{2d},\] где \(\varepsilon_0\) — диэлектрическая постоянная.
Аналогично, емкость полностью выдвинутой внешней пары равна \[C_2 = \frac{S\varepsilon_0}{4d},\] а максимальная емкость батареи составляет, соответственно, \(C_1 + C_2\).
Тогда для искомого отношения максимальной и минимальной емкостей получим: \[\frac{C_{max}}{C_{min}} = \frac{C_1 + C_2}{C_1} = \frac{\cancel{S\varepsilon_0}/ (4 \cancel{d}) + \cancel{S\varepsilon_0}/ (2 \cancel{d})}{\cancel{S\varepsilon_0}/ (2 \cancel{d})} = \frac{1/4 + 1/2}{1/2} = 1{,}5.\]
Погрешность \(0{,}01\).
\(1{,}50\pm 0{,}01\).
Горелка теплового аэростата способна поддерживать среднюю температуру воздуха в его оболочке не более, чем на \(\Delta t = 70\,°\text{C}\) выше, чем температура окружающего шар воздуха. Аэростат имеет объем \(V = 645\) м\(^3\), а общая масса его оболочки, корзины и полезной нагрузки \(M = 150\textrm{\,кг}\). Определите, при какой максимальной температуре окружающей среды аэростат сможет взлететь?
Абсолютный ноль температур \(T_0 = -273\,°\text{C}\), атмосферное давление \(p_0 = 100\textrm{\,кПа}\), молярная масса воздуха \(\mu = 29\textrm{\,г/моль}\), универсальная газовая постоянная \(R = 8{,}31\textrm{\,Дж/(моль}\cdot \text{К})\).
Оболочки монгольфьеров (тепловых аэростатов) представляют собой открытые сосуды, поэтому давление внутри и снаружи оболочки должно совпадать (и равняться \(p_0\)). Тогда из уравнения Менделеева – Клапейрона \[p_0 V = \frac{m}{\mu} R T,\] где \(T\) — абсолютная термодинамическая температура газа, \(m\) — его масса.
Легко выразить массу \(m_1\) воздуха внутри оболочки и массу \(m_2\) вытесненного атмосферного воздуха \[\begin{aligned} m_1 &= \frac{\mu p_0 V}{R (T_0 + \Delta t)}, \\ m_2 &= \frac{\mu p_0 V}{R T_0}, \end{aligned}\] где \(T_0\) — искомая температура окружающего воздуха.
Для того чтобы аэростат мог подняться в воздух, необходимо, чтобы вес вытесняемого им воздуха превысил его общий вес (включая вес газа в оболочке) \[m_2\cancel{g} = M\cancel{g} + m_1\cancel{g} \Rightarrow \frac{\mu p_0 V}{R T_0} = M + \frac{ \mu p_0 V}{R (T_0 + \Delta t)},\] где \(g\) — ускорение свободного падения (сразу сокращающееся во всех слагаемых).
Домножим это выражение на \(R T_0(T_0 + \Delta T)\) и получим квадратное уравнение относительно \(T_0\)
\[\mu p_0 V (\cancel{T_0} + \Delta t) = M R T_0 (T_0 + \Delta t) + \cancel{\mu p_0 V T_0}.\]
В канонической форме: \[T_0^2 + T_0 \Delta t - \frac{\mu p_0 V \Delta t}{MR} = 0.\]
Остается найти (методом дискриминанта) единственный положительный корень этого уравнения \[T_0 = -\frac{\Delta t}{2} + \frac{1}{2}\sqrt{\Delta t^2 + \frac{4 \mu p_0 V}{MR} \Delta t} \approx 291\textrm{\,К} \approx 18\,°\text{C}.\]
Погрешность \(0{,}1\,°\text{C}\).
\((18{,}0 \pm 0{,}1)\,°\text{C}\).
Спутник, движущийся вокруг Земли по высокой круговой орбите, перевели на другую круговую орбиту, в результате чего его кинетическая энергия увеличилась на \(5\%\). На сколько процентов увеличился модуль потенциальной энергии взаимодействия спутника с планетой, если она считается равной нулю на бесконечном удалении от планеты?
Обозначим радиус орбиты спутника \(R\), его орбитальную скорость \(v\), его массу \(m\), а массу планеты \(M\). На спутник действует сила всемирного тяготения \[F = G\frac{mM}{R^2},\] где \(G\) — гравитационная постоянная, связанная с центростремительным ускорением \(v^2/R\) спутника вторым законом Ньютона \[\cancel{m}\frac{v^2}{\cancel{R}} = G\frac{\cancel{m}M}{R^{\cancel{2}}}.\]
Из этого выражения легко видеть, что квадрат орбитальной скорости спутника \(v^2\) обратно пропорционален радиусу орбиты. Разумеется, кинетическая энергия спутника \(mv^2/2\) прямо пропорциональна этому квадрату скорости и, следовательно, тоже обратно пропорциональна \(R\).
Чтобы понять, как потенциальная энергия спутника зависит от радиуса его орбиты, проще всего обратить внимание на аналогию между гравитацией и электростатическими силами. Сила Кулона взаимодействия двух точечных зарядов зависит от расстояния между ними и обратно пропорциональна квадрату разделяющего их расстояния, точно так же, как сила всемирного тяготения. Одновременно потенциальная энергия взаимодействия этих зарядов обратно пропорциональна первой степени расстояния между ними, следовательно, то же справедливо и для гравитации. В результате видно, что модуль потенциальной энергии обратно пропорционален \(R\), как и кинетическая энергия. Следовательно, при изменении орбиты спутника он изменится ровно во столько же раз.
Погрешность \(0{,}01\%\).
\((5{,}00 \pm 0{,}01)%\).
В сложной трансмиссии две шестеренки А и Б вращаются в различных частях механизма так, что угловая скорость вращения шестеренки А в \(3\) раза выше, чем шестеренки Б, но линейная скорость зубцов шестеренки Б в \(2\) раза выше, чем шестеренки А. Найдите отношение центростремительного ускорения зубцов шестеренки А к центростремительному ускорению зубцов шестеренки Б.
Два хорошо известных выражения для центростремительного ускорения \(a\) \[a = \frac{v^2}{R} = \omega^2R,\] где \(R\) — радиус траектории, \(v\) — линейная скорость, \(\omega\) — угловая скорость. Перемножив эти выражения, получим \[a^2 = \frac{v^2}{\cancel{R}} \omega^2 \cancel{R} \Rightarrow a = v \omega.\]
Таким образом, центростремительное ускорение равно произведению линейной скорости на угловую, из чего следует \[\frac{a_\textrm{А}}{a_\textrm{Б}} = \frac{v_\textrm{А}}{v_\textrm{Б}} \cdot \frac{\omega_\textrm{А}}{\omega_\textrm{Б}} = \frac{1}{2} \cdot \frac{3}{1} = 1{,}5.\]
Погрешность \(0{,}01\).
\(1{,}50 \pm 0{,}01\).
Заряженный металлический шарик закреплен на конце тонкой шелковой нити и несет заряд \(q = 20\textrm{\,мкКл}\). Другой конец нити закреплен к потолку. Определите массу шарика, если при помещении такого маятника в однородное электрическое поле, вектор напряженности которого направлен строго горизонтально и равен по модулю \(E = 2{,}5\textrm{\,кВ/м}\), сила натяжения нити после установления равновесия оказывается равна \(T = 130\textrm{\,мН}\). Ускорение свободного падения \(g = 9{,}8\textrm{\,м/с}^2\).
На шарик действуют три силы: горизонтально направленная сила электростатического взаимодействия \(q\vec{E}\), вертикально вниз направленная сила тяжести \(m\vec{g}\) и направленная вдоль нити сила ее натяжения \(\vec{T}\). Разумеется, маятник может быть в равновесии, только если векторная сумма этих сил равна нулю, то есть эти три вектора образуют замкнутый треугольник \[q\vec{E} + m\vec{g} + \vec{T} = \vec{0}.\]
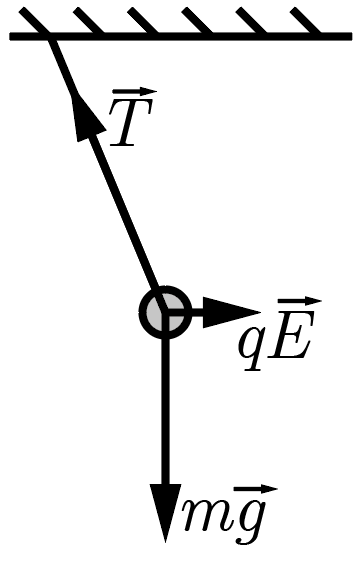
Поскольку направления \(\vec{E}\) и \(\vec{g}\) известны, этот треугольник прямоугольный, а \(\vec{T}\) — его гипотенуза. Тогда из теоремы Пифагора \[q^2E^2 + m^2g^2 = T^2 \Rightarrow m = \frac{\sqrt{T^2 - q^2E^2}}{g} \approx 12{,}2\textrm{\,г.}\]
Погрешность \(0{,}2\textrm{\,г}.\)
\((12{,}2 \pm 0{,}2)\textrm{\,г}\).
Автомобиль с автопилотом запрограммирован таким образом, что при движении по прямой на трассе он всегда старается поддерживать дистанцию между собой и движущимся непосредственно перед ним автомобилем ровно такой же, как между собой и движущимся непосредственно за ним автомобилем. В некоторый момент движения скорости всех трех этих автомобилей были равны. Определите ускорение автомобиля, движущегося непосредственно за автопилотируемым, если модули ускорения самого автопилотируемого автомобиля и движущегося непосредственно перед ним в этот момент оба оказались равны \(a = 0{,}2\textrm{\,м/с}^2\), но дистанция между ними при этом начала сокращаться. Колеса автомобилей движутся без проскальзывания, и автопилоту удается соблюдать требования своей программы.
Программа автомобиля означает, что (до тех пор, пока это позволяет мощность двигателя и сцепление колес) координата \(x\) вдоль оси, совпадающей с дорогой, автомобиля с автопилотом равна среднему арифметическому координат \(x_1\) идущего впереди и \(x_2\) идущего позади \[x = \frac{x_1 + x_2}{2}.\]
Поскольку такая кинематическая связь справедлива в любые два момента времени \(t_1\) и \(t_2\), для средней скорости \(v\) автомобиля на автопилоте в проекции на \(0x\) на любом промежутке времени можно записать \[v_x = \frac{x(t_2) - x(t_1)}{t_2 - t_1} = \frac{x_1(t_2) + x_2(t_2) - x_1(t_1) - x_2(t_1)}{2(t_2-t_1)} = \frac{v_{x1} + v_{x2}}{2},\] где использована та же система индексов. Таким образом, средняя скорость на любом промежутке времени и, следовательно, мгновенная скорость в любой момент времени автомобиля на автопилоте в проекции на \(0x\) равна среднему арифметическому мгновенной скорости в этой же проекции впереди и позади идущих автомобилей. Повторение этих рассуждений приводит к аналогичному результату для ускорений \[a_x = \frac{a_{x1} + a_{x2}}{2}.\]
Выразим из этого уравнения проекцию на \(0x\) искомого ускорения замыкающего автомобиля \(a_{x2}\) \[a_{x2} = 2a_x - a_{x1} \label{acceleraiton}.\]
По условиям задачи в рассматриваемый момент скорости всех трех автомобилей равны, а ускорения \(a_1\) и \(a\) совпадают по модулю, но дистанция начинает сокращаться. Это возможно только если передний автомобиль тормозит — имеет отрицательную проекцию ускорения на направление движения, а автопилотируемый автомобиль, напротив, ускоряется (имеет положительную проекцию). Тогда напрямую из \eqref{acceleraiton} получим \[a_{x2} = 2a_x - a_{x1} = 2a - (-a) = 3a = 0{,}6\textrm{\,м/с}^2.\]
Погрешность \(0{,}01\textrm{\,м/с}^2.\)
\((0{,}60 \pm 0{,}01)\textrm{\,м/с}^2\).
В лифте, движущемся вверх с некоторым ускорением \(a\), сонаправленным его скорости, уронили без начальной скорости относительно лифта мячик с высоты \(h_1 = 0{,}6\textrm{\,м}\) над уровнем пола лифта. Мячик абсолютно упруго ударился о пол, но своим ударом спровоцировал срабатывание системы аварийной остановки, в результате чего в момент удара ускорение лифта резко поменяло направление на противоположное, а его модуль возрос втрое. После отскока мячик поднялся до высоты \(h_2 = 1{,}8\textrm{\,м}\). Определите \(a\). Ускорение свободного падения \(g = 9{,}8\textrm{\,м/с}^2\).
В системе отсчета, связанной с лифтом, начальное ускорение мяча равно \(g + a\). Проходя с этим ускорением расстояние \(h_1\), мяч приобретает скорость (относительно лифта) \(v\), которую легко вычислить из соотношения \[\frac{v^2}{2} = (g+a)h_1.\]
В момент удара резко меняется ускорение, но не скорость лифта, поэтому значение \(v\) при абсолютно упругом ударе по модулю остается неизменным.
В процессе подъема мяч уже имеет относительно лифта ускорение \(g - 3a\), что позволяет записать аналогично \[\frac{v^2}{2} = (g-3a)h_2.\] Совмещая эти равенства, получим окончательно \[(g+a)h_1 = (g-3a)h_2 \Rightarrow a(h_1 + 3h_2) = g(h_2-h_1) \Rightarrow a = g\frac{h_2-h_1}{h_1 + 3h_2} = 1{,}96\textrm{\,м/c$^2$}.\]
Погрешность \(0{,}02\) м/c\(^2\).
\((1{,}96\pm 0{,}02)\) м/c\(^2\).
Капля воды при температуре немного ниже температуры кипения упала на раскаленную поверхность, в результате чего \(\alpha = 10^{-5}\) ее массы практически мгновенно испарилось. Известно, что \(\eta = 3\%\) полученной каплей энергии пошло на работу расширяющегося пара над оставшейся частью капли.
На какую высоту «подпрыгнет» капля вертикально вверх в результате такого испарения, если сопротивлением воздуха ее движению, а также потерями тепла в окружающую среду и работой пара против воздуха можно пренебречь?
Удельная теплота парообразования воды равна \(L = 2{,}26\textrm{\,МДж/кг}\), ускорение свободного падения \(g = 9{,}8\textrm{\,м/с}^2\).
Согласно первому началу термодинамики та теплота, полученная каплей, которая не пошла на работу расширяющегося пара над жидкой частью капли, ушла на изменение ее внутренней энергии; в данном случае — на испарение. Таким образом, можно записать для для этой части энергии \[\Delta U = (1 - \eta)Q = Lm\alpha, \label{evaporation}\] где \(m\) — масса капли до испарения, а \(Q\) — общая полученная каплей теплота. Отсюда легко найти \(Q\) \[Q = \frac{Lm\alpha}{1 - \eta}.\]
В то же время работа пара над каплей полностью идет на увеличение ее механической энергии, которая в верхней точке траектории чисто потенциальна \[A = \eta Q = (1-\alpha)m g h.\]
Выражая из этого уравнения \(h\) и подставляя в него \(Q\), получаем \[h = \frac{\eta Q}{(1-\alpha)m g} = \frac{L\alpha\eta}{(1-\alpha)(1 - \eta)g} \approx 7{,}1\textrm{\,см}.\]
Разумеется, если величину \(1 - \alpha\) в этом выражении считать просто единицей, ответ не изменится в пределах любой разумной погрешности.
Погрешность \(0{,}5\textrm{\,см}.\)
\((7{,}1 \pm 0{,}5)\textrm{\,см}\).