Инженерный тур. 1 этап
Измерение частоты оборотов паровой турбины происходит следующим образом: на роторе турбины установлена шестерня с определенным количеством зубьев, напротив шестерни установлен датчик Холла, фиксирующий магнитное поле и его напряженность. Каждый зуб, проходя мимо датчика, меняет магнитное поле, что влечет изменение напряжения на датчике. Датчик преобразует частоту оборотов в электрические прямоугольные импульсы. По количеству этих импульсов можно определить частоту вращения турбины. Для этого применяется электронное устройство — частотомер. Назовите главный компонент (микросхему), который используется в электрической схеме частотомера.
Счетчик.
Управление скоростью вращения турбины осуществляется с помощью электромагнитного клапана, у которого есть две команды: «открыть» и «закрыть». Им соответствуют высокий (1) и низкий (0) логические уровни электрического сигнала соответственно. Необходимо разработать программу, автоматизирующую управление данным клапаном для защиты турбины от превышения частоты вращения. В нормальной эксплуатации (НЭ) значение частоты должно быть не выше 1650 об/мин, и клапан должен быть открыт. При превышении данного значения клапан необходимо закрыть. Следует также учесть, что у турбины есть сервисный режим (СР) для проведения испытания механических бойков, при котором пороговое значение частоты вращения поднимается до 1685 об/мин. Условные обозначения: НЭ — 0, СР — 1.
Программу следует разрабатывать на языке С.
Программа должна принимать ТОЛЬКО целочисленные аргументы типа int.
На выходе программы необходимо получить цифру в формате int: «1» либо «0», что соответствует открытию или закрытию клапана.
Ниже представлено решение на языке C.
#define OPEN 1
#define CLOSE 0
#define NORMAL_MODE 0
#define NORMAL_MODE_LIMIT 1650
#define SERVICE_MODE_LIMIT 1685
int getValveState(int frecuency, int mode) // функция, которая принимает значение частоты (frecuency) и режима (mode). Возвращает состояние открыть или закрыть
{
if(mode == NORMAL_MODE) // если мы попали в нормальный режим
{
if(frecuency > NORMAL_MODE_LIMIT) // если значение частоты больше предела, нужно закрыть клапан, иначе открыть его.
{
return CLOSE;
}
return OPEN;
}
else // если попали в сервисный режим
{
if(frecuency > SERVICE_MODE_LIMIT) // если значение частоты больше предела, нужно закрыть клапан, иначе открыть его.
{
return CLOSE;
}
return OPEN;
}
}
| № теста | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Аргумент 1 | 500 | 500 | 725 | 725 | 950 | 950 | 1400 | 1400 | 1650 | 1650 |
| Аргумент 2 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| Результат | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| № теста | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Аргумент 1 | 1660 | 1660 | 1685 | 1685 | 1850 | 1850 | 2075 | 2075 | 2300 | 2300 |
| Аргумент 2 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| Результат | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Лопасть вращается со скоростью 1400 об/мин, а ее радиус составляет 60 см.
- Определите полное ускорение точки. Ответ дайте с точностью до целых в метрах в секунду за секунду.
Используя центр окружности в качестве начала координат, определите, по какому закону меняется значение координаты \(X\) со временем (какая функция описывает зависимость \(x(t)\)). Достаточно указать только вид зависимости без аргументов.
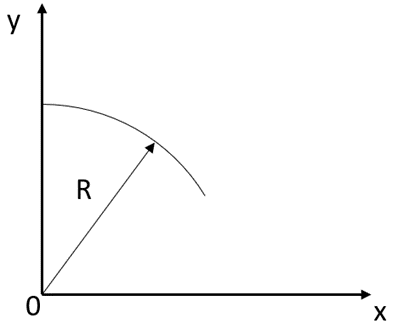 Рис. 1.1.
Рис. 1.1.- Турбина начинает вращаться из неподвижного положения и развивает скорость 1400 об/мин за 120 с. Определите полное ускорение точки в момент \(t = 100\) c. Ответ дайте с точностью до целых в метрах в секунду за секунду.
- Используя центр окружности в качестве начала координат, определите угол между вектором скорости и положительным направлением оси \(X\) в момент времени \(t = 100\) c. Ответ дайте с точностью до целых в градусах с учетом знака.
- Лопасть вращается с постоянной скоростью — вектор скорости в каждый момент времени изменяет только направление, сохраняя свое значение по модулю. Полное ускорение материальной точки будет складываться только из нормального (центростремительного) ускорения, которое можно найти по формуле: \[\label{eq:yat_0101} a = \frac{v^2}{R}.\] Переведем единицы измерения из оборотов в минуту: \[1400 \, \text{об/мин} = \frac{1400 \cdot 360 \cdot \pi}{180 \cdot 60} \, \text{рад/с} = 146{,}6 \, \text{рад/с}.\] Чтобы получить линейную скорость, умножим угловую скорость на радиус: \[v = \omega R = 146{,}6 \cdot 0{,}6 = 87{,}9 \, \text{м/с}.\] Подставим полученное значение в формулу для вычисления нормального ускорения: \[a_n = \frac{(87{,}9)^2}{0{,}6} = 12887 \, \text{м/с}^2.\]
Вектор скорости точки в любой момент времени направлен по касательной к траектории движения. Отобразим этот вектор и спроецируем на заданные оси.
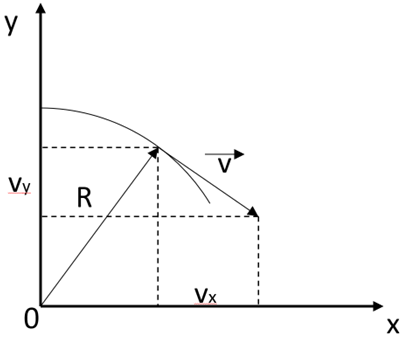 Рис. 1.2.
Рис. 1.2.\(V_x\) можно выразить через один из двух углов прямоугольного треугольника. Так как скорость и координата однозначно связаны, зависимость будет одна и та же с точностью до множителя перед тригонометрической функцией. Ответ: синус/косинус, \(\sin\)/\(\cos\).
- В данном случае, в отличие от п.1, вектор скорости изменяется не только по направлению, но и по модулю, и полное ускорение складывается из двух составляющих — тангенциального и нормального. Решение для поиска нормального ускорения приведено в п.1. Тангенциальную составляющую ускорения можно найти по формуле: \[a_\tau = \frac{\Delta v}{\Delta t} = \frac{87{,}9}{120} = 0{,}73 \, \text{м/с}^2.\] Скорость в момент \(t = 100\) с найдем, умножив тангенциальную составляющую ускорения на время: \[v(100) = a_\tau t = 73 \, \text{м/с}.\] По формуле \eqref{eq:yat_0101} найдем нормальную составляющую ускорения: \[a_n = \frac{73^2}{0{,}6} = 8882 \, \text{м/с}^2.\] Модуль полного ускорения точки можно получить по теореме Пифагора: \[a = \sqrt{a_n^2 + a_\tau^2} = \sqrt{8882^2 + 0{,}73^2} = 8882 \, \text{м/с}^2.\]
- Закон движения точки по окружности можно записать следующим образом: \[x(t) = R \cos(\omega t),\] \[y(t) = R \sin(\omega t).\] Получим скорость, дифференцируя по \(t\): \[v_x(t) = -R \omega \sin(\omega t),\] \[v_y(t) = R \omega \cos(\omega t).\] Подставляя условия и результаты из предыдущих пунктов, получим: \[v_x(100) = -0{,}6 \cdot 146{,}6 \sin(146{,}6\cdot 100) = -85{,}4\, \text{м/с},\] \[v_y(100) = 0{,}6 \cdot 146{,}6 \cos(146{,}6\cdot 100) = 21{,}1 \, \text{м/с}.\] Определим тангенс угла и через него значение угла в градусах: \[\operatorname{tg}(\varphi)=\frac{v_x}{v_y} =-4{,}05,\] \[\varphi=\arctan(-4{,}05)=-76°.\] Также принимается ответ 104°.
- 12887\(\pm\) 100 м/с\(^2\);
- любой из ответов: синус, косинус, sin, cos;
- 8882\(\pm\) 100 м/с\(^2\);
- \(-76°\) или 104°.






