Предметный тур. Информатика. 3 этап
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Два катера начинают движение параллельными курсами на расстоянии \(r\) м друг от друга. Правому катеру требуется совершить маневр с поворотом на 90° влево, тем самым он пересечет траекторию левого катера. Правый катер двигается быстрее, поэтому он может опередить левый катер и далее выполнить поворот по дуге окружности. Чтобы маневр был безопасным, требуется, чтобы в момент пересечения траекторий катеров расстояние между ними также было не меньше, чем \(r\).
Напишите программу, которая найдет, через какое время после начала движения правый катер должен начать поворот.
Для лучшего понимания посмотрите схему, представленную на рис. 1.1.
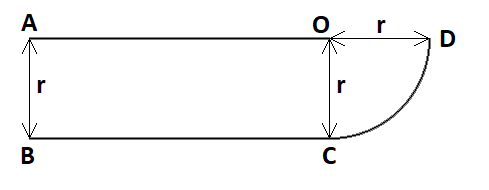
Левый катер проплыл по прямой от точки \(A\) к точке \(O\) со скоростью \(u\) м/с. Правый катер за это же время проплыл по прямой со скоростью \(v\) м/с от точки \(B\) до точки \(C\) и далее по дуге окружности от точки \(C\) до точки \(D\). Программа должна найти время, за которое правый катер проплывет отрезок \(BC\).
Подсказка. Чтобы использовать в программе на Python константу \(\pi\), напишите в первой строчке следующий фрагмент кода.
from math import piФормат входных данных
В одной строке через пробел на вход поступает три натуральных числа \(r\), \(u\), \(v\) — расстояние между катерами и радиус поворота, скорость левого катера, скорость правого катера, \(100\leqslant r\leqslant 10000\), \(1\leqslant u < v\leqslant 20\).
Формат выходных данных
Выведите одно вещественное число — время, за которое правый катер проплывет отрезок \(BC\). Ответ будет засчитан, если разность между выведенным числом и точным значением не превысит \(0{,}001\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
200 4 5 |
251.32741228718345 |
Примечания
Поясним ответ к тестовому примеру.
Правый катер проплыл \(251{,32741228718345}\) с по прямой и \[\frac{200\pi}{2\cdot 5}=62{,83185307179586}\text{~с по дуге.}\]
Тогда левый катер плыл по прямой \[251{,32741228718345}+62{,83185307179586}=314{,1592653589793} \text{ с.}\]
Тогда длина отрезка \(AO\) равна \[4\cdot 314{,1592653589793}=1256{,6370614359173},\] а отрезка \(BC\) \[251{,}32741228718345\cdot 5=1256{,6370614359173}.\]
Длины отрезков совпали, то есть время соответствует траекториям на схеме.
Обозначим за \(x\) длину отрезка \(BC\). Дуга составляет четверть окружности, и ее длина равна \(\pi \dfrac{r}{v}\). Таким образом, расстояние, пройденное правым катером, равно \[x+\pi \dfrac r2.\] Время движения правого катера равно \[\dfrac {x+\pi \dfrac r2}{v}=\dfrac{2x+\pi r}{2v}.\] Левый катер за это время проплыл расстояние \(\dfrac{u(2x+\pi r)}{2v}\), которое равно \(x\), что позволяет записать следующее уравнение.
\[x=\frac{u(2x+\pi r)}{2v}.\]
Решив полученное уравнение, получим формулу для вычисления \(x\). \[x=\frac{\pi r u}{2(v-u)}.\]
Чтобы найти искомое время, \(x\) надо поделить на \(v\).
Пример программы-решения
Ниже представлено решение на языке Python.
from math import pi
r, u, v = map(int,input().split())
ans = (pi*r*u) / (2*(v-u)*v)
print(ans)Первый тест совпадает с тестом из условия задачи. Баллы за него не начисляются.
Программа проверяется на \(10\) тестах. Успешное прохождение каждого теста оценивается в \(1\) балл.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Гоночный автомобиль должен проехать по ровной трассе \(s\) км. Это расстояние требуется проехать как можно скорее, однако расход топлива на километр обычно возрастает с увеличением скорости, и имеющегося запаса топлива может не хватить, чтобы проехать всю трассу на максимальной скорости. У автомобиля \(n\) режимов движения. В \(i\)-том режиме автомобиль тратит \(r_i\) мл топлива, чтобы проехать 1 км за \(t_i\) с. Бак автомобиля вмещает \(v\) л топлива.
Напишите программу, которая найдет, за какое минимальное время автомобиль сможет преодолеть требуемую дистанцию. Гарантируется, что емкости бака хватит, чтобы проехать \(s\) км хотя бы в самом экономичном режиме. Расстояние, проезжаемое автомобилем в каждом из режимов, может не быть целым.
Подсказка. Эта задача относится к классу задач линейного программирования. Неизвестными переменными \(x_1, \ldots, x_n\) здесь будут расстояния, пройденные автомобилем в каждом из режимов. В задаче два ограничения: на расстояние и на объем бака. В теории линейного программирования доказывается, что количество ненулевых значений переменных в оптимальном ответе будет меньше или равно, чем количество ограничений. Таким образом, для достижения оптимального времени в этой задаче автомобиль может двигаться не более, чем в двух различных режимах.
Формат входных данных
В первой строке на вход поступают три натуральных числа \(n\), \(s\), \(v\) — количество режимов движения, длина дороги и имеющееся количество топлива, \(2\leqslant n\leqslant 100\), \(1\leqslant s\leqslant 1000\), \(1\leqslant v \leqslant 1000000\).
Далее в \(n\) строках записаны описания режимов движения. Описание \(i\)-го режима состоит из двух чисел \(t_i\) и \(r_i\) — время, за которое автомобиль проезжает 1 км в этом режиме, и объем сжигаемого за это время топлива, \(10\leqslant t_i\leqslant 200\), \(10\leqslant r_i\leqslant 1000\).
Гарантируется, что \(s\cdot\min r_i\leqslant v\), то есть требуемое расстояние можно проехать в самом экономичном режиме.
Формат выходных данных
Выведите одно вещественное число — наименьшее возможное время, за которое автомобиль преодолеет заданное расстояние. Ответ будет засчитан, если разность между выведенным числом и точным значением не превысит \(0{,}001.\)
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 100 15000 60 150 50 200 100 50 |
6000 |
2 |
7 100 15000 20 300 69 100 30 250 60 150 50 200 100 50 80 75 |
5599.999999999999 |
Примечания
Рассмотрим первый тестовый пример. Чтобы получить оптимальное время, можно использовать второй и третий режим движения. Во втором режиме автомобиль будет ехать \(100\cdot\dfrac{2}{3}\) км, а в третьем — \(100\cdot\dfrac{1}{3}\) км. При этом будет потрачено ровно \(15000\) мл топлива. \[100\cdot\frac{2}{3}\cdot 100 + 100\cdot\frac{1}{3}\cdot 250 = 45000\cdot\frac{1}{3} = 15000.\]
Время движения составит: \[100\cdot\frac{2}{3}\cdot 69 + 100\cdot\frac{1}{3}\cdot 30 = 5600.\]
Выведенный ответ отличается от точного значения менее, чем на \(0{,}001\), поэтому он считается верным.
Можно показать, что меньшее значения времени получить невозможно.
Во втором тестовом примере оптимальным вариантом будет проехать весь путь в первом режиме движения.
С учетом ограничений решение этой задачи может заключаться в переборе всех пар режимов движения. Обозначим объем сжигаемого топлива и время для первого режима за \(r_i\) и \(t_i\), а для второго режима — за \(r_j\) и \(t_j\). Будем считать, что \(s r_i < v\), а \(s r_j > v\). Если \(s r_i\geqslant v\), то достаточно использовать один режим движения.
Обозначим за \(x\) расстояние, пройденное в первом режиме. Тогда расстояние, пройденное во втором режиме, будет равно \(s-x\). Тогда \(xr_i+(s-x)r_j=v\). Решив уравнение, получим формулу \[x=\frac{v-sr_i}{r_j-r_i}.\]
Из нее можно получить время движения \(t = xt_i+(s-x)t_j\). Требуется перебрать все пары режимов и найти минимум из полученных значений \(t\). Необходимо также учесть, что может оказаться оптимальным проехать все расстояние, используя один режим.
Пример программы-решения
Ниже представлено решение на языке Python.
n, s, v = map(int,input().split())
p = [tuple(map(int,input().split())) for _ in range(n)]
p.sort(key = lambda x:x[1])
ans = 10**18
for i in range(n):
if p[i][1]*s <= v and p[i][0]*s < ans:
ans = p[i][0]*s
for i in range(n):
if p[i][1]*s>=v:
break
for j in range(i+1,n):
if p[j][1]*s>v:
x = (v-p[i][1]*s) / (p[j][1]-p[i][1])
t = p[j][0]*x+p[i][0]*(s-x)
if t<ans:
ans = t
print(ans)Два первых теста совпадают с тестами из условия задачи. Баллы за них не начисляются.
Программа проверяется на \(15\) тестах. Успешное прохождение каждого теста оценивается в \(1\) балл.
В тестах №№ 3–8 задано ровно два режима движения.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Петя опять прогулял информатику, и Антон в учебно-воспитательных целях создал для него виртуальный мир \(k\)-значных ловушек. Мир выглядит как последовательность комнат, в каждой из которых находится \(k\)-значная ловушка. У каждой ловушки имеется \(k\) состояний, пронумерованных цифрами от \(0\) до \(k-1\). Петя должен пройти по всем комнатам от первой до последней. Если в некоторой комнате имеется ловушка с состоянием, равным нулю, то Петя, войдя в эту комнату, проваливается в ловушку и переносится в начало последовательности, после чего начинает двигаться по комнатам заново. Состояние ловушки при этом изменяется на \(k-1\).
Если же ловушка в некоторой комнате имела состояние \(s>0\), то Петя проходит через эту комнату, однако состояние ловушки при этом становится равным \(s-1\).
Петя может досрочно покинуть этот странный мир, если правильно ответит, сколько раз ему придется попадать в ловушки, перед тем как он сможет дойти до выхода. Он уже осознал ошибочность своего поведения и теперь просит написать программу, которая по текущему состоянию ловушек в комнатах даст ответ на поставленный вопрос. Программа должна предоставить решение для \(t\) независимых тестовых случаев.
Формат входных данных
В первой строке на вход подается одно натуральное число \(t\) — количество тестовых случаев, \(1\leqslant t\leqslant 100\). Далее записаны сами тесты, каждый из которых занимает две строки. В первой строке записаны два натуральных числа \(n\) и \(k\) — количество комнат и показатель мира \(k\)-значных ловушек, \(1\leqslant n\leqslant 500\), \(2\leqslant k\leqslant 10\).
Во второй строке записаны \(n\) целых чисел \(a_1,\ldots,a_n\) — состояния ловушек в комнатах в некоторый момент времени, когда Петя стоит у входа в первую комнату, \(0\leqslant a_i < k\).
Гарантируется, что числа подобраны таким образом, что ответ не превысит \(10^{18}\).
Формат выходных данных
Для каждого тестового случая программа должна вывести в отдельной строке одно целое число, равное количеству попаданий в ловушки до момента выхода из последней комнаты.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 4 3 2 1 0 1 3 2 1 0 0 4 9 1 1 1 1 |
3 6 0 |
Примечания
Рассмотрим первый тестовый пример. В свой первый проход Петя пройдет две комнаты и попадет в ловушку в третьей.
Состояние ловушек при этом станет 1 0 2 1. В свой второй проход Петя пройдет одну комнату и попадет в ловушку во второй.
Состояние ловушек при этом станет 0 2 2 1. В свой третий проход Петя попадет в ловушку в самой первой комнате.
Состояние ловушек при этом станет 2 2 2 1. Теперь открытых ловушек нет, и Петя дойдет до выхода. В ответ выводится количество попаданий в ловушки, то есть \(3\).
Задача может быть решена с использованием стандартного алгоритма целочисленного бинарного поиска. Функция test(s) будет возвращать истину, если, входя в первую комнату \(s\) раз, Петя сможет выйти из последней комнаты. Эта функция, очевидно, является монотонной, поэтому применение бинарного поиска является корректным. Ответом будет максимальное значение \(s\), при котором test(s) вернет ложь.
Сама функция test может быть реализована циклически. Если Петя войдет в некоторую комнату \(s\) раз, то он попадет в ловушку \(\displaystyle\left\lceil\frac{s-a}{k}\right\rceil\) раз, где \(a\) — начальное состояние ловушки, а \(k\) — ее параметр. Тогда в следующую комнату Петя войдет \(s - \displaystyle\left\lceil\frac{s-a}{k}\right\rceil\) раз и так далее. Если переменная \(s\) станет равна нулю, то Петя не сможет дойти до выхода из последней комнаты.
Пример программы-решения
Ниже представлено решение на языке Python.
def test(s):
for a in lst:
s -= (s-a+k-1)//k
return s>0
t = int(input())
for _ in range(t):
n, k = map(int,input().split())
lst = [int(x) for x in input().split()]
left = 0
right = 10**18
while right-left > 1:
mid = (left+right)//2
if test(mid):
right=mid
else:
left=mid
print(left)Первый тест совпадает с тестом из условия задачи. Баллы за него не начисляются.
Программа проверяется на \(20\) тестах. Успешное прохождение каждого теста оценивается в \(1\) балл.
В тестах №№ 2–9 во всех тестовых случаях \(k=2\). Дополнительно в тестах №№ 2–5 количество комнат в каждом тестовом случае не превосходит \(10\).
В тестах №№ 10–15 количество комнат в каждом тестовом случае не превосходит \(15\).
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 128 Мбайт.
Антон разрабатывает виртуальный музей с самыми известными культурными достопримечательностями человечества. Сегодня его внимание привлекла терракотовая армия — тысячи глиняных статуй воинов, расположенных у мавзолея Цинь Шихуанди — основателя империи Цинь.

Чтобы сделать экспозицию более динамичной, он решил, что воины должны двигаться по следующей схеме. Представим себе поле, состоящее из \(n\) ячеек, расположенных в одну линию. В начальный момент времени в каждой ячейке поля находится один воин. Далее за каждый такт происходят следующие изменения.
Воин, стоящий на первой клетке падает, сраженный, и пропадает с поля, а оставшиеся воины перемещаются так, чтобы выполнялись следующие условия:
- За один шаг воин перемещается в следующую клетку. За такт каждый воин может сделать несколько шагов или ни одного.
- В первой и последней клетках поля всегда должно находиться по одному воину.
- Количество пустых клеток между любой парой соседних воинов должно быть примерно одинаковым. Это означает, что наибольшее количество свободных клеток между двумя соседними воинами и наименьшее должны различаться не более, чем на единицу.
- Суммарное количество шагов, сделанных всеми воинами, на каждом отдельном такте должно быть минимальным.
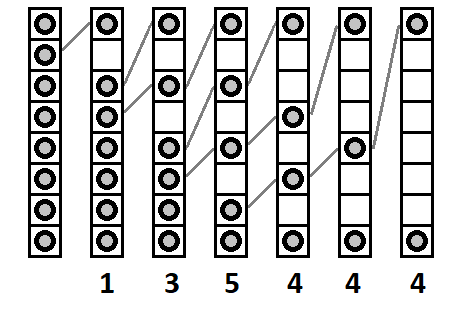
Для лучшего понимания посмотрите на схему перемещений за \(6\) тактов при \(n=8\) (см. рис. 1.3). Числа на схеме указывают суммарное количество шагов.
Антона заинтересовал вопрос, а сколько всего шагов сделают воины на каждом такте от \(1\) до \(n-2\). Напишите программу, которая даст на него ответ.
Формат входных данных
На вход поступает единственное натуральное число \(n\), \(3\leqslant n\leqslant 200000\).
Формат выходных данных
Программа должна вывести в одной строке через пробел \(n-2\) натуральных числа — суммарное количество шагов, сделанное воинами на каждом такте демонстрации от \(1\) до \(n-2\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
8 |
1 3 5 4 4 4 |
Примечания
Тестовый пример рассмотрен на схеме 1.3.
Для решения этой задачи можно применить следующий подход. Пронумеруем все позиции на поле, начиная с нуля. Будем считать сумму номеров позиций, на которых стоят воины после каждого такта. При этом будем учитывать снятых с поля воинов как стоящих на позиции \(n-1\). Тогда количество шагов на каждом такте будет разностью сумм номеров между текущим состоянием и предыдущим.
Пусть \(i\) — номер текущего такта. Воина, стоящего в клетке \(0\), не учитываем в сумме. Тогда количество воинов будет равно \(n-1-i\). Представим число \(n-1\) в виде \[n-1 = m(n-1-i)+k.\] Это означает, что \(n-1-i-k\) воинов находятся на расстоянии \(m\) друг от друга, а \(k\) воинов — на расстоянии \(m+1\). Чтобы получить такую расстановку, можно сначала расставить \(n-1-i\) воинов на позиции \(m\), \(2m\), \(3m\) и так далее, а после дополнительно сдвинуть \(k\) воинов на \(1\), \(2\), \(3\) и так далее. Тогда сумма номеров позиций может быть вычислена с использованием формулы суммы арифметической прогрессии следующим образом: \[i(n-1)+m(n-i)(n-i-1)/2+k(k+1)/2.\]
Пример программы-решения
Ниже представлено решение на языке Python.
n = int(input())
sm=[n*(n-1)//2]
for i in range(1,n-1):
m = (n-1) // (n-1-i)
k = (n-1) % (n-1-i)
sm.append(i*(n-1) + m*(n-i)*(n-i-1)//2 + k*(k+1)//2)
print(' '.join(str(sm[i+1]-sm[i]) for i in range(n-2)))Первый тест совпадают с тестом из условия задачи. Баллы за него не начисляются.
Программа проверяется на \(25\) тестах. Успешное прохождение каждого теста оценивается в \(1\) балл.
В тестах №№ 2–11 размер поля \(n\) не превосходит 100.
В тестах №№ 12–16 размер поля \(n\) не превосходит 10000.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 128 Мбайт.
«Хорошо, хоть яйца не разбегаются», — устало подумал Иван-царевич, отстреливая стотысячного зайца.
Много тысячелетий назад Кощей Бессметный осознал свою уязвимость. Герою достаточно пронзить стрелой зайца, утку, разбить яйцо — и все. Тогда он решил усилить свою защиту. Он создал много объектов трех видов: «яйца», «зайцы», «утки». При этом каждый объект может содержать в себе произвольное количество других объектов. Например, в зайце могут скрываться еще два зайца, утка и яйцо, внутри них — новые зайцы утки и яйца и так далее. После поражения внешнего объекта все внутренние немедленно выскакивают наружу. При этом зайцы и утки быстро разбегаются или разлетаются в разные стороны, и попробуй их догони! Яйца же остаются на месте, и бегать за ними не придется. Единственным самым внешним объектом является некоторое яйцо, а смерть Кощея наступит, когда будут поражены все объекты.
Конечно же, это была завязка сюжета для логической игры с элементами виртуальной реальности.
В нашей игре объединенный штаб всех сил добра разрабатывает план сражения с Кощеем. Команде магических хакеров удалось выкрасть схему размещения объектов в защите Кощея. При ближайшем рассмотрении рунические символы на ней оказались обыкновенными скобками. Яйцо записывается как пара из круглых скобок (), заяц — квадратных [], а утка — фигурных {}. Вложенность скобок показывает вложенность объектов. Например, последовательность ([{}{}][]{([{}])}) задает яйцо, в котором находится первый заяц с двумя утками внутри, второй заяц без вложенных объектов и утка, внутри которой находится яйцо, в том яйце еще один заяц, а в нем — еще одна утка.
Команда магов-артефакторов создала волшебные стрелы, которые никогда не промахиваются, а команда магов-лекарей усилила способности и силу Ивана-царевича. Теперь сражение можно представить в виде следующей модели. В начале каждой минуты Иван-царевич произвольно выбирает и поражает один из объектов, находящихся на поверхности. Далее в течении минуты он выбирает и догоняет новый объект, чтобы поразить его в начале следующей минуты. Усиленные способности Ивана-царевича позволяют ему всегда догнать зайца или утку за минуту, независимо от расстояния на которое те убежали, однако на это потребуется некоторое количество энергии. Будем считать, что если заяц или утка оказались на поверхности в момент времени \(i\), а поражены были в момент времени \(j\), то это потребовало \(j-i\) единиц энергии. Яйца не убегают, поэтому их поиск не требует энергии.
Вы — маг-стратег, от которого требуется составить план сражения, то есть последовательность поражения объектов, при которой Иван-царевич потратит минимальное количество энергии. Поскольку объектов может быть много, вам придется написать программу для решения указанной задачи.
Формат входных данных
На вход поступает правильная скобочная последовательность c тремя видами скобок. Длина последовательности не превосходит \(300000\). Первый и последний символ — это круглая открывающая и соответствующая ей закрывающая скобка. Количество уровней вложенности скобок не превосходит \(1000\).
Формат выходных данных
Выведите одно целое число — минимальное количество энергии, которое потратит Иван-царевич для поражения всех объектов.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
([][]([])) |
11 |
Примечания
Рассмотрим тестовый пример ([{}{}][]{([{}])}).
В момент времени \(0\) Иван-царевич разобьет внешнее яйцо. На поверхности окажутся три объекта: [{}{}], [] и {([{}])}.
В момент времени \(1\) Иван-царевич может поразить утку и потратить на это \(1-0=1\) единицу энергии. На поверхности останутся объекты: [{}{}], [] и ([{}]).
В момент времени \(2\) Иван-царевич может поразить второго зайца и потратить на это \(2-0=2\) единицы энергии. На поверхности останутся объекты: [{}{}] и ([{}]).
В момент времени \(3\) Иван-царевич может поразить оставшегося зайца и потратить на это \(3-0=3\) единицы энергии. На поверхности останутся объекты: {}, {} и ([{}]). Заметим, что утки появились в момент времени \(3\).
В момент времени \(4\) Иван-царевич может поразить одну из уток и потратить на это \(4-3=1\) единицу энергии. На поверхности останутся объекты: {} и ([{}]).
В момент времени \(5\) Иван-царевич может поразить оставшуюся утку и потратить на это \(5-3=2\) единицы энергии. На поверхности останется одно яйцо: ([{}]).
В момент времени \(6\) Иван-царевич разобьет яйцо и не потратит на это энергии. На поверхности останется один заяц: [{}].
В момент времени \(7\) Иван-царевич поразит зайца и потратит на это \(7-6=1\) единицу энергии. На поверхности останется одна утка: {}.
В момент времени \(8\) Иван-царевич поразит последнюю утку и потратит на это \(8-7=1\) единицу энергии.
Всего Иван-царевич потратил \(1+2+3+1+2+1+1=11\) единиц энергии.
Сделаем несколько замечаний. Во-первых, каждое яйцо может рассматриваться как независимый объект, поскольку его уничтожение можно отложить на произвольное время без потерь энергии.
Во-вторых, в каждый момент времени на поверхности должно находиться как можно меньше объектов, поэтому, начав ликвидацию некоторого объекта, следует немедленно уничтожать и все вложенные объекты, кроме яиц.
В-третьих, следует устранять объекты в порядке возрастания их размера с учетом вложенности.
Для решения задачи можно использовать алгоритм обхода дерева в глубину. Само дерево здесь неявно задано с использованием скобочного выражения, поэтому текущей позицией вершины в дереве будем считать позицию некоторой открывающей скобки. В прилагаемой программе эта позиция хранится в переменной cp. Каждый рекурсивный вызов будет обрабатывать некоторое правильное скобочное подвыражение, изменяя переменную cp.
В переменной ans накапливается ответ. Функция dfs возвращает размер поддерева, при этом учитываются только фигурные и квадратные скобки в соответствии с первым замечанием.
Время нахождения на поверхности непосредственных потомков текущего объекта отмеряется от момента уничтожения этого объекта в соответствии со вторым замечанием.
Для подсчета времени нахождения на поверхности непосредственных потомков упорядочим их по возрастанию количества вложенных объектов. Если обозначить эти значения \(c_1, c_2, \ldots, c_m\), то первый объект будет уничтожен через 1 с, второй — через \((1+c_1)\) с, третий — через \((1+c_1+c_2)\) с и так далее. Эти величины добавляются к ответу.
Пример программы-решения
Ниже представлено решение на языке Python.
seq = input()
cp = 0
ans = 0
def dfs():
global cp,ans
cp+=1
cnt = []
while True:
if seq[cp]=='(':
dfs()
elif seq[cp]=='[' or seq[cp]=='{':
cnt.append(dfs())
else:
break
cnt.sort()
s = 1
for c in cnt:
ans+=s
s+=c
cp+=1
return s
dfs()
print(ans)Первый тест совпадают с тестом из условия задачи. Баллы за него не начисляются.
Программа проверяется на \(40\) тестах. Успешное прохождение каждого теста оценивается в \(0{,}5\) балла. Если программа прошла все тесты, то начисляется еще 10 баллов.
В тестах №№ 2–11 длина строки не превосходит 300.
В тестах №№ 12–21 длина строки не превосходит 3000.
В тестах №№ 22–31 длина строки не превосходит 30000.






