Предметный тур. Физика. 3 этап
Сосуд доверху заполнили жидкостью плотности \(\rho = 1{,}2\) г/см\(^3\). Далее в него поместили шарик, объем которого в четыре раза меньше объема сосуда. Средняя плотность содержимого сосуда стала равна \(\rho_1 = 1{,}5\) г/см\(^3\). Определите плотность шарика \(\rho_{\text{ш}}\). Если вместо шарика в сосуд поместить кубик такого же объема, то средняя плотность содержимого сосуда станет равна \(\rho_2 = 1{,}7\) г/см\(^3\). Определите плотность кубика \(\rho_{\text{к}}\). Какой станет средняя плотность \(\rho_3\) содержимого сосуда, если в него поместить одновременно шарик и кубик?
Обозначим объем шарика и кубика за \(V\), тогда объем сосуда будет \(4V\). Для средней плотности содержимого сосуда и шарика запишем \[\rho_1 = \frac{\rho \cdot 3V + \rho_{\text{ш}}V}{4V} = \frac{3\rho + \rho_{\text{ш}}}{4}.\] Плотность шарика: \[\rho_{\text{ш}} = 4\rho_1 - 3\rho = 2{,}4~\text{г/см}^3.\] Для средней плотности содержимого сосуда и кубика запишем \[\rho_2 = \frac{\rho \cdot 3V + \rho_{\text{к}}V}{4V} = \frac{3\rho + \rho_{\text{к}}}{4}.\] Плотность кубика: \[\rho_{\text{к}} = 4\rho_2 - 3\rho = 3{,}2~\text{г/см}^3.\] Для средней плотности содержимого сосуда, шарика и кубика запишем \[\rho_3 = \frac{\rho \cdot 2V + \rho_{\text{ш}}V + \rho_{\text{к}}V}{4V} = \frac{2\rho + \rho_{\text{ш}} + \rho_{\text{к}}}{4}.\] Складывая два первых уравнения и вычитая третье уравнение, получим \[\rho_1 + \rho_2 - \rho_3 = \rho \quad \rightarrow \quad \rho_3 = \rho_1 + \rho_2 - \rho,\] \[\rho_3 = 2{,}0~\text{г/см}^3.\]
\(\rho_{\text{ш}} = 2{,}4\) г/см\(^3\), \(\rho_{\text{к}} = 3{,}2\) г/см\(^3\), \(\rho_3 = 2{,}0\) г/см\(^3\).
| Обозначим объем шарика и кубика за \(V\), тогда объем сосуда будет \(4V\) | 1 балл |
| \(\rho_1 = \frac{\rho \cdot 3V + \rho_{\text{ш}}V}{4V} = \frac{3\rho + \rho_{\text{ш}}}{4}\) | 3 балла |
| \(\rho_{\text{ш}} = 4\rho_1 - 3\rho = 2{,}4~\text{г/см}^3\) | 1 балл |
| \(\rho_2 = \frac{\rho \cdot 3V + \rho_{\text{к}}V}{4V} = \frac{3\rho + \rho_{\text{к}}}{4}\) | 3 балла |
| \(\rho_{\text{к}} = 4\rho_2 - 3\rho = 3{,}2~\text{г/см}^3\) | 1 балл |
| \(\rho_3 = \frac{\rho \cdot 2V + \rho_{\text{ш}}V + \rho_{\text{к}}V}{4V} = \frac{2\rho + \rho_{\text{ш}} + \rho_{\text{к}}}{4}\) | 3 балла |
| \(\rho_1 + \rho_2 - \rho_3 = \rho \rightarrow \rho_3 = \rho_1 + \rho_2 - \rho\) | 2 балла |
| \(\rho_3 = 2{,}0~\text{г/см}^3\) | 1 балл |
| Всего | 15 баллов |
Две нелинейных элемента имеют вольтамперные характеристики \(U_1 = \alpha_1I^2\) и \(U_2 = \alpha_2I^2\), где \(\alpha_1 = 200\) В/А\(^2\), \(\alpha_2 = 700\) В/А\(^2\). Элементы соединили последовательно и подключили к источнику с напряжением \(U = 2{,}25\) В.
- Определите мощности, выделяющиеся на нелинейных элементах.
Затем нелинейный элемент с вольтамперной характеристикой \(U_1 = \alpha_1I^2\), где \(\alpha_1 = 200\) В/А\(^2\) соединили последовательно с резистором с сопротивлением \(R = 90\) Ом и подключили к источнику с напряжением \(U = 18\) В.
- Определите ток \(I\) в полученной цепи.
- Определите мощности, выделяющиеся на нелинейном элементе \(P_{\text{НЭ}}\) и резисторе \(P_R\).
При последовательном соединении элементов в цепи для общего тока и общего напряжения имеем: \[I = I_1 = I_2,\] \[U = U_1 + U_2.\] Ток, текущий через нелинейные элементы: \[I = \left(\frac{U}{\alpha_1 + \alpha_2}\right)^{1/2},\] \[I = 50~\text{мА}.\] Мощности, выделяющиеся на нелинейных элементах: \[P = IU = \alpha I^3,\] \[P_1 = I_1U_1 = \alpha_1I^3 = 25~\text{мВт},\] \[P_2 = I_2U_2 = \alpha_2I^3 = 87{,}5~\text{мВт}.\]
При последовательном соединении нелинейного элемента и резистора имеем: \[U = \alpha_1I^2 + IR.\] Решая квадратное уравнение \(\alpha_1I^2 + IR - U = 0\), получим: \[I = \frac{-R \pm \sqrt{R^2 + 4\alpha_1U}}{2\alpha_1}.\] Так как \(I > 0\), то \(I = 0{,}15\) А. Мощность, выделяющаяся на нелинейном элементе: \[P_{\text{НЭ}} = IU_1 = \alpha_1I^3 = 0{,}675~\text{Вт}.\] Мощность, выделяющаяся на резисторе: \[P_R = I^2R = 2{,}025~\text{Вт}.\]
- \(P_1 = 25\) мВт, \(P_2 = 87{,}5\) мВт.
- \(I = 0{,}15\) А.
- \(P_{\text{НЭ}} = 0{,}675\) Вт, \(P_R = 2{,}025\) Вт.
| \(I = I_1 = I_2\) | 1 балл |
| \(U = U_1 + U_2\) | 1 балл |
| \(I = \left(\frac{U}{\alpha_1 + \alpha_2}\right)^{1/2}\) | 1 балл |
| \(I = 50\) мА | 1 балл |
| \(P = IU = \alpha I^3\) | 1 балл |
| \(P_1 = I_1U_1 = \alpha_1I^3 = 25\) мВт | 1 балл |
| \(P_2 = I_2U_2 = \alpha_2I^3 = 87{,}5\) мВт | 1 балл |
| \(U = \alpha_1I^2 + IR\) | 2 балла |
| \(I = \frac{-R \pm \sqrt{R^2 + 4\alpha_1U}}{2\alpha_1}\) | 2 балла |
| Так как \(I > 0\), то | 1 балл |
| \(I = 0{,}15\) А | 1 балл |
| \(P_{\text{НЭ}} = IU_1 = \alpha_1I^3 = 0{,}675\) Вт | 1 балл |
| \(P_R = I^2R = 2{,}025\) Вт | 1 балл |
| Всего | 15 баллов |
В сосуд поместили лед, имеющий температуру \(t_{\text{л}} = -6~°\)C. Затем в него налили воду при комнатной температуре \(t_{\text{в}} = 24~°\)C. В результате теплообмена в сосуде установилась температура \(t_1 = 6~°\)C. Определите, во сколько раз масса воды больше массы льда. Далее в сосуд налили еще столько же воды при комнатной температуре. Какая температура \(t_2\) установится в сосуде? Удельная теплоемкость льда \(c_{\text{л}} = 2100\) Дж/(кг\(\cdot°\)C), воды — \(c_{\text{в}} = 4200\) Дж/(кг\(\cdot°\)C), удельная теплота плавления льда \(\lambda = 340\) кДж/кг. Теплоемкостью сосуда и тепловыми потерями пренебречь.
Температура плавления льда \(t_0 = 0~°\)C.
Из уравнения теплового баланса для воды и льда: \[m_{\text{в}}c_{\text{в}}(t_{\text{в}} - t_1) = m_{\text{л}}c_{\text{л}}(t_0 - t_{\text{л}}) + m_{\text{л}}\lambda + m_{\text{л}}c_{\text{в}}(t_1 - t_0)\] найдем отношение массы воды к массе льда: \[\frac{m_{\text{в}}}{m_{\text{л}}} = \frac{-c_{\text{л}}t_{\text{л}} + \lambda + c_{\text{в}}t_1}{c_{\text{в}}(t_{\text{в}} - t_1)},\] \[\frac{m_{\text{в}}}{m_{\text{л}}} = 5.\]
При доливании воды из уравнения теплового баланса: \[m_{\text{в}}c_{\text{в}}(t_{\text{в}} - t_2) = (m_{\text{в}} + m_{\text{л}})c_{\text{в}}(t_2 - t_1)\] определим конечную температуру: \[t_2 = \frac{t_{\text{в}}\frac{m_{\text{в}}}{m_{\text{л}}} + t_1\left(\frac{m_{\text{в}}}{m_{\text{л}}} + 1\right)}{2\frac{m_{\text{в}}}{m_{\text{л}}} + 1},\] \[t_2 = 14{,}2~°\text{C}.\]
\(\dfrac{m_{\text{в}}}{m_{\text{л}}} = 5, t_2 = 14{,}2~°\text{C}\).
| Температура плавления льда \(t_0 = 0~°\)C | 2 балла |
| \(m_{\text{в}}c_{\text{в}}(t_{\text{в}} - t_1) = m_{\text{л}}c_{\text{л}}(t_0 - t_{\text{л}}) + m_{\text{л}}\lambda + m_{\text{л}}c_{\text{в}}(t_1 - t_0)\) | 4 балла |
| \(\frac{m_{\text{в}}}{m_{\text{л}}} = \frac{-c_{\text{л}}t_{\text{л}} + \lambda + c_{\text{в}}t_1}{c_{\text{в}}(t_{\text{в}} - t_1)}\) | 3 балла |
| \(\frac{m_{\text{в}}}{m_{\text{л}}} = 5\) | 2 балла |
| \(m_{\text{в}}c_{\text{в}}(t_{\text{в}} - t_2) = (m_{\text{в}} + m_{\text{л}})c_{\text{в}}(t_2 - t_1)\) | 4 балла |
| \(t_2 = \frac{t_{\text{в}}\frac{m_{\text{в}}}{m_{\text{л}}} + t_1\left(\frac{m_{\text{в}}}{m_{\text{л}}} + 1\right)}{2\frac{m_{\text{в}}}{m_{\text{л}}} + 1}\) | 3 балла |
| \(t_2 = 14{,}2~°\text{C}\) | 2 балла |
| Всего | 20 баллов |
Катер из пункта A в пункт B двигался со скоростью 40 м/мин. Далее из пункта B в пункт C он перемещался со скоростью 69 м/мин. А расстояние из пункта C в пункт D он преодолел со скоростью 60 м/мин.
Определите среднюю скорость катера на всем пути, если расстояние между пунктами A и B составляет 25% всего пути, а перемещение из пункта B в пункт C заняло третью часть всего времени движения.
Из условия задачи имеем:
движение из пункта A в пункт B (\(v_1 = 40\) м/мин) \(t_1 = \dfrac{S_1}{v_1} = \dfrac{S}{4v_1};\)
движение из пункта B в пункт C (\(v_2 = 69\) м/мин) \(S_2 = v_2t_2 = \dfrac{v_2t}{3};\)
движение из пункта C в пункт D (\(v_3 = 60\) м/мин) \(S_3 = S - S_1 - S_2 = \dfrac{3S}{4} - \dfrac{v_2t}{3};\) \(t_3 = \dfrac{S_3}{v_3} = \dfrac{3S}{4v_3} - \dfrac{v_2t}{3v_3}.\)
Общее время движения автомобиля \[t = t_1 + t_2 + t_3 = \frac{S}{4v_1} + \frac{t}{3} + \frac{3S}{4v_3} - \frac{v_2t}{3v_3}.\]
Так как \[v_{\text{ср}} = \frac{S}{t},\] то из уравнения \[1 = \frac{v_{\text{ср}}}{4v_1} + \frac{1}{3} + \frac{3v_{\text{ср}}}{4v_3} - \frac{v_2}{3v_3}\] получим \[v_{\text{ср}} = \frac{4v_1(v_2 + 2v_3)}{3(3v_1 + v_3)},\] \[v_{\text{ср}} = 56~\text{м/мин}.\]
\(v_{\text{ср}} = 56\) м/мин.
| \(t_1 = \frac{S_1}{v_1} = \frac{S}{4v_1}\) | 2 балла |
| \(S_2 = v_2t_2 = \frac{v_2t}{3}\) | 2 балла |
| \(S_3 = S - S_1 - S_2 = \frac{3S}{4} - \frac{v_2t}{3}\) | 3 балла |
| \(t_3 = \frac{S_3}{v_3} = \frac{3S}{4v_3} - \frac{v_2t}{3v_3}\) | 2 балла |
| \(t = t_1 + t_2 + t_3 = \frac{S}{4v_1} + \frac{t}{3} + \frac{3S}{4v_3} - \frac{v_2t}{3v_3}\) | 3 балла |
| \(v_{\text{ср}} = \frac{S}{t}\) | 2 балла |
| \(1 = \frac{v_{\text{ср}}}{4v_1} + \frac{1}{3} + \frac{3v_{\text{ср}}}{4v_3} - \frac{v_2}{3v_3}\) | 3 балла |
| \(v_{\text{ср}} = \frac{4v_1(v_2 + 2v_3)}{3(3v_1 + v_3)}\) | 5 баллов |
| \(v_{\text{ср}} = 56\) м/мин | 3 балла |
| Всего | 25 баллов |
В сосуд с вертикальными стенками и площадью основания \(S = 300\) см\(^2\) налили глицерин плотностью \(\rho_{\text{г}} = 1{,}2\) г/см\(^3\). Затем в него опустили плотик (\(\rho_{\text{п}} = 0{,}4\) г/см\(^3\)). В результате уровень глицерина в сосуде изменился на \(\Delta h = 1\) см. Определите объем плотика \(V_{\text{п}}\). Затем на плотик сверху положили кусок льда (\(\rho_{\text{л}} = 0{,}9\) г/см\(^3\)). В результате плотик погрузился в глицерин полностью, а лед — на половину своего объема. Определите объем льда \(V_{\text{л}}\). Определите окончательное изменение уровня глицерина в сосуде \(\Delta H\) (по отношению к начальному уровню), когда весь лед растает.
Из условия плавания плотика \[\rho_{\text{п}}V_{\text{п}}g = \rho_{\text{г}}S\Delta h g\] определим объем плотика: \[V_{\text{п}} = \frac{S\Delta h\rho_{\text{г}}}{\rho_{\text{п}}},\] \[V_{\text{п}} = 900~\text{см}^3.\] Из условия плавания плотика и льда \[\rho_{\text{п}}V_{\text{п}}g + \rho_{\text{л}}V_{\text{л}}g = \rho_{\text{г}}(V_{\text{п}} + 0{,}5V_{\text{л}})g\] определим объем льда: \[V_{\text{л}} = \frac{V_{\text{п}}(\rho_{\text{г}} - \rho_{\text{п}})}{\rho_{\text{л}} - 0{,}5\rho_{\text{г}}},\] \[V_{\text{л}} = 2400~\text{см}^3.\]
При таянии льда образуется вода плотности \(\rho_{\text{в}} = 1{,}0\) г/см\(^3\). Объем образовавшейся воды \[V_{\text{в}} = \frac{\rho_{\text{л}}V_{\text{л}}}{\rho_{\text{в}}} = 2160~\text{см}^3.\]
Так как плотность воды меньше плотности глицерина, то вся вода в сосуде расположится выше уровня глицерина. Так как объем воды больше объема плотика, а плотность плотика меньше плотности воды, то плотик будет плавать только в воде.
Таким образом, окончательное изменение уровня глицерина \[\Delta H = 0~\text{см}.\]
\(V_{\text{п}} = 900~\text{см}^3, V_{\text{л}} = 2400~\text{см}^3, \Delta H = 0~\text{см}\).
| \(\rho_{\text{п}}V_{\text{п}}g = \rho_{\text{г}}S\Delta h g\) | 3 балла |
| \(V_{\text{п}} = \frac{S\Delta h\rho_{\text{г}}}{\rho_{\text{п}}}\) | 3 балла |
| \(V_{\text{п}} = 900\) см\(^3\) | 2 балла |
| \(\rho_{\text{п}}V_{\text{п}}g + \rho_{\text{л}}V_{\text{л}}g = \rho_{\text{г}}(V_{\text{п}} + 0{,}5V_{\text{л}})g\) | 4 балла |
| \(V_{\text{л}} = \frac{V_{\text{п}}(\rho_{\text{г}} - \rho_{\text{п}})}{\rho_{\text{л}} - 0{,}5\rho_{\text{г}}}\) | 3 балла |
| \(V_{\text{л}} = 2400\) см\(^3\) | 2 балла |
| При таянии льда образуется вода плотности \(\rho_{\text{в}} = 1{,}0\) г/см\(^3\) | 1 балл |
| \(V_{\text{в}} = \frac{\rho_{\text{л}}V_{\text{л}}}{\rho_{\text{в}}} = 2160\) см\(^3\) | 2 балла |
| Так как плотность воды меньше плотности глицерина, то вся вода в сосуде расположится выше уровня глицерина; так как объем воды больше объема плотика, а плотность плотика меньше плотности воды, то плотик будет плавать только в воде | 2 балла |
| \(\Delta H = 0\) см | 3 балла |
| Всего | 25 баллов |
Мячик бросили с воздушного шара, находящегося в покое на высоте \(H\), со скоростью \(v_0 = 20\) м/с под углом \(\alpha = 30°\) к горизонту. Через время \(t = 2\) c мячик ударился о землю. Определите, с какой скоростью \(v\) и под каким углом \(\beta\) к горизонту мячик упал на землю. На какой высоте \(H\) находился воздушный шар?
Предположим, что мячик бросили под углом к горизонту вверх. Уравнения движения мячика по вертикальной оси: \[y = H + v_0\sin\alpha t - gt^2/2.\] В момент падения мячика на землю \(y = 0\), таким образом: \[H = gt^2/2 - v_0\sin\alpha t = 0,\] что противоречит условию задачи.
Следовательно, мячик бросили под углом к горизонту вниз. Уравнения движения мячика по вертикальной оси \[y = H - v_0\sin\alpha t - gt^2/2.\]
Высота, с которой бросили мячик \[H = gt^2/2 + v_0\sin\alpha t = 40~\text{м}.\]
Проекция скорости мячика при падении на землю на горизонтальную ось \[v_x = v_0\cos\alpha \approx 17{,}3~\text{м/с}.\]
Проекция скорости мячика при падении на землю на вертикальную ось \[v_y = -v_0\sin\alpha - gt = -30~\text{м/с}.\]
Скорость падения мячика на землю \[v = (v_x^2 + v_y^2)^{1/2} \approx 34{,}6~\text{м/с}.\]
Угол падения мячика на землю \[\operatorname{tg}\beta = |v_y|/v_x \approx 1{,}73\quad (\beta = 60°).\]
Примечание
Скорость падения мячика на землю можно найти из закона сохранения энергии \(mv_0^2/2 + mgH = mv^2/2 \rightarrow v = (v_0^2 +2gH)^{1/2} \approx 34{,}6\) м/с.
\(H = 40~\text{м}, v \approx 34{,}6~\text{м/с}, \operatorname{tg}\beta \approx 1{,}73~ (\beta = 60°)\).
| \(y = H + v_0\sin\alpha t - gt^2/2\) | 2 балла |
| \(H = gt^2/2 - v_0\sin\alpha t = 0\), что противоречит условию задачи | 1 балл |
| \(y = H - v_0\sin\alpha t - gt^2/2\) | 2 балла |
| Высота, с которой бросили мячик \(H = gt^2/2 + v_0\sin\alpha t = 40\) м | 2 балла |
| \(v_x = v_0\cos\alpha \approx 17{,}3\) м/с | 1 балл |
| \(v_y = -v_0\sin\alpha - gt = -30\) м/с | 1 балл |
| \(v = (v_x^2 + v_y^2)^{1/2} \approx 34{,}6\) м/с | 3 балла |
| \(\operatorname{tg}\beta = |v_y|/v_x \approx 1{,}73 ~(\beta = 60°)\) | 3 балла |
| Всего | 15 баллов |
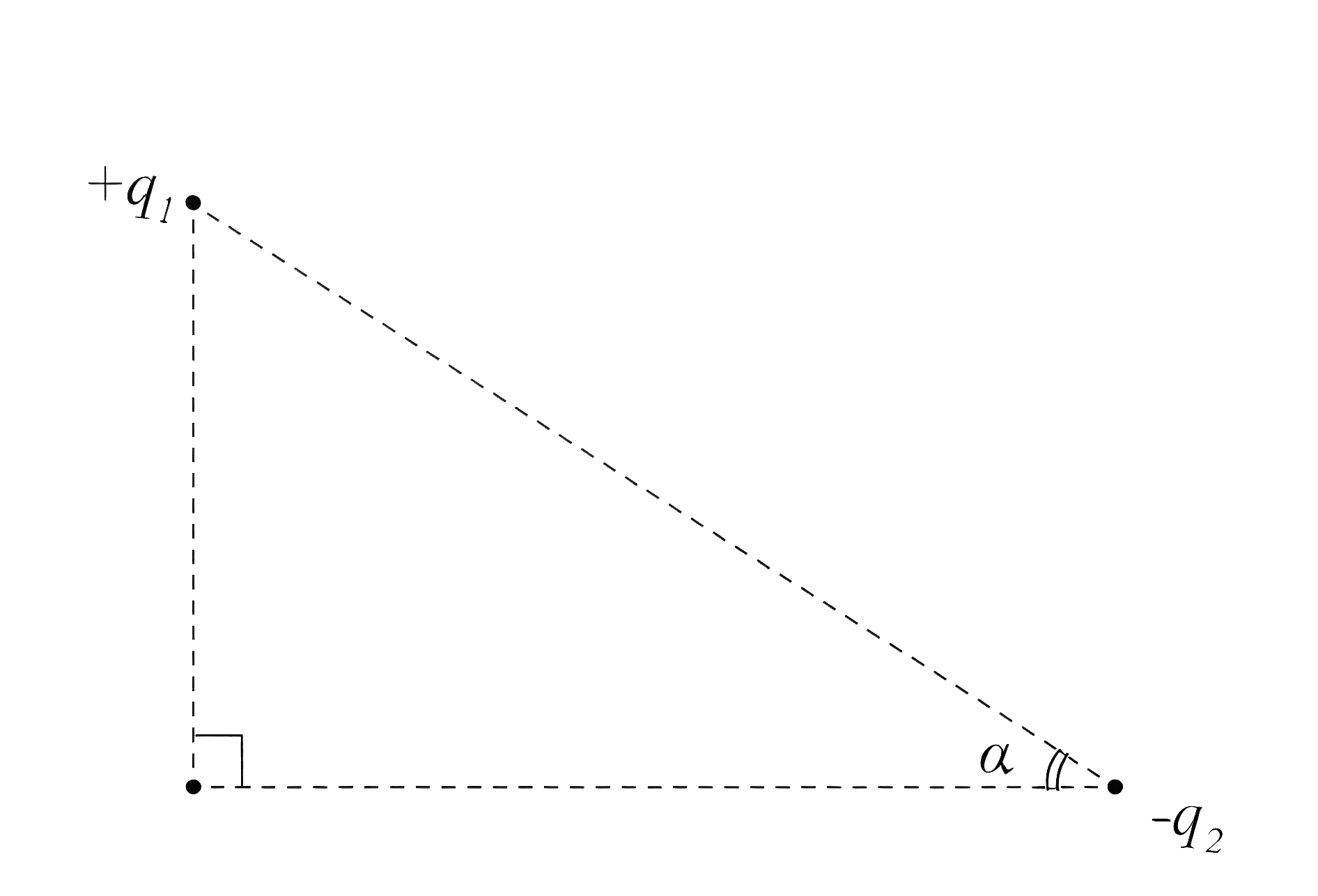
Точечные заряды \(+q_1\) и \(-q_2\) поместили в вершины прямоугольного треугольника, лежащих на его гипотенузе. Заряд \(-q_2\) находится в вершине треугольника, угол которого равен \(\alpha = 30°\). При каком отношении модулей зарядов \(q_2/q_1\) напряженность поля в третьей вершине треугольника будет направлена параллельно гипотенузе?
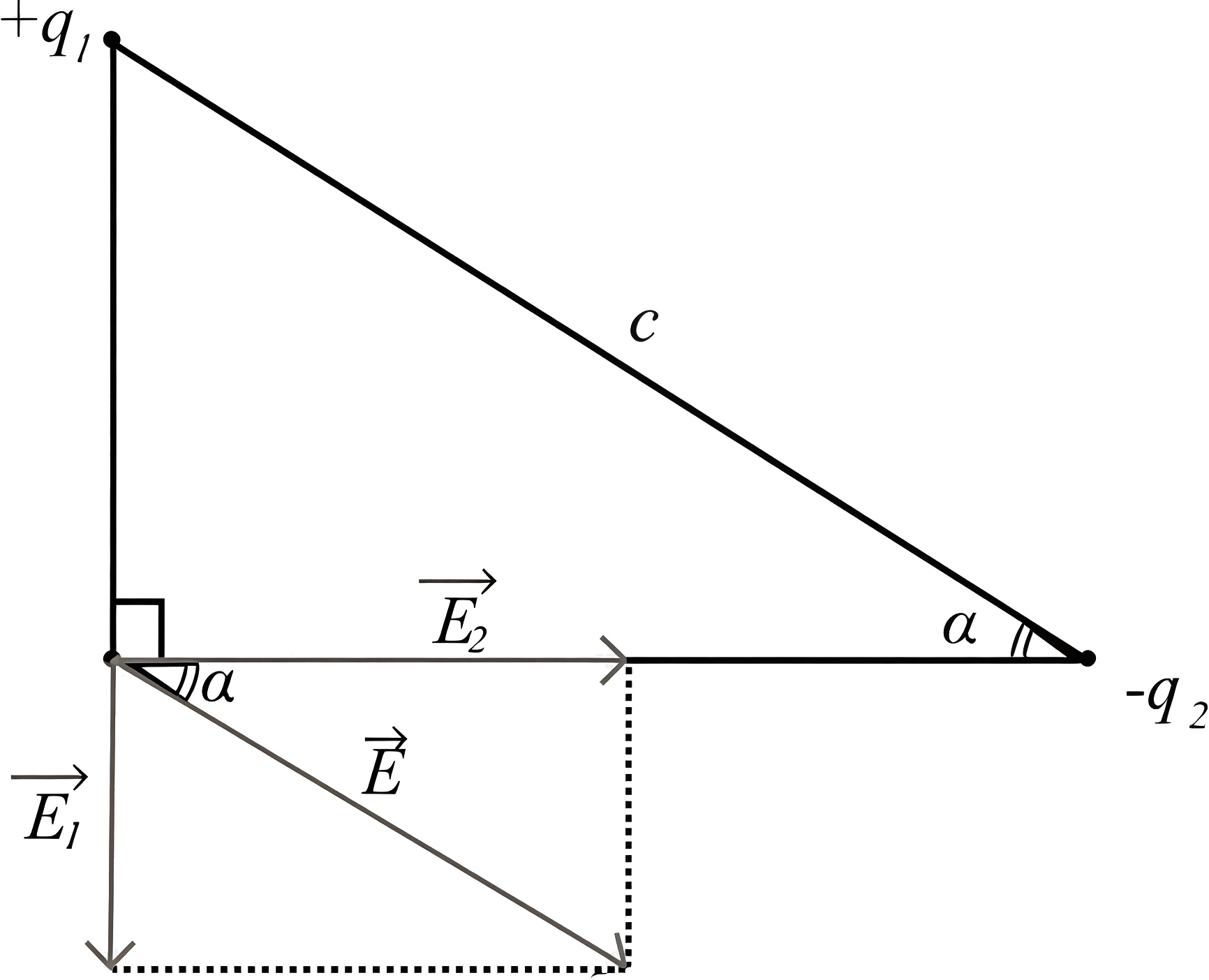
Обозначим: \(c\) — гипотенуза прямоугольного треугольника. Поле, создаваемое зарядом \(+q_1\), в вершине прямого угла \[E_1 = kq_1/(c \sin\alpha)^2.\]
Поле, создаваемое зарядом \(-q_2\), в вершине прямого угла \[E_2 = kq_2/(c \cos\alpha)^2.\]
Используя принцип суперпозиции \(\vec{E} = \vec{E_1} + \vec{E_2}\), определим напряженность электрического поля в вершине прямого угла.
Так как треугольник прямоугольный и поле \(\vec{E}\) направлено параллельно гипотенузе, то \(\operatorname{tg}\alpha = E_1/E_2\).
Из уравнения \(\operatorname{tg}\alpha = E_1/E_2 = (q_1 \cos^2\alpha)/(q_2 \sin^2\alpha) = (q_1/q_2)\operatorname{ctg}^2\alpha\) получим \[q_2/q_1 = \operatorname{ctg}^3\alpha = 3\sqrt{3} \approx 5{,}2.\]
\(q_2/q_1 = 3\sqrt{3} \approx 5{,}2\).
| \(E_1 = kq_1/(c \sin\alpha)^2\) | 2 балла |
| \(E_2 = kq_2/(c \cos\alpha)^2\) | 2 балла |
| \(\vec{E} = \vec{E_1} + \vec{E_2}\) | 3 балла |
| \(\operatorname{tg}\alpha = E_1/E_2\) | 2 балла |
| \(\operatorname{tg}\alpha = E_1/E_2 = (q_1 \cos^2\alpha)/(q_2 \sin^2\alpha) = (q_1/q_2)\operatorname{ctg}^2\alpha\) | 3 балла |
| \(q_2/q_1 = \operatorname{ctg}^3\alpha = 3\sqrt{3} \approx 5{,}2\) | 3 балла |
| Всего | 15 баллов |
Две нелинейных элемента имеют вольтамперные характеристики \(U_1 = \alpha_1I^2\) и \(U_2 = \alpha_2/I^2\), где \(\alpha_1 = 300\) В/A\(^2\), \(\alpha_2 = 0{,}03\) В\(\cdot\)А\(^2\). Элементы соединили последовательно и подключили к источнику с напряжением \(U\).
- При каком напряжением \(U_a\) источника по цепи идет ток \(I_a = 200\) мА?
- При каком минимальном напряжении \(U_{\text{min}}\) в цепи может течь ток?
- Определите мощности, выделяющиеся на элементах при \(U = U_{\text{min}}\).
При последовательном соединении элементов в цепи для общего тока и общего напряжения имеем \[\begin{gather} I = I_1 = I_2;\\ U = U_1 + U_2;\\ U_a = \alpha_1I_a^2 + \alpha_2/I_a^2;\\ U_a = 12,75~\text{В}. \end{gather}\]
Из уравнения \(U = \alpha_1I^2 + \alpha_2/I^2\) получим биквадратное уравнение для тока \(\alpha_1I^4 - UI^2 + \alpha_2 = 0\).
Напряжение будет минимальным, если уравнение будет иметь один корень, то есть дискриминант будет равен нулю: \[\begin{gather} D = U^2 - 4\alpha_1\alpha_2 = 0;\\ U_{\text{min}} = (4\alpha_1\alpha_2)^{1/2} = 6~\text{В};\\ I_{\text{min}} = (U/(2\alpha_1))^{1/2} = 100~\text{мА}. \end{gather}\]
Мощность, выделяющаяся на нелинейных элементах: \[\begin{gather} P_1 = I_1U_1 = \alpha_1I_{\text{min}}^3 = 300~\text{мВт};\\ P_2 = I_2U_2 = \alpha_2/I_{\text{min}} = 300~\text{мВт}. \end{gather}\]
\(U_a = 12{,}75~\text{В}, U_{\text{min}} = 6~\text{В}, P_1 = 300~\text{мВт}, P_2 = 300~\text{мВт}\).
| \(I = I_1 = I_2\) | 2 балла |
| \(U = U_1 + U_2\) | 2 балла |
| \(U_a = \alpha_1I_a^2 + \alpha_2/I_a^2\) | 2 балла |
| \(U_a = 12{,}75\) В | 2 балла |
| \(\alpha_1I^4 - UI^2 + \alpha_2 = 0\) | 2 балла |
| \(D = U^2 - 4\alpha_1\alpha_2 = 0\) | 2 балла |
| \(U_{\text{min}} = (4\alpha_1\alpha_2)^{1/2} = 6\) В | 4 балла |
| \(I_{\text{min}} = (U/(2\alpha_1))^{1/2} = 100\) мА | 2 балла |
| \(P_1 = I_1U_1 = \alpha_1I_{\text{min}}^3 = 300\) мВт | 2 балла |
| \(P_2 = I_2U_2 = \alpha_2/I_{\text{min}} = 300\) мВт | 2 балла |
| Всего | 20 баллов |
Грузики массами \(m_1 = m\) и \(m_2 = 2m\) прикрепили к концам невесомой нерастяжимой нити, перекинутой через блок массой \(M = 3m\). К блоку прикладывают силу \(F = 8{,}5mg\), направленную вертикально вверх. Определите в установившемся режиме движения силу натяжения нити, ускорения грузиков и блока. Ускорение свободного падения \(g\).
Обозначим: \(T\) — сила натяжения нити, \(a_1\), \(a_2\) и \(a\) — ускорения грузов и блока соответственно направленные вертикально вверх.
Запишем уравнения движения блока и грузов: \[\begin{gather} Ma = F - Mg - 2T;\\ m_1a_1 = T - m_1g;\\ m_2a_2 = T - m_2g. \end{gather}\]
Так как блок связан с грузами нерастяжимой нитью, то его ускорение связано с ускорениями грузов: \[a = (a_1 + a_2)/2.\]
Решая систему записанных уравнений, получим: \[\begin{gather} T = 4/17\cdot F = 2mg;\\ a = g/2;\\ a_1 = g;\\ a_2 = 0. \end{gather}\]
\(T = 2mg\), \(a_1 = g\), \(a_2 = 0\), \(a = g/2\).
| \(Ma = F - Mg - 2T\) | 3 балла |
| \(m_1a_1 = T - m_1g\) | 3 балла |
| \(m_2a_2 = T - m_2g\) | 3 балла |
| \(a = (a_1 + a_2)/2\) | 4 балла |
| \(T = 4/17F = 2mg\) | 3 балла |
| \(a = g/2\) | 3 балла |
| \(a_1 = g\) | 3 балла |
| \(a_2 = 0\) | 3 балла |
| Всего | 25 баллов |
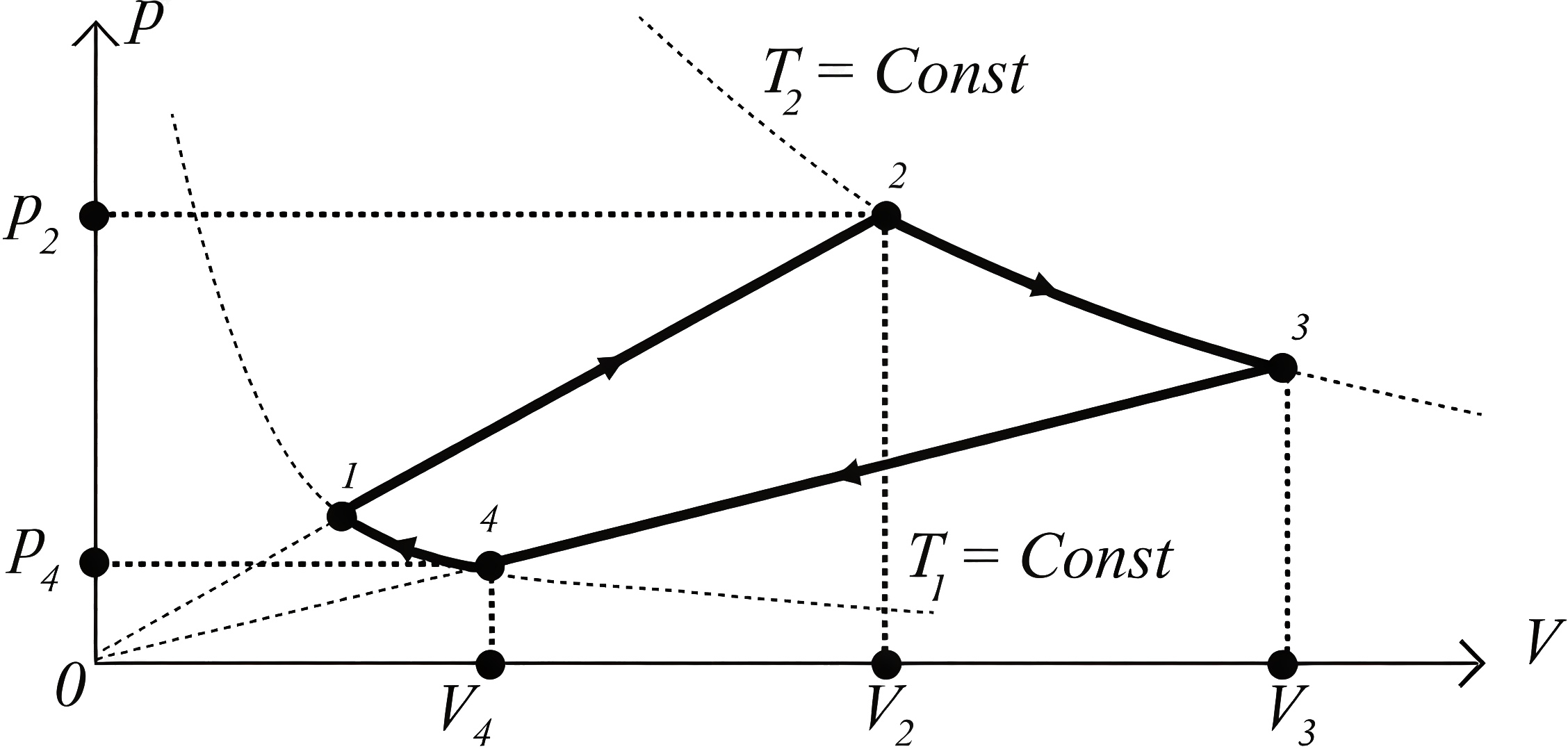
Идеальный газ участвует в замкнутом процессе \(1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1\). На участках \(1 \rightarrow 2\) и \(3 \rightarrow 4\) температура газа пропорциональна квадрату объема, а процессы \(2 \rightarrow 3\) и \(4 \rightarrow 1\) изотермические. Найдите максимальное давление \(p_{\text{max}}\) газа в цикле, если известно, что минимальное давление \(p_{\text{min}} = 1\) атм, объемы в состояниях 2 и 4 равны \(V_2 = 60\) дм\(^3\) и \(V_4 = 30\) дм\(^3\), а максимальный объем \(V_{\text{max}} = 90\) дм\(^3\).
Уравнение состояния идеального газа \[pV = \nu RT.\]
Для процессов, в которых температура газа пропорциональна квадрату объема (\(T = \alpha V^2\)) получим \[pV = \nu R\alpha V^2 \rightarrow p = \alpha\nu RV = \beta V\] (давление пропорционально объему).
Рассмотрим процесс в осях \(pV\).
Исходя из данных задачи, имеем \[\begin{gather} p_4 = p_{\text{min}},\\ p_2 = p_{\text{max}},\\ V_3 = V_{\text{max}}. \end{gather}\]
Так как на участке \(3 \rightarrow 4\) давление пропорционально объему, то \[p_3/p_4 = V_3/V_4 \rightarrow p_3 = p_4V_3/V_4 = p_{\text{min}}V_{\text{max}}/V_4.\]
Так как участок \(2 \rightarrow 3\) — изотермический, то \[p_2V_2 = p_3V_3\quad (\text{или}~ p_{\text{max}}V_2 = p_3V_{\text{max}})\]
Окончательно получим \[\begin{gather} p_{\text{max}} = p_3V_{\text{max}}/V_2 = p_{\text{min}}(V_{\text{max}})^2/(V_2V_4),\\ p_{\text{max}} = 4,5~\text{атм}. \end{gather}\]
\(p_{\text{max}} = 4{,}5~\text{атм}\).
| \(p_4 = p_{\text{min}}\) | 2 балла |
| \(p_2 = p_{\text{max}}\) | 2 балла |
| \(V_3 = V_{\text{max}}\) | 2 балла |
| \(p_3/p_4 = V_3/V_4 \rightarrow p_3 = p_4V_3/V_4 = p_{\text{min}}V_{\text{max}}/V_4\) | 4 балла |
| \(p_2V_2 = p_3V_3\quad (\text{или}\quad p_{\text{max}}V_2 = p_3V_{\text{max}})\) | 4 балла |
| \(p_{\text{max}} = p_3V_{\text{max}}/V_2 = p_{\text{min}}(V_{\text{max}})^2/(V_2V_4)\) | 3 балла |
| \(p_{\text{max}} = 4{,}5\) атм | 2 балла |
| Всего | 25 баллов |