Предметный тур. Информатика. 3 этап

Информатика. 8–11 классы

Задача 1.1.(10 баллов)

Повседневная активность жителей города

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

В современном городе люди используют разные способы передвижения: пешком, на велосипеде или на общественном транспорте. В городском исследовании собрали данные о том, какими из этих способов передвижения пользуется каждый житель.

Требуется провести анализ собранных данных и ответить на некоторые вопросы:

Сколько жителей пользуются ровно двумя способами передвижения?
Сколько жителей активно используют все три способа?
Какой способ передвижения является самым популярным?

Формат входных данных

Первая строка входных данных содержит целое число \(N\) — количество жителей, принявших участие в исследовании (\(1 \leqslant N \leqslant 1000\)).

Следующие \(N\) строк содержат по три символа 1 или 0, описывающих способы передвижения для каждого жителя:

первый символ — ходит пешком;
второй символ — пользуется велосипедом;
третий символ — использует общественный транспорт.

Формат выходных данных

Выведите три числа через пробел:

количество жителей, использующих ровно два способа передвижения;
количество жителей, использующих все три способа передвижения;
индекс самого популярного способа передвижения: 1 (пешком), 2 (велосипед), 3 (общественный транспорт); если популярность одинакова, выведите минимальный индекс.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	8 110 101 011 111 100 010 001 110	4 1 1

Решение

Для решения задачи нужно выполнить несколько шагов.

Даны N строк, каждая из которых представляет данные о том, как конкретный житель города передвигается, с помощью трех символов:
- 1 означает использование способа передвижения;
- 0 — не использование.
Каждая строка имеет три символа, что соответствует трем способам передвижения:
- первый символ — житель города передвигается пешком;
- второй символ — житель города передвигается на велосипеде;
- третий символ — житель города передвигается на общественном транспорте.
Нахождение количества жителей, использующих ровно два способа передвижения.

Можно посчитать количество единиц в каждой строке. Если их ровно два, это значит, что человек использует два способа передвижения.
Нахождение количества жителей, использующих все три способа передвижения.

Если в строке все символы равны единице, это означает, что человек использует все три способа передвижения.
Нахождение самого популярного способа передвижения. Для каждого способа передвижения (пешком, на велосипеде, на транспорте) считаем, сколько людей использует этот способ.

После этого находим максимальное значение и выводим соответствующий индекс. Если популярность равна для нескольких способов, выводим минимальный индекс.

Пример программы-решения

Ниже представлено решение на языке Python.

Python

# Ввод данных
n = int(input())  # Количество жителей города

# Инициализация счетчиков
count_two_modes = 0  # Жители, использующие ровно два способа передвижения
count_three_modes = 0  # Жители, использующие все три способа передвижения
walk_count = 0  # Количество жителей, ходящих пешком
bike_count = 0  # Количество жителей, использующих велосипед
transport_count = 0  # Количество жителей, пользующихся общественным транспортом

# Обработка данных о жителях
for _ in range(n):
    modes = input().strip()  # Строка из трех символов (например, "110")
    walk = int(modes[0])  # Пешком
    bike = int(modes[1])  # Велосипед
    transport = int(modes[2])  # Общественный транспорт

    # Подсчет популярности каждого способа передвижения
    walk_count += walk
    bike_count += bike
    transport_count += transport

    # Подсчет жителей, использующих ровно два способа передвижения
    if walk + bike + transport == 2:
        count_two_modes += 1

    # Подсчет жителей, использующих все три способа передвижения
    if walk + bike + transport == 3:
        count_three_modes += 1

# Определение самого популярного способа передвижения
most_popular = 1  # По умолчанию: пешком
max_count = walk_count

if bike_count > max_count:
    most_popular = 2  # Велосипед
    max_count = bike_count

if transport_count > max_count:
    most_popular = 3  # Общественный транспорт

# Вывод результатов
print(count_two_modes, count_three_modes, most_popular)

Задача 1.2.(15 баллов)

Загадочный пассажиропоток

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

В городе есть \(N\) автобусных остановок, расположенных вдоль одной улицы. Для анализа пассажиропотока транспортная компания хочет выяснить, на скольких отрезках подряд суммарное число пассажиров в автобусах равно \(P\).

Каждый день сотрудники собирают данные о числе пассажиров в автобусах, которые находятся на остановках. Теперь они просят помочь с анализом данных.

Формат входных данных

В первой строке содержатся два целых числа \(N\) и \(P\) (\(1 \leqslant N \leqslant 10000\), \(1 \leqslant P \leqslant 10^6\)) — количество остановок и целевое число пассажиров.

Во второй строке записаны \(N\) чисел — количество пассажиров на автобусах у каждой остановки. Числа находятся в диапазоне от 1 до 999 включительно.

Формат выходных данных

Выведите одно число — количество отрезков остановок, на которых суммарное число пассажиров равно \(P\).

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	6 25 5 10 10 5 15 10	3
2	5 12 3 4 5 6 7	1

Примечания

В первом примере существуют три подходящих отрезка:

(5, 10, 10) — с первой по третью остановку;
(10, 10, 5) — со второй по четвертую остановку;
(15, 10) — с пятой по шестую остановку.

Во втором примере единственный подходящий отрезок: (3, 4, 5) — с первой по третью остановку.

Решение

Программа использует метод двух указателей для эффективного поиска всех подотрезков массива, сумма которых равна заданному числу \(P\).

Пример программы-решения

Ниже представлено решение на языке Python.

Python

def count_subarrays_with_sum(n, k, numbers):
    left = 0
    current_sum = 0
    count = 0
    
    for right in range(n):
        current_sum += numbers[right]
        
        while current_sum > k and left <= right:
            current_sum -= numbers[left]
            left += 1
        
        if current_sum == k:
            count += 1
    
    return count

# Чтение входных данных
n, k = map(int, input().split())
numbers = list(map(int, input().split()))

# Вывод результата
print(count_subarrays_with_sum(n, k, numbers))

Задача 1.3.(20 баллов)

Фестиваль и транспортный коллапс

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

В городе проходит масштабный фестиваль, из-за которого движение по одной из центральных улиц ограничено: в 1 мин может проезжать не более \(b\) машин. Однако поток машин на улицу продолжается, и образуется пробка.

В начале \(i\)-й минуты на улицу въезжает \(a_i\) машин, и они становятся в очередь для проезда (пробку).

За 1 мин по улице могут проехать не более \(b\) машин. Остальные остаются ждать в пробке.

В конце \(n\)-й минуты организаторы фестиваля полностью перекрывают движение по улице. Все автомобили, оставшиеся в пробке, стоят на месте еще 1 мин, после чего отправляются в объезд.

Вычислите суммарное время, которое все автомобили провели в пробке на этой улице.

Формат входных данных

В первой строке даны два целых числа \(n\) и \(b\) — количество минут, в течение которых улица остается открытой, и количество машин, которые могут проехать за 1 мин (\(1 \leqslant n \leqslant 10000\), \(1 \leqslant b \leqslant 10^6\)).

Во второй строке даны n целых чисел \(a_i\) — количество машин, которые въезжают на улицу в начале \(i\)-й минуты (\(0 \leqslant a_i \leqslant 10^6\)).

Формат выходных данных

Выведите одно целое число — суммарное время, которое все машины провели в пробке.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	3 4 1 5 9	22

Примечания

Улица открыта в течение 3 мин.

За 1 мин может проехать 4 машины.

Первый этап (первая минута):

Въезжает 1 машина.
Время в пробке: 1 машина \(\times\) 1 мин = 1 мин.
За 1 мин 1 машина успевает проехать, к концу минуты пробки нет (0 машин).

Второй этап (вторая минута):

Въезжает 5 машин.
Время в пробке: 5 машин \(\times\) 1 мин = 5 мин.
За 1 мин 4 машины уезжают, к концу минуты 1 машина остается в пробке.

Третий этап (третья минута):

В пробке остается 1 машина, въезжают еще 9 машин (всего 10 машин).
Время в пробке: 10 машин \(\times\) 1 мин = 10 мин.
За 1 мин 4 машины уезжают, к концу минуты 6 машин остаются в пробке.

Четвертый этап (улица перекрывается):

Оставшиеся 6 машин стоят еще 1 мин.
Время в пробке: 6 машин \(\times\) 1 мин = 6 мин.

Общий итог (суммарно по этапам):

\(1 + 5 + 10 + 6 = 22\) мин.

Решение

Для каждой минуты поддерживаем переменную очередь, которая показывает, сколько машин скопилось в пробке.

В начале \(i\)-й минуты добавляем новые машины в очередь.

Затем выпускаем из пробки \(min(b, \text{ очередь})\) машин.

Оставшиеся машины остаются ждать.

Каждая машина добавляет к общему времени количество минут, которые она пробыла в пробке.

После завершения \(n\)-й минуты все оставшиеся в пробке машины добавляют к времени еще 1 мин, потому что они ждут перед объездом.

Пример программы-решения

Ниже представлено решение на языке Python.

Python

def total_wait_time(n, b, arrivals):
    queue = 0  # количество машин в пробке
    total_time = 0  # суммарное время пребывания машин в пробке
    
    for i in range(n):
        queue += arrivals[i]  # машины въезжают на улицу в начале i-й минуты
        passed = min(queue, b)  # за минуту могут проехать не более b машин
        total_time += queue  # все машины в пробке ждут минимум 1 минуту
        queue -= passed  # убираем машины, которые смогли проехать
    
    # После n минут улицу перекрывают, оставшиеся машины ждут еще 1 минуту
    total_time += queue  # добавляем время ожидания перед объездом
    
    return total_time

# Чтение входных данных
n, b = map(int, input().split())
arrivals = list(map(int, input().split()))

# Вычисление и вывод результата
print(total_wait_time(n, b, arrivals))

Задача 1.4.(25 баллов)

Восстание древних механизмов

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

В далеком будущем, на одной из колонизированных планет, археологи обнаружили древний механизм — цепь боевых роботов. Эти роботы стоят вдоль разрушенного транспортного туннеля. Каждый робот расположен на координате \(x_i\) и имеет энергетический заряд \(h_i\), который определяет его зону влияния.

Любопытные инженеры решили активировать цепь, чтобы изучить ее работу. Они отправили тестовый сигнал первому роботу на левой стороне туннеля. При активации робот выпускает волну энергии, которая включает всех роботов, расположенных в пределах \(x_i + h_i\). Каждый активированный робот в свою очередь создает новую волну энергии, распространяя эффект дальше.

Однако планам инженеров помешал взлом хакером системы. Хакер отправил сигнал активации последнему роботу на правой стороне туннеля. Этот робот тоже выпустил энергетическую волну, но она распространяется назад, активируя роботов на координатах \(x_i - h_i\).

Теперь две волны активации движутся навстречу друг другу. Роботы, оказавшиеся в зоне действия обеих волн, продолжают распространять энергию в обе стороны. Определите, сколько всего роботов будет активировано в результате этой цепной реакции.

Формат входных данных

Первая строка содержит одно целое число \(N\) (\(2 \leqslant N \leqslant 10^4\)) — количество боевых роботов.

Следующие \(2N\) строк содержат два набора целых чисел.

Первые \(N\) строк содержат координаты роботов \(x_i\) (\(0 \leqslant x_i \leqslant 10^9\)).

Следующие \(N\) строк содержат энергетический заряд роботов \(h_i\) (\(0 \leqslant h_i \leqslant 10^9\)). Гарантируется, что координаты образуют возрастающую последовательность (никакие два робота не имеют одинаковых координат).

Формат выходных данных

Выведите одно целое число — общее число роботов будет активировано в результате цепной реакции.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	4 1 5 7 8 2 3 1 1	3

Примечания

Рис. 1.1.

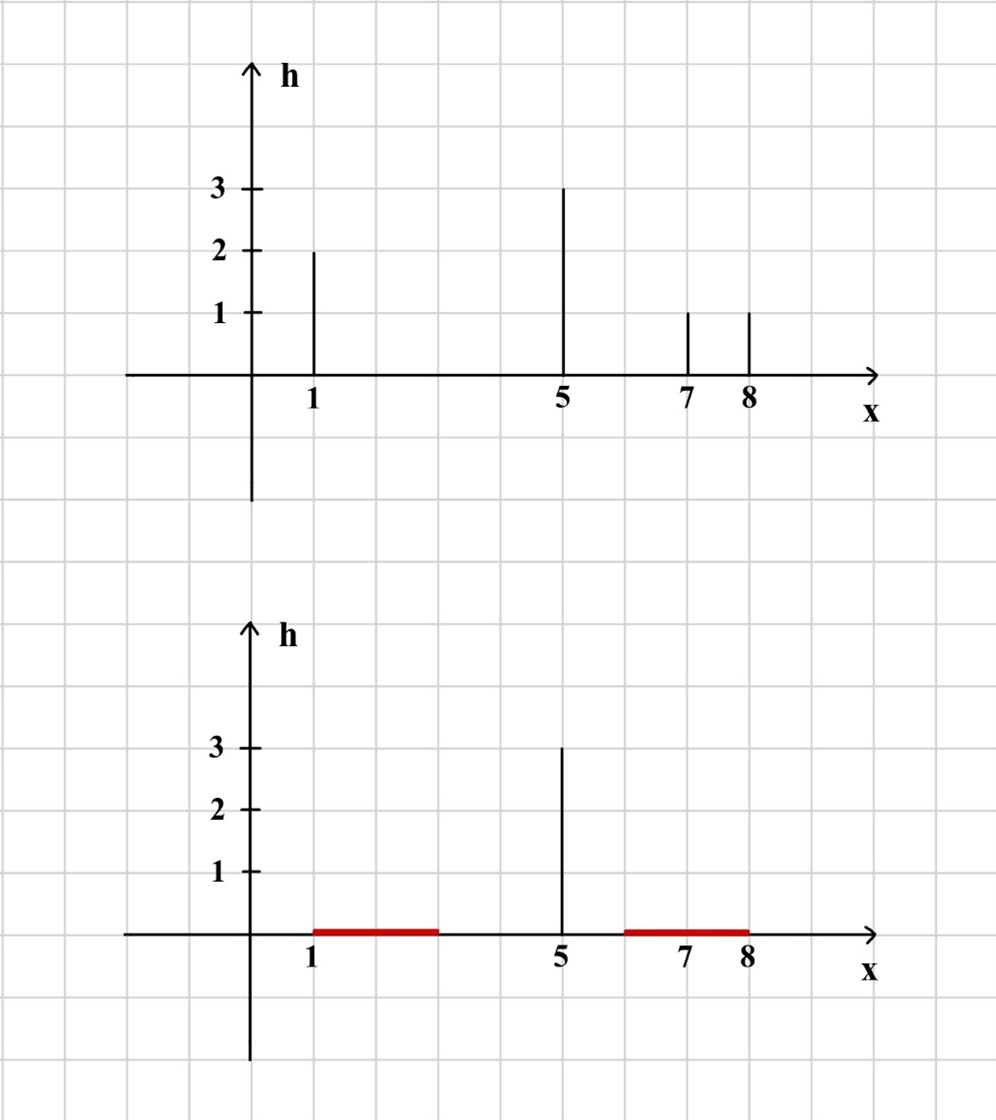
В примере заряд первого робота, равный 2, не достигнет следующего, поэтому слева будет активирован только первый робот (от тестового сигнала инженеров). Заряд робота, которого активировали хакеры и стоящего на координате 8, достигнет робота, стоящего на координате 7, заряд которого равный 1, в свою очередь, не достигнет робота на координате 5. На рис. 1.1 показаны роботы до активации и их итоговое состояние (красным отмечены места распространения энергетической волны).

Решение

Ввод данных — считывается количество роботов \(N\), их позиции \(x\), и заряды \(h\).
Проведем симуляцию энергетической волны с левой стороны. Цикл while проходит по роботам слева направо, обновляя border, который отслеживает дальность воздействия заряда. Цикл продолжается, пока текущая позиция робота \(x[i]\) находится в пределах границы border.
Проведем симуляцию энергетической волны с правой стороны. Аналогично цикл while идет справа налево, уменьшая border, и учитывает роботов, попавших под воздействие правой волны.
Суммируется количество роботов, попавших под воздействие волны слева (\(i\)) и справа (\(n-1-j\)). Итоговое значение ограничивается \(N\) (на случай, если обе волны перекрывают друг друга).

Пример программы-решения

Ниже представлено решение на языке Python.

Python

# Ввод данных
n = int(input("Введите количество роботов: "))
x = [int(input(f"Введите координату {i + 1}: ")) for i in range(n)]
h = [int(input(f"Введите заряд {i + 1}: ")) for i in range(n)]

# Волна с левой стороны
border = x[0]
i = 0
while i < n and x[i] <= border:
    border = max(border, x[i] + h[i])
    i += 1

# Волна с правой стороны
border = x[-1]
j = n - 1
while j >= 0 and x[j] >= border:
    border = min(border, x[j] - h[j])
    j -= 1

# Итоговый подсчет
result = min(n, i + (n - 1 - j))
print("Общее количество активированных роботов:", result)

Задача 1.5.(30 баллов)

Город мечты

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

Городской архитектор Петр работает над развитием умного города. Ему предстоит выбрать \(n\) проектов для реализации: это могут быть парки, транспортные развязки, велодорожки, пешеходные зоны и др.

Каждый проект обладает дизайнерской привлекательностью и функциональной полезностью.

Петр принимает решения в течение \(n\) дней. В зависимости от настроения он выбирает один из двух вариантов:

Если он в настроении создавать красоту, то выбирает проект с максимальной дизайнерской привлекательностью.
Если он в настроении делать город удобнее, то выбирает проект с максимальной функциональной полезностью.

Если среди доступных проектов несколько с одинаковым значением выбранного параметра, Петр отдаст предпочтение проекту с наибольшим значением второго параметра. Если и этот параметр совпадает, он выберет тот, что был предложен раньше.

Задача — определить порядок, в котором архитектор реализует проекты.

Формат входных данных

В первой строке вводится одно целое число \(n\) — количество городских проектов (\(1 \leqslant n \leqslant 10^4\)).

Во второй строке через пробел перечислены \(n\) целых чисел \(a_i\) — значения дизайнерской привлекательности проектов (\(1 \leqslant a_i \leqslant 10^9\)).

В третьей строке в том же формате даны \(n\) целых чисел \(b_i\) — значения функциональной полезности проектов (\(1 \leqslant b_i \leqslant 10^9\)).

В последней строке через пробел перечислены \(n\) целых чисел \(p_i\) — настроение архитектора в каждый из дней.

Если \(p_i = 1\), Петр выбирает проект с максимальной функциональной полезностью (\(b_i\)).
Если \(p_i = 0\), Петр выбирает проект с максимальной дизайнерской привлекательностью (\(a_i\)).

Формат выходных данных

Выведите \(n\) различных целых чисел от 1 до \(n\), разделенных пробелами.

Число на \(i\)-й позиции означает номер проекта, который Петр реализует в \(i\)-й день.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	5 1 2 3 4 5 5 4 3 2 1 1 0 1 0 0	1 5 2 4 3
2	6 3 10 6 2 10 1 3 5 10 7 5 9 0 0 1 1 0 1	2 5 3 6 1 4

Решение

Для решения задачи используем две приоритетные очереди (max-heap), чтобы эффективно выбирать алгоритмы в зависимости от настроения Петра.

Подготовка данных

Создаем две кучи:
- interest_heap — хранит алгоритмы, отсортированные по убыванию интересности (если интересности равны, сортируем по полезности, а затем — по индексу);
- utility_heap — хранит алгоритмы, отсортированные по убыванию полезности (если полезности равны, сортируем по интересности, а затем — по индексу).
Преобразуем списки в кучи (heapq.heapify), что позволяет быстро извлекать наибольший элемент.
Обход дней и выбор алгоритмов

Для каждого дня проверяем настроение Петра:
- если \(p_i\) = 1, выбираем алгоритм с максимальной полезностью (utility_heap);
- если \(p_i\) = 0, выбираем алгоритм с максимальной интересностью (interest_heap).
Используем heapq.heappop, чтобы извлечь алгоритм с наибольшим значением. Проверяем, был ли алгоритм уже изучен. Если нет, добавляем его в order и отмечаем как изученный.
Вывод результата.

После обработки всех дней выводим последовательность номеров алгоритмов в порядке их изучения.

Пример программы-решения

Ниже представлено решение на языке Python.

Python

import heapq

def vasya_learning_order(n, a, b, p):
    interest_heap = [(-a[i], -b[i], i + 1) for i in range(n)]
    utility_heap = [(-b[i], -a[i], i + 1) for i in range(n)]
    heapq.heapify(interest_heap)
    heapq.heapify(utility_heap)
    studied, order = set(), []
    
    for mood in p:
        heap = utility_heap if mood else interest_heap
        while heap:
            _, _, idx = heapq.heappop(heap)
            if idx not in studied:
                studied.add(idx)
                order.append(idx)
                break
    
    print(*order)

n = int(input())
a = list(map(int, input().split()))
b = list(map(int, input().split()))
p = list(map(int, input().split()))
vasya_learning_order(n, a, b, p)