Предметный тур. Информатика. 1 этап
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Рассмотрим модель движения тела. Будем фиксировать такие параметры, как координата, скорость, ускорение и ускорение ускорения (рывок). Если некоторый параметр равен \(a\) и имеет скорость изменения \(v\), то в следующий момент времени этот параметр будет равен \(a + v\).
Например, если тело имело координату, равную 10, скорость, равную 20, ускорение, равное 30 и ускорение ускорения, равное 40, то в следующий момент оно будет иметь координату 30, скорость 50 и ускорение 70. Ускорение ускорения будем считать в этой задаче постоянной величиной.
Задача довольно проста: тело в начальный момент времени 0 находится в точке с координатой 0, скоростью 0 и ускорением 0. На это тело действует постоянное ускорение ускорения, равное 6. Требуется определить, в точке с какой координатой окажется это тело в момент времени \(t\).
Формат входных данных
В единственной строке находится одно число \(t\), где \(0 \leqslant t \leqslant 10^6\).
Формат выходных данных
Вывести одно число — координату, в которой окажется тело в момент времени \(t\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
6 |
120 |
2 |
2 |
0 |
3 |
1000000 |
999997000002000000 |
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int t;
cin >> t;
cout << ((t * (t - 1)) * (t - 2)) << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
У деда Василия есть два прямоугольных куска стекла. Один из них имеет размеры \(a \times b\), другой — \(c \times d\). Дед собирается из этих кусков сделать окно с двойным остеклением. Он хочет, чтобы окно было обязательно квадратным и как можно большим по размеру. Дед должен вырезать из имеющихся у него прямоугольников два одинаковых квадрата максимально возможного размера. Нужно написать программу, которая по заданным \(a,~b,~c,~d\) найдет максимальные размеры квадратного окна. Имейте ввиду, что оба квадрата могут быть вырезаны и из одного прямоугольного куска стекла.
Формат входных данных
На вход подаются две строки. В первой строке находятся размеры первого прямоугольника \(a,~b\) через пробел, во второй — размеры второго прямоугольника \(c,~d\) через пробел, где \(1 \leqslant a, b, c, d \leqslant 10^{9}\).
Формат выходных данных
Вывести одно число — максимальную сторону квадратного двойного окна, которое можно вырезать из заданных на входе прямоугольных кусков стекла. Ответ может быть нецелым, требуется вывести его с точностью 1 знак после десятичной точки.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
5 10 9 6 |
5 |
2 |
4 10 9 6 |
4.5 |
Комментарии
Второй пример показывает, что иногда лучше вырезать оба квадрата из одного и того же куска стекла.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
double a, b, c, d;
cin >> a >> b >> c >> d;
double a0 = min({a, b, c, d});
double a1 = min(max(a, b) / 2.0, min(a, b));
double a2 = min(max(c, d) / 2.0, min(c, d));
double ans = max({a0, a1, a2});
if( (int)ans == ans ){
int ians = ans;
cout << ians << endl;
return 0;
}
cout.precision(1);
cout << fixed<< ans << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
После событий известной сказки А. С. Пушкина старик решил принципиально не пользоваться услугами золотой рыбки. Поэтому для того чтобы изготовить новое корыто, он честно заготовил \(n\) одинаковых досок.
Но гостивший в это время у старика со старухой внук решил, что ему нужно научиться пилить. И, не сказав ничего своему деду, внук быстро распилил каждую из досок на две части. В итоге у старика оказались \(2 n\) кусков досок. Самое интересное, что все эти куски оказались разными по длине, но имели целочисленные размеры. К сожалению, старик забыл, какова была исходная длина целых досок.
Формат входных данных
В первой строке задается целое число \(n\) — исходное количество целых досок, где \(1 \leqslant n \leqslant 10^5\).
Во второй строке заданы \(2 n\) целых чисел \(d_i\) — длины всех кусков, которые получились после «тренировки» внука, где \(1 \leqslant d_i \leqslant 10^9\). Гарантируется, что эти числа попарно различны, и их можно разбить на пары одинаковых по сумме чисел. Все эти части досок пронумерованы от 1 до \(2 n\) в том порядке, в котором они заданы на входе.
Формат выходных данных
В первую строку вывести одно число — исходную длину целых досок.
В следующих \(n\) строках вывести пары номеров кусков досок, которые составляют по длине целые доски. Номера выводить через один пробел, внутри пары сначала должен идти меньший номер, затем больший. Пары должны быть выведены в порядке возрастания первых номеров в парах.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 4 8 2 3 6 7 |
10 1 5 2 3 4 6 |
Комментарии
Отсортируем куски и далее будем брать один из начала и второй к нему из конца.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int n;
cin >> n;
vector<pair<int, int> > v(2 * n);
for(int i = 0; i < 2 * n; i++){
int d;
cin >> d;
v[i] = {d, i + 1};
}
sort(v.begin(), v.end());
vector<pair<int, int> > ans(n);
for(int i = 0; i < n; i++){
ans[i] = {v[i].second, v[2 * n - i - 1].second};
if(ans[i].first > ans[i].second){
swap(ans[i].first, ans[i].second);
}
}
sort(ans.begin(), ans.end());
cout << v[0].first + v.back().first<< endl;
for(int i = 0; i < n; i++){
cout << ans[i].first<<' '<< ans[i].second<< endl;
}
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Технология производства некоторой металлической детали предполагает вытачивание ее из металлической заготовки. При этом образуются стружки, которые не стоит выкидывать. Ведь из \(a\) комплектов стружек (оставшихся после обработки \(a\) заготовок) можно бесплатно выплавить еще одну заготовку, которую снова можно использовать для выточки детали и создания еще одного комплекта стружек.
Заготовки можно купить на оптовом складе, при этом в целях привлечения клиентов, проводится акция «купи \(b\) заготовок, тогда еще одну получишь бесплатно».
Требуется изготовить \(c\) деталей. Нужно определить минимальное число заготовок, которые нужно купить за деньги, чтобы с учетом бонусных заготовок и экономии на стружках можно было изготовить требуемое число деталей.
Формат входных данных
В одной строке через пробел заданы три целых числа \(a\), \(b\), и \(c\) такие, что \(2 \leqslant a \leqslant 10^{18}\), \(1 \leqslant b,~ c \leqslant 10^{18}\).
Формат выходных данных
Вывести одно целое число — минимальное количество заготовок, которые нужно купить, чтобы с учетом всех бонусов и экономии выточить \(c\) конечных деталей.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
4 5 41 |
26 |
Примечания
В примере из условия нужно закупить 26 заготовок. Тогда за каждые пять купленных заготовок будет предоставлена одна бесплатная, итого по акции добавится еще пять заготовок, то есть получится 31 заготовка. Далее из 31 заготовки выточится 31 деталь, останется 31 комплект стружек. Из каждых четырех комплектов выплавится дополнительная заготовка, получится семь заготовок и три комплекта стружек. Из семи заготовок выточится семь деталей и останется семь комплектов стружек, три комплекта стружек осталось с первого шага, итого 10 комплектов стружек. Из них выплавится еще две заготовки, дающие две детали и два комплекта стружек. Собрав эти два комплекта с двумя, оставшимися от 10, получим еще одну заготовку, из которой выточится еще одна деталь. Останется один комплект стружек, который уже никак не получится использовать. Итого будет произведена 31 + 7 + 2 + 1 = 41 деталь.
Комментарии
Методом бинарного поиска можно подобрать минимальное необходимое количество исходных заготовок.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
int f1(int M, int a){
int res = 0, z = 0;
while(1){
if(M == 0 && z < a){
return res;
}
res += M;
M = M + z;
z = M % a;
M = M / a;
}
}
int f2(int M, int b){
return M + M / b;
}
signed main(){
int a, b, c;
cin >> a >> b >> c;
int L = 0, R = 1;
while(f1(R, a) <= c){
R *= 2;
}
while(R - L > 1){
int M = (R + L) / 2;
if(f1(M, a) < c){
L = M;
}
else{
R = M;
}
}
int z = R;
L = 0, R = 1;
while(f2(R, b) <= z){
R *= 2;
}
while(R - L > 1){
int M = (R + L) / 2;
if(f2(M, b) < z){
L = M;
}
else{
R = M;
}
}
cout << R << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Одному таксисту приснился красочный сон. Во сне он живет и работает в некотором городе, где абсолютно все улицы с односторонним движением. Эти улицы устроены так, что невозможно проехать с какого-либо перекрестка так, чтобы вернуться обратно на этот же перекресток, то есть в дорожной сети города нет циклов.
Таким образом, если с перекрестка \(A\) можно попасть по направлению движения улиц на перекресток \(B\), то люди вызывают такси, иначе их везет специальный муниципальный подземный транспорт бесплатно.
В связи с такими странными правилами, таксистам в этом городе разрешено законом везти пассажира по любому маршруту, не нарушающему направления движения. Все в этом городе привыкли к такой ситуации и абсолютно спокойно относятся к тому, что таксисты везут их самым длинным путем. Разумеется, заработок таксиста за одну поездку прямо пропорционален ее длине. Для упрощения будем считать, что стоимость 1 км поездки составляет ровно 1 руб.
Схема дорог города задана. Перекрестки города пронумерованы числами от 1 до \(n\). Таксист в своем сне находится на перекрестке номер \(S\). Напишите программу, которая подскажет ему, сколько он максимально сможет заработать, когда ему придет заказ от клиента. Так как он не знает, куда попросит его везти клиент, нужно для каждого перекрестка от 1 до \(n\) указать максимальную стоимость поездки до этого перекрестка из пункта \(S\) на такси. Если по правилам на такси добраться из пункта \(S\) до какого-то перекрестка нельзя, вывести \(-1\).
Формат входных данных
Дорожная сеть задана следующим образом: в первой строке находятся два числа через пробел \(n\) и \(m\) — число перекрестков и число улиц в городе, где \(2 \leqslant n, m \leqslant 2 \cdot 10^5\).
В следующих \(m\) строках задана очередная односторонняя улица в виде трех чисел \(A\), \(B\), \(d\) через пробел, где \(A\) — начало улицы, \(B\) — конец улицы и \(d\) — ее длина. \(1 \leqslant A, B \leqslant n\), \(1 \leqslant d \leqslant 10^9\). Гарантируется, что в этой дорожной сети нет циклов. Некоторые пары перекрестков могут быть соединены двумя и более односторонними улицами. Дорожная сеть может быть неплоской за счет мостов и тоннелей.
В последней строке ввода содержится номер стартового перекрестка \(S\), \(1 \leqslant S \leqslant n\).
Формат выходных данных
Вывести \(n\) чисел в одну строку через пробел. \(i\)-е число обозначает длину самого длинного пути с перекрестка номер \(S\) до перекрестка номер \(i\). Если до перекрестка номер \(i\) от \(S\) нельзя доехать, не нарушая правила движения, вывести \(-1\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
10 20 9 10 15 9 8 3 8 10 7 7 8 4 7 10 10 5 8 2 5 9 10 5 6 5 7 6 5 4 6 8 3 6 4 3 4 6 5 3 2 2 5 2 2 3 3 3 1 5 1 4 2 2 1 7 4 7 4 6 8 1 5 |
7 -1 2 9 0 18 13 19 10 26 |
Комментарии
Задача решается методом динамического программирования на ориентированном ациклическом графе.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n, m;
vector<vector<pair<int, int> > > G;
vector<int> order, used;
void dfs(int a){
used[a] = 1;
for(auto to : G[a]){
if(!used[to.first]){
dfs(to.first);
}
}
order.push_back(a);
}
signed main(){
cin >> n >> m;
G.resize(n + 1);
used.resize(n + 1, 0);
for(int i = 0; i < m; i++){
int a, b, d;
cin >> a >> b >> d;
G[a].push_back({b, d});
}
int s;
cin >> s;
dfs(s);
reverse(order.begin(), order.end());
vector<int> dp(n + 1, -1);
dp[s] = 0;
for(auto el : order){
for(auto to : G[el]){
dp[to.first] = max(dp[to.first], dp[el] + to.second);
}
}
for(int i = 1; i <= n; i++){
cout << dp[i] <<' ';
}
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Маленький Андрей изучает геометрические фигуры при помощи игры на планшете. У него есть прямоугольные треугольники четырех цветов и ориентаций: желтые, зеленые, красные и синие. Для каждой разновидности треугольников есть заданное количество экземпляров этих треугольников. Более точно: у Андрея есть \(a\) желтых, \(b\) зеленых, \(c\) красных и \(d\) синих треугольников. Помимо этого у него есть прямоугольная таблица \(n \times m\).
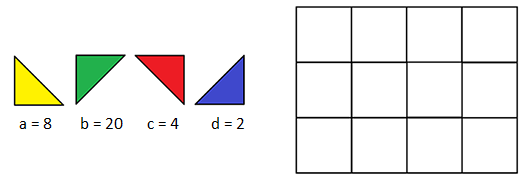
Треугольники одного цвета имеют одну и ту же ориентацию, которую нельзя поменять. Андрей может только взять очередной треугольник и переместить его параллельным сдвигом в одну из ячеек этой прямоугольной таблицы. При этом в одну ячейку можно поместить либо вместе желтый и красный треугольники, либо вместе зеленый и синий, либо один любой треугольник из имеющихся.
Андрей хочет расположить в ячейках таблицы как можно больше треугольников из тех, что у него имеются. Нужно подсказать ему максимальное количество треугольников, которые получится разместить в таблице.
Формат входных данных
В первой строке содержатся четыре целых числа \(a\), \(b\), \(c\) и \(d\) через пробел — количество желтых, зеленых, красных и синих треугольников соответственно.
Во второй строке содержатся два целых числа \(n\) и \(m\) через пробел — размеры прямоугольной таблицы.
Все числа в пределах от 1 до \(10^9\).
Формат выходных данных
Вывести одно число — максимальное количество треугольников, которые можно при заданных условиях разместить в таблице.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
8 20 4 2 3 4 |
18 |
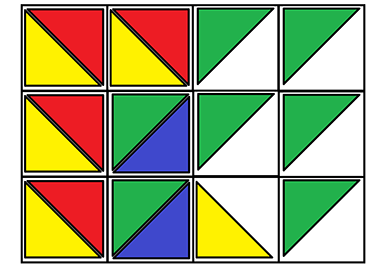
Примечания
На рис. 2.2 представлен один из примеров размещения 18 треугольников из 34 заданных на входе.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int a, b, c, d, n, m;
cin >> a >> b >> c >> d >> n >> m;
if(a > c){
swap(a, c);
}
if(b > d){
swap(b, d);
}
int f = a + b;
int k = n * m;
if(k <= f){
cout << k * 2;
return 0;
}
k -= f;
c -= a;
d -= b;
cout << f * 2 + min(k, c + d) << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Одна старая задача имеет следующий вид:
«Разбить число 45 на сумму четырех слагаемых так, что если к первому прибавить 2, из второго вычесть 2, третье умножить на 2, а четвертое разделить на 2, то получится одно и то же число».
Ответ к этой задаче — четыре числа 8, 12, 5 и 20. Можно убедиться, что в сумме они дают число 45, а если с каждым из них проделать соответствующую арифметическую операцию, то получится одно и то же число 10.
Необходимо решить чуть более общую задачу: даны числа \(n\) и \(k\). Нужно представить число \(n\) в виде суммы четырех целых неотрицательных слагаемых \(a~+~b~+~c~+~d\) таких, что \(a + k = b - k = c \cdot k = d / k\). Гарантируется, что для заданных \(n\) и \(k\) такое разбиение существует.
Формат входных данных
В одной строке через пробел два числа \(n\) и \(k\), где \(1 \leqslant n \cdot k \leqslant 10^{18}\).
Формат выходных данных
Вывести через пробел в одну строку четыре целых неотрицательных числа \(a,~b,~c,~d\) таких, что \(a + b + c + d = n\) и \(a + k = b - k = c \cdot k = d\, /\, k\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
45 2 |
8 12 5 20 |
2 |
128 7 |
7 21 2 98 |
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int n, k;
cin >> n >> k;
int x = (k * n) / (k * k + 2 * k + 1);
cout << x - k <<' '<< x + k <<' '<< x / k <<' '<< x * k << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
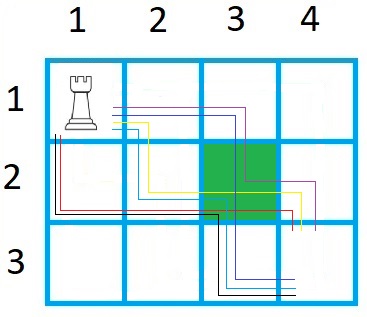
Шахматная ладья находится в левом верхнем углу прямоугольного поля, разбитого на клетки размером \(n \times m\). \(n\) обозначает число строк, \(m\) — число столбцов. Она хочет попасть в правую нижнюю клетку этого поля кратчайшим путем. Ладья может передвигаться либо вправо, либо вниз на любое количество клеток. Ладья обязана посетить заданную клетку с координатами \((x, y)\), где \(x\) — номер строки этой клетки, а \(y\) — номер ее столбца.
Требуется найти количество способов построить путь ладьи из левого верхнего угла в правый нижний, которые проходят через обязательную клетку с заданными координатами.
Формат входных данных
В первой строке находятся два числа через пробел: \(n\) — число строк и \(m\) — число столбцов прямоугольного поля, \(2 \leqslant n,~ m \leqslant 25\). Во второй строке через пробел находятся координаты \((x, y)\) обязательной для посещения клетки, где \(1 \leqslant x \leqslant n\), \(1 \leqslant y \leqslant m\). Координаты \(x\) и \(y\) не совпадают с координатами левой верхней и правой нижней клеток.
Формат выходных данных
Вывести одно число — количество кратчайших путей ладьи из верхней левой в правую нижнюю клетку, проходящих через заданную клетку.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 4 2 3 |
6 |
Примечания
На рис. 2.3 представлены шесть путей, которыми ладья может пройти по полю размером \(3 \times 4\), обязательно посещая по пути клетку \((2, 3)\).
Комментарии
Задачу можно решить как комбинаторными методами (произведение биномиальных коэффициентов), так и динамическим программированием.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
vector<vector<int> > bc(51, vector<int>(51, 0));
bc[0][0] = 1;
for(int i = 1; i <= 50; i++){
for(int j = 0; j < 51; j++){
bc[i][j] += bc[i - 1][j];
if(j - 1 >= 0){
bc[i][j] += bc[i - 1][j - 1];
}
}
}
int n, m, x, y;
cin >> n >> m >> x >> y;
int d1 = bc[x - 1 + y - 1][x - 1];
int d2 = bc[n - x + m - y][n - x];
int ans = d1 * d2;
cout << ans << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Десять танцоров репетируют на сцене новый танец. Каждый танцор одет в футболку, на которой написана одна из цифр от 1 до 9, цифры могут повторяться. Изначально они стоят в некотором порядке слева направо, и их цифры образуют некоторое десятизначное число \(A\). Далее во время всего танца участники либо разбиваются на пять пар рядом стоящих танцоров и одновременно меняются местами внутри своих пар, либо самый левый танцор перемещается на самую правую позицию и становится самым правым танцором.
Сын постановщика танца от скуки на бумаге выписывает все получающиеся при каждом перемещении десятизначные числа. Так как танец длинный, то в итоге на бумаге окажутся все возможные числа, которые в принципе могут появится при этих условиях. Нужно найти разницу между самым большим и самым маленьким из этих чисел.
Формат входных данных
На вход подается одно десятизначное число \(A\), обозначающее начальное расположение танцоров. В числе могут встречаться цифры от 1 до 9, некоторые из них могут повторяться.
Формат выходных данных
Вывести одно число, равное разности самого большого и самого маленького из чисел, которые могут быть получены во время танца.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1456531355 |
5182160085 |
Примечания
Самое маленькое число, которое можно получить в примере, равно 1353155456, самое большое равно 6535315541.
Покажем, как получить эти числа из исходного числа 1456531355. Сначала получим самое большое следующим образом: две левых цифры, 1 и 4, переместим вправо, получим 5653135514, потом поменяем в парах цифры местами и получим самое большое — 6535315541. Далее опять поменяем порядок в парах и в числе 5653135514 переместим три левых цифры 5, 6 и 5 вправо, получим 3135514565 и здесь снова поменяем порядок в парах, получим самое маленькое — 1353155456. Таким образом, искомая разница равна 5182160085.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
string s;
cin >> s;
string mx = s, mn = s;
for(int i = 0; i < 5; i++){
for(int j = 0; j < 10; j++){
mx = max(mx, s);
mn = min(s, mn);
if(j < 9){
s = s.substr(1) + s[0];
}
}
for(int j = 0; j < 5; j++){
swap(s[2 * j], s[2 * j + 1]);
}
}
stringstream ssmn;
ssmn << mn;
int imn;
ssmn >> imn;
stringstream ssmx;
ssmx << mx;
int imx;
ssmx >> imx;
cout << imx - imn << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 3 с.
Ограничение по памяти: 64 Мбайт.
Иннокентий работает в отделе сортировки перестановок, подотделе сортировки вставками. Его задача заключается в сортировке перестановок, предоставленных заказчиками. Перестановкой длины \(n\) называется такая последовательность чисел, в которой встречаются все числа от 1 до \(n\) без повторений в некотором порядке.
Перестановка считается отсортированной, если в ней все числа расположены по возрастанию, то есть она имеет вид \(1, \ldots, n\).
Иннокентий начинает рабочий день с пустой последовательности чисел. За день он сортирует вставками перестановку длины \(n\). В начале каждой операции вставки он получает очередное число \(a_i\) из перестановки заказчика, после чего обрабатывает его, вставляя в отсортированную последовательность из ранее полученных чисел. После каждого такого добавления последовательность уже обработанных чисел должна быть отсортирована по возрастанию.
Перед тем как вставить число \(a_i\) в последовательность, он может выбрать, с какого края последовательности начать вставку. Далее он устанавливает число \(a_i\) с этого края и последовательно меняет вставляемое число с рядом стоящим числом \(b_j\) до тех пор, пока число \(a_i\) не встанет на свое место. На каждую перестановку вставляемого числа \(a_i\) с числом \(b_j\) Иннокентий тратит \(b_j\) единиц энергии.
Дана перестановка длины \(n\) из чисел \(a_i\) в том порядке, в котором Иннокентий их будет обрабатывать. Подскажите ему, какое минимальное количество энергии ему потребуется потратить, чтобы отсортировать всю перестановку.
Формат входных данных
В первой строке находится одно целое число \(n\) — длина перестановки, где \(1 \leqslant n \leqslant 2 \cdot 10^5\).
Во второй строке содержится \(n\) целых чисел \(a_i\) через пробел в том порядке, в котором они поступают на обработку Иннокентию. Гарантируется, что эти числа образуют перестановку длины \(n\), то есть каждое число от 1 до \(n\) содержится в заданном наборе ровно один раз.
Формат выходных данных
Вывести одно число — минимальные суммарные энергозатраты Иннокентия для сортировки вставками заданной на входе перестановки.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
9 2 9 1 5 6 4 3 8 7 |
43 |
Примечания
Первым устанавливается число 2. Оно ни с чем не меняется местами, поэтому затрат нет.
Далее устанавливается число 9. Выбираем правый край и ставим его туда без потерь энергии.
Затем устанавливаем число 1. Выбираем левый край, ставим его туда и снова потерь нет.
Теперь нужно вставить число 5. Если его вставлять с правого края, придется менять местами с 9, а если с левого, то с 1 и 2, что суммарно явно лучше. Итого затраты на вставку 5 равны 3.
Число 6 снова лучше вставить слева, затраты на его вставку равны 8.
Число 4 вставим слева за 3.
Число 3 так же слева за 3.
А вот число 8 лучше вставить справа за 9.
И осталось число 7. Если вставлять слева, то затратим 21, а если справа, то всего 17.
Итого на сортировку заданной перестановки потратили: 0 + 0 + 0 + 3 + 8 + 3 + 3 + 9 + 17 = 43.
Комментарии
Построим дерево отрезков на сумму, при обработке числа \(a\) будем находить, какая сумма на данный момент меньше: от 1 до \(a - 1\) или от \(a + 1\) до \(n\). Прибавим ее к ответу и поместим в позицию \(a\) это число \(a\).
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int LG = 19;
int N = (1 << LG);
vector<int> tr(2 * N, 0);
void upd(int pos, int x){
pos += N;
tr[pos] = x;
pos /= 2;
while(pos){
tr[pos] = {tr[2 * pos]+ tr[2 * pos + 1]};
pos /= 2;
}
}
int get(int l, int r){
l += N;
r += N;
int res = 0;
while(l <= r){
if(l % 2 == 1){
res += tr[l];
}
if(r % 2 == 0){
res += tr[r];
}
l = (l + 1) / 2;
r = (r - 1) / 2;
}
return res;
}
signed main(){
int n, a;
cin >> n;
int ans = 0;
for(int i = 0; i < n; i++){
cin >> a;
int sl = get(0, a - 1);
int sr = get(a + 1, N - 1);
ans += min(sl, sr);
upd(a, a);
}
cout << ans << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Рассмотрим классическую задачу прохождения группы с одним фонариком по туннелю. Есть четыре человека, и у них есть один фонарик. Нужно перевести всю группу на другой конец туннеля. По туннелю можно проходить только с фонариком и только либо вдвоем, либо в одиночку. По этой причине придется сделать пять рейсов по туннелю: три рейса туда и два рейса обратно. Туда идут двое, обратно — один, возвращая фонарик еще не прошедшей части группы. У каждого из четырех человек своя скорость передвижения по туннелю, но некоторые скорости могут совпадать. Двое идут со скоростью самого медленного в этой паре. Нужно найти минимальное время, за которое можно перевести группу по туннелю.
Здесь, в зависимости от скоростей персонажей, есть две стратегии. Проиллюстрируем их на примерах.
Пусть есть люди \(A,~ B,~ C,~ D\). У \(A\) — время прохождения туннеля 1 мин, у \(B\) — 4 мин, у \(C\) — 5 мин, у \(D\) — 10 мин. Здесь работает наиболее очевидная стратегия: самый быстрый переводит текущего и возвращается с фонариком обратно за следующим. При этой стратегии нужно проходить так:
- \(A\), \(B\) туда, затрачено 4 мин;
- \(A\) обратно, затрачена 1 мин;
- \(A\), \(C\) туда, затрачено 5 мин;
- \(A\) обратно, затрачена 1 мин;
- \(A\), \(D\) туда, затрачено 10 мин.
Общее время \(4 + 1 + 5 + 1 + 10 = 21\) мин.
Но не всегда эта стратегия оптимальна. Уменьшим время прохождения туннеля персонажем B до 2 мин. По вышеопределенной стратегии будет 19 мин (\(2 + 1 + 5 + 1 + 10 = 19\)), но имеется более быстрое решение:
- \(A\), \(B\) туда, затрачено 2 мин;
- \(A\) обратно, затрачена 1 мин;
- \(C\), \(D\) туда, затрачено 10 мин;
- \(B\) обратно, затрачено 2 мин;
- \(A\), \(B\) туда, затрачено 2 мин.
Общее время \(2 + 1 + 10 + 2 + 2 = 17\) мин.
Заметим, что для предыдущего примера такая стратегия не работает: \(4 + 1 + 10 + 4 + 4 = 23\) мин.
Если же персонаж \(B\) проходит туннель за 3 мин (а все остальные так же, как и в примерах), то независимо от стратегии будет затрачено 20 мин. В этом случае считаем, что работает первая стратегия.
Поразмыслив, станет понятно, от какого условия зависит выбор стратегии. Далее будем всегда считать, что \(A\) движется не медленнее \(B\), \(B\) движется не медленнее \(C\), \(C\) движется не медленнее \(D\).
Дано время прохождения туннеля персонажами \(A\), \(C\), \(D\). Нужно найти границу border для \(B\) такую, что если определить для \(B\) время прохождения строго меньшее, чем border, то выгодна вторая стратегия, иначе — первая.
Формат входных данных
В одной строке задано три целых чисел через пробел — время прохождения туннеля персонажами \(A\), \(C\), \(D\). Времена даны по неубыванию. Все числа на входе в пределах от 1 до 100.
Формат выходных данных
Вывести одно число — границу border для \(B\) такую, что если определить время прохождения им туннеля строго меньше, чем border, нужно использовать вторую стратегию, иначе — первую. Ответ может быть нецелым, поэтому вывести его нужно с одним знаком после десятичной точки.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1 5 10 |
3 |
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int A, C, D;
cin >> A >> C >> D;
cout.precision(1);
cout << fixed << (A + C) / 2.0 << endl;
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
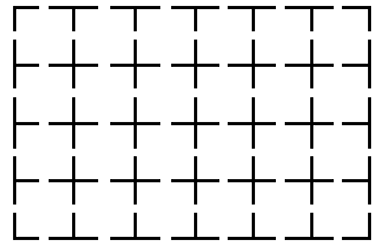
Компания по производству пазлов решила освоить принципиально новый тип головоломок. Для этого берется прямоугольная решетка размера \(n \times m\), каждый ее столбец и строка разрезаются посередине пополам. После этого образуются фигуры трех типов: четыре уголка, \(2 \cdot (n + m - 2)\) т-образных фигур и \((n - 1) \cdot (m - 1)\) крестиков.
Тому, кто решает головоломку, требуется сложить из этих фигур исходную прямоугольную решетку. При этом необходимо использовать абсолютно все имеющиеся в наличии фигуры.
Формат входных данных
В первой строке заданы через пробел два числа \(a\) — количество т-образных фигур и \(b\) — количество крестиков, которые находятся в одном из пазлов. При этом в наборе всегда есть еще четыре уголка. Известно, что этот комплект позволяет собрать прямоугольную решетку размера \(n \times m\), где \(1 \leqslant n,~m \leqslant 10^9\).
Формат выходных данных
Требуется по числам \(a\) и \(b\) найти размеры исходной решетки \(n\) и \(m\). Будем всегда считать, что \(n \leqslant m\), то есть нужно вывести в одну строку через пробел два числа, первое из которых не превосходит второго, и вместе они задают размеры загаданной решетки.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
16 15 |
4 6 |
2 |
0 0 |
1 1 |
Комментарии
Задачу можно решить либо бинарным поиском, либо при помощи квадратного уравнения.
Ниже представлено решение на языке C++ при помощи бинпоиска.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int a, b;
cin >> a >> b;
int L = 0, R = a / 4 + 1;
while(R - L > 1){
int M = (R + L) / 2;
int D = a / 2 - M;
if(M * D <= b){
L = M;
}
else{
R = M;
}
}
cout << L + 1 <<' '<< a / 2 - L + 1 << endl;
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Мечта Карлсона наконец-то сбылась! Мама Малыша испекла восемь пирогов прямоугольной формы и в один из них воткнула свечку. После того как Карлсон съел семь пирогов, он решил-таки поделиться кусочком оставшегося восьмого пирога с Малышом. Но, будучи в хорошем настроении, он вынул из пирога свечу и предложил ему решить задачку.
«Так как я самый щедрый Карлсон в мире, то делить оставшийся пирог будешь ты. Но учти, ты должен разрезать пирог одним прямым разрезом так, чтобы линия прошла через один из углов и точку, где стояла свечка. После этого я выберу себе один из двух кусочков, а оставшийся, так и быть, достанется тебе».
Малыш не против этого замысла, однако считает, что разрезать пирог нужно как можно более справедливо, то есть так, чтобы разница между меньшим и большим кусками была как можно меньше. Подскажите Малышу, какой минимальной разницы между площадями кусков он сможет добиться.
Формат входных данных
В первой строке находятся два числа \(n\) и \(m\) через пробел — размеры прямоугольного пирога. Пирог размещен на координатной плоскости так, что его левый нижний угол находится в точке \((0, 0)\), а правый верхний — в точке \((n, m)\), где \(2 \leqslant n,~ m \leqslant 1000\).
Во второй строке находятся два числа \(x\) и \(y\) через пробел — координаты свечки, где \(1 \leqslant x \leqslant n - 1\), \(1 \leqslant y \leqslant m - 1\), то есть свечка находится строго внутри пирога.
Формат выходных данных
Вывести одно вещественное число с точностью не менее трех знаков после десятичной точки — минимальную разницу между площадями двух получающихся после разрезания кусков, которую сможет получить Малыш.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
8 5 7 2 |
12.571 |
2 |
2 2 1 1 |
0.000 |
Примечания
На рис. 3.2 представлены четыре варианта разделения пирога для первого примера из условия. Можно видеть, что самый близкий к справедливому способ разделения связан с разрезом из левого верхнего угла. Площадь треугольника в этом случае будет равна \(96\, /\, 7\), площадь четырехугольника равна \(184\,/\,7\), и разница равна \(88\, /\, 7\), что при округлении до трех знаков равно 12,571.
Комментарии
Геометрия: для каждого из четырех случаев аккуратно находим катеты прямоугольного треугольника при помощи пропорции, затем находим площадь этого треугольника и, вычитая из всего прямоугольника эту площадь, находим площадь второго куска. Далее выбираем наиболее оптимальное отношение площадей.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int INF = 1e18;
double katy(double x, double y, double n){
return n * y / x;
}
double n, m, x, y;
double ans = INF;
double k1, k2;
void upd(){
if(k1 < m){
double st =k1 * n / 2;
ans = min(ans, n * m - 2 * st);
}
else{
double st =k2 * m / 2;
ans = min(ans, n * m - 2 * st);
}}
signed main(){
cin >> n >> m >> x >> y;
k1 = katy(x, y, n);
k2 = katy(y, x, m);
upd();
k1 = katy(n - x, y, n);
k2 = katy(y, n - x, m);
upd();
k1 = katy(x, m - y, n);
k2 = katy(m - y, x, m);
upd();
k1 = katy(n - x, m - y, n);
k2 = katy(m - y, n - x, m);
upd();
cout.precision(3);
cout << fixed << ans<< endl;
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
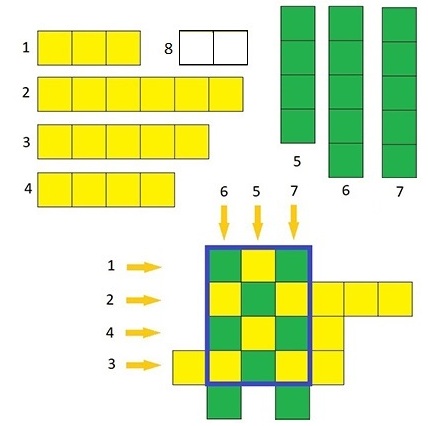
У Маши есть \(n\) полосок бумаги. \(i\)-я полоска имеет ширину 1 и длину \(a_i\). Маша разделит эти полоски на две части и покрасит некоторые в желтый, а оставшиеся — в зеленый цвет. Она сама выберет, какие полоски как покрасить. Далее она хочет из этих полосок сплести максимально большую плетенку. Она расположит полоски одного цвета в некотором порядке горизонтально, а полоски другого цвета в некотором порядке вертикально. После этого она переплетет горизонтальные и вертикальные полоски так, что они будут чередоваться то сверху, то снизу, образуя в местах пересечения шахматную раскраску. Наконец, она обрежет выступающие края полосок так, что останется прямоугольная плетенка с ровными краями. Каждая клетка полученной плетенки должна иметь два слоя.
Маша хочет сплести максимально большую по площади прямоугольную плетенку. Подскажите ей, плетенку какой площади она сможет сделать. Заметим, что она может при создании плетенки использовать не все имеющиеся у нее полоски.
Формат входных данных
В первой строке на вход подается число \(n\) — количество полосок бумаги у Маши, где \(2 \leqslant n \leqslant 2\cdot 10^5\). Во второй строке через пробел заданы \(n\) целых чисел \(a_i\) через пробел — длины полосок, где \(1 \leqslant a_i \leqslant 10^9\).
Формат выходных данных
Вывести одно число — площадь прямоугольника, форму которого может иметь самая большая плетенка Маши.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
8 3 6 5 4 4 5 5 2 |
12 |
Примечания
На рис. 3.3 представлен один из вариантов получения самой большой плетенки для полосок из примера. Синим обозначена граница полученной максимальной плетенки. Ее размер \(3 \times 4\), и ее площадь 12. При ее создании Маша не должна использовать полоску номер 8, по этой причине неважно, как она раскрашена.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int n;
cin >> n;
deque<int> v(n);
for(int i = 0; i < n; i++){
cin >> v[i];
}
sort(v.begin(), v.end());
int ans = 0;
int cnth = 0, minh;
while(1){
if(v.size() == 0){
break;
}
cnth++;
minh = v.back();
v.pop_back();
while(v.size() > 0 && v[0] < cnth){
v.pop_front();
}
ans = max(ans, cnth * min(minh, (int)v.size()));
}
cout << ans << endl;
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 3 с.
Ограничение по памяти: 64 Мбайт.
Маша и Витя запоминают слова английского языка в оригинальной игровой форме. За день им нужно выучить \(n\) слов, где \(20 \leqslant n \leqslant 100\), каждое из которых имеет длину от 5 до 8 символов. Маша выбирает из этого набора наугад несколько попарно различных слов (также от 5 до 8) и собирает их в одну строку без пробелов. Далее она переставляет буквы в этой строке так, что слова оказываются полностью перепутанными, и дает эту строку Вите. Теперь Витя должен восстановить все слова, которые выбрала Маша.
Но у Вити плохо получается, а Маша уже забыла, какие слова она выбрала. Нужно им помочь — написать программу, которая восстановит слова, выбранные Машей.
Формат входных данных
В первой строке находится строка, которую Маша предложила Вите. Во второй строке содержится число \(n\) — количество слов, которые нужно выучить детям, \(20 \leqslant n \leqslant 100\).
В следующих \(n\) строках содержатся эти слова по одному в строке. Все слова в этом наборе различны. Слова отсортированы в лексикографическом (алфавитном) порядке. Все слова состоят из маленьких букв от a до z. Обратите внимание, что в тестах к этой задаче все заданные слова реально существуют в английском языке и случайным образом выбраны из словаря.
Гарантируется, что длина каждого слова из предложенного набора (словаря) в пределах от 5 до 8, строка, которую получила Маша, может быть получена путем перестановки букв некоторых различных слов из предложенного словаря, причем, набор выбранных Машей слов определяется по ней однозначно. Количество слов, из которых составлена Машина строка, находится в пределах от 5 до 8.
Формат выходных данных
Вывести все слова, выбранные Машей, в алфавитном порядке по одному в строке.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
stirbaexsudueoeidgomttcrnrwlunapntetacwri 24 bridge cranky document drawing farmer fighter figurine gravy havoc minimum reactant reply republic sonata soprano split subset tailor texture tomorrow trout vicinity wrist writer |
document drawing republic sonata texture wrist |
Комментарии
В случае, выделенном в условии (слова являются случайными, взятыми из английского словаря), задача решается рекурсией с перебором вариантов.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
string frs;
int n;
vector<string> dict;
vector<int> msk(26, 0);
int cnt = 0;
vector<vector<int> > amsk;
vector<string> ans;
bool bigok = 0;
void p(int pos){
if(!bigok){
if(cnt == 0){
sort(ans.begin(), ans.end());
bigok = 1;
return;
}
for(int i = pos; i < n; i++){
string ts = dict[i];
bool ok = 1;
for(int j = 0; j < 26; j++){
if(amsk[i][j] > msk[j]){
ok = 0;
}
}
if(ok){
ans.push_back(ts);
for(int j = 0; j < 26; j++){
msk[j] -= amsk[i][j];
cnt -= amsk[i][j];
}
p(i + 1);
if(!bigok){
for(int j = 0; j < 26; j++){
msk[j] += amsk[i][j];
cnt += amsk[i][j];
}
ans.pop_back();
}
}
}
}
}
signed main(){
cin >> frs;
cin >> n;
amsk.resize(n, vector<int>(26, 0));
string ts;
for(int i = 0; i < n; i++){
cin >> ts;
dict.push_back(ts);
}
for(int i = 0; i < n; i++){
for(auto el : dict[i]){
amsk[i][el - 'a']++;
}
}
for(auto el : frs){
msk[el - 'a']++;
cnt++;
}
p(0);
for(auto el : ans){
cout << el << endl;
}
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Одному портному заказали сделать одноцветный флаг. Особенность этого флага в том, что он должен быть квадратным. У портного есть два прямоугольных куска ткани заданного цвета. Один из них имеет размеры \(a \times b\), другой — \(c \times d\). Так как клиент будет платить пропорционально площади изготовленного флага, портной хочет сначала сшить имеющиеся у него прямоугольные куски, соединив их двумя какими-то сторонами, а затем из полученного полотна вырезать и сделать флаг с максимально большой стороной. Определить сторону получившегося у него флага.
Формат входных данных
На вход подаются две строки. В первой строке находятся размеры первого прямоугольника — целые числа \(a\), \(b\) через пробел, во второй — размеры второго прямоугольника, также целые числа \(c\), \(d\) через пробел, где \(1 \leqslant a, b, c, d \leqslant 10^9\).
Формат выходных данных
Вывести одно число — сторону самого большого квадрата, который можно получить по условию задачи.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
2 4 3 6 |
4 |
2 |
2 2 3 6 |
3 |
Примечания
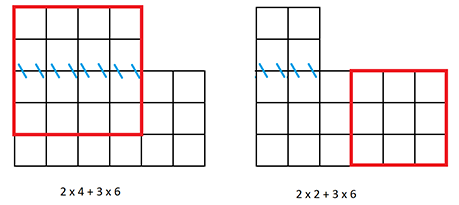
На рис. 4.1 представлены иллюстрации для тестов из условия. Синими штрихами обозначено место сшивки двух кусков. Красный квадрат выделяет один из вариантов вырезания максимального квадрата.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int a, b, c, d;
cin >> a >> b >> c >> d;
int ans = max(min(a, b), min(c, d));
int p1 = min(a + c, min(b, d));
int p2 = min(a + d, min(b, c));
int p3 = min(b + c, min(a, d));
int p4 = min(b + d, min(a, c));
ans = max({ans, p1, p2, p3, p4});
cout << ans << endl;
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
В данной задаче будем упрощенно считать, что ДНК представляется строкой длины от 10 до 100, состоящей из букв A, C, G, T.
Пусть даны две ДНК \(D_1\) и \(D_2\) одной и той же длины \(n\). Выберем некоторое произвольное число \(i\) от 1 до \(n - 1\) и поменяем местами префиксы (начала) этих ДНК длины \(i\). Будем говорить, что полученные новые две строки образованы путем скрещивания двух исходных по префиксу длины \(i\).
Например, пусть \(D_1 =\) AACGGTAGGT, а \(D_2 =\) TCCCGGAACA. Выберем \(i = 4\) и поменяем местами префиксы длины 4. Получим две новые ДНК, одна из которых будет иметь вид AACGGGAACA, а вторая — TCCCGTAGGT. Для наглядности были выделены части первой из них.
Полученные новые ДНК снова могут быть скрещены по любому префиксу длины от 1 до \(n - 1\).
Теперь можно рассмотреть популяцию из нескольких ДНК. Выберем из них две, произведем их скрещивание по префиксу какой-либо длины и поместим две новые ДНК в исходную популяцию. В данной задаче будем считать, что количество ДНК не увеличивается, то есть старые две ДНК заменяются на новые две ДНК.
Дана исходная популяция из \(m\) ДНК, каждая имеет одну и ту же длину \(n\). После некоторого количества попарных скрещиваний была получена новая популяция. Но при итоговой обработке данных сведения об одной ДНК из новой популяции были потеряны. Задача состоит в отыскании этой потерянной ДНК по оставшимся \(m - 1\) ДНК из новой популяции.
Формат входных данных
В первой строке через пробел даны два числа \(n\) — длина ДНК и \(m\) — количество ДНК в исходной популяции, где \(10 \leqslant n \leqslant 100\), \(2 \leqslant m \leqslant 100\).
В следующих \(m\) строках содержится описание исходной популяции ДНК, каждая задается строкой длины \(n\), состоящей из символов A, C, G и T.
Далее следует разделяющая строка, содержащая \(n\) символов «\(-\)».
Далее следует еще \(m - 1\) строк, описывающих новую (заключительную) популяцию без одной ДНК.
Гарантируется, что данные верны, то есть \(m - 1\) последняя ДНК является некоторой новой популяцией ровно без одной ДНК, полученной из исходной популяции, заданной в \(m\) первых строках.
Формат выходных данных
Вывести недостающую утерянную ДНК.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
10 2 AACGGTAGGT TCCCGGAACA ---------- TCCCGTAGGT |
AACGGGAACA |
2 |
10 4 AACCGGTTAA ACGTACGTAC AAACCCGGGT CATTACTGGA ---------- AAGCGCTTAA CCACACGTGC AACTAGGGGT |
AATTCCTGAA |
Комментарии
Для каждой позиции нужно найти недостающую букву из первого набора ДНК. Для этого удобнее всего использовать функцию xor.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int n, m;
cin >> n >> m;
vector<string> v1(m);
for(int i = 0; i < m; i++){
cin >> v1[i];
}
string d;
cin >> d;
vector<string> v2(m - 1);
for(int i = 0; i < m - 1; i++){
cin >> v2[i];
}
for(int j = 0; j < n; j++){
int ss = 0;
for(int i = 0; i < m; i++){
ss ^= (int)(v1[i][j]);
}
for(int i = 0; i < m - 1; i++){
ss ^= (int)(v2[i][j]);
}
cout << (char)(ss);
}
cout << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Рассмотрим следующий вариант известной задачи на перемещение по туннелю группы из четырех человек. В общем виде она выглядит так: четыре туриста хотят пройти по темному туннелю. Имеется один фонарик. По туннелю можно перемещаться либо вдвоем, либо по одному, при этом у тех, кто движется в туннеле, должен быть фонарик в руках. По этой причине движение должно быть следующим: двое переходят туда, один возвращается обратно и приносит фонарик тем, кто еще не перешел. После этого указанный маневр повторяется снова.
У каждого участника своя скорость движения в туннеле. Пусть участники проходят туннель за \(A\), \(B\), \(C\) и \(D\) мин. Если идут двое, то они движутся со скоростью того, кто идет медленнее. Требуется по заданным временам прохождения туннеля каждого из участников перевести их максимально быстро через туннель.
Немного усложним данную задачу. Введем фактор усталости. А именно, любой участник, пройдя по туннелю, устает и в следующий раз идет уже медленнее. После каждого прохождения туннеля время прохождения любого участника увеличивается на \(E\) мин. Например, если участник до начала движения проходит туннель за 1 мин, а показатель усталости \(E\) равен 3 мин, то первый раз участник пройдет туннель за 1 мин, второй раз — за 4 мин, третий раз — за 7 мин и т. д.
По заданным \(A\), \(B\), \(C\), \(D\) и \(E\) узнать, за какое минимальное время можно провести всю группу через туннель согласно указанным правилам.
Формат входных данных
На вход подаются пять чисел. В первой строке через пробел четыре числа \(A\), \(B\), \(C\) и \(D\) — время прохождения туннеля каждым из четырех участников до того, как они начали движение. Во второй строке содержится число \(E\) — величина, на которую увеличивается время прохождения туннеля каждым участником после каждого перемещения. При этом \(1 \leqslant A, B, C, D \leqslant 1000\), \(0 \leqslant E \leqslant 1000\).
Формат выходных данных
Вывести одно число — минимальное время прохождения туннеля всей группой.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
8 9 10 1 3 |
44 |
2 |
8 9 10 1 0 |
29 |
Примечания
В первом примере при прохождении туннеля каждый турист устает и движется медленнее на 3 мин. Покажем, как перевести группу при этом за 44 мин.
Каждую ситуацию будем обозначать следующим образом: слева от двоеточия находятся туристы, которые стоят в начале туннеля, а справа — те, что стоят в конце туннеля. Туриста будем обозначать при помощи числа, соответствующего его текущему времени прохождения туннеля.
Тогда исходная ситуация имеет вид 1, 8, 9, 10 :.
Сначала идут туристы 1 и 8, каждый после перехода устает на 3 мин, получим ситуацию 9, 10 : 4, 11, затрачено 8 мин.
Обратно возвращается турист 4, он устает еще на 3 мин. Ситуация становится 7, 9, 10 : 11, затрачено 8 + 4 = 12 мин.
Теперь идут туристы 7 и 9, получится ситуация 10 : 10, 11, 12, затрачено \(8 + 4 + 9 = 21\) мин.
Возвращается турист 10, получится 10, 13 : 11, 12, затрачено \(8 + 4 + 9 + 10 = 31\) мин.
Наконец, оставшиеся двое туристов 10 и 13 за 13 мин переходят туннель, итого затрачено 8 + 4 + 9 + 10 + 13 = 44 мин.
Комментарии
Задача решается рекурсивным перебором всех вариантов прохождения.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int INF = 1e18;
vector<int> v(4);
int e, ans = INF;
void p(vector<int> &vl, vector<int> &vr, int tv){
if(vl.size() == 2){
ans = min(ans, tv + *max_element(vl.begin(), vl.end()));
return;
}
for(int i = 0; i < vl.size() - 1; i++){
for(int j = i + 1; j < vl.size(); j++){
vector<int> vl1;
for(int k = 0; k < vl.size(); k++){
if(k != i && k != j){
vl1.push_back(vl[k]);
}
}
vector<int> vr1 = vr;
vr1.push_back(vl[i] + e);
vr1.push_back(vl[j] + e);
int tmp = max(vl[i], vl[j]);
sort(vr1.rbegin(), vr1.rend());
vl1.push_back(vr1.back() + e);
vr1.pop_back();
p(vl1, vr1, tv + tmp + vl1.back() - e);
}
}
}
signed main(){
for(int i = 0; i < 4; i++){
cin >> v[i];
}
sort(v.begin(), v.end());
cin >> e;
vector<int> vl = v, vr;
p(vl, vr, 0);
cout << ans;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
При постройке моста используются два типа пролетов: П-образные (они прочные, но дорогие) и Т-образные (они дешевле, но менее надежные). Мост должен начинаться и заканчиваться П-образными пролетами. Любой Т-образный пролет должен иметь хотя бы один П-образный пролет в качестве соседнего.
Длина проектируемого моста — \(n\) пролетов. Муниципалитет выделил средства на постройку \(a\) П-образных и \(b\) Т-образных пролетов. При этом \(a + b = n\). Требуется выяснить, сколькими способами при этих условиях можно скомпоновать мост. Два способа компоновки моста отличаются, если в одной на некоторой позиции стоит П-образный пролет, а в другой на этой же позиции стоит Т-образный пролет.
Формат входных данных
В одной строке через пробел заданы два числа: \(a\) — число П-образных пролетов и \(b\) — число Т-образных пролетов, на постройку которых выделены средства, где \(2 \leqslant a \leqslant 10^6\), \(0 \leqslant b \leqslant 10^6\).
Формат выходных данных
Вывести одно число — количество вариантов компоновки моста. Так как ответ может быть очень большим, требуется вывести остаток от его деления на 1000000007 (\(10^9 + 7\)).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
4 3 |
7 |
Примечания
Для примера из условия имеется 7 вариантов компоновки моста (пробелы добавлены для лучшего восприятия вариантов):
П Т Т П Т П П
П Т Т П П Т П
П Т П Т Т П П
П Т П П Т Т П
П П Т П Т Т П
П П Т Т П Т П
П Т П Т П Т П
Комментарии
При заданных ограничениях задача решается только при помощи комбинаторики с вычислениями по модулю.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int INF = 1e18;
const int MOD = 1e9 + 7;
vector<int> f(2e6 + 1, 1);
int binpow (int a, int n) {
int res = 1;
while (n > 0) {
if (n % 2 == 1)
(res *= a) %= MOD;
(a *= a) %= MOD;
n /= 2;
}
return res;
}
int bc(int n, int k){
int res = f[n];
int p1 = binpow(f[k], MOD - 2);
int p2 = binpow(f[n - k], MOD - 2);
(res *= p1) %= MOD;
(res *= p2) %= MOD;
return res;
}
signed main(){
for(int i = 1; i <= 2e6; i++){
f[i] = (f[i - 1] * i) % MOD;
}
int a, b;
int ans = 0;
cin >> a >> b;
a--;
for(int i = 0; i < a + 1; i++){
if(2 * i <= b){
int d = bc(a, i);
if(b - 2 * i <= a - i){
(d *= bc(a - i, b - 2 * i) ) %= MOD;
(ans += d) %= MOD;
}
}
}
cout << ans << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 8 с.
Ограничение по памяти: 64 Мбайт.
По прямому участку улицы, которую будем считать отрезком \(AB\) длины \(d\), прогуливаются \(n\) джентльменов. \(i\)-й джентльмен движется со скоростью \(v_i\). Скорости всех джентльменов попарно различны. Дойдя до любого конца улицы, каждый джентльмен поворачивает и идет в обратную сторону.
При каждой встрече два джентльмена приветствуют друг друга, приподнимая головной убор. Приветствие происходит и в том случае, когда один джентльмен обгоняет другого. Если два джентльмена встречаются в момент их одновременного поворота, то происходит два приветствия: одно до поворота, другое — после поворота. Если происходит одновременная встреча трех и более джентльменов, то они приветствуют друг друга попарно, то есть каждый каждого. Допустим, если одновременно встретились четыре джентльмена где-то посреди улицы, произойдет шесть попарных приветствий. Если же эти четыре джентльмена встретились в момент их одновременного поворота, произойдет уже двенадцать приветствий.
В этой задаче считаем, что все действия происходят без остановок, то есть и повороты и приветствия происходят мгновенно. Джентльмены одновременно начинают свою прогулку из точки \(A\) в момент 0. В этот момент они уже производят свои первые попарные приветствия, то есть в момент 0 уже произведено \(n \cdot (n - 1) / 2\) приветствий. Момент старта не считается моментом поворота, то есть на старте число приветствий не удваивается. Джентльмены гуляют достаточно долго, чтобы произошло любое заданное количество приветствий.
Требуется найти момент, в который было произведено \(k\)-е по порядку приветствие.
Формат входных данных
В первой строке ввода через пробел содержится два целых числа: \(d\) — длина отрезка \(AB\) и \(n\) — количество прогуливающихся джентльменов, где \(1 \leqslant d \leqslant 200\), \(2 \leqslant n \leqslant 2000\).
Во второй строке находятся \(n\) целых чисел \(v_i\) через пробел — скорости каждого джентльмена, где \(1 \leqslant v_i \leqslant 2000\). Гарантируется, что все скорости попарно различны. Скорости даны в порядке возрастания, то есть \(v_1 < v_2 < \ldots < v_n\).
В третьей строке содержится одно целое число \(k\) — номер требуемого приветствия, для которого нужно найти момент, когда оно произойдет, где \(1 \leqslant k \leqslant 10^9\).
Формат выходных данных
Вывести одно вещественное число — время, когда произойдет \(k\)-е по порядку приветствие. Ответ вывести с точностью не менее двух знаков после десятичной точки.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
5 4 2 5 8 10 6 |
0.000 |
2 |
5 4 2 5 8 10 7 |
0.556 |
3 |
5 4 2 5 8 10 11 |
1.000 |
4 |
5 4 2 5 8 10 15 |
1.429 |
5 |
5 4 2 5 8 10 17 |
1.667 |
6 |
5 4 2 5 8 10 19 |
1.667 |
7 |
5 4 2 5 8 10 21 |
2.000 |
Примечания
На рис. 4.2 приведено положение джентльменов из примеров в моменты времени 0, 1 и 2. Джентльмены обозначены своими скоростями. Стрелками обозначены направления их движения в соответствующий момент. Перечислим и пронумеруем в порядке возрастания моменты попарных приветствий этих джентльменов до момента времени 2 включительно. Если два и более приветствия происходят одновременно, неважно какое из них конкретно имеет номер \(k\), главное, что они происходят в один и тот же определенный момент времени.
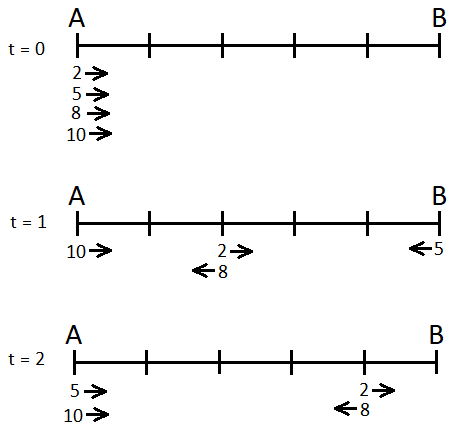
- 2 и 5 приветствуют друг друга в момент 0 (изображено на рис. 4.2).
- 2 и 8 приветствуют друг друга в момент 0 (изображено на рис. 4.2).
- 2 и 10 приветствуют друг друга в момент 0 (изображено на рис. 4.2).
- 5 и 8 приветствуют друг друга в момент 0 (изображено на рис. 4.2).
- 5 и 10 приветствуют друг друга в момент 0 (изображено на рис. 4.2).
- 8 и 10 приветствуют друг друга в момент 0 (изображено на рис. 4.2).
- 8 и 10 приветствуют друг друга в момент 0.556.
- 5 и 10 приветствуют друг друга в момент 0.667.
- 5 и 8 приветствуют друг друга в момент 0.769.
- 2 и 10 приветствуют друг друга в момент 0.833.
- 2 и 8 приветствуют друг друга в момент 1.000 (изображено на рис. 4.2).
- 8 и 10 приветствуют друг друга в момент 1.111.
- 2 и 10 приветствуют друг друга в момент 1.250.
- 5 и 10 приветствуют друг друга в момент 1.333.
- 2 и 5 приветствуют друг друга в момент 1.429.
- 5 и 8 приветствуют друг друга в момент 1.538.
- 2 и 8 приветствуют друг друга в момент 1.667.
- 2 и 10 приветствуют друг друга в момент 1.667.
- 8 и 10 приветствуют друг друга в момент 1.667 (в момент 1.667 встретятся одновременно три джентльмена 2, 8 и 10).
- 2 и 8 приветствуют друг друга в момент 2.000 (изображено на рис. 4.2).
- 5 и 10 приветствуют друг друга в момент 2.000 (до поворота).
- 5 и 10 приветствуют друг друга в момент 2.000 (после поворота, изображено на рис. 4.2).
Комментарии
Задача решается при помощи бинпоиска с квадратичным нахождением ответа в каждой его итерации.
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
const double EPS = 1e-7;
double x(double M, int V, int d){
double dst = V * M;
int cnt = floor((dst + EPS) / d);
double pin = dst - cnt * d;
if(cnt % 2 == 0){
return pin;
}
else{
return d - pin;
}
}
int F(double M, vector<int> &v, int d){
int res = 0;
for(int i = 0; i < v.size(); i++){
double dst = v[i] * M;
int cnt = floor((dst + EPS) / d);
res += cnt * i;
double tx = x(M, v[i], d);
for(int j = 0; j < i; j++){
double txj = x(M, v[j], d);
if(cnt % 2 == 0){
res += txj <= tx + EPS;
}
else{
res += txj >= tx - EPS;
}
}
}
return res;
}
signed main(){
int d, n;
cin >> d >> n;
vector<int> v(n);
for(int i = 0; i < n; i++){
cin >> v[i];
}
int k;
cin >> k;
double L = 0, R = 1;
while(F(R, v, d) <= k){
R *= 2;
}
R *= 2;
while(R - L > 1e-4){
double M = (R + L) / 2.0;
if(F(M, v, d) < k){
L = M;
}
else{
R = M;
}
}
cout.precision(10);
cout << fixed << L << endl;
}