Предметный тур. Информатика. 3 этап
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 256 Мбайт.
В одном из лабораторных центров умного города ученики разработали искусственный интеллект, который анализирует возраст зданий по их фотографиям, помогая в прогнозировании их технического обслуживания. Однако из-за ошибки в коде система дает лишь косвенные подсказки о возрасте объекта.
После загрузки фотографий очередного здания были получены следующие подсказки:
- возраст здания ближе к \(x\) годам, чем к \(y\);
- разница между возрастом здания и \(z\), умноженная на \(k\), более, чем в \(p\) раз больше половины возраста здания.
Вот такая замудренная подсказка! Ошибку, конечно, нужно найти и исправить, а сейчас разработайте временное решение: по указанным подсказкам определите возраст здания. Считаем, что подсказки верны.
Формат входных данных
Входные данные представляют собой пять строк с одним целым числом в каждой строке \(x\), \(y\), \(z\), \(k\), \(p\) соответственно. Каждое из чисел — целое положительное и не превосходит 200. Гарантируется, что ответ при заданных числах существует.
Формат выходных данных
Выведите единственное целое положительное число — возраст здания. Если возможных вариантов несколько — выведите минимальный. Гарантируется, что все здания в городе имеют возраст, не превышающий 120.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
70 30 76 4 3 |
51 |
2 |
101 16 141 9 5 |
59 |
Примечания
«Ближе к \(x\) годам, чем к \(y\)» — подразумевается, что если возраст здания \(H\), то \(|H-x|<|H-y|\).
Переберем возможный возраст здания, начиная с 1 до 120, до тех пор, пока не выполнятся все условия, а именно: \(|H-x|<|H-y|\) и \(|H-z|\cdot k\cdot 2>H\cdot p\).
Сложность решения: \(\mathcal{O}(C)\).
Пример программы-решения
Ниже представлено решение на языке Python.
def solve():
x, y, z, k, p = [int(input()) for i in range(5)]
for H in range(1, 121):
if abs(H - x) >= abs(H - y):
continue
dif = abs(H - z)
if dif * k * 2 > H * p:
print(H)
return
if __name__ == '__main__':
solve()Проверка в задаче полная — тестирование не прерывается при неверном ответе. Баллы будут начисляться пропорционально количеству пройденных тестов. Баллы за тестовые примеры не предусмотрены. Всего оцениваемых тестов 20 штук.
Максимальный балл за задачу — 13.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 256 Мбайт.
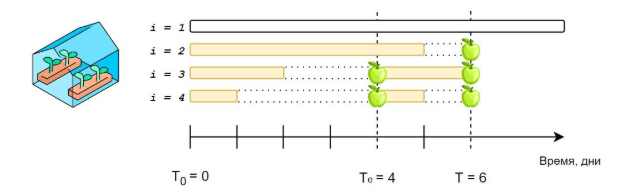
В умном городе запущен экспериментальный агротехнический комплекс с теплицей. В теплице установлены \(n\) горшочков, в каждом из которых растет особый вид растения, дающий плоды. Растение в горшочке \(i\) вырастает и дает первые плоды за \(t_i\) дней, после этого растение ждет, пока соберут его плоды. Если растение \(i\) выросло, и его плоды собрали, то оно не растет, но продолжает давать плоды каждый раз через ровно \(t_i\) дней с момента прошлого сбора его плодов.
Изначально в нулевой день экспериментаторы посадили в этой теплице все \(n\) растений. Общая длительность эксперимента составляет \(T\) дней. Экспериментаторы хотят собрать из теплицы максимальное число плодов за эти \(T\) дней, однако, чтобы минимизировать внешние воздействия на микроклимат, в теплицу разрешается зайти в теплицу и собрать поспевшие плоды лишь единожды между днями 0 и \(T\).
По рис. 1.1 видно, что оптимально посетить теплицу в день 4 (также можно в день 2 или 3) и собрать плоды с горшков 3 и 4. В последний — шестой — день плоды собираются с растений в горшках 2, 3 и 4.
Определите, какое максимальное число плодов можно суммарно собрать за \(T\) дней, если в теплицу можно зайти не более одного раза для сбора плодов растений, не включая дни 0 и \(T\). Заметьте, что в последний день эксперимента разрешается заходить в теплицу и собирать все поспевшие плоды.
Формат входных данных
В первой строке содержатся два целых числа \(n\), \(T\) (\(1\leqslant n\leqslant 2\cdot 10^5;~1\leqslant T\leqslant 10^9\)) — количество горшочков в теплице и время в днях, доступное для выращивания плодов растений.
Во второй строке содержатся n целых чисел \(t_i\) (\(1\leqslant ti\leqslant 10^9\)) — время вырастания и созревания плодов каждого растения.
Формат выходных данных
Выведите максимальное число плодов, которые можно собрать, согласно описанным условиям.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
4 6 8 5 2 1 |
5 |
2 |
4 4 10 6 4 9 |
1 |
3 |
5 10 8 3 3 2 5 |
9 |
Примечания
Обратите внимание, что если у растения не собрать плоды, то оно не начнет выращивать новые плоды, пока кто-то не соберет текущие плоды.
После того как растение \(i\) посадили в нулевой день, в день \(t_i\) растение вырастает, и в этот же день с него уже можно собрать первые плоды.
Условие задачи сводится к тому, чтобы собрать двойной урожай с максимального числа растений. Легко показать, что собрать двойной урожай можно только с растений, время созревания которых принадлежит некоторому отрезку \([0;~X]\).
Не будем рассматривать такие \(t_i > T\), так как с таких растений ни разу нельзя собрать урожай.
Время, в которое стоит зайти в теплицу и собрать урожай — это такое максимальное \(t_i\leqslant \displaystyle \frac T2\) (но не всегда только это значение, тем не менее, оно всегда не хуже). Если ни одного такого значения нет, то можно зайти в теплицу, когда угодно или не заходить ни разу, так как двойной урожай собрать нельзя.
Сложность решения: \(\mathcal{O}(n\cdot \log n)\) или \(\mathcal{O}(n)\), если не делать сортировку.
Пример программы-решения
Ниже представлено решение на языке Python.
import sys
def solve():
n, T = map(int, sys.stdin.readline().split())
t = list(map(int, sys.stdin.readline().split()))
t.sort()
while len(t) > 0 and t[-1] > T:
t.pop()
res = len(t)
for i in range(len(t)):
if t[i] << 1 <= T:
res += 1
else:
break
sys.stdout.write(str(res) + '\n')
return
if __name__ == '__main__':
solve()Ниже представлена таблица оценки за группы тестов.
| Группа | Дополнительные ограничения | Баллы |
|---|---|---|
| 1 | n=2 | 2 |
| 2 | \(n\leqslant 10;~T\leqslant 100\) | 3 |
| 3 | \(n\leqslant 1000\) | 5 |
| 4 | — | 7 |
Проверка в каждой группе тестов полная — тестирование не прерывается при неверном ответе. Баллы будут начисляться пропорционально количеству пройденных тестов. Балл за задачу — сумма баллов за каждую подгруппу. Баллы за тестовые примеры не предусмотрены.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 256 Мбайт.
В игре «Гексокрафт 2D», где все объекты представлены шестиугольными блоками, Вася построил на сервере пирамиду, состоящую из таких блоков. Однако его друг Петя, развлекаясь с различными механиками игры, случайно уничтожил несколько блоков в постройке Васи.
Вася расстроился — давайте поможем ему и оценим ущерб в цифрах. Главное, по его словам, починить основание пирамиды, так что сосредоточимся именно на нем. Изначально пирамида состояла из n уровней. Уровни в пирамиде нумеруются с верхнего — он имеет номер 1, соответственно самый нижний уровень имеет номер \(n\). Блоки в каждом уровне \(h\) нумеруются слева направо, начиная с 1 и заканчивая \(h\).
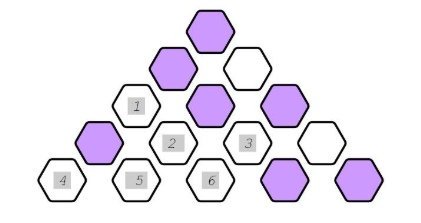
Каждый блок в пирамиде может быть или заполнен, или быть пустым. Состояние каждого блока будет известно. Некоторые пустые блоки можно заполнить за один ход, но для того чтобы заполнить блок \(i\) на уровне \(h>1\), должны быть заполнены блоки \(i-1\) (если существует) и \(i\) (если существует) на уровне \(h-1\).
Определите минимальное число ходов для заполнения всех \(n\) блоков нижнего уровня пирамиды.
Формат входных данных
В первой строке входных данных содержится целое число \(n\) \((1\leqslant n\leqslant 1000)\) — количество уровней в пирамиде. Далее содержатся \(n\) строк, описывающие начальное состояние пирамиды: в \(i\)-й строке содержится бинарная строка \(s_i\) длины \(i\), если \(j\)-й блок \(i\)-го уровня пирамиды заполнен, то \(s_{i,j}=1\), иначе \(s_{i,j}=0\). Гарантируется, что блок пирамиды в самом верхнем уровне всегда заполнен (\(s_{1{,}1}=1\)).
Формат выходных данных
Выведите единственное целое число — минимальное число ходов для того, чтобы заполнить \(n\) блоков нижнего уровня пирамиды.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
2 1 01 |
1 |
2 |
4 1 00 101 1011 |
4 |
3 |
5 1 10 011 1000 00011 |
6 |
Задачу можно решить рекурсивно.
Пусть текущий ответ равен нулю. Определим \(F(i, j)\) — это функция, которая заполняет все блоки, необходимые для заполнения \(j\)-го блока в \(i\)-м уровне пирамиды, включая сам этот блок. Принцип ее работы таков:
- если текущий блок уже заполнен — возвращаем 0;
- если вызов некорректен (например, на \(i\)-м уровне нет \(j\)-го блока) — возвращаем 0;
- если текущий блок пустой, то надо убедиться в том, что заполнены блоки выше него — заполняем текущий блок и возвращаем \(1+F(i-1, j-1)+F(i-1, j)\).
Будем по порядку рассматривать блоки нижнего уровня пирамиды слева направо, как только очередной блок пустой — будем запускать функцию \(F\) из текущего блока и прибавлять к ответу возвращаемое ей значение.
Также задачу можно решить без рекурсии — итеративно, заполняя необходимые блоки уровень за уровнем, начиная с нижнего.
Сложность решения: \(\mathcal{O}(n^2)\).
Пример программы-решения
Ниже представлено решение на языке Python.
import sys
def solve():
n = int(sys.stdin.readline())
f = [[0 for i in range(h + 1)] for h in range(n)]
for i in range(n):
s = str(sys.stdin.readline().strip())
for j in range(i + 1):
if s[j] == '1':
f[i][j] = 1
need_to_fill = set()
for i in range(n):
if f[-1][i] == 0:
need_to_fill.add(i)
cur_level = n - 1
res = 0
while len(need_to_fill) != 0:
fill_in_next_level = set()
res += len(need_to_fill)
for i in need_to_fill:
if i - 1 >= 0:
if f[cur_level - 1][i - 1] == 0:
fill_in_next_level.add(i - 1)
f[cur_level - 1][i - 1] = 1
if i < len(f[cur_level - 1]):
if f[cur_level - 1][i] == 0:
fill_in_next_level.add(i)
f[cur_level - 1][i] = 1
need_to_fill, fill_in_next_level = fill_in_next_level, set()
cur_level = cur_level - 1
sys.stdout.write(str(res) + '\n')
return
if __name__ == '__main__':
solve()Ниже представлена таблица оценки за группы тестов.
| Группа | Дополнительные ограничения | Баллы |
|---|---|---|
| 1 | \(n\leqslant 3\) | 4 |
| 2 | \(n\leqslant 5\) | 4 |
| 3 | \(n\leqslant 50\) | 4 |
| 4 | — | 10 |
Проверка в каждой группе тестов полная — тестирование не прерывается при неверном ответе. Баллы будут начисляться пропорционально количеству пройденных тестов. Балл за задачу — сумма баллов за каждую подгруппу. Баллы за тестовые примеры не предусмотрены.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 256 Мбайт.
В умном городе работают две вышки интернета, которые обслуживают \(n\) кварталов города. Сейчас администрация планирует установку третьей вышки, и им нужна помощь.
Каждая вышка описывается перестановкой1 из \(n\) элементов, элемент последовательности определяет приоритет, которым обладает обслуживание соответствующего квартала. Чем число больше, тем выше приоритет и, соответственно, выше качество интернет-соединения. Первая вышка описывается перестановкой \(a\), вторая вышка — перестановкой \(b\), третья вышка — перестановкой \(c\).
Общее качество интернета в умном городе сейчас (до установки третьей вышки) определяется последовательностью из \(s\) из \(n\) элементов, где \(s_i=max(a_i, b_i)\), а эффективностью третьей вышки является количество индексов \(i\) таких, что \(c_i > s_i\). Задача: определить оптимальную конфигурацию третьей вышки для достижения ее максимальной эффективности. Если возможных вариантов несколько — допускается вывести любой из них.
Формат входных данных
В первой строке содержится единственное целое число \(n\) (\(1\leqslant n\leqslant 10^5\)) — количество кварталов в умном городе. Во второй строке содержатся \(n\) целых чисел \(a\) (\(1\leqslant a\leqslant n\)) — конфигурация первой вышки. В третьей строке содержатся \(n\) целых чисел \(b\) (\(1\leqslant b\leqslant n\)) — конфигурация второй вышки. Гарантируется, что \(a\) и \(b\) являются перестановками.
Формат выходных данных
Выведите любую перестановку для конфигурации третьей вышки, которая максимизирует значение эффективности третьей вышки.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 1 2 3 3 2 1 |
1 3 2 |
2 |
6 1 5 2 3 4 6 2 6 3 1 5 4 |
3 1 4 5 6 2 |
3 |
5 1 2 3 4 5 1 2 3 4 5 |
2 3 4 5 1 |
Обозначим массив \(m\) такой, что \(m_i=max(a_i, b_i)\). Найдем минимальное значение в этом массиве — пусть это \(m_x=y\), тогда присвоим \(p_x\) такое значение, что больше \(y\), но не больше \(n\), и его еще не использовали. Затем повторим операцию со вторым по самой малой величине значением в \(m\). И так далее, пока не сможем больше сделать ни одного присваивания в \(p\). Остальные значения в \(p\) (незаполненные) можно заполнить любыми числами, чтобы в конце была перестановка, какие именно числа и в каком порядке — на ответ не повлияет.
Чтобы быстро находить \(k\)-е минимальное число в \(m\) и знать его индекс, можно запомнить с каждым значением его индекс (сделать пару «значение» — «индекс») и отсортировать по неубыванию «значений».
Сложность решения: \(\mathcal{O}(n\cdot \log{n})\).
Пример программы-решения
Ниже представлено решение на языке Python.
import sys
def solve():
n = int(sys.stdin.readline())
a = list(map(int, sys.stdin.readline().split()))
b = list(map(int, sys.stdin.readline().split()))
for i in range(n):
a[i] = [max(a[i], b[i]), i]
a.sort()
b = [-1 for i in range(n)]
not_used = set([i for i in range(1, n + 1)])
st = min(a[0][0], n) + 1
for v, ind in a:
while st <= v:
st += 1
if st > n:
break
else:
not_used.discard(st)
b[ind] = st
st += 1
for i in range(n):
if b[i] == -1:
b[i] = not_used.pop()
sys.stdout.write(' '.join(map(str, b)) + '\n')
return
if __name__ == '__main__':
solve()Ниже представлена таблица оценки за группы тестов.
| Группа | Дополнительные ограничения | Баллы |
|---|---|---|
| 1 | \(n=3\) | 2 |
| 2 | \(n\leqslant 10\) | 4 |
| 3 | \(n\leqslant 500\) | 6 |
| 4 | — | 11 |
Проверка в каждой группе тестов полная — тестирование не прерывается при неверном ответе. Баллы будут начисляться пропорционально количеству пройденных тестов. Балл за задачу — сумма баллов за каждую подгруппу. Баллы за тестовые примеры не предусмотрены.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 256 Мбайт.
На складском пространстве умного города имеется один свободный автономный грузовой автомобиль, который можно сдавать в аренду для перевозки грузов между поселениями. Грузовик отправляется в путешествие, но ему нужно вернуться в умный город через \(T\) ч, так как его услугами снова потребуется воспользоваться в умном городе.
В умном городе есть \(n\) поселений, некоторые из них соединены дорогами. Два поселения соединяет не более, чем одна дорога. Всего дорог \(m\) штук, и каждая из них описывается своим числом \(w_i\) — временем в часах для перемещения между соответствующими поселениями.
Заказы на перевозку грузов есть всегда, поэтому считаем, что каждая поездка между двумя поселениями считается как выполненный заказ. Полагаем, что погрузка и разгрузка выполняются моментально, а грузовику не требуется время на техническое обслуживание.
Определите, какое максимальное число заказов может выполнить грузовик в пределах отведенного времени.
Формат входных данных
В первой строке входных данных содержится единственное целое число \(n\) — количество поселений, \(2\leqslant n\leqslant 100\). Во второй строке содержится единственное целое число \(m\) — количество дорог между всеми поселениями, \(1\leqslant m\leqslant \dfrac{n(n-1)}2\). Умный город является поселением с номером один.
Далее следуют \(m\) строк, описывающих дороги между поселениями. Каждая дорога описывается тремя целыми числами u, v, w (\(1\leqslant u < v\leqslant n;~1\leqslant w\leqslant 200\)), где \(u\) и \(v\) — это номера двух поселений, между которыми есть дорога, а \(w\) — время в часах для перемещения по этой дороге. Гарантируется, что каждая пара \((u, v)\) присутствует во входных данных не более одного раза.
В последней строке содержится единственное целое число \(T (1\leqslant T\leqslant 100\)) — время в часах, отводимое на аренду грузового автомобиля.
Формат выходных данных
Выведите единственное целое число — максимальное число заказов, которые может выполнить грузовик в указанное время. Помните, что через \(T\) часов грузовик должен быть на складе умного города.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 3 1 2 8 2 3 2 1 3 1 5 |
4 |
2 |
3 3 1 2 8 2 3 2 1 3 1 6 |
6 |
3 |
5 7 1 2 4 1 3 9 3 5 2 2 3 1 4 5 13 1 4 8 2 5 1 10 |
4 |
Пусть \(dp[i][j]\) — максимальное число заказов, которое можно выполнить в поселении \(j\) в момент времени \(i\). Матрица \(dp\) имеет размер \((T+1)\times n\), изначально заполнена \(-inf\), кроме ячейки \(dp[0][0]\) — там находится значение 0.
Будем последовательно перебирать \(i\) с 1 до \(T\) включительно.
Внутри будем также перебирать текущее поселение \(j\).
Посмотрим на каждое поселение \(u\) из текущего, в которое можем переместиться.
Можем обновить \(dp[i][j] = max(dp[i - 1][j],~dp[i][j], dp[i - w_{ju}][u] + 1).\)
Некоторые особые случаи:
- \(dp[i - w_{j\rightarrow u}][u]\) рассматривается только когда \(i - w_{j\rightarrow u}\) больше или равно нулю;
- \(dp[i - w_{j\rightarrow u}][u] + 1\) — слагаемое (+1) используется только когда текущая комната не является стартовой (т. е. в ней есть кнопка).
Сложность решения: \(\mathcal{O}(T\cdot m)\).
Так как цикл на \(T\) итераций, в нем рассматривается каждое ребро два раза, остальными операциями пренебрегаем.
Пример программы-решения
Ниже представлено решение на языке Python.
import sys
INF = 1 << 90
def solve():
n = int(sys.stdin.readline())
m = int(sys.stdin.readline())
g = [[] for i in range(n)]
for i in range(m):
u, v, w = map(int, sys.stdin.readline().split())
u, v = u - 1, v - 1
g[u].append([v, w])
g[v].append([u, w])
T = int(sys.stdin.readline())
dp = [[-INF for i in range(n)] for time in range(0, T + 1)]
dp[0][0] = 0
for time in range(1, T + 1):
for node in range(n):
dp[time][node] = max(dp[time - 1][node], dp[time][node])
for u, w in g[node]:
if time - w < 0:
continue
dp[time][node] = max(dp[time][node], dp[time - w][u] + 1)
sys.stdout.write(str(dp[T][0]) + '\n')
return
if __name__ == '__main__':
solve()Ниже представлена таблица оценки за группы тестов.
| Группа | Дополнительные ограничения | Баллы |
|---|---|---|
| 1 | \(n\leqslant 3\) | 2 |
| 2 | \(n\leqslant 5;~T\leqslant 10\) | 3 |
| 3 | \(n\leqslant 10;~m=n-1\) | 6 |
| 4 | — | 14 |
Проверка в каждой группе тестов полная — тестирование не прерывается при неверном ответе. Баллы будут начисляться пропорционально количеству пройденных тестов. Балл за задачу — сумма баллов за каждую подгруппу. Баллы за тестовые примеры не предусмотрены.
- Перестановкой длины \(n\) является массив из \(n\) целых чисел, в котором каждое число от 1 до \(n\) встречается ровно один раз.↩︎