Предметный тур. Физика. 3 этап
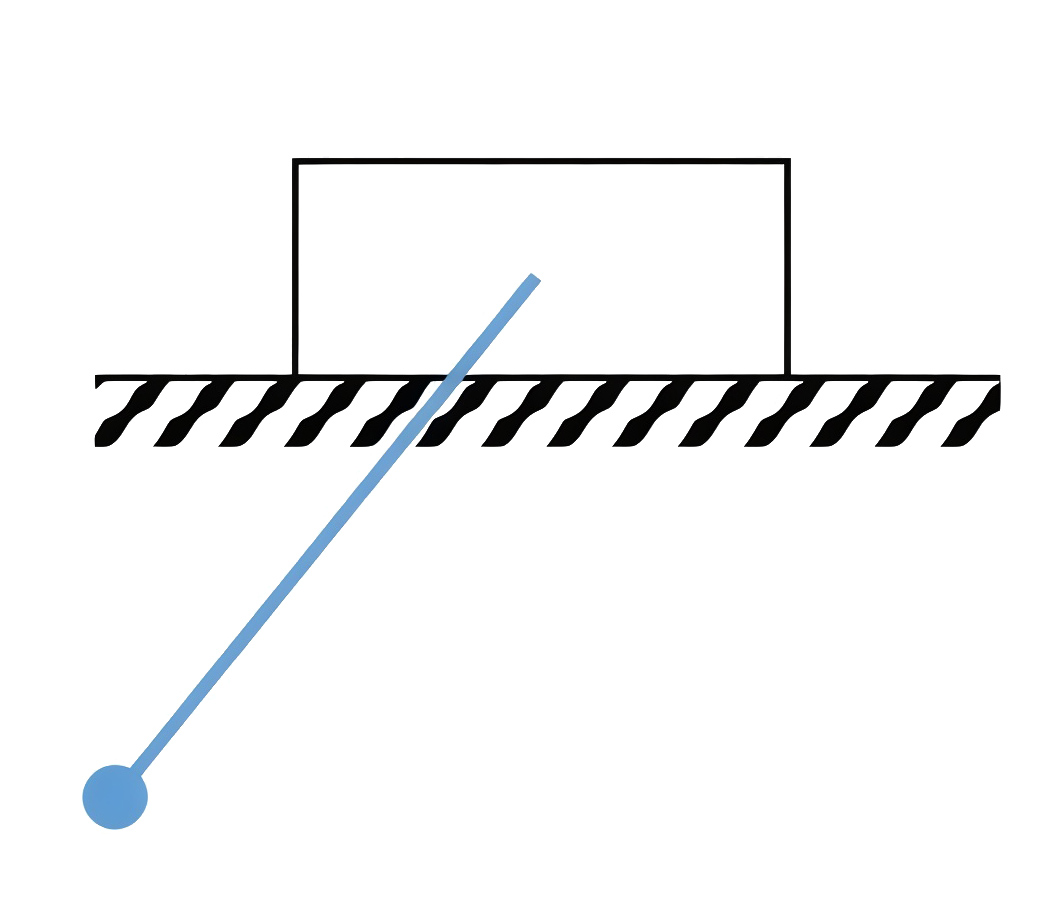
В умном городе поставили новые необычные качели. Но прежде чем пускать на них ребят, для их безопасности, надо все просчитать! Упрощенная схема качелей выглядит так: на абсолютно гладкой поверхности лежит брусок массой \(M\), к которому прикреплен математический маятник длиной \(L\) и массой \(m\) (см. рис. 1.1). Найдите скорость бруска относительно поверхности земли в момент времени, когда угловая скорость маятника в нижней точки равна \(\omega\).
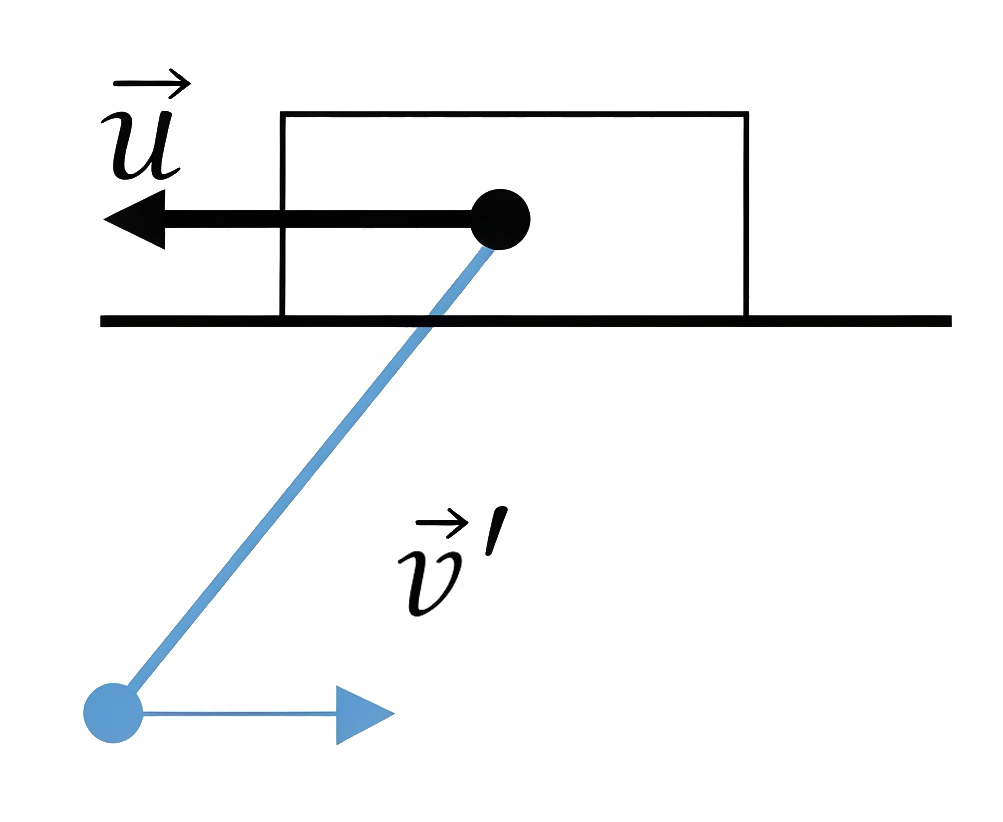
На рис. 1.1 \(\vec u\) — скорость бруска относительно земли, \(\vec{v^{\prime}}\) — скорость маятника относительно бруска.
Найдем скорость маятника относительно земли: \[v =v '-u\text{,~где}~v '=\omega L\rightarrow v =\omega L-u.\]
Запишем закон сохранения импульса относительно \(CO\), связанной с землей: \[uM=m(\omega L-u).\]
Преобразуем: \[uM+mu=m\omega L.\]
Найдем: \[u=m\omega \frac L{m+M}.\]
\(m\omega \dfrac L{m+M}.\)
| Критерий | Баллы | Подзадача |
|---|---|---|
| 1 | 8 | Найдена скорость маятника относительно земли |
| 2 | 8 | Записан закон сохранения импульса |
| 3 | 4 | Получено выражение для скорости бруска |
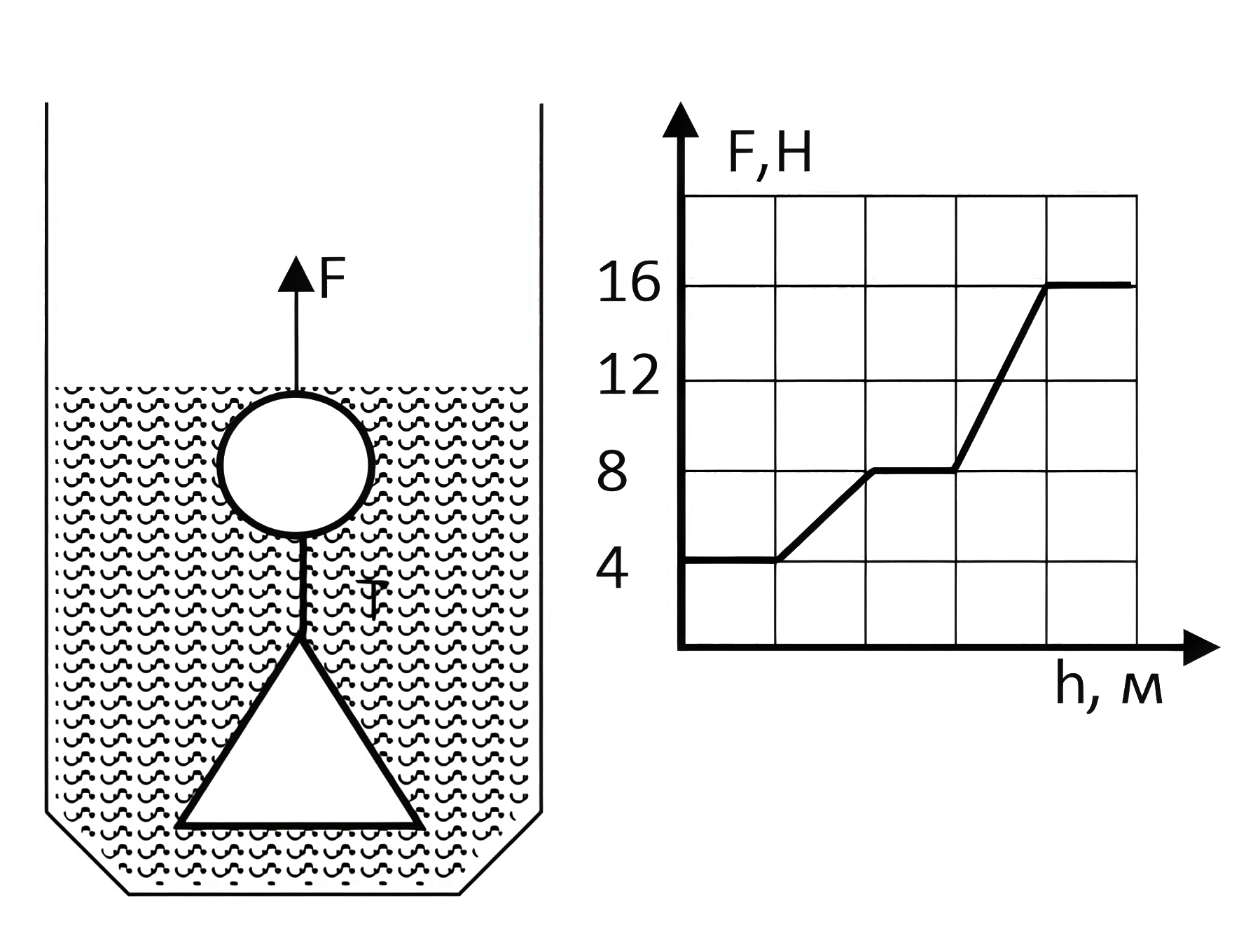
В умном городе провели эксперимент. Из сосуда, заполненного жидкостью, равномерно достают два связанных невесомой нитью груза, сделанных из одного материала, к одному из которых прикреплен динамометр (см. рис. 1.3).
Зависимость показаний динамометра \(F\) от высоты подъема представлена на графике. Найдите натяжение нити \(T\) в момент времени, когда первый груз полностью выйдет из жидкости. Ответ округлите до десятых.
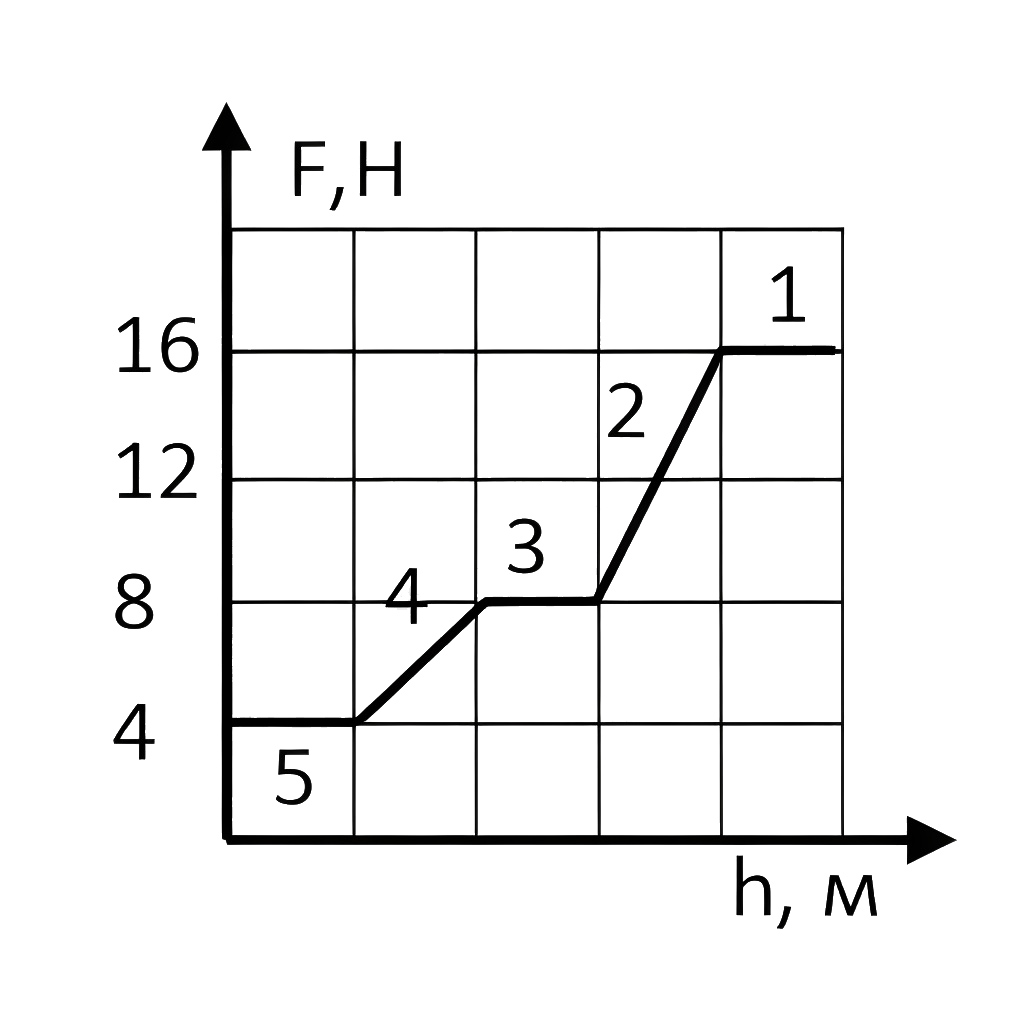
Сила \(F\) остается постоянной, пока не изменяется сила Архимеда, действующая на грузы. Поэтому горизонтальные участки 1, 3, 5 на рис. 1.4 отвечают случаям, когда уровень жидкости находится ниже нижнего груза, между верхним и нижним грузами и выше верхнего груза соответственно. Наклонные участки 2 и 4 соответствуют частичному погружению нижнего и верхнего грузов.
На участке 1 сила \(F = 16\) H равна сумме весов верхнего \(P_1\) и нижнего \(P_2\) грузов: \[\label{yg8-030201} 16=P_1+P_2.\]
На участке 3 сила \(F = 8\) H равна сумме \(P_1\) и \(P_2\) за вычетом силы Архимеда \(F_{A2}\), действующей на нижний груз: \[\label{yg8-030202} 8=P_1+P_2-F_{A2}.\]
На участке 5 сила \(F = 4\) H равна сумме \(P_{_1}\) и \(P_{_2}\) за вычетом силы Архимеда \(F_{A1}\) и \(F_{A2}\), действующих на нижний и верхний груз: \[\label{yg8-030203} 4=P_1+P_2-F_{A1}-F_{A2}.\]
Вычитая \eqref{yg8-030202} из \eqref{yg8-030201}, получим \(F_{A2} = 8\) H.
А вычитая \eqref{yg8-030203} из \eqref{yg8-030202}, получим \(F_{A1} = 4\) H.
На третьем участке графика верхний груз полностью вышел из жидкости, и искомая сила натяжения \(T\) нижней нити равна разности сил тяжести и Архимеда, действующих на груз: \[\label{yg8-030204} T=P_2-F_{A2}.\]
Чтобы найти \(P_2\), заметим, что так как грузы выполнены из одинакового материала, отношение весов грузов \(\dfrac {P_2}{ P_1}\) равно отношению их объемов, а следовательно, сил Архимеда: \[\label{yg8-030205} \frac{P_2}{P_1}=\frac{F_{A2}}{F_{A1}}=2.\]
Из \eqref{yg8-030201} и \eqref{yg8-030205} найдем вес нижнего груза: \(P_2=10{,}7\text{ H.}\)
Подставив найденные значения \(P_2\) и \(F_{A2}\) в \eqref{yg8-030204}, получим \(T = 2{,}7\) Н.
Примечание
Соотношение \eqref{yg8-030205} также можно получить, сравнивая наклоны кривой на участках 2 и 4 графика, представленного на рис. 1.4.
2,7 Н.
| Критерий | Баллы | Подзадача |
|---|---|---|
| 1 | 1 | Установлено, какой участок графика соответствует положению грузов в жидкости |
| 2 | 2 | Записано уравнение сил для полностью извлеченных из воды грузов |
| 3 | 2 | Записано уравнение сил для случая, когда из воды извлечен только верхний груз |
| 4 | 2 | Записано уравнение сил для случая, когда оба груза под водой |
| 5 | 2 | Найдены значения сил Архимеда, действующих на каждый груз |
| 6 | 3 | Найдено значение натяжения нити \(T\) |
| 7 | 3 | Получено соотношение объемов грузов |
Все мы в умном городе любим иногда вечером посмотреть короткие ролики в любимых социальных сетях. Нам попался один интересный ролик, где раскаленный шарик кладут на лед. Мы решили рассчитать, как глубоко этот шарик сможет «проплавить» лед, прежде чем остановится.
Возьмем оловянную картечь массой 70 г, нагреем до температуры 200 °C и положим на лед. Определите глубину (самую нижнюю точку), на которую картечь погрузится в лед, если удельная теплоемкость олова 230 Дж/(кг\(~°\)C), плотность олова 7,3 г/см\(^3\), плотность льда 0,9 г/см\(^3\), удельная теплота плавления льда \(3{,}3\cdot 10^5\) Дж/кг. Температура окружающей среды 0 °C. Картечь считайте шаром.
Так как картечь — шар, радиус этого шара равен \[r=\sqrt[3]{\frac{3-V_c}{4\pi}},\] где \(V_c=\dfrac M{\rho_0}\). Отсюда \[\label{yg8-030301} r=\sqrt[3]{\frac{3M}{4\pi\rho_0}}.\]
Поставим значение \(r=\displaystyle\sqrt[3]{\frac {3\cdot 0{,}07}{4 \pi 7300}}=0{,}013\) м.
Картечь радиуса \(r\) расплавит объем льда, состоящий из объема цилиндра \(\pi r^2h\) и объема половины шара \(\dfrac 23\pi r^3\), т. е. \(\pi r^2h+\dfrac 23 \pi r^3\), где \(h\) — высота цилиндра.
Для плавления льда нужно потратить количество теплоты равное: \[\label{yg8-030302} Q=\lambda(\pi r^2h+\frac 23 \pi r^3)\rho_1,\] где \(\lambda\) — удельная теплота плавления льда, \(\rho_1\) — плотность льда.
Количество теплоты, выделенное картечью при остывании: \[\label{yg8-030303} Q=\frac 43 \pi r^3\rho_0c(t-t_1),\] где \(c\) — удельная теплоемкость олова.
Приравнивая \eqref{yg8-030302} и \eqref{yg8-030303}, получим \[\frac{4}{3}\pi r^3\rho_0c(t-t_1)=\lambda (\pi r^2h+\frac 23\pi r^3)\rho_1,\] откуда \[\label{yg8-030304} h=\frac{r(4\rho_0c(t-t_1)-2\lambda\rho_1)}{3\lambda\rho_1}.\]
Подставим \eqref{yg8-030301} в \eqref{yg8-030304}: \[h=\sqrt[3]{\displaystyle\frac{3M}{4\pi\rho_0}}\cdot \frac{4\rho_0c(t-t_1)-2\lambda\rho_1}{3\lambda\rho_1}.\]
Подставим численные значения: \[h=\sqrt[3]{\displaystyle\frac{3\cdot 0{,}07}{4\pi \cdot 7300}}\cdot \frac{4\cdot 7300\cdot 230\cdot 200-2\cdot 3{,}3\cdot 10^5\cdot 900} {3\cdot 3{,}3\cdot 10^5\cdot 900}=0{,}011\text{ м.}\]
Глубина погружения картечи \(H=0{,}013+0{,}011=0{,}024\) м (высота цилиндра плюс радиус шара).
0,024 м.
| Критерий | Баллы | Подзадача |
|---|---|---|
| 1 | 3 | Записано выражение \eqref{yg8-030301} для радиуса шара |
| 2 | 4 | Записано выражение для объема льда |
| 3 | 4 | Записано выражение для нахождения количества теплоты, потраченной на плавление льда |
| 4 | 4 | Записано выражение для нахождения количества теплоты, отданной картечью |
| 5 | 6 | Получено выражение для высоты цилиндра h |
| 6 | 3 | Найдено числовое значение h |
| 7 | 1 | Найдена глубина погружения картечи |
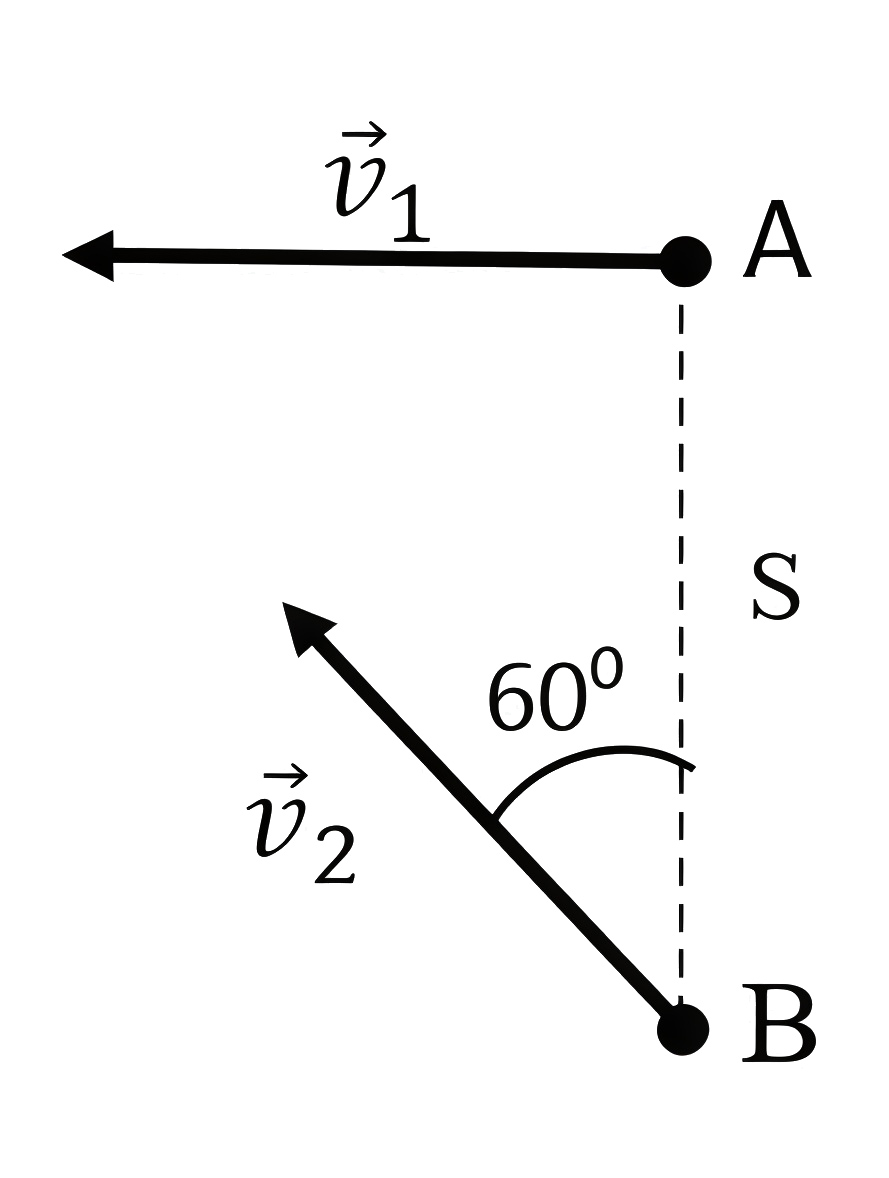
В умном городе стало много квадрокоптеров, и понадобилось срочно разработать алгоритм, помогающий предотвратить их столкновение. Два квадрокоптера летают на одной высоте с постоянными и одинаковыми по модулю скоростями: \[|\vec{v_1}|=|\vec{v_2}|=|\vec{v}|.\]
В какой момент времени расстояние между ними будет минимальным и чему оно будет равно, если их начальное взаимное расположение показано на рис. 1.6? В начальный момент времени расстояние между ними \(S\).
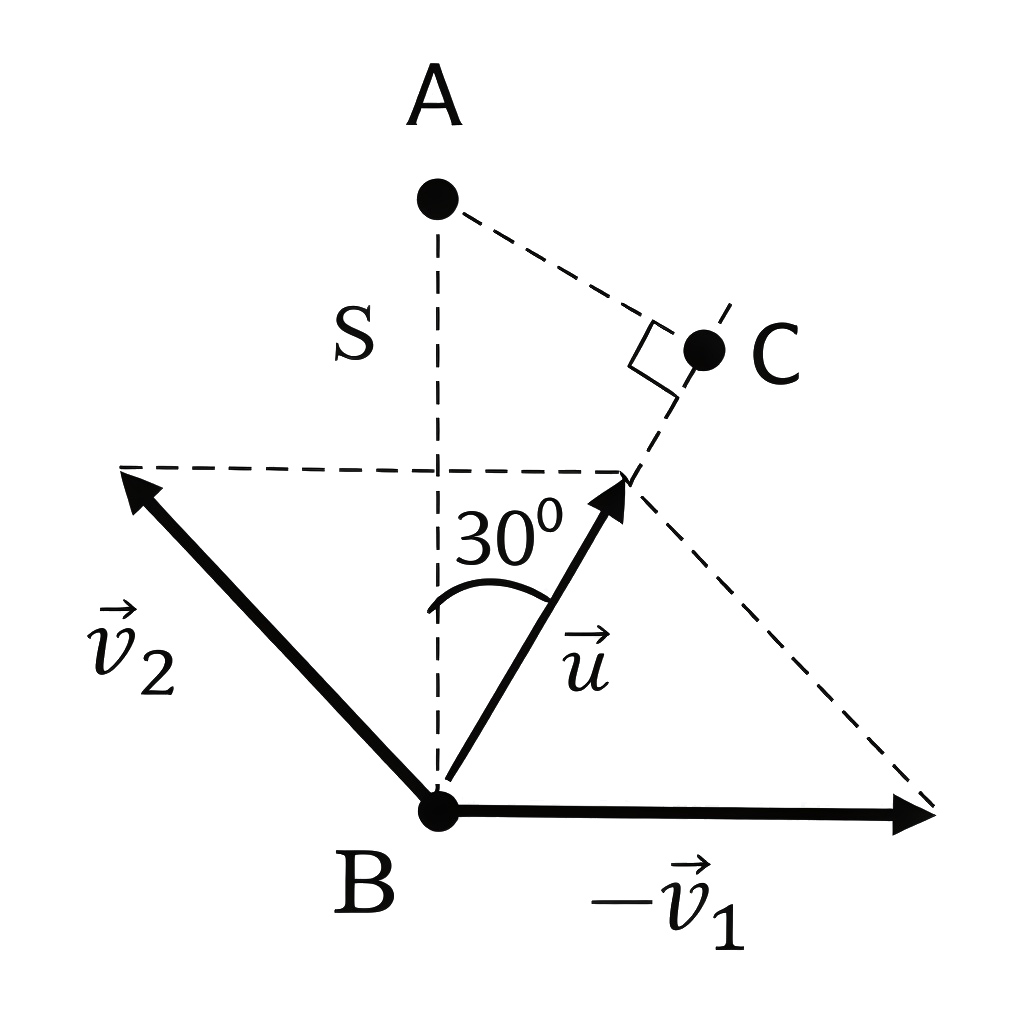
Перейдем в систему отсчета, связанную с «коптером» 1. Ее начало отсчета поместим в точку \(A\). На рисунке скорость \(\vec{u}\) — это относительная скорость, которая по модулю равна \(v\) и направлена под углом \(30°\) к линии \(AB=S\). Найдем минимальное расстояние между «коптерами». Для этого опустим перпендикуляр \(AC\) из \(A\) на продолжение скорости \(u\). Из рис. 1.7 \(AC=S\cdot \sin{30}°=\dfrac S2\).
Время, за которое они сблизятся на минимальное расстояние: \[t=\frac{S\cdot \cos{30}°}v=\frac{\sqrt{3}S}{2v}.\]
\(t=\dfrac{\sqrt{3}S}{2v}\).
| Критерий | Баллы | Подзадача |
|---|---|---|
| 1 | 3 | Проведены рассуждения о выборе системы отсчета |
| 2 | 2 | Нарисован рисунок |
| 3 | 2 | Показано минимальное расстояние на рисунке между «коптерами» |
| 4 | 4 | Найдено аналитическое выражение для минимального расстояние и проведены расчеты |
| 5 | 4 | Найдено время |
Для умного города разработали модульный электрический нагреватель, нагревательные элементы которого можно подключать по-разному. Систему испытывали с двумя нагревательными элементами разных сопротивлений. При включении только первого элемента электрический нагреватель нагрелся до температуры 110 °C, а если включить только второй — нагреется до температуры 200 °C. До какой температуры нагреется электрический нагреватель, если нагревательные элементы будут включены последовательно или параллельно? Температуру окружающей среды примите равной 20 °C.
Пусть сопротивление нагревательных элементов будет соответственно \(R_1\) и \(R_2\), а напряжение в цепи \(U\). Тогда \[\label{yg8-030501} \frac{U^2}{R_1}=B(t_1-t_0),\] \[\label{yg8-030502} \frac{U^2}{R_2}=B(t_2-t_0).\]
Последовательное соединение: \[\label{yg8-030503} \frac{U^2}{R_1+R_2}=B(t_3-t_0).\]
Параллельное соединение: \[\label{yg8-030504} \frac{U^2(R_1+R_2)}{R_1R_2}=B(t_4-t_0),\] где \(t_3\), \(t_4\) — температуры, до которых нагреется электрический нагреватель, \(B\) — коэффициент пропорциональности.
Выразим из \eqref{yg8-030501} и \eqref{yg8-030502} \(\displaystyle\frac B{U^2}\) и приравняем левые части: \[\frac{t_1-t_0}{R_1}=\frac{t_2-t_0}{R_2}\Rightarrow\frac{R_2}{R_1}=\frac{180}{90}=2.\]
Выразим из \eqref{yg8-030503} и \eqref{yg8-030504} \(\displaystyle\frac B{U^2}\) и приравняем левые части к \eqref{yg8-030501}: \[\frac{90}{R_1}=\frac{t_3-t_0}{R_1+R_2}\Rightarrow t_3=290~°\text{C},\] \[\frac{90}{R_1}=\frac{(t_4-t_0)(R_1+R_2)}{R_1R_2}\Rightarrow t_4=80~°\text{C}.\]
- при последовательном — \(t=290~°\)C;
- при параллельном — \(t=80~°\)C.
| Критерий | Баллы | Подзадача |
|---|---|---|
| 1 | 1 | Записаны уравнения, описывающие связь тепловой мощности с температурой для отдельных включений первого и второго элементов |
| 2 | 3 | Записано уравнение, описывающее связь тепловой мощности с температурой при последовательном включении элементов |
| 3 | 3 | Записано уравнение, описывающее связь тепловой мощности с температурой при параллельном включении элементов |
| 4 | 6 | Найдено аналитическое выражение для температуры при последовательном включении элементов |
| 5 | 3 | Произведен расчет температуры при последовательном включении элементов |
| 6 | 6 | Найдено аналитическое выражение для температуры при параллельном включении элементов |
| 7 | 3 | Произведен расчет температуры при параллельном включении элементов |
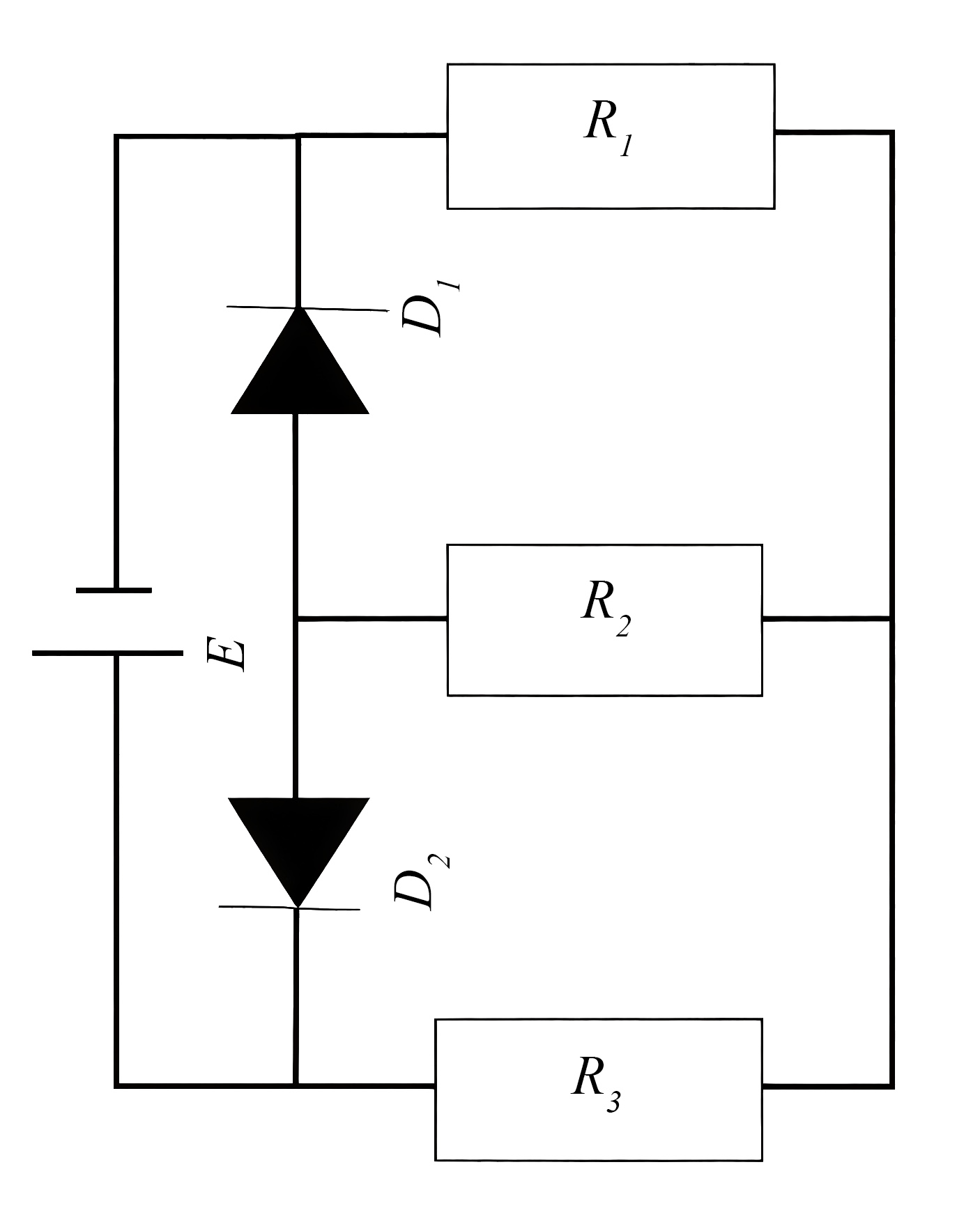
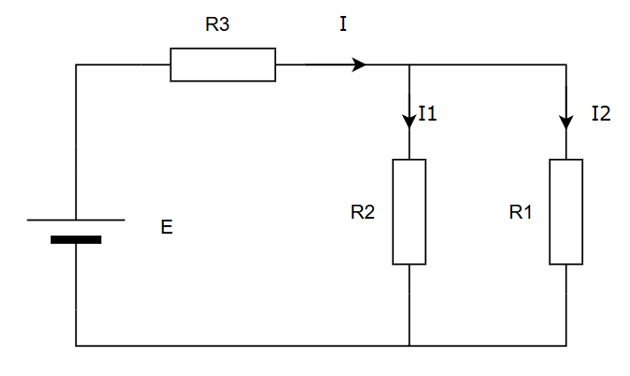
В схеме, изображенной на рис. 2.1, найдите ток, идущий через сопротивление \(R_2\).
ЭДС батареи \(E = 9\) В, остальные параметры элементов схемы показаны на рисунке. \(R_1=R_3=2R\), \(R_2=R= 4{,}5\) Ом. Диоды и ЭДС являются идеальными.
Диод \(D_2\) закрыт, диод \(D_1\) открыт.
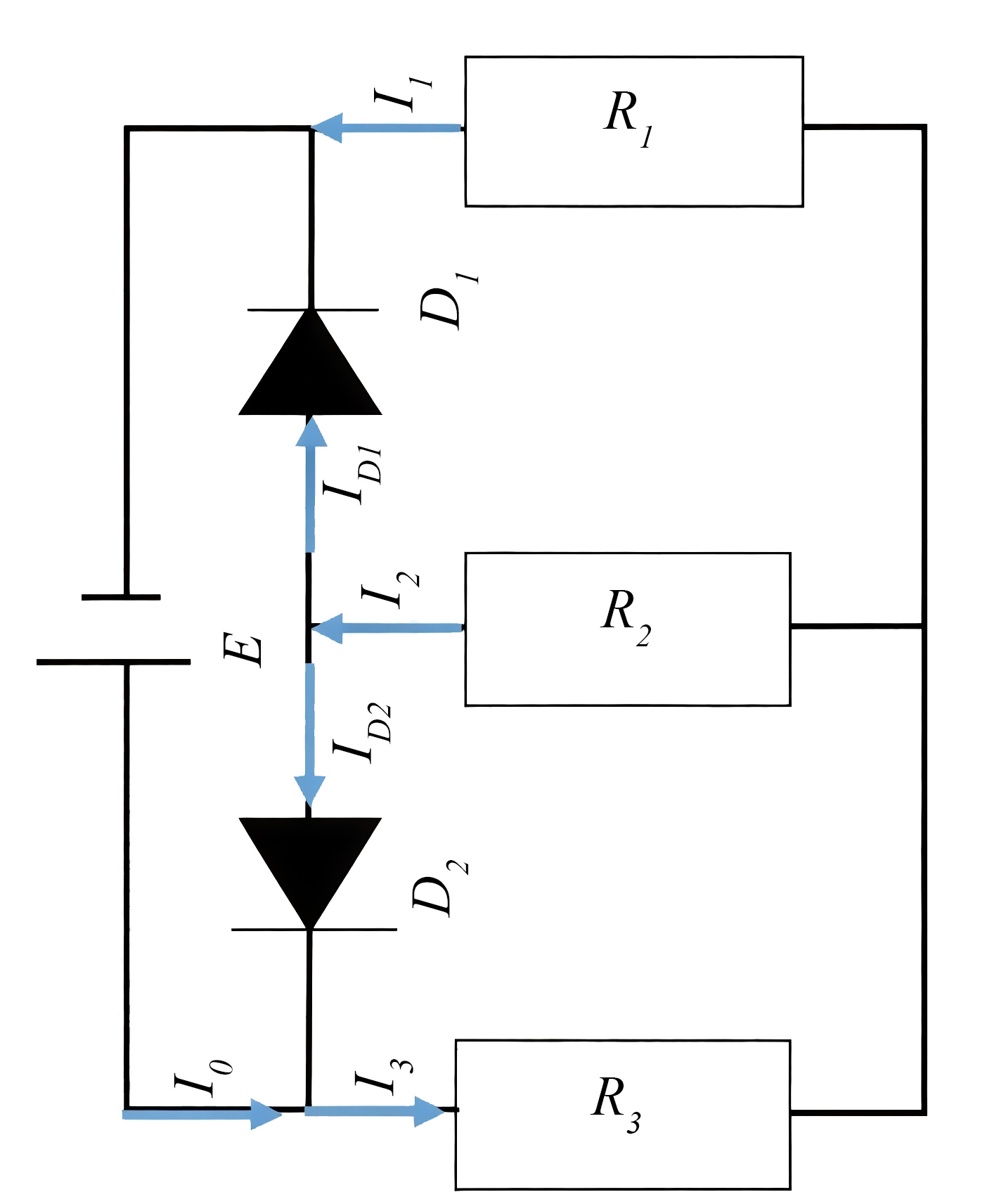
Альтернативная схема представлена на рис. 2.2.
Система уравнений по законам Кирхгофа: \[I=I_1+I_2;\] \[E=R_1I_1+R_3I;\] \[E=R_2I_2+R_3I.\]
Решая систему уравнений, получим: \[I=\frac{E(R_1+R_2)}{R_1 R_3+R_1 R_2+R_2 R_3};\] \[I_1=\frac{ER_2}{R_1 R_3+R_1 R_2+R_2 R_3};\] \[I_2=\frac{ER_1}{R_1 R_3+R_1 R_2+R_2 R_3}.\]
Расставим токи в цепи.
Запишем систему уравнений по законам Кирхгофа: \[\label{yg10-030301} I_0+I_{D2}=I_3 ;\]
\[\label{yg10-030102} I_{D1}+I_{D2}=I_2 ;\]
\[\label{yg10-030103} I_1+I_2=I_3;\]
\[\label{yg10-030104} E=R_1I_1+R_3I_3;\]
\[\label{yg10-030105} E=R_2I_2+R_3I_3;\]
\[\label{yg10-030106} 0=R_1I_1-R_2I_2.\]
Подставим численные значения в уравнений \eqref{yg10-030104}–\eqref{yg10-030106}, получим: \[\label{yg10-030107} 9=9I_1+9I_3\Rightarrow 1=I_1+I_3;\]
\[\label{yg10-030108} 9=4{,}5I_2+9I_3\Rightarrow 2=I_1+2I_3;\]
\[\label{yg10-030109} 0=9I_1-4{,}5I_2\Rightarrow I_2=2I_1.\]
Подставим \eqref{yg10-030109} в \eqref{yg10-030103}: \[I_3=3I_1,\] а теперь подставим в \eqref{yg10-030107} \(I_1=\displaystyle\frac 14 \text{ А},\) из \eqref{yg10-030109} следует, что \(I_2=\displaystyle\frac 12 \text{ А}.\)
Примечания
\[0=R_2I_2+R_3I_3.\]
Так как сумма двух положительных величин не может быть равной 0, ток через диод 2 не идет (токи \(I_3\) и \(I_2\) не могут быть отрицательными), поэтому получаем первое решение.
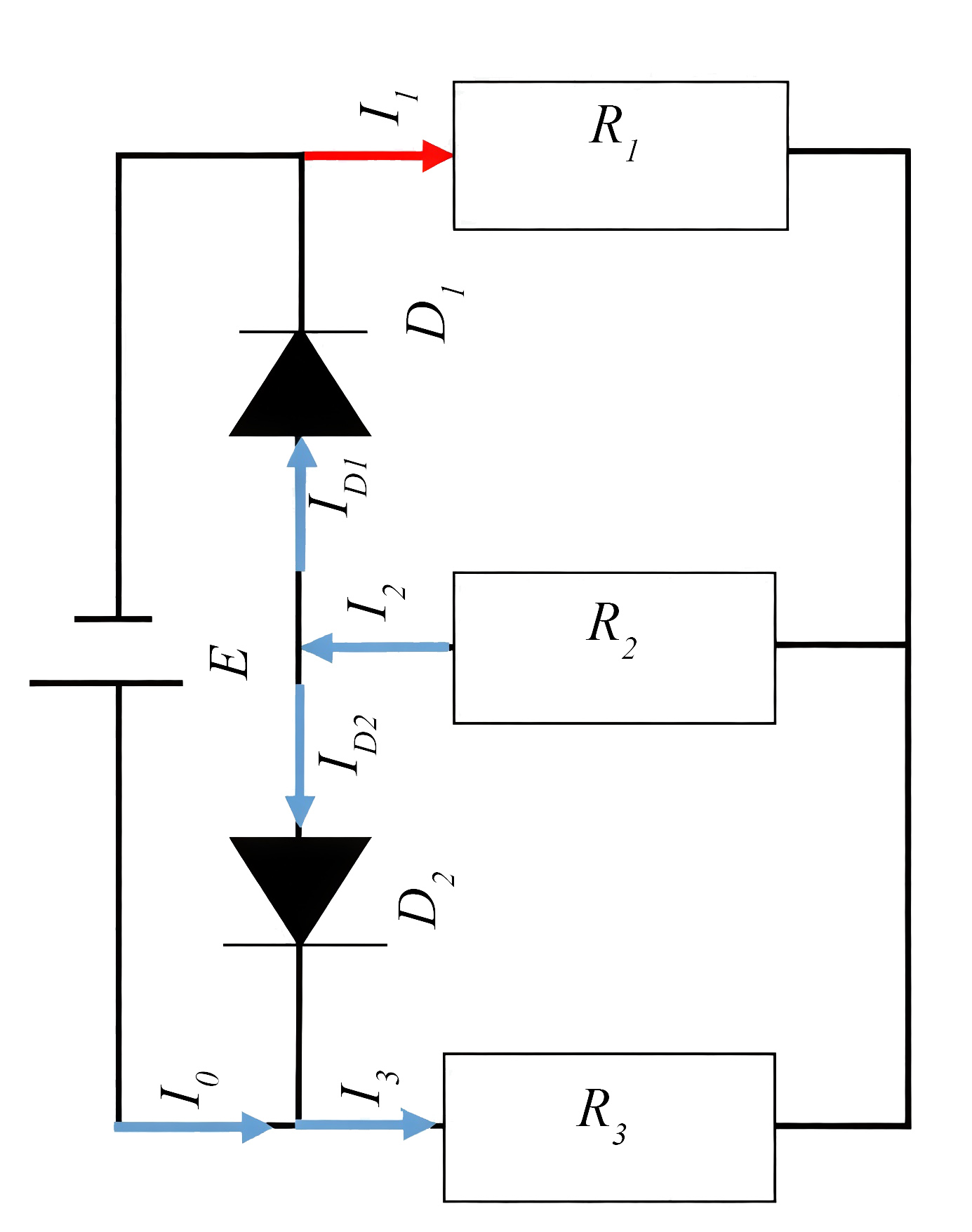
Возможно другое направление токов в схеме.
Запишем систему уравнений по законам Кирхгофа: \[\label{yg10-030110} I_0+I_{D2}=I_3 ;\]
\[\label{yg10-030111} I_{D1}+I_{D2}=I_2 ;\]
\[\label{yg10-030112} I_2=I_1+I_3;\]
\[\label{yg10-030113} E=R_1I_1+R_3I_3;\]
\[\label{yg10-030114} E=R_2I_2+R_3I_3;\]
\[\label{yg10-030115} 0=R_2I_2+R_3I_3;\]
\[\label{yg10-030116} 0=R_1I_1+R_2I_2.\]
Сумма двух положительных величин не может быть равной 0, поэтому из равенства \eqref{yg10-030116} вытекает противоречие (уравнение неверное).
Сумма двух одних и тех же величин равна разным значениям, поэтому из \eqref{yg10-030114} и \eqref{yg10-030115} вытекает противоречие.
Единственное правильное направление токов представлено в решении 1.
0,5 А.
| Критерий | Баллы | Подзадача |
|---|---|---|
| 1 | 6 | Правильно расставлены возможные направления токов в цепи и представлена эквивалентная схема |
| 2 | 6 | Правильно записаны законы Кирхгофа |
| 3 | 4 | Правильно найдено выражение для тока |
| 4 | 4 | Правильно рассчитан ток |
В умном городе решили добывать электроэнергию из магнитного поля. Для этого собрали экспериментальную установку. В однородном магнитном поле индукцией 6 мТл перпендикулярно силовым линиям находится квадратная рамка из латунной проволоки со стороной 30 см. Какой заряд протечет по рамке за время ее поворота на угол 45°? Площадь поперечного сечения латунной проволоки 4 мм\(^2\), удельное сопротивление 0,025 (Ом\(\cdot\)мм\(^2\))/м. Результат округлите до целого и представьте в милликулонах (мКл).
\[\label{yg10-030201} I=\frac{\Delta q}{\Delta t}\Rightarrow \Delta q=I\cdot \Delta t.\]
Сила тока в проводнике найдем по закону Ома: \[\label{yg10-030202} I=\frac{|\varepsilon_i|}R.\]
Площадь квадрата \(S=a^2\).
Сопротивление проволоки: \[\label{yg10-030203} R=\rho \frac l{S_c} =\rho \frac{4a}{S_c}.\]
\(S_c\) — площадь поперечного сечения проводника.
ЭДС индукции: \[\label{yg10-030204} \varepsilon_i = -\frac{\Delta \Phi}{\Delta t} = \frac{\Phi_1 - \Phi_2}{\Delta t},\] где: \[\Phi_1=B\cdot S\cdot \cos{0},\] \[\Phi_2=B\cdot S\cdot \cos{45}.\]
Подставив \eqref{yg10-030202}, \eqref{yg10-030203} и \eqref{yg10-030204} в \eqref{yg10-030201} получим:
\[\Delta q=I\Delta t=- \frac{\Delta\Phi}{\Delta tR}\Delta t =\displaystyle\frac{\Phi_1-\Phi_2}R =\displaystyle\frac{B\cdot S}R(\cos{0}-\cos{45}) =\frac{B\cdot S_c\cdot a}{4\rho \cdot l}\cdot \frac{2-\sqrt{2}}2;\]
\[\Delta q=\frac{6\cdot 10^{-3}\cdot 4\cdot 10^{-6}\cdot 0{,}3}{4\cdot 0{,}025\cdot 10^{-6}}\cdot \frac{2-\sqrt{2}}2=0{,}021\text{ Кл}.\]
21 мКл.
| Критерий | Баллы | Подзадача |
|---|---|---|
| 1 | 6 | Правильно записаны формулы расчета ЭДС индукции, силы тока и сопротивления |
| 2 | 2 | Правильно записана формула расчета сопротивления |
| 3 | 8 | Правильно записана формула нахождения протекающего по проводнику заряда |
| 4 | 4 | Правильно выполнены расчеты |
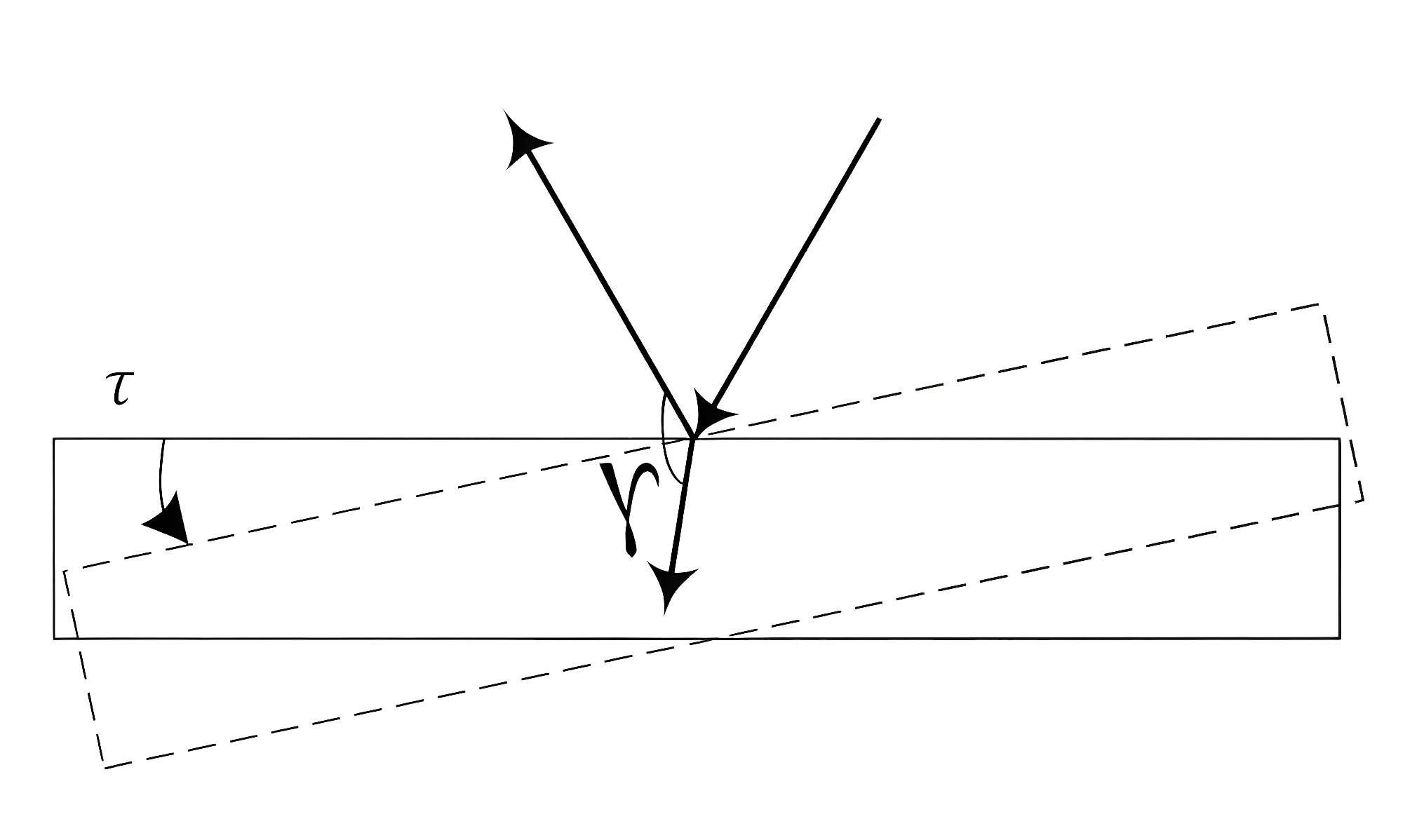
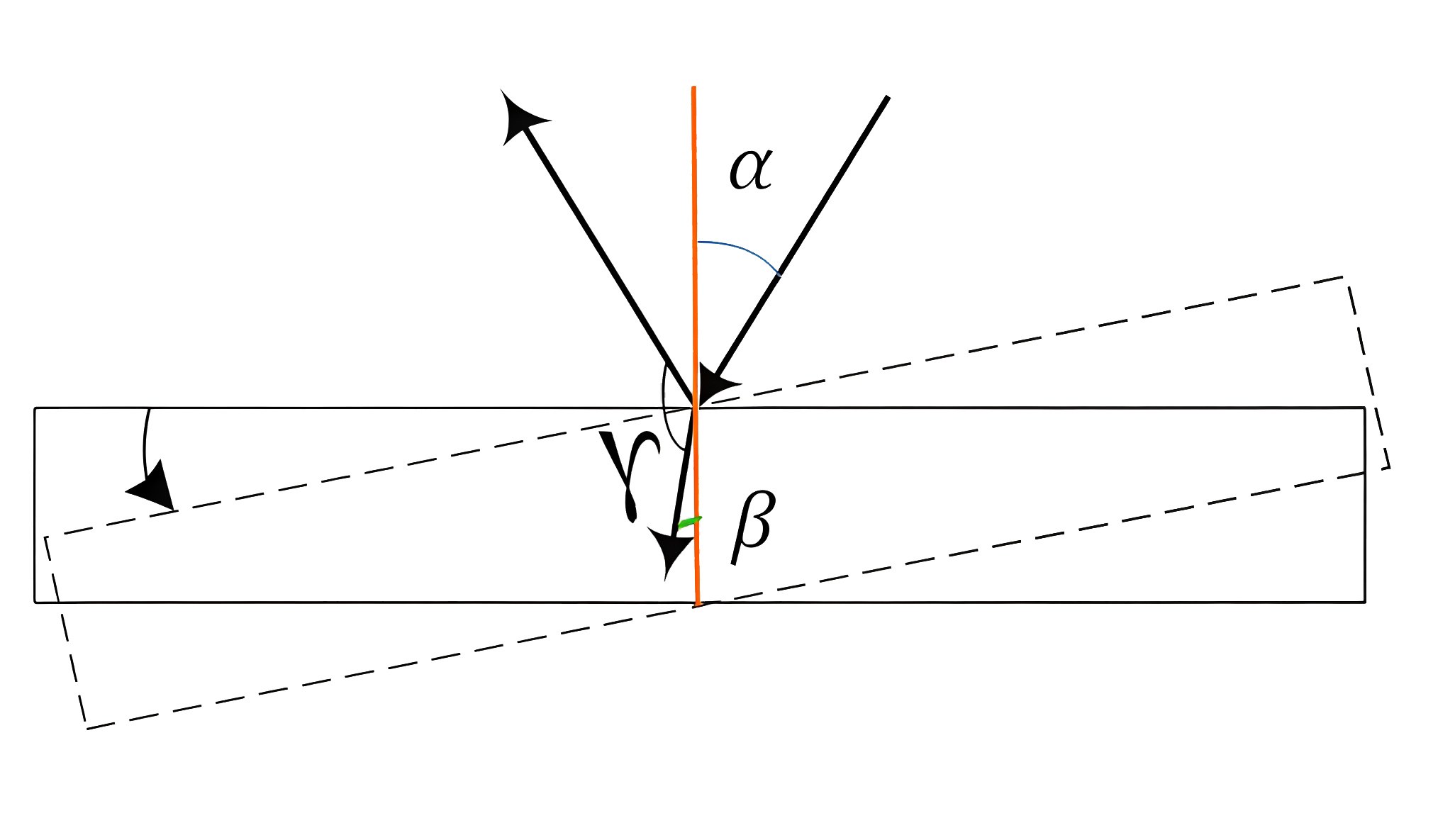
Инженеры умного города проектируют прибор, измеряющий угол между падающим и отраженным лучом. При очередном испытании прибора использовали погруженную в воду плоскопараллельную пластинку из акрилового стекла. При горизонтальном положении пластинки прибор измерил угол в 60° 30\(^\prime\). Найдите изменение угла \(\gamma\), образованного отраженным и преломленным лучами (как показано на рис. 2.5), если повернуть пластинку на \(\tau=15°\). Показатели преломления воды (\(n_\text{в}\)) и акрилового стекла (\(n_\text{с}\)) равны 1,33 и 1,49 соответственно. Ответ представьте в виде 0° 0\(^\prime\), округлите до целого значения угловых минут.
Из рис. 2.6 видно, что первоначальный угол падения \(\alpha=30°~15^\prime\).
Так как стеклянная поверхность повернулась, то на такой же угол повернулся перпендикуляр, опущенный на нее, следовательно, угол падения изменился на такое же значение и равен \(\alpha_1=45°~15^\prime\).
Найдем угол \(\gamma\): \[\gamma=2\pi -\alpha-\beta,\] где \(\beta\) — это угол преломления.
\[\frac{\sin{\alpha}}{\sin{\beta}}=\frac{n_\text{с}}{n_\text{в}}\Rightarrow \sin{\beta}=\frac{n_\text{в}}{n_\text{с}}\sin{\alpha}.\]
Такие же рассуждения проводим после поворота пластины: \[\gamma_1=2\pi-\alpha_1-\beta_1,\]
\[\frac{\sin{\beta_1}}{\sin{\beta_1}}=\frac{n_\text{с}}{n_\text{в}}\Rightarrow \sin{\beta_1}=\frac{n_\text{в}}{n_\text{с}}\sin{\beta_1}.\]
Найдем изменение угла \(\gamma\): \[\gamma-\gamma_1=\alpha_1+\beta_1-\alpha-\beta.\]
Подставим численные значения: \[\gamma-\gamma_1=45{,}25+39{,}34-30{,}25-26{,}726=27{,}617\text{ или}~27°~37^\prime.\]
\(27°~37^\prime.\)
| Критерий | Баллы | Подзадача |
|---|---|---|
| 1 | 5 | Правильно найдены углы \(\alpha\) и \(\beta\) |
| 2 | 5 | Правильно найдены углы \(\alpha_1\) и \(\beta_1\) |
| 3 | 5 | Правильно найдено выражение для \(\gamma-\gamma_1\) и выполнены расчеты |
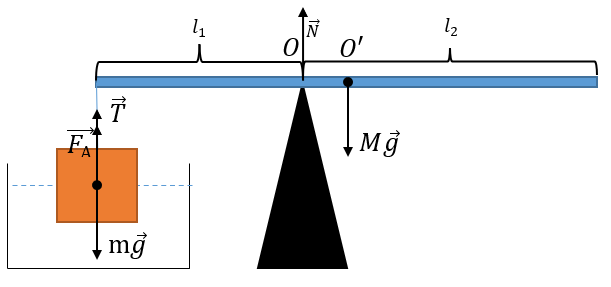
Коллеги из соседнего умного города подарили нам весы собственной разработки, но совсем не объяснили, как они работают, а значит, надо разобраться. Сделали все по инструкции. Однородный медный куб со стороной 1 см подвесили на неравноплечих весах и погрузили куб в воду наполовину. В каком отношении должны делиться плечи весов, чтобы весы находились в равновесии? Также в опоре весов установлен динамометр. Что он показывает, когда весы находятся в равновесии? Примите плотность воды за 1 г/см\(^3\), плотность меди — 8,9 г/см\(^3\), ускорение свободного падения — 10 м/с\(^2\) и массу коромысла — 2 г.
Центр масс коромысла точка \(O'\) находится на расстоянии \(\displaystyle\frac{l_1+l_2}2\) от краев и на \(\displaystyle\frac{l_2-l_1}2\) от точки подвеса куба.
Запишем второй закон Ньютона для куба в проекции на ось: \[\label{yg10-030401} T+F_A-mg=0 \Rightarrow T=mg-F_A,\] где \[\label{yg10-030402} F_A=\rho_{\text{ж}}g\displaystyle\frac V2=\rho_{\text{ж}}g\frac{a^3}2.\]
Запишем уравнение моментов для точки \(O\): \[\label{yg10-030403} Tl_1=Mg\frac{l_2-l_1}2.\]
Подставим в \eqref{yg10-030403} \eqref{yg10-030401} и \eqref{yg10-030402}: \[\left(\rho_{\text{к}}ga^3-\rho_{\text{ж}}g\frac{a^3}2\right)l_1=Mg\frac{l_2-l_1}2.\]
Упростим: \[\label{yg10-030404} \frac{l_2}{l_1}=\frac{a^3(2\rho_{\text{к}}-\rho_{\text{ж}})}{M}+1.\]
Подставим данные и рассчитаем: \[\frac{l_2}{l_1}=\frac{10^{-6}(2\cdot 8900-1000)}{0{,042}}+1=1{,}4.\]
Запишем второй закон Ньютона для коромысла в проекции на ось: \[N-T-Mg=0;\] \[\label{yg10-030405} N=T+Mg=(\rho_{\text{к}}-\displaystyle\frac{\rho_{\text{ж}}}2)ga^3+Mg.\]
Подставим данные и рассчитаем: \[N=10^{-5} (8900-500)+0{,}042\cdot 10=0{,}504 \text{ Н}.\]
\(0{,}504 \text{ Н}\).
| Критерий | Баллы | Подзадача |
|---|---|---|
| 1 | 4 | Нарисован рисунок к задаче и расставлены силы |
| 2 | 3 | Записан второй закон Ньютона для куба |
| 3 | 3 | Записано уравнение моментов |
| 4 | 3 | Получено выражение для нахождения отношения плеч |
| 5 | 2 | Найдено численное значение отношения плеч |
| 6 | 2 | Записан второй закон Ньютона для коромысла |
| 7 | 3 | Получена и посчитана сила реакции |
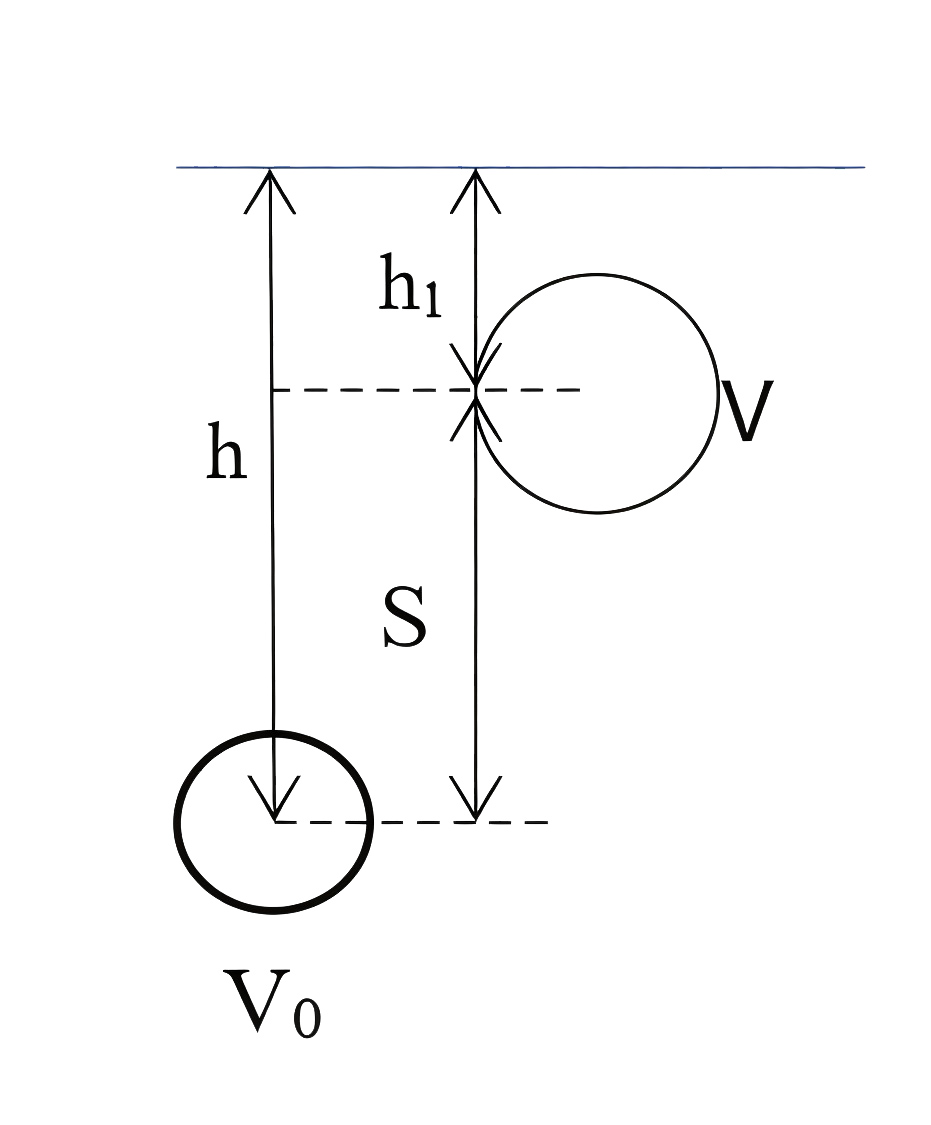
На побережье умного города поселился кит. Кит очень любит пускать пузыри. Мы заметили, что пузырь воздуха меняет размер в зависимости от глубины. Так, кит плывущий на глубине \(h\), выпускает пузырь воздуха. Пузырь поднимается к поверхности океана. Считая, что температура в течении всего подъема не меняется, определите, какой путь пузырь прошел, если его объем увеличился в \(\eta\) раз. Оцените ускорение, которое приобретет пузырь в конце подъема, если пренебрегать сопротивлением воды в расчетах. Возможно, информация о том, что киты редко погружаются глубже 100 м, поможет сделать правильный вывод. Молярная масса воздуха \(\mu\) и атмосферное давление \(P_0\).
Уравнение Менделеева – Клайперона: \[PV=\frac m{\mu}RT;\]
\[V=\frac m{\mu P}RT;\]
\[S=h-h_1;\]
\[P=P_0+\rho gh\text{ и }P_1=P_0+\rho gh_1;\]
\[\frac{V_1}V=\eta=\frac{P_1}P = \frac{P_0+\rho gh}{P_0+\rho gh_1};\]
\[h_1=\frac{P_0+\rho gh-\eta P_0}{\rho g\eta};\]
\[S=\frac{\eta-1}{\eta}(h+\frac{P_0}{\rho g});\]
\[\frac{V\mu P_1}{RT}=m;\]
\[F_A-mg=ma\Rightarrow a=\frac{\rho gV}m-g;\]
\[a=g\left(\frac{\rho TR}{\mu (P_0+\rho gh_1)}-1\right).\]
Подставим произвольные численные значения: \(h_1= 10\) м, \(T= 300\) K. \[a=9{,}81\left(\frac{1000\cdot 300\cdot 8{,}31}{0{,}029(10^5+1000\cdot 9{,}81\cdot 10)}-1\right)=7670\text{ м/с}^2.\]
Вывод: ускорение получилось много больше ускорения свободного падения, следовательно, сопротивлением воды пренебрегать нельзя.
\(7670\text{ м/с}^2\).
| Критерий | Баллы | Подзадача |
|---|---|---|
| 1 | 4 | Записано выражение для давления на глубине \(h\) и \(h_1\) |
| 2 | 4 | Найдено отношение давлений |
| 3 | 8 | Найдено выражение для \(S\) |
| 4 | 6 | Записан второй закон Ньютона и найдено выражение для \(a\) |
| 5 | 4 | Сделан правильный вывод |