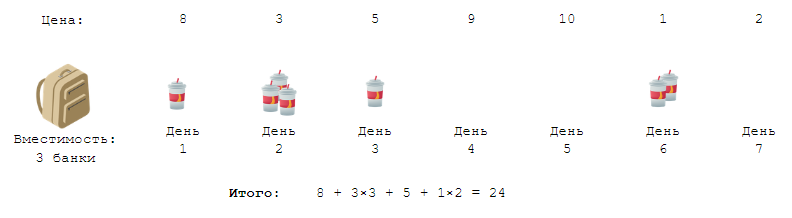Инженерный тур. 2 этап
Командные задачи второго этапа инженерного тура открыты для решения. Соревнование доступно на платформе Яндекс.Контест: https://contest.yandex.ru/contest/69929/enter/.
Определим функцию \(\hbar(N)\) как значение выражения \(1 \oplus 2 \oplus \dots \oplus N\), где \(\oplus\) обозначает логическое исключающее «или».
Для скольких \(N\) от \(1\) до \(2^{60}\) включительно значение функции \(\hbar(N)\) принимает значение \(0\)?
Примечания
Результат функции \(xor\) между двумя бинарными числами — это число, полученное путем применения \(xor\) (исключающего «или») попарно между каждым битом двух чисел. Например, \(11_{10} \oplus 6_{10} = 13_{10}\), так как \(11_{10} = 1011_2\) и \(6_{10} = 110_2\), а \(1011_2 \oplus 0110_2 = 1101_2 = 13_{10}\).
Приведенная функция для всех чисел от \(1\) до \(2^k\) принимает значение \(0\) ровно \(2^{k-2}\) раза. В частности, для всех чисел от \(1\) до \(2^{60}\) значение \(0\) будет получено \(2^{58} = 288230376151711744\) раза.
288230376151711744.
В шахматном турнире принимали участие шесть человек: Антон, Богдан, Вера, Глеб, Даша и Ева. Каждый сыграл с каждым по одной игре. За победу в игре победитель получает 2 очка, а проигравший — 0, в случае ничьи оба игрока получают по 1 очку.
Турнир был закрытым, и его результаты неизвестны, но из интервью, данных каждым игроком, получена некоторая информация о турнире. Гарантируется, что все игроки сказали правду. Ниже приведены утверждения каждого из них.
- Антон: «Я не сыграл ни одной игры вничью, а еще не занял последние два места, поэтому я доволен».
- Богдан: «Я опередил моего давнего соперника Антона. Кроме того, я не проиграл ни одной игры».
- Вера: «Сложилось так, что все получили разное количество очков в конце турнира, и места определись однозначно».
- Глеб: «Я не проиграл ни одной игры, тем не менее я не смог занять первое место».
- Даша: «Я выиграла у своей подруги Евы, мне кажется, она немного расстроилась».
- Ева: «У меня ни разу не получилось выиграть, но я сыграла вничью с Глебом, который очень хорошо играет в шахматы».
Из предложенных ниже утверждений выберите те, про которые можно сказать, что они верны вне зависимости от исходов конкретных игр (разумеется, при соблюдении истинности ответов участников).
Варианты ответа (множественный выбор):
- В турнире выиграл или Богдан, или Глеб.
- Последнее место заняла Ева.
- Глеб мог занять второе место.
- В турнире победил мальчик.
- Вера могла оказаться на первом месте.
- Богдан и Глеб сыграли между собой вничью.
- Глеб выиграл игру у Антона.
- Первые три места заняли мальчики.
Опровергнем ряд утверждений примером, см. таблицу 1.1.
| А | Б | В | Г | Д | Е | Место | Очки | |
|---|---|---|---|---|---|---|---|---|
| А | 0 | 0 | 0 | 2 | 4 | 4 | 4 | |
| Б | 2 | 1 | 1 | 1 | 1 | 3 | 6 | |
| В | 2 | 1 | 1 | 1 | 2 | 1 | 8 | |
| Г | 2 | 1 | 1 | 2 | 1 | 2 | 7 | |
| Д | 0 | 1 | 0 | 0 | 2 | 5 | 3 | |
| Е | 0 | 1 | 0 | 1 | 0 | 6 | 2 |
Неверные утверждения:
- В турнире выиграл или Богдан, или Глеб.
- В турнире победил мальчик.
- Первые три места заняли мальчики.
Этот пример также подтверждает следующие утверждения:
- Глеб мог занять второе место.
- Вера могла оказаться на первом месте.
Заметим, что хоть следующие ниже утверждения выполнены в примере, это не доказывает их истинность при любом другом исходе игр ввиду их формулировки:
- Последнее место заняла Ева.
- Богдан и Глеб сыграли между собой вничью.
- Глеб выиграл игру у Антона.
Рассмотрим их по отдельности:
- «Глеб выиграл игру у Антона»: это верное утверждение, потому что Антон не мог сыграть вничью, а Глеб не проиграл ни одной игры.
- «Богдан и Глеб сыграли между собой вничью»: это тоже верное утверждение, потому что Богдан и Глеб не проиграли ни одной игры, но они провели между собой игру на турнире — единственный исход в таком случае ничья.
- «Последнее место заняла Ева»: опровергнем это утверждение примером, см. таблицу 1.2.
| А | Б | В | Г | Д | Е | Место | Очки | |
|---|---|---|---|---|---|---|---|---|
| А | 0 | 0 | 0 | 2 | 2 | 4 | 4 | |
| Б | 2 | 2 | 1 | 2 | 1 | 1 | 8 | |
| В | 2 | 0 | 1 | 2 | 1 | 3 | 6 | |
| Г | 2 | 1 | 1 | 2 | 1 | 2 | 7 | |
| Д | 0 | 0 | 0 | 0 | 2 | 6 | 2 | |
| Е | 0 | 1 | 1 | 1 | 0 | 5 | 3 |
3, 5, 6, 7.
Петя открыл для себя вкусный напиток «Милки» (молочный коктейль), который продается в магазине неподалеку от его дома. Он решил пить его каждый день в течение \(n\) дней по одной банке в день.
Однако в этом магазине действует активное ценообразование, то есть цены на все товары, включая «Милки», меняются каждый день. К счастью, тетя Пети работает в этом магазине и знает цены на «Милки» на ближайшие \(n\) дней. Теперь Петя тоже знает эти цены.
Но есть одно ограничение: в один день Петя может купить не более \(k\) банок «Милки», потому что именно столько помещается в его рюкзак, а ходить в магазин чаще одного раза в день он не хочет.
Помогите Пете определить минимальную сумму денег, которая ему понадобится, чтобы пить «Милки» каждый день в течение следующих \(n\) дней.
Формат входных данных
В первой строке входных данных содержатся два целых числа \(n, k\) (\(1 \leqslant n, k \leqslant 10^5\)) — количество дней и размер рюкзака Пети. Во второй строке входных данных содержатся \(n\) целых чисел \(p_i\) (\(1 \leqslant p_i \leqslant 10^9\)) — цена напитка «Милки» в \(i\)-й день.
Формат выходных данных
Выведите единственное целое число — минимальное число денег, необходимое Пете, чтобы иметь возможность пить по банке «Милки» в каждый из следующих \(n\) дней.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
6 2 2 4 3 9 10 7 |
18 |
2 |
5 3 5 4 3 2 1 |
15 |
3 |
7 3 8 3 5 9 10 1 2 |
24 |
Рассмотрим один из вариантов решения этой задачи.
Определим пустую очередь с приоритетом \(h\) — эта очередь будет работать с парами чисел, выполняя операции вставки и извлечения за \(\mathcal{O}(\log|h|)\).
Начнем итерироваться по массиву \(p\), начиная с первого элемента. Запомним, что в день \(i\) цена на напиток равна \(p_i\), и в этот день можно было купить \(k\) банок — выполним вставку в очередь \(h\) пары чисел \((p_i, k)\). Затем выполним операцию извлечения пары \((price, rem)\) (цена напитка в какой-то день и количество банок, которое можно было купить в этот день) из очереди \(h\) — ввиду природы очереди с приоритетом, \(price\) будет наименьшим из всех существующих \(price\) в очереди \(h\), прибавим к ответу \(price\), если при этом \(rem \geqslant 2\), то в тот же день, которому соответствует цена \(price\), можно было купить еще минимум одну банку — запомним это и выполним вставку в \(h\) пары \((price, rem-1)\).
Сложность: \(\mathcal{O}(n \cdot \log n)\).
Ниже представлено решение на языке Python.
import sys
from heapq import heappop, heappush
n, k = map(int, sys.stdin.readline().split())
p = list(map(int, sys.stdin.readline().split()))
res = 0
h = []
for i in range(n):
heappush(h, (p[i], k))
price, rem = heappop(h)
res += price)
if rem > 1:
heappush(h, (price, rem - 1))
print(res)
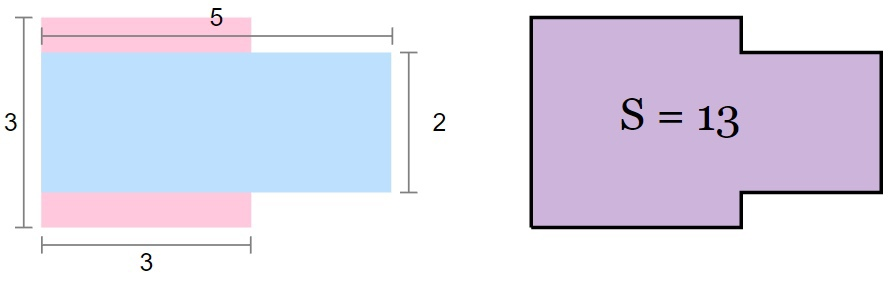
На столе лежат \(n\) прямоугольников из цветного картона, каждый прямоугольник имеет целочисленные длины сторон.
Все прямоугольники раскладываются так, что стороны каждого прямоугольника или параллельны, или перпендикулярны сторонам любого другого. Прямоугольники могут частично или полностью лежать друг на друге.
Определите минимальную площадь фигуры (необязательно прямоугольника), ограничивающей все лежащие прямоугольники при их оптимальном расположении. Фигуру назовем ограничивающей, если внутрь нее помещаются все прямоугольники.
Формат входных данных
В первой строке входных данных содержится целое число \(n\) (\(1 \leqslant n \leqslant 2 \cdot 10^5\)) — количество прямоугольников.
Далее следуют \(n\) строк с описанием каждого прямоугольника: в \(i\)-й строке содержится два целых числа \(w_i, h_i\) (\(1 \leqslant w_i, h_i \leqslant 10^9\)) — длины смежных сторон прямоугольника \(i\).
Формат выходных данных
Выведите единственное целое число — минимальную площадь фигуры, покрывающей все прямоугольники.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
2 5 4 3 3 |
20 |
2 |
2 3 3 2 5 |
13 |
3 |
4 5 7 5 4 3 10 16 2 |
56 |
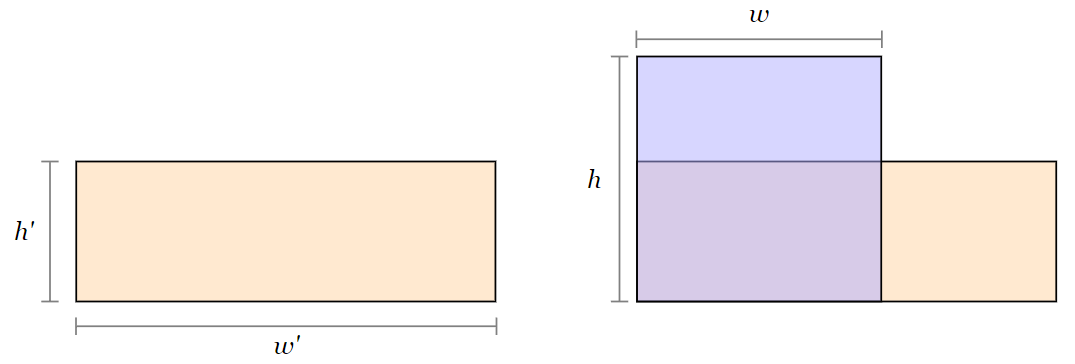
Можно доказать, что оптимальной стратегией для минимизации площади является расположение всех прямоугольников с фиксацией в одном углу (возможно, существует несколько способов, но этот также является оптимальным).
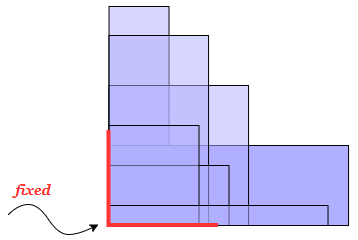
Предположим, \(h_i \leqslant w_i\), если это не так, то поменяем числа в каждой такой паре, чтобы ширина каждого прямоугольника была не меньше, чем высота. После этого отсортируем все прямоугольники в первую очередь по невозрастанию ширины, а затем — по невозрастанию высоты.
Выберем первый прямоугольник, который имеет наибольшую ширину. Если таких прямоугольников несколько, то выберем самый высокий из них. Пусть ширина этого прямоугольника равна \(w'\), а высота — \(h'\). Запомним эти значения.
Затем мы будем последовательно рассматривать остальные прямоугольники в порядке их сортировки. Если текущий прямоугольник имеет ширину \(w\) и высоту \(h\) (\(w \geqslant h\)), а \(h \leqslant h''\), то это означает, что текущий прямоугольник полностью помещается внутри уже существующей фигуры и не увеличивает ее площадь. Поэтому такие прямоугольники пропустим.
Более интересен случай, когда \(h > h'\), в такой ситуации прибавим к ответу площадь прямоугольника, ограниченного по оси \(X\) с \(w\) по \(w'\) и по оси \(Y\) с \(0\) по \(h'\).
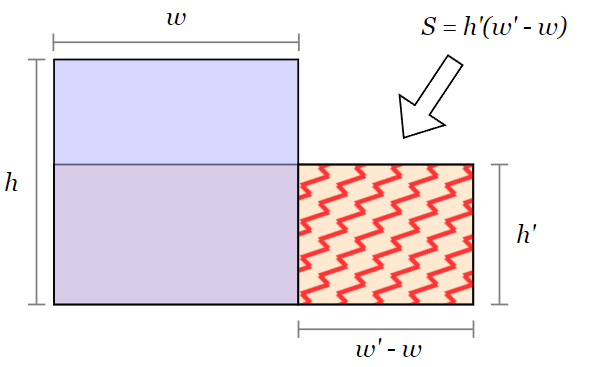
Заменим \(w'\) на \(w\), то есть присвоим переменной \(w'\) значение \(w\). Аналогично присвоим переменной \(h'\) значение \(h\). Продолжая этот процесс для оставшихся прямоугольников, можно вычислить площадь всей фигуры за исключением последнего прямоугольника, который совпадает с самым высоким.
В конце прибавим к ответу \(w' \cdot h'\) — это площадь «неучтенного» прямоугольника.
Сложность: \(\mathcal{O}(n \cdot \log n)\).
Ниже представлено решение на языке Python.
import sys
n = int(sys.stdin.readline())
d = []
for i in range(n):
w, h = map(int, sys.stdin.readline().split())
if w >= h:
w, h = h, w
d.append([w, h])
d.sort(key=lambda x: (-x[0], -x[1]))
res = 0
a, b = d[0]
for w, h in d[1:]:
if h > b:
res += b * (a - w)
b = h
a = w
res += a * b
print(res)
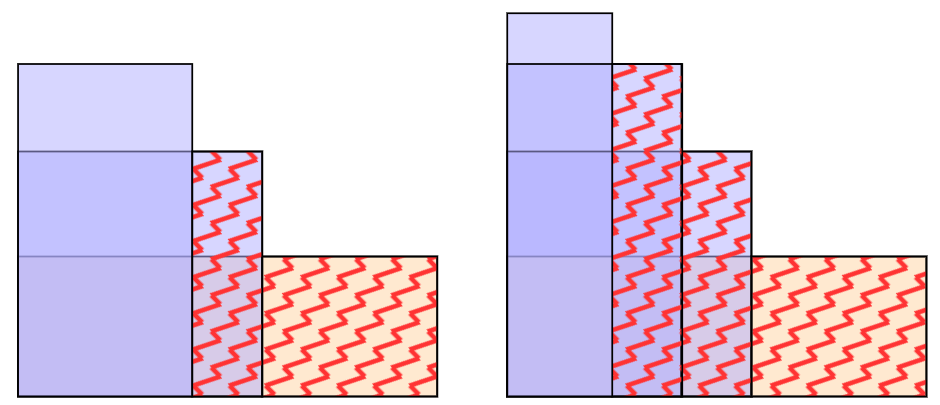
Построим фигурку из блоков конструктора весьма необычным способом: изначально берем крепежную деталь — фундамент конструкции, который является отрезком длины \(w\), затем поднимаемся на возвышенность и сбрасываем с нее поочередно \(n\) блоков конструктора. Они падают вниз и прикрепляются к первой задетой ими детали; если блок не задевает ни одну деталь, то он бесследно пропадает.
Считаем, что изначально деталь фундамента занимает отрезок \([0; w]\), блок \(i\)-й по счету падает вниз в вертикальном отрезке \([l_i; r_i]\). Падающий блок задевает деталь, если внутрь отрезка \([l_i; r_i]\) попадает строго больше одной точки детали.
Если каждый блок конструктора, в том числе и фундамент, имеет одинаковую высоту, равную 1, то какой высоты получилась фигура?
Формат входных данных
В первой строке входных данных содержится целое число \(w\) (\(1 \leqslant w \leqslant 10^9\)) — длина крепежной детали. Крепежная деталь занимает отрезок \([0;w]\).
Во второй строке входных данных содержится целое число \(n\) (\(0 \leqslant n \leqslant 10^5\)) — количество сбрасываемых блоков.
Далее следуют \(n\) строк, в \(i\)-й строке содержится описание \(i\)-го блока как два целых числа \(l_i, r_i\) (\(-10^9 \leqslant l_i < r_i \leqslant 10^9\)) — левая и правая граница вертикального отрезка, в котором падает блок \(i\).
Формат выходных данных
Выведите единственное целое число — высоту фигуры после сброса всех \(n\) блоков.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 4 -1 2 -3 0 2 4 -2 1 |
4 |
2 |
4 3 -2 5 -3 -2 5 7 |
2 |
3 |
4 5 2 5 4 7 -2 1 0 3 1 2 |
4 |
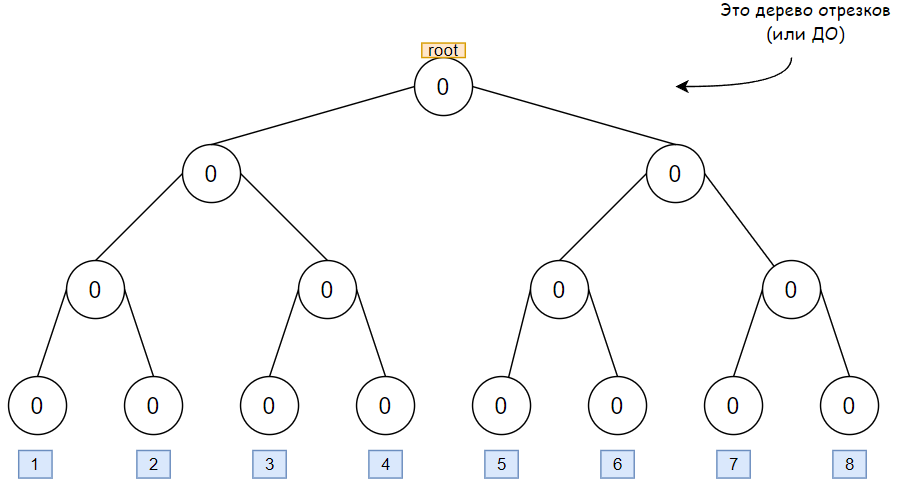
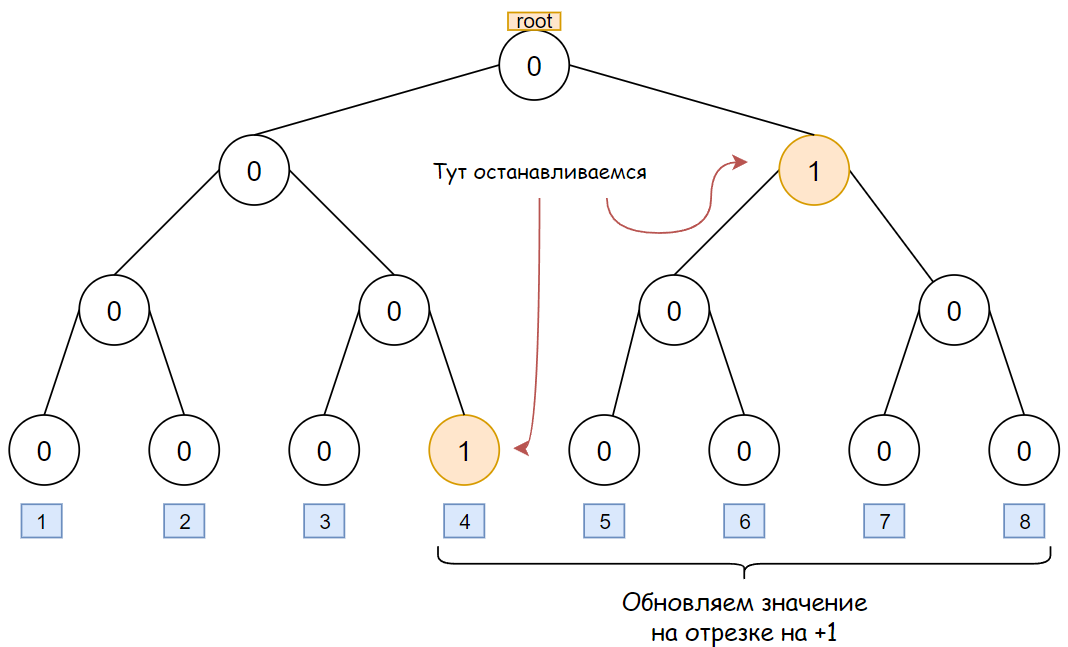
Нужно уметь быстро прибавлять на отрезке. Идея, которая напрашивается сразу — дерево отрезков (ДО), однако в стандартном виде это будет работать слишком медленно.
Во-первых, координаты находятся в диапазоне от \(-10^9\) до \(10^9\), что не позволит задать координаты и использовать в дереве явно. Применим сжатие координат — рассмотрим все координаты, которые встречаются в задаче, отсортируем их и переназначим значения: так, самой малой координате будет соответствовать 1, второй по величине будет соответствовать 2 и так далее. Итого имеем не более \(2n\) различных координат.
Во-вторых, пусть даже с \(2n\) различными координатами, ДО в привычном виде все еще не справится с задачей, так как блок в общем случае занимает не одну координату, а отрезок, то есть нужно обновлять значения в ДО для каждой точки в отрезке, а это не пройдет по времени и ничем не лучше реализации без ДО.
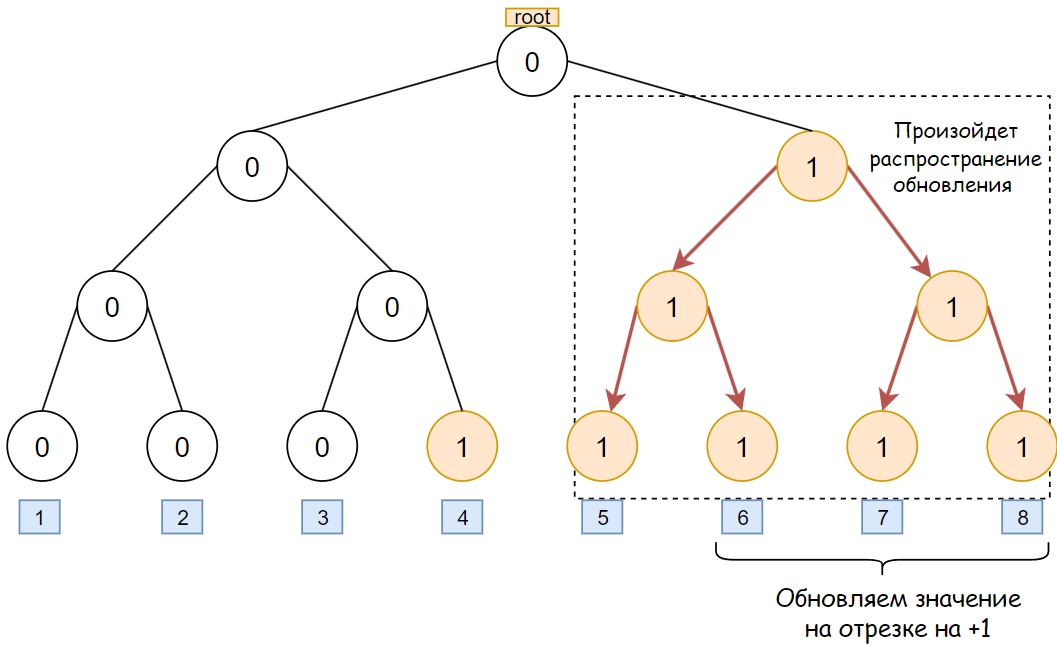
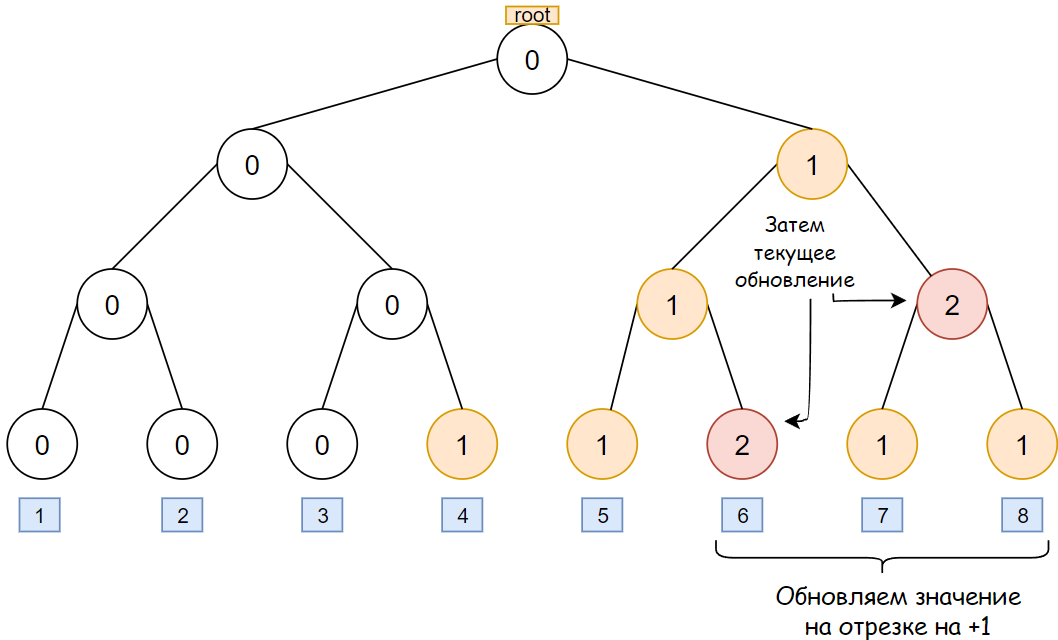
Применим оптимизацию, позволяющую прибавлять \(+1\) в ДО не в одной точке, а на отрезке. Эта оптимизация использует идею «ленивых вычислений» или «отложенных» (https://ru.algorithmica.org/cs/segment-tree/lazy-propagation/, pdf-версия веб-страницы: https://disk.yandex.ru/i/Nj8_d-2lzCfb9w), а именно: когда текущая вершина в ДО покрывает целиком часть отрезка, на котором выполняется прибавление, то значение в этой вершине увеличивается, а далее не спускаемся в дочерние вершины. Такая операция сопряжена с рядом возможных случаев: если в текущей вершине уже было записано обновление ранее — то спускаем его в дочерние вершины, а только после записываем в текущую вершину новое значение. Вообще, всегда оказавшись в какой-то вершине, спускаем обновления вниз по дереву.
Ответ на задачу — максимальное число в вершине дерева.
Всего тратим время на сортировку координат \(n \cdot \log n\).
Затем \(n\) раз выполняем операции на дереве. Каждая операция затрагивает \(4 \cdot \log n\) вершин дерева.
Сложность: \(\mathcal{O}(n \cdot \log n)\).
Ниже представлено решение на языке Python.
import sys
class SegmentTree:
def __init__(self, size):
self.size = size
self.tree = [0] * (4 * size)
self.lazy = [None] * (4 * size)
def _apply(self, node, start, end, value):
self.tree[node] = value
if start != end:
self.lazy[node * 2] = value
self.lazy[node * 2 + 1] = value
self.lazy[node] = None
def _update_range(self, node, start, end, l, r, value):
if self.lazy[node] is not None:
self._apply(node, start, end, self.lazy[node])
if start > end or start > r or end < l:
return
if start >= l and end <= r:
self._apply(node, start, end, value)
return
mid = (start + end) // 2
self._update_range(node * 2, start, mid, l, r, value)
self._update_range(node * 2 + 1, mid + 1, end, l, r, value)
self.tree[node] = max(self.tree[node * 2], self.tree[node * 2 + 1])
def update_range(self, l, r, value):
self._update_range(1, 0, self.size - 1, l, r, value)
def _query_range(self, node, start, end, l, r):
if start > end or start > r or end < l:
return -float('inf')
if self.lazy[node] is not None:
self._apply(node, start, end, self.lazy[node])
if start >= l and end <= r:
return self.tree[node]
mid = (start + end) // 2
left_query = self._query_range(node * 2, start, mid, l, r)
right_query = self._query_range(node * 2 + 1, mid + 1, end, l, r)
return max(left_query, right_query)
def query_range(self, l, r):
return self._query_range(1, 0, self.size - 1, l, r)
def solve():
w = int(sys.stdin.readline())
n = int(sys.stdin.readline())
lr = []
uniq = {0, w - 1}
for i in range(n):
l, r = map(int, sys.stdin.readline().split())
lr.append([l, r])
uniq.add(l)
uniq.add(r - 1)
sorted_uniq = sorted(list(uniq))
new_x = {sorted_uniq[i]: i for i in range(len(sorted_uniq))}
seg_tree = SegmentTree(len(uniq))
seg_tree.update_range(l=sorted_uniq.index(0),
r=sorted_uniq.index(w - 1),
value=1)
for l, r in lr:
nl, nr = new_x[l], new_x[r - 1]
mx = seg_tree.query_range(nl, nr)
if mx >= 1:
seg_tree.update_range(nl, nr, mx + 1)
max_height = seg_tree.query_range(0, len(uniq))
print(max_height)
return max_height
if __name__ == '__main__':
solve()
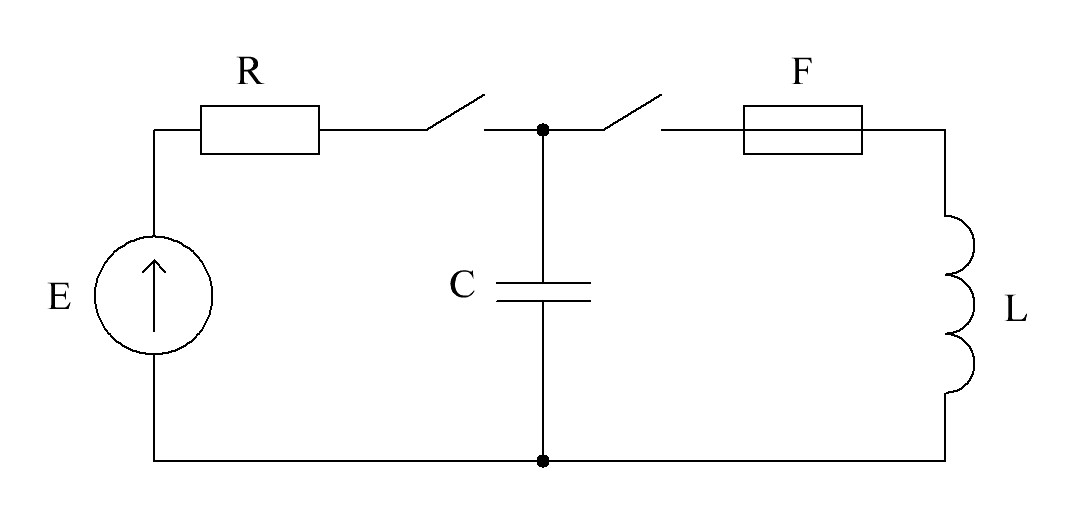
Была собрана цепь, представленная на рис. 1.13. В начальный момент времени оба ключа открыты. В какой-то момент времени первый ключ замыкается и держится закрытым до тех пор, пока ток через резистор \(R\) не станет меньше в \(k_1\) раз максимального значения. После этого первый ключ открывается, и закрывается второй. Предохранитель рассчитан на ток \(I\). Какой заряд на конденсаторе \(C\) будет в момент перегорания предохранителя?
Формат входных данных
На вход в строчку через пробел подаются следующие переменные:
- \(R\) — сопротивление в омах (Ом), вещественное число от 1 до \(10^6\);
- \(k_1\) — вещественное число от 2 до \(10^6\);
- \(I\) — ток в амперах (А), вещественное число от \(10^{-6}\) до \(10^2\);
- \(E\) — напряжение в вольтах (В), вещественное число от \(10^{-6}\) до \(10^3\);
- \(C\) — емкость в фарадах (Ф), вещественное число от \(10^{-6}\) до \(10^2\);
- \(L\) — индуктивность в генри (Гн), вещественное число от \(10^{-6}\) до \(10^{2}\).
Формат выходных данных
На выход необходимо вывести заряд на конденсаторе в кулонах с точностью до шести знаков после запятой.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1000 2 0.1 12 0.001 0.001 |
0.005999 |
Напряжение конденсатора после закрытия первого ключа: \[U_{Co} = E \cdot \left(1 - \frac{1}{k_1}\right).\]
Полная энергия колебательной системы: \[W = \frac{C \cdot U_{Co}^2}{2}.\]
Энергия, запасенная в конденсаторе в момент разрыва предохранителя: \[W_C = W - \frac{L \cdot I^2}{2}.\]
Заряд на конденсаторе: \[q = \sqrt{2 \cdot W_C \cdot C}.\]
Ниже представлено решение на языке C++.
#include <stdio.h>
#include <cmath>
int main() {
float R, k, I, E, C, L, U, W, Wc, q;
scanf("%f", &R);
scanf("%f", &k);
scanf("%f", &I);
scanf("%f", &E);
scanf("%f", &C);
scanf("%f", &L);
U=E*(1-1/k);
W=C*U*U/2;
Wc=W-L*I*I/2;
q=sqrt(Wc*C*2);
printf("%.6f", q);
return 0;
}
Один заядлый любитель чая и гор отправился в путешествие со своими любимыми аккумулятором, чайником и кружкой. Местность, по которой он гуляет, представлена на рис. 1.14 в виде сверху, с указанием высоты каждого квадрата.
Горе-путешественника поднимает ветром и переносит в случайное место на этих горах. Оказавшись в клетке номер \(N\), путешественник не растерялся и тут же включил чайник, налив в него воды ровно на одну кружку чая, и запитал его от аккумулятора. Емкость аккумулятора \(Q\) мАч с напряжением 12 В. Объем кружки чая 0,4 л, начальная температура воды \(20\) °С, плотность воды \(1000\) кг/м\(^3\), а удельная теплоемкость воды \(4200\) Дж/(кг\(\cdot°\)C). Включив чайник, он понял, что из-за высоты гор вода закипает при другой температуре, а именно, температура кипения изменяется на 10 °С при изменении высоты на 300 м, при этом на высоте 1000 м температура кипения равна 100 °С, температура изменяется по линейному закону. Вот такие вот странные горы.
Наш любитель чая решил во что бы то ни стало выпить максимальное количество кружек, при этом он будет пить чай в каждой посещенной им области, передвигаться между ними он может только по горизонтали и вертикали. Путешественник может оставаться в одной области и пить там неограниченное количество кружек чая, насколько хватит аккумулятора. Определите максимальное число выпитых кружек чая.
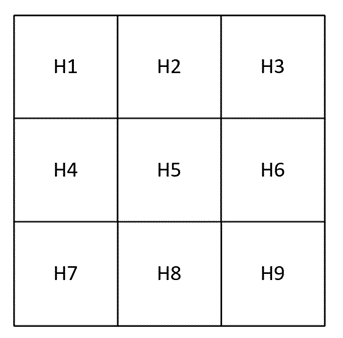
Формат входных данных
На вход приходит число \(N\) от 1 до 9, означающее местонахождение любителя чая, числа \(H1, H2, \dots, H9\), означающие высоту области над уровнем моря в метрах и емкость аккумулятора \(Q\) в миллиампер-час (мАч).
- \(N\) — число от 1 до 9;
- \(H1, H2, H3\) — числа от 0 до 2000;
- \(H4, H5, H6\) — числа от 0 до 2000;
- \(H7, H8, H9\) — числа от 0 до 2000;
- \(Q\) — число от 10000 до 100000.
Формат выходных данных
Целое число, максимальное количество выпитых кружек чая.
Для начала необходимо пересчитать матрицу высот в матрицу энергетических затрат по формуле: \[Q_{\text{кип}} = C \cdot m \cdot \Delta t,\] где:
- \(Q_{\text{кип}}\) — количество энергии на кипячение воды в чайнике, Дж;
- \(C\) — удельная теплоемкость воды, Дж/(кг\(\cdot°\)C);
- \(\Delta t\) — разница между температурой кипения воды на данной высоте и начальной температурой воды, °C.
Для определения \(\Delta t\) воспользуемся следующей формулой: \[\Delta t = \frac{1000 - h}{30} + 80,\] где \(h\) — высота горы, м.
Также необходимо знать количество запасенной энергии в аккумуляторе в джоулях (Дж): \[Q_{\text{ак}} = Q \cdot 3{,}6 \cdot V,\] где \(Q\) — емкость аккумулятора, мАч, \(V\) — напряжение аккумулятора, В.
Решение заключается в переборе возможных вариантов прохождения. Приведенное ниже решение представляет собой рекурсивный проход с оценкой пути. В зависимости от положения любителя чая на поле (в матрице) \(3\times 3\) клетки необходимо учитывать возможность его движения. Оценка пути заключается в вычислении количества выпитых чашек чая.
Ниже представлено решение на языке Python.
n = int(input())
h = [(1000 - x) / 30 + 80 for _ in range(3) for x in map(int, input().split())]
q = int(input())
C_water = 4200
m_water = 0.4
V = 12
Q = q * 3.6 * V
q_for_cup = [C_water * m_water * h[i] for i in range(9)]
def walking(n, tea_drink, energy_remain, used):
best = tea_drink + int(energy_remain / q_for_cup[n])
if q_for_cup[n] > energy_remain:
return best
for dn in [1, -1, 3, -3]:
if not 0 <= n + dn <= 8:
continue
if abs(dn) != 3 and not 0 <= n % 3 + dn <= 2:
continue
if (1 << n + dn) & (used) != 0:
continue
best = max(best, walking(n + dn, tea_drink + 1, energy_remain - q_for_cup[n], used | (1 << n + dn)))
return best
print(walking(n, 0, Q, 1 << n))
Иногда инженерам приходится решать задачу, используя только то, что есть непосредственно под рукой или на складе. Именно такая ситуация случилась у инженера Бори. К нему обратились сотрудники из ботанического сада с просьбой как можно быстрее собрать устройство, которое бы измеряло температуру и влажность в оранжерее, поскольку предыдущее вышло из строя, а некоторые растения очень прихотливы. Осмотрев углы своего КБ на наличие датчиков, Борис нашел только два датчика температуры DS18B20 и BMP280. И тут он вспомнил, что есть такое замечательное устройство, как психрометр (https://ru.wikipedia.org/wiki/Психрометр). «Это то, что нужно!» — воскликнул Борис. И, нагуглив таблицу зависимости плотности насыщенного пара от температуры, принялся писать код. Но так как в КБ сейчас очень много срочных заказов, Боря обратился за помощью к участникам Олимпиады, чтобы вы написали программу, которая бы по разности температур и атмосферному давлению выдавала влажность в помещении.
| t, °C | \(\rho\), г/м\(^3\) | t, °C | \(\rho\), г/м\(^3\) | t, °C | \(\rho\), г/м\(^3\) |
|---|---|---|---|---|---|
| \(-30\) | 0,28 | \(-8\) | 2,54 | 14 | 12,1 |
| \(-28\) | 0,35 | \(-6\) | 2,99 | 16 | 13,6 |
| \(-26\) | 0,43 | \(-4\) | 3,51 | 18 | 15,4 |
| \(-24\) | 0,52 | \(-2\) | 4,13 | 20 | 17,3 |
| \(-22\) | 0,64 | 0 | 4,84 | 22 | 19,4 |
| \(-20\) | 0,77 | 2 | 5,6 | 24 | 21,8 |
| \(-18\) | 0,94 | 4 | 6,4 | 26 | 24,4 |
| \(-16\) | 1,13 | 6 | 7,3 | 28 | 27,2 |
| \(-14\) | 1,36 | 8 | 8,3 | 30 | 30,3 |
| \(-12\) | 1,63 | 10 | 9,4 | ||
| \(-10\) | 2,14 | 12 | 10,4 |
Формат входных данных
\(t_1\) — температура сухого термометра, вещественное число с двумя знаками после запятой от \(-30\) до \(30\) °C.
\(t_2\) — температура сухого термометра, вещественное число с двумя знаками после запятой от \(-30\) до \(30\) °C (\(t_2 < t_1\)).
\(P\) — атмосферное давление в текущий момент времени, вещественное число с двумя знаками после запятой. Принять, что в оранжерее естественная вентиляция без сквозняков. Входные данные подаются в одну строку через пробел.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
20 19 760 |
90% |
2 |
27.36 17.34 750.49 |
25% |
3 |
24.02 17.01 750.68 |
40% |
4 |
17.36 10.34 740.49 |
26% |
5 |
-4.01 -7.02 758.00 |
7% |
Для решения данной задачи необходимо было воспользоваться предложенной статьей и таблицей зависимости плотности насыщенного пара от температуры. Из статьи про психрометр надо было подметить два момента:
- начение психрометрического коэффициента равно 0,0011 (по условию в оранжерее естественная вентиляция без сквозняков);
- формула для расчета значения влажности: \[\varphi = 100 \left( \frac{d_w}{d_s} - \alpha \cdot B \frac{t - t_w}{d_s} \right).\]
В этой формуле уже известны две температуры (\(t\) и \(t_w\)), атмосферное давление, а также психрометрический коэффициент. Остается найти плотность насыщенного пара. Для этого была предоставлена таблица соответствия плотности насыщенного пара от температуры, но в качестве входных данных может выступать любое вещественное число от \(-30\) до \(30\).
Первое, что приходит в голову — округлять температуру до ближайшего целого четного, но точнее будет использовать кусочно-линейную функцию. Такой подход активно используется для преобразования аналоговых сигналов с помощью микроконтроллеров. Суть в том, что, зная приращение по температуре и по плотности, можно найти наклон линейной функции для участка температур в 2°. Из таких небольших участков составляется кусочно-линейная функция, стремящаяся к нелинейной функции изменения плотности насыщенного пара. Значения плотностей насыщенного пара, а также наклоны линейных функций заносятся в соответствующие массивы. На основе известной температуры рассчитывается, к какой линейной функции принадлежит необходимая плотность насыщенного пара, и через линейную функцию находится ее приближенное значение. Все известные величины подставляются в формулу, и вычисляется относительная влажность воздуха. При выводе значение округляется до целых.
Ниже представлено решение на языке C.
#include <stdio.h>
#include <stdint.h>
#include <math.h>
#define ALPHA 0.0011
#define DEFAULT_PREASURE 760
#define VALID_INDEX(index, max) ((index > max) ? max : index)
float density_table[] = {0.28, 0.35, 0.43, 0.52, 0.64, 0.77, 0.94, 1.13, 1.36, 1.63, 2.14, 2.54,
2.99, 3.51, 4.13, 4.84, 5.6, 6.4, 7.3, 8.3, 9.4, 10.4, 12.1, 13.6, 15.4, 17.3, 19.4, 21.8, 24.4,
27.2};
float k_table[] = {0.035, 0.04, 0.045, 0.06, 0.065, 0.085, 0.095, 0.115, 0.135, 0.255, 0.2,
0.225, 0.26, 0.31, 0.355, 0.38, 0.4, 0.45, 0.5, 0.55, 0.5, 0.85, 0.75, 0.9, 0.95, 1.05, 1.2, 1.3,
1.4, 1.55};
int main(){
float t1, t1w;
float P1 = DEFAULT_PREASURE;
scanf("%f%f%f", &t1, &t1w, &P1);
uint8_t i1, i1w;
i1 = VALID_INDEX((uint8_t)(t1 + 30) / 2, 29);
i1w = VALID_INDEX((uint8_t)(t1w + 30) / 2, 29);
float d1, d1w;
d1 = k_table[i1] * (t1 - (-30 + 2 * i1)) + density_table[i1];
d1w = k_table[i1w] * (t1w - (-30 + 2 * i1w)) + density_table[i1w];
float phi = 100.0f * (d1w - 0.0011 * P1 * (t1 - t1w)) / d1;
printf("%.0f%%\n", phi);
return 0;
}
Борис, как и многие его ровесники, мечтал стать пилотом. Мечте не суждено было сбыться, но из этой мечты исходит его хобби. Борис занимается авиамоделизмом. В преддверии отпуска он днями и ночами набрасывал какие-то идеи по улучшению своего планера «Добрыня». Но для того чтобы понимать, улучшилась ситуация или нет, необходим бортовой компьютер. Он будет писать логи полета, из которых можно будет сделать соответствующий вывод
Борис обратился к участникам Олимпиады с просьбой помочь ему написать часть программы для бортового компьютера. К бортовому компьютеру с Arduino nano на борту будет подключен трехосевой акселерометр ADXL335 (https://disk.yandex.ru/d/4wGwp_aq_ShAlQ/adxl335.pdf). Arduino считывает показания с трех аналоговых выводов, пересчитывает полученные значения в проекции ускорения по трем осям (в метрах в секунду за секунду), а также вычисляет углы планера: тангаж и крен (в градусах).
Примечания
Гарантируется, что напряжение питания Arduino 5 В, датчика 3,3 В, а рыскание отсутствует.
Формат входных данных
\(N\) — количество обрабатываемых показаний.
\(N\) строчек по три значения.
\(x_1\) — показания АЦП по оси \(X\), 10-битное беззнаковое целое.
\(x_2\) — показания АЦП по оси \(Y\), 10-битное беззнаковое целое.
\(x_3\) — показания АЦП по оси \(Z\), 10-битное беззнаковое целое.
Формат выходных данных
\(N\) строчек по пять значений.
\(a_x\) — проекция ускорения по оси \(X\), м/с\(^2\) до двух знаков после запятой.
\(a_y\) — проекция ускорения по оси \(Y\), м/с\(^2\) до двух знаков после запятой.
\(a_z\) — проекция ускорения по оси \(Z\), м/с\(^2\) до двух знаков после запятой.
Roll — крен, град. с точностью до одного знака до запятой.
Pitch — тангаж, град. с точностью до одного знака до запятой.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1 263 306 342 |
-7.01 -0.14 5.60 1 51 |
Для решения данной задачи необходимо понять, каким образом ускорение, измеряемое акселерометром, преобразуется в напряжение на входе. Для этого обратимся к документации на акселерометр, которая была приложена к заданию. Акселерометр рассчитан на ускорение до 3g. Смещение нуля, согласно документации, составляет 1,65 В, при питании в 3,3 В. Приращение напряжения от изменения ускорения по оси 300 мВ/g. Отсюда выведем формулу расчета: \[a = \frac{\left(\frac{adc \cdot 5}{1023} - 1{,}65\right)}{0{,}300} \cdot 9{,}8 = \frac{\left(\frac{adc \cdot 5000}{1023} - 1650\right)}{300} \cdot 9{,}8 = \left(\frac{adc \cdot 50}{3069} - 5\right) \cdot 9{,}8.\] Для каждого показания АЦП по трем осям рассчитывается ускорение в метрах секунду за секунду. Далее применим формулу из application note для расчета крена и тангажа. Эти формулы справедливы для большинства акселерометров и легко находятся в статьях: \[roll = \operatorname{arctg} \left( \frac{a_y}{a_z} \right);\] \[pitch = \operatorname{arctg} \left( \frac{-a_x}{\sqrt{a_y^2+a_z^2}} \right).\]
Подставляя в эти формулы рассчитанные ранее ускорения, вычисляются углы крен и тангаж в радианах, остается только пересчитать радианы в градусы.
Ниже представлено решение на языке C++.
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#define PI 3.1415926535
#define PI_2 (PI / 2.0)
#define PI_4 (PI / 4.0)
#define ABS(x) ((x < 0) ? -x : x)
#define SQR(x) (x * x)
#define CONV(x) ((x - 1) / (x + 1))
#define DEGREES(x) ((float)x * 180.0f / PI)
#define ATAN(x) (x * (0.9992150 + SQR(x) * (-0.3211819 + SQR(x) * (0.1462766 + SQR(x) * (-0.0389929)))))
float fast_rsqrt(float number){
const float x2 = number * 0.5F;
const float threehalfs = 1.5F;
union {
float f;
uint32_t i;
} conv = {number};
conv.i = 0x5f3759df - ( conv.i >> 1 );
conv.f *= threehalfs - x2 * conv.f * conv.f;
return conv.f;
}
float fast_atan(float number){
if (number > 0)
return PI_4 + ATAN(CONV(number));
else
return -(PI_4 + ATAN(CONV(-number)));
}
int main(){
uint32_t N;
scanf("%u", &N);
uint32_t* array = (uint32_t*)calloc(N * 3, sizeof(uint32_t));
for (uint32_t i = 0; i < N * 3; i += 3)
scanf("%u %u %u", &array[i], &array[i + 1], &array[i + 2]);
for (uint32_t i = 0; i < N * 3; i += 3){
float ax_x = ((float)array[i] * 50 / 3069 - 5) * 9.8;
float ax_y = ((float)array[i + 1] * 50 / 3069 - 5) * 9.8;
float ax_z = ((float)array[i + 2] * 50 / 3069 - 5) * 9.8;
float roll = fast_atan(ax_y / -ax_z);
float pitch = fast_atan(-ax_x * fast_rsqrt(SQR(ax_y) + SQR(ax_z)));
printf("%.2f %.2f %.2f %.0f %.0f\n", ax_x, ax_y, ax_z, DEGREES(roll), DEGREES(pitch));
}
free(array);
return 0;
}
Беспилотных автомобилей в умном городе становится все больше и больше. Они уже классно ездят по прямой и поворачивают, пока никто не мешает. Но последнее время здесь ужасные пробки из-за того, что беспилотные автомобили не могут разобраться на перекрестке, кто же должен ехать первым. Надо было учить ПДД, прежде чем садиться за руль!
В умном городе существует несколько типов нерегулируемых перекрестков, среди которых наиболее распространены обычные (состоящие из двух пересекающихся дорог) и T-образные перекрестки. На таких перекрестках отсутствуют светофоры, но у некоторых дорог есть знаки приоритета. Задача заключается в разработке алгоритма, который будет управлять движением беспилотных автомобилей на перекрестках, получая информацию от умного регулировщика о типе перекрестка и наличии приоритетных полос.
Формат входных данных
От умного регулировщика поступает JSON-сообщение, содержащее следующую информацию:
- Тип перекрестка (
type): может быть обычным (regular) или T-образным (T-shaped). - Перечень приоритетных полос (
priority_lanes): массив строк, указывающий, какие полосы движения имеют приоритет. Если список пустой, значит, ни одна из полос не имеет приоритет. - Количество автомобилей на перекрестке (
vehicle_count): общее количество автомобилей на перекрестке. Информация о каждом автомобиле:
vehicle_id: уникальный идентификатор автомобиля;lane: полоса, на которой находится автомобиль;direction: направление, в которое движется автомобиль (например,west,northи т. д.).
Дороги в умном городе могут быть в восьми направлениях:
north— север,north-east— северо-восток,east— восток,south-east— юго-восток,south— юг,south-west— юго-запад,west— запад,north-west— северо-запад.
Считать, что каждая дорога имеет две полосы движения: в прямом и во встречном направлениях.
Задача — разработать алгоритм, который на основании входных данных определит порядок проезда автомобилей через перекресток и вернет его в формате JSON. В случае, если два и более автомобилей могут разъехаться одновременно, не создавая помеху друг другу, регулировщик должен назначить им равный приоритет. Любой автомобиль может ехать из любой полосы в любую полосу.
Формат выходных данных
Алгоритм должен вернуть JSON-ответ, содержащий порядок проезда автомобилей через перекресток. Ответ должен содержать порядок движения автомобилей. Порядок появления автомобилей в ответе сортируется по vehicle_id. В ответе не может несколько раз появиться один и тот же автомобиль, но у разных автомобилей может быть одинаковый приоритет (если они могут двигаться одновременно, не создавая помеху друг другу). При формировании ответа необходимо соблюдать следующую разметку (количество и места пробелов должны строго соответствовать примеру, см. рис. 1.15).

Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
"intersection": "type": "regular", "priority_lanes": ["north", "south"], "vehicle_count": 4 , "vehicles": [ "vehicle_id": 1, "lane": "north", "direction": "west" , "vehicle_id": 2, "lane": "east", "direction": "north" , "vehicle_id": 3, "lane": "south", "direction": "east" , "vehicle_id": 4, "lane": "west", "direction": "south" ] |
"order": [ "vehicle_id": 1, "priority": 1 , "vehicle_id": 2, "priority": 1 , "vehicle_id": 3, "priority": 1 , "vehicle_id": 4, "priority": 1 ] |
Все тестовые задания созданы на основе официальных заданий из теоретических билетов ГИБДД на право управления транспортным средством категории B. В частности, были использованы задания на нерегулируемые перекрестки. Соответственно, все правила, определяющие порядок проезда, указаны в ПДД на момент 2024 года.
Основная идея решения в следующем: на перекрестке возможны восемь направлений. Для каждого направления условно можно выделить две полосы: въезд и выезд. Так как на территории Российской Федерации движение правостороннее, то въезд всегда будет «правее» или «дальше по часовой стрелке», чем выезд.
Таким образом, можно представить все возможные направления в виде окружности, на которой с равным шагом расположены 16 точек. Каждая из точек обозначает въезд или выезд для каждого направления. Каждый из автомобилей стремится отправиться из начальной точки в конечную. Начальную и конечную точку можно соединить линией и получить отрезок или вектор.
Примем изначально приоритет каждого автомобиля равным 1 (должен проехать первым). Далее необходимо проверить, пересекаются ли отрезки/вектора автомобилей. Если они не пересекаются, значит, автомобили на перекрестке могут разъехаться, не пересекая траекторию друг друга (в реальности, конечно, может существовать перекресток, где такое окажется невозможным, но команда разработчиков провела наблюдение за несколько перекрестками и решила, что такое допущение работает в подавляющем большинстве случаев). Автомобили, чьи траектории не пересекаются, могут оставить равный приоритет между собой.
В случае, если траектории все-таки пересеклись, необходимо определить, чей приоритет останется более высоким. В ПДД это определяется «помехой справа». Простыми словами помехой справа является такая помеха, которая в моменте находится справа от водителя. Если водитель 1 едет прямо в одном направлении, а перпендикулярно ему едет водитель 2 с правой стороны, водитель 1 должен уступить дорогу, т. к. водитель 2 является для него помехой справа.
С точки зрения программирования для определения помехи справа можно использовать разные способы. Самым простым, с точки зрения реализации, является расчет векторного произведения двух векторов движения. Если векторное произведение положительное, то помехой справа является один автомобиль, если отрицательное, то другой. Здесь может возникнуть сложная ситуация при расчете, если конечная точка у обоих автомобилей одинаковая. Для устранения этой проблемы каждый вектор/отрезок можно немного продлить.
Таким образом стоит проверить каждую пару автомобилей. Во избежание неточностей при решении рекомендуем сделать проверку итерационной. Так, в каждой итерации приоритет автомобиля может увеличиться только на 1. Всего итерационным образом нужно провести проверки 3 раза, что по условию задачи будет достаточным (максимум 4 автомобиля, максимальный приоритет может быть 4).
С точки зрения распределения приоритета, с учетом существования главной дороги, логика значительно не меняется, за исключением того факта, что оба автомобиля с главной дороги распределяют приоритет между собой согласно правилам, описанным выше; автомобиль с главной дороги имеет приоритет относительно автомобиля со второстепенной дороги безусловно; автомобили со второстепенной дороги распределяют приоритет согласно правилам, описанным выше. Далее остается только сформировать посылку по правилам, приведенным в задании.
В коде ниже есть закомментированные строки, выводящие промежуточные результаты. Это позволяет лучше понять логику кода.
Ниже представлено решение на языке Python.
import json
import math
def polar_to_cartesian(radius, angle_deg):
"""Преобразует полярные координаты в декартовые."""
angle_rad = math.radians(angle_deg)
x = radius * math.cos(angle_rad)
y = radius * math.sin(angle_rad)
return x, y
def is_intersecting_and_right(line1, line2):
"""
Проверяет, пересекаются ли траектории, включая проверку "помеха справа"
для продленных линий в случае совпадения конечных точек.
"""
def determinant(a, b, c, d):
return a * d - b * c
def vector_cross_product(ax, ay, bx, by):
"""Векторное произведение для определения относительного положения точки."""
return ax * by - ay * bx
def are_points_equal(p1, p2, epsilon=1e-6):
"""Сравнивает два пункта с учетом допустимой погрешности."""
return abs(p1[0] - p2[0]) < epsilon and abs(p1[1] - p2[1]) < epsilon
def extend_point(p1, p2, factor=1.0):
"""Продлевает точку p2 на основе направления от p1 к p2."""
dx = p2[0] - p1[0]
dy = p2[1] - p1[1]
return (p2[0] + dx * factor, p2[1] + dy * factor)
x1, y1, x2, y2 = *line1[0], *line1[1]
x3, y3, x4, y4 = *line2[0], *line2[1]
# Проверяем совпадение конечных точек
if are_points_equal((x2, y2), (x4, y4)):
'''print("Конечные точки совпадают. Проверяем продленные линии.")'''
# Продление линий
extended1 = extend_point((x1, y1), (x2, y2), factor=0.1)
extended2 = extend_point((x3, y3), (x4, y4), factor=0.1)
'''print(f"Продленная точка для линии 1: {extended1}")
print(f"Продленная точка для линии 2: {extended2}")'''
# Проверяем пересечение для продленных линий
vec1_x, vec1_y = extended1[0] - x1, extended1[1] - y1
vec2_x, vec2_y = extended2[0] - x3, extended2[1] - y3
cross = vector_cross_product(vec1_x, vec1_y, vec2_x, vec2_y)
return True, cross < 0
# Проверяем пересечение обычным образом
det = determinant(x2 - x1, x3 - x4, y2 - y1, y3 - y4)
if det == 0:
return False, False
t = determinant(x3 - x1, x3 - x4, y3 - y1, y3 - y4) / det
u = determinant(x2 - x1, x3 - x1, y2 - y1, y3 - y1) / det
if 0 <= t <= 1 and 0 <= u <= 1:
vec1_x, vec1_y = x2 - x1, y2 - y1
vec2_x, vec2_y = x4 - x3, y4 - y3
cross = vector_cross_product(vec1_x, vec1_y, vec2_x, vec2_y)
return True, cross < 0
return False, False
def process_intersection(data, iterations=3):
radius = 1
step_angle = 22.5
# Определение точек и превосходства
lanes_map = {
"north": 0, "north-east": 2, "east": 4,
"south-east": 6, "south": 8, "south-west": 10,
"west": 12, "north-west": 14
}
directions_map = {
"north": 1, "north-east": 3, "east": 5,
"south-east": 7, "south": 9, "south-west": 11,
"west": 13, "north-west": 15
}
superior_points = {lanes_map[lane] for lane in data["intersection"]["priority_lanes"]}
'''print(f"Точки превосходства: {superior_points}")'''
# Формирование траекторий
vehicles = data["vehicles"]
trajectories = []
for vehicle in vehicles:
start_idx = lanes_map[vehicle["lane"]]
end_idx = directions_map[vehicle["direction"]]
start_point = polar_to_cartesian(radius, start_idx * step_angle)
end_point = polar_to_cartesian(radius, end_idx * step_angle)
trajectories.append((start_point, end_point, start_idx))
'''print(f"Траектория автомобиля {vehicle['vehicle_id']}: стартовая точка {start_idx}, конечная точка {end_idx}")'''
# Итеративный процесс перераспределения приоритетов
priorities = [1] * data["intersection"]["vehicle_count"]
for iteration in range(iterations):
'''print(f"\nИтерация {iteration + 1}")'''
new_priorities = priorities[:]
for i in range(len(trajectories)):
for j in range(i + 1, len(trajectories)):
start_idx_i = trajectories[i][2]
start_idx_j = trajectories[j][2]
# Проверяем "превосходство" только если траектории пересекаются
intersects, is_right = is_intersecting_and_right(
(trajectories[i][0], trajectories[i][1]),
(trajectories[j][0], trajectories[j][1])
)
if intersects:
if new_priorities[i] == new_priorities[j]: # Меняем приоритет только если они равны
if (start_idx_i in superior_points) != (start_idx_j in superior_points):
if start_idx_i not in superior_points:
if new_priorities[i] <= iteration + 2:
new_priorities[i] += 1
'''print(f"Траектория {j + 1} имеет превосходство над траекторией {i + 1}. Приоритет траектории {i + 1} увеличен до {new_priorities[i]}.")'''
elif start_idx_j not in superior_points:
if new_priorities[j] <= iteration + 2:
new_priorities[j] += 1
'''print(f"Траектория {i + 1} имеет превосходство над траекторией {j + 1}. Приоритет траектории {j + 1} увеличен до {new_priorities[j]}.")'''
else:
if is_right:
if new_priorities[i] <= iteration + 2:
new_priorities[i] += 1
'''print(f"Автомобиль {vehicles[j]['vehicle_id']} помеха справа для автомобиля {vehicles[i]['vehicle_id']}. Приоритет {vehicles[i]['vehicle_id']} увеличен до {new_priorities[i]}.")'''
else:
if new_priorities[j] <= iteration + 2:
new_priorities[j] += 1
'''print(f"Автомобиль {vehicles[i]['vehicle_id']} помеха справа для автомобиля {vehicles[j]['vehicle_id']}. Приоритет {vehicles[j]['vehicle_id']} увеличен до {new_priorities[j]}.")'''
priorities = new_priorities[:]
# Формирование результата
result = {"order": []}
for i, vehicle in enumerate(vehicles):
result["order"].append({
"vehicle_id": vehicle["vehicle_id"],
"priority": priorities[i]
})
'''print(f"\nИтоговые приоритеты: {result['order']}")'''
return result
# Пример входных данных
with open("input.txt", encoding="UTF-8") as file_in:
input_data = json.load(file_in)
# Вывод результата
output = process_intersection(input_data)
print(json.dumps(output, indent=2))