Инженерный тур. 1 этап
На некоторой площадке по продаже видеоигр есть игры четырех категорий: [Singleplayer], [Adventure], [Strategy], [Multiplayer]. В базе данных системы площадки ведется полный учет по всем играм.
В ежемесячном отчете стажер компании построил круговую диаграмму, отображающую долю игр по категориям, но каждая игра может иметь не одну категорию. Более подробно:
- любая игра обязательно принадлежит к одной из категорий [Singleplayer] или [Multiplayer], но не сразу к двум;
- кроме категории [Singleplayer] или [Multiplayer] игра может иметь одну или две (а может не иметь) категории [Adventure] и [Strategy].
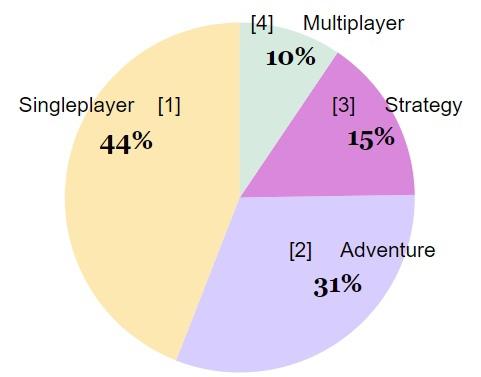
Если построить круговую диаграмму, отображающую долю игр с категорией [Singleplayer] и [Multiplayer], то какую долю в процентах будет занимать [Singleplayer]?
Поскольку игры с метками [Singleplayer] и [Multiplayer] не пересекаются, и каждая игра имеет только одну из этих меток, их процентное соотношение не изменится, если исключить из графика другие метки.
На общей диаграмме [Singleplayer] и [Multiplayer] вместе занимают 54%. Если исключить другие метки, то на графике они будут занимать 100%. Это означает, что их доля увеличится в \(k=100/54\) раза больше. Следовательно, процентное соотношение [Singleplayer] и [Multiplayer] также увеличится в \(k\) раз.
Процентное отношение [Singleplayer] будет равно: \[44\cdot k=\frac{44\cdot 100}{54}=81{,}4814\%.\]
В ответе следует указать 81,48.
81,48.
Маска строки \(\omega\) — это шаблон, который определяет формат или структуру строки \(s\), состоящей из строчных латинских символов. В маске \(\omega\) могут использоваться следующие символы:
- \(*\) (звездочка) — заменяет ноль или несколько любых символов;
- \(?\) (вопросительный знак) — заменяет один любой символ;
- \([a-z]\) (буква от
aдоz) — заменяет одну соответствующую букву.
Например, строка abb удовлетворяет маскам \(*\), \(a?b\), \(*b\), \(?bb*\), а к маске \(?*a*\) подходят строки ba, caba.
Определите, сколько строк длины от 1 до 4 удовлетворяют маске \(\omega=?*a*\).
Дана маска \([?*a*]\), где знак вопроса может быть заменен на один из 26 символов. Оставшаяся часть маски \([*a*]\) обозначает любую строку, в которой есть хотя бы одна буква «\(a\)».
Так как требуется найти количество строк длиной от 1 до 4, соответствующих маске \([?*a*]\), а знак вопроса уже определен, то требуется определить, сколько строк длины от 1 до 3 соответствуют маске \([*a*]\).
Строк длины 1 с буквой a: 1.
Строк длины 2 с буквой a: \(26^2-25^2=51\).
Строк длины 3 с буквой a: \(26^3-25^2=1951\).
Итого \([*a*]\) преобразуется в одну из \((1+51+1951)=2003\) строк.
Итоговый ответ на задачу: \(26\cdot 2003=52078\).
52078.
Малыш Макс собирает пирамидки из стержней и колец разного диаметра. У Макса есть \(a\) стержней и \(b\) колец, все стержни одинаковы и способны собрать на себя три кольца, а вот кольца могут быть разного диаметра. Причем Макс считает, что собранная пирамидка является красивой, если она состоит из трех колец, и кольца в ней идут строго по увеличению диаметра, если смотреть сверху вниз.
Определите максимальное число красивых пирамидок \(n\), которые может собрать Макс. Все \(n\) красивых пирамидок должны быть собранными одновременно, то есть каждое кольцо и каждый стержень могут быть задействованы не более, чем в одной пирамидке.
Формат входных данных
В первой строке входных данных содержатся два целых числа \(a\), \(b\) (\(0\leqslant a, b\leqslant 10^5\)) — количество стержней и колец в распоряжении Макса соответственно.
Во второй строке содержатся \(b\) целых чисел \(c_i\) (\(1\leqslant c_i\leqslant 10^9\)) — диаметры колец.
Формат выходных данных
Выведите единственное целое число — максимальное число красивых пирамидок.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 12 1 1 2 5 6 6 6 6 7 8 9 9 |
3 |
2 |
1 3 18 15 3 |
1 |
3 |
2 11 10 14 3 5 2 10 20 10 4 13 13 |
2 |
Задачу можно решить с помощью бинарного поиска по ответу, это следует из следующего замечания: если можно собрать \(p\) пирамидок, то, очевидно, можно собрать и \((p-1)\), и если нельзя собрать \(p\) пирамидок, то тем более нельзя собрать и \((p+1)\).
Попробуем понять, получится ли собрать определенное количество пирамидок, равное \(p\). Для этого будем действовать по принципу жадности: отсортируем все кольца независимо от того, в каком порядке они будут расположены — по возрастанию или по убыванию. В результате получится отсортированный массив колец \(c\).
Затем пройдемся по этому массиву и оденем каждое кольцо \(c_i\) на стержень, на котором находится минимальное количество колец. Если на этом стержне уже есть кольцо того же диаметра, что и \(c_i\), то пропустим это кольцо. Если в итоге на каждом стержне окажется по три кольца, то получится собрать \(p\) пирамидок.
Рассмотрим два неверных подхода к решению задачи.
- Одевать кольца на стержень с максимальным числом колец. Контрпример: \(c=[1,~2,~3,~4,~4,~4,~5,~5,~5]\), если в распоряжении есть минимум три стержня, то ответ 3 достижим: \((1,~4,~5)\), \((2,~4,~5)\), \((3,~4,~5)\), а при неверном подходе получится пирамидка \((1,~2,~3)\) и незаконченная пирамидка \((4,~5,~\_)\).
- Посчитать для кольца каждого диаметра, сколько раз можно его использовать — для колец одного диаметра, которых всего менее \(a\) штук, можно их использовать столько раз, сколько их встречается, для колец одного диаметра, которых более \(a\) штук, их используем не более \(a\) раз (иначе по принципу Дирихле будет пирамидка с двумя кольцами одного диаметра) — посчитаем, сколько есть «доступных» колец и поделим на 3, получив число полных пирамидок. Контрпример: \(a=2\), \(c=[1,~1,~2]\). Очевидно, что ни одной пирамидки собрать нельзя, но идея подхода посчитает, что кольца с диаметром 1 можно использовать дважды и кольцо диаметра 2 — всего три кольца, а значит, можно собрать пирамидку.
Сложность: \(\mathcal{O}\left(b\cdot \log{b}+b\cdot \log{\left(min\left(a,~\dfrac{b}{3}\right)\right)}\right)\).
Ниже представлено решение на языке Python.
import sys
a, b = map(int, sys.stdin.readline().split())
c = list(map(int, sys.stdin.readline().split()))
c.sort()
l, r = 1, min(b // 3, a)
while l <= r:
m = (l + r) // 2
cycles = 0
p = [0 for i in range(m)]
it = 0
for i in range(b):
if p[it] < c[i]:
p[it] = c[i]
it += 1
if it == m:
it = 0
cycles += 1
if cycles < 3:
r = m - 1
else:
l = m + 1
print(max(0, r))
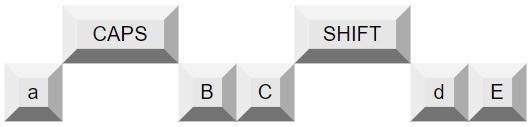
Необходимо напечатать строку \(s\) длины \(n\), состоящую из символов в двух разных регистрах: заглавных и строчных латинских букв. Изначально на клавиатуре включен нижний регистр (печатаются строчные буквы).
За одно нажатие клавиши на клавиатуре можно:
- нажать клавишу
SHIFT, которая переключит регистр для одного следующего напечатанного символа; - нажать клавишу
CAPS, которая переключает регистр для всех следующих печатаемых символов; - нажать клавишу с буквой на клавиатуре, тогда она напечатается в установленном регистре.
Определите минимальное число нажатий клавиш для того, чтобы напечатать строку \(s\).
Формат входных данных
В первой строке входных данных содержится целое число \(n\) (\(1\leqslant n\leqslant 10^5\)) — количество символов в строке s.
Во второй строке содержится строка \(s\) длины \(n\). Строка состоит только из строчных и заглавных букв латинского алфавита.
Формат выходных данных
Выведите единственное целое число — минимальное число нажатий клавиш на клавиатуре для того, чтобы напечатать строку \(s\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
5 ABCDE |
6 |
2 |
5 aBCdE |
7 |
3 |
7 AAAAaAA |
9 |
Задачу можно решить методом динамического программирования. Определим два массива \(upper\) и \(lower\), оба размера \((n+1)\), следующим образом:
- \(upper_i\) — минимальное количество нажатий на клавиатуре для печати первых \(i\) символов строки \(s\) с установленным в конце верхним регистром;
- \(lower_i\) — минимальное количество нажатий на клавиатуре для печати первых \(i\) символов строки \(s\) с установленным в конце нижним регистром.
База динамики. Изначально \(lower_0=0\), \(upper_0=1\), так как изначально клавиатура установлена на нижний регистр, и печатать ничего не нужно, остальные значения \(lower\) и \(upper\) не определены.
Переход динамики. Будем просматривать строку \(s\) слева направо. Пусть сейчас мы смотрим на \(i\)-й символ строки, тогда есть два варианта событий:
Символ \(s_{(i-1)}\) (у строки 0-индексация) в нижнем регистре, тогда \(lower_i\) обновится на минимальное значение из следующих:
- \((lower_{(i-1)}+1)\) — поскольку уже напечатаны \((i-1)\) символов, и у клавиатуры был установлен нижний регистр, то текущий символ напечатаем за одно нажатие;
- \((upper_{(i-1)}+2)\) — используем нажатие на
CAPSдля переключения регистра на нижний. После того как напечатаны \((i-1)\) символов и включен верхний регистр, нажимаем на клавишу символа.
\(upper_i\) же примет минимальное значение из следующих:
- \((lower_i+1)\) — используем ответ для \(lower_i\), но тратим одно действие на нажатие
CAPS, переключая регистр на верхний; - \((upper_{(i-1)}+2)\) — берем ответ для \(upper_{(i-1)}\), нажимаем на
SHIFT, затем на клавишу с символом. Это требует два действия, и после нажатия на клавишу с символом регистр переключается обратно.
- Символ \(s_{(i-1)}\) в верхнем регистре. Тогда делаем все то же самое, что описано выше, но подменяем понятия \(lower\) и \(upper\).
Ответ на задачу — минимум из \(lower_n\) и \(upper_n\). Также можно использовать не два, но один двухмерный массив, как показано в решении ниже.
Сложность: \(\mathcal{O}(n)\).
Ниже представлено решение на языке Python.
import sys
n = int(sys.stdin.readline())
s = str(sys.stdin.readline().strip())
dp = [[0 for i in range(n + 1)], [0 for i in range(n + 1)]]
dp[1][0] = 1
for i in range(n):
if s[i].lower() == s[i]:
# буква в нижнем регистре
dp[0][i + 1] = 1 + min(dp[0][i], 1 + dp[1][i])
dp[1][i + 1] = min(dp[0][i + 1] + 1, 2 + dp[1][i])
else:
# буква в верхнем регистре
dp[1][i + 1] = 1 + min(dp[1][i], 1 + dp[0][i])
dp[0][i + 1] = min(dp[1][i + 1] + 1, 2 + dp[0][i])
print(min(dp[0][-1], dp[1][-1]))
В маленькой стране N есть клуб гиревого спорта «Гиря и Гора», в котором преподает поднятие тяжестей небезызвестный в известных кругах уважаемый Мхал Саныч. В клубе занимаются \(n\) атлетов, каждый \(i\)-й атлет имеет личный рекорд поднятия гири — целое число \(a_i\).
Так как скоро олимпиада, то президент страны N поручил отобрать \(k\) атлетов так, чтобы все \(k\) атлетов имели различные личные рекорды по поднятию гири. Мхал Саныч хочет выбрать таких \(k\) атлетов, чтобы наибольшая разница между личными рекордами любых двух атлетов в команде была как можно меньше, при этом должно выполняться поручение президента.
Определите, какую минимальную разницу между максимальным и минимальным личными рекордами атлетов можно получить, выбрав \(k\) атлетов с различными личными рекордами из \(n\) имеющихся.
Формат входных данных
В первой строке входных данных содержатся два целых числа \(n\), \(k\) (\(1\leqslant n, k\leqslant 10^5\)) — количество атлетов в клубе «Гиря и Гора» и количество атлетов для отбора на олимпиаду соответственно.
Во второй строке содержатся \(n\) целых чисел \(a\) (\(1\leqslant a_i\leqslant 10^9\)) — личные рекорды каждого атлета по поднятию гири.
Формат выходных данных
Выведите единственное целое число — минимальную из максимальных разниц в наборе из \(k\) атлетов с попарно различными личными рекордами. Если ни одного такого набора не существует, то выведите -1.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
5 2 3 9 6 10 1 |
1 |
2 |
11 3 4 9 1 1 2 4 5 5 1 2 6 |
2 |
3 |
4 3 1 2 2 1 |
-1 |
Отсортируем массив \(a\) и будем искать в нем такой отрезок \([l,\,r]\), на котором встречается ровно \(k\) различных чисел, а разница между \(a[r]\) и \(a[l]\) будет максимальной разницей в этом наборе. По всем таким наборам нужно найти минимальную разницу.
Решим задачу методом двух указателей. Создадим \(left=0\) и будем итерироваться по массиву переменной \(right\), поддерживая на отрезке \(k\) различных чисел (это можно сделать, используя счетчик и, например, словарь с количеством вхождений каждого элемента на отрезке).
Если на отрезке менее \(k\) различных чисел, то сдвигаем \(right+1\), иначе, если на отрезке \(k\) различных чисел, то пытаемся обновить ответ, как минимум, из того, что в нем находится и \(a[right]\), и \(a[left]\), затем сдвигаем \(left+1\).
Сложность: \(\mathcal{O}(n+n\cdot \log n)\), что то же самое, что \(\mathcal{O}(n\cdot \log n)\).
Ниже представлено решение на языке Python.
import sys
n, k = map(int, sys.stdin.readline().split())
a = list(map(int, sys.stdin.readline().split()))
a.sort()
mn = 1 << 60
f = {}
r = 0
for i in range(n):
if a[i] not in f or f[a[i]] == 0:
f[a[i]] = 1
k -= 1
else:
f[a[i]] += 1
while k == 0:
mn = min(mn, a[i] - a[r])
if f[a[r]] == 1:
k += 1
f[a[r]] -= 1
r += 1
if mn == 1 << 60:
print(-1)
else:
print(mn)
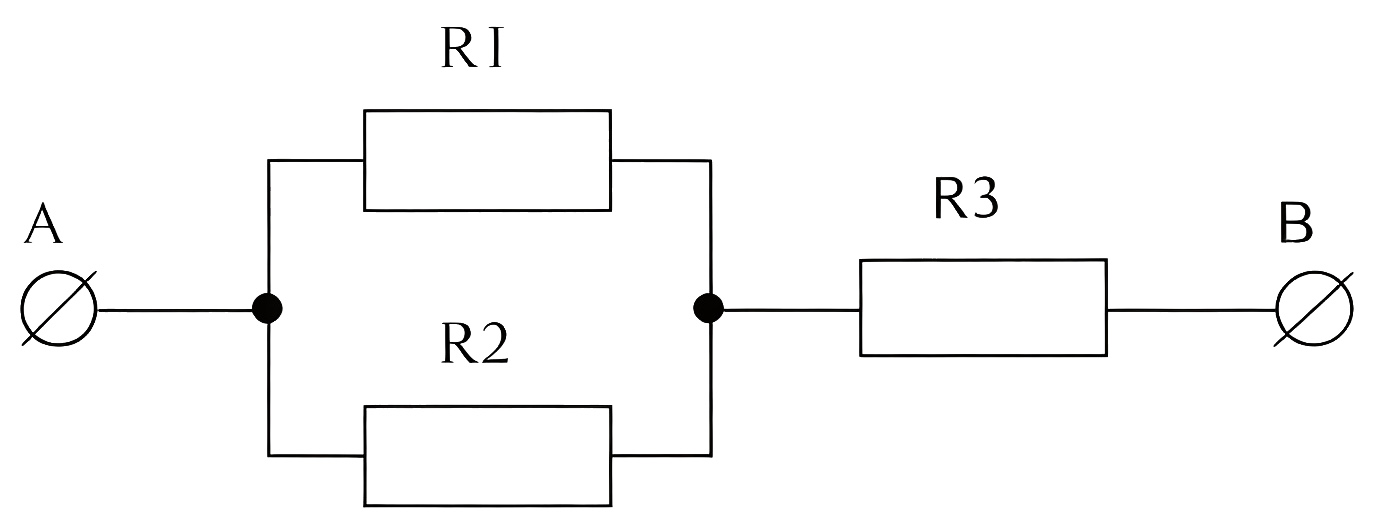
В умном доме есть сушилка для одежды, ее схема представлена на рис. 1.4. К концам схемы приложено постоянное напряжение. Сопротивление \(R_1=3R\), а сопротивление остальных элементов \(R_2=R_3=R\). Какое количество теплоты выделится на \(R_1\) за 2 мин, если за 30 с на \(R_3\) выделилось 220 Дж? Ответ укажите в джоулях.
По закону Джоуля – Ленца: \[\begin{gather} Q_1=I^2_1\cdot R_1\cdot t_1;\\ Q_3=I^2_3\cdot R_3\cdot t_3. \end{gather}\] Так как элементы \(R_1\) и \(R_2\) соединены параллельно и подключены к элементу \(R_3\) последовательно, то \[I_3=I_1+I_2 ~\text{и}~ U_1=U_2.\] Из закона Ома: \[\begin{gather} I_1\cdot R_1=I_2\cdot R_2~\Rightarrow~ I_1=\frac{I_2\cdot R}{3R}=\frac{1}{3} I_2;\\ I_3=I_2+\frac{1}{3} I_2=\frac{4}{3} I_2~\Rightarrow~ I_2=\frac{3}{4} I_3~\Rightarrow~ I_1=\frac{1}{4} I_3;\\ Q_1=\left(\frac{1}{4} I_3 \right)^2\cdot 3R_3\cdot t_1=\left(\frac{1}{4} I_3 \right)^2\cdot 3R_3\cdot t_3 \frac{t_1}{t_3} =\frac{3}{16} \cdot Q_3\cdot \frac{t_1}{t_3};\\ Q_1=\frac{3}{16}\cdot 220\cdot \frac{120}{30}=165 \text{~Дж}. \end{gather}\]
165 Дж.
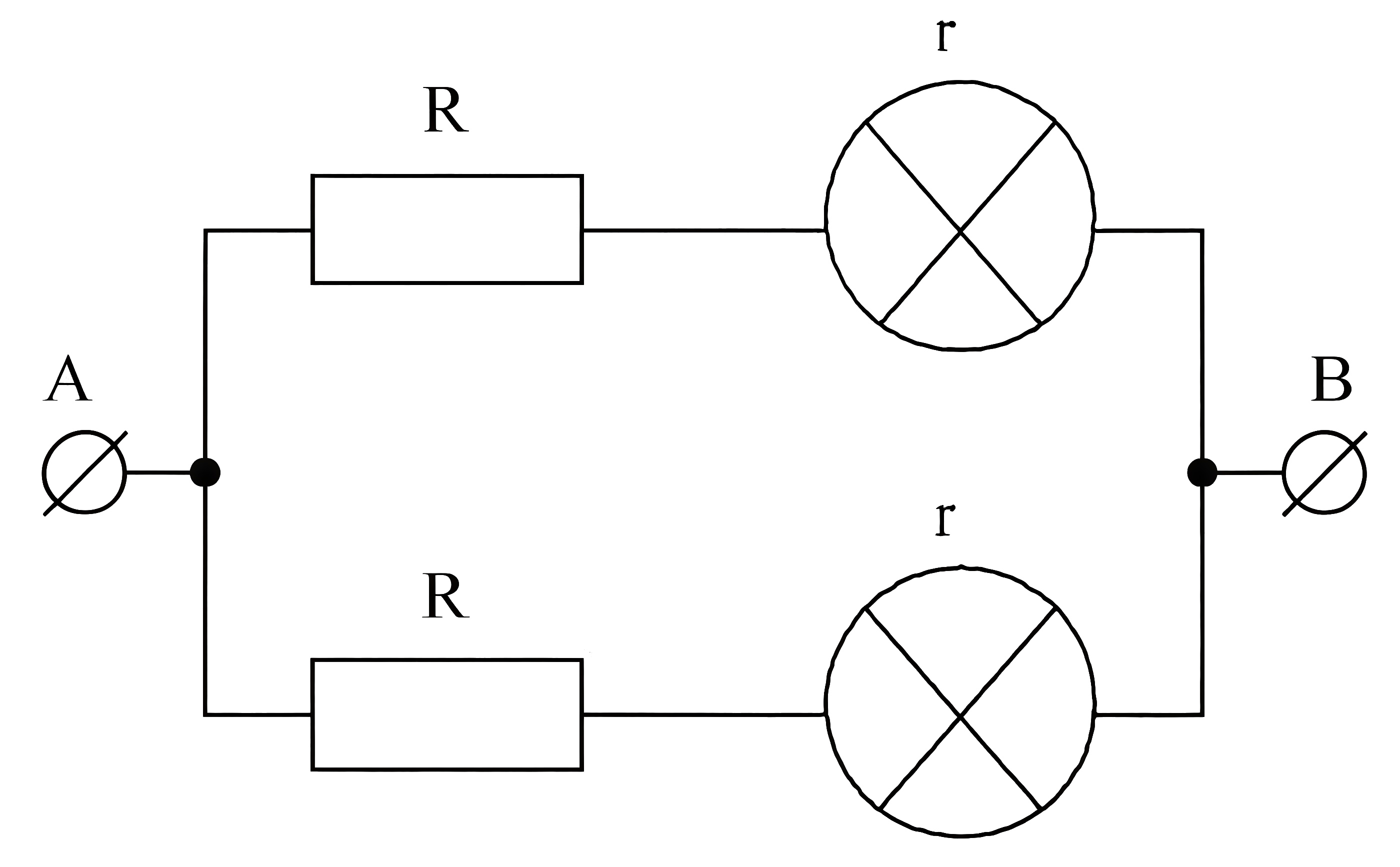
Инженер разработал схему, представленную на рис. 1.5. Напряжение источника считаем постоянным. Сопротивление резисторов составляет \(R= 100\) Ом. Известно, что если в этой цепи вместо одной из ламп подключить резистор с сопротивлением \(R\), то мощность, выделяемая во всей цепи, увеличится в \(k = 5\) раз. Найдите сопротивление лампы \(r\), ответ дайте в омах.
Общее сопротивление цепи в первом случае равно: \[R_1=\frac{R+r}{2}.\]
Мощность в цепи равна: \[P_1=\frac{U^2}{R_1} =\frac{2\cdot U^2}{R+r},\] где U — напряжение между точками \(A\) и \(B\).
После того как одну из ламп заменили резистором, общее сопротивление цепи стало равным: \[R_2=\frac{2R\cdot (R+r)}{3R+r},\] а мощность: \[P_2=\frac{U^2 (3R+r)}{2R\cdot (R+r)}.\]
По условию \[P_2=k\cdot P_1.\]
Тогда \[\frac{U^2 (3R+r)}{2R\cdot (R+r)}=k\cdot \frac{2\cdot U^2}{R+r},\] отсюда получаем: \[r=(4k-3)\cdot R=(4\cdot 5-3)\cdot 100= 1{,}7 \text{~кОм}.\]
1700 Ом.
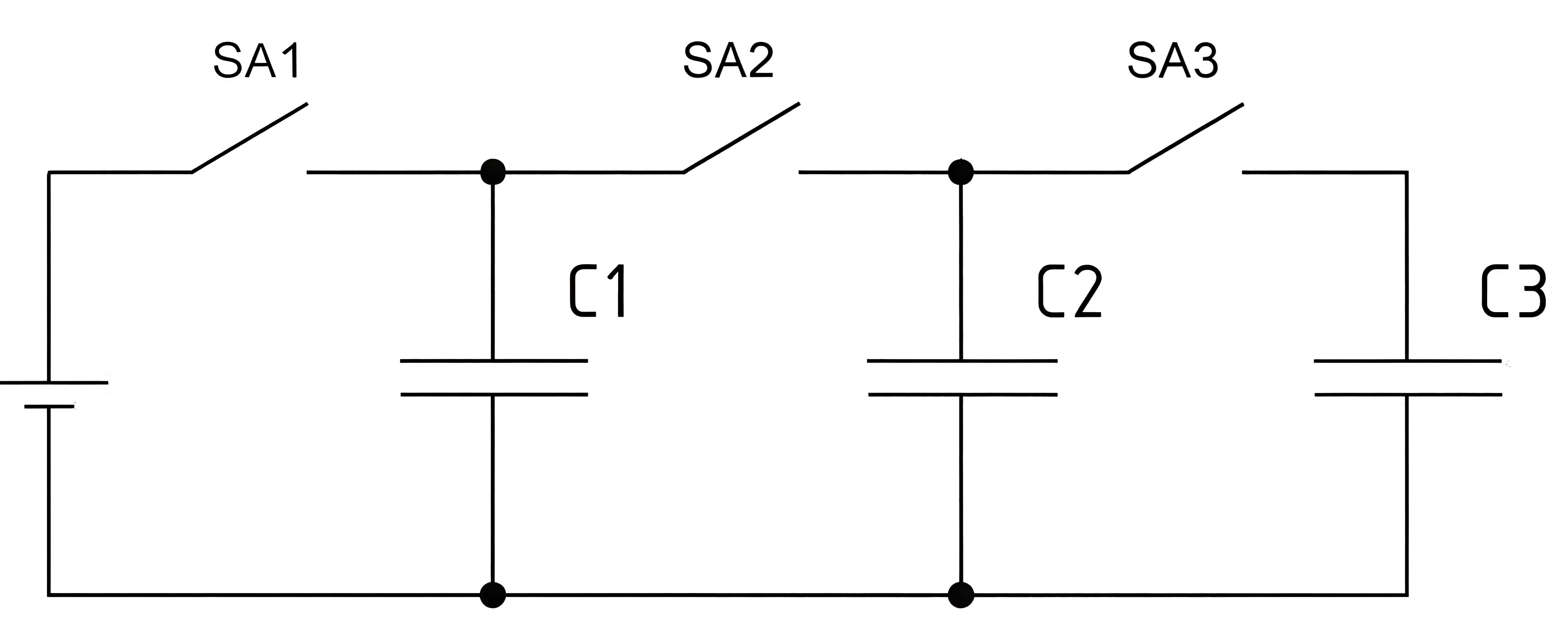
В умном городе было три аккумулятора, между которыми нужно было распределить заряд. Для этого их соединили по следующей схеме — рис. 1.6. ЭДС источника составляет 12 В. Емкость второго конденсатора в 2 раза больше первого и в 3 раза меньше третьего. Ключи поочередно быстро замкнули и разомкнули, сначала — первый, затем — второй и в конце — третий. Найдите напряжение на всех трех конденсаторах в вольтах.
Емкости конденсаторов равны: \[\begin{gather} C_2=2C_1;\\ C_3=3C_2=6C_1. \end{gather}\] Найдем заряд на первом конденсаторе после того, как замкнули первый ключ: \[q_0=C_1\cdot U_{\text{ист}}.\]
Затем найдем отношение зарядов после замыкания второго ключа, зная, что после этого напряжение на \(C_1\) и \(C_2\) стало одинаковым: \[\frac{q_1}{C_1} =\frac{q_2}{C_2} ~\Rightarrow~\frac{q_1}{q_2} =\frac{C_1}{C_2} =\frac{1}{2}~\Rightarrow~q_1=\frac{1}{2} q_2.\]
Известно, что \[q_0=q_1+q_2~\Rightarrow~q_2=\frac{2}{3} q_0 \text{~и~} q_1=\frac{1}{3} q_0.\]
Найдем заряды на конденсаторах после замыкания третьего ключа: \[\frac{q'_2}{q_3} =\frac{C_2}{C_3 }=\frac{1}{3}~\Rightarrow~q'_2=\frac{1}{3} q_3.\] Известно, что \[q_2=q'_2+q_3~\Rightarrow~q_3=\frac{3}{4} q_2=\frac{1}{2} q_0\] и \[q'_2=\frac{1}{4} q_2=\frac{1}{6} q_0.\] Находим напряжения на каждом конденсаторе: \[\begin{gather} U_{C_1}=\frac{C_1 \cdot U_{\text{ист}}}{3\cdot C_1}=4 \text{~В},\\ U_{C_2}=\frac{C_1\cdot U_\text{ист}}{6\cdot C_2} = \frac{U_\text{ист}}{12}=1 \text{~В},\\ U_{C_3}=\frac{C_1\cdot U_\text{ист}}{2\cdot C_3} = \frac{U_\text{ист}}{12}=1 \text{~В}. \end{gather}\]
\(U_{C_1}=4\) В, \(U_{C_2}=1\) В, \(U_{C_3}=1\) В.
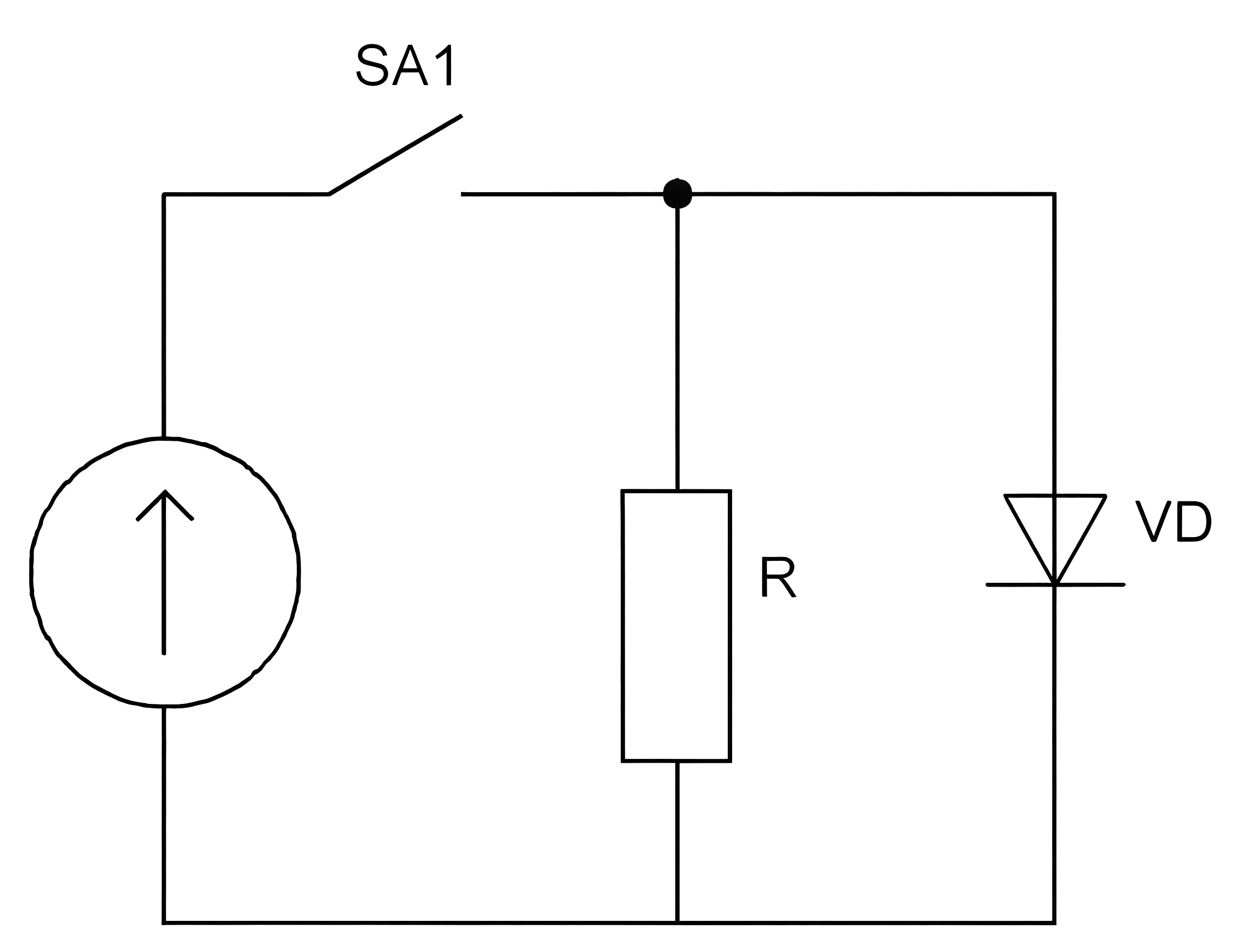
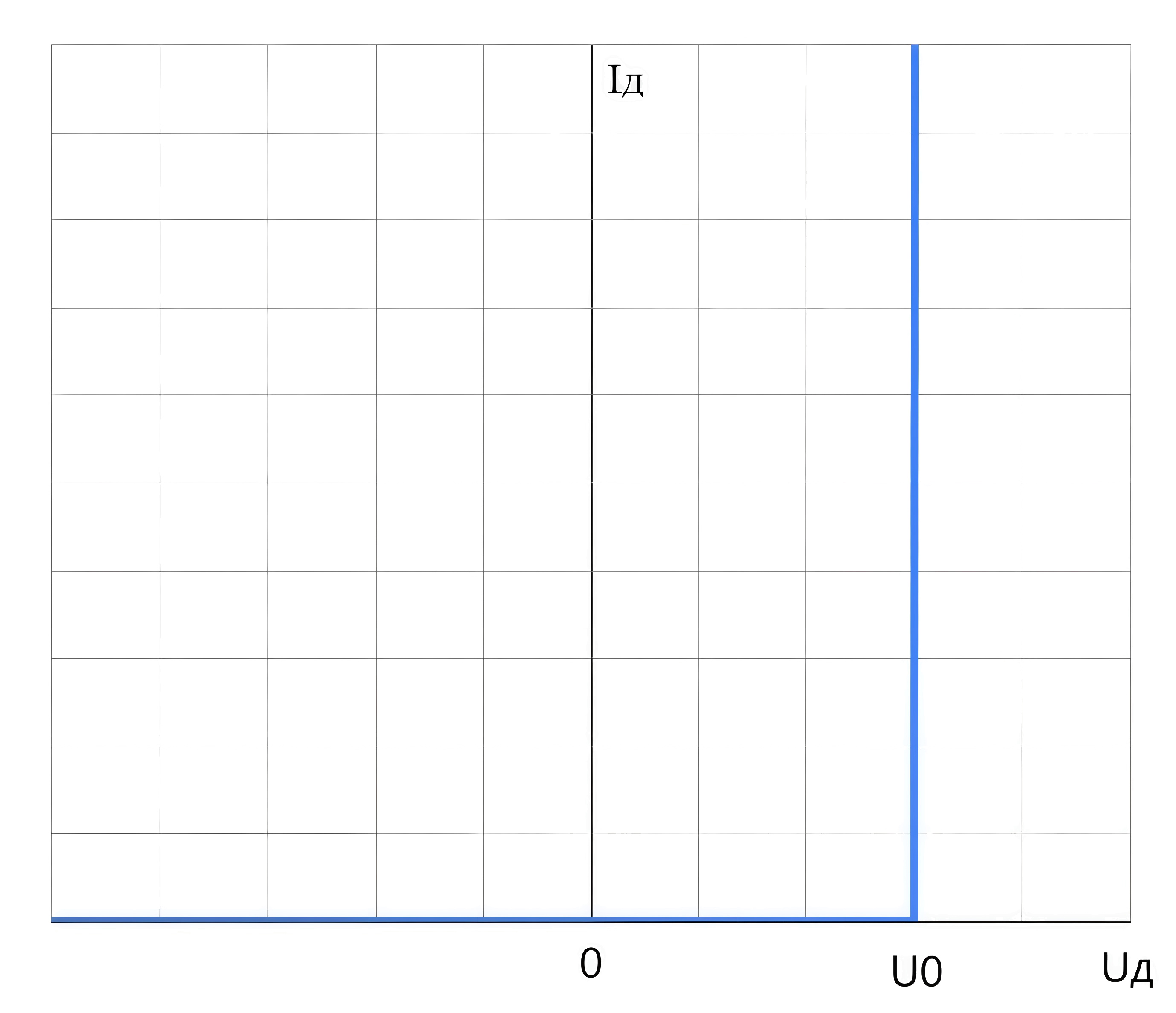
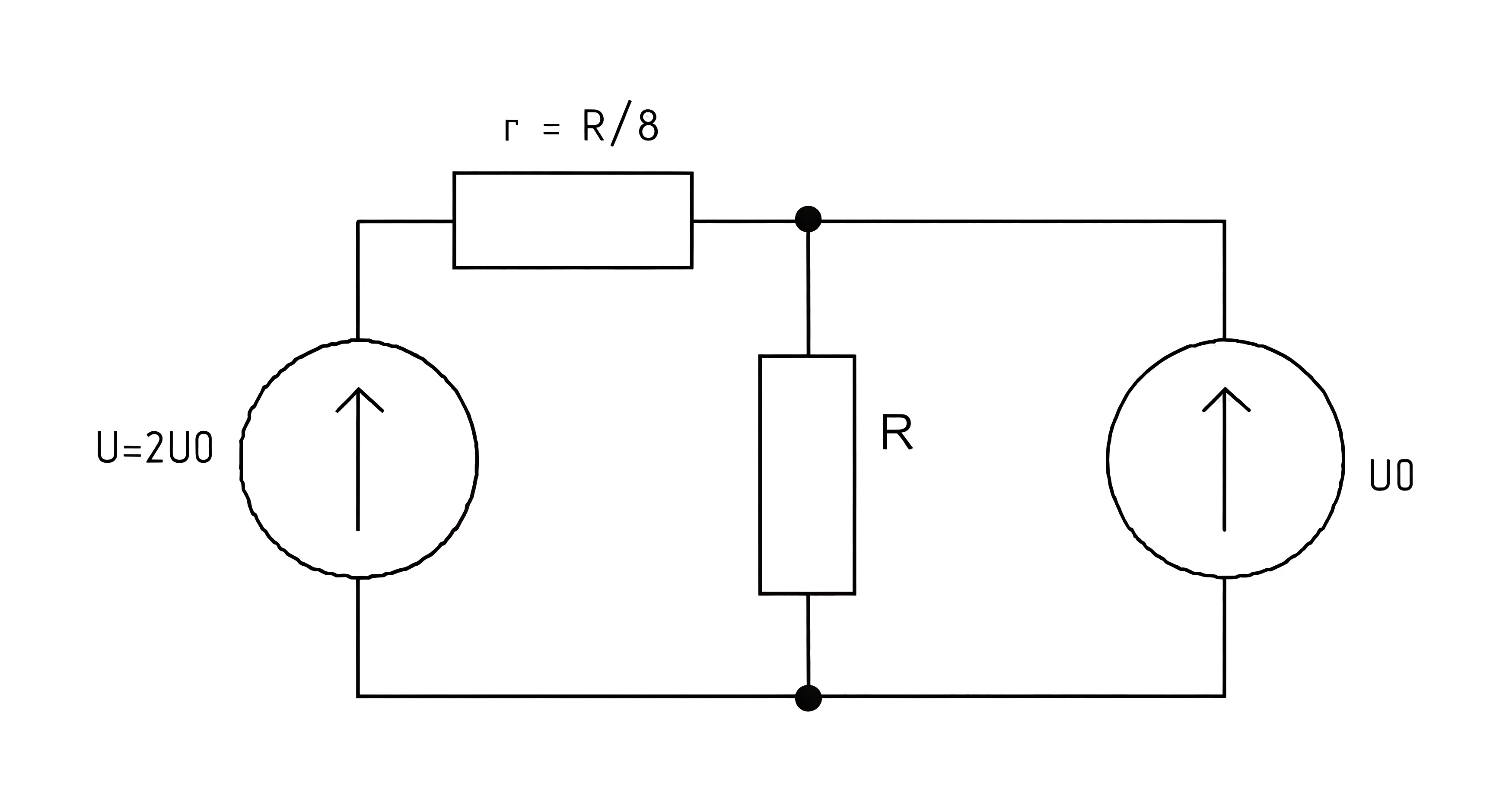
Инженер спроектировал схему, представленную на рис. 1.7, вольт-амперная характеристика диода изображена на рис. 1.8. Известно, что напряжение источника в два раза больше порогового напряжения \(U_0\), а внутреннее сопротивление источника в восемь раз меньше сопротивления резистора. Найдите отношение мощностей \(P_R/P_\text{диод}\). Ответ округлите до десятых.
Диод, очевидно, находится в открытом состоянии.
Мощности, выделяемые на элементах: \[P_R=U_0\cdot I_R\] и \[P_\text{д}=U_0\cdot I_\text{д}.\] Отсюда \[\frac{P_R}{P_\text{д}} =\frac{I_R}{I_\text{д}}.\] Эквивалентная схема.
Методом наложенных контуров находим токи: \[I_R=0+\frac{U_0}{R}\] и \[I_\text{д}=\frac{16U_0}{R}-\frac{9R\cdot U_0}{R^2},\] \[\frac{P_R}{P_\text{д}} =\frac{I_R}{I_\text{д}} = \frac{\frac{U_0}{R}}{\left(\frac{16U_0}{R}-\frac{9R\cdot U_0}{R^2} \right)}\approx 0{,}1.\]
0,1.
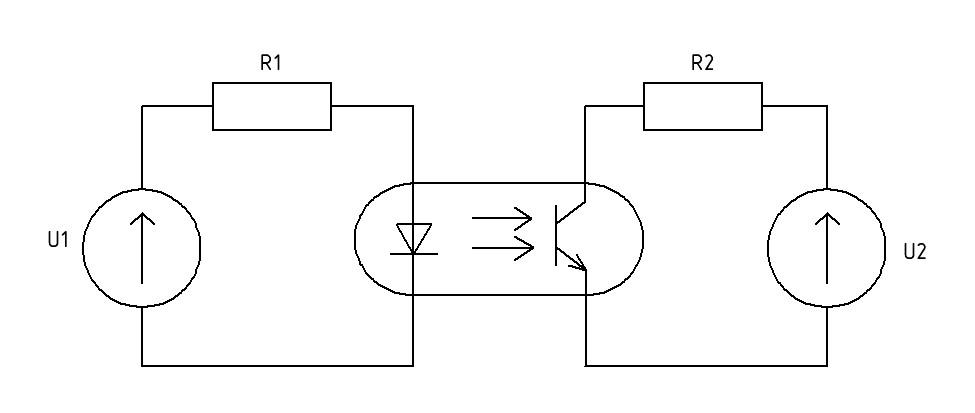
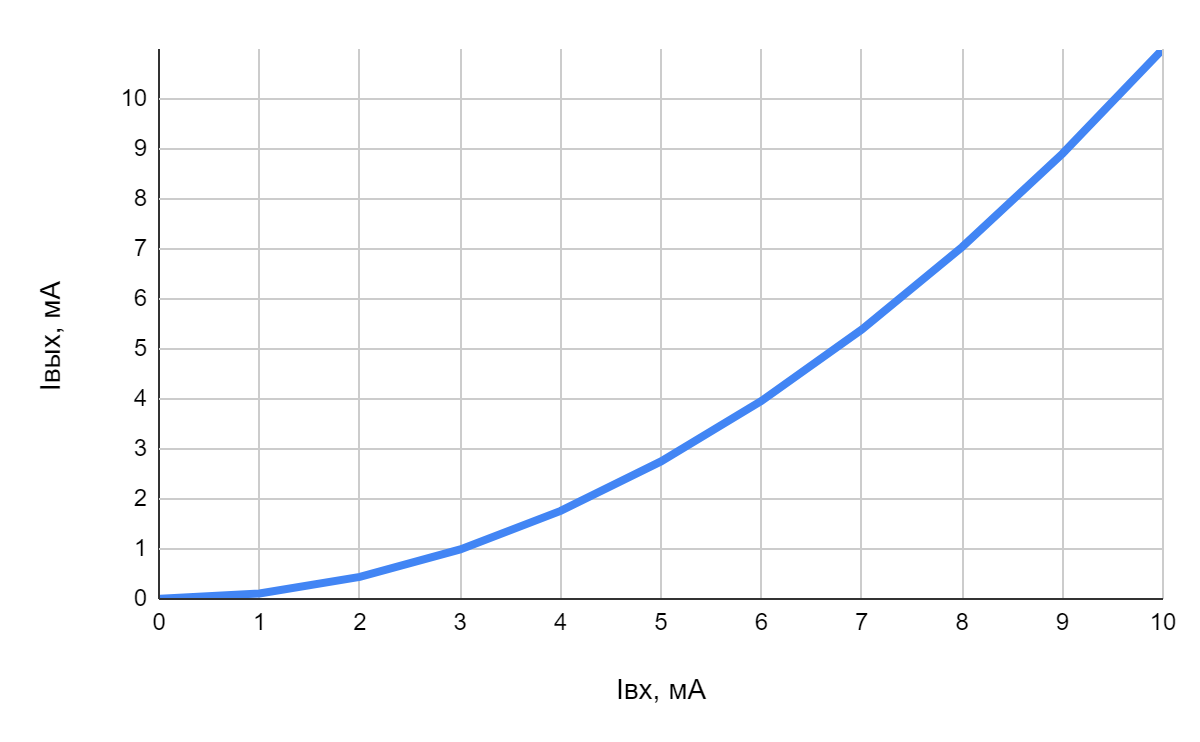
В умном городе используется схема с оптопарой, представленная на рис. 1.10. Имеется зависимость входного тока оптопары от выходного (рис. 1.11). Известно, что напряжение входного источника равно 32 В, а выходного — 15 В, сопротивление \(R_1=4\) кОм, \(R_2=3\) кОм. Найдите ток в выходной ветви в миллиамперах.
Найдем ток во входной цепи: \[I_\text{вх}=\frac{U_1}{R_1} =\frac{32}{4000}=8 \text{~мА}.\] По графику находим выходной ток, он равен 7 мА, но необходимо проверить, возможен ли такой ток. Найдем максимально возможный ток в выходной цепи: \[I_\text{вых}=\frac{U_2}{R_2} =\frac{15}{3000}=5 \text{~мА}.\] Можно сделать вывод, что фототранзистор вышел в насыщение, и ток в выходной цепи составляет 5 мА.
5 мА.