Инженерный тур. 2 этап

Поручено разработать систему автоматической параллельной парковки автомобиля на дороге небольшого виртуального городка.

• Парктроник — датчик расстояний до препятствий на автомобиле.
• Сплошная — осевая разметка дорожного движения, разделяющая встречные потоки.
• Датчик разметки — датчик, измеряющий расстояние от автомобиля до сплошной линии разметки.
• Коллайдер — физические границы, по которым считается столкновение объектов.

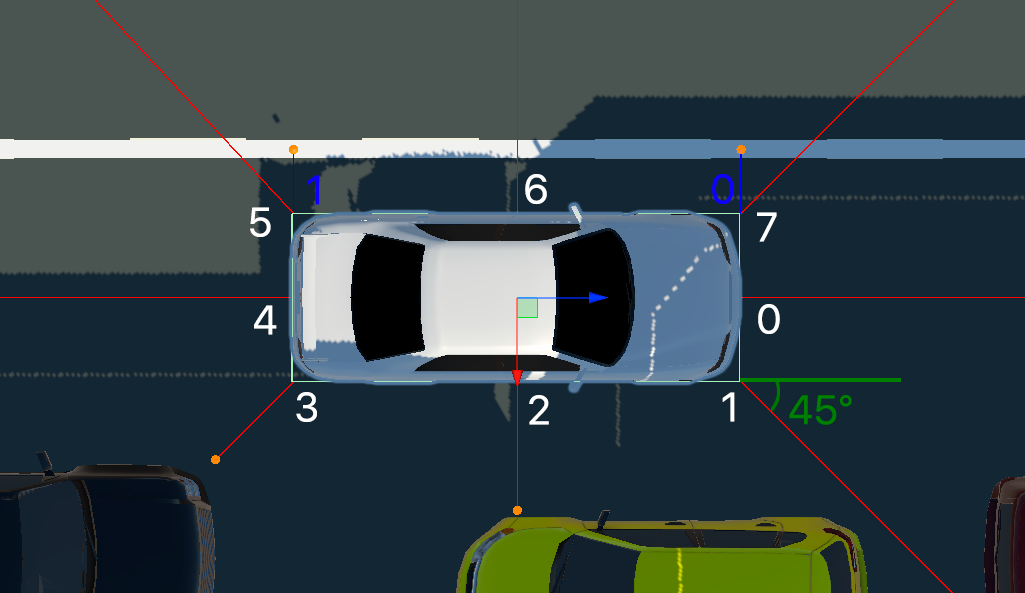
На автомобиле расположены 8 парктроников, а также 2 датчика разметки. Для упрощения задачи коллайдер автомобиля представляет собой параллелепипед размерами (1,811328 м в ширину, 4,819343 м в длину и 1,191418 м в высоту).

Все датчики расположены на высоте \(\approx 0{,}27\) м от нижней грани коллайдера. Парктроники располагаются по одному на каждой боковой грани по центру, а также в боковых ребрах под углом 45° к продолжению граней. Датчики разметки расположены на двух боковых ребрах, ближайших к сплошной по направлению движения автомобиля (движение правостороннее), и направлены в плоскости передней и задней боковой грани.

Датчики разметки игнорируют любые препятствия и выполняют измерения сквозь них, парктроники же считывают первое попадание до препятствия и возвращают расстояние до него.

Если расстояние до препятствия больше 10 м, то парктроники возвращают значение, близкое к 10.

Локация, в которой происходит парковка, представляет собой прямую проезжую часть шириной 12,5 м (каждая полоса 6,25 м) и длиной 50 м. Парковочная зона огорожена двумя блоками и знаком «Парковка».

Парковку можно выполнять только внутри этой области. Длина парковочной зоны составляет 40 м, расположение зоны одинаково для всех тестов. Внутри этой области могут находиться другие припаркованные транспортные средства. Каждое ТС расположено строго параллельно сплошной, его коллайдер также представляет собой параллелепипед, границы которого не находятся ближе 3 м от сплошной, а также не выходят за пределы проезжей части. Припаркованные ТС могут быть различных размеров.

К проезжей части примыкает тротуарная зона, в которой также могут располагаться различные объекты.

Перед началом парковки автомобиль расположен параллельно сплошной, центр автомобиля находится на расстоянии 1,6 м от нее. Передний край коллайдера находится на линии начала парковочной зоны.

Для управления автомобилем доступны два метода, реализованных в классе CarController:

• void SetSpeed(float value) — задает скорость движения автомобилем в километрах в час. Отрицательные значения value задают движение в обратном направлении.
• void SetStearingAngle(float value) — задает направление поворота руля. value может изменяться от \(-1\) до \(1\), где \(-1\) — крайнее левое положение (максимальный выворот колес влево), 1 — крайнее правое положение.
• float GetParkingSensorDistance(int index) — возвращает текущее показание парктроника с номером index. Нумерация начинается с \(0\) (передний парктроник) и идет по часовой стрелке. Если парктроник с запрошенным индексом отсутствует, возвращается \(-1\).
• float GetDistanceToLine(int index) — возвращает текущее показание датчика разметки с номером index. \(0\) соответствует переднему датчику, 1 — заднему.

Данные с датчиков обновляются после каждого выполнения FixedUpdate().

Примечания

Поведение функции SetSpeed приближено к поведению при управлении автомобилем в ручном режиме. При вызове функции SetSpeed происходит набор скорости автомобилем до установленного значения путем нажатия на полный газ. Как только разгон до нужной скорости будет выполнен, автомобиль сразу же начинает сбавлять скорость путем подачи полного газа на обратный ход. В тот момент когда скорость становится ниже заданной, автомобиль снова начинает ее набирать. Таким образом, после разгона до нужной скорости \(v_{\text{заданная}}\) автомобиль продолжает ее поддерживать в пределах \(|v_{\text{факт}}-v_{\text{заданная}}| < 0{,}3\). Вызов функции SetSpeed обрабатывается сразу, т. е. если, например, задана скорость, равная 40 и, не дожидаясь ее полного набора, установлена скорость \(0\), то автомобиль сразу начнет процесс снижения скорости.

При вызове функции SetStearingAngle происходит поворот колес до установленного положения. Полный выворот от начального положения до одного из краевых составляет примерно 0,4 c. Функция обрабатывает все запросы по очереди, т. е. если находитесь в процессе движения из состояния \(0\) в состояние \(1\), и не дожидаясь завершения полного поворота колес вызываете переход в состояние \(-1\), то сначала колеса выкручиваются в положение, соответствующее состоянию \(1\), и только затем начинают выкручиваться до состояния \(-1\).

Внутри парковочной зоны необходимо найти пространство, в которое можно будет припарковать автомобиль. Гарантируется, что парковочное место, достаточное для осуществления парковки с помощью вышеуказанных функций, существует. Требуется припарковать автомобиль параллельно сплошной по направлению движения, ближайшая точка коллайдера должна быть не ближе, чем 3 м от сплошной, при этом автомобиль должен находится строго внутри проезжей части (не заезжать на тротуар). Также требуется припарковать автомобиль на расстоянии от 0,3 до 0,35 м до ближайшего препятствия позади автомобиля. По завершении парковки нужно вызвать функцию EndOfParking(), находящуюся в классе CarController.

Тестирование проводится на наборе сцен, соответствующих указанному описанию. Требуется выполнить процедуру поиска парковочного места и самой парковки за 50 с.

Результат теста будет оцениваться по качеству осуществленной парковки. Если автомобиль после парковки попадает в указанную зону и находится на нужном расстоянии от препятствия сзади (измерение берется по парктронику № 4), то в случае, если угол автомобиля отклоняется не более, чем на 1° от идеальной параллельной парковки, получаете максимальный балл за тест. За большее отклонение по каждому из параметров предусматривается штраф.

В процессе парковки нельзя сталкиваться с любыми другими объектами на сцене.

Также нельзя выезжать любой частью хитбокса на встречную полосу за сплошную. При нарушении этих требований симуляция завершается с результатом в 0 баллов.

Кроме этого, нельзя устанавливать скорость движения автомобиля свыше 60 км/ч в любую из сторон.

Все решение должно находиться в классе Solution. Этот класс не должен содержать публичные методы, значения которых устанавливаются из редактора движка. Также запрещается обращаться к любым объектам на сцене, в том числе запрашивать и/или изменять компоненту Transform, а также создавать свои игровые объекты. Можно использовать только данный экземпляр CarController и вызывать указанные в нем методы.

Проект с демонстрационной сценой доступен по ссылке: https://github.com/ntomaterials/tvr-25-stage2.

Можно открыть сцену в папке Assets/Scenes для тестирования своего решения. Писать код с решением нужно в файл Assets/Scripts/Solution.cs. Для моделирования различных дорожный ситуаций можно расставлять на сцене объекты с машинами, находящиеся в папке Assets/Prefabs.

Примечания

Внимание! Не изменяйте остальные файлы и другие игровые объекты. Изменения, внесенные куда-либо кроме файла Solution.cs, не учитываются.

Автомобильная компания участвует в гонках для рекламы своего продукта. В этом году спрос на гонщиков был выше обычного, и компании достался потенциальный пилот Петя, который, однако, не умеет быстро просчитывать траектории.

Траекторией считается линия, описываемая центром автомобиля. Известно, что гоночный трек имеет постоянную ширину \(w\) и ровно \(n\) поворотов с заданными внешними радиусами \(R_i\). В начальный момент времени координаты старта совпадают с центром автомобиля. В конце пути координаты финиша также совпадают с координатами центра автомобиля.

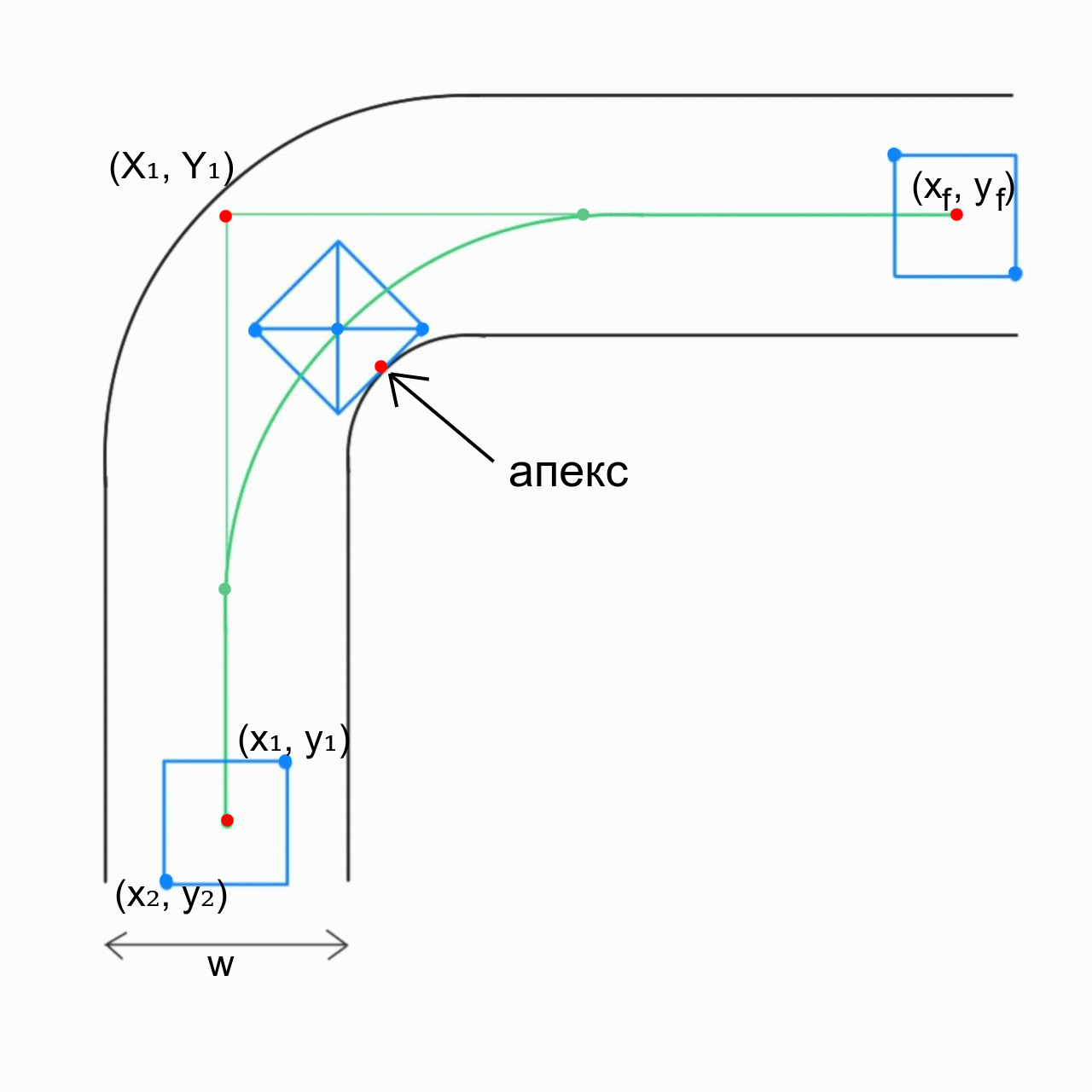
На прямых участках Петя старается ехать ровно по осевой линии трека, однако, приближаясь к поворотам, корректирует траекторию в сторону поворота. Эта траектория представляет собой дугу окружности, проходящую таким образом, чтобы при движении по ней автомобиль внешней стороной касался апекса (точки, ближайшей к внутреннему краю дороги).

На границах трека установлены ограничители, поэтому выходить за его границы нельзя. Траектория считается корректной, только если каждый поворот начинается из центра трека и завершается в центре трека.

Необходимо написать программу, которая определяет угол поворота левого переднего колеса \(i\) для каждого поворота на треке. Именно это колесо задает движение автомобиля в гонках.

Важно учитывать, что у разных колес свой угол поворота, так как они описывают окружности разного радиуса. Например, если левое колесо расположено ближе к апексу, то угол его поворота больше угла поворота правого колеса, поскольку левое колесо описывает окружность меньшего радиуса.

Также необходимо подсчитать общую длину траектории \(s\).

Чем лучше и быстрее выполнена работа, тем выше шансы на повышение внутри компании!

Формат входных данных

В первой строке входного файла находятся четыре числа \((x_1, y_1, x_2, y_2)\) — координаты переднего правого и левого заднего колеса автомобиля соответственно, эти же числа задают границы автомобиля.

Вторая строка содержит число \(w\) — ширину трека.

В третьей строке даны два числа \((x_f, y_f)\) — координаты финиша.

В четвертой строке находится число \(n\) — количество поворотов.

В следующих \(n\) строках находятся по 3 числа \((X_i, Y_i, R_i)\) — координаты поворота в прямолинейной траектории и внешний радиус поворота.

Формат выходных данных

В первой строке выходного файла содержится число \(s\) — длина получившейся траектории, округленная до пятого знака после запятой.

В следующих \(n\) строках указаны значения \(i\) — угол поворота переднего левого колеса на \(i\)-м повороте в радианах, округленный до пятого знака после запятой.

Если заданную траекторию построить невозможно, необходимо вывести только \(-1\).

\[0 < w \leqslant 1000;\] \[0 \leqslant n \leqslant 10^4;\] \[-10^6 < x_1, y_1, x_2, y_2, x_f, y_f, X_i, Y_i < 10^6;\] \[w < R_i < 100.\]

Тестовые данные

1

3 2 1 0
4
13 10
1
2 10 6

17.24700
0.13407

2

5 4 0 1
5.21
3 5.432
2
38.3553 38.3553 6.5
51.3362 -9.9137 6.5

134.91777
0.41026
0.41892

Старый друг Дмитрий попросил Руслана разработать дизайн для дисков на его машину в формате векторного изображения SVG. К сожалению, Руслан ничего не смыслит в дизайне и компьютерной графике, но зато хорошо разбирается в формулах и математике. Ему удалось вывести точное математическое описание с формулами и зависимостями, чтобы в точности можно было следовать этому описанию и нарисовать то, что Руслан представляет у себя в голове. Помогите Руслану получить векторное изображение.

• Размер векторного изображения составляет \(200\times 200\) единиц.
• Граница фигуры представляет собой кольцо шириной \(20\) единиц. Внешний радиус кольца равен \(90\) единиц, а его центр расположен в центре изображения.

• На изображении располагаются восемь квадратичных кривых Безье. Каждая \(k\)-ая кривая (где \(k = 0, 1, \dots, 7\)) строится следующим образом:

  • Начало кривой лежит на окружности с радиусом \(90\) единиц. Дуга между верхней точкой окружности и началом кривой, движущаяся по часовой стрелке, опирается на угол \(\dfrac{\pi \cdot k}{4}\).
  • Конец кривой находится в центре изображения.
  • Контрольная точка расположена на окружности с центром в центре изображения и радиусом \(60\) единиц. Дуга между верхней точкой этой окружности и контрольной точкой, движущаяся по часовой стрелке, опирается на угол \(\left(\dfrac{\pi \cdot k}{4} - \dfrac{\pi}{4}\right)\). Отрицательный угол означает движение против часовой стрелки от верхней точки.
  • Ширина каждой кривой Безье составляет \(20\) единиц.
• При расчете координат, связанных с построением кривых и окружностей, все дробные числа округляются до ближайшего целого.

• Область изображения внутри кольца, но вне полос кривых, закрашивается с использованием линейного градиента.
• Градиент строится на всем полотне изображения, но область за пределами кольца остается незакрашенной.

• Требования к линейному градиенту:

  • используются опорные точки с цветами: #cfd8dc, #ffffff, #cfd8dc, #9e9e9e, #757575, равномерно распределенные от 0% до 100%;
  • направление градиента задается начальной точкой \(\{0, 0\}\) и конечной \(\{200, 200\}\).
• Кольцо и полосы кривых окрашиваются с помощью радиального градиента, центр которого находится в центре изображения и имеет радиус, равный половине ширины изображения.

• Используется радиальный градиент.
• Градиент задается с использованием элемента <stop> (https://developer.mozilla.org/en-US/docs/Web/SVG/Element/stop). Этот элемент определяет цвет и позицию, используемую на градиенте.
• Всего используется 510 стопов и для каждого \(i\)-го стопа (\(i=0, 1, \dots, 509\)) атрибут offset задается равным \(i/510\).
• Цвет каждого стопа (атрибут stop-color: https://developer.mozilla.org/en-US/docs/Web/SVG/Attribute/stop-color) определяется функцией: \[f(i) = \sqrt{i} \cdot \cos\left(\dfrac{i}{1 + \dfrac{1}{50}i}\right).\] Полученный набор значений для каждого \(i\) нормируется линейным преобразованием \(\phi\) так, чтобы \(\phi(f(i)) = 0\), а \(\phi(f(i)) = 255\). Затем применяется пороговое преобразование \(\psi(i) = \lfloor \phi(i) \rfloor\) (округление вниз). Итоговый цвет имеет значения каналов RGB, равное \(\left(\psi(i), \left\lfloor \dfrac{i}{2} \right\rfloor, 255 - \psi(i)\right)\).

Изображение проверяется на основе попиксельного сравнения растрированного изображения с эталонным решением. В качестве метрики используется величина dssim по каждому цветовому каналу.

Формат выходных данных

Решение должно быть представлено в виде текстового файла формата SVG (расширение .svg). Размер файла не должен превышать 10000 байт.

Юный программист Руслан занимается разработкой приложения виртуальной реальности, и, как в любом хорошем VR-приложении, он хочет добавить пользовательский интерфейс, который бы плавно следовал за поворотом головы. Игрок находится внутри некоторой сферы \(S: x^2+y^2+z^2=R^2\). В начальный момент времени голова Игрока имеет координаты \((x_0^p, y_0^p, z_0^p )\), взгляд исходит из центра головы и имеет направление \(\vec{l}=(x_0^d, y_0^d, z_0^d )\), заданное вектором единичной длины.

Пользовательский интерфейс представляет собой пространственный прямоугольник шириной \(w\) и высотой \(h\). Его центр в начальный момент времени совпадает с точкой пересечения луча, выходящего из центра головы по направлению \(\vec{l}\), и сферы \(S\).

В любой момент времени центр пользовательского интерфейса находится на поверхности сферы, а сам прямоугольник расположен в касательной плоскости к сфере \(S\) таким образом, что его верхняя сторона всегда параллельна плоскости пола \(Oxy\). Далее игрок начинает произвольным образом двигаться и вращать головой так, что она не выходит за границы сферы.

Известна информация о положении головы \((x_f^p, y_f^p, z_f^p )\) и направлении взгляда \((x_f^d, y_f^d, z_f^d )\) для каждого кадра \(f=1{,}2,\dots\). Если в какой-то кадр \(f_{i-1}\) точка пересечения взгляда и плоскости пользовательского интерфейса находится внутри или на границе прямоугольника, а в следующем кадре \(f_i\) — за его границей, то происходит запуск начала отсчета задержки перед движением интерфейса в новое положение, которое составляет \(k\) кадров, начиная с \(f_i\).

Если до завершения отсчета точка пересечения взгляда и плоскости пользовательского интерфейса вернулась в границы прямоугольника, то отсчет сбрасывается, и процедура ожидания повторяется.

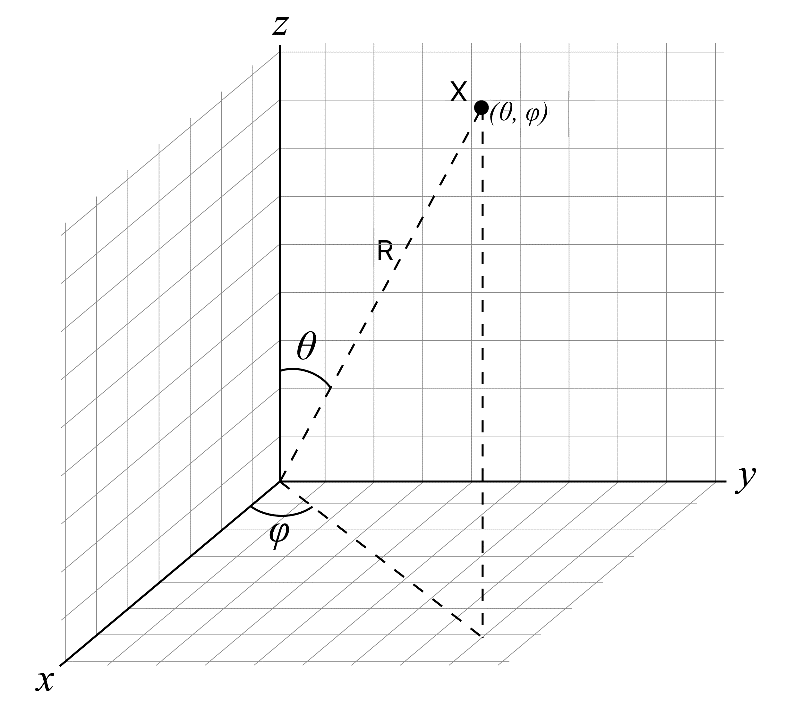
По прошествии задержки пользовательский интерфейс начинает свое движение. Рассмотрим произвольный кадр \(f_j\). Пусть \(P=(x_{f_j}^{UI}, y_{f_j}^{UI}, z_{f_j}^{UI} )\in S\) — координаты центра пользовательского интерфейса, \(Q=(x_{f_j}^s, y_{f_j}^s, z_{f_j}^s )\in S\) — координаты пересечения взгляда со сферой. Тогда можно сопоставить точкам \(P\) и \(Q\) пары чисел \((\theta_P, \varphi_P )\) и \((\theta_Q, \varphi_Q )\). \(0°\leqslant\theta_X\leqslant180°\) для точки \(X\) вычисляется как угол между осью \(Oz\) и отрезком, соединяющим начало координат и точку \(X\), \(0°\leqslant\varphi_X<360°\) вычисляется как угол между осью \(Ox\) и проекцией отрезка, соединяющего начало координат с точкой \(X\), на плоскость \(Oxy\) (см. рис. 1.5).

Таким образом, получаем двумерное пространство \(O\theta\varphi\). Если соединить точки \((\theta_P, \varphi_P )\) и \((\theta_Q, \varphi_Q )\) в этом пространстве кратчайшей прямой линией, то получим отрезок, задающий изменение от положения \(P\) до положения \(Q\). Вдоль этой линии пользовательский интерфейс движется с постоянной скоростью \(v\) градусов в кадр. Длина отрезка в пространстве \(O\theta\varphi\) измеряется с помощью евклидовой нормы. Необходимо рассчитать, какое положение, заданное углами, будет у центра пользовательского интерфейса в следующем кадре и переместить его туда в конце текущего кадра.

Далее наступает момент времени следующего кадра \(f_{j+1}\), и вышеописанная процедура повторяется для новых положений пользовательского интерфейса и пересечения взгляда со сферой. Как только в пространстве \(O\theta\varphi\) расстояние до \(Q\) оказывается меньше, чем расстояние, проходимое интерфейсом за один кадр, пользовательский интерфейс фиксируется в пространстве и снова ожидает момент, при котором взгляд окажется за границей прямоугольника.

Помогите Руслану рассчитать, где будут находиться вершины прямоугольника пользовательского интерфейса в момент завершения расчета последнего кадра.

Формат входных данных

В первой строке находятся четыре вещественных числа \(w, h, R, v\) и одно целое неотрицательное число \(k\).

Следующая пара строк содержит по три вещественных числа в каждой: в первой даны числа \((x_0^p, y_0^p, z_0^p)\) — начальное положение головы, во второй — \((x_0^d, y_0^d, z_0^d)\) — начальное направление взгляда.

Затем для каждого \(f\) парами следуют строки: в первой даны числа \((x_f^p, y_f^p, z_f^p)\) — текущее положение головы, во второй — \((x_f^d, y_f^d, z_f^d)\) — текущее направление взгляда.

Формат выходных данных

Требуется вывести четыре строки, в каждой из которых содержится положение вершины прямоугольника пользовательского интерфейса. Первой выводится левая верхняя вершина, остальные — в порядке обхода по часовой стрелке (см. рис. 1.4).

Каждая координата округляется до пятого знака после запятой.

\[\begin{gather} 0 < w, h \leqslant 30;\\ 0 < R \leqslant 20;\\ 0 \leqslant v \leqslant 90;\\ 0 \leqslant k \leqslant 200;\\ (x_f^p )^2 + (y_f^p )^2 + (z_f^p )^2 < R^2;\\ (x_f^d )^2 + (y_f^d )^2 + (z_f^d )^2 = 1, f \geqslant 0. \end{gather}\]

Гарантируется, что центр пользовательского интерфейса и пересечения взгляда со сферой ни в какой момент времени не проходит через точки \((0, 0, R)\) и \((0, 0, -R)\).

Если существует два оптимальных пути движения, то выбирайте тот, который не проходит через скачок \(\varphi\).

Тестовые данные

1

1 1 1 90 0
0 0 0
1 0 0
0 0 0
0 1 0

-0.50000 1.00000 0.50000
0.50000 1.00000 0.50000
0.50000 1.00000 -0.50000
-0.50000 1.00000 -0.50000

2

1 1 1 45 2
0 0 0
1 0 0
0 0 0
0 1 0
0 0 0
0 1 0
0 0 0
0 1 0
0 0 0
-1 0 0
0 0 0
0 1 0
0 0 0
0 1 0
0 0 0

-0.50000 1.00000 0.50000
0.50000 1.00000 0.50000
0.50000 1.00000 -0.50000
-0.50000 1.00000 -0.50000

Необходимо разработать 3D-модель поршня по представленному чертежу: https://disk.yandex.ru/d/CdQvxqRGSeLQpg/Поршень.pdf. Масштаб чертежа — \(10:1\). Окружность в 3D-редакторе необходимо строить по 100 точкам. Количество сегментов для выполнения закругления должно быть равно 100. Центр основания поршня совпадает с началом координат. Точка привязки 3D-модели — в центре основания поршня. Ось отверстия в поршне параллельна оси \(OY\). Весь поршень должен быть окрашен с использованием материала, приведенного в документе: https://disk.yandex.ru/d/CdQvxqRGSeLQpg/piston.mtl. Файл с материалом называется solve.mtl.

Для тестирования качества модели будет задействована программа, которая генерирует множество рендеров модели с различных ракурсов и попиксельно сравнивает совпадения цвета с рендером эталонной модели. Итоговым результатом является значение процента совпадения с эталонным решением, усредненное по всем рендерам. (0 баллов начисляется за полное несовпадение, 100 баллов — за полное совпадение).

Убедитесь, что решение содержит правильно ориентированные нормали к поверхности.

Формат выходных данных

В качестве решения следует отправлять файл формата OBJ (расширение .obj). Размер файла не должен превышать 999997 байт.

Вася — таксист с большой душой. Он обожает водить машину, чувствовать город под колесами, но глубоко внутри он настоящий программист. Поэтому всем своим пассажирам он говорит, что является успешным программистом, а таксует так, для души.

Но именно сегодня навигатор у Васи сломался, и теперь ему нужно быстро написать программу, которая найдет кратчайший путь из точки \(A\) в точку \(B\), дабы не опозориться перед пассажиром. Помогите ему в этом деле.

Город в плане представляет собой прямоугольник с высотой \(H\) и шириной \(W\), где каждая клетка — это перекресток. Все было бы хорошо, но Вася знает, что сейчас в городе из-за аварий, ремонтов, пришельцев закрыты \(N\) перекрестков с номерами \(a_1, a_2, \ldots, a_N\). Нумерует перекрестки он по принципу: \[a = i\cdot w +j,\] когда перекресток находится на пересечении \(i\) улицы и \(j\) улицы.

Также Вася напомнил, что существует правило проезда перекрестка, которое гласит: необходимо уступать всем машинам, оказавшимся справа. Поэтому если Вася подъезжает на перекресток, то дальше он может сразу (за 1 единицу времени) повернуть направо, пропустить машину и проехать прямо (2 единицы времени), пропустить машину справа, затем встречную, а затем повернуть налево (3 единицы времени), пропустить машины со всех направлений и развернуться (4 единицы).

Формат входных данных

В первой строке подаются два целых числа: \(1\leqslant H, W\leqslant 3\cdot 10^3\), разделенные пробелом.

Во второй строке идут три целых числа: \(1\leqslant A, B\leqslant H\cdot W, 0\leqslant N\leqslant \min(H, W)/2\).

В третьей строке идут \(N\) целых чисел: \(1\leqslant a_i\leqslant H\cdot W\).

Формат выходных данных

Выведите одно целое число — кратчайшее расстояние от точки \(A\) до точки \(B\). Если добраться невозможно, то выведите \(-1\).

Примечания

Вася может выбрать исходное направление своего такси.