Инженерный тур. 1 этап
Юный программист Вася решил научиться рисовать в виртуальной реальности. В его виртуальном мире присутствует холст, плоскость которого задается уравнением \(Ax+By+Cz+D=0\). Для рисования он использует свой VR-контроллер, из которого выходит луч. Пока что Вася умеет рисовать только вершины некоторого выпуклого многоугольника и хочет научится измерять его площадь.
Для этого Вася во время рисования точек в моменты времени \(t=0, 1, 2, \ldots\) регистрирует положение своего контроллера \((x_t^c,~y_t^c,~z_t^c )\), а также направление луча, задаваемое координатами вектора \(\vec{l} =(x_t^d,~y_t^d,~z_t^d )\). По этим данным он хочет узнать, где расположены точки пересечения луча контроллера и холста, а затем вычислить площадь полученного многоугольника. Помогите Васе найти площадь многоугольника.
Формат входных данных
В первой строке находятся четыре вещественных числа \(A, B, C, D\), задающие плоскость холста \(Ax+By+Cz+D=0\).
Затем для каждого \(t\) парами следуют строки: первая строка содержит три вещественных числа \((x_t^c,~y_t^c,~z_t^c )\) — координаты VR-контроллера, вторая строка содержит три вещественных числа \((x_t^d,~y_t^d,~z_t^d )\) — направление луча, выходящего из контроллера, \(t\geqslant 3\).
Формат выходных данных
Требуется вывести одно число — площадь многоугольника, округленную до третьего знака после запятой.
\[-100\leqslant A,~B,~C,~D \leqslant 100,\] \[-5000\leqslant x_t^c,~y_t^c,~z_t^c,~x_t^d,~y_t^d,~z_t^d \leqslant 5000.\]
Гарантируется, что точки расположены в порядке обхода вершин многоугольника.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1 0 0 -1 0 0 0 1 1 1 0 0 0 1 -1 1 0 0 0 1 -1 -1 0 0 0 1 1 -1 |
4.000 |
2 |
3.2 4.565 1 -3 -3.244614 -2.767102 1.13509 0.3167339 0.9443344 0.08894986 -3.326412 -2.63829 1.458332 0.1545813 0.8854616 0.4382492 -3.11875 -2.769511 1.697183 0.3951633 0.6238662 0.6742678 -2.932171 -2.947675 1.509933 0.7221898 0.5187265 0.4575639 -3.087754 -2.836136 1.203994 0.6005476 0.7946372 0.08885031 |
8.343 |
Задача сводится к нахождению набора точек на заданной плоскости, образующих выпуклый многоугольник. Поскольку известно положение контроллера и направление луча в сторону плоскости для каждого \(t\), можно построить параметрическое уравнение прямой:
\[\left\{ \begin{aligned} x&=x_t^c+x_t^d\cdot s,\\ y&=y_t^c+y_t^d\cdot s,\\ z&=z_t^c+z_t^d\cdot s \end{aligned} \right.\]
и пересечь ее с плоскостью: \[Ax+By+Cz+D= 0,\] то есть решаем уравнение: \[A(x_t^c+x_t^d\cdot s)+B(y_t^c+y_t^d\cdot s)+C(z_t^c+z_t^d\cdot s)+D= 0.\]
Решая уравнение относительно \(s\) и подставляя в уравнение прямой, получим точку пересечения луча и плоскости.
Осталось найти площадь многоугольника. Поскольку многоугольник является выпуклым, то его можно разбить на треугольники, проводя диагонали из любой вершины. Тогда общая площадь равна сумме площадей треугольников, которые можно вычислить, например, по формуле Герона.
Решение доступно по ссылке: https://disk.yandex.ru/d/BBXZXaGyE0KJdg.
Король Артур выбирает новую цепочку для своей сокровищницы. Сейчас у него есть одна большая древовидная цепь, каждое звено которой пронумеровано и имеет какую-то положительную ценность, а корнем этой цепи является звено 1. Артур хочет отрезать от нее и забрать непрерывную цепочку длиной \(2\cdot k\).
Однако Артур всегда думает о балансе, поэтому он выбирает ее по-особому. Его правило таково: нужно взять ровно \(2\cdot k\) подряд идущих звеньев. Началом выбранной цепочки должно быть звено, ближайшее к корню из этих \(2\cdot k\) звеньев. При этом первые \(k\) звеньев увеличивают ценность сокровищницы, а последние \(k\) — уменьшают ее ценность, так как они становятся слишком старыми и ломкими (их ценность умножается на \(-1\)).
Помогите королю Артуру выбрать такую часть цепочки, чтобы разница между положительными и отрицательными звеньями была максимальной!
Примечание
Выбранная Артуром цепочка должна быть непрерывной линией с двумя концами.
Формат входных данных
Первая строка содержит \(t\) — количество наборов входных данных.
Каждый набор входных данных сначала содержит два целых числа \(n\) и \(k\) — количество звеньев и длина половины искомой цепочки.
Затем идут \(n\) целых положительных чисел — ценность \(i\) звена.
После идет \((n-1)\) пара целых чисел \(a_i\), \(b_i\) — какие два звена соединены.
Формат выходных данных
Требуется вывести одно число — максимальную ценность цепочки, которую может отрезать Артур. Если он не сможет взять никакую цепочку, то выведите \(-1\).
\[\begin{gather} 1\leqslant t\leqslant 10^4,\\ 1\leqslant n\leqslant 10^6,\\ 1\leqslant a_i,~b_i\leqslant n,\\ 1\leqslant k\leqslant n,\\ 1\leqslant c_i\leqslant 10^9. \end{gather}\] Гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(10^6\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 3 1 3 3 1 2 12 7 1 3 2 1 3 1 2 12 7 1 2 2 3 5 3 5 4 3 2 1 3 5 5 4 1 3 2 4 |
-5 5 -1 |
2 |
1 10 2 679 873 214 210 13 529 76 163 148 25 6 3 8 1 5 3 1 4 8 7 2 3 3 9 9 1 9 10 |
600 |
Для решения задачи необходимо обойти цепочку с помощью алгоритма dfs из звена с номером 1. На каждом шаге нужно лишь знать \((2\cdot k-1)\) предка, чтобы узнать ценность цепочки, заканчивающейся в этой вершине. При переходе в одного из ребенка текущего звена меняется только один предок. При выходе из вершины нужно вернуть самого старого предка и откинуть нового, чтобы можно было обработать других детей. Но даже зная всех предков, постоянно пересчитывать ценность цепочки слишком долго. Поэтому нужно использовать три очереди. Первая очередь — для \((k-1)\) ближайших родителей и текущей вершины. Вторая очередь — для \(k\) старших родителей. Третья очередь — для более старших родителей.
При переходе в ребенка нужно из предыдущей вершине вычесть самого старого предка — начало второй очереди, прибавить \(k\)-го предка, умноженного на 2 — начало первой очереди, умноженное на 2, вычесть текущую вершину. При этом начало второй очереди добавляется в конец третей очереди, начало первой — в конец второй.
При выходе из вершины проделываем все в обратном порядке: конец третьей очереди переходит в начало второй очереди, конец второй — в начало первой. При переходах главное — учитывать, что это возможно, имея ввиду, что уже есть \(2\times k\) предков.
Решение доступно по ссылке: https://disk.yandex.ru/d/zkxfZk__pNdNdA.
Код генератора тестов: https://disk.yandex.ru/d/dmW7xEdg4v3LGw.
В славном королевстве случился пожар. Единственный, кто может его потушить — волшебник Мэрлин, но сейчас он находится на вершине своей башни. Ему нужно быстро спуститься в правый нижний угол башни и потушить огонь.
Башня Мэрлина состоит из кучи вертикальных платформ и лестниц. Волшебник уже стар, поэтому ему особенно сложно подниматься и спускаться по лестницам. Из-за этого он хочет узнать, какое наименьшее количество лестниц ему придется преодолеть.
Формат входных данных
Первая строка входных данных содержит два целых числа \(n\) и \(m\). Следующие \(n\) строк содержат по \(m\) символов каждая — описание башни. Описание может быть:
- «
-» — вертикальная платформа. С нее можно перейти только вправо и влево, если там также есть вертикальная платформа. - «
*» — начало или конец лестницы на вертикальной платформе. Здесь Мэрлин может начать поднимать/спускаться или двигаться как на обычной платформе. - «
|» — лестница. По лестнице можно двигаться только вверх и вниз, если там есть другие лестницы или их начало или конец. - «
+» — лестница, за которой вертикальная платформа. Нельзя спрыгнуть с лестницы на платформу и обратно залезть с нее на лестницу. - «
#» — пустота. По ней нельзя пройти, проползти или перепрыгнуть.
Формат выходных данных
Требуется вывести одно число — минимальное количество лестниц. Если он не может добраться до выхода из башни, то выведите -1.
\[1\leqslant n,\,m\leqslant 10^3.\]
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
9 14 -*-#-*#–*---- #|###|###|#### -*—*##-*-*– #|#|#######|## #|#|#|#####|## -*-#***#*–*-* #|##|#|#|####| -*##*#*-+----* -*–*#–*----* |
8 |
2 |
5 5 +++++ +++++ +++++ +++++ +++++ |
-1 |
Примечания
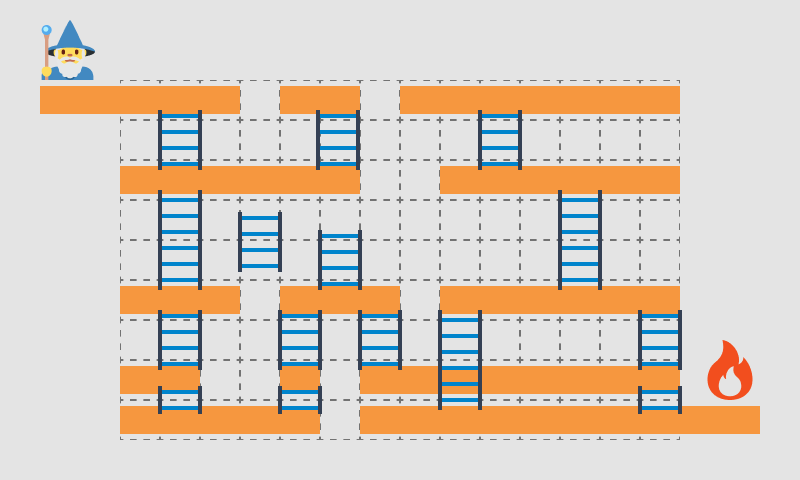
Визуализация первого примера.
Для решения задачи необходимо все горизонтальные поверхности превратить в вершины (1 непрерывная поверхность = 1 вершина), лестницы преобразовать в ребра. Тогда для получения ответа достаточно запустить bfs из первой вершины в последнюю.
Считать все вершины несложно, так как вершина может находиться только в одном ряду, а значит, просто считывая данные, можно получить их все. Для закрепления ребер достаточно отслеживать появление «*» и запоминать, из какой вершины началась лестница; так как она идет строго вертикально вниз, то это тоже можно сделать при считывании входных.
Решение доступно по ссылке: https://disk.yandex.ru/d/f78zT11-ZZrJeg.