Предметный тур. Математика. 3 этап
Школьник проспал и вышел в школу на полчаса позже, чем обычно. Он решил ускориться, чтобы не опоздать, взял электросамокат и доехал до школы со средней скоростью 20 км/ч, но тем не менее опоздал на 10 мин. На следующий день он опять проспал и вышел в школу в то же время, что и в предыдущий день. На этот раз он решил еще больше ускориться и преодолел путь до школы на электросамокате со средней скоростью 25 км/ч, но все равно опоздал на 4 мин. Каково расстояние от дома школьника до школы?
Для нахождения длины пути используем стандартную формулу \(S=v\cdot t,\) где \(S\) — путь, \(t\) — время, а \(v\) — скорость. Пусть в первый день школьник добрался до школы за \(a\) ч. Тогда получаем, что расстояние до школы равно \(S=20a\) км. На следующий день время, за которое он добрался до школы, уменьшилось на 6 мин, то есть на 0,1 ч. Таким образом, его путь равнялся \(S=25(a-0{,}1).\) Так как это один и тот же путь, приравняем эти выражения: \(20a=25(a-0{,}1).\) Из этого уравнения найдем \(a=0{,}5\) ч. Отсюда длина пути до школы \(S=20a=20\cdot 0{,}5=10\) км.
10 км.
- Верно нашли уравнение или систему уравнений для решения задачи, но решили неправильно — 5 баллов.
- Верно нашли решение — 10 баллов.
Теннисный матч играется в три сета, победителем считается тот, кто выиграет два сета из трех. Если один и тот же игрок выигрывает первые два сета, играть третий сет становится бессмысленным, игра заканчивается, и выигравший два сета объявляется победителем. Объясните, что более вероятно: игра закончится в два сета или в три? Предположите для простоты, что вероятность игроком выиграть сет постоянна и не меняется от сета к следующему сету.
Пусть \(W\) — событие, состоящие в том, что игрок 1 выиграет один сет. Пусть вероятность \(P(W)\) этого события равна \(p\) и не меняется от сета к сету. Пусть \(L\) — событие, состоящие в том, что игрок 1 проиграет один сет, и пусть вероятность этого события \(P(L)=1-p\) также не меняется от сета к сету. Тогда вероятность того, что этот игрок выиграет два сета подряд равна \(P(WW)=p^2,\) а вероятность того, что этот игрок проиграет два сета подряд равна \(P(LL)=(1-p)^2,\) то есть вероятность того, что игра закончится в 2 сета равна \(P(2)=p^2+(1-p)^2=p^2+1-2p+p^2=2p^2-2p+1.\)
Найдем вероятность того, что игра закончится в три сета. \[P(WLW)=P(LWW)=p^2(1-p),\] \[P(LWL)=P(WLL)=p(1-p)^2,\] следовательно, вероятность того, что игра закончится в три сета равна \[P(3)=2p^2(1-p)+2p(1-p)^2=2p(1-p)(p+1-p)=2p-2p^2.\]
Найдем разность этих вероятностей: \[P(2)-P(3)=2p^2-2p+1-2p+2p^2=4p^2-4p+1=(2p-1)^2\geqslant 0.\] Следовательно, \(P(2)\geqslant P(3)\) и \(P(2)=P(3)\) только если \(p=0{,}5.\)
Более вероятно, что игра закончится в два сета.
- Верно нашли одну из вероятностей: что игра закончится в два сета или что игра закончится в три сета. Угадали, что более вероятно, что игра закончится в два сета, но математически не обосновали — 5 баллов.
- Верно нашли вероятности того, что игра закончится в два сета и что игра закончится в три сета, но не смогли их грамотно сравнить — 10 баллов.
- Верно нашли вероятности того, что игра закончится в два сета и что игра закончится в три сета, и показали, что первая вероятность больше второй — 15 баллов.
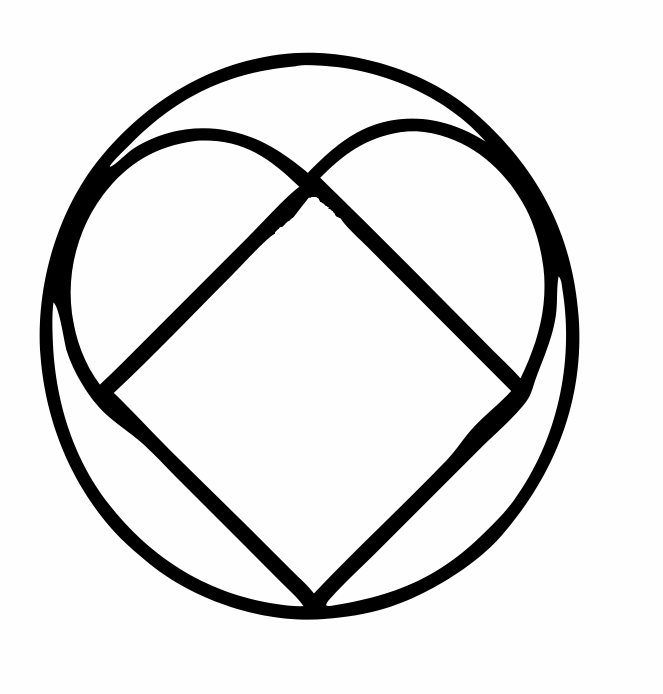
Нужно соорудить сердечко на день всех влюбленных следующим образом: взять квадрат со стороной 1, повернуть его на \(45°\), чтобы получился ромб, к верхним сторонам ромба приклеить полукруги диаметра 1 так, чтобы получилось сердечко. Теперь его необходимо вставить в кольцо. Какого радиуса кольцо следует взять, чтобы сердечко оказалось вписанным в кольцо?
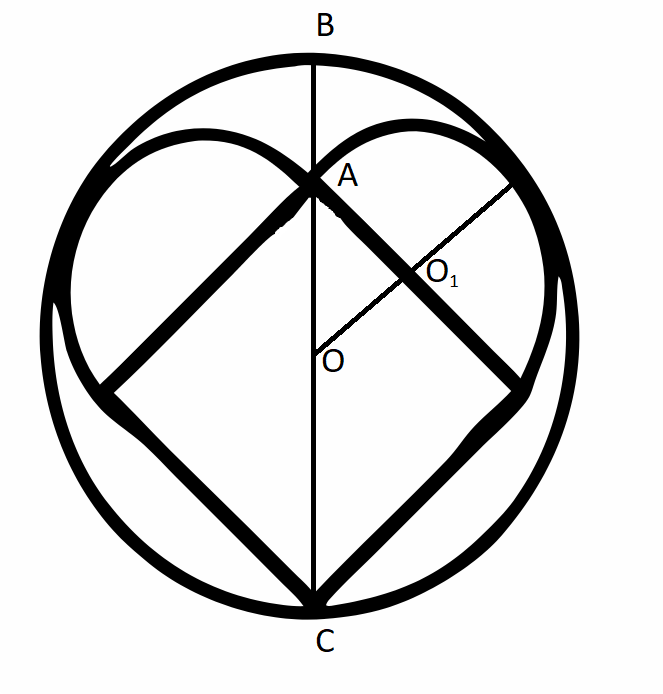
Обозначим радиус большого круга, куда нужно вписать сердечко, за \(R,\) центр большого круга — за \(O,\) а центр одного из полукругов — за \(O_1.\) Полукруг вписан в большой круг, поэтому их радиусы, перпендикулярные к касательной к большому кругу в точке касания, лежат на одной прямой. Диаметр меньшего круга равен стороне квадрата, равной 1, поэтому его радиус — 0,5. Следовательно, расстояние между центрами кругов равно \(OO_1=R-0{,}5.\) Проведем вертикальный диаметр по центру большого круга, а следовательно, по центру сердечка, \(BC\) (см. рис. 1.2). Обозначим точку в вершине ромба на этой линии за \(A.\) \(AC=\sqrt{2}\) как диагональ квадрата со стороной 1. \(\sqrt{2}+AB=2R,\) следовательно, \(AB=2R-\sqrt{2}.\) Тогда \(AO=R-(2R-\sqrt{2})=\sqrt{2}-R.\)
Рассмотрим треугольник \(\triangle AOO_1.\) Угол \(\angle OAO_1=\theta=45°,\) так как \(AO\) — биссектриса угла квадрата, \(AO_1=0{,}5\) как радиус меньшего круга, \(AO=\sqrt{2}-R,\ OO_1=R-0{,}5.\) По теореме косинусов \[c^2=a^2+b^2-2ab\cos\theta.\] Подставим все известные нам значения: \[(R-0{,}5)^2=(\sqrt{2}-R)^2+0{,}25-(\sqrt{2}-R)\sqrt{2}/2.\] Раскроем скобки: \[R^2-R+0{,}25=2-2\sqrt{2}R+R^2+0{,}25-1+\sqrt{2}R/2.\] Упрощая, получим: \[-R=1-3\sqrt{2}R/2,\] откуда \[R(3\sqrt{2}/2-1)=1,\] следовательно, \[R=\frac{2}{3\sqrt{2}-2}.\] Домножая на сопряженный множитель, получим \[R=\frac{2}{3\sqrt{2}-2}\cdot \frac{3\sqrt{2}+2}{3\sqrt{2}+2}=\frac{3\sqrt{2}+2}{7}\approx 0{,}892.\]
\(R=\frac{2}{3\sqrt{2}-2}=\frac{3\sqrt{2}+2}{7}\approx 0{,}892.\)
- Верно нашли уравнение или систему уравнений для решения задачи, но решили неверно — 10 баллов.
- Верно нашли решение — 20 баллов.
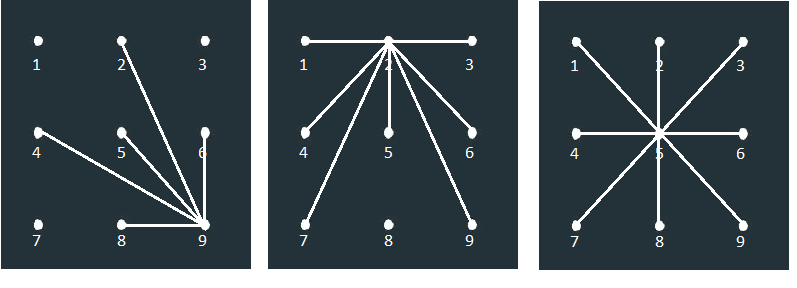
Для разблокировки андроида может использоваться графический ключ — тип пароля, при котором пользователь сопоставляет некоторый рисунок с заранее выбранными жестами. Жесты в данном случае — это движения, которые совершают проводя пальцами или стилусом по экрану, на котором расположены в три ряда 9 точек (узлов), как на рисунке 1.3. Для удобства узлам присвоены номера.

Правила составления графического ключа следующие:
- Ключ должен охватывать не менее 4 узлов.
- Каждая вершина может быть выбрана лишь единожды, например, если из узла 5 идем в узел 1, а затем в узел 9, то узел 5 не считается, несмотря на то, что проводим пальцем по нему, когда ведем от узла 1 в узел 9, получится комбинация 519.
- Путь между двумя последовательными узлами может идти только по прямой, и первая вершина, которая встретится на пути, и будет следующей, если только эта же вершина не встречалась в графическом ключе ранее (см. п. 2), например, из узла 1 нельзя перейти сразу в узел 3, так как на пути лежит узел 2: получится комбинация 123.
Ответьте на следующие вопросы:
- будет ли комбинаций из двух узлов больше 60;
- будет ли число комбинаций из четырех узлов больше 500;
- можно ли доказать, что количество комбинаций из четырех узлов больше 1000?
Для начала заметим, что любую угловую точку можно соединить только с пятью другими точками (см. рис. 1.4). Угловых точек четыре.
Рис. 1.4. Дополнительный рисунок к задачеЛюбую боковую точку между двумя угловыми можно соединить с семью другими точками (см. рис. 1.4). Таких точек четыре. И наконец, центральную точку можно соединить с любой из восьми оставшихся (см. рис. 1.4). Итого получаем, что число комбинаций из двух узлов равно: \(5\cdot 4+7\cdot 4+8=56,\) что меньше шестидесяти. Поэтому такие короткие графические ключи и не используются.
- Прикинем, сколько может быть комбинаций из четырех вершин. Из пункта а) знаем, что из первого узла можно перейти как минимум в пять других узлов. Далее, из второго выбранного узла можно будет перейти как минимум в четыре других узла (если один из пяти возможных уже был использован в качестве первого узла). Из третьего выбранного узла можно перейти в хотя бы пять других узлов, как максимум два из которых заблокированы. Начать можно с любого из девяти узлов. Итого получаем: \(9 \cdot 5 \cdot 4 \cdot 3 = 540,\) что больше пятисот комбинаций.
Но на самом деле их больше. Например, из угловой вершины с пятью доступными узлами нельзя перейти в другую угловую вершину, поэтому если начнем с угловой, то для второй точки будет как минимум шесть новых доступных узлов, после чего можно будет перейти как минимум в вершину с пятью доступными узлами, из которых как максимум один использован. Итого получаем: \(5 \cdot 6 \cdot 4 = 120.\) (Либо получим \(5 \cdot (8 - 1) \cdot ( 5- 1)\) комбинаций, что больше, чем \(120\), либо \(5 \cdot (7 - 1) \cdot (7 - 2)\) комбинаций, что тоже больше, чем \(120\).) Если это число умножим на четыре изначально доступных угловых узла, то уже получим \(480\) комбинаций, и это только начиная с углового узла!
Если же начнем с бокового центрального узла (коих четыре), то второй узел можно выбрать семью способами, после чего окажемся в точке с пятью соседями минимум, один из которых уже использован, и наконец, из узла с пятью соседями можно перейти только в узел с не менее, чем семью соседями, из которых как максимум два использованы, итого получим: \(4\cdot 7\cdot (5-1)\cdot (7-2)=560\) комбинаций. Либо с бокового узла перейдем опять на боковой, а затем на угловой, у которого два соседа уже могут быть использованы. Тогда получим: \(4\,\cdot\, 7\cdot (7-1)\cdot (5-2)=504\) комбинаций. Это минимальное количество комбинаций в данном случае.
И наконец, начав с центрального узла, вторым можно выбрать любой из оставшихся восьми, после чего можем оказаться в узле с пятью соседями, из которых один использован, и далее перейдем в узел с семью соседями, из которых два могут быть использованы, получаем: \(8\cdot (5-1)\cdot (7-2)=160\) комбинаций. (Либо получим \(8\cdot (7-1)\cdot (5-2)=144\) вариантов, либо, как в случае комбинации \(519\), получим: \(8\cdot (5-1)\cdot (5-2)=96\) различных вариантов.) Итого минимально получим: \(480+504+96=1080\) комбинаций, что больше тысячи!
- число комбинаций из двух узлов равно \(56\), что меньше \(60\);
- число комбинаций из четырех узлов более \(500\);
- число комбинаций из четырех узлов не менее \(1080\), что больше \(1000\).
- Верно нашли число комбинаций из двух узлов — 10 баллов.
- Верно нашли число комбинаций из двух узлов, верно доказали, что число комбинаций из четырех узлов более \(500\) — 20 баллов.
- Верно нашли число комбинаций из двух узлов, верно доказали, что число комбинаций из четырех узлов более \(1000\) — 25 баллов.
В компьютерной игре, чтобы открылась сокровищница, нужно переключить четыре тумблера — это рычаги, которые поворачиваются из позиции «вверх» в позицию «вниз» или наоборот. Проблема в том, что переключать можно только по три тумблера одновременно. Например, если два первых тумблера направлены вверх, а два вторых — вниз: \(\uparrow \uparrow \downarrow \downarrow,\) то можно переключить первые три, тогда получим комбинацию \(\downarrow \downarrow \uparrow \downarrow,\) или, например, первый, третий и четвертый, тогда получим комбинацию \(\downarrow \uparrow \uparrow \uparrow.\)
Ответьте на следующие вопросы:
- за какое минимальное число ходов можно переключить все четыре тумблера из позиции «вверх»: \(\uparrow \uparrow \uparrow \uparrow\) в позицию «вниз»: \(\downarrow \downarrow \downarrow \downarrow;\)
- если бы было не четыре, а \(n\) тумблеров, и переключать их можно было по \((n-1)\)-му, при каких \(n\) невозможно перевести все тумблеры из позиции «вверх» в позицию «вниз», и если можно, то за какое минимальное число ходов?
- Обозначим за \(a_i\) шаг, когда переключаются все тумблеры, кроме \(i\)-го. Тогда последовательность шагов \(a_4,a_3,a_2,a_1\) переключит каждый тумблер ровно три раза, следовательно, если все тумблеры были изначально подняты, то они все станут опущены: \(\uparrow \uparrow \uparrow \uparrow\), \(\downarrow \downarrow \downarrow \uparrow\), \(\uparrow \uparrow \downarrow \downarrow\), \(\downarrow \uparrow \uparrow \uparrow\), \(\downarrow \downarrow \downarrow \downarrow\). Понадобится 4 хода.
Пусть \(n\) — нечетное. Тогда после первого хода опущенных вниз тумблеров будет \(d_1=n-1\) — число четное, а поднятых вверх — \(u_1=1.\) После следующего хода либо опущенных тумблеров будет \(d_2=0,\) а поднятых — \(u_2=n,\) либо опущенных тумблеров будет \(d_2=1+1=2,\) а поднятых — \(u_2=n-2.\) Докажем по индукции, что число опущенных вниз тумблеров тогда всегда будет четным. Пусть на \(k\)-м шаге число опущенных тумблеров \(d_k\) — четное, а поднятых \(u_k\) — нечетное, так как \(d_k+u_k=n\) — нечетное. Тогда на \((k+1)\)-й итерации, если переключить все \(d_k\) из опущеных тумблеров и \(n-d_k-1\) из поднятых, то получим \(d_{k+1}=n-d_k-1\) — число четное, так как \(n-1\) — четное и \(d_k\) — четное, а разность двух четных чисел дает четное число. А если переключим все \(u_k\) из поднятых и \(n-u_k-1\) из опущенных, то \(d_{k+1}=u_k+(d_k-n+u_k+1)\) — тоже число четное, так как \(2u_k\) — число четное, \(d_k+1\) — нечетное, \(n\) — тоже, разность двух нечетных чисел — число четное, а сумма двух четных — опять четное. То есть в любом случае, если начинаем с четного количества опущенных тумблеров, оно всегда остается четным, поэтому никогда все \(n\) тумблеров не будут опущены, если \(n\) — нечетное число.
Теперь рассмотрим случай, если \(n\) — четное число. Покажем, что за \(n\) шагов можно обратить все тумблеры, то есть если вначале они все были подняты вверх, то через \(n\) ходов все тумблеры будут опущены вниз. Повторим действия пункта а): \(a_n, a_{n-1}, \ldots ,a_1.\) Тогда каждый переключатель поменяет свою позицию \(n-1\) (нечетное) число раз, следовательно, окажется опущенным вниз. Покажем, что это минимальное число ходов, за которое можно опустить все тумблеры. Пусть \(S_i\) — число ходов типа \(a_i\) — то есть когда переключают все тумблеры, кроме \(i\)-го. И пусть существует решение проблемы за \(S\) ходов, где \(S=S_1+S_2+\ldots +S_n.\) Следовательно, тумблер \(i\) переключается в \(S-S_i\) ходах, и так как в итоге он обратил свою позицию, то \(S-S_i\) — нечетное число. Тогда сумма таких чисел \((S-S_1)+(S-S_2)+\ldots +(S-S_n)=nS-(S_1+S_2+\ldots +S_n)=nS-S=(n-1)S.\) В этом равенстве слева стоит сумма из четного (\(n\)) количества нечетных чисел, следовательно, число четное, а справа — произведение нечетного числа (\(n-1\)) на \(S,\) следовательно, \(S\) — четное число. А так как \(S-S_i\) — нечетное число, получаем, что каждое \(S_i\) должно быть числом нечетным для любого \(i.\) Следовательно, минимальное значение для каждого \(S_i\) — это единица (\(S_i\) не может равняться нулю). А тогда \(S=S_1+S_2+\ldots +S_n\geqslant 1+1+\ldots +1=n,\) то есть \(S\geqslant n,\) а значит, \(n\) ходов — минимальное количество ходов, за которое можно обратить все тумблеры.
- 4 хода;
- все тумблеры нельзя обратить, если \(n\) — нечетное число, а если \(n\) — четное, то за \(n\) ходов можно обратить все тумблеры, и это минимальное число ходов, за которые все тумблеры можно обратить.
- Верно нашли решение пункта 1 — 5 баллов.
- Верно нашли решение пункта 1. Догадались, что нечетное количество тумблеров нельзя обратить, а четное — можно, но не смогли это строго доказать — 10 баллов.
- Верно нашли решение пункта 1. Доказали что-то одно: либо, что нечетное количество тумблеров нельзя обратить, либо, что для любого четного числа — можно — 15 баллов.
- Верно нашли решение пункта 1. Доказали, что нечетное количество тумблеров нельзя обратить, а любое четное число — можно обратить за \(n\) ходов — 20 баллов.
- Верно нашли решение пункта 1. Доказали, что нечетное количество тумблеров нельзя обратить, а любое четное число — можно. Показали, что для четного количества тумблеров \(n,\) это можно сделать за \(n\) ходов, и доказали, что это минимальное число ходов — 30 баллов.
Одометр — это прибор для измерения количества оборотов колеса. С его помощью может быть найден пройденный транспортным средством путь. Допустим, одометр в машине сломался, и теперь пропускает цифру 4 в каждой позиции. Сколько километров реально было пройдено машиной, если сейчас цифра на счетчике \(2025\)?
Можно решать эту задачу по-разному, но здесь представлено решение через модульную арифметику. Перейдем в арифметику по модулю 9 (так как теперь в каждой позиции числа не десять, как в привычном нам десятичном исчислении, а девять цифр). \[2025=^{mod\ 9}=2\cdot (9)^3+0\cdot (9)^2+2\cdot (9)^1+4\cdot (9)^0=1480.\] В последней позиции считаем четыре цифры вместо пяти, так как в первые пять цифр входит четверка, которую одометр пропускает.
Предложим и другой способ решения. Можно посчитать четырехзначные числа, не превышающее \(2000\), без цифры 4 в каждой позиции. Тогда на первой позиции слева могут быть только две цифры: \(1\) или \(2\), а на каждой следующей позиции — по девять цифр: \(0, 1, 2, 3, 5, 6, 7, 8, 9.\) Итого получим \(2 \cdot 9 \cdot 9 \cdot 9=1458\) чисел. А из 25 чисел после \(2000\) в каждой десятке (с \(0\) и \(1\) на второй справа позиции) засчитается только по девять чисел, и от \(2021\) до \(2025\) засчитается только четыре числа. Итого получим: \(9+9+4=22\) числа. Всего получится \(1458+22=1480\) чисел.
1480 км.
- Найденное значение верно обосновано, но в результате арифметической ошибки отличается от ответа — 5 баллов.
- Решение задачи найдено верно и полностью обосновано — 10 баллов.
Пусть один пришелец высадился на нашу планету. И пусть на следующий день с ним могут произойти следующие трансформации равновероятно:
- он может умереть;
- он может остаться в живых, но не размножиться;
- он может создать себе один клон;
- или он может создать себе два клона.
Его клоны дальше размножаются по той же схеме, что и первый пришелец. Какова вероятность, что раса пришельцев вымрет на Земле?
Пусть \(p,\ 0\leqslant p \leqslant 1,\) — вероятность того, что определенный пришелец и все потомки этого пришельца вымрут. Тогда через день один пришелец:
- вымрет с вероятностью 0,25,
- сохранится с вероятностью 0,25,
- удвоится с вероятностью 0,25,
- утроится с вероятностью 0,25.
После чего в перспективе раса пришельцев в первом случае вымрет с вероятностью 1, во втором случае вымрет с вероятностью \(p,\) в третьем случае каждый из двоих пришельцев вымрет с вероятностью \(p,\) то есть раса пришельцев вымрет с вероятностью \(p^2,\) так как эти события независимы. И наконец, в четвертом случае каждый из троих пришельцев вымрет с вероятностью \(p,\) то есть раса пришельцев вымрет с вероятностью \(p^3.\) Таким образом, получаем, что вероятность того, что определенный пришелец и все потомки этого пришельца вымрут, равна \(p=0{,}25(1+p+p^2+p^3).\)
Решая это кубическое уравнение, которое после упрощения примет вид \(p^3+p^2-3p+1=0,\) можно заметить, что \(p=1\) является его корнем. Разделим столбиком многочлен \(p^3+p^2-3p+1\) на \(p-1,\) и получим многочлен второго порядка \(p^2+2p-1.\) Корнями квадратного уравнения \(p^2+2p-1=0\) являются \(p=-1+\sqrt{2}\) и \(p=-1-\sqrt{2}\) (посторонний корень). Как всегда в уравнениях с вероятностями выбираем наименьший из подходящих корней, и получаем, что вероятность того, что раса пришельцев вымрет на Земле равна \(p=\sqrt{2}-1\approx 0{,}414\) или 41,4%.
\(p=\sqrt{2}-1\approx 0{,}414.\)
- Нашли верное уравнение для поиска вероятности, но оно неверно решено, или выбран не тот корень — 10 баллов.
- Нашли верное решение, и оно полностью обосновано — 20 баллов.
Пусть необходимо создать виртуальный тур по музею. Для этого надо отснять все арт-объекты под наиболее выгодным углом зрения.
Предположим, что арт-объект высотой \(c\) см в музее висит на стене, причем нижняя сторона арт-объекта находится выше на \(b\) см от уровня высоты центра объектива камеры оператора, и оператор может отойти от объекта на достаточное расстояние прямо по линии, перпендикулярной стене на уровне центральной вертикальной линии арт-объекта.
На каком расстоянии от стены следует находиться камере оператора, чтобы арт-объект был виден лучше всего, то есть чтобы вертикальный угол зрения на объект был максимальным? Решите в общем случае и в случае, если \(b=18\), \(c=14\).
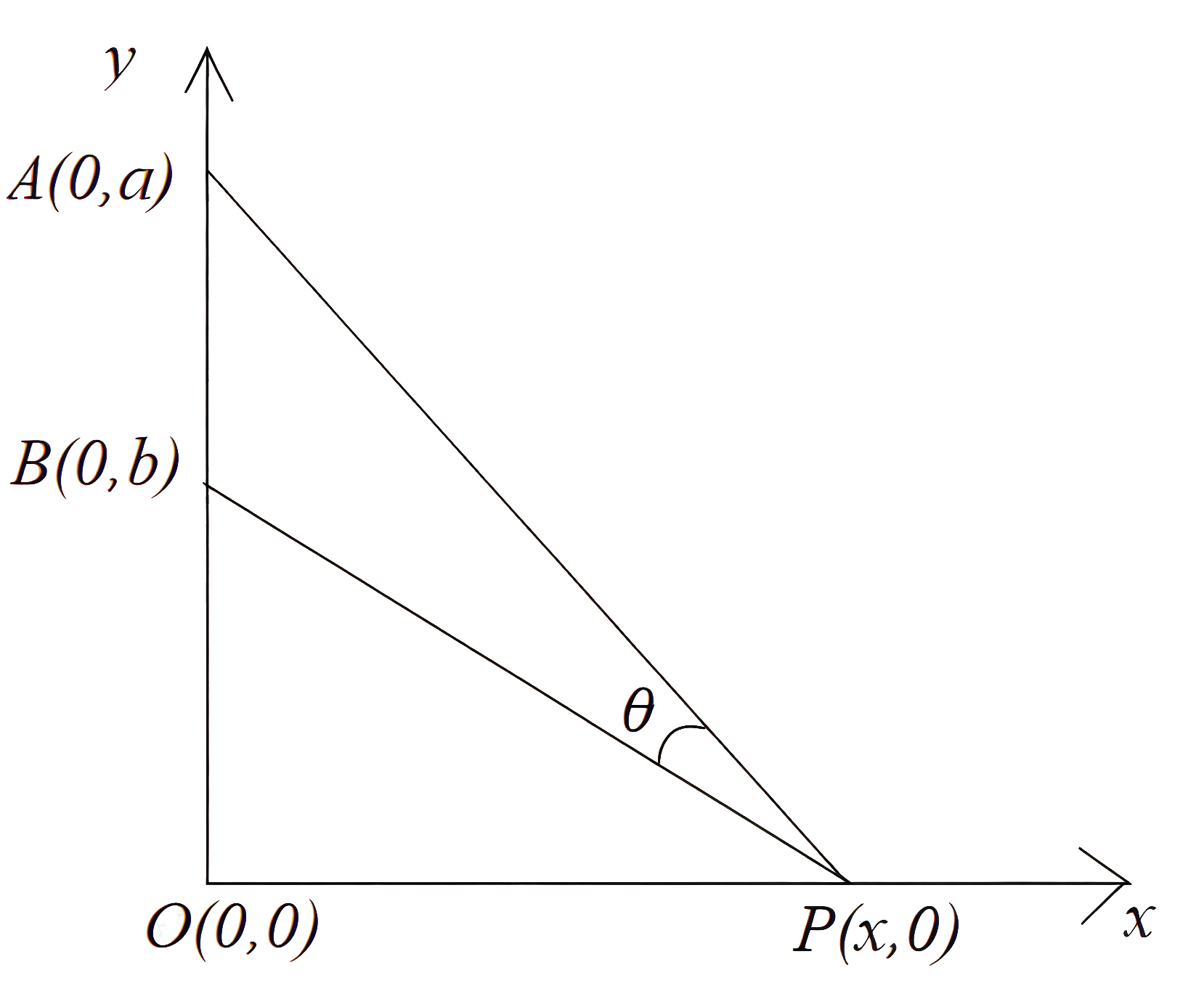
Рассмотрим декартову систему координат (см. рис. 2.1), где точка \(P(x, 0)\) представляет положение камеры оператора, точка \(B(0, b)\) — центр нижней стороны арт-объекта, а точка \(A(0, a),\) где \(a=b+c,\) — центр его верхней стороны, начало координат \(O\) — это та точка стены, на которой висит арт-объект, что находится на уровне камеры оператора.
Пусть угол \(\angle BPA=\theta, 0<\theta<90°.\) Нужно найти, когда угол \(\theta\) максимален, а это будет, когда максимален тангенс этого угла.
Пусть угол \(\angle OPA=\alpha,\) угол \(\angle OPB=\beta,\) тогда \(\operatorname{tg} \theta =\operatorname{tg} (\alpha-\beta).\) Из треугольника \(\triangle APO\) \(\operatorname{tg} \alpha=a/x,\) а из треугольника \(\triangle BPO\) \(\operatorname{tg} \beta=b/x.\) Применим формулу: \[\operatorname{tg} (\alpha-\beta)=\frac{\operatorname{tg} \alpha-\operatorname{tg} \beta}{1+\operatorname{tg}\alpha \cdot \operatorname{tg} \beta}.\] Получим: \[\operatorname{tg} (\theta)=\frac{\frac{a}{x}-\frac{b}{x}}{1+\frac{ab}{x^2}}=\frac{x(a-b)}{x^2+ab}=f(x).\]
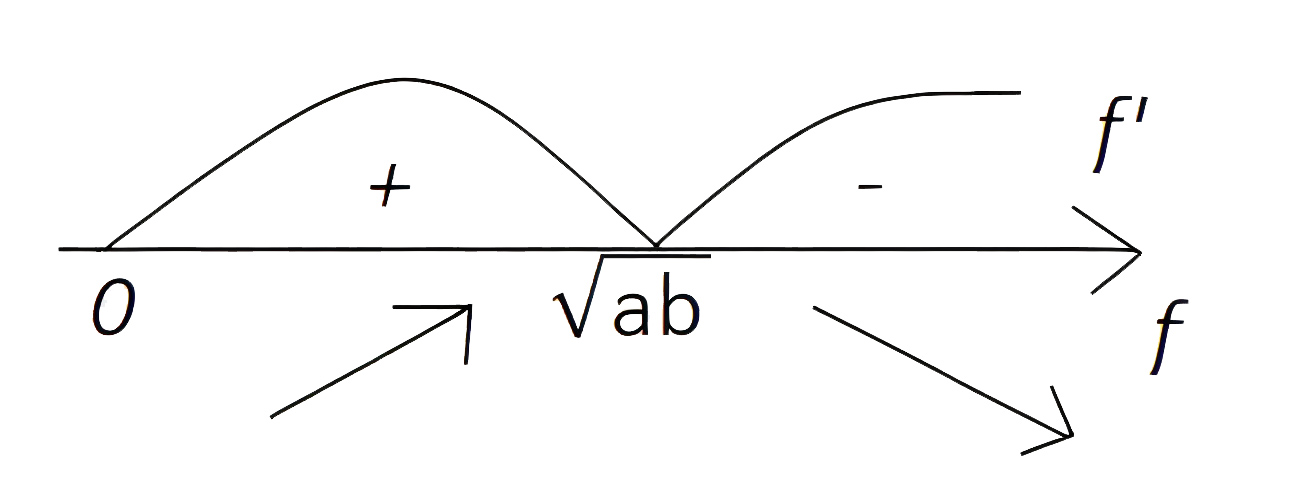
Обозначим полученное выражение за \(f(x).\) Нужно найти такое значение \(x>0,\) при котором функция максимальна. Найдем производную этой функции и приравняем к нулю: \[f^\prime=\frac{(a-b)(x^2+ab)-2x^2(a-b)}{(x^2+ab)^2}=\frac{(a-b)(ab-x^2)}{(x^2+ab)^2}=0.\] Найдем единственную подходящую стационарную точку \(x=\sqrt{ab}.\) Разместим ее на оси и посмотрим знаки производной справа и слева от этой точки (см. рис. 2.2).
Получим, что \(x=\sqrt{ab}\) — точка максимума функции \(f(x).\) Подставляя в эту формулу \(a=b+c\), делаем вывод: чтобы арт-объект был виден лучше всего, камере нужно находиться от стены на расстоянии \(x=\sqrt{b(b+c)},\) где \(b\) — высота по стене от уровня камеры до центра нижней стороны арт-объекта, а \(c\) — высота арт-объекта. Например, если \(b=18, c=14, a=18+14=32,\) то \(x=\sqrt{18\cdot 32}=24\) см.
Камере нужно находиться от стены на расстоянии \(x=\sqrt{b(b+c)},\) где \(b\) — высота по стене от камеры до центра нижней стороны арт-объекта, а \(c\) — высота самого арт-объекта. Если \(b=18, c=14,\) то \(x=24\) см.
- Нашли выражение для тангенса угла зрения смотрящего на арт-объект относительно \(b\) и \(c\), но не нашли значение, обеспечивающее максимальный тангенс угла зрения — 10 баллов.
- Нашли и полностью обосновали решение задачи — 20 баллов.
Новогодняя елка зажигается, если включатся все 12 кнопок, соединенных последовательно в переключателе. Однако в переключателе что-то сломалось, и нажатие на кнопку меняет ее статус с «включено» (горит зеленым) на «выключено» (горит красным) или наоборот только:
- если это крайняя кнопка справа (ее можно переключить в любой момент);
- если это такая кнопка, что кнопка непосредственно справа от нее зеленая, в то время как все остальные кнопки справа от нее (если есть) — красные.
Например, в такой конфигурации, где К означает, что кнопка горит красным, а З — что кнопка горит зеленым,
| К | З | К | К | З | К | К | З | К | К | К | К |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
можно нажать только кнопки 7 и 12. Кнопки 1 и 4 нажать нельзя, так как, несмотря на то, что непосредственно справа от них горит зеленая кнопка, далее не все кнопки красные.
Вначале все кнопки красные. Можно ли включить елку в принципе, и если можно, то за какое минимальное число шагов (под шагом понимается нажатие одной из 12 кнопок)?
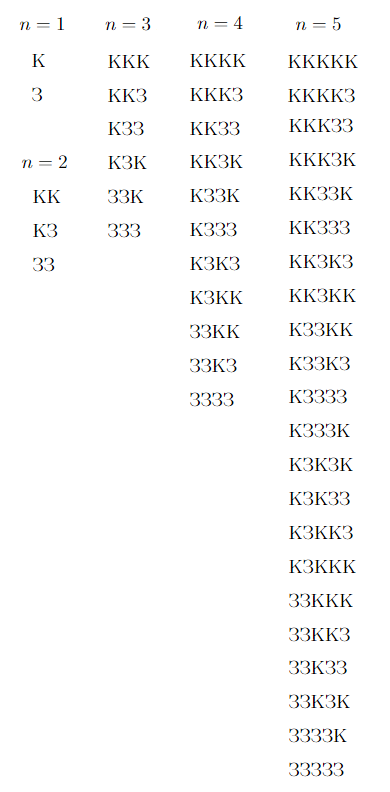
Рассмотрим вначале случаи с меньшим числом кнопок. Обозначим за \(n\) — количество кнопок, а за \(M(n)\) — минимальное количество ходов для включения елки при таком количестве кнопок на переключателе. При \(n=1\) кнопка одна, она горит красным, но при нажатии включится, и станет гореть зеленым, так как это крайняя кнопка справа, следовательно, \(M(1)=1.\) При \(n=2\) вначале обе кнопки горят красным: КК, нажимаем на крайнюю правую, получим конфигурацию КЗ, далее можем нажать на левую, так как кнопка непосредственно справа от нее горит зеленым, получаем конфигурацию ЗЗ, и вот, елочка горит! Следовательно, \(M(2)=2.\) Запишем еще раз все ходы (см. рис. 2.4). При \(n=3\) ходы следующие (см. рис. 2.4), следовательно, \(M(3)=5.\) Ходы при \(n=4\) и \(n=5\) также отображены на рисунке 2.4, получаем, что \(M(4)=10, M(5)=21.\)
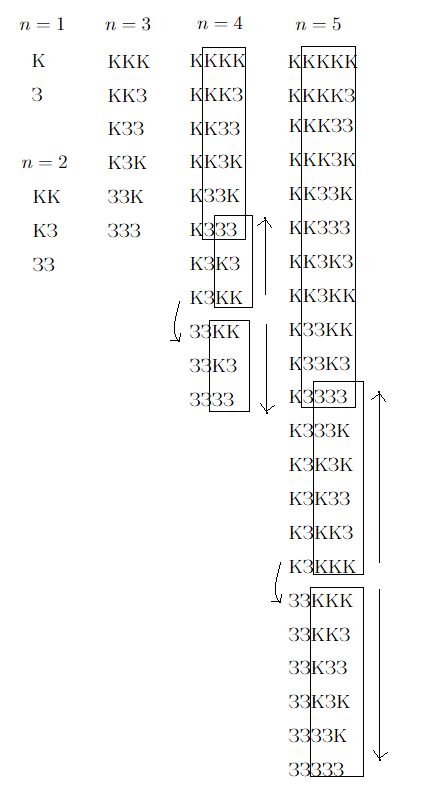
На примере \(n=5\) посмотрим, можно ли ограничиться меньшим числом ходов. Можно заметить, что нечетные ходы — единственно возможные, в четных конфигурациях другой возможный ход возвращает в предыдущую конфигурацию. Следовательно, это минимальное число ходов, за которое можно зажечь елку. Попробуем увидеть закономерности в количестве ходов в зависимости от количества кнопок. Например, при \(n=5\) вначале делаем с четырьмя правыми кнопками те же шаги, что при \(n=4,\) далее с тремя правыми кнопками повторяем шаги как при \(n=3,\) только в обратном порядке, потом появляется возможность переключить крайнюю левую кнопку на зеленый, после чего опять делаем с тремя правыми кнопками шаги как при \(n=3,\) только на этот раз в прямом порядке (см. рис. 2.5).
Можно заметить, что при \(n=4\) происходит что-то подобное: вначале делаем с тремя правыми кнопками те же шаги, что при \(n=3,\) далее с двумя правыми кнопками повторяем шаги как при \(n=2,\) только в обратном порядке, потом появляется возможность переключить крайнюю левую кнопку на зеленый, после чего опять делаем с двумя правыми кнопками шаги как при \(n=2,\) только на этот раз в прямом порядке. Из чего видим такую закономерность в числе ходов в зависимости от количества кнопок: \(M(n)=M(n-1)+2\cdot M(n-2)+1,\) где \(M(1)=1, M(2)=2.\) Проверим при \(n=3:\) \[M(3)=M(2)+2\cdot M(1)+1=2+2\cdot 1+1=5,\] при \(n=4:\) \[M(4)=M(3)+2\cdot M(2)+1=5+2\cdot 2+1=10,\] при \(n=5:\) \[M(5)=M(4)+2\cdot M(3)+1=10+2\cdot 5+1=21,\] все верно. Теперь последовательно по этой рекуррентной формуле найдем, что при \(n=6:\) \[M(6)=M(5)+2\cdot M(4)+1=21+2\cdot 10+1=42,\] при \(n=7:\) \[M(7)=M(6)+2\cdot M(5)+1=42+2\cdot 21+1=85,\] при \(n=8:\) \[M(8)=M(7)+2\cdot M(6)+1=85+2\cdot 42+1=170,\] при \(n=9:\) \[M(9)=M(8)+2\cdot M(7)+1=170+2\cdot 85+1=341,\] при \(n=10:\) \[M(10)=M(9)+2\cdot M(8)+1=341+2\cdot 170+1=682,\] при \(n=11:\) \[M(11)=M(10)+2\cdot M(9)+1=682+2\cdot 341+1=1365,\] и наконец, при \(n=12\) получим: \[M(12)=M(11)+2\cdot M(10)+1=1365+2\cdot 682+1=2730.\]
Елка зажжется за 2730 ходов.
- Нашли верная последовательность ходов для \(n=1, 2, 3, 4\) или для большего \(n\), но закономерность в количестве ходов в зависимости от количества кнопок не нашли, или нашли неверно — 5 баллов.
- Верно нашли закономерность в количестве ходов в зависимости от количества кнопок, но уравнение не решили, решили неправильно, или неверно подсчитали число ходов для 12 кнопок — 10 баллов.
- Нашли верное решение и его полностью обосновали — 20 баллов.
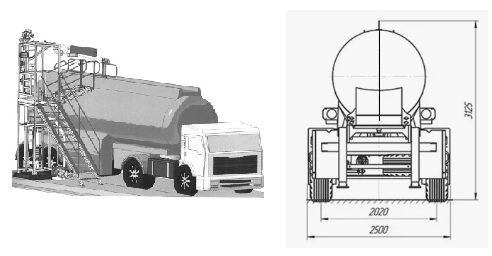
Нужно создать прибор, который по мокрой части прямого стержня (называемого уровнемером), опущенного вертикально по диаметру горизонтально лежащей цилиндровой бочки (например, автоцистерны с бензином), сможет выдавать информацию, какую часть объема бочки заполнили.
Для начала работы над прибором необходимо ответить на вопросы:
- Если четверть измеряющего стержня окажется мокрой, то какая часть объема цилиндровой бочки будет заполнена?
- Если четверть объема цилиндровой бочки будет заполнена, то какая часть стержня по отношению к диаметру цилиндра окажется мокрой?
Замечание: для части 2 достаточно найти выражение решения, зависящее от величины угла сегмента круга, соответствующего заполненному уровню бочки, и указать уравнение для нахождения этого угла, которое может быть решено примерно.
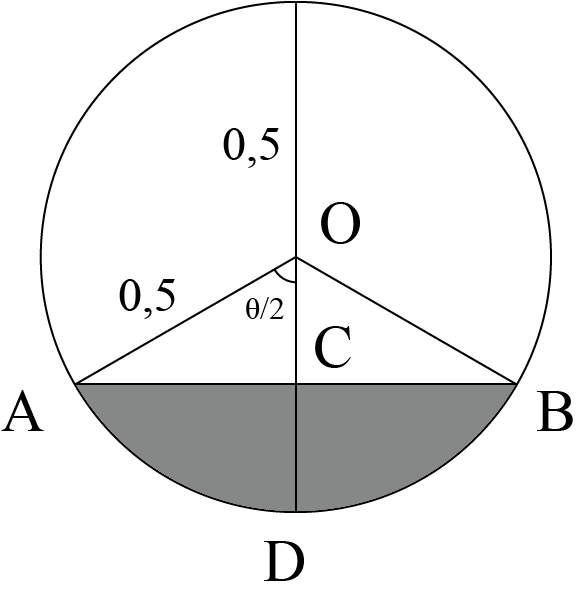
Примем длину измерительного стержня, опущенного в бочку на всю ее высоту и, соответственно, диаметр цилиндра, за единицу. Объем цилиндра равен \(V=\pi r^2 h,\) где \(r\) — радиус цилиндра — равен 0,5, а \(h\) — высота цилиндра. Так как бочка лежит горизонтально, она заполняется жидкостью по всей длине \(h,\) следовательно, если четверть измеряющего стержня будет мокрой, то сегмент, соответствующий уровню заполненной жидкости, будет иметь высоту, равную 0,25.
Обозначим также центр круга за \(O;\) линию, соответствующую уровню заполненной жидкости, за \(AB,\) где точки \(A\) и \(B\) лежат на окружности, а середина отрезка \(AB\) — точка \(C\) — лежит на вертикальном диаметре круга, то есть на измерительном стержне. Нижний конец стержня — точку на окружности — обозначим за \(D.\) Примем угол \(\angle AOB\) — за \(\theta.\) Тогда в прямоугольном треугольнике \(\triangle AOC\) \(AO=r=0{,}5, OC=0{,}25, \angle OAC=30^{\circ},\) так как напротив него лежит сторона, равная половине гипотенузы.
Следовательно, угол \(\angle AOC=60^{\circ}=\theta/2,\) а угол \(\theta=120°.\) Тогда площадь сегмента круга с хордой \(AB\) равна \[\begin{gather} S=\frac{r^2}{2}(\pi \frac{\theta}{180°} -\sin\theta)=0,125(2\pi /3-\sin 120^{\circ})=\\=0,125(2\pi /3-\sin 60^{\circ})=0,125(2\pi /3-\sqrt{3}/2). \end{gather}\] Разделив это на площадь круга \(\pi r^2=0{,}25\pi,\) получим \[\frac{1}{3}-\frac{\sqrt{3}}{4\pi}\approx 0{,}196\] или 19,6% площади круга. Следовательно, если четверть измеряющего стержня будет мокрой, то будет заполнено \[\frac{1}{3}-\frac{\sqrt{3}}{4\pi}\approx 0{,}196\] или 19,6% цилиндровой бочки.
Четверть бочки будет заполнена, когда заполнится четверть круга в боковом перпендикулярном сечении цилиндра. Теперь надо найти часть высоты \(OD,\) соответствующую уровню заполненной жидкости, это отрезок \(CD.\) Обозначим длину отрезка \(OC\) за \(b,\) и угол \(\angle AOB\) — как и ранее, за \(\theta.\) Тогда площадь сегмента круга с хордой \(AB\) равна \[S=\frac{r^2}{2}(\pi \frac{\theta}{180°}- \sin \theta),\] что по условию равно четверти площади круга, т. е. \(S=\pi r^2 /4.\) Приравнивая эти значения, получим, что \(\theta -\sin\theta=\pi/2.\)
Это уравнение можно решить приблизительно графически, найдя точку пересечения синусоиды \(y=\sin \theta\) и прямой \(y=\theta -\pi/2.\) Подходящее значение \(\theta=2{,}31.\) Далее в прямоугольном треугольнике \(\triangle AOC\) \(AO=0{,}5, OC=b, \angle AOC=\theta/2.\) Тогда \[b=0{,}5\cos(\theta/2)\approx 0{,}202.\]
Следовательно, четверть бочки будет заполнена, когда длина мокрой части стержня будет \[0{,}5-0{,}5\cos(\theta/2)=\sin^2(\theta/4)\approx 0{,}298\] или 29,8% от длины стержня, опущенного в бочку до упора.
- Если четверть измеряющего стержня будет мокрой, то будет заполнено \(\dfrac{1}{3}-\dfrac{\sqrt{3}}{4\pi}\approx 0{,}196\) или 19,6% цилиндровой бочки.
- Четверть бочки будет заполнена, когда длина мокрой части стержня будет \(0{,}5-0{,}5\cos(\theta/2)=\sin^2(\theta/4),\) где \(\theta\) находится из уравнения: \(\theta -\sin\theta=\pi/2,\) или длина мокрой части стержня равна 29,8% от всей длины стержня, опущенного в бочку до упора.
- Решили пункт 1 — 10 баллов.
- Решили пункт 1, нашли выражение решения для пункта 2, зависящее от величины угла сегмента круга, но уравнение для нахождения этого угла не нашли — 20 баллов.
- Решили пункт 1, нашли выражение решения для пункта 2, зависящее от величины угла сегмента круга, нашли уравнение для нахождения этого угла, но не обязательно решили в числах или решили примерно — 30 баллов.