Предметный тур. Математика. 3 этап

Раскладывая число 2025 на два сомножителя, можем найти, что подходит, например, случай \(2025 = 9 \cdot 225\) и \(2 + 2 + 5 = 9\).

Предположим, что все программисты получили разное число конфет, тогда их наименьшее количество равно \(0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45\) конфет, что противоречит условию. Значит, найдутся программисты, получившие одинаковое число конфет.

Заметим, что если у натурального числа нечетное число делителей, то данное число является квадратом некоторого числа.

Пусть \(n = a^2\), \(n + 2024 = b^2\). Распишем их разность: \[b^2 - a^2 = (b - a)(b + a) = 2024.\]

Заметим, что числа \(b - a\) и \(b + a\) имеют одинаковую четность и натуральные, тогда это два натуральных четных числа (нечетными быть не могут, так как их произведение четно).

Разложим правую часть равенства на простые множители: \[2024 = 2 \cdot 2 \cdot 2 \cdot 11 \cdot 23.\]

Так как в левой части равенства стоит два четных множителя, то эти числа нужно разбить на две группы так, чтобы произведение чисел в каждой группе было четным. Разместим сначала в каждую группу по одной двойке, и тогда нужно разбить произведение \(2 \cdot 11 \cdot 23\) на два множителя, причем больший множитель — это \((a + b)\), а меньший — \((a - b)\). Сделать это можно четырьмя способами:

• 1 и \(2 \cdot 11 \cdot 23\);
• 2 и \(11 \cdot 23\);
• 11 и \(2 \cdot 23\);
• \(2 \cdot 11\) и 23.

В каждом способе однозначно определяются \(a\) и \(b\), а значит, и однозначно определяем \(n\).

Вариант 1. По условию задачи \(0 \leqslant x + y \leqslant 1\). Тогда \((x + y)^2 \leqslant 1\).

С другой стороны, заметим, что \(4xy \leqslant (x + y)^2\). Отсюда следует, что \(4xy \leqslant 1\). Так как числа \(x\) и \(y\) неотрицательные, то умножим левую и правую часть последнего неравенства на \(2xy\) и получим, что \(8x^2 y^2 \leqslant 2xy\). Оценим требуемое выражение: \[x^2 + 8x^2 y^2 + y^2 \leqslant x^2 + 2xy + y^2 \leqslant (x + y)^2 \leqslant 1.\]

Таким образом, максимальное значение выражения равно 1 и достигается, например, при \(x = 1\), \(y = 0\).

Вариант 2. Рассмотрим свойства функции \(f(x, y) = x^2 + 8x^2 y^2 + y^2\). Она является монотонно возрастающей по \(x\) и по \(y\) при \(x, y \geqslant 0\). Это значит, что максимальное значение достигается там, где \(x + y = 1\). Выразив \(y = 1 - x\) и подставив в функцию \(f(x, y)\), получим функцию: \[\phi(x) = x^2 + 8x^2 (1 - x)^2 + (1 - x)^2.\]

Заметим, что \(\phi(x) = \phi(1 - x)\), то есть функция \(\phi(x)\) симметрична. Это означает, что ее можно упростить, сделав замену \(z = x - \dfrac{1}{2}\): \[\left(z + \frac{1}{2}\right)^2 + 8\left(z + \frac{1}{2}\right)^2 \left(z - \frac{1}{2}\right)^2 + \left(z - \frac{1}{2}\right)^2 = 8z^4 - 2z^2 + 1 = g(z), z^2 \in \left[0, \dfrac{1}{4}\right].\]

Эта функция является биквадратным трехчленом, его вершина в точке \(z^2 = -\dfrac{-2}{2 \cdot 8} = \dfrac{1}{8}\). В этой точке достигается его минимум, а максимум достигается на концах отрезка: \(g_{\text{max}} = g(0) = g\left(\dfrac{1}{4}\right) = 1\).

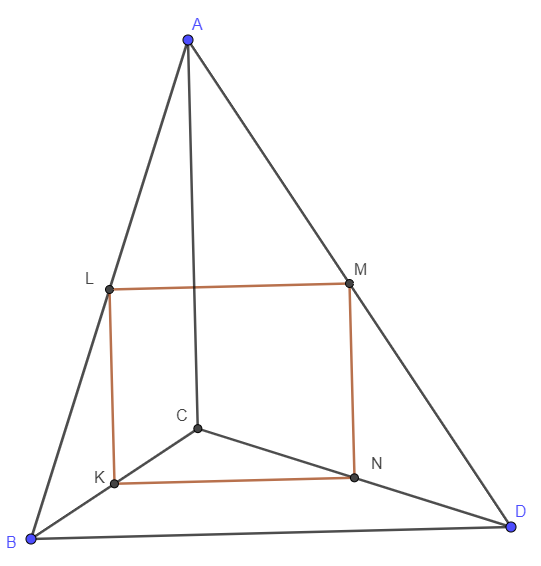
Рис. 1.1.

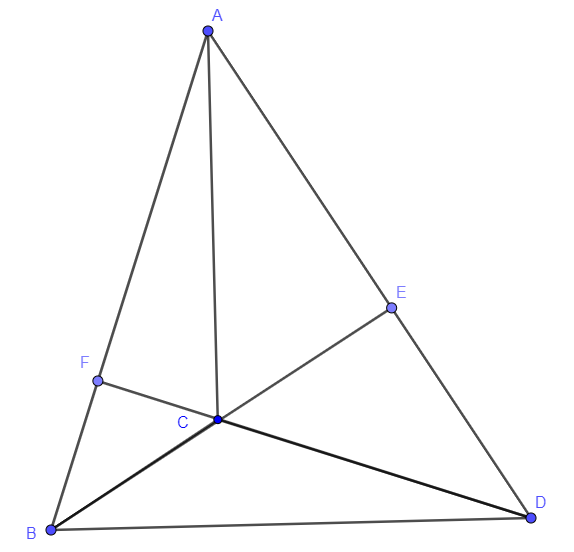
Рис. 1.2.

Обозначим середины сторон \(AB\), \(BC\), \(CD\) и \(DA\) через \(L\), \(K\), \(N\), \(M\) соответственно (рис. 1.1). Заметим, что каждая из сторон четырехугольника \(LKNM\) является средней линией в некотором треугольнике и выполняются условия: \(LM = KN = \dfrac{1}{2} BD\), \(LK = MN = \dfrac{1}{2} AC\). Тогда чтобы доказать, что \(LKNM\) — квадрат, достаточно показать равенство и перпендикулярность \(BD\) и \(AC\).

Продлим \(BC\) и \(DC\) до противоположных сторон и точки пересечения обозначим соответственно через \(E\) и \(F\) (рис. 1.2). Заметим, что так как по условию \(\angle ABE = \angle BAE = 45°\), то \(\angle AEB = 90°\), то есть \(BE \perp AD\). Аналогично, так как \(\angle ADF = \angle DAF = 45°\), то \(\angle AFD = 90°\), то есть \(DF \perp AB\). Таким образом, получаем, что \(C\) — это точка пересечения высот (ортоцентр) в треугольнике \(ABD\). И тогда по свойству ортоцентра \(AC \perp BD\).

Заметим, что треугольники \(AEC\) и \(BED\) равны по первому признаку (\(AE = BE\) из равнобедренного прямоугольного треугольника \(AEB\) и \(CE = DE\) из равнобедренного прямоугольного треугольника \(CED\), а \(\angle BED = \angle AEC = 90°\)). Следовательно, \(AC = BD\) как соответствующие элементы. Таким образом, получаем, что \(AC \perp BD\) и \(AC = BD\). Что и требовалось доказать.

\(2025 = 3^4 \cdot 5^2 = 3^{7-3} \cdot 5^{7-5}\). Для функции \(f(x) = x^{7-x}\) выполняются указанные условия.

Замечание: существуют и другие функции, например, \(f(x) = 3x^2\).

Заметим, что каждая дробь имеет вид: \[\frac{n}{(n-2)! + (n-1)! + n!}.\]

Преобразуем данную дробь:

\[\begin{aligned} \frac{n}{(n-2)! + (n-1)! + n!} &= \frac{n}{(n-2)!(1 + n - 1 + n^2 - n)} =\\ &= \frac{n}{(n-2)!n^2} = \frac{1}{(n-2)!n} = \frac{1}{(n-1)!} - \frac{1}{n!}. \end{aligned}\]

Заменим в исходном выражении каждую дробь по данному правилу:

\[\begin{aligned} &\frac{3}{1!+2!+3!} + \frac{4}{2!+3!+4!} + \cdots + \frac{2025}{2023!+2024!+2025!} = \\ &= \left(\frac{1}{2!} - \frac{1}{3!}\right) + \left(\frac{1}{3!} - \frac{1}{4!}\right) + \cdots + \left(\frac{1}{2024!} - \frac{1}{2025!}\right) = \frac{1}{2!} - \frac{1}{2025!}. \end{aligned}\]

Заметим, что если у натурального числа нечетное число делителей, то данное число является квадратом некоторого числа.

Пусть \(n = a^2\), \(n + 2024 = b^2\). Распишем их разность: \[b^2 - a^2 = (b - a)(b + a) = 2024.\]

Заметим, что числа \(b - a\) и \(b + a\) имеют одинаковую четность и натуральные, тогда это два натуральных четных числа (нечетными быть не могут, так как их произведение четно).

Разложим правую часть равенства на простые множители: \[2024 = 2 \cdot 2 \cdot 2 \cdot 11 \cdot 23.\]

Так как в левой части равенства стоит два четных множителя, то эти числа нужно разбить на две группы так, чтобы произведение чисел в каждой группе было четным. Разместим сначала в каждую группу по одной двойке, и тогда нужно разбить произведение \(2 \cdot 11 \cdot 23\) на два множителя, причем больший множитель — это \((a + b)\), а меньший — \((a - b)\). Сделать это можно четырьмя способами:

• 1 и \(2 \cdot 11 \cdot 23\);
• 2 и \(11 \cdot 23\);
• 11 и \(2 \cdot 23\);
• \(2 \cdot 11\) и 23.

В каждом случае однозначно определяются \(a\) и \(b\), а значит, и однозначно определяем \(n\).

Пусть точка \(O\) — центр рассматриваемой окружности, \(OE\) — расстояние от точки \(O\) до хорды \(BC\) и \(OB\) — радиус окружности. Тогда требуемое отношение из прямоугольного треугольника \(OEB\) будет равно \(\dfrac{OE}{OB} = \sin \angle OBE\).

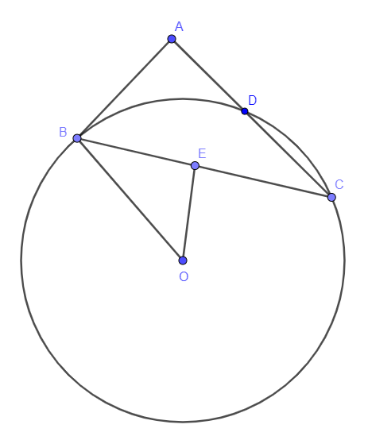
Из точки \(A\) к окружности проведена касательная \(AB\) и секущая \(AC\), причем \(AD : DC = 4 : 3\). Обозначим: \(AD = 4x\), \(AC = 7x\). Тогда по теореме о касательной и секущей имеем: \[AB^2 = AD \cdot AC = 4x \cdot 7x = 28x^2 \text{, т.\,е. } AB = 2\sqrt{7}x.\]

Запишем площадь треугольника \(ABC\): \[S = \frac{1}{2} AB \cdot AC \cdot \sin \angle BAC = \frac{1}{2} \cdot 2\sqrt{7}x \cdot 7x \cdot \sin \angle BAC = 7\sqrt{7}x^2 \cdot \sin \angle BAC.\]

Из основного тригонометрического тождества найдем \(\sin \angle BAC\): \[\sin \angle BAC = \sqrt{1 - \cos^2 \angle BAC} = \sqrt{1 - \left(\frac{\sqrt{7}}{14}\right)^2} = \frac{3\sqrt{21}}{14}.\]

Зная, что по условию задачи площадь треугольника \(ABC\) равна \(42\sqrt{3}\), получим уравнение: \[42\sqrt{3} = 7\sqrt{7}x^2 \cdot \frac{3\sqrt{21}}{14}.\]

Решая данное уравнение, найдем \(x = 2\).

Таким образом, треугольник \(ABC\) имеет стороны \(AB = 4\sqrt{7}\) и \(AC = 14\). По теореме косинусов найдем его третью сторону: \[\begin{gather} BC^2 = AB^2 + AC^2 - 2 \cdot AB \cdot AC \cdot \cos \angle BAC = (4\sqrt{7})^2 + 14^2 - 2 \cdot 4\sqrt{7} \cdot 14 \cdot \frac{\sqrt{7}}{14} = 252,\\ BC = 6\sqrt{7}. \end{gather}\]

Запишем теорему синусов для треугольника \(ABC\): \[\frac{AC}{\sin \angle ABC} = \frac{BC}{\sin \angle BAC}.\]

Найдем из этого равенства \(\sin \angle ABC\): \[\sin \angle ABC = \frac{AC}{BC} \cdot \sin \angle BAC = \frac{14}{6\sqrt{7}} \cdot \frac{3\sqrt{21}}{14} = \frac{\sqrt{3}}{2}.\]

Таким образом, получаем, что \(\angle ABC = 60°\).

Тогда так как \(AB\) — касательная к окружности, то: \[\angle OBE = \angle ABO - \angle ABC = 30° \text{ и } \frac{OE}{OB} = \sin 30° = 0{,}5.\]

Сделав замену \(t = \sin^2 \left(\dfrac{x}{3}\right)\), получим квадратное уравнение относительно \(t\): \[16t^2 - 4t(\cos^2 (4x) + \cos (4x)) + 1 = 0\]

Дискриминант этого уравнения будет неположительным в силу ограниченности функции \(y = \cos x\). Действительно: \[D = 16(\cos^2 (4x) + \cos (4x))^2 - 64 \leqslant 0.\]

Значит, единственное решение для \(t\) получается при \(\cos (4x) = 1\). При этом \(t = \dfrac{1}{4}\), то есть \(\sin \left(\dfrac{x}{3}\right) = \pm \dfrac{1}{2}\).

Таким образом, получаем первую систему уравнений: \[\begin{cases} \cos (4x) = 1, \\ \sin \left(\dfrac{x}{3}\right) = \dfrac{1}{2} \end{cases}\] и \[\begin{cases} \cos (4x) = 1,\\ \sin \left(\dfrac{x}{3}\right) = -\dfrac{1}{2}. \end{cases}\]

Решая данные системы уравнений, получим четыре серии решений: \[x_{1{,}2} = \pm \frac{\pi}{2} + 6\pi n, \quad x_{3{,}4} = \pm \frac{5\pi}{2} + 6\pi k, \quad k, n \in \mathbb{Z}.\]