Предметный тур. Информатика. 3 этап
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Научный институт проектирует полигон для испытания оборудования беспроводной связи. Для испытаний на полигоне требуется разместить две прямоугольные площадки, имеющие размеры \(a_1\times b_1\) и \(a_2\times b_2\). Они могут соприкасаться, но не должны пересекаться. Полигон также должен иметь форму прямоугольника, и стороны площадок должны быть параллельны или перпендикулярны сторонам полигона.
Проектировщики хотят сделать полигон минимальным по площади, но так, чтобы на нем поместились обе площадки. Напишите программу, которая найдет наименьшую возможную площадь полигона по заданным размерам площадок.
Программа должна решить задачу для \(t\) независимых наборов входных данных.
Формат входных данных
В первой строке на вход подается единственное натуральное число \(t\) — количество наборов входных данных (\(1\leqslant t\leqslant 10000\)). Далее записаны сами наборы входных данных. Каждый набор состоит из двух строк. В первой строке через пробел записаны два натуральных числа \(a_1\) и \(b_1\) — размеры первой площадки. Во второй строке аналогично записаны еще два числа \(a_2\) и \(b_2\) — размеры второй площадки. Все числа не превосходят \(10000\).
Формат выходных данных
Для каждого набора входных данных выведите в единственной строке ответ — минимальную площадь полигона.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
2 6 4 3 5 4 2 3 2 |
42 14 |
Примечание
Рисунки ниже поясняют тестовые случаи.
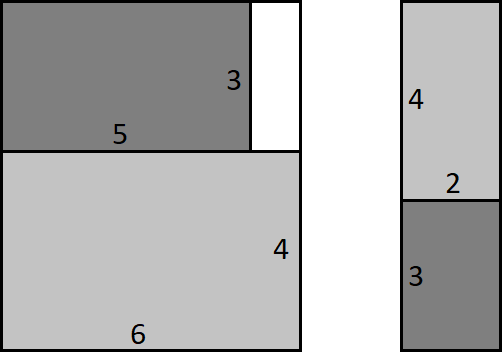
Обозначим стороны первого прямоугольника за \(a_1\) и \(b_1\), а второго — за \(a_2\) и \(b_2\). Прямоугольники можно соединить по сторонам четырьмя способами: \(a_1a_2\), \(a_1b_2\), \(b_1a_2\) и \(b_1b_2\). В результате получится прямоугольник, где длина одной стороны будет максимумом из длин соединяемых сторон, а длина второй стороны будет суммой длин оставшихся сторон. В программе надо перебрать четыре указанных способа и выбрать из них лучший.
Пример программы-решения
Ниже представлено решение на языке Python.
t = int(input())
for _ in range(t):
a1,b1 = map(int,input().split())
a2,b2 = map(int,input().split())
print(min((a1+a2)*max(b1,b2),
(b1+b2)*max(a1,a2),
(a2+b1)*max(a1,b2),
(a1+b2)*max(a2,b1)))Тест с номером 1 совпадает с тестом из условия задачи. Баллы за него не начисляются.
Успешное прохождение каждого теста с номерами 2–11 оценивается в 1 балл.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Алиса, Алена и Алина играют в следующую игру. Перед игроками в ряд расположено \(n\) кучек камней, пронумерованных от \(1\) до \(n\), \(n\geqslant 3\). За \(a_i\) обозначим количество камней в \(i\)-й кучке. Сначала Алиса выбирает себе некоторую кучку камней, которая не является самой левой или самой правой. Обозначим номер кучки, выбранной Алисой, за \(k\), \(2\leqslant k\leqslant n-1\). Далее Алена выбирает любую кучку камней слева от кучки, выбранной Алисой, а Алина аналогично выбирает одну кучку справа. Обозначим номера кучек Алены и Алины за \(m\) и \(r\), \(1\leqslant m < k
Выигрышем станет сумма камней в трех выбранных кучах. Игра является кооперативной, то есть цель игроков — максимизация совместного выигрыша.
Напишите программу, которая найдет номера кучек, выбранных Алисой, Аленой и Алиной. Она должна ответить на \(t\) независимых запросов во входных данных.
Формат входных данных
В первой строке на вход подается единственное натуральное число \(t\) — количество наборов входных данных (\(1\leqslant t\leqslant 10000\)). Далее записаны сами наборы входных данных. Каждый набор состоит из двух строк. В первой строке записано одно натуральных число \(n\) — количество кучек с камнями (\(3\leqslant n \leqslant 200000\)).
Во второй строке через пробел записано \(n\) натуральных чисел \(a_1, \ldots, a_n\) — количество камней в каждой кучке, \(1\leqslant a_i\leqslant 10^9\). Гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(200000\).
Формат выходных данных
Для каждого набора входных данных выведите с отдельной строке три числа \(k\), \(m\) и \(r\) — номера кучек камней, которые возьмет Алиса, Алена и Алина, \(1 \leqslant m < k < r \leqslant n\). Обратите внимание, что числа должны выводиться в требуемом порядке, а именно: сначала \(k\), потом \(m\) и \(r\).
Если возможно несколько правильных решений, то вывести можно любое из них.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 3 5 1 4 5 1 2 3 4 5 5 2 2 2 3 1 |
2 1 3 4 3 5 3 2 4 |
Примечания
В первом тестовом случае всего три числа. Алиса может выбрать только второе число.
Во втором тестовом случае Алиса выберет четверку, а Алена и Алина тройку и пятерку соответственно. Сумма будет равна \(12\), и улучшить этот результат нельзя.
В третьем тестовом случае Алиса выберет двойку, а Алена и Алина двойку и тройку соответственно. Сумма будет равна \(7\), и улучшить этот результат нельзя.
Очевидно, что сумма будет максимальной, если девочки выберут три самых больших числа. Поскольку Алиса выбирает число первой, она должна выбрать то число из этой тройки, которое находится в середине.
Таким образом, программа должна найти номера трех самых больших чисел, упорядочить эти номера по возрастанию и вывести сначала второй номер, потом первый и, наконец, третий.
В прилагаемой программе в пятой строке номера чисел сортируются в порядке возрастания их значений.
Пример программы-решения
Ниже представлено решение на языке Python.
t = int(input())
for _ in range(t):
n = input()
x = [int(a) for a in input().split()]
x = sorted(list(range(len(x))),key = lambda i:x[i])
x = sorted(x[-3:])
print(x[1]+1,x[0]+1,x[2]+1)Тест с номером 1 совпадает с тестом из условия задачи. Баллы за него не начисляются.
Успешное прохождение каждого теста с номерами 2–13 оценивается в 1 балл.
В тестах с номерами 2–5 все числа \(a_i\) являются различными.
В тестах с номерами 2–9 сумма \(n\) по всем тестовым случаям не превосходит 20000.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Антон пишет программу для управления гоночными машинками. Недавно он добавил модуль для выполнения обгонов и хочет его протестировать. Интерфейс модуля очень прост и содержит всего одну команду «обогнать». Выполняя эту команду, некоторая машинка обгоняет ровно одну другую машинку, двигающуюся впереди. Если перед машинкой, которая должна выполнить эту команду, нет другой машинки, то команда игнорируется.
Машинки двигаются по достаточно большому гоночному кругу, строго друг за другом с одинаковой скоростью, за исключением моментов обгонов. Это означает, что машинка, двигающаяся первой, не видит и не может обогнать машинку, которая едет последней. Все они пронумерованы последовательными числами от \(1\) до \(n\). Каждая окрашена в один из трех цветов Российского флага, и количество машинок каждого цвета совпадает. Чтобы отправить команду на обгон, программа должна просто указать номер машинки, которая будет его выполнять.
Для эффектной демонстрации своего модуля Антон просит вас написать программу, которая составит такую последовательность обгонов, чтобы машинки на финише были упорядочены по цветам, как на флаге России сверху вниз. Количество обгонов при этом должно быть минимальным. В момент старта машинки выстроены по своим порядковым номерам.
Программа должна ответить на \(t\) независимых запросов во входных данных.
Формат входных данных
В первой строке на вход подается единственное натуральное число \(t\) — количество наборов входных данных (\(1\leqslant t\leqslant 333\)). Далее записаны сами наборы входных данных. Каждый набор входных данных представлен в виде строки, состоящей из символов w, b, r. Гарантируется, что строка не пустая, и ее длина делится на \(3\). Также гарантируется, что сумма длин всех строк во входных данных не превосходит \(1000\).
Будем считать, что нумерация символов в строке начинается с единицы. Тогда символ w в \(i\)-й позиции означает, что машинка с номером \(i\) белая. Аналогично символы b и r означают машинки синего и красного цветов.
Формат выходных данных
Ответ на каждый запрос во входных данных должен быть записан в одной строке в виде последовательности целых чисел. Первым числом в последовательности должно быть минимальное количество обгонов \(r\). Далее должно быть записано еще \(r\) чисел — номера машинок, на которые подается команда об обгоне. Номера должны быть записаны в порядке, в котором они будут отправляться.
Если ответов с минимальным количеством обгонов несколько, то можно вывести любой.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 rwbbrw wbr wbrwbr |
7 2 6 6 6 6 3 4 0 3 4 4 5 |
Примечания
Последовательность обгонов в первом тестовом случае отображена на рис. 1.1. Эта последовательность не является единственной, возможны и другие ответы.
Во втором тестовом случае машинки уже стоят в нужном порядке, и обгоны не требуются.
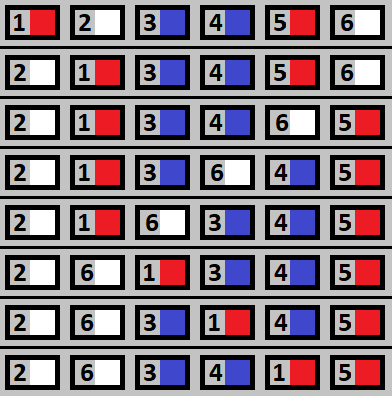
Фактически в этой задаче нужно реализовать произвольный алгоритм, выполняющий сортировку данных обменом соседних элементов. При этом требуется формировать специфическую последовательность номеров, поэтому алгоритмы из библиотеки не подойдут.
В прилагаемой программе формируется список из пар, состоящих из номера машинки и ее цвета. Далее выполняется алгоритм, похожий на сортировку вставками. Сначала выбираются все машинки белого цвета и перемещаются в начало последовательности. Далее такие же действия выполняются с синими машинками. На каждом шаге известна позиция, в которую надо переместить машинку, что упрощает реализацию алгоритма.
Пример программы-решения
Ниже представлено решение на языке Python.
t = int(input())
for _ in range(t):
s = list(enumerate(input()))
ans = []
k = 0
for c in 'wb':
for i in range(len(s)):
if s[i][1]==c:
ans+=[s[i][0]+1]*(i-k)
b = s[i]
for j in range(i,k,-1):
s[j]=s[j-1]
s[k]=b
k+=1
print(s)
print(len(ans),*ans)Тест с номером 1 совпадает с тестом из условия задачи. Баллы за него не начисляются.
Успешное прохождение каждого теста с номерами 2–19 оценивается в 1 балл.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 128 Мбайт.
На занятиях по схемотехнике Алиса разработала компьютер, способный выполнять два вида команд. Сегмент данных ее компьютера состоит из \(128\) двадцатиразрядных беззнаковых целых чисел, пронумерованных от 0 до \(127\). Программа состоит из команд, пронумерованных от \(1\) до \(n\). Команда с номером \(i\) всегда записывает \(i\)-е число в сегменте данных, поэтому программа состоит не более, чем из 127 команд. Нулевое число в сегменте данных считается входной информацией и помещается в сегмент данных до начала выполнения программы.
Первая команда имеет вид (\(i\) r \(k\) \(m\)), где \(i\) — порядковый номер команды; r — ее обозначение (rotate); \(k\) — некоторое целое неотрицательное число, \(k < i\); \(m\) — целое неотрицательное число, \(0\leqslant m\leqslant 19\). По этой команде из сегмента данных извлекается число под номером \(k\), его биты циклически сдвигаются на \(m\) разрядов влево, результат записывается в сегмент данных под номером \(i\).
Операция циклического сдвига влево может быть описана следующим образом. Пусть задано \(n\)-разрядное число \(a_{n-1}\cdots a_1 a_0\). Необходимо выполнить его циклический сдвиг влево на \(m\) бит. Выделим из числа \(m\) старших бит \(a_{n-1}\cdots a_{n-m}\) и запишем их в начало. Получим циклический сдвиг \(a_{n-m-1}\cdots a_1 a_0 | a_{n-1}\cdots a_{n-m}\). Например, циклическим сдвигом числа \(00101101\) на три бита влево будет число \(01101|001\). Вертикальная черта поставлена для наглядности.
Вторая команда имеет вид (\(i\) x \(k\) \(t\)), где \(i\) — порядковый номер команды; x — ее обозначение (eXclusive or); \(k\) и \(t\) некоторые целые неотрицательные числа, \(k < i\), \(t < i\). По этой команде из сегмента данных извлекаются числа под номером \(k\) и \(t\), для них выполняется операция поразрядного исключающего «или», результат записывается в сегмент данных под номером \(i\).
Булевская операция Xor (исключающее «или») определяется таблицей истинности 1.1.
| x | y | f |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Другими словами, исключающее «или» двух булевских значений равно единице, если ровно одно из них равно единице.
Побитовая операция исключающего «или» для двух чисел определяется над их двоичными представлениями. Заданная операция применяется к каждой паре соответствующих битов обоих чисел.
Например, \(100\) xor \(50\) можно вычислить следующим образом: \(100=(01100100)_2\), \(50=(00110010)_2\).
\[\begin{array}{cccccccc} 0&1&1&0&0&1&0&0\\ 0&0&1&1&0&0&1&0\\\hline 0&1&0&1&0&1&1&0 \end{array}\] В итоге \((01010110)_2=86\).
Отметим, что в языках С++ и Python операция побитового исключающего «или» для двух переменных x и y записывается при помощи символа крышки x^y.
В качестве примера рассмотрим программу, которая получает число \(589827\) из заданного числа \(5\). В столбцах dec и bin (таблица 1.2) записано десятичное и двоичное представление числа, полученного в результате исполнения команды.
| num | com | dec | bin |
|---|---|---|---|
| 0 | 5 | 00000000000000000101 | |
| 1 | r 0 1 | 10 | 00000000000000001010 |
| 2 | x 0 1 | 15 | 00000000000000001111 |
| 3 | r 2 3 | 120 | 00000000000001111000 |
| 4 | x 1 3 | 114 | 00000000000001110010 |
| 5 | r 4 15 | 589827 | 10010000000000000011 |
Преподавателю понравился компьютер Алисы, но он попросил ее продемонстрировать его возможности. Для этого она должна написать \(n\) различных программ, чтобы получить заданные числа \(a_1, \cdots, a_n\) из одного и того же заданного числа \(x\). Преподаватель дал достаточно много чисел, и Алиса не успевает написать для них программы. Напишите программу, которая будет автоматически генерировать требуемые программы. Обратите внимание: в задаче не требуется находить кратчайшую программу. Необходимо лишь позаботиться о том, чтобы количество команд в ней не превосходило 127.
Формат входных данных
В первой строке на вход поступает единственное натуральное число \(x\) — исходное число для программ Алисы, \(1\leqslant x \leqslant 2^{20}-1\).
Во второй строке на вход поступает единственное натуральное число \(n\) — количество чисел для получения которых требуется написать программы, \(1\leqslant n\leqslant 2000\).
В третьей строке на вход поступают числа \(a_1, \ldots, a_n\), для получения которых требуется написать программу, \(0\leqslant a_i\leqslant 2^{20}-1\).
Формат выходных данных
Для каждого из чисел во входных данных требуется вывести полученные программы. В первой строке вывода требуется указать одно число \(s\) — количество команд в программе, \(-1\leqslant s\leqslant 127\). Если его невозможно получить за 127 или менее команд, то \(s\) должно быть равно (\(-1\)). Далее в \(s\) строках требуется записать команды программы в указанном формате без порядкового номера команды. Требуемое число должно быть получено последней командой программы.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
5 4 0 1 5 589827 |
1 x 0 0 -1 0 5 r 0 1 x 0 1 r 2 3 x 1 3 r 4 15 |
Примечания
Для первого числа одна команда x 0 0 дает ноль, так как a^a равно нулю для любого \(a\).
Для второго числа можно доказать, что получить \(1\) невозможно.
Третье число совпадает с исходным. Можно ничего не делать.
Программа для четвертого числа разобрана в примере.
Обозначим операцию циклического сдвига числа \(x\) на \(k\) бит за \(x\triangleleft k\).
Очевидно имеют место тождества \[(x\oplus y)\triangleleft k = (x \triangleleft k)\oplus (y\triangleleft k),\] \[(x\triangleleft a) \triangleleft b = x \triangleleft (a+b).\]
Тогда, используя эти тождества, можно преобразовать любую формулу к виду \[(x\triangleleft k_1)\oplus (x\triangleleft k_2)\oplus\ldots\oplus(x\triangleleft k_m).\]
Теперь можно перебрать все формулы такого вида и для каждой формулы найти число, которое получается в результате ее вычисления. В прилагаемой программе в списке r хранятся все циклические сдвиги \(x\), а каждая формула указанного вида кодируется в виде числа, двоичная запись которого содержит единицы на позициях \(k_1, \ldots, k_m\). В списке x для каждого возможного двадцатизначного двоичного числа хранится код его формулы или (\(-1\)), если это число невозможно получить.
Вторая часть программы выводит ответ в виде формулы указанного вида.
Пример программы-решения
Ниже представлено решение на языке Python.
bits = 20
r = [0]*bits
r[0] = int(input())
for i in range(bits-1):
r[i+1]=((r[i]>>(bits-1))+(r[i]<<1))&(2**bits-1)
x = [-1]*(2**bits)
for p in range(2**bits):
t = 0
for k in range(bits):
if ((p>>k)&1)==1:
t^=r[k]
x[t]=p
n = int(input())
for p in map(int,input().split()):
if x[p]==-1:
print(-1)
else:
print(bits+bin(x[p]).count('1'))
for i in range(bits-1):
print('r',i,1)
print('x',0,0)
n=bits
for k in range(bits):
if ((x[p]>>k)&1)==1:
print('x',k,n)
n+=1Тест с номером 1 совпадает с тестом из условия задачи. Баллы за него не начисляются.
Успешное прохождение каждого теста с номерами 2–31 оценивается в 1 балл.
В тестах с номерами 2–3 выполняется \(x=1\).
В тестах с номерами 4–7 выполняется \(x=3\).
В тестах с номерами 8–11 выполняется \(x=7\).
В тестах с номерами 12–19 выполняется \(n\leqslant 20\).
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 256 Мбайт.
Алиса пишет программу по заданному алгоритму. На вход алгоритму подается некоторое целое число \(x\) и последовательность \(a_1, \ldots, a_n\). Алгоритм является циклическим. На каждом шаге цикла для \(i\) от \(1\) до \(n\) переменная \(x\) сравнивается с \(a_i\) и, если \(x \geqslant a_i\), то \(x=x-a_i\). Полученное после завершения цикла значение переменной \(x\) является ответом. Ниже записан текст этой программы в виде функции на языке Python.
def algo(x, A):
for a in A:
if x>= a:
x -= a
return x==0Алисе задалась вопросом, сколько существует значений \(x\), при которых алгоритм для фиксированной последовательности \(a_1, \ldots, a_n\) дает ответ \(0\). Ей кажется, что для этого придется перебрать все возможные значения \(x\) от \(0\) до \(\sum_{i=1}^n a_i\), но она понимает, что такая программа будет работать слишком долго.
Сможете ли вы написать программу, которая решит задачу, поставленную Алисой, быстрее?
Программа должна ответить на \(t\) независимых запросов во входных данных.
Формат входных данных
В первой строке на вход подается единственное натуральное число \(t\) — количество наборов входных данных (\(1\leqslant t\leqslant 100\)).
Далее записаны сами наборы входных данных. Каждый набор входных данных состоит из двух строк. В первой из них записано одно натуральное число \(n\) — количество элементов в последовательности (\(1\leqslant n\leqslant 200000\)). Вторая строка набора содержит последовательность натуральных чисел \(a_1, \ldots, a_n\) (\(1\leqslant a_i\leqslant 10^6\)).
Гарантируется, что сумма \(n\) по всем наборам входных данных не превышает \(200000\). Также гарантируется, что сумма всех значений \(a_i\) во входном файле не превышает \(2\cdot 10^8\).
Формат выходных данных
Для каждого набора входных данных выведите ответ в виде одного целого числа. Числа можно выводить как в одной строке через пробел, так и в разных.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 5 1 2 3 4 5 5 5 4 3 2 1 4 5 1 5 1 |
6 16 8 |
Примечания
В первом тестовом случае ответ \(0\) может быть получен при начальных значениях \(x\), равных \(0\), \(1\), \(3\), \(6\), \(10\), \(15\).
Во втором тестовом случае ответ \(0\) может быть получен при всех начальных значениях \(x\) от \(0\) до \(15\).
В третьем тестовом случае ответ \(0\) может быть получен при начальных значениях \(x\), равных \(0\), \(1\), \(2\), \(5\), \(6\), \(7\), \(11\), \(12\).
Рассмотрим решение этой задачи методом динамического программирования. Обозначим за \(dp(k, x)\) количество чисел, из которых можно получить число \(x\), выполнив данную программу для первых \(k\) чисел заданного списка. Очевидно \(dp(0, x)=1\). Проанализировав программу, можно прийти к формуле
\[dp(k,x)=\left\{\begin{array}{ll} dp(k-1, x)+dp(k-1, x+a_k), & x < a_k,\\ dp(k-1, x+a_k), & x\geqslant a_k.\\ \end{array}\right.\] Действительно, если после очередного шага было получено число \(x < a_k\), то на этом шаге вычитание могло выполняться или не выполняться. В противном случае вычитание производилось наверняка. Ответом будет \(dp(n, 0)\).
Отметим, что если эту формулу записать в виде программы без преобразований, то количество сложений будет равно \(\sum_{i=1}^n a_i\). С учетом ограничений на сумму такое количество сложений может быть выполнено за отведенное время. Таким образом, надо найти реализацию, при которой данные не будут перемещаться по памяти. Также заметим, что если \(s\geqslant \max a_i\), то \(dp(k, s)=1\). Это означает, что для всех \(s\), больших \(10^6\), значением \(dp(k, s)\) будет единица. Таким образом, достаточно хранить \(10^6\) значений, а единицы добавлять при необходимости.
Рассмотрим преобразование данных на одном шаге. \[\begin{array}{ccccccccccccc} d_0 & d_1 & \cdots & d_{a-1} & d_a & d_{a+1} & \cdots& d_{r-a}& d_{r-a+1}&\cdots & d_r & 1 & \cdots\\ d_0+d_a & d_1+d_{a+1} & \cdots & d_{a-1}+d_{2a-1} & d_{2a} & d_{2a+1} & \cdots & d_r & 1 &\cdots & 1 & 1 & \cdots\\ \\ \end{array}\] Можно заметить, что если первые \(a\) элементов добавить к следующим \(a\) элементам, а потом удалить, а также добавить \(a\) единиц в конец последовательности, то получим требуемое преобразование. Для реализации можно использовать кольцевой буфер требуемого размера.
Пример программы-решения
Ниже представлено решение на языке Python.
maxval = 1000002
t = int(input())
for _ in range(t):
n = int(input())
rng = [1]*maxval
pos = 0
for a in map(int,input().split()):
for i in range(a):
rng[(pos+a)%maxval]+=rng[pos%maxval]
rng[pos%maxval]=1
pos+=1
print(rng[pos%maxval],end=' ')Тест с номером 1 совпадает с тестом из условия задачи. Баллы за него не начисляются.
Успешное прохождение каждого теста с номерами 2–31 оценивается в 1 балл.
В тестах с номерами 2–9 сумма \(n\) по всем тестовым случаям не превосходит 1000, при этом выполняется \(a_i\leqslant 1000\) и сумма всех \(a_i\) по всем тестовым случаям не превосходит \(50000\).
В тестах с номерами 10–15 сумма \(n\) по всем тестовым случаям не превосходит 20000, при этом выполняется \(a_i\leqslant 1000\).
В тестах с номерами 16–21 сумма \(n\) по всем тестовым случаям не превосходит 100000, при этом выполняется \(a_i\leqslant 1000\).






