Предметный тур. Математика. 3 этап
Двигатель новаторского суборбитального летательного аппарата может работать в двух режимах: самолетном и ракетном. В первом он сжигает топливо, используя в качестве окислителя забортный воздух, при этом удельная теплота сгорания топлива в этой реакции составляет \(q_1 = 40\textrm{\,МДж/кг}\). Второй режим активируется, когда аппарат поднимается на высоту, плотность воздуха на которой недостаточна для поддержания стабильного сгорания топлива. В этом режиме в качестве окислителя начинает использоваться жидкий реактив, хранящийся в баках на борту самолета. Удельная теплота сгорания (в расчете на массу топлива) в этой реакции составляет \(q_2 = 60\textrm{\,МДж/кг}\), но для ее поддержания приходится расходовать окислитель, массой в \(n = 1{,}5\) превышающий массу окисляемого им топлива.
Для выполнения полетного задания двигателям аппарата придется произвести одинаковое количество теплоты в самолетном и ракетном режимах. Определите, в какой объемной пропорции необходимо разделить общее доступное для хранения реагентов пространство на борту аппарата между топливом и окислителем, чтобы добиться максимального запаса хода при таких требованиях. Плотность топлива \(\rho_\textrm{т} = 900\) кг/м\(^3\), плотность окислителя \(\rho_\textrm{о} = 1200\) кг/м\(^3\). Считайте, что зависимость расхода аппаратом топлива от массы реагентов в его баках пренебрежимо мала.
Пускай количество теплоты, производимое двигателем в каждом режиме, равно \(Q\). Для самолетного режима эта величина может быть выражена как \[Q = q_1 m_\textrm{т1} = q_1 \rho_\textrm{т} V_\textrm{т1} \Rightarrow V_\textrm{т1} = \frac{Q}{q_1 \rho_\textrm{т}},\] где \(m_\textrm{т1}\) и \(V_\textrm{т1}\) — масса и объем сжигаемого в этом режиме топлива соответственно.
Для ракетного режима объем потребляемого топлива равен аналогично \[V_\textrm{т2} = \frac{Q}{q_2 \rho_\textrm{т}}.\]
Таким образом, общий объем \(V_\textrm{т}\), который необходимо выделить под топливо, равен \[V_\textrm{т} = V_\textrm{т1} + V_\textrm{т2} = V_\textrm{т2} \left(\frac{q_2}{q_1} + 1\right).\]
Объем, требуемый для хранения окислителя, легко вычислить из известной пропорции масс. Обозначим \(m_\textrm{о}\) и \(V_\textrm{о}\) массу и объем окислителя соответственно. Нам известно, что \(m_\textrm{о} = n m_\textrm{т2}\). Перепишем это равенство через объемы: \[\rho_\textrm{о} V_\textrm{о} = n \rho_\textrm{т} V_\textrm{т2} \Rightarrow V_\textrm{о} = V_\textrm{т2} \frac{n \rho_\textrm{т}}{\rho_\textrm{о}}.\]
Осталось найти отношение двух полученных объемов: \[\frac{V_\textrm{т}}{V_\textrm{о}} = \frac{\cancel{V_\textrm{т2}}(1 + q_2/q_1)}{\cancel{V_\textrm{т2}} n \rho_\textrm{т}/\rho_\textrm{о}} = \frac{20}{9}.\]
\[V_\textrm{т} : V_\textrm{о} = \frac{1 + q_2/q_1}{n \rho_\textrm{т}/\rho_\textrm{о}} = 20 : 9 \approx 2{,}22.\]
| Продемонстрировано понимание понятия «удельная теплота сгорания» (верно записана связь теплоты и массы топлива) | 5 баллов |
| Верно записана связь масс топлива и окислителя с их объемами | 3 балла |
| Точно: в общем виде или простой дробью получен правильный ответ | 7 баллов |
| Правильный ответ получен только численно с погрешностью не более \(0{,}05\) | 4 балла |
| Всего | 15 баллов |
Если соответствующие шаги успешно проделаны только для части режимов работы двигателя — за них ставится пропорциональная часть максимального балла на усмотрение проверяющего.
Ракета-носитель выводит спутник на круговую орбиту радиуса \(r = 7000\textrm{\,км}\) таким образом, что до достижения заданной высоты орбиты двигатели ракеты создают силу, направленную строго вертикально (от центра Земли). Уже достигнув заданной высоты с нулевой вертикальной скоростью, последняя ступень ракеты включает свои двигатели, за короткое время увеличивающие импульс спутника на некую постоянную величину \(\Delta p\) в строго горизонтальном направлении. Инженерами было установлено, что, действуя по данному алгоритму, ракета способна вывести на указанную орбиту спутник максимальной массы \(m = 600\textrm{\,кг}\), если запускать его с космодрома, находящегося на полюсе планеты. Спутник какой максимальной массы сможет запустить по такому же алгоритму ракета, стартующая с космодрома, находящегося на экваторе? Экваториальный радиус Земли \(R = 6380\textrm{\,км}\), ее масса \(M = 6\cdot 10^{24}\textrm{\,кг}\), гравитационная постоянная \(G = 6{,}67\cdot10^{-11}\) Н\(\cdot\)м\(^2\)/кг\(^2\).
Найдем сначала орбитальную скорость \(v\) спутника на орбите радиуса \(r\). Для этого приравняем центростремительное ускорение этого спутника \(a = v^2/r\) к ускорению свободного падения на соответствующей высоте:
\[\frac{v^2}{r} = G\frac{M}{r^2} \Rightarrow v = \sqrt{\frac{GM}{r}}.\]
В случае старта с полюса спутник не имеет изначальной горизонтальной компоненты скорости, а значит, всю эту скорость спутник получает благодаря горизонтальному импульсу последней ступени: \[\Delta p = m v = m \sqrt{\frac{GM}{r}}.\]
При старте с экватора спутник изначально имеет горизонтальную составляющую скорости \(v_0\), обусловленную суточным вращением космодрома относительно центра планеты: \[v_0 = \frac{2\pi R}{T},\] где \(T = 24\textrm{\,ч}\). Следовательно, импульс \(\Delta p\) должен обеспечить только повышение скорости от \(v_0\) до \(v\): \[\Delta p = m_1 (v - v_0) \Rightarrow m_1 = \frac{\Delta p}{v-v_0} = m \sqrt{\frac{GM}{r}} \left(\sqrt{\frac{GM}{r}} - \frac{2\pi R}{T}\right)^{-1}.\]
\[m_1 = m \sqrt{\frac{GM}{r}} \left(\sqrt{\frac{GM}{r}} - \frac{2\pi R}{T}\right)^{-1} \approx 639\textrm{\,кг}.\]
| Продемонстрировано понимание причин различных масс спутника при старте с экватора и полюса | 2 балла |
| Верно найдена связь орбитальной скорости с высотой | 6 баллов |
| Верно найдена скорость спутника, обусловленная его суточным вращением | 3 балла |
| Верно записана связь всех скоростей с импульсом в задаче | 3 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 20 баллов |
Частичный успех на каждом из этих шагов может оцениваться в долю от максимального балла за соответствующий шаг на усмотрение проверяющего. Например, верно записан закон всемирного тяготения, но орбитальную скорость выразить не удалось, получен верный ответ в общем виде, но при подстановке чисел допущена арифметическая ошибка и т. п. Аналогично в последующих задачах.
В некоторых ракетных двигателях используется метод транспирационного охлаждения. Он состоит в том, что жидкий охладитель продавливается сквозь пористую стенку охлаждаемого прибора, образуя на ее поверхности равномерную тонкую пленку, которая, испаряясь, уносит избыточное тепло агрегата равномернее и эффективнее, чем большинство других методов.
Инженерами в качестве такого охладителя был выбран жидкий аммиак, имеющий удельную теплоту парообразования и конденсации \(L = 1{,}37\textrm{\,МДж/кг}\) и плотность \(\rho = 683\) кг/м\(^3\). Аммиак движется сквозь поры специального керамического покрытия с постоянной скоростью \(v = 1\textrm{\,мм/с}\). Определите, каким должен быть средний диаметр круглых сквозных пор в этом покрытии, чтобы при их поверхностной плотности \(\sigma = 10^6\) м\(^{-2}\) система охлаждения могла обеспечить плотность теплового потока \(f = 10\) кВт/м\(^2\). Теплоту, идущую на изменение температуры аммиака, считать пренебрежимо малой по сравнению с теплотой его испарения.
Круглая пора с диаметром \(d\) имеет площадь \(S_0 = \pi d^2/4\). За некоторое время \(t\) сквозь каждую такую пору проходит объем аммиака \[V = vtS_0 = \frac{\pi d^2}{4} vt.\] Этот объем содержит в себе массу \(m = \rho V\) вещества, а значит, при испарении отводит количество теплоты \[Q_0 = L \rho V = \frac{\pi d^2}{4} L\rho vt.\] Поверхностная плотность \(\sigma\) — есть отношение числа \(N\) пор на элементе поверхности к площади \(S\) этой поверхности: \[\sigma = \frac{N}{S}.\] Следовательно, с площади \(S\) поверхности за время \(t\) отводится тепло \[Q = NQ_0 = \frac{\pi d^2}{4} L\rho v \sigma S t.\] Плотность потока тепла \(f\) (как можно судить из названия и единиц измерения) представляет собой отношение количества теплоты, уходящего с поверхности двигателя, ко времени и площади соответствующей поверхности: \[f = \frac{Q}{S t} = \frac{\pi d^2}{4} L\rho v \sigma,\] откуда окончательно \[d = \sqrt{\frac{4f}{\pi L\rho v \sigma}} \approx 0{,}12\textrm{\,мм}.\]
Примечание: поры такого диаметра и плотности расположения покрывают приблизительно 1% общей площади поверхности керамики.
\[d = \sqrt{\frac{4f}{\pi L\rho v \sigma}} \approx 0{,}12\textrm{\,мм}.\]
| Верно записана связь между удельной теплотой парообразования и количеством отводимой теплоты | 3 балла |
| Верно записана связь диаметра пор, скорости течения жидкости и ее объемного расхода | 6 баллов |
| Продемонстрировано понимание терминов «поверхностная плотность» и «плотность теплового потока» | по 3 балла |
| Получен правильный ответ | 7 баллов |
| Всего | 22 балла |
Спутниковая группировка состоит из \(n = 12\) одинаковых спутников, движущихся по одной и той же круговой орбите над экватором Земли. Согласно техническим требованиям, спутники группировки должны быть разделены равными расстояниями друг от друга, и каждая пара ближайших друг к другу спутников должна непрерывно обмениваться исследовательскими данными по радиоканалу. При этом используемые частоты радиосвязи отражаются от слоя ионосферы Земли, расположенного на постоянной высоте \(h = 80\textrm{\,км}\) от поверхности планеты, но проходят через более высокие слои. Спутники выводят на самую низкую орбиту, удовлетворяющую этим требованиям. В некоторый момент \(m = 4\) спутника группировки потребовалось вывести из эксплуатации. Определите, на какую величину \(\Delta v\) и в какую сторону необходимо изменить орбитальные скорости остальных спутников, чтобы вновь удовлетворить техническим требованиям на самой низкой возможной орбите. Экваториальный радиус Земли \(R = 6380\textrm{\,км}\), ее масса \(M = 6\cdot 10^{24}\textrm{\,кг}\), гравитационная постоянная \(G = 6{,}67\cdot10^{-11}\) Н \(\cdot\) м\(^2\)/кг\(^2\).
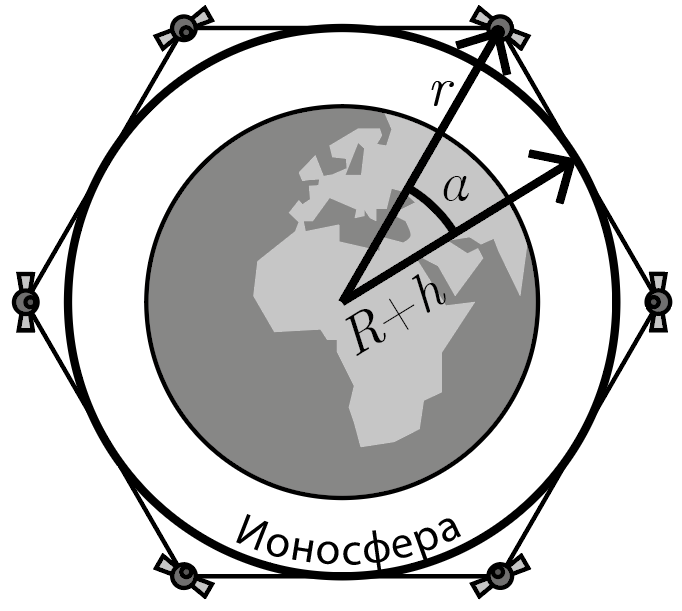
Поскольку спутники находятся на одной круговой орбите и разделены равными расстояниями, можно говорить, что они находятся в вершинах правильного \(n-\)угольника. Чтобы обеспечить нахождение ближайших друг к другу спутников в зоне взаимной видимости, прямая, соединяющая их (сторона \(n-\)угольника), не должна пересекать сферу с радиусом \(R + h\) и центром в центре планеты, от которой отражаются радиосигналы. Наиболее низкое расположение спутников, при котором это возможно, такое, что упомянутый \(n-\)угольник описан около соответствующей сферы. На рис. 1.1 для наглядности приведен пример для \(n = 6\), а вид Земли и масштаб не соблюдены.
Угол \(\alpha\) образуется между двумя векторами (см. рис. 1.1). Один из них направлен из центра планеты на точку касания отрезка между соседними спутниками с ионосферой. Второй — на один из спутников. Этот угол равен половине угловой меры дуги орбиты, разделяющей два соседних спутника:
\[\alpha = \frac{\pi}{n}.\] Через этот угол легко выразить связь между радиусом \(R+h\) ионосферы и радиусом \(r\) орбиты спутников: \[R+h = r \cos\alpha \Rightarrow r = \frac{R+h}{\cos(\pi/n)}.\]
Зная радиус орбиты, легко определить и соответствующую ему орбитальную скорость \(v\) (как в задаче 2) в зависимости от числа спутников \(n\): \[v(n) = \sqrt{\frac{GM}{r(n)}} = \sqrt{\frac{GM \cos(\pi/n)}{R+h}},\]
откуда получим окончательно \[\Delta v = v(n-m) - v(n) = \sqrt{\frac{GM}{R+h}}\left( \cos^{1/2} \left(\frac{\pi}{n-m}\right) - \cos^{1/2} \left(\frac{\pi}{n}\right) \right).\]
\[\Delta v = \sqrt{\frac{GM}{R+h}}\left( \cos^{1/2} \left(\frac{\pi}{n-m}\right) - \cos^{1/2} \left(\frac{\pi}{n}\right) \right) \approx -170\textrm{\,м/с}.\]
То есть орбитальную скорость необходимо уменьшить на \(170\textrm{\,м/с}\).
| Продемонстрировано понимание геометрии расположения спутников на орбите относительно ионосферы | 4 балла |
| Верно найдена связь орбитальной скорости с радиусом орбиты | 5 баллов |
| Верно найдена связь орбитальной скорости с радиусом ионосферы и числом спутников в группировке | 4 балла |
| Получен правильный ответ | 7 баллов |
| Всего | 20 баллов |
Стратостат, предназначенный для изучения атмосферного электричества, представляет собой шар объемом \(V = 400\) м\(^3\), заполненный гелием. Стратостат соединен с землей длинным проводом, электрическое сопротивление которого, согласно требованиям эксперимента, должно быть равно \(R = 600\textrm{\,Ом}\). Изначально для этого использовался медный провод, в результате чего максимальная высота подъема аппарата оказывалась ограничена значением \(H_1 = 16\textrm{\,км}\). До какой высоты сможет подняться тот же аппарат, если изготовить провод из алюминия? Плотность меди \(\rho_\textrm{м} = 8960\) кг/м\(^3\), плотность алюминия \(\rho_\textrm{а} = 2700\) кг/м\(^3\), удельное сопротивление меди \(r_\textrm{м} = 1{,}7\cdot 10^{-8}\) Ом\(\cdot\)м, удельное сопротивление алюминия \(r_\textrm{а} = 2{,}65\cdot 10^{-8}\) Ом\(\cdot\)м. На высотах полета аппарата плотность воздуха \(\rho\) снижается с высотой на \(\Delta \rho = 0{,}02\) кг/м\(^3\) на каждый километр высоты.
Высота, до которой может подняться стратостат, определяется балансом между его подъемной силой \(F = \rho(h) g V\) и общим поднимаемым им весом \(P\). Здесь \(\rho(h)\) — плотность воздуха на высоте \(h\). Этот вес включает в себя вес \(mg\) самого стратостата (включая оболочку, оборудование и наполняющий оболочку газ) и вес \(\rho_\textrm{п} g h S\) провода, где \(\rho_\textrm{п}\) — плотность металла, из которого он изготовлен, \(S\) — площадь его поперечного сечения, а \(h\) — высота подъема стратостата, совпадающая с минимальной длиной провода, позволяющего соединить аппарат с Землей: \[m g + \rho_\textrm{п} g h S = \rho(h) g V.\] Площадь поперечного сечения провода можно найти из требований на его сопротивление: \[R = \frac{r h}{S} \Rightarrow S = \frac{r h}{R},\] где \(r\) — удельное сопротивление. Отсюда \[m \cancel{g} = \rho(h) \cancel{g} V - \frac{\rho_\textrm{п} \cancel{g} r h^2}{R}.\]
Масса \(m\) в левой части этого уравнения не зависит от материала провода и высоты подъема стратостата. Поэтому, обозначив \(H_2\) максимальную высоту, доступную стратостату с алюминиевым проводом, приравняем массы, выраженные из этого уравнения для двух описанных случаев, и получим \[\rho (H_1) V - \frac{\rho_\textrm{м} r_\textrm{м}H_1^2}{R} = \rho (H_2) V - \frac{\rho_\textrm{а} r_\textrm{а}H_2^2}{R}.\] Перепишем это уравнение в более удобной форме: \[\frac{1}{R}(r_\textrm{м}\rho_\textrm{м} H_1^2 - r_\textrm{а}\rho_\textrm{а} H_2^2) + V (H_1 - H_2) \frac{\Delta \rho}{\Delta h} = 0,\] где \(\Delta h = 1\textrm{\,км}\), воспользовавшись тем, что разницу в плотностях на высотах \(H_1\) и \(H_2\) удобно записать напрямую через известную нам величину \(\Delta \rho\): \[\rho(H_1) - \rho(H_2) = (H_2 - H_1) \frac{\Delta \rho}{\Delta h}.\] Обратите внимание: увеличение высоты приводит к уменьшению плотности воздуха, поэтому порядок следования \(H_1\) и \(H_2\) в правой и левой частях уравнения различен.
Полученное уравнение является квадратным относительно \(H_2\) и имеет единственный положительный корень \[H_2 = \frac{-\Delta p/\Delta h RV +\sqrt{\Delta p^2/\Delta h^2 R^2V^2 + 4 \Delta p / \Delta h H_1 R V r_\textrm{а} \rho_\textrm{а} + 4 H_1^2 r_\textrm{м} \rho_\textrm{м}r_\textrm{а} \rho_\textrm{а}}}{2 r_\textrm{а} \rho_\textrm{а}} \approx 18{,}8\textrm{\,км}.\]
Его, разумеется, проще получить, подставив промежуточные значения непосредственно в квадратное уравнение.
\(H_2 \approx 18{,}8\textrm{\,км}.\)
| Продемонстрировано понимание природы ограничений на максимальную высоту подъема стратостата | 3 балла |
| Верно записано условие равновесия стратостата | 3 балла |
| Верно записана связь между полным и удельным сопротивлениями провода | 4 балла |
| Хотя бы в одном уравнении верно учтено изменение плотности воздуха с высотой | 5 баллов |
| Получен правильный ответ | 10 баллов |
| Всего | 25 баллов |
Научный аэростат исследует высокие слои атмосферы планеты на предмет концентрации в них ионов. Для этого на его корпусе установлен зонд в виде двух параллельных друг другу металлических пластин, разделенных небольшим воздушным зазором. Зонд подключен к высокоточным вольтметру и амперметру, непрерывно измеряющим напряжение между пластинами и силу протекающего между ними тока. На малых высотах, на которых воздух практически не ионизирован, зонд является конденсатором с емкостью \(C = 50\textrm{\,пФ}\), не пропускающим ток. На рабочей высоте измерения показали, что зонд является резистором с эффективным сопротивлением \(R = 9\textrm{\,МОм}\). Найдите удельное сопротивление воздуха на этой высоте. Электрическая постоянная \(\varepsilon_0 = 8{,}85\cdot 10^{-12}\textrm{\,Ф/м}\).
Емкость плоского воздушного конденсатора задается выражением \[C = \frac{S\varepsilon_0}{d},\] где \(S\) — площадь его обкладок, а \(d\) — ширина зазора между ними.
Удельное сопротивление частично ионизированного разреженного газа заведомо значительно выше, чем металла, поэтому потенциал в пределах одной обкладки зонда можно считать постоянным с высокой точностью. В этом случае сопротивление резистора, образованного ионизированной воздушной прослойкой между ними, задается выражением \[R = \frac{\rho d}{S} = \frac{\rho \varepsilon_0}{C},\] где \(\rho\) — искомое удельное сопротивление. Отсюда получим окончательно \[\rho = \frac{RC}{\varepsilon_0} \approx 5{,}08\cdot 10^7 \textrm{\,Ом $\cdot$ м}.\]
\[\rho = \frac{RC}{\varepsilon_0} \approx 5{,}08\cdot 10^7 \textrm{\,Ом $\cdot$ м}.\]
Примечательно, что этот результат на самом деле не зависит от формы обкладок зонда, но доказательство этого факта выходит за рамки школьной программы.
| Верно записана формула для емкости плоского конденсатора | 3 балла |
| Верно записана формула сопротивления резистора | 3 балла |
| Обоснована возможность применения предыдущей формулы | 1 балл |
| Получен правильный ответ | 6 баллов |
| Всего | 13 баллов |
Указание: существует более общее решение, основывающееся на применении теоремы Гаусса, закона Ома в дифференциальной форме и определений емкости и сопротивления. Если оно применено полностью корректно — за задачу следует ставить полный балл. Если часть его обоснована — балл ставится на усмотрение проверяющего из той же общей логики: 6 баллов за правильность ответа и до 7 баллов за обоснованность решения.
Многие типы двигателей, широко применяемые в авиации — газотурбинные, турбореактивные и прямоточные воздушно-реактивные — используют в своей основе термодинамический цикл Брайтона, состоящий из двух изобар и двух адиабат. В цикле 12341 этого рода провели дополнительную изобару 56, «разделившую» его на два меньших цикла 15641 и 52365, КПД которых оказались одинаковы. Найдите КПД этих циклов если известно, что КПД исходного цикла 12341 равняется \(\eta\).
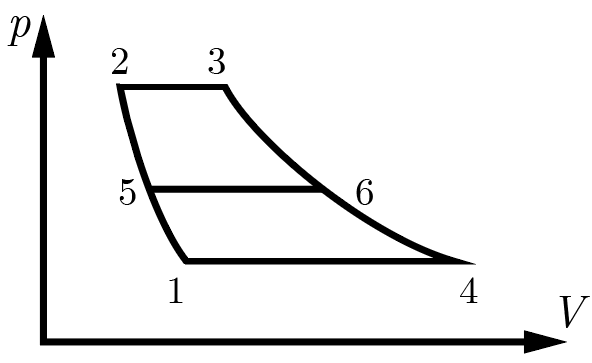
КПД термодинамического цикла удобно найти по формуле \[\eta = 1 - \frac{Q_\textrm{о}}{Q_\textrm{п}},\] где \(Q_\textrm{о, п}\) — количества теплоты, отданные газом холодильнику и полученное им от нагревателя соответственно.
Рассмотрим сначала исходный цикл 1234. На адиабатических участках цикла газ не получает и не теряет теплоту, соответственно, весь теплообмен рабочего тела с окружающей средой сосредоточен на изобарных участках 2–3 и 4–1. Тогда перепишем КПД цикла в виде
\[\eta = 1-\frac{Q_{41}}{Q_{23}},\] где \(Q_{41}, Q_{23}\) — модули количества полученной или отданной газом теплоты на соответствующих участках цикла.
Аналогично КПД циклов \(15641\) и \(52365\) равны \[\eta^\prime = 1 - \frac{Q_{41}}{Q_{56}}= 1 - \frac{Q_{56}}{Q_{23}}.\]
Следовательно, \[\frac{Q_{41}}{Q_{56}} = \frac{Q_{56}}{Q_{23}} \Rightarrow Q_{56} = \sqrt{Q_{41} Q_{23}}.\] Выражая \(Q_{41}\) через КПД исходного цикла: \(Q_{41} = Q_{23}(1-\eta)\), получим \[Q_{56} = Q_{23}\sqrt{1-\eta} \Rightarrow \eta^\prime = 1 - \frac{\cancel{Q_{23}} \sqrt{1-\eta}}{\cancel{Q_{23}}} = 1-\sqrt{1-\eta}.\]
\(\eta^\prime = 1-\sqrt{1-\eta}\).
| Верно записано любое определение КПД теплового двигателя | 3 балла |
| Верно записана формула для КПД именно цикла Брайтона через характеристики пронумерованных процессов или состояний | 3 балла |
| Найдена пропорция между количествами теплоты на трех изобарах или эквивалентная ей | 4 балла |
| Получен правильный ответ | 7 баллов |
| Всего | 17 баллов |
Исследовательский беспилотный планер начинает свое движение над южным полюсом Земли и по кратчайшей траектории достигает научной станции, расположенной строго на экваторе, вблизи бразильского города Макапа. Быстро проделав необходимые измерения и повернув по малому радиусу, он затем направляется, также по кратчайшей траектории, в следующую станцию, расположенную в Кении, тоже на экваторе; после этого вновь быстро проводит измерения и возвращается по кратчайшей траектории на Южный полюс. При этом линия возвращения беспилотника пересеклась на полюсе с линией его старта под прямым углом.
Определите общее время движения беспилотника, если известно, что все время в пути он двигался равномерно на пренебрежимо малых высотах, и в момент обоих поворотов беспилотника Солнце находилось над ним в зените, но не оказывалось над ним в зените в других точках отрезка Бразилия – Кения. Длина экватора Земли \(L = 40\,076\textrm{\,км}\), длина меридиана \(l = 20\,004\textrm{\,км}\).
Точки поворота беспилотника находятся на экваторе, поэтому траектория беспилотника состояла из двух меридианальных дуг, соединяющих эти точки с полюсом, и одной экваториальной дуги, соединяющей их друг с другом. Суммарная длина меридианальных дуг равна \(l\), так как каждая из них составляет ровно половину меридиана.
Важно, что длина экваториальной дуги \(x\) не может быть найдена при помощи теоремы Пифагора или других соотношений евклидовой планиметрии, поскольку движение беспилотника происходит на сфере, и характерные расстояния этого движения сопоставимы с радиусом этой сферы. Вместо этого можно заметить, что длина этой дуги относится к общей длине экватора, так же как разница в широтах между двумя точками поворота относится к \(2 \pi\), а эта разница в широтах есть не что иное, как угол между меридианами, вдоль которых взлетает и садится беспилотник: \[\frac{x}{L} = \frac{\pi/2}{2 \pi} \Rightarrow x = \frac{L}{4}.\]
Согласно условию, Солнце оказалось в зените в моменты обоих поворотов, но не между ними, при этом на участке Бразилия – Кения беспилотник двигался с запада на восток (навстречу Солнцу). Это значит, что угловая скорость видимого движения Солнца над беспилотником складывалась из угловой скорости его видимого движения, обусловленного вращением Земли и угловой скорости движения беспилотника относительно поверхности планеты, а за время \(t\) этого перелета относительно беспилотника Солнце совершило один полный оборот: \[\frac{2 \pi}{t} = \frac{\pi}{2t} + \frac{2\pi}{T},\] где \(T = 1\textrm{\,сут}\).
Отсюда \[t = T\left(1 - \frac{1}{4}\right) \Rightarrow v = \frac{x}{t} = \frac{L}{3T},\] где \(v\) — линейная скорость беспилотника относительно поверхности Земли.
После того как была найдена скорость и длина траектории, легко дать ответ на вопрос задачи: \[t_\textrm{о} = \frac{l + x}{v} = 3T\frac{l+L/4}{L} \approx 54\textrm{\,ч} \approx 1{,}94\cdot 10^5\textrm{\,с}.\]
\[t_\textrm{о} = 3T\frac{l+L/4}{L} \approx 54\textrm{\,ч} \approx 1{,}94\cdot 10^5\textrm{\,с}.\]
| Продемонстрировано понимание траектории беспилотника (она изображена или описана) и невозможности использования планиметрии для нахождения ее длины | 4 балла |
| Верно найдена длина всех участков траектории | 3 балла |
| Верно записан закон сложения линейных или угловых скоростей для экваториального участка маршрута | 3 балла |
| Верно найдено время в пути или скорость на этом участке | 4 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 20 баллов |
Если участник продемонстрировал явное понимание необходимости сложения угловых скоростей для нахождения скорости планера на экваториальном участке, но допустил незначительную алгебраическую ошибку, например, перепутал знак, на этом этапе — за критерии 3 и 4 он может получить до 4 баллов суммарно.
Первые два закона Кеплера (сформулированные для спутника Земли) гласят:
- Невозмущенная орбита спутника Земли является эллипсом, в одном из фокусов которого находится центр планеты.
- За равные промежутки времени радиус-вектор космического аппарата (с началом в центре планеты) заметает равные площади.
Космический аппарат, находящийся на круговой земной орбите радиусом \(R = 10000\) км, провел маневр расстыковки, разделившись на два независимых отсека, каждый из которых получил небольшое приращение скорости. Для первого отсека это приращение оказалось направлено строго по ходу его орбитального движения, а для второго — строго против этого хода. При этом орбиты спутников изменились так, что скорость каждого из спутников в перигее оказалась на \(k = 1\%\) раз больше, чем в апогее. Найдите расстояние между апогеем первого спутника и перигеем второго.
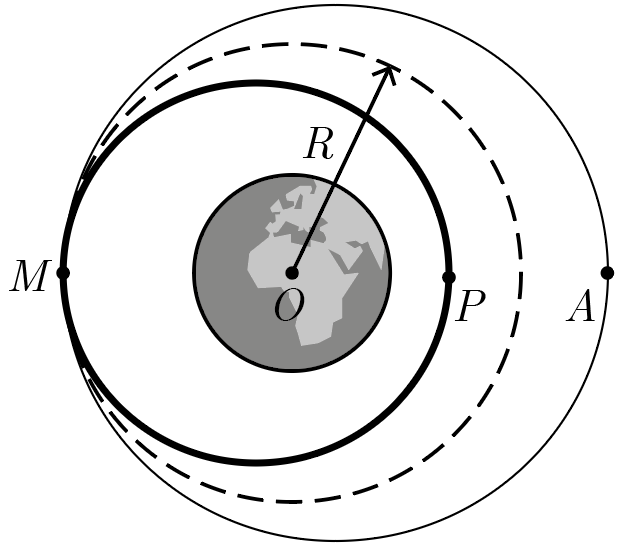
На рис. 2.2 (не в масштабе) тонкой линией изображена орбита первого отсека, толстой — второго, пунктиром средней толщины — их общая изначальная круговая орбита. \(M\) — точка расстыковки спутников, \(A\) — апогей орбиты первого спутника, \(P\) — перигей орбиты второго. Расстояние \(AP\) является искомой величиной задачи. Это расстояние сильно преувеличено для наглядности.
При движении по круговой орбите вектор скорости спутника всегда ортогонален его радиус-вектору, проведенному из центра планеты. Векторы \(\Delta \vec{v}\) приращения скоростей обоих отсеков коллинеарны вектору их орбитальной скорости в момент расстыковки, это значит, что и сразу после маневра, когда орбиты спутников уже изменились, их мгновенные скорости направлены перпендикулярно радиус-векторам и, следовательно, векторам действующих на них сил тяжести.
Из этого вытекает, что в момент расстыковки сила тяжести не совершает над отсеками работы, поэтому и не изменяются кинетические энергии отсеков, а это возможно только в моменты максимального сближения (перигей) и максимального отдаления (апогей) спутника от планеты. При этом для первого спутника скорость оказалась немного выше скорости его движения по круговой орбите и, следовательно, при постоянном центростремительном ускорении центр кривизны его траектории сместился немного дальше центра планеты, а значит, точка расстыковки \(M\) является для него перигеем. Для второго, наоборот, скорость оказалась несколько меньше скорости его движения по круговой орбите, поэтому точка \(M\) оказалась для него апогеем.
Рассмотрим малый отрезок времени \(t\) вблизи перигея или апогея орбиты спутника. В этот момент мгновенная скорость спутников, как было установлено, ортогональна радиус-вектору, поэтому площадь \(S\) заметаемого им сектора может быть найдена по формуле \[S = \frac{vtr}{2},\] где \(r\) — расстояние от спутника до центра планеты. Поэтому по второму закону Кеплера, скорости \(v_A\) и \(v_P\), которые имеет любой спутник в апогее и перигее соответственно связаны с расстояниями \(r_A\), \(r_P\) от центра планеты до этих точек его орбиты соотношениями \[v_A r_A = v_P r_P.\]
Следовательно, расстояния \(r_P\) и \(r_A\) для двух отсеков находятся в пропорции \[\frac{r_{A1}}{r_{P1}} = \frac{v_{P1}}{v_{A1}} = 1+k = \frac{v_{P2}}{v_{A2}} = \frac{r_{A2}}{r_{P2}},\] где индексы \(1, 2\) указывают на принадлежность величины к орбите первого или второго спутников соответственно. Но \(r_{P1} = r_{A2} = R\) и, следовательно, \[r_{A1} = R(1+k); \quad r_{P2} = R/(1+k).\]
Тогда окончательно \[l = r_{A1} - r_{P2} = R\left(1+k - \frac{1}{1+k}\right) \approx 199\textrm{\,км}.\]
\[l= R\left(1+k - \frac{1}{1+k}\right) \approx 199\textrm{\,км}.\]
| Верно изображены или описаны словами с указанием ключевых для задачи точек орбиты двух отсеков после расстыковки | 5 баллов |
| Положение ключевых точек на этих орбитах физически обосновано | 5 баллов |
| Из второго закона Кеплера или закона сохранения момента импульса найдена связь между модулем скорости и радиус-вектором в разных точках эллиптической орбиты | 6 баллов |
| То же утверждение записано без доказательства | 3 балла |
| Получен правильный ответ | 7 баллов |
| Всего | 23 балла |
Частичный успех на каждом из шагов может оцениваться в долю от максимального балла за соответствующий шаг на усмотрение проверяющего. Например, верно найдена орбита только одного из сегментов, получен верный ответ в общем виде, но при подстановке чисел допущена арифметическая ошибка и т. п. Аналогично в остальных задачах.
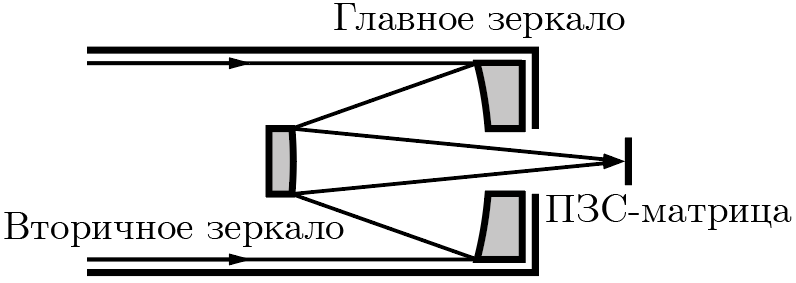
Космический телескоп находится на околоземной орбите и изготовлен по схеме Ричи – Кретьена (см. рис. 2.3). Она состоит из кольцевого главного зеркала с оптической силой \(D_1 = 0{,}2\textrm{\,дптр}\) и внешним диаметром \(d_1 = 1{,}2 \textrm{\,м}\) и вторичного зеркала с оптической силой \(D_2 = -0{,}1\textrm{\,дптр}\) и диаметром \(d_2 = 0{,}4\textrm{\,м}\), расположенном на расстоянии \(l = 3\textrm{\,м}\) от главного. Внутренний диаметр главного зеркала совпадает с диаметром вторичного.
Оптическая система отъюстирована таким образом, что пучок световых лучей, приходящих параллельно главной оптической оси телескопа фокусируется ею точно в центр светочувствительной ПЗС-матрицы, расположенной за главным зеркалом. Орбита телескопа оказалась ориентирована таким образом, что через некоторое время телескоп окажется сориентирован строго на Солнце, и если ничего не предпринять — фокусировка столь мощного источника света выведет ПЗС-матрицу из строя. К сожалению, за годы эксплуатации жесткое космическое излучение нарушило работу маневровых двигателей и электромотора, контролирующего крышку объектива, поэтому единственной возможностью спасти матрицу оказались юстировочные сервоприводы, способные смещать ПЗС-матрицу вдоль оптической оси телескопа.
На какое минимальное расстояние необходимо сместить матрицу вдоль этой оси, если общая плотность потока мощности, попадающего на телескоп от Солнца и фокусируемой его оптикой, равна \(I = 1200\) Вт/м\(^2\), а предельная плотность мощности, попадание которой на ПЗС-матрицу не приведет к ее выгоранию равна \(I^\prime = 3\) Вт/мм\(^2\)?
Общий световой поток, попадающий на матрицу, равен произведению плотности светового потока на площадь его поперечного сечения. В частности, этот поток можно выразить через площадь главного зеркала и начальную плотность потока \(I\), либо через площадь пятна, в которое фокусируется кольцевой световой пучок внешнего диаметра \(d_1\) и внутреннего диаметра \(d_2\), отраженный главным зеркалом телескопа и критическую допустимую плотность потока \(I^\prime\) соответственно. Обозначив диаметр этого пятна \(d\), запишем условие «выживания» матрицы в виде \[\cancel{\frac{\pi}{4}}d^2I^\prime = \cancel{\frac{\pi}{4}}d_1^2I \Rightarrow d = d_1\sqrt{\frac{I}{I^\prime}}.\] Оба эти пятна имеют форму геометрически подобных колец, поэтому нет необходимости учитывать их внутренние радиусы.
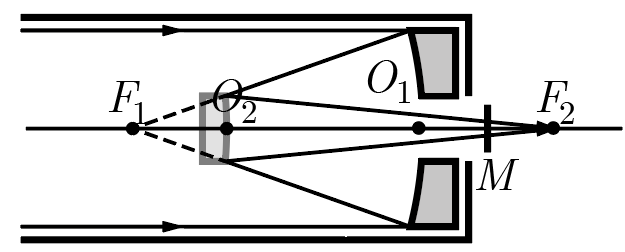
Чтобы выразить диаметр \(d\), рассмотрим подробнее ход лучей в телескопе. Главным зеркалом, оптический центр которого обозначен на рис. 2.4 как \(O_1\), они собираются в точке \(F_1\), такой, что \(O_1F_1 = 1/D_1\).
Эта точка служит мнимым источником для вторичного зеркала (с оптическим центром в точке \(O_2\)), поэтому расстояние \(O_2F_2\) может быть найдено по формуле тонкой линзы (которая для выпуклых и вогнутых зеркал выполняется с точностью до замены области пропускания лучей на область их отражения): \[D_2 =-\frac{1}{O_2F_1} + \frac{1}{O_2F_2} \Rightarrow O_2F_2 = \left(D_2 + \frac{1}{O_2F_1}\right)^{-1} = \left(D_2 + \frac{1}{1/D_1 - l}\right)^{-1}.\]
Из подобия треугольников, образованных лучами, отраженными от вторичного зеркала, плоскостью этого зеркала и ПЗС-матрицей, следует \[\frac{d_2}{d} = \frac{O_2 F_2}{MF_2},\] где \(M\) — точка расположения центра матрицы.
Таким образом, искомый отрезок \(F_2M\) равен \[MF_2 = O_2F_2 \frac{d}{d_2} = \left(D_2 + \frac{1}{1/D_1 - l}\right)^{-1}\cdot \frac{d_1}{d_2} \sqrt{\frac{I}{I^\prime}} = 15\textrm{\,см}.\]
\[x = \left(D_2 + \frac{1}{1/D_1 - l}\right)^{-1}\cdot \frac{d_1}{d_2} \sqrt{\frac{I}{I^\prime}} = 15\textrm{\,см}.\]
| Продемонстрировано понимание связи между плотностью потока и площадью светового пятна | 5 баллов |
| Верно найден фокус главного зеркала | 3 балла |
| Верно записана формула тонкой линзы с учетом мнимости источника вторичного зеркала | 6 баллов |
| Формула тонкой линзы записана, но с ошибкой в знаках | 3 балла |
| Верно использовано подобие необходимых для решения задачи треугольников | 4 балла |
| Получен правильный ответ | 9 баллов |
| Всего | 27 баллов |