Предметный тур. Химия. 1 этап
У каждого вещества — неорганического или органического — должно быть свое название. Иначе ни химики, ни обычные люди не будут понимать друг друга. Для этого и существует номенклатура веществ (на латыни nomenclatura — называние имен). Многие вещества имеют исторически сложившиеся «собственные имена», которые известны как тривиальные названия. Они не вытекают из каких-либо единых систематических принципов, не выражают строения соединения и чрезвычайно разнообразны. В настоящее время используется систематическая международная номенклатура ИЮПАК (IUPAC) — Международный союз теоретической и прикладной химии (International Union of Pure and Applied Chemistry), позволяющая дать веществу однозначное название и отражающая его принадлежность к определенному классу веществ, то есть строение.
Соотнесите тривиальные названия веществ с их систематическими названиями.
В ответе укажите сочетание буквы тривиального названия с соответствующей цифрой систематического названия через тире; между сочетаниями для различных веществ поставьте запятую. Например: A — 1, B — 2, C — 3 и т. д.
Тривиальное название вещества:
- Негашеная известь.
- Веселящий газ.
- Бурый газ, лисий хвост.
- Поташ.
- Пищевая сода.
- Гашеная известь.
- Едкий натр.
- Индийская селитра.
- Чилийская селитра.
- Известняк.
Систематическое название:
- Гидроксид натрия.
- Гидроксид кальция.
- Карбонат кальция.
- Гидрокарбонат натрия.
- Карбонат калия.
- Нитрат натрия.
- Нитрат калия.
- Оксид кальция.
- Оксид азота (I).
- Оксид азота (IV).
A — 8, B — 9, C — 10, D — 5, E — 4, F — 2, G — 1, H — 7, I — 6, J — 3.
В современном мире технологии и инженерии сплавы металлов играют важнейшую роль. Эти материалы сочетают свойства различных металлов, создавая уникальные характеристики, которые невозможно достичь с помощью чистых веществ. Сплавы — это не просто комбинации элементов, а инновационные решения для множества проблем, стоящих перед инженерами и учеными. Использование сплавов дает возможность создавать материалы с уникальным набором физико-химических характеристик, чтобы оптимизировать производственные процессы и повысить эффективность изделий. Это причина того, почему они так широко распространены в самых разнообразных областях: от строительства до высоких технологий.
Силумин (сплав на основе алюминия и кремния) представляет собой важный материал, сочетающий в себе прочность, устойчивость и легкость, что обеспечивает его широкое применение в различных областях промышленности и дизайна. Благодаря прочности, низкому весу, коррозионной стойкости силумин используется в автомобилестроении, авиастроении, кораблестроении, в космической промышленности.
Для анализа образца силумина, содержащего алюминий и кремний, массой 30 г его растворили в 400 г 15%-го раствора едкого натра, при этом выделился газ объемом 38,4 л (н. у.).
Определите массовую долю алюминия в сплаве (в процентах). Число округлите до целых.
Составим уравнения реакций:
\[\ce{2Al + 2NaOH + 6H2O -> 2Na[Al(OH)4] + 3H2 ^};\] \[\ce{Si + 2NaOH + H2O -> Na2SiO3 + 2H2 ^};\] \[n(\ce{H_2})=\displaystyle\frac{38{,}4\text{~л}}{22{,}4 \text{~л/моль}} = 1{,}714\text{~моль}.\]
Если \(n( \ce{Al} ) = x\) моль, \(n(\ce{Si}) = y\) моль, тогда: \[\left\{\begin{aligned} &27 x + 28y = 30, \\ &1,5 x + 2y = 1,714. \end{aligned}\right.\]
\(x=1\) моль, \(y = 0{,}107\) моль. \[m (\ce{Al}) = n \cdot M = 1 \cdot 27 = 27\text{~г};\] \[\omega (\ce{Al}) = \displaystyle\frac{27}{30} = 0{,}9\text{ или }90\%.\]
90.
Определите массовую долю кремния в сплаве (в процентах). Число округлите до целых.
Составим уравнения реакций: \[\ce{2Al + 2NaOH + 6H2O -> 2Na[Al(OH)4] + 3H2 ^};\] \[\ce{Si + 2NaOH + H2O -> Na2SiO3 + 2H2 ^};\] \[n(\ce{H_2})=\displaystyle\frac{38{,}4\text{~л}}{22{,}4 \text{~л/моль}} = 1{,}714\text{~моль}.\]
Если \(n(\ce{Al}) = x\) моль, \(n(\ce{Si}) = y\) моль, тогда: \[\left\{\begin{aligned} &27 x + 28y = 30, \\ &1,5 x + 2y = 1,714. \end{aligned}\right.\]
\(x=1\) моль, \(y = 0{,}107\) моль. \[m (\ce{Si}) = n \cdot M = 0{,}107 \cdot 28 = 2{,}996 \approx 3\text{~г};\] \[\omega (\ce{Si}) = \displaystyle\frac 3{30} = 0{,}1\text{ или }10 \%.\]
10.
Определите массовую долю гидроксида натрия в полученном растворе (в процентах). Число округлите до десятых.
Составим уравнения реакций:
\[\ce{2Al + 2NaOH + 6H2O -> 2Na[Al(OH)4] + 3H2 ^};\] \[\ce{Si + 2NaOH + H2O -> Na2SiO3 + 2H2 ^};\] \[n(\ce{H_2})=\displaystyle\frac{38{,}4\text{~л}}{22{,}4 \text{~л/моль}} = 1{,}714\text{~моль}.\]
Если \(n(\ce{Al}) = x\) моль, \(n(\ce{Si}) = y\) моль, тогда: \[\left\{\begin{aligned} &27 x + 28y = 30, \\ &1,5 x + 2y = 1,714. \end{aligned}\right.\]
\(x=1\) моль, \(y = 0{,}107\) моль. \[\begin{gather} m (\ce{NaOH})_{\text{в исх. растворе}} = 400 \cdot 0,15 = 60\text{~г};\\ m (\ce{NaOH})_{\text{прореагир.}} = (1 + 0,107 \cdot 2) \cdot 40 = 48,56\text{~г};\\ m (\ce{NaOH})_{\text{оставшегося}} = 60 - 48,56 = 11,44\text{~г};\\ \omega (NaOH) = \displaystyle\frac{11,44\cdot 100}{400+30-1,714\cdot2}= 2,7 \%. \end{gather}\]
2,7.
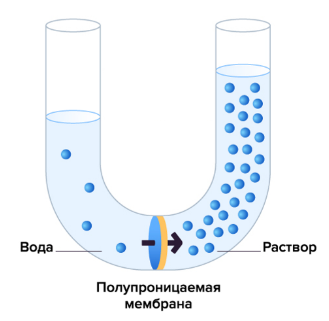
Рассмотрим такую систему: мембрана, по разные стороны от которой расположены растворы с разным содержанием растворенного вещества. Поры полупроницаемой мембраны пропускают молекулы растворителя, но не молекулы растворенного вещества. Из-за того, что концентрации растворов различны, растворитель (например, вода) начнет диффундировать (перетекать) из более разбавленного раствора в более концентрированный и разбавлять его до тех пор, пока концентрация не станет равной по обе стороны мембраны. Это явление называют осмосом.
Мембраны всех живых клеток используют осмос для контроля поглощения необходимых веществ, поэтому он играет очень важную роль в медицине, биотехнологии и агротехнологии, особенно в гидропонике. Но осмос значим и в быту: с древности с его помощью консервировали пищу — в соленой среде вода вытекает из клеток, что приводит к сморщиванию (весь материал внутри клетки отслаивается от клеточной стенки) и потере жизнедеятельности микроорганизмов (этот процесс называют плазмолизом).
Рассчитайте массу поваренной соли,необходимую для приготовления 1,5 л рассола для засаливания огурцов (плотность \(\rho = 1055\) г/л), массовая доля соли в котором составляет 7,5%. Ответ запишите в граммах с точностью до десятых.
Рассчитаем массу раствора \[m_{\text{р-ра}}=\rho V= 1055\cdot 1{,}5=1582{,5}\text{~г.}\]
Масса соли составляет: \[m(NaCl)=m_{\text{р-ра}}\omega (NaCl)=1582{,5}\cdot 0{,}075=118{,}7\text{~г.}\]
118,7. Диапазон 118–119.
Осмотическим давлением называют величину избыточного давления на раствор, отделенный от чистого растворителя полупроницаемой мембраной, при котором прекращается осмос, то есть диффузия растворителя через мембрану. Голландский химик Якоб Хендрик Вант-Гофф установил, что для разбавленных растворов осмотическое давление прямо пропорционально молярной концентрации частиц (молекул, ионов) растворенного вещества: \(\pi=CRT\), где \(\pi\) — осмотическое давление, кПа; \(C\) — молярная концентрация частиц (молекул, ионов) растворенного вещества, моль/л; \(R\) —универсальная газовая постоянная, 8,314 Дж/(моль\(\cdot\)К); \(T\) — температура, К. Это открытие было отмечено первой Нобелевской премией по химии.
При внутривенном введении используют изотонические растворы — растворы, осмотическое давление которых соответствует давлению плазмы крови — в такой среде вода не поступает в клетку и не выводится из клетки, что предотвращает от повреждения эритроциты. Изотонический 5%-й раствор глюкозы применяют для улучшения антитоксической функции печени, восполнения водного и энергетического дефицита, для разведения и растворения лекарственных препаратов.
Рассчитайте величину осмотического давления 5%-го водного раствора глюкозы (\(\ce{C6H12O6}\)) при температуре 37 °С (плотность \(\rho = 1018\) г/л). Ответ приведите в килопаскалях (кПа) с точностью до целых.
Рассчитаем массу 1 л раствора \(m_{\text{р-ра}}=\rho V=1018\cdot 1{,}0=1018\) г.
Масса глюкозы составляет \[m(\ce{C_6 H_12 O_6})=m_{\text{р-ра}}\omega(\ce{C_6 H_12 O_6})=1018\cdot 0{,}05=50{,}9\text{~г.}\]
Количество вещества глюкозы \[n(\ce{C_6 H_12 O_6})=\frac{m(\ce{C_6 H_12 O_6})}{M(\ce{C_6 H_12 O_6})}=\frac{50{,}9}{6\cdot 12+12+6\cdot 16}=0{,}283\text{~моль,}\] соответственно, молярная концентрация раствора \[C(\ce{C_6 H_12 O_6})=\frac{n(\ce{C_6 H_12 O_6})}V=\frac{0{,}283}1=0{,}283\text{~моль/л.}\]
Осмотическое давление \[\pi=CRT=0{,}283\cdot 8{,}314\cdot (273+37)=729{,}4\text{~кПа.}\]
729. Диапазон 710–750.
Водные растворы полимера гидроксиэтилкрахмала вводят внутривенно для предотвращения шока при значительной кровопотере, например, в случае травмы, поскольку это способствует нормализации и улучшению гемодинамических показателей, уменьшает вязкость плазмы, снижает агрегацию тромбоцитов и эритроцитов. Осмотическое давление раствора полимера мало, поэтому в состав также включают неорганические соли, чтобы сделать раствор препарата изотоничным крови.
Установите молярную массу гидроксиэтилкрахмала в граммах на моль (г/моль) с точностью до целых, если осмотическое давление раствора, содержащего 15,0 г полимера в 250 мл раствора, составляет 1,022 кПа при 20 °C.
Молярная концентрация раствора полимера \[C=\frac{\pi}{RT}=\frac{1{,}022}{8{,}314\cdot (273+20)}=0{,}42 \text{~ммоль/л},\]
т. е. количество вещества полимера \[n=CV=0{,}42\cdot 0{,}25=0{,}105\text{~ммоль.}\]
Тогда молярная масса \(M=\displaystyle\frac mn=\displaystyle\frac{15}{0{,}105}\cdot 1000=142857\) г/моль.
142857. Диапазон 140000–147000.
Ортофосфорная кислота используется в самых разных областях — в производстве удобрений и чистящих средств, для деревообработки и очистки металла от ржавчины, в стоматологии для реставрации зубов и в ювелирном деле при пайке. Также она зарегистрирована в качестве пищевой добавки E338, которую можно встретить в составе мармеладов, сиропов и напитков, хлебобулочных изделий, сыров и плавленых сырков.
Пищевую фосфорную кислоту производят термическим способом, позволяющим получить концентрированный продукт с меньшим содержанием примесей — для этого расплавленный белый фосфор сжигают в воздухе и подвергают образующийся оксид фосфора (V) гидратации.
Этот процесс упрощенно можно описать следующими реакциями: \[\ce{4P + 5O2 -> 2P2O5};\] \[\ce{P2O5 + 3H2O -> 2H3PO4}.\]
Рассчитайте объем воздуха, который необходимо подавать в башню (камеру сжигания) в 1 ч для сжигания фосфора, содержащего 0,5% негорючих примесей (расход фосфора 3000 кг/ч). Ответ приведите в кубических метрах при нормальных условиях с точностью до целых. Учтите, что для предотвращения образования оксида фосфора (III) в башню подают двукратный избыток воздуха по сравнению с расчетным количеством.
В расчете на 1 ч количество вещества фосфора составляет \[n(\ce{P})=\frac mM=\frac{3000\cdot 0{,}995}{31}=96{,}29\text{~кмоль},\]
тогда \[\begin{gather} n_\text{теор}(\ce{O_2})=\frac 54n(\ce{P})=120,36\text{~кмоль},\\ n_\text{практ}(\ce{O_2})=2n_\text{теор}(\ce{O_2})=2\cdot 120,36=240,72\text{~кмоль}. \end{gather}\] Объем кислорода:
\[V(\ce{O_2})=n_\text{практ}(\ce{O_2})V_0=240{,}72\cdot 1000\cdot 22{,}4=5392128\text{~л,}\] объем воздуха \[V_\text{возд}=\frac{V(\ce{O_2})}{\chi(\ce{O_2})}=\frac {5392128}{0{,}21\cdot 1000}=25677\text{~м}^3.\]
25677. Диапазон 24380–26970.
Рассчитайте массу 75%-го раствора фосфорной кислоты, образующегося в башне, в килограммах в час (кг/ч) с точностью до целых.
Количество вещества фосфорной кислоты соответствует количеству фосфора \(n(\ce{H_3PO_4})=n(\ce{P})=96{,}29\) кмоль/ч, тогда: \[\begin{gather} m(\ce{H_3PO_4})=n(\ce{H_3PO_4})M=96,29\cdot (3+31+16\cdot 4)=9436,42 \text{~кг/ч,}\\ m_\text{р-ра}(\ce{H_3PO_4})=\frac{m(\ce{H_3PO_4})}{\omega(\ce{H_3PO_4})}=\frac{9436,42}{0,75}=12581 \text{~кг/ч.} \end{gather}\]
12581. Диапазон 12577–12585.
Использование теплоты, выделяющейся при сгорании фосфора, позволяет значительно увеличить энергоэффективность проведения процесса. Рассчитайте массу угля, содержащего 5% негорючих примесей, которую удастся сэкономить при полном использовании тепла сгорания фосфора. Ответ приведите в килограммах в час (кг/ч) с точностью до целых. Теплота сгорания белого фосфора в указанных условиях составляет 1764 кДж/моль, углерода 394 кДж/моль.
Количество теплоты, выделяющейся при сгорании фосфора, составляет \[Q=Q_Pn(P)=96{,}29\cdot 1764=169802~\text{МДж/ч},\] тогда \[\begin{gather} n(\ce{C})=\frac Q{Q_C}=\frac{169802\cdot 1000}{394}=430970\text{~моль/ч,}\\ m(\ce{C})=n(\ce{C})M=430970\cdot 12=5172\text{~кг/ч,}\\ m_\text{уголь}=\frac{m(\ce{C})}{\omega(\ce{C})}=\frac{5172}{0,95}=5444\text{~кг/ч.} \end{gather}\]
5444. Диапазон 5440–5448.
В качестве пищевой добавки ортофосфорная кислота выступает регулятором кислотности и консервантом: кислая среда препятствует размножению микроорганизмов и порче продукта. Именно наличие фосфорной кислоты в составе обуславливает способность газированных напитков растворять ржавчину и очищать бытовые поверхности, о которой снято много интернет-роликов.

Впрочем, имеются сведения о стимулировании фосфорной кислотой вымывания кальция из организма и ее негативном влиянии на зубную эмаль при чрезмерном употреблении.
Рассчитайте концентрацию ионов водорода в 0,01 моль/л растворе фосфорной кислоты, если известно, что степень диссоциации кислоты по первой ступени составляет 57%, а диссоциацией по второй и третьей ступени можно пренебречь. Ответ приведите в миллимоль на литр (ммоль/л) с точностью до десятых.
Запишем уравнение диссоциации фосфорной кислоты по первой ступени: \[\ce{H3PO4 <--> H+ + H2PO4-}.\]
Степень диссоциации представляет собой отношение количества вещества, распавшегося на ионы, к общему количеству растворенного вещества: \[\alpha_I=\frac{n(\ce{H_2PO_4^-})}{n_0(\ce{H_3PO_4}) }.\]
В расчете на 1 л раствора \[n_0(\ce{H_3PO_4})=CV=0{,}01\cdot 1=0{,}01~\text{моль};\] \[\begin{split} n(\ce{H^+})=n(\ce{H_2PO_4^-})=\alpha_In_0(\ce{H_3PO_4})=0{,}57\cdot 0{,}01=\\ =0{,}0057\text{~моль} =5{,}7\text{~ммоль.} \end{split}\]
5,7.
Врач, геолог, химик, педагог...
Этот ученый отличался разносторонностью своих интересов. Поступил на медицинский факультет в Дерптском университете, чтобы иметь возможность изучать химию. В начале своей научной деятельности в Иркутске одновременно с врачебной практикой проводил химические и минералогические исследования — изучал химический состав минеральных вод и минералов, в том числе открытых им в экспедициях по Уралу и Сибири. Его рвение в химии было отмечено, по приглашению Академии наук он возвратился в Петербург, чтобы посвятить свою жизнь именно этой науке. Активно занимался вопросами методики преподавания химии; учебник «Основания чистой химии», выпущенный им, произвел фурор в академическом сообществе и выдержал семь изданий.
Педагогический талант химика был отмечен весьма высоко — ему выпала честь обучать естественным наукам наследника русского престола, будущего императора Александра II.
Мировую известность этому химику принесло открытие закона, который имеет большое значение не только в химии, но и в инженерии для эффективного проектирования и оптимизации всевозможных систем и устройств, так как позволяет рассчитать теплоту химических процессов, не проводя их! Этот закон имеет применение и в медицине, как теоретическая основа определения калорийности продуктов питания.
Назовите этого ученого:
- Александр Ерминингельдович Арбузов;
- Александр Михайлович Бутлеров;
- Федор Федорович Бейльштейн;
- Александр Порфирьевич Бородин;
- Герман Иванович Гесс;
- Дмитрий Иванович Менделеев;
- Сергей Васильевич Лебедев;
- Юрий Анатольевич Овчинников;
- Игорь Михайлович Скурихин;
- Михаил Семенович Цвет.
E.
У каждого вещества — неорганического или органического — должно быть свое название. Иначе ни химики, ни обычные люди не будут понимать друг друга. Для этого и существует номенклатура веществ (на латыни \(nomenclatura\) — называние имен). Многие вещества имеют исторически сложившиеся «собственные имена», которые известны как тривиальные названия. Они не вытекают из каких-либо единых систематических принципов, не выражают строения соединения и чрезвычайно разнообразны. В настоящее время используется систематическая международная номенклатура ИЮПАК (IUPAC) — Международный союз теоретической и прикладной химии (International Union of Pure and Applied Chemistry), позволяющая дать веществу однозначное название и отражающая его принадлежность к определенному классу веществ, то есть строение.
Соотнесите тривиальные названия биологически значимых природных веществ с их систематическими названиями.
В ответе укажите сочетание буквы тривиального названия с соответствующей цифрой систематического названия через тире; между сочетаниями для различных веществ поставьте запятую. Например: A — 1, B — 2, C — 3 и т. д.
Тривиальное название вещества:
- Молочная кислота
- Пировиноградная кислота (ПВК)
- Аланин
- Щавелевая кислота
- Щавелевоуксусная кислота (ЩУК)
- Янтарная кислота
- Глутаровая кислота
- Глицин
- Фумаровая кислота
- Адипиновая кислота
Систематическое название:
- Пентандиовая кислота
- Бутандиовая кислота
- Гександиовая кислота
- 2-оксобутандиовая кислота
- Этандиовая кислота
- Бутендиовая кислота
- 2-аминоэтановая кислота
- 2-гидроксипропановая кислота
- 2-оксопропановая кислота
- 2-аминопропановая кислота
A — 8, B — 9, C — 10, D — 5, E — 4, F — 2, G — 1, H — 7, I — 6, J — 3.

В современном мире технологии и инженерии сплавы металлов играют важнейшую роль. Эти материалы сочетают свойства различных металлов, создавая уникальные характеристики, которые невозможно достичь с помощью чистых веществ. Сплавы — это не просто комбинации элементов, а инновационные решения для множества проблем, стоящих перед инженерами и учеными. Их использование дает возможность создавать материалы с уникальным набором физико-химических характеристик, что позволяет оптимизировать производственные процессы и повысить эффективность изделий. Это причина того, почему сплавы так широко распространены в самых разнообразных областях: от строительства до высоких технологий.
Авиаль — группа сплавов системы алюминий-магний-кремний. Название образовано от сокращения словосочетания «авиационный алюминий». Они отличаются высокой пластичностью и удовлетворительной коррозионной стойкостью. Из авиалей изготавливают кованые и штампованные детали сложной формы, например, лопасти винтов вертолетов. Также эти сплавы активно используют для замены нержавеющей стали в корпусах мобильных телефонов.
Для анализа сплава группы «Авиаль», содержащего алюминий, кремний и магний, его образец массой 13,776 г растворили в избытке соляной кислоты, при этом выделился газ объемом 16,9 л (н. у.). Нерастворившийся остаток поместили в раствор гидроксида натрия, при этом выделился газ объемом 268,8 мл (н. у.).
Определите массовую долю кремния в сплаве (в процентах). Число округлите до десятых.
В соляной кислоте растворяются металлы алюминий и магний. Нерастворившийся остаток — это кремний.
Кремний растворяется в растворе гидроксида натрия:
\[\ce{Si + 2NaOH + H2O -> Na2SiO3 + 2H2 ^}. \label{ch1011_010201}\]
По уравнению \eqref{ch1011_010201} \(n(\ce{H_2})= \displaystyle\frac{0{,}2688\text{~л}}{22{,}4\text{~л/моль}} = 0{,}012\) моль. \[\begin{gather} n(\ce{Si}) =\frac 12 n(\ce{H_2}) = \frac{0,012}2\text{~моль} = 0,006\text{~моль};\\ m (\ce{Si}) = n \cdot M = 0,006 \cdot 28 = 0,168\text{~г};\\ \omega (\ce{Si}) = \displaystyle\frac{0,168}{13,776} = 0,01219\text{~ или~}1,219 \approx 1,2\%. \end{gather}\]
1,2.
Определите массовую долю алюминия в сплаве (в процентах). Число округлите до целых.
В соляной кислоте растворяются металлы алюминий и магний. Нерастворившийся остаток — это кремний:
\[\ce{2Al + 6 HCl -> 2AlCl3 + 3H2 ^ }; \label{ch1011_010202}\] \[\ce{Mg + 2 HCl -> MgCl2 + H2 ^ }. \label{ch1011_010203}\]
По уравнению \eqref{ch1011_010201} \(n(\ce{H_2})= \displaystyle\frac{0{,}2688\text{~л}}{22{,}4\text{~л/моль}} = 0{,}012\) моль. \[\begin{gather} n(\ce{Si}) =\frac 12 n(\ce{H_2}) = \frac{0,012}2\text{~моль} = 0,006\text{~моль};\\ m (\ce{Si}) = n \cdot M = 0,006 \cdot 28 = 0,168\text{~г};\\ \omega (\ce{Si}) = \displaystyle\frac{0,168}{13,776} = 0,01219\text{~ или~}1,219 \approx 1,2\%. \end{gather}\] Таким образом, масса алюминия и магния составляет: \[13{,}776 - 0{,}168 = 13{,}608\text{ г.}\]
По уравнениям \eqref{ch1011_010202}, \eqref{ch1011_010203} \[n(\ce{H_2}) = \displaystyle\frac{16{,}9\text{~л}}{22{,}4\text{~л/моль}} = 0{,}7545~\text{моль}.\]
Если \(n(Al) = x\) моль, \(n(Mg) = y\) моль, тогда: \[\left\{\begin{aligned} &27 x + 24y = 13{,}608, \\ &1{,}5 x + y = 0{,}7545. \end{aligned}\right.\]
\(x=0{,}5\) моль, \(y = 0{,}0045\) моль. \[\begin{gather} m (Al) = n \cdot M = 0,5 \cdot 27 = 13,5\text{~г};\\ \omega (Al) = \displaystyle\frac{13,5}{13,776} = 0,9799\text{~ или~}97,99 \approx 98\%. \end{gather}\]
98.
Определите массовую долю магния в сплаве (в процентах). Число округлите до десятых.
По уравнению \eqref{ch1011_010203} \(n(\ce{H_2})= \displaystyle\frac{0{,}2688\text{~л}}{22{,}4\text{~л/моль}} = 0{,}012\) моль. \[\begin{gather} n(Si) =\frac 12 n(\ce{H_2}) = \frac{0,012}2\text{~моль} = 0,006\text{~моль};\\ m (Si) = n \cdot M = 0,006 \cdot 28 = 0,168\text{~г};\\ \omega (Si) = \displaystyle\frac{0,168}{13,776} = 0,01219\text{~ или~}1,219 \approx 1,2\%. \end{gather}\] Таким образом, масса алюминия и магния составляет \(13{,}776 - 0{,}168 = 13{,}608\) г.
По уравнениям \eqref{ch1011_010201}, \eqref{ch1011_010202} \(n(\ce{H_2}) = \displaystyle\frac{16{,}9\text{~л}}{22{,}4\text{~л/моль}} = 0{,}7545\) моль.
Если \(n(Al) = x\) моль, \(n(Mg) = y\) моль, тогда: \[\left\{\begin{aligned} &27 x + 24y = 13{,}608, \\ &1{,}5 x + y = 0{,}7545. \end{aligned}\right.\]
\(x=0{,}5\) моль, \(y = 0{,}0045\) моль. \[\begin{gather} m (Mg) = n \cdot M = 0,0045 \cdot 24 = 0,108\text{~г};\\ \omega (Mg) = \displaystyle\frac{0,108}{13,776} = 0,0078~\text{или}~0,78 \approx 0,8 \%. \end{gather}\]
0,8.

Осмотическим давлением называют величину избыточного давления на раствор, отделенный от чистого растворителя полупроницаемой мембраной, при котором прекращается осмос, то есть диффузия растворителя через мембрану. Голландский химик Якоб Хендрик Вант-Гофф установил, что для разбавленных растворов осмотическое давление прямо пропорционально молярной концентрации частиц (молекул, ионов) растворенного вещества: \[\pi=CRT,\] где \(\pi\) — осмотическое давление, кПа; \(C\) — молярная концентрация частиц (молекул, ионов) растворенного вещества, моль/л; \(R\) — универсальная газовая постоянная, 8,314 Дж/(моль\(\cdot\)К); \(T\) — температура, К. Это открытие было отмечено первой Нобелевской премией по химии.
Мембраны всех живых клеток используют осмос для контроля поглощения необходимых веществ, поэтому он играет очень важную роль в медицине, биотехнологии и агротехнологии, особенно в гидропонике. Осмос помогает растениям расти и всасывать воду корневой системой — поскольку в клеточном соке концентрация солей и сахаров выше, чем в почвенном растворе. Это важно учитывать при внесении удобрений — если осмотическое давление почвенного раствора станет слишком большим, поступление воды в растение прекратится, и оно погибнет (например, как в засоленных почвах).
Рассчитайте осмотическое давление раствора удобрения (300 г мочевины в 10 л воды) при температуре 25 °C. Ответ приведите в килопаскалях (кПа) с точностью до целых.
Количество вещества мочевины: \[n(\ce{NH_2CONH_2})=\frac{m(\ce{NH_2CONH_2})}{M}=\frac{300}{16\cdot 2+28}=5{,}0~\text{моль},\] соответственно молярная концентрация раствора \[C(\ce{NH_2CONH_2})=\frac{n(\ce{NH_2CONH_2})}{V}=\frac{5{,}0}{10}=0{,}5~\text{моль/л}.\]
Осмотическое давление \(\pi=CRT=0{,}5\cdot 8{,}314\cdot (273+25)=1239\) кПа.
1239. Диапазон 1235–1243.
В медицине в терапевтических целях иногда используют гипертонические растворы — растворы, осмотическое давление которых превышает давление плазмы крови — в такой среде вода выходит через мембрану из клетки, и клетка сжимается. Гипертонический раствор хлорида натрия применяют для снятия отека в офтальмологии, как осмотический диуретик, для коррекции состояния систем организма при операциях и в реанимационных целях.

Рассчитайте массовую долю хлорида натрия в разбавленном растворе, осмотическое давление которого при температуре 37 °С составляет 9472 кПа (плотность примите \(\rho=1075\) г/л). Ответ приведите в процентах с точностью до десятых.
Рассчитаем концентрацию частиц в растворе, исходя из величины осмотического давления: \[C=\frac{\pi}{RT}=\frac {9472}{8{,}314\cdot (273+37)}=3{,}68\textrm{\,~моль/л.}\]
Хлорид натрия — электролит, диссоциирующий в растворе на ионы \(\ce{Na^+}\) и \(\ce{Cl^-}\). Поскольку точная степень диссоциации в информации не указана, а раствор является разбавленным, ее можно принять равной 100%.
Тогда концентрация хлорида натрия составляет: \[C(\ce{NaCl})=\frac C2=\frac {3{,}68}2=1{,}84\textrm{\,~моль/л,}\] а масса соли в 1 л раствора равна \[m(\ce{NaCl})=n(\ce{NaCl})\cdot M=C(\ce{NaCl})\cdot V\cdot M=1{,}84\cdot 1\cdot (23+35{,}5)=107{,}64\textrm{\,~г}.\]
Массовая доля в растворе
\[\omega=\frac{m\ce{NaCl}}{m_\text{р-ра}}=\frac{107{,}64}{1\cdot 1075}\cdot 100=10{,}0 \%.\]
10,0. Диапазон 9,7–10,3.
Измерение осмотического давления является одним из распространенных методов определения молекулярной массы полимера, влияющей на его свойства. Например, поливинилхлорид с высокой молекулярной массой обладает более высокой твердостью, эластичностью и температурой стеклования, при меньшей растворимости в органических растворителях. Мембранный осмометр основан на измерении разности давлений — например, по разности высот в капиллярах раствора и растворителя, поскольку гидростатическое давление уравновешивает осмотическое.
Установите молекулярную массу поливинилхлорида в килограммах на моль (кг/моль) с точностью до десятых, если разность высот жидкости в осмометре для его раствора в циклогексане, содержащего 2,5 г в 250 мл раствора, составляет 1,97 см при 25 °С. Плотность циклогексана и раствора 779 \(\text{кг/м}^3\).
Гидростатическое давление столба жидкости уравновешивает осмотическое давление, для удобства расчета используем единицы измерения системы СИ:
\[\pi=CRT=\rho g \Delta h=779\cdot 9{,}8\cdot (1{,}97\cdot 10^{-2})=148\textrm{\,~Па.}\]
Молярная концентрация раствора полимера составляет
\[C=\frac {\pi}{RT}=\frac {148}{8{,}314\cdot (273+25)}=0{,}0598\textrm{\,~моль/м}^3,\]
то есть количество вещества полимера
\[n=CV=0{,}0598\cdot \frac{0{,}25}{1000}=0{,}015\textrm{\,~ммоль.}\]
Тогда молекулярная масса
\[M=\frac mn=\frac {2{,}5}{0{,}015}=166{,}7\textrm{\,~кг/моль.}\]
166,7. Диапазон 162,0–172,0.
Ортофосфорная кислота используется в самых разных областях — в производстве удобрений и чистящих средств, для деревообработки и очистки металла от ржавчины, в стоматологии для реставрации зубов и в ювелирном деле при пайке. Также она зарегистрирована в качестве пищевой добавки E338, которую можно встретить в составе мармеладов, сиропов и напитков, хлебобулочных изделий, сыров и плавленых сырков.
Пищевую фосфорную кислоту производят термическим способом, позволяющим получить концентрированный продукт с меньшим содержанием примесей — для этого расплавленный белый фосфор сжигают в воздухе и подвергают образующийся оксид фосфора (V) гидратации.
Рассчитайте объем воздуха, который необходимо подавать при нормальных условиях в башню (камеру сжигания) в 1 ч для сжигания фосфора, если известно, что расход образующегося в башне 75%-го раствора фосфорной кислоты составляет 3000 кг/ч. Ответ приведите в кубических метрах. Учтите, что для предотвращения образования оксида фосфора (III) в башню подают двукратный избыток воздуха по сравнению с расчетным количеством.
Запишем уравнения происходящих реакций: \[\begin{gather} \ce{P4 + 5O2 -> P4O10};\\ \ce{P4O10 + 6H2O -> 4H3PO4}. \end{gather}\] Масса фосфорной кислоты: \[m(\ce{H_3PO_4})=m_\text{р-ра}\omega_{\ce{H_3PO_4}}=3000\cdot 0{,}75=2250 \text{~кг/ч.}\] Количество вещества фосфорной кислоты: \[n(\ce{H_3PO_4})=\frac{m(\ce{H_3PO_4})}{M}=\frac{2250}{3+31+16\cdot 4}=22{,}96 \text{~кмоль/ч},\] что соответствует расчетному количеству вещества кислорода \[\begin{gather} n_\text{теор}(\ce{O_2})=\frac 54n(\ce{H_3PO_4})=\frac 5{4}22,96=28,70\text{~кмоль/ч,}\\ n_\text{практ}(\ce{O_2})=2n_\text{теор}(\ce{O_2})=2\cdot 28,70 =57,40 \text{~кмоль/ч}. \end{gather}\] Объем кислорода \[V(\ce{O_2})=n_\text{практ}(\ce{O_2})V_0=57{,}40\cdot 1000\cdot 22{,}4=1285714\text{ л,}\] объем воздуха \[V_\text{возд}=\frac {V(\ce{O_2})}{\chi(\ce{O_2})}=\frac {1285714}{0{,}21\cdot 1000}=6122 \text{~м}^3.\]
6122. Диапазон 5800–6500.
Использование теплоты, выделяющейся при сгорании фосфора, позволяет значительно увеличить энергоэффективность проведения процесса. При стандартных условиях рассчитайте теплоту, которая выделяется в ходе проходящих реакций при образовании указанного в подзадаче 1 количества фосфорной кислоты, используя данные таблицы. Ответ выразите в мегаджоулях (МДж) с точностью до целых.
| Вещество | \(\ce{P4O10}\)\(_\text{(тв)}\) | \(\ce{H3PO4}\)\(_\text{(ж)}\) | \(\ce{H2O}\)\(_\text{(ж)}\) |
|---|---|---|---|
| Теплота образования, кДж/моль | 2984,03 | 1266,90 | 285,83 |
В соответствии со следствием из закона Г. И. Гесса теплоту каждой из протекающих реакций можно выразить как разность между суммами теплот образования продуктов и реагентов с учетом стехиометрических коэффициентов: \[\begin{gather} \Delta_rQ=\Sigma n_i Q_f(\text{прод})-\Sigma n_j Q_f(\text{реаг});\\ \Delta_{r1}Q=Q_f(\ce{P_4 O_{10(\text{тв})}})-Q_f(\ce{P_{4(\text{тв})}})-5Q_f(\ce{O_{2(\text{г})}});\\ \Delta_{r2}Q=4Q_f(\ce{H_3PO_{4(\text{ж})}})-6Q_f(\ce{H_2 O_{(\text{ж})}})-Q_f(\ce{P_4 O_{10 (\text{тв})}}). \end{gather}\] С учетом того, что теплоты образования простых веществ равны нулю, получим: \[\begin{gather} \Delta_{r1}Q=2984,03\text{~кДж/моль,}\\ \Delta_{r2}Q=4\cdot 1266,90-6\cdot 285,83-2984,03=368,59\text{~кДж/моль.} \end{gather}\] В расчете на 4 моль фосфорной кислоты \[Q_R=\Delta_{r1}Q+\Delta_{r2}Q=3352{,62}~\text{кДж/моль}.\]
Тогда \[Q=Q_R\cdot \dfrac{n(\ce{H_3PO_4})}4=3352{,62}\cdot \dfrac{22{,}96}4=19243~\text{МДж}.\]
19243. Диапазон 19200–19280.
В качестве пищевой добавки ортофосфорная кислота выступает регулятором кислотности и консервантом: кислая среда препятствует размножению микроорганизмов и порче продукта.
Именно наличие фосфорной кислоты в составе обуславливает способность газированных напитков растворять ржавчину и очищать бытовые поверхности, о которой снято много интернет-роликов. Впрочем, имеются сведения о стимулировании фосфорной кислотой вымывания кальция из организма и ее негативном влиянии на зубную эмаль при чрезмерном употреблении.

Рассчитайте \(pH\) с точностью до десятых 0,5 моль/л раствора фосфорной кислоты, если известно, что константа диссоциации кислоты по первой ступени составляет \(7{,}52\cdot 10^{-3}\), а диссоциацией по второй и третьей ступени можно пренебречь.
Запишем уравнение диссоциации фосфорной кислоты по первой ступени: \[\ce{H3PO4 <--> H+ + H2PO4-}.\] Выражение для константы диссоциации: \[K_I=\frac {[\ce{H2PO4-}][\ce{H+}]}{[\ce{H3PO4}]},\] где в квадратных скобках указаны равновесные концентрации.
Тогда \[\begin{gather} [\ce{H2PO4-}]=[\ce{H+}], [\ce{H3PO4}]=\ce{C0}-[\ce{H+}];\\ K_I=\frac{[\ce{H+}]^2}{\ce{C0}-[\ce{H+}]}=7,52\cdot 10^{-3}. \end{gather}\] Решение уравнения при \(\ce{C0}=0{,}5\) моль/л позволяет найти \[[\ce{H+}]=0{,}058\text{~моль/л,}\] откуда \[pH=-lg ([\ce{H+}])\approx 1{,}2.\]
1,2.
Врач, геолог, химик, педагог...
Этот ученый отличался разносторонностью своих интересов. Поступил на медицинский факультет в Дерптском университете, чтобы иметь возможность изучать химию. В начале своей научной деятельности в Иркутске одновременно с врачебной практикой проводил химические и минералогические исследования — изучал химический состав минеральных вод и минералов, в том числе открытых им в экспедициях по Уралу и Сибири. Его рвение в химии было отмечено, по приглашению Академии наук он возвратился в Петербург, чтобы посвятить свою жизнь именно этой науке. Активно занимался вопросами методики преподавания химии; учебник «Основания чистой химии», выпущенный им, произвел фурор в академическом сообществе и выдержал семь изданий. Педагогический талант химика был отмечен весьма высоко — ему выпала честь обучать естественным наукам наследника русского престола, будущего императора Александра II.
Мировую известность этому химику принесло открытие закона, который имеет большое значение не только в химии, но и в инженерии для эффективного проектирования и оптимизации всевозможных систем и устройств, так как позволяет рассчитать теплоту химических процессов, не проводя их! Этот закон имеет применение и в медицине, как теоретическая основа определения калорийности продуктов питания.
Назовите этого ученого:
- Александр Ерминингельдович Арбузов;
- Александр Михайлович Бутлеров;
- Федор Федорович Бейльштейн;
- Александр Порфирьевич Бородин;
- Герман Иванович Гесс;
- Дмитрий Иванович Менделеев;
- Сергей Васильевич Лебедев;
- Юрий Анатольевич Овчинников;
- Игорь Михайлович Скурихин;
- Михаил Семенович Цвет.
E.
В древности во времена засухи люди использовали любые методы, чтобы вызвать дождь — приносили в жертву животных, пели песни, читали заклинания и проводили обряды. Неудивительно, ведь засуха означала отсутствие урожая и голодную смерть в скором будущем. Но сегодня у ученых есть сразу несколько методов для создания искусственного дождя.
Искусственный дождь или «посев облаков» — это целенаправленное производство дождя. Для создания облаков используются химические вещества, которые могут быть сброшены с самолетов или наземных систем рассеивания, таких как генераторы или канистры, выпущенные ракетами или зенитным оружием. Наиболее часто используемые химикаты для создания облаков — это сухой лед (твердый диоксид углерода) и йодид серебра. В Дубае регулярно идет искусственный дождь, который запускается при помощи беспилотников. О таком дожде власти предупреждают заранее. В России осадки, вызванные искусственным способом, используют при тушении крупных лесных пожаров.

Какой объем (в литрах) газообразного \(\ce{CO2}\) (н. у.) необходим для получения 22 кг сухого льда? Ответ округлите до целых.
Определяем количество вещества, а затем объем \(\ce{CO2}\): \[\begin{gather} n(\ce{CO2})= \frac mM = \frac {22000}{44} = 500\text{~моль};\\ V (\ce{CO2}) = n \cdot VM = 500 \cdot 22,4 = 11200\text{~л.} \end{gather}\]
11200.
Какой объем (в кубических метрах) займет 22 кг газообразного \(\ce{CO2}\) при температуре 28 °С и давлении 750 мм рт. ст? Ответ округлите до десятых.
Пересчет объема газа при изменении условий (температуры и давления) можно производить по формуле объединенного газового закона Бойля – Мариотта и Гей-Люссака: \[\frac {p\cdot V}T = \frac {p_0\cdot V_0}{T_0},\] где \(p_0\), \(T_0\), \(V_0\) — давление, температура и объем при нормальных условиях.
\[V (\ce{CO2}) =\frac{760 \cdot 11200 \cdot 301}{750 \cdot 273} = 12513\text{~л~или~}12{,}5\text{~м}^3.\]
12,5.
Какой объем (в литрах) занимает 22 кг сухого льда, если его плотность составляет 1,561 г/см\(^3\)? Ответ округлите до целых.
Объем сухого льда, представляющего собой твердое вещество, определяем через его плотность: \[V (\ce{CO2})\text{(тв)} = \frac m\rho = \frac{22000}{1{,}561} = 14093~\text{см}^3~\text{или}~14\text{~л.}\]
14.
Какое количество теплоты поглотится при возгонке 1 кг сухого льда, если тепловой эффект реакции возгонки составляет 25,96 кДж/моль? Ответ выразите килоджоулях (кДж) и округлите до целых.
Исходя из термохимического уравнения: \[CO_{2\text{(тв)} } = CO_{2\text{(газ)}}- 25{,}96~\text{кДж},\] количество теплоты на один кг составляет: \[\displaystyle\frac{1000 \cdot 25{,}96}{44} = 590~\text{кДж}.\]
590.
Аммофос — это комплексное удобрение, источник важнейших веществ для питания растений, в составе которого есть азот с фосфором. Эти водорастворимые компоненты очень важны для жизнедеятельности растений. Химическая формула удобрения — \(\ce{NH4H2PO4 + (NH4)2HPO4}\). Азот отвечает за быстрый рост, а фосфор — за развитие корневой системы. Обеспечивая растения азотом и фосфором, аммофос способствует наращиванию зеленой массы, развитию и укреплению корневой системы. Это удобрение позволяет повысить урожайность и иммунитет растений, устойчивость к стрессам, вызванным колебаниями температуры. Кроме того, подкормки аммофосом приводят к увеличению клетчатки и белков в овощах и злаках, продлевают сроки хранения.
В некоторой смеси дигидрофосфата аммония и гидрофосфата аммония число атомов азота \(6{,}02\cdot 10^{23}\), а число атомов фосфора — \(5{,}418\cdot 10^{23}\). Вычислите массу смеси (в граммах). Ответ округлите до десятых.
Определим количество вещества атомов азота и фосфора: \[\begin{gather} n (\ce{N}) = \frac{6,02 \cdot 10^{23}}{6,02 \cdot 10^{23}} = 1\text{~моль};\\ n (\ce{P}) = \frac{5,418 \cdot 10^{23}}{6,02 \cdot 10^{23}} = 0,9 \text{~моль}. \end{gather}\] Если \(n(\ce{NH4H2PO4}) = x\) моль, а \(n(\ce{(NH4)2HPO4}) = y\) моль, тогда: \[\left\{\begin{aligned} &x + 2y = 1, \\ &x + y = 0{,}9. \end{aligned}\right.\]
\(x=0{,}8\) моль, \(y = 0{,}1\) моль. \[\begin{gather} m (\ce{NH4H2PO4}) = n \cdot M = 0,8 \cdot 115 = 92\textrm{\,г};\\ m (\ce{(NH4)2HPO4}) = n \cdot M = 0,1 \cdot 132= 13,2\textrm{\,г}\\ m (\text{смеси}) = 92 + 13,2 = 105,2\textrm{\,г.} \end{gather}\]
105,2.
В некоторой смеси дигидрофосфата аммония и гидрофосфата аммония число атомов азота \(6{,}02\cdot 10^{23}\), а число атомов фосфора — \(5{,}418\cdot 10^{23}\). Вычислите массовую долю дигидрофосфата аммония в смеси (в процентах по массе). Ответ округлите до целых.
Определим количество вещества атомов азота и фосфора: \[\begin{gather} n (\ce{N}) = \frac{6,02 \cdot 10^{23}}{6,02 \cdot 10^{23}} = 1\text{~моль};\\ n (\ce{P}) = \frac{5,418 \cdot 10^{23}}{6,02 \cdot 10^{23}} = 0,9 \text{~моль}. \end{gather}\] Если \(n(\ce{NH4H2PO4}) = x\) моль, а \(n(\ce{(NH4)2HPO4}) = y\) моль, тогда: \[\left\{\begin{aligned} &x + 2y = 1 ,\\ &x + y = 0{,}9. \end{aligned}\right.\]
\(x=0{,}8\) моль, \(y = 0{,}1\) моль. \[\begin{gather} m (\ce{NH4H2PO4}) = n \cdot M = 0,8 \cdot 115 = 92\textrm{\,г};\\ m (\ce{(NH4)2HPO4}) = n \cdot M = 0,1 \cdot 132= 13,2\textrm{\,г};\\ m (\text{смеси}) = 92 + 13,2 = 105,2\textrm{\,г};\\ \omega (\ce{NH4H2PO4}) = \frac{92}{105,2} = 0,8745\text{~или~}87,45 \%\approx 87 \%. \end{gather}\]
87. Диапазон 87–88.
В некоторой смеси дигидрофосфата аммония и гидрофосфата аммония число атомов азота \(6{,}02\cdot 10^{23}\), а число атомов фосфора — \(5{,}418\cdot 10^{23}\). Вычислите массовую долю гидрофосфата аммония в смеси (в процентах по массе). Ответ округлите до целых.
Определим количество вещества атомов азота и фосфора: \[\begin{gather} n (\ce{N}) = \frac{6,02 \cdot 10^{23}}{6,02 \cdot 10^{23}} = 1\text{~моль};\\ n (\ce{P}) = \frac{5,418 \cdot 10^{23}}{6,02 \cdot 10^{23}} = 0,9 \text{~моль}. \end{gather}\] Если \(n(\ce{NH4H2PO4}) = x\) моль, а \(n(\ce{(NH4)2HPO4}) = y\) моль, тогда: \[\left\{\begin{aligned} &x + 2y = 1, \\ &x + y = 0{,}9. \end{aligned}\right.\]
\(x=0{,}8\) моль, \(y = 0{,}1\) моль. \[\begin{gather} m (\ce{NH4H2PO4}) = n \cdot M = 0,8 \cdot 115 = 92\textrm{\,г};\\ m (\ce{(NH4)2HPO4}) = n \cdot M = 0,1 \cdot 132= 13,2\textrm{\,г};\\ m (\text{смеси}) = 92 + 13,2 = 105,2\textrm{\,г};\\ \omega (\ce{NH4H2PO4}) = \frac{13,2}{105,2} = 0,1254\text{~или~}12,54 \%\approx 13 \%. \end{gather}\]
13. Диапазон 12–13.
Рассмотрим такую систему: мембрана, по разные стороны от которой расположены растворы с разным содержанием растворенного вещества. Поры полупроницаемой мембраны пропускают молекулы растворителя, но не молекулы растворенного вещества. Из-за того, что концентрации растворов различны, растворитель (например, вода) начнет диффундировать (перетекать) из более разбавленного раствора в более концентрированный и разбавлять его до тех пор, пока концентрация не станет равной по обе стороны мембраны. Это явление называют осмосом.

Мембраны всех живых клеток используют осмос для контроля поглощения необходимых веществ, поэтому он играет очень важную роль в медицине, биотехнологии и агротехнологии, особенно в гидропонике. Но осмос значим и в быту: с древности с его помощью консервировали пищу — в соленой среде вода вытекает из клеток, что приводит к сморщиванию (весь материал внутри клетки отслаивается от клеточной стенки) и потере жизнедеятельности микроорганизмов (этот процесс называют плазмолизом).
Рассчитайте массу поваренной соли, необходимую для приготовления 2,0 л рассола для засаливания огурцов (плотность \(\rho = 1027\) г/л), массовая доля соли в котором составляет 4,5%. Ответ приведите в граммах с точностью до десятых.
Рассчитаем массу раствора \[m_{\text{р-ра}}=\rho V= 1027\cdot 2{,}0=2054\text{~г.}\]
Масса соли составляет: \[m(NaCl)=m_{\text{р-ра}}\omega (NaCl)=2054\cdot 0{,}045=92{,}4\text{~г.}\]
92,4. Диапазон 92–93.
Осмотическим давлением называют величину избыточного давления на раствор, отделенный от чистого растворителя полупроницаемой мембраной, при котором прекращается осмос, то есть диффузия растворителя через мембрану. Голландский химик Якоб Хендрик Вант-Гофф установил, что для разбавленных растворов осмотическое давление прямо пропорционально молярной концентрации частиц (молекул, ионов) растворенного вещества: \(\pi=CRT\), где \(\pi\) — осмотическое давление, кПа; \(C\) — молярная концентрация частиц (молекул, ионов) растворенного вещества, моль/л; \(R\) —универсальная газовая постоянная, 8,314 Дж/(моль\(\cdot\)К); \(T\) — температура, К. Это открытие было отмечено первой Нобелевской премией по химии.

В терапевтических целях иногда используют гипертонические растворы — растворы, осмотическое давление которых превышает давление плазмы крови — в такой среде вода выходит через мембрану из клетки, и клетка сжимается. Гипертонический 20%-й раствор глюкозы вводят при внутричерепном кровоизлиянии, гипогликемии, заболеваниях печени для улучшения антитоксической функции печени, стимулирования процесса обмена веществ и расширения сосудов, а также в качестве источника углеводов.
Рассчитайте величину осмотического давления 20%-го водного раствора глюкозы (\(\ce{C6H12O6}\)) при температуре 37 °С (плотность \(\rho =1080\) г/л). Ответ выразите в килопаскалях (кПа) с точностью до целых.
Рассчитаем массу 1 л раствора \[m_{\text{р-ра}}=\rho V=1080\cdot 1{,}0=1080~\text{г}.\]
Масса глюкозы составляет \[m(\ce{C_6 H_12 O_6})=m_{\text{р-ра}}\omega(\ce{C_6 H_12 O_6})=1080\cdot 0{,}20=216\text{~г.}\]
Количество вещества глюкозы \[n(\ce{C_6 H_12 O_6})=\frac{m(\ce{C_6 H_12 O_6})}{M(\ce{C_6 H_12 O_6})}=\frac{216}{6\cdot 12+12+6\cdot 16}=1{,}2\text{~моль,}\]
соответственно молярная концентрация раствора \[C(\ce{C_6 H_12 O_6})=\frac{n(\ce{C_6 H_12 O_6})}V=\frac{1{,}2}1=1{,}2\text{~моль/л.}\]
Осмотическое давление \[\pi=CRT=1{,}2\cdot 8{,}314\cdot (273+37)=3092{,8}\text{~кПа.}\]
3093. Диапазон 3070–3110.
Водные растворы полимера поливинилпирролидона (повидон, препарат «Гемодез») вводят внутривенно для связывания токсинов, циркулирующих в крови и быстрого выведения их из организма, усиления почечного кровотока при шоке, заболеваниях печени, сепсисе и пневмонии. Осмотическое давление раствора полимера мало, поэтому в состав также включают неорганические соли, чтобы сделать раствор препарата изотоничным крови.
Установите молярную массу поливинилпирролидона, если осмотическое давление раствора, содержащего 0,6 г полимера в 100 мл раствора, составляет 1,731 кПа при 22 °C. Ответ выразитев граммах на моль (г/моль) с точностью до целых.
Молярная концентрация раствора полимера
\[C=\frac{\pi}{RT}=\frac{1{,}731}{8{,}314\cdot (273+22)}=0{,}71\text{~ммоль/л},\] то есть количество вещества полимера \(n=CV=0{,}71\cdot 0{,}1=0{,}071\) ммоль.
Тогда молярная масса \(M=\frac mn=\displaystyle\frac{0{,}6}{0{,}071}\cdot 1000=8499\) г/моль.
8499. Диапазон 8300–8700.
Ортофосфорная кислота используется в самых разных областях — в производстве удобрений и чистящих средств, для деревообработки и очистки металла от ржавчины, в стоматологии для реставрации зубов и в ювелирном деле при пайке. Также она зарегистрирована в качестве пищевой добавки E338, которую можно встретить в составе мармеладов, сиропов и напитков, хлебобулочных изделий, сыров и плавленых сырков.
Пищевую фосфорную кислоту производят термическим способом, позволяющим получить концентрированный продукт с меньшим содержанием примесей — для этого расплавленный белый фосфор сжигают в воздухе и подвергают образующийся оксид фосфора (V) гидратации.
Этот процесс упрощенно можно описать следующими реакциями: \[\begin{gather} \ce{4P + 5O2 -> 2P2O5};\\ \ce{P2O5 + 3H2O -> 2H3PO4}. \end{gather}\]
При нормальных условиях рассчитайте объем воздуха, который необходимо подавать в башню (камеру сжигания) в 1 ч для сжигания фосфора, содержащего 0,9% негорючих примесей (расход фосфора 2450 кг/ч). Ответ выразите в кубических метрах. Учтите, что для предотвращения образования оксида фосфора (III) в башню подают двукратный избыток воздуха по сравнению с расчетным количеством.
В расчете на один час количество вещества фосфора составляет \[n(P)=\frac mM=\frac{2450\cdot 0{,}995}{31}=78{,}32\text{~кмоль},\] тогда \[\begin{gather} n_\text{теор}(\ce{O_2})=\frac 54n(\ce{P})=97,90\text{~кмоль};\\ n_\text{практ}(\ce{O_2})=2n_\text{теор}(\ce{O_2})=2\cdot 97,90=195,80\text{~кмоль}. \end{gather}\] Объем кислорода: \[V(\ce{O_2})=n_\text{практ}(\ce{O_2})V_0=195{,}80\cdot 1000\cdot 22{,}4=4385974\text{~л,}\] объем воздуха \[V_\text{возд}=\frac{V(\ce{O_2})}{\chi(\ce{O_2})}=\frac {4385974}{0{,}21\cdot 1000}=20886\text{~м}^3.\]
20886. Диапазон 19840–21932.
Рассчитайте массу 75%-го раствора фосфорной кислоты, образующегося в башне. Ответ приведите в килограммах в час (кг/ч) с точностью до целых.
Количество вещества фосфорной кислоты соответствует количеству фосфора \[n(\ce{H_3PO_4})=n(P)=78{,}32~ \text{кмоль/ч},\] тогда: \[\begin{gather} m(\ce{H_3PO_4})=n(\ce{H_3PO_4})M=78,32\cdot (3+31+16\cdot 4)=7675,36 \text{~кг/ч};\\ m_\text{р-ра}(\ce{H_3PO_4})=\frac{m(\ce{H_3PO_4})}{\omega(\ce{H_3PO_4})}=\frac{7675,36}{0,75}=10234\text{~кг/ч.} \end{gather}\]
10234. Диапазон 10230–10238.
Использование теплоты, выделяющейся при сгорании фосфора, позволяет значительно увеличить энергоэффективность проведения процесса. Рассчитайте массу угля, содержащего 7% негорючих примесей, которую удастся сэкономить при полном использовании тепла сгорания фосфора. Ответ выразите в килограммах в час (кг/ч) с точностью до целых. Теплота сгорания белого фосфора в указанных условиях составляет 1764 кДж/моль, углерода 394 кДж/моль.
Количество теплоты, выделяющейся при сгорании фосфора, составляет \[Q=Q_Pn(P)=78{,}32\cdot 1764=138156~ \text{МДж/ч},\] тогда \[\begin{gather} n(C)=\frac Q{Q_C}=\frac{138156\cdot 1000}{394}=350650\text{~моль/ч};\\ m(C)=n(C)M=350650\cdot 12=4208\text{~кг/ч};\\ m_\text{уголь}=\frac{m(C)}{\omega(C)}=\frac{4208}{0,93}=4524\text{~кг/ч.} \end{gather}\]
4524. Диапазон 4490–4558.
В качестве пищевой добавки ортофосфорная кислота выступает регулятором кислотности и консервантом: кислая среда препятствует размножению микроорганизмов и порче продукта. Именно наличие фосфорной кислоты в составе обуславливает способность газированных напитков растворять ржавчину и очищать бытовые поверхности, о которой снято много интернет-роликов. Впрочем, имеются сведения о стимулировании фосфорной кислотой вымывания кальция из организма и ее негативном влиянии на зубную эмаль при чрезмерном употреблении.

Рассчитайте концентрацию ионов водорода в 0,005 моль/л растворе фосфорной кислоты, если известно, что степень диссоциации кислоты по первой ступени составляет 69%, а диссоциацией по второй и третьей ступени можно пренебречь. Ответ выразите в миллимоль на литр (ммоль/л) с точностью до десятых.
Запишем уравнение диссоциации фосфорной кислоты по первой ступени: \[\ce{H3PO4 <--> H+ + H2PO4-}.\] Степень диссоциации представляет собой отношение количества вещества, распавшегося на ионы, к общему количеству растворенного вещества: \[\alpha_I=\frac{n(\ce{H_2PO_4^-})}{n_0(\ce{H_3PO_4}) }.\]
В расчете на 1 л раствора \(n_0(\ce{H_3PO_4})=CV=0{,}005\cdot 1=0{,}005\) моль, \[\begin{split} n(\ce{H^+})=n(\ce{H_2PO_4^-})=\alpha_In_0(\ce{H_3PO_4})=0{,}69\cdot 0{,}005=\\ =0{,}0034\text{~моль} =3{,}4\text{~ммоль.} \end{split}\]
3,4.
Этот выдающийся ученый начинал как математик и физик: степень кандидата он получил в Казанском университете за сочинение о законах движениях планет и других небесных тел. Химией он стал заниматься по настоянию своего наставника и ректора университета Н. Н. Лобачевского. Так зарождалась Казанская химическая школа.
Будучи мастером органического синтеза, этот исследователь впервые осуществил реакцию бензоиновой конденсации и бензидиновую перегруппировку, получил «летучее горчичное масло» и разработал метод замещения атомов галогенов в органических соединениях водородом. Примечательно, что этот ученый был учителем химии А. Нобеля и даже внес свой вклад в применение нитроглицерина в качестве взрывчатого вещества. Однако мировую известность ему принесло открытие реакции превращения ароматических нитросоединений в аминосоединения, впоследствии названной его именем. Эта реакция позволила получить «бензидам», известный нам как анилин, и впоследствии положила начало промышленному синтезу многочисленных продуктов его превращений. В наши дни из анилина получают красители, лекарственные и взрывчатые вещества, а также полиуретаны. Научные заслуги признаны химиками всего мира. Знаменитый немецкий ученый А. В. Гофман скажет: «Если бы ... не сделал ничего более, кроме превращения нитробензола в анилин, то и тогда его имя осталось бы записанным золотыми буквами в истории химии».
Помимо науки этот академик активно занимался организационной и общественной работой, способствуя развитию органической химии, был одним из организаторов Русского химического общества и первым его президентом. Среди его учеников А. М. Бутлеров, Н. Н. Бекетов, А. П. Бородин, А. Н. Энгельгардт, Л. Н. Шишков. Впоследствии Бутлеров отметит: «Имя ... будут всегда чтить те, которым дороги и близки к сердцу успехи и величие науки в России».
Назовите этого ученого:
- Александр Павлович Виноградов;
- Александр Михайлович Зайцев;
- Николай Дмитриевич Зелинский;
- Карл Карлович Клаус;
- Николай Александрович Меншуткин;
- Сергей Васильевич Лебедев;
- Николай Николаевич Зинин;
- Владимир Васильевич Марковников;
- Дмитрий Иванович Менделеев;
- Алексей Евграфович Фаворский.
G.
В древности во времена засухи люди использовали любые методы, чтобы вызвать дождь — приносили в жертву животных, пели песни, читали заклинания и проводили обряды. Неудивительно, ведь засуха означала отсутствие урожая и голодную смерть в скором будущем. Но сегодня у ученых есть сразу несколько методов для создания искусственного дождя.
Искусственный дождь или «посев облаков» — это целенаправленное производство дождя. Для создания облаков используются химические вещества, которые могут быть сброшены с самолетов или наземных систем рассеивания, таких как генераторы или канистры, выпущенные ракетами или зенитным оружием. Наиболее часто используемые химикаты для создания облаков — это сухой лед (твердый диоксид углерода) и йодид серебра. В Дубае регулярно идет искусственный дождь, который запускается при помощи беспилотников. О таком дожде власти предупреждают заранее. В России осадки, вызванные искусственным способом, используют при тушении крупных лесных пожаров.

Для получения иодида серебра образец аргентита (серебросодержащего минерала, представляющий собой модификации сульфида серебра) сначала подвергли обжигу для удаления серы. Остаток поместили в 35%-й раствор азотной кислоты массой 90 г, при этом выделилось 2,24 л газа, нерастворимого в воде, а осадок растворился полностью.
Определите относительную плотность газа по водороду, выделившегося при обработке обожженного остатка руды 35%-й азотной кислотой. Ответ округлите до целых.
При обжиге сульфида серебра образуется не оксид металла, а сам металл (так как оксид термически неустойчив): \[\ce{Ag2S + O2 = 2 Ag + SO2}.\]
Газ, образующийся при обработке серебра 35%-й азотной кислотой, — \(\ce{NO}\): \[\ce{3Ag + 4HNO3 -> 3AgNO3 + NO ^ + 2H2O}.\]
Относительная плотность \(\ce{NO}\) по водороду составляет: \[\ce{DH2}= \frac{M(\ce{NO})}{M(\ce{H2})} = \frac{30}2 = 15.\]
15.
Какая масса образца аргентита была взята для получения йодида серебра по данному условию? Ответ округлите до десятых.
При обжиге сульфида серебра образуется не оксид металла, а сам металл (так как оксид термически неустойчив): \[\ce{Ag2S + O2 = 2 Ag + SO2}.\]
Газ, образующийся при обработке серебра 35%-й азотной кислотой, — \(\ce{NO}\): \[\begin{gather} \ce{3Ag + 4HNO3 -> 3AgNO3 + NO ^ + 2H2O};\\ n(\ce{NO}) = \frac {2,24}{22,4} = 0,1\textrm{\, моль};\\ n (\ce{AgNO3}) = n (\ce{Ag}) = 3\cdot n (\ce{NO}) = 3 \cdot 0,1 = 0,3\textrm{\, моль};\\ n (\ce{Ag2S}) = \frac 12 n (\ce{Ag}) = \frac {0,3}2 = 0,15\textrm{\, моль};\\ m (\ce{Ag2S}) = n \cdot M = 0,15\cdot 248 = 37,2\textrm{\, г.} \end{gather}\]
37,2.
После завершения реакции к полученному раствору добавили 415 г 15%-го раствора йодида калия, при этом, помимо выпадения осадка, наблюдали выделение бесцветного газа. Определите массу образовавшегося йодида серебра в граммах. Ответ округлите до десятых.
При обжиге сульфида серебра образуется не оксид металла, а сам металл (так как оксид термически неустойчив): \[\ce{Ag2S + O2 = 2 Ag + SO2}. \label{chem1011_020101}\] Газ, образующийся при обработке серебра 35% азотной кислотой — \(\ce{NO}\): \[\ce{3Ag + 4HNO3 -> 3AgNO3 + NO ^ + 2H2O}. \label{chem1011_020102}\] \[\begin{gather} n(\ce{NO}) = \frac {2,24}{22,4} = 0,1\textrm{\, моль};\\ n (\ce{AgNO3}) = n (\ce{Ag}) = 3\cdot n (\ce{NO}) = 3 \cdot 0,1 = 0,3\textrm{\, моль};\\ n (\ce{Ag2S}) = \frac 12 n (\ce{Ag}) = \frac {0,3}2 = 0,15\textrm{\, моль};\\ m (\ce{Ag2S}) = n \cdot M = 0,15\cdot 248 = 37,2\textrm{\, г.} \end{gather}\] По уравнению \eqref{chem1011_020102}: \[n (\ce{HNO3}) = 4 \cdot n (\ce{NO}) = 4 \cdot 0{,}1 = 0{,}4\textrm{\, моль.}\]
В исходном растворе: \[n (\ce{HNO3})=\frac{90 \cdot 0{,}35}{63} = 0{,}5~\text{моль}~-~\text{в избытке.}\] \[n (\ce{HNO3})\text{непрор.} = 0{,}5 - 0{,}4 = 0{,}1\textrm{\, моль.}\]
При добавлении к раствору, полученному растворением серебра в азотной кислоте, раствора иодида калия образуется иодид серебра: \[\begin{gather} \ce{AgNO3 + KI -> AgI v + KNO3};\\ n (\ce{KI}) = \frac{415 \cdot 0,15}{166} = 0,375~\text{моль}~-~\text{в избытке;}\\ n (\ce{AgI}) = n (\ce{AgNO3}) = 0,3\textrm{\, моль};\\ m (\ce{AgI}) = n \cdot M = 0,3 \cdot 235 = 70,5\textrm{\, г.} \end{gather}\]
70,5.
После завершения реакции к полученному раствору добавили 415 г 15%-го раствора йодида калия, при этом, помимо выпадения осадка, наблюдали выделение бесцветного газа. Определите массовую долю вещества в процентах в конечном растворе после отделения всех нерастворимых веществ. Ответ округлите до сотых.
При обжиге сульфида серебра образуется не оксид металла, а сам металл (так как оксид термически неустойчив), получаем \eqref{chem1011_020101}.
Газ, образующийся при обработке серебра 35%-й азотной кислотой, — \(\ce{NO}\), получаем \eqref{chem1011_020102}:
\[\begin{gather} n(\ce{NO}) = \frac {2,24}{22,4} = 0,1\textrm{\, моль};\\ n(\ce{AgNO3}) = n(\ce{Ag}) = 3\cdot (\ce{NO}) = 3 \cdot 0,1 = 0,3\textrm{\, моль};\\ n (\ce{Ag2S}) = \frac 12 n (\ce{Ag}) = \frac {0,3}2 = 0,15\textrm{\, моль};\\ m (\ce{Ag2S}) = n \cdot M = 0,15\cdot 248 = 37,2\textrm{\, г.} \end{gather}\] По уравнению \eqref{chem1011_020102}: \[n (\ce{HNO3}) = 4 \cdot n (\ce{NO}) = 4 \cdot 0{,}1 = 0{,}4\textrm{\, моль.}\]
В исходном растворе: \[\begin{gather} n (\ce{HNO3})=\frac{90 \cdot 0,35}{63} = 0,5~\text{моль}~-~\text{в избытке;}\\ n (\ce{HNO3})_{\text{непрор.}} = 0,5 - 0,4 = 0,1\textrm{\, моль.} \end{gather}\] При добавлении к раствору, полученному растворением серебра в азотной кислоте, раствора иодида калия образуется иодид серебра: \[\begin{gather} \ce{AgNO3 + KI -> AgI v + KNO3};\\ n (\ce{KI}) = \frac{415 \cdot 0,15}{166} = 0,375~\text{моль}~-~\text{в избытке;}\\ n (\ce{AgI}) = n (\ce{AgNO3}) = 0,3\text{ моль};\\ m (\ce{AgI}) = n \cdot M = 0,3 \cdot 235 = 70,5\text{ г};\\ n(\ce{KI})_{\text{прореаг}} = n(\ce{AgNO3}) = 0,3\text{ моль};\\ n(\ce{KI})_{\text{непрореаг}} = 0,3 - 0,375 = 0,075\text{ моль.} \end{gather}\] Выделение бесцветного газа при добавлении раствора иодида калия объясняется его взаимодействием с азотной кислотой, оставшейся в растворе: \[\ce{6 KI + 8 HNO3 -> 3I2 v + 2 NO ^ + 6 KNO3 + 4 H2O}. \label{chem1011_020103}\] \[\begin{gather} n(\ce{KI})_{\text{прореаг}} = n(\ce{AgNO3}) = 0,3 \text{~моль};\\ n(\ce{KI})_{\text{непрореаг}}= 0,3 - 0,375 = 0,075 \text{~моль};\\ n(\ce{HNO3})_{\text{непрореаг}} = 0,5 - 0,4 = 0,1 \text{~моль.} \end{gather}\] В уравнении \eqref{chem1011_020103} реагенты провзаимодействовали полностью, т. о. в конечном растворе содержится только нитрат калия. \[\begin{gather} n (\ce{KNO3}) = 0,3 + 0,075 = 0,375\text{ моль};\\ m (\ce{KNO3}) = n\cdot M = 0,375\cdot 101 = 37,875\text{ г};\\ m (\text{р-ра}) = m (\ce{Ag}) + m (\text{р-ра} \ce{HNO3}) - m(\ce{NO})_{\text{по(\ref{chem1011_020102})} } + m (\text{р-ра} \ce{KI}) - m(\ce{AgI})-\\ - m(\ce{I2}) - m(\ce{NO})_{\text{по (\ref{chem1011_020103})}} = 0,3\cdot 108 + 90 + 415 - 70,5 - 254\cdot 0,0375 -\\ - 30\cdot (0,1+0,025) = 453,625\text{ г};\\ \omega(\ce{KNO3}) = \frac{37,875}{453,625} = 0,08349\text{ или }8,35 \%. \end{gather}\]
8,35.
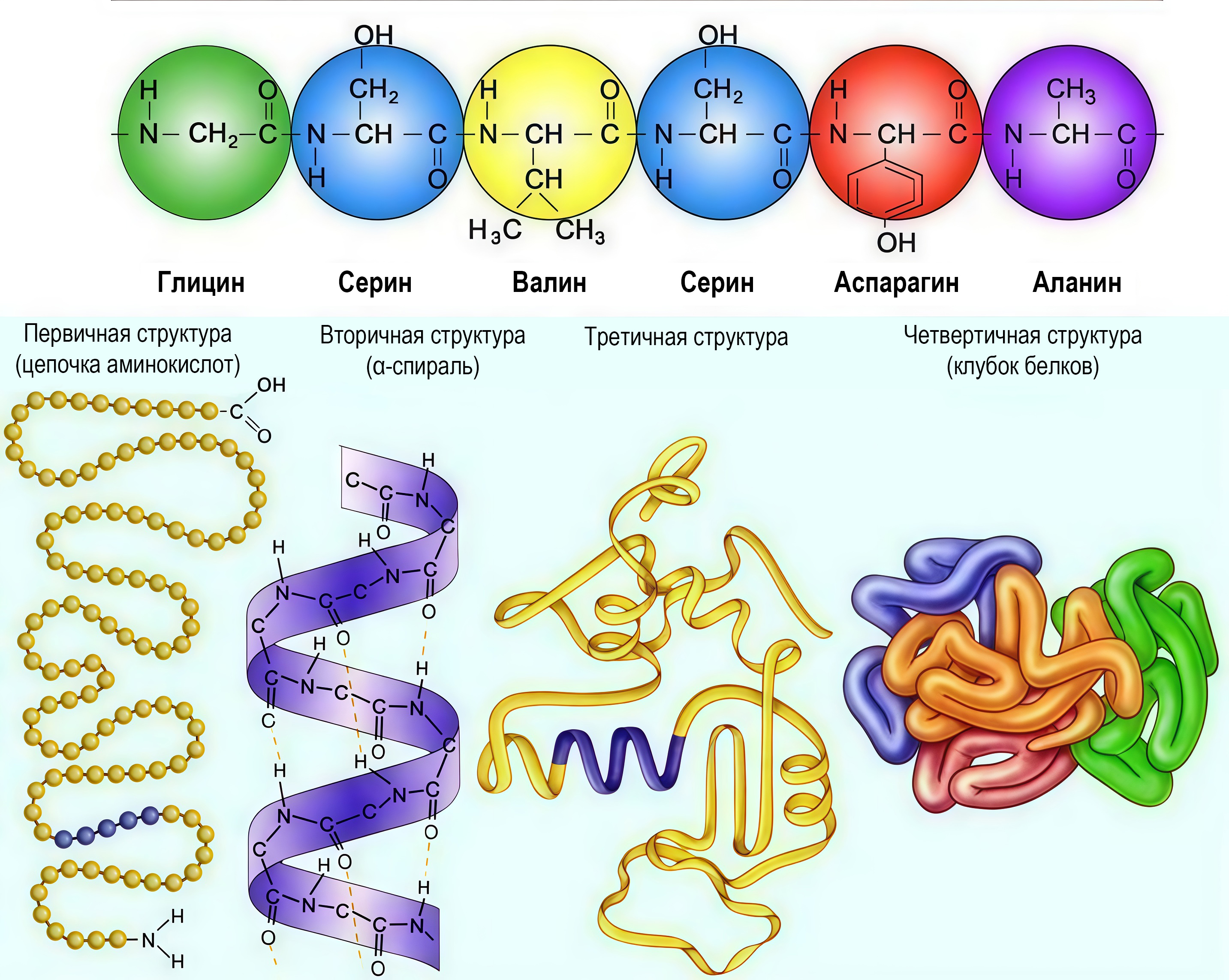
В живых организмах белки играют важнейшую роль среди макромолекул, обеспечивая множество жизненно важных функций. Основатель русской биохимической школы Александр Яковлевич Данилевский в 1888 году впервые высказал предположение о наличии в молекуле белка связи \(\ce{-NH-CO-}\), которая позднее получила название пептидной связи. В 1902 году немецкий химик Эмиль Фишер сформулировал полипептидную теорию строения белка, согласно которой белки — это гигантские полипептидные цепи, состоящие из \(\alpha\)-аминокислот. В настоящее время известны порядка 300 аминокислот, однако в образовании природных белков участвуют только 20 из них, которые называются белокобразующими.
Последовательность этих аминокислот определяет уникальные свойства каждого белка. Некоторые аминокислоты могут быть синтезированы в организме, в то время как другие являются незаменимыми и должны поступать с пищей. Содержание белка в растениях считается важным показателем качества сельскохозяйственной продукции. Высокое содержание белка указывает на питательную ценность растения и способность обеспечивать необходимые аминокислоты для организма человека и животных.
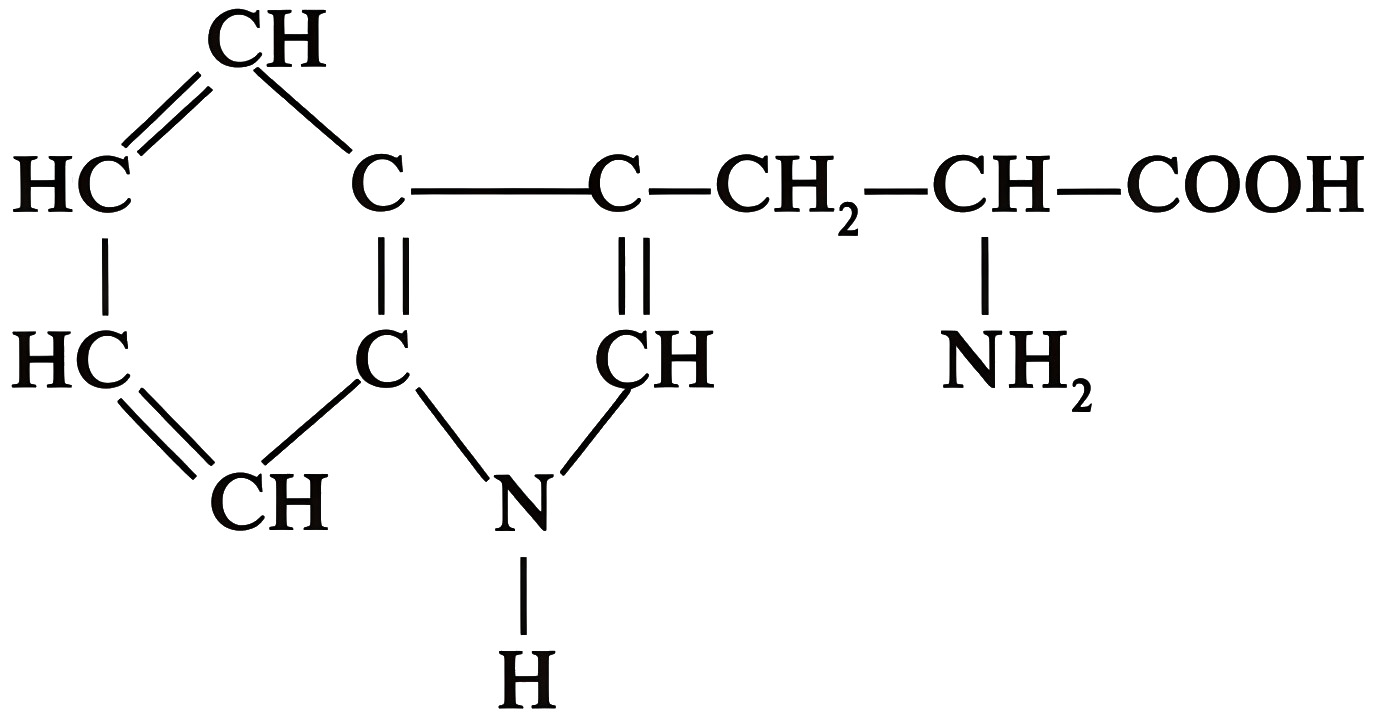
Некоторая белокобразующая аминокислота содержит 64,71% углерода, 5,88% водорода, 15,69% кислорода. Определите молекулярную формулу аминокислоты. Запишите ее в формате \(\ce{C1H2O3N4}\).
\[\begin{gather} \omega (\ce{N}) = 100 - 64,71 - 5,88 - 15,69 = 13,72 \%;\\ n (\ce{C}) : n (\ce{H}) : n (\ce{O}) : n (\ce{N}) = \frac{64,71}{12} : \frac{5,88}{1} : \frac{15,69}{16} : \frac{13,72}{14} =\\ = 5,3925 : 5,88 : 0,98 : 0,98 = 11 : 12 : 2 : 2. \end{gather}\] Молекулярная формула аминокислоты — \(\ce{C11H12O2N2}\).
\(\ce{C11H12O2N2}.\)
Некоторая белокобразующая аминокислота содержит 64,71% углерода, 5,88% водорода, 15,69 % кислорода. Запишите тривиальное название данной аминокислоты (строчными буквами).
\[\begin{gather} \omega (\ce{N}) = 100 - 64,71 - 5,88 - 15,69 = 13,72 \%;\\ n (\ce{C}) : n (\ce{H}) : n (\ce{O}) : n (\ce{N}) = \frac{64,71}{12} : \frac{5,88}{1} : \frac{15,69}{16} : \frac{13,72}{14} =\\ = 5,3925 : 5,88 : 0,98 : 0,98 = 11 : 12 : 2 : 2. \end{gather}\] Молекулярная формула аминокислоты — \(\ce{C11H12O2N2}\).
Это триптофан, ароматическая аминокислота, имеет структурную формулу, представленную на рис. 4.1.
Триптофан.
Среди перечисленных реакций выберите номер реакции, являющейся качественной и одновременно специфической для данной аминокислоты:
- нингидриновая,
- биуретовая,
- ксантопротеиновая,
- цистеиновая.
В ответе укажите только номер реакции.
3.
Рассмотрим такую систему: мембрана, по разные стороны от которой расположены растворы с разным содержанием растворенного вещества. Поры полупроницаемой мембраны пропускают молекулы растворителя, но не молекулы растворенного вещества. Из-за того, что концентрации растворов различны, растворитель (например, вода) начнет диффундировать (перетекать) из более разбавленного раствора в более концентрированный и разбавлять его до тех пор, пока концентрация не станет равной по обе стороны мембраны. Это явление называют осмосом.

Осмотическим давлением называют величину избыточного давления на раствор, отделенный от чистого растворителя полупроницаемой мембраной, при котором прекращается осмос, то есть диффузия растворителя через мембрану. Голландский химик Якоб Хендрик Вант-Гофф установил, что для разбавленных растворов осмотическое давление прямо пропорционально молярной концентрации частиц (молекул, ионов) растворенного вещества: \[\pi=CRT,\] где \(\pi\) — осмотическое давление, кПа; \(C\) — молярная концентрация частиц (молекул, ионов) растворенного вещества, моль/л; \(R\) — универсальная газовая постоянная, 8,314 Дж/(моль\(\cdot\)К); \(T\) — температура, К. Это открытие было отмечено первой Нобелевской премией по химии.
Мембраны всех живых клеток используют осмос для контроля поглощения необходимых веществ, поэтому он играет очень важную роль в медицине, биотехнологии и агротехнологии, особенно в гидропонике. Осмос помогает растениям расти и всасывать воду корневой системой — поскольку в клеточном соке концентрация солей и сахаров выше, чем в почвенном растворе. Это важно учитывать при внесении удобрений — если осмотическое давление почвенного раствора станет слишком большим, поступление воды в растение прекратится, и оно погибнет (например, как в засоленных почвах).
Рассчитайте осмотическое давление раствора удобрения (130 г мочевины в 5 л воды) при температуре 20 °C. Ответ приведите в килопаскалях (кПа) с точностью до целых.
Количество вещества мочевины: \[n(\ce{NH_2CONH_2})=\frac{(\ce{NH_2CONH_2})}{M}=\frac{130}{16\cdot 2+28}=2{,}2~\text{моль},\] соответственно молярная концентрация раствора \[C(\ce{NH_2CONH_2})=\frac{n(\ce{NH_2CONH_2})}V=\frac{2{,}2} 5=0{,}44\text{~моль/л.}\] Осмотическое давление \(\pi=CRT=0{,}44\cdot 8{,}314\cdot (273+20)=1072\) кПа.
1072. Диапазон 1069–1075.
В медицине при внутривенном введении используют изотонические растворы — растворы, осмотическое давление которых соответствует давлению плазмы крови — в такой среде вода не поступает в клетку и не выводится из клетки, что предотвращает от повреждения эритроциты. Изотонический раствор хлорида натрия применяют как дезинтоксикационное средство, для коррекции состояния систем организма в случае обезвоживания и как растворитель других лекарственных препаратов.

Рассчитайте массовую долю хлорида натрия в разбавленном растворе, осмотическое давление которого при температуре 37 °С составляет 749 кПа (плотность примите \(\rho=1000\) г/л). Ответ приведите в процентах с точностью до сотых.
Рассчитаем концентрацию частиц в растворе, исходя из величины осмотического давления: \[C=\frac{\pi}{RT}=\frac {749}{8{,}314\cdot (273+37)}=0{,}29\text{~моль/л.}\]
Хлорид натрия — электролит, диссоциирующий в растворе на ионы \(\ce{Na^+}\) и \(\ce{Cl^-}\). Поскольку точная степень диссоциации в информации не указана, а раствор является разбавленным, ее можно принять равной 100%.
Тогда концентрация хлорида натрия составляет: \[C(\ce{NaCl})=\frac C2=\frac {0{,}29}2=0{,}145\text{~моль/л,}\] тогда масса соли в 1 л раствора \[m(\ce{NaCl})=n(\ce{NaCl})\cdot M=C(\ce{NaCl})\cdot V\cdot M=0{,}145\cdot 1\cdot (23+35{,}5)=8{,}48\text{~г}.\]
Массовая доля в растворе: \[\omega=\frac{m\ce{NaCl}}{m_\text{р-ра}}=\frac{8{,}48}{1\cdot 1000}\cdot 100=0{,}85\%.\]
0,85. Диапазон 0,81–0,89.
Измерение осмотического давления является одним из распространенных методов определения молекулярной массы полимера, влияющей на его свойства. Например, полистирол с высокой молекулярной массой обладает повышенной жесткостью и более высокой температурой плавления по сравнению с полистиролом с низкой молекулярной массой. Более того, с увеличением молекулярной массы полистирола увеличивается и его вязкость, что приводит к трудностям в переработке. Мембранный осмометр основан на измерении разности давлений — например, по разности высот в капиллярах раствора и растворителя, поскольку гидростатическое давление уравновешивает осмотическое.
Установите молекулярную массу полистирола, если разность высот жидкости в осмометре для его раствора в толуоле, содержащего 3,5 г в 500 мл раствора, составляет 2,46 см при 20 °С. Ответ выразите в килограммах на моль (кг/моль) с точностью до десятых. Плотность толуола и раствора 867 \(\text{кг/м}^3\).
Гидростатическое давление столба жидкости уравновешивает осмотическое давление, для удобства расчета используем единицы измерения системы СИ: \[\pi=CRT=\rho g \Delta h=867\cdot 9{,}8\cdot (2{,}46\cdot 10^{-2})=209\text{~Па.}\]
Молярная концентрация раствора полимера составляет \[C=\frac {\pi}{RT}=\frac {209}{8{,}314\cdot (273+20)}={0{,}0858}\text{~моль/м}^3,\] то есть количество вещества полимера \[n=CV={0{,}0858}\cdot \frac{0{,}5}{1000}={0{,}0429}\text{~ммоль.}\] Тогда молекулярная масса \[M=\frac mn=\frac {3{,}5}{{0{,}0429}}=81{,}6\text{~кг/моль.}\]
81,6. Диапазон 79,8–82,2.
Ортофосфорная кислота используется в самых разных областях — в производстве удобрений и чистящих средств, для деревообработки и очистки металла от ржавчины, в стоматологии для реставрации зубов и в ювелирном деле при пайке. Также она зарегистрирована в качестве пищевой добавки E338, которую можно встретить в составе мармеладов, сиропов и напитков, хлебобулочных изделий, сыров и плавленых сырков.
Пищевую фосфорную кислоту производят термическим способом, позволяющим получить концентрированный продукт с меньшим содержанием примесей — для этого расплавленный белый фосфор сжигают в воздухе и подвергают образующийся оксид фосфора (V) гидратации.
При нормальных условиях рассчитайте объем воздуха, который необходимо подавать в башню (камеру сжигания) для сжигания фосфора в 1 ч, если известно, что расход образующегося в башне 75%-го раствора фосфорной кислоты составляет 4000 кг/ч. Ответ приведите в кубометрах с точностью до целых. Учтите, что для предотвращения образования оксида фосфора (III) в башню подают двукратный избыток воздуха по сравнению с расчетным количеством.
Запишем уравнения происходящих реакций: \[\begin{gather} \ce{P4 + 5O2 -> P4O10};\\ \ce{P4O10 + 6H2O -> 4H3PO4}. \end{gather}\]
Масса фосфорной кислоты: \[m(\ce{H_3PO_4})=m_\text{р-ра}\omega_{\ce{H_3PO_4}}=4000\cdot 0{,}75=3000 \text{~кг/ч.}\]
Количество вещества фосфорной кислоты: \[n(\ce{H_3PO_4})=\frac{m(\ce{H_3PO_4})}{M}=\frac{3000}{3+31+16\cdot 4}=30{,}61 \text{~кмоль/ч},\] что соответствует расчетному количеству вещества кислорода \[\begin{gather} n_\text{теор}(\ce{O_2})=\frac 54n(\ce{H_3PO_4})=38,26\text{~кмоль/ч};\\ n_\text{практ}(\ce{O2})=2n_\text{теор}(\ce{O2})=2\cdot 38,26 =76,52 \text{~кмоль/ч}. \end{gather}\]
Объем кислорода \[V(\ce{O_2})=n_\text{практ}(\ce{O2})V_0=76{,}52\cdot 1000\cdot 22{,}4=1714160\text{~л,}\] объем воздуха \[V_\text{возд}=\frac {V(\ce{O2})}{\chi(\ce{O2})}=\frac {1714160}{0{,}21\cdot 1000}=8163 \text{~м}^3.\]
8163. Диапазон 7700–8600.
Использование теплоты, выделяющейся при сгорании фосфора, позволяет значительно увеличить энергоэффективность проведения процесса. При стандартных условиях рассчитайте теплоту, которая выделяется в ходе проходящих реакций при образовании указанного в подзадаче № 1 количества фосфорной кислоты. Используйте данные таблицы, ответ выразите в мегаджоулях (мДж) с точностью до целых.
| Вещество | \(\ce{P4O10}\)\(_\text{(тв)}\) | \(\ce{H3PO4}\)\(_\text{(ж)}\) | \(\ce{H2O}\)\(_\text{(ж)}\) |
|---|---|---|---|
| Теплота образования, кДж/моль | 2984,03 | 1266,90 | 285,83 |
В соответствии со следствием из закона Г. И. Гесса теплоту каждой из протекающей реакции можно выразить как разность между суммами теплот образования продуктов и реагентов с учетом стехиометрических коэффициентов: \[\begin{gather} \Delta_rQ=\Sigma n_i Q_f(\text{прод})-\Sigma n_j Q_f(\text{реаг});\\ \Delta_{r1}Q=Q_f(\ce{P_4 O_{10(\text{тв})}})-Q_f(\ce{P_{4(\text{тв})}})-5Q_f(\ce{O_{2(\text{г})}});\\ \Delta_{r2}Q=4Q_f(\ce{H_3PO_{4(\text{ж})}})-6Q_f(\ce{H_2 O_{(\text{ж})}})-Q_f(\ce{P_4 O_{10 (\text{тв})}}). \end{gather}\] С учетом того, что теплоты образования простых веществ равны нулю, получим: \[\begin{gather} \Delta_{r1}Q=2984,03\text{~кДж/моль};\\ \Delta_{r2}Q=4\cdot 1266,90-6\cdot 285,83-2984,03=368,59\text{~кДж/моль.} \end{gather}\]
В расчете на 4 моль фосфорной кислоты \[Q_R=\Delta_{r1}Q+\Delta_{r2}Q=3352{,62}~\text{кДж/моль}.\]
Тогда \[Q=Q_R\cdot \displaystyle\frac{n(\ce{H_3PO_4})}4=3352{,62}\cdot \displaystyle\frac{30{,}61}4=25658~\text{МДж}.\]
25658. Диапазон 25620–25700.
В качестве пищевой добавки ортофосфорная кислота выступает регулятором кислотности и консервантом: кислая среда препятствует размножению микроорганизмов и порче продукта. Именно наличие фосфорной кислоты в составе обуславливает способность газированных напитков растворять ржавчину и очищать бытовые поверхности, о которой снято много интернет-роликов. Впрочем, имеются сведения о стимулировании фосфорной кислотой вымывания кальция из организма и ее негативном влиянии на зубную эмаль при чрезмерном употреблении.

Рассчитайте \(pH\) с точностью до десятых 1,25 моль/л раствора фосфорной кислоты, если известно, что константа диссоциации кислоты по первой ступени составляет \(7{,}52\cdot 10^{-3}\), а диссоциацией по второй и третьей ступени можно пренебречь.
Запишем уравнение диссоциации фосфорной кислоты по первой ступени: \[\ce{H3PO4 <--> H+ + H2PO4-}.\]
Выражение для константы диссоциации: \[K_I=\frac {[\ce{H2PO4-}][\ce{H+}]}{[\ce{H3PO4}]},\] где в квадратных скобках указаны равновесные концентрации. Тогда \[\begin{gather} [ \ce{H2PO4-} ]=[\ce{H+}], [\ce{H3PO4}]=\ce{C0}-[\ce{H+}];\\ K_I=\frac{[\ce{H+}]^2}{\ce{C0}-[\ce{H+}]}=7,52\cdot 10^{-3}. \end{gather}\] Решение уравнения при \(\ce{C0}=1{,}25\) моль/л позволяет найти \[[\ce{H+}]=0{,}093\text{~моль/л,}\] откуда \(pH=-lg ([\ce{H+}])\approx 1.\)
1.
Этот выдающийся ученый начинал как математик и физик: степень кандидата он получил в Казанском университете за сочинение о законах движениях планет и других небесных тел. Химией он стал заниматься по настоянию своего наставника и ректора университета Н. Н. Лобачевского. Так зарождалась Казанская химическая школа.
Будучи мастером органического синтеза, этот исследователь впервые осуществил реакцию бензоиновой конденсации и бензидиновую перегруппировку, получил «летучее горчичное масло» и разработал метод замещения атомов галогенов в органических соединениях водородом. Примечательно, что этот ученый был учителем химии А. Нобеля и даже внес свой вклад в применение нитроглицерина в качестве взрывчатого вещества. Однако мировую известность ему принесло открытие реакции превращения ароматических нитросоединений в аминосоединения, впоследствии названной его именем. Эта реакция позволила получить «бензидам», известный нам как анилин, и впоследствии положила начало промышленному синтезу многочисленных продуктов его превращений. В наши дни из анилина получают красители, лекарственные и взрывчатые вещества, а также полиуретаны. Научные заслуги признаны химиками всего мира. Знаменитый немецкий ученый А. В. Гофман скажет: «Если бы ... не сделал ничего более, кроме превращения нитробензола в анилин, то и тогда его имя осталось бы записанным золотыми буквами в истории химии».
Помимо науки этот академик активно занимался организационной и общественной работой, способствуя развитию органической химии, был одним из организаторов Русского химического общества и первым его президентом. Среди его учеников А. М. Бутлеров, Н. Н. Бекетов, А. П. Бородин, А. Н. Энгельгардт, Л. Н. Шишков. Впоследствии Бутлеров отметит: «Имя ... будут всегда чтить те, которым дороги и близки к сердцу успехи и величие науки в России».
Назовите этого ученого:
- Александр Павлович Виноградов;
- Александр Михайлович Зайцев;
- Николай Дмитриевич Зелинский;
- Карл Карлович Клаус;
- Николай Александрович Меншуткин;
- Сергей Васильевич Лебедев;
- Николай Николаевич Зинин;
- Владимир Васильевич Марковников;
- Дмитрий Иванович Менделеев;
- Алексей Евграфович Фаворский.
G.
В стремительно развивающемся мире городского сельского хозяйства, известного как сити-фермерство, вода играет роль не просто ресурса, а ключевого фактора, определяющего успешность выращивания. Однако не только количество воды, но и ее качество напрямую влияет на рост и развитие растений. Это особенно актуально для сити-фермерства, где растения выращиваются в замкнутых системах с ограниченным объемом воды, что делает качество воды первостепенным фактором. Одной из важнейших характеристик качества воды является ее жесткость, которая определяется содержанием в ней солей кальция и магния.
Высокая жесткость воды может создавать ряд проблем при выращивании растений, как в традиционных, так и в гидропонных системах, поскольку приводит к повышению pH раствора. Это делает недоступными для растения многие важные питательные вещества, например, железо, марганец и цинк. В результате растение испытывает дефицит микроэлементов, что проявляется в замедленном росте, хлорозе — пожелтении листьев, а также повышенной уязвимости к болезням. Информацию о жесткости воды учитывают при приготовлении питательных растворов, так как необходимо знать точную концентрацию избыточных минералов, присутствующих в используемой воде. Кроме того, присутствие солей кальция и магния увеличивает риск отложения нерастворимых солей, который приводит к засорению и блокировке оросительного оборудования.
Для устранения временной (гидрокарбонатной) жесткости 1 л воды, содержащей катионы кальция и магния, прокипятили в течение длительного времени. При этом образовался осадок массой 14,2 мг и выделился углекислый газ объемом 3,36 мл (н. у.).Определите массу ионов кальция в миллиграммах (мг), обуславливающих временную жесткость воды. Ответ округлите до целых.
При нагревании гидрокарбонаты разлагаются: \[\ce{Ca(HCO3)2}\ce{->[t]}\ce{CaCO3 + CO2 + H2O}; \label{ch89_030101}\] \[\ce{Mg(HCO3)2} \ce{->[t]} \ce{MgCO3 + CO2 + H2O}; \label{ch89_030102}\] \[n(\ce{CO2}) = \frac{3{,}36\text{ мл}}{22{,}4\text{ л/моль}} = 0{,}15\text{ ммоль.}\]
По уравнению реакции \eqref{ch89_030101} \(n(\ce{Ca(HCO3)2}) = n(\ce{CaCO3}) = n(\ce{CO2})\).
По уравнению реакции \eqref{ch89_030102} \(n(\ce{Mg (HCO3)2}) = n(\ce{MgCO3}) = n(\ce{CO2})\).
Пусть \(n(\ce{CaCO3}) = x\) ммоль, \(n(\ce{MgCO3}) = y\) ммоль, тогда: \[\left\{\begin{aligned} &100 x + 84y = 14{,}2, \\ &x + y = 0{,}15. \end{aligned}\right.\] \(x=0{,}1\) ммоль, \(y = 0{,}05\) ммоль. \[m (\ce{Ca^{2+}} ) = n \cdot M = 0{,}1 \cdot 40 = 4\text{ мг.}\]
4.
Определите массу ионов магния в миллиграммах (мг), обуславливающих временную жесткость воды. Ответ округлите до десятых.
Продолжая решения предыдущей подзадачи, получим: \[m (\ce{Mg^{2+}} )= n \cdot M = 0{,}05 \cdot 24 = 1{,}2\text{ мг.}\]
1,2. Диапазон 1,2–1,4.
В соответствии с содержанием ионов кальция и магния (в миллиграммах), определите тип исследуемой воды (при условии, что жесткость обусловлена только гидрокарбонатами) по следующей шкале:
- до 3 мг/л — мягкая;
- 3–6 мг/л — средней жесткости;
- от 6 мг/л — жесткая.
В ответе приведите цифру, соответствующую типу воды.
Суммарная масса катионов кальция и магния составляет \(4 + 1{,}2 = 5{,}2\) мг, что обуславливает среднюю жесткость воды.
2.
Раствор для гидропоники представляет собой специальную жидкость, предназначенную для полноценного питания растений, в которую входят минеральные соли и другие необходимые компоненты. В традиционном земледелии растения получают все необходимые для роста вещества из почвы, но гидропоника позволяет обходиться без нее, обеспечивая растения питательными веществами непосредственно через корневую систему в водной среде. Это особенно полезно в условиях ограниченного пространства или неблагоприятных почвенных условий. При создании питательного раствора для гидропоники важно учитывать специфику каждой культуры, так как разные растения требуют различных соотношений макро- и микроэлементов. Для достижения оптимального результата в гидропонике необходимо не только правильно подбирать компоненты, но и следить за их концентрацией. Неправильные пропорции могут привести к дефициту или избытку полезных веществ, что негативно скажется на здоровье растений. На протяжении многих лет различные ученые и агрономы разработали множество формул для питательных растворов, адаптированных для разных систем гидропоники. Например, известные формулы, такие как формула Туманова, Кнопа, Кидсона, Пюрдье, Шварца, Пильгрима и другие, каждая из которых имеет свои особенности и преимущества. Эти формулы учитывают не только потребности конкретных культур, но и условия их выращивания, такие как температура, влажность и освещение.
Таким образом, раствор для гидропоники — это не просто смесь, а целая наука, требующая глубоких знаний о потребностях растений и условиях их роста.
Один из растворов для гидропоники — раствор Кнопа — предполагает следующее содержание солей в одном литре раствора:
- нитрата кальция — 1 г;
- нитрата калия — 0,25 г;
- сульфата магния — 0,25 г;
- дигидрофосфата калия — 0,25 г;
- хлорида калия — 0,125 г.
Рассчитайте массовые доли элементов (в процентах) в полученном растворе. Плотность раствора примите за 1 г/мл.
Вычислите массовую долю элемента кальция в растворе (в процентах). Ответ округлите до тысячных.
Для определения массовой доли кальция определим количество 1 г нитрата кальция, а затем массу элемента кальция: \[\begin{gather} n (\ce{Ca(NO3)2}) =\frac 1{164} =0,0060975\text{~моль }\approx 0,0061\text{~моль};\\ m (\ce{Ca}) = n \cdot M = 0,0060975 \cdot 40= 0,2439\text{~г};\\ m (\text{раствора}) = V \cdot \rho = 1000\text{ мл }\cdot 1\text{ г/мл }= 1000\text{~г};\\ \omega (\ce{Ca}) = \frac{0,2439\cdot 100}{1000} = 0,02439 \% \approx 0,024\%. \end{gather}\]
\(0{,}024\pm 0{,}001.\)
Вычислите массовую долю элемента калия в растворе (в процентах). Ответ округлите до тысячных.
Для определения массовой доли калия необходимо учитывать, что этот элемент содержится в нитрате, дигидрофосфате и хлориде. Определим количество веществ, а затем суммарную массу элемента калия: \[\begin{gather} n (\ce{KNO3}) = \frac{0,25}{101} = 0,0024752\text{~моль} \approx 0,0025\text{~моль};\\ n (\ce{KH2PO4}) = \frac{0,25}{136} = 0,0018382\text{~моль} \approx 0,0018\text{~моль};\\ n (\ce{KCl}) = \frac{0,125}{74,5} = 0,0016778\text{~моль} \approx 0,0017\text{~моль};\\ n (\ce{K}) = 0,0024752 + 0,0018382 + 0,0016778 = 0,0059912 \approx 0,006\text{~моль} \end{gather}\] или, с учетом округления: \[\begin{gather} n (\ce{K}) = 0,0025 + 0,0018 + 0,0017 = 0,006\text{~моль};\\ m (\ce{K}) = n \cdot M = 0,006 \cdot 39= 0,234~\text{г};\\ m (\text{раствора}) = V \cdot \rho = 1000~\text{мл}~\cdot 1\text{~г/мл} = 1000 ~\text{г};\\ \omega (\ce{K}) = \frac{0,234\cdot 100}{1000} = 0,0234 \% \approx 0,023 \%. \end{gather}\]
\(0{,}023\pm 0{,}001.\)
Вычислите массовую долю элемента магния в растворе (в процентах). Ответ округлите до тысячных.
Для определения массовой доли магния определим количество сульфата магния, а затем массу элемента магния: \[\begin{gather} n (\ce{MgSO4}) = \frac{0,25}{120} = 0,0020833\text{~моль}\approx 0,0021\text{~моль};\\ m (\ce{Mg}) = n \cdot M = 0,0020833 \cdot 24= 0,0499992\approx 0,05\text{~г};\\ m (\text{раствора}) = V \cdot \rho = 1000\text{~мл} \cdot 1\text{~г/мл} = 1000\text{~г};\\ \omega(\ce{Mg}) = \frac{0,05\cdot 100}{1000} = 0,005\%. \end{gather}\]
\(0{,}005\pm 0{,}001.\)
Вычислите массовую долю элемента азота в растворе (в процентах). Ответ округлите до тысячных.
Для определения массовой доли азота необходимо учитывать, что этот элемент содержится в нитратах кальция и калия. Определим количество веществ, а затем суммарную массу элемента азота: \[\begin{gather} n (\ce{Ca(NO3)2}) =\frac 1{164} = 0,0060975\text{~моль}\approx 0,0061\text{~моль};\\ n (\ce{KNO3}) = \frac {0,25}{101} = 0,0024752\text{~моль}\approx 0,0025\text{~моль};\\ n (\ce{N}) = 0,0060975 \cdot 2 + 0,0024752 = 0,0146702\approx 0,0147\text{~моль} \end{gather}\] или, с учетом округления: \[\begin{gather} n (\ce{N})= = 0,0061 \cdot 2 + 0,0025 = 0,0147\text{~моль};\\ m (\ce{N}) = n \cdot M = 0,0147 \cdot 14= 0,2058\text{~г};\\ m (\text{раствора}) = V \cdot \rho = 1000\text{~мл} \cdot 1\text{~г/мл} = 1000\text{~г};\\ \omega(\ce{N}) = \frac{0,2058\cdot 100}{1000} = 0,02058 \%\approx 0,021 \%. \end{gather}\]
\(0{,}021\pm 0{,}001.\)
Вычислите массовую долю элемента фосфора в растворе (в процентах). Ответ округлите до тысячных.
Для определения массовой доли фосфора определим дигидрофосфата калия, а затем массу элемента фосфора: \[\begin{gather} n (\ce{KH2PO4}) = \frac{0,25}{136} = 0,0018382\text{~моль} \approx 0,0018\text{~моль};\\ m (\ce{P}) = n \cdot M = 0,0018382 \cdot 31= 0,0569842\approx 0,057\text{~г};\\ m (\text{раствора}) = V \cdot \rho = 1000\text{~мл} \cdot \text{1~г/мл} = 1000\text{~г};\\ \omega(\ce{P}) = \frac{0,057\cdot 100}{1000} = 0,0057 \% \approx 0,006\%. \end{gather}\]
\(0{,}006 \pm 0{,}001.\)
Рассмотрим такую систему: мембрана, по разные стороны от которой расположены растворы с разным содержанием растворенного вещества.

Поры полупроницаемой мембраны пропускают молекулы растворителя, но не молекулы растворенного вещества. Из-за того, что концентрации растворов различны, растворитель (например, вода) начнет диффундировать (перетекать) из более разбавленного раствора в более концентрированный и разбавлять его до тех пор, пока концентрация не станет равной по обе стороны мембраны. Это явление называют осмосом.
Мембраны всех живых клеток используют осмос для контроля поглощения необходимых веществ, поэтому он играет очень важную роль в медицине, биотехнологии и агротехнологии, особенно в гидропонике. Но осмос значим и в быту: с древности с его помощью консервировали пищу — в соленой среде вода вытекает из клеток, что приводит к сморщиванию (весь материал внутри клетки отслаивается от клеточной стенки) и потере жизнедеятельности микроорганизмов (этот процесс называют плазмолизом).
Рассчитайте массу поваренной соли, необходимую для приготовления 1,75 л рассола для засаливания огурцов (плотность \(\rho=1041\) г/л), массовая доля соли в котором составляет 6,0%. Ответ приведите в граммах с точностью до десятых.
Рассчитаем массу раствора \(m_{\text{р-ра}}=\rho V=1041\cdot 1{,}75=1821{,}8\) г.
Масса соли составляет: \[m(\ce{NaCl})=m_{\text{р-ра}}\omega (\ce{NaCl})=1821{,8}\cdot 0{,}06=109{,}3\text{~г.}\]
109,3. Диапазон 109–110.
Осмотическим давлением называют величину избыточного давления на раствор, отделенный от чистого растворителя полупроницаемой мембраной, при котором прекращается осмос, то есть диффузия растворителя через мембрану. Голландский химик Якоб Хендрик Вант-Гофф установил, что для разбавленных растворов осмотическое давление прямо пропорционально молярной концентрации частиц (молекул, ионов) растворенного вещества: \[\pi=CRT,\] где \(\pi\) — осмотическое давление, кПа; \(C\) — молярная концентрация частиц (молекул, ионов) растворенного вещества, моль/л; \(R\) — универсальная газовая постоянная, 8,314 Дж/(моль\(\cdot\)К); \(T\) — температура, К. Это открытие было отмечено первой Нобелевской премией по химии.
В терапевтических целях иногда используют гипертонические растворы — растворы, осмотическое давление которых превышает давление плазмы крови — в такой среде вода выходит через мембрану из клетки, и клетка сжимается. Гипертонический 10%-й раствор глюкозы вводят для регидратации в случае потери жидкости, для разведения и растворения вводимых парентерально лекарственных препаратов, а также в качестве источника углеводов.

Рассчитаем массу 1 л раствора: \[m_{\text{р-ра}}=\rho V=1037\cdot 1{,}0=1037\text{~г.}\]
Масса глюкозы составляет: \[m(\ce{C6H12O6})=m_{\text{р-ра}}\omega (\ce{C6H12O6})=1037\cdot 0{,}10=103{,}7\text{~г.}\]
Количество вещества глюкозы: \[n(\ce{C6H12O6})=\frac{m(\ce{C6H12O6})}{M(\ce{C6H12O6})}=\frac{103{,}7}{6\cdot 12+12+6\cdot 16}=0{,}574\text{~моль,}\] соответственно молярная концентрация раствора
\[C(\ce{C6H12O6})=\frac{n(\ce{C6H12O6})}V=\frac{0{,}574}1=0{,}574\text{~моль/л.}\]
Осмотическое давление \(\pi =CRT=0{,}574\cdot 8{,}314\cdot (273+25)=1423{,2}\) кПа.
1423. Диапазон 1403–1443.
Полимер поливиниловый спирт является дезинтоксикатором: его водные растворы вводят внутривенно для связывания токсинов из-за способности связывать в комплексы вещества различной природы. Это также способствует улучшению реологических свойств крови. Осмотическое давление раствора полимера мало, поэтому в состав также включают неорганические соли, чтобы сделать раствор препарата изотоничным крови.
Установите молярную массу поливинилового спирта в граммах на моль (г/моль) с точностью до целых, если осмотическое давление раствора, содержащего 6,00 г полимера в 200,0 мл раствора, составляет 6,873 кПа при 37 °С.
Молярная концентрация раствора полимера: \[C=\frac{\pi}{RT}=\frac{6{,}873}{8{,}314\cdot (273+37)}=2{,}67\text{~ммоль/л},\] то есть количество вещества полимера: \[n=CV=2{,}67\cdot 0{,}2=0{,}534\text{~ммоль.}\]
Тогда молярная масса \[M=\frac mn=\frac{6{,}00}{0{,}534}\cdot 1000=11236\text{~кг/моль.}\]
11236. Диапазон 11036–11436.
Ортофосфорная кислота используется в самых разных областях — в производстве удобрений и чистящих средств, для деревообработки и очистки металла от ржавчины, в стоматологии для реставрации зубов и в ювелирном деле при пайке. Также она зарегистрирована в качестве пищевой добавки E338, которую можно встретить в составе мармеладов, сиропов и напитков, хлебобулочных изделий, сыров и плавленых сырков.
Пищевую фосфорную кислоту производят термическим способом, позволяющим получить концентрированный продукт с меньшим содержанием примесей — для этого расплавленный белый фосфор сжигают в воздухе и подвергают образующийся оксид фосфора (V) гидратации.
Этот процесс упрощенно можно описать следующими реакциями: \[\begin{gather} \ce{4P + 5O2 -> 2P2O5};\\ \ce{P2O5 + 3H2O -> 2H3PO4}. \end{gather}\]
При нормальных условиях рассчитайте объем воздуха, который необходимо подавать в башню (камеру сжигания) в 1 ч для сжигания фосфора, содержащего 1,2% негорючих примесей (расход фосфора 3750 кг/ч). Ответ выразите в кубических метрах с точностью до целых. Учтите, что для предотвращения образования оксида фосфора (III) в башню подают двукратный избыток воздуха по сравнению с расчетным количеством.
В расчете на один час количество вещества фосфора составляет \[n(P)=\frac mM=\frac{3750\cdot 0{,}988}{31}=119{,}52\text{~кмоль},\] тогда \[\begin{gather} n_\text{теор}(\ce{O_2})=\frac 54n(\ce{P})=149,40\text{~кмоль};\\ n_\text{практ}(\ce{O_2})=2n_\text{теор}(\ce{O_2})=2\cdot 149,40=298,8\text{~кмоль}. \end{gather}\] Объем кислорода: \[V(\ce{O_2})=n_\text{практ}(\ce{O_2})V_0=298{,}8\cdot 1000\cdot 22{,}4=6 693 120\text{~л,}\] объем воздуха \[V_\text{возд}=\frac{V(\ce{O_2})}{\chi(\ce{O_2})}=\frac {6693120}{0{,}21\cdot 1000}=31872\text{~м}^3.\]
31872. Диапазон 29640–34100.
Рассчитайте массу 80%-го раствора фосфорной кислоты, образующегося в башне, в килограммах в час (кг/ч) с точностью до целых.
Количество вещества фосфорной кислоты соответствует количеству фосфора \(n(\ce{H_3PO_4})=n(P)=119{,}52\) кмоль/ч, тогда: \[\begin{gather} m(\ce{H_3PO_4})=n(\ce{H_3PO_4})M=119,52\cdot (3+31+16\cdot 4)=11713 \text{~кг/ч};\\ m_\text{р-ра}(\ce{H_3PO_4})=\frac{m(\ce{H_3PO_4})}{\omega(\ce{H_3PO_4})}=\frac{11713}{0,80}=14641\text{~кг/ч.} \end{gather}\]
14641. Диапазон 14637–14645.
Использование теплоты, выделяющейся при сгорании фосфора, позволяет значительно увеличить энергоэффективность проведения процесса. Рассчитайте массу угля, содержащего 3% негорючих примесей, которую удастся сэкономить при полном использовании тепла сгорания фосфора. Ответ выразите в килограммах в час (кг/ч) с точностью до целых. Теплота сгорания белого фосфора в указанных условиях составляет 1764 кДж/моль, углерода 394 кДж/моль.
Количество теплоты, выделяющейся при сгорании фосфора, составляет \[Q=Q_Pn(P)=119{,}52\cdot 1764=210833~\text{МДж/ч},\] тогда \[\begin{gather} n(C)=\frac Q{Q_C}=\frac{210833\cdot 1000}{394}=535110\text{~моль/ч};\\ m(C)=n(C)M=535110\cdot 12=6421\text{~кг/ч};\\ m_\text{уголь}=\frac{m(C)}{\omega(C)}=\frac{6421}{0,90}=6620\text{~кг/ч.} \end{gather}\]
6620. Диапазон 6616–6624.
В качестве пищевой добавки ортофосфорная кислота выступает регулятором кислотности и консервантом: кислая среда препятствует размножению микроорганизмов и порче продукта. Именно наличие фосфорной кислоты в составе обуславливает способность газированных напитков растворять ржавчину и очищать бытовые поверхности, о которой снято много интернет-роликов.
Впрочем, имеются сведения о стимулировании фосфорной кислотой вымывания кальция из организма и ее негативном влиянии на зубную эмаль при чрезмерном употреблении.

Рассчитайте концентрацию ионов водорода в миллимоль на литр (ммоль/л) с точностью до десятых в 0,015 моль/л растворе фосфорной кислоты, если известно, что степень диссоциации кислоты по первой ступени составляет 50%, а диссоциацией по второй и третьей ступени можно пренебречь.
Запишем уравнение диссоциации фосфорной кислоты по первой ступени: \[\ce{H3PO4 <--> H+ + H2PO4-}.\]
Степень диссоциации представляет собой отношение количества вещества, распавшегося на ионы, к общему количеству растворенного вещества: \[\alpha_I=\frac{n(\ce{H_2PO_4^-})}{n_0(\ce{H_3PO_4}) }.\]
В расчете на 1 л раствора \(n_0(\ce{H_3PO_4})=CV=0{,}015\cdot 1=0{,}015\) моль, \[\begin{gather} n(\ce{H^+})=n(\ce{H_2PO_4^-})=\alpha_In_0(\ce{H_3PO_4})=0,50\cdot 0,015=\\ =0,0075\text{~моль} =7,5\text{~ммоль.} \end{gather}\]
7,5.
В стенах Казанского университета, где начинал свой путь будущий ученый, царила атмосфера, далекая от современного представления о химической лаборатории. Два рабочих стола, калильные печи, одна большая печь и песчаная баня без тяги — вот и весь скромный арсенал для проведения экспериментов. Опыты, требующие вытяжной вентиляции, проводились прямо на улице, независимо от времени года. Холодная зима или палящее солнце — наука не знала границ. В 1853 году отец ученого, желая обеспечить сыну более стабильное будущее, уговаривал его сменить направление деятельности и отказал во всяческой материальной поддержке. Но, вопреки всем уговорам, юноша, движимый неугасимой жаждой познания, твердо решил посвятить себя науке. В 1844 году он поступил в Петербургский университет, но уже через три года перешел в Казанский, где стал учеником знаменитого российского химика-органика Николая Николаевича Зинина. Казалось бы, естественным продолжением было бы изучение органической химии, следуя по стопам своего учителя. Однако молодой ученый, не ограничиваясь рамками одного направления, увлекся физической химией, тогда еще только формирующейся областью знания. И хотя немцы утверждают, что приоритет в развитии физической химии принадлежит Вильгельму Оствальду, наш ученый уже в 1865 году, когда Оствальд был еще ребенком, читал студентам систематический курс по этой дисциплине.
Важным фактором, способствовавшим его успехам, была не только страсть к науке, но и способность использовать подручные средства для достижения поставленных задач. Так, исследуя явление алюминотермии, он прибегнул к изогнутому ружейному стволу в качестве реакционного сосуда. Ученый также изучал восстановительные способности других металлов, что позволило ему разработать «вытеснительный ряд металлов». Этот ряд, составленный по возрастанию активности металлов, стал неотъемлемой частью химии, помогая прогнозировать и анализировать химические реакции.
По мнению И. А. Каблукова, имя этого ученого «будет стоять в истории науки рядом с именами Д. И. Менделеева и А. М. Бутлерова и будет занесено золотыми буквами в историю науки в России».
Назовите этого ученого:
- Федор Федорович Бейльштейн;
- Николай Николаевич Бекетов;
- Александр Порфирьевич Бородин;
- Владимир Иванович Вернадский;
- Александр Абрамович Воскресенский;
- Николай Дмитриевич Зелинский;
- Сергей Васильевич Лебедев;
- Юрий Анатольевич Овчинников;
- Игорь Михайлович Скурихин;
- Алексей Евграфович Фаворский.
B.
В стремительно развивающемся мире городского сельского хозяйства, известного как сити-фермерство, вода играет роль не просто ресурса, а ключевого фактора, определяющего успешность выращивания.
Однако не только количество воды, но и ее качество напрямую влияет на рост и развитие растений. Это особенно актуально для сити-фермерства, где растения выращиваются в замкнутых системах с ограниченным объемом воды, что делает качество воды первостепенным фактором. Одной из важнейших характеристик качества воды является ее жесткость, которая определяется содержанием в ней солей кальция и магния.
Высокая жесткость воды может создавать ряд проблем при выращивании растений, как в традиционных, так и в гидропонных системах. Высокое содержание кальция и магния в воде может приводить к повышению pH раствора, что делает недоступными для растения многие важные питательные вещества, например, железо, марганец и цинк. В результате растение испытывает дефицит микроэлементов, что проявляется в замедленном росте, хлорозе — пожелтении листьев, а также повышенной уязвимости к болезням. Информацию о жесткости воды учитывают при приготовлении питательных растворов, так как необходимо знать точную концентрацию избыточных минералов, присутствующих в используемой воде. Кроме того, присутствие солей кальция и магния увеличивает риск отложения нерастворимых солей, который приводит к засорению и блокировке оросительного оборудования.
Для определения жесткости воды можно использовать метод комплексонометрического титрования, который основывается на реакциях комплексообразования между ионами, содержащимися в анализируемом растворе, и титрантом. В данном случае титрантом является раствор ЭДТА (этилендиаминтетрауксусной кислоты). ЭДТА образует стабильные комплексные соединения с ионами кальция и магния в соотношении \(1:1\). Это позволяет точно измерять количество этих ионов в воде, что является важным для оценки жесткости. Процесс титрования включает в себя поэтапное добавление титранта к образцу воды, пока не произойдет полное взаимодействие между ионами кальция и магния и ЭДТА. Завершение реакции фиксируется с помощью металлоиндикаторов, таких как эриохром черный Т и мурексид. Эти индикаторы изменяют цвет в зависимости от наличия ионов кальция и магния, что позволяет визуально определить момент окончания титрования. Для раздельного определения содержания кальция и магния в воде проводят два титрования в разных условиях. В одном в качестве индикатора используется эриохром черный \(\ce{T}\). В этом случае в результате титрования определяется общее количество ионов кальция и магния. Во втором подходе используется мурексид, который также реагирует с обоими ионами, но с некоторыми модификациями. Перед титрованием в раствор добавляется едкий натр (\(\ce{NaOH}\)), что приводит к осаждению магния в виде гидроксида. Таким образом, в этом случае титруется только кальций, а содержание магния можно вычислить по разнице. Титрование обычно проводят трижды для повышения точности результатов, после чего рассчитывается средний объем использованного титранта. Расчет содержания кальция и магния осуществляют по формулам: \[\begin{gather} m(\ce{Ca^{2+}}) \text{в~мг~в~1~л} = \frac{ C_{\text{ЭДТА}} \cdot V_{\text{ЭДTA1}} \cdot 1000 \cdot M_{\ce{Ca^{2+}}}}{V_{\text{пробы}}};\\ m (\ce{Mg^{2+}})\text{в~мг~в~1~л} = \frac{C_{\text{ЭДТА}} \cdot (V_{\text{ЭДТА2}} - V_{\text{ЭДTA1}} ) \cdot 1000 \cdot M_{\ce{Mg^{2+}}}}{V_{\text{пробы}}}, \end{gather}\] где
- \(C_{\text{ЭДTA1}}\) — молярная концентрация ЭДТА, моль/л;
- \(V_{\text{ЭДTA1}}\) — средний объем ЭДТА, пошедший на титрование с мурексидом, мл;
- \(V_{\text{ЭДTA2}}\) — средний объем ЭДТА, пошедший на титрование с эриохромом черным Т, мл;
- \(M_{\ce{Ca^{2+}}}\), \(M_{Mg^{2+}}\) — молярные массы кальция и магния, г/моль.
Определите в миллиграммах массу ионов кальция, содержащуюся в 1 л воды, если при трехкратном титровании пробы воды объемом 100 мл с металлоиндикатором мурексидом 0,005 М раствором ЭДТА при \(pH = 12\) до перехода красной окраски раствора в фиолетовую объемы ЭДТА составили: 2,9 мл, 2,7 мл, 2,8 мл. Ответ округлите до десятых.
Комплексометрическое титрование воды раствором ЭДТА с использование мурексида при \(pH=12\) позволяет определить содержание кальция при совместном нахождении в пробе магния, так как при данном значении \(pH\) магний осаждается в виде гидроксида.
Средний объем титранта, пошедшего на титрование, составляет \[V_{\text{ЭДTA1}} = \frac{2{,}9 + 2{,}7 + 2{,}8}3 = 2{,}8\text{~мл.}\]
Массу кальция определяем по формуле: \[\begin{gather} m (\ce{Ca^{2+}})\text{~в~мг~в~1~л} = \frac{C_{\text{ЭДTA1}} \cdot V_{\text{ЭДTA1}} \cdot 1000 \cdot M_{\ce{Ca^{2+}}}}{V_{\text{пробы}}} =\\ =\frac{0,005 \cdot 2,8 \cdot 1000 \cdot 40}{100} = 5,6\text{~мг.} \end{gather}\]
5,6. Диапазон 5,4–5,8.
Определите в миллиграммах массу ионов магния, содержащуюся в 1 л воды, если при трехкратном титровании пробы воды объемом 100 мл с металлоиндикатором мурексидом 0,005 М раствором ЭДТА при \(ph = 12\) до перехода красной окраски раствора в фиолетовую объемы ЭДТА составили: 2,9 мл, 2,7 мл, 2,8 мл; а с металлоиндикатором эриохромом черным \(\ce{T}\) 0,005 М раствором ЭДТА при \(ph = 10\) до перехода красной окраски в синюю объемы ЭДТА составили: 4,5 мл, 4,4 мл, 4,3 мл. Ответ округлите до сотых.
Комплексометрическое титрование воды раствором ЭДТА с использование эриохрома черного \(\ce{T}\) при \(pH=10\) позволяет определить суммарное содержание кальция и магния в пробе, магний рассчитывают по разнице с предыдущим титрованием.
Средний объем титранта, пошедшего на титрование, составляет \[V_{\text{ЭДTA1}} = \frac{4{,}5 + 4{,}4 + 4{,}3}3 = 4{,}4\text{ мл.}\]
Массу магния определяем по формуле: \[\begin{gather} m (\ce{Mg^{2+}})\text{~в~мг~в~1~л} = \frac{C_{\text{ЭДTA1}} \cdot (V_{\text{ЭДTA2}}-V_{\text{ЭДTA1}}) \cdot 1000 \cdot M_{\ce{Mg^{2+}}}}{V_{\text{пробы}}}=\\ =\frac{0,005 \cdot (4,4-2,8) \cdot 1000 \cdot 24}{100} = 1,92\text{~мг.} \end{gather}\]
1,92. Диапазон 1,90–1,94.
При необходимости умягчить воду можно воспользоваться одним из химических методов устранения жесткости воды — добавлением к воде раствора соды. При этом ионы кальция и магния осаждаются в виде нерастворимых солей. Определите массу осадка, образовавшегося при добавлении к 10 л воды, содержащей \(7{,}525\cdot 10^{20}\) ионов кальция и \(9{,}632\cdot 10^{20}\) ионов магния, раствора кальцинированной соды, взятой в избытке. Ответ выразите в миллиграммах (мг) и округлите до целых.
Кальцинированная сода — карбонат натрия, катионы кальция и магния образуют с ней нерастворимые карбонаты: \[\label{chem_030101} \ce{Ca^{2+} + Na2CO3 -> CaCO3 v + 2 Na+};\] \[\label{chem_030102} \ce{Mg^{2+} + Na2CO3 -> MgCO3 v + 2 Na+};\] \[\begin{gather} n(\ce{Ca^{2+}}) = \frac{7,525 \cdot 10^{20}}{6,02 \cdot 10^{23}} = 0,00125\text{ моль}= 1,25\text{ ммоль};\\ n(\ce{Mg^{2+}}) = \frac{9,632 \cdot 10^{20}}{6,02 \cdot 10^{23}} = 0,0016\text{ моль}= 1,6\text{ ммоль};\\ n(\ce{CaCO3}) = n(\ce{Ca^{2+}})=1,25\text{~ммоль};\\ m (\ce{CaCO3}) = n \cdot M = 1,25 \cdot 100 = 125\text{~мг};\\ n(\ce{MgCO3}) = n(\ce{Mg^{2+}})=1,16\text{~ммоль};\\ m (\ce{MgCO3}) = n \cdot M = 1,16 \cdot 84 = 134,4\text{~мг};\\ m(\text{осадка})= 125 + 134,4 = 259,4\text{~мг~}\approx 259\text{~мг~в~}10\text{~л воды.} \end{gather}\]
259. Диапазон 258–260.
Для устранения временной жесткости воды, обусловленной содержанием гидрокарбонатов кальция и магния, 1 л воды прокипятили в течение длительного времени в закрытом сосуде. При этом образовался осадок массой 28,4 мг и выделился углекислый газ объемом 6,72 мл (н. у.). Определите суммарную массу ионов кальция и магния, устраненных кипячением из 1 л воды. Ответ выразите в миллиграммах (мг) и округлите до десятых.
При нагревании гидрокарбонаты кальция и магния разлагаются по формулам \eqref{chem_030101} и \eqref{chem_030102}. \[n(\ce{CO2}) = \frac{6{,}72\text{~мл}}{22{,}4\text{~л/моль}} = 0{,}3\text{~ммоль.}\]
Пусть \(n(\ce{CaCO3}) = x\) ммоль, \(n(\ce{MgCO3}) = y\) ммоль.
По уравнению \eqref{chem_030101} \(n(\ce{CO2}) = n(\ce{CaCO3}) = x\text{~ммоль.}\)
По уравнению \eqref{chem_030102} \(n(\ce{CO2}) = n(\ce{MgCO3}) = y\text{~ммоль}\), тогда: \[\left\{\begin{aligned} &100 x + 84y = 28,4,\\ &x + y = 0,3. \end{aligned}\right.\]
\(x=0{,}2\) ммоль, \(y = 0{,}1\) ммоль. \[\begin{gather} n (\ce{Ca^{2+}} ) = n(\ce{CaCO3}) = 0,2\text{~ммоль};\\ n (\ce{Mg^{2+}}) = n(\ce{MgCO3}) = 0,1\text{~ммоль};\\ m (\ce{Ca^{2+}} ) = n \cdot M = 0,2 \cdot 40 = 8\text{~мг};\\ m (\ce{Mg^{2+}} )= n \cdot M = 0,1 \cdot 24 = 2,4\text{~мг};\\ m (\ce{Ca^{2+}} ) + m (\ce{Mg^{2+}} ) = 8 + 2,4 = 10,4\text{~мг.} \end{gather}\]
10,4. Диапазон 10,2–10,6.
Аминокислоты играют ключевую роль в современных биотехнологиях, становясь основой для множества инновационных процессов и продуктов. Их применение охватывает широкий спектр областей, среди которых особенно выделяются производство вакцин, создание терапевтических белков и разработка различных биофармацевтических препаратов. Например, в последние годы значительное внимание уделяется использованию аминокислот в разработке мРНК-вакцин, которые продемонстрировали свою эффективность в борьбе с COVID-19. Кроме того, аминокислоты активно задействуются в производстве моноклональных антител, которые применяются для лечения различных заболеваний, включая рак и аутоиммунные расстройства. Эти антитела, созданные на основе специфических аминокислотных последовательностей, способны целенаправленно связываться с определенными молекулами в организме, что делает их мощным инструментом в терапии. Исследования в области аминокислот не ограничиваются только медициной. Они также находят применение в сельском хозяйстве, где аминокислоты используются для создания высококачественных кормов, способствующих улучшению здоровья животных и увеличению продуктивности. В сфере пищевых технологий аминокислоты применяются для улучшения вкусовых качеств продуктов, а также для обогащения их питательными веществами. С учетом быстрого развития науки и технологий, можно ожидать, что в будущем мы увидим новые, ранее невообразимые, сферы и методы применения аминокислот.
Небольшой фрагмент белка \(A\), состоящий из двух аминокислот массой 10,8 г, сожгли в достаточном количестве кислорода. В процессе горения образовалось 11,2 л (н. у.) углекислого газа, 9 г воды и 1,12 л азота (н. у.). В присутствии соляной кислоты исходное вещество подверглось гидролизу с образованием единственной соли.
Определите молярную массу исходного вещества \(A\) в граммах на моль (г/моль). Ответ запишите с точностью до целых.
Фрагмент из двух аминокислот — дипептид. Определим количества образующихся в результате сжигания дипептида веществ и количества элементов, входящих в его состав. \[\begin{gather} n (\ce{CO2}) = n (\ce{C}) =\frac {11,2}{22,4} = 0,5\text{ моль; }m (\ce{C}) = n \cdot M = 0,5 \cdot 12 = 6\text{ г};\\ n (\ce{H2O}) = \frac 9{18} = 0,5\text{ моль; }n (\ce{H}) = 2 \cdot n (\ce{H2O}) = 2\cdot 0,5 = 1\text{ моль};\\ m(\ce{H}) = n \cdot M = 1 \cdot 1 = 1\text{ г};\\ n (\ce{N2}) = \frac{1,12}{22,4} = 0,05\text{ моль; }n (\ce{N}) = 2 \cdot n (\ce{N2}) = 2\cdot 0,05 = 0,1\text{ моль};\\ m (\ce{N}) = n \cdot M = 0,1 \cdot 14 = 1,4\text{ г};\\ m (\ce{O}) =10,8 - 6 - 1 - 1,4 = 2,4\text{ г};\\ n (\ce{O}) = \frac{2,4}{16} = 0,15\text{ моль};\\ n (\ce{C}) : n (\ce{H}) : n (\ce{O}) : n (\ce{N}) = 0,5 : 1 : 0,15 : 0,1 = 5 : 10 : 1,5 : 1 (\times 2);\\ n (\ce{C}) : n (\ce{H}) : n (\ce{O}) : n (\ce{N}) = 10 : 20 : 3 : 2. \end{gather}\]
Молекулярная формула дипептида — \(\ce{C10H20O3N2}\).
Молекулярная масса дипептида \(M(\ce{C10H20O3N2}) = 216\) г/моль.
216. Диапазон 215–217.
Определите, какая аминокислота образует фрагмент белка \(A\), укажите ее тривиальное название.
При гидролизе дипептида \(\ce{C10H20O3N2}\) образуется только одна соль, следовательно, дипептид состоит из одинаковых аминокислот, содержащих по 5 атомов углерода. \[\ce{C10H20O3N2 + 2HCl + H2O -> 2 [C5H12O2N]Cl}.\]
Молекулярная формула аминокислоты, соответствующая образовавшейся соли — \(\ce{C5H11O2N}\).
Аминокислота, имеющая брутто-формулу \(\ce{C5H11O2N}\) — валин.
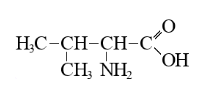
Валин относится к группе незаменимых аминокислот, то есть эта аминокислота не синтезируется в организме человека и должна поступать с пищей.
\(L\)-валин — это аминокислота, которая коммерчески важна, его можно использовать в качестве кормовой добавки для животных, ингредиента косметических средств и специальных питательных веществ в фармацевтической и сельскохозяйственной областях. \(L\)-валин может улучшать функцию лактации у племенных животных и рассматривался как одна из лимитирующих аминокислот в кормах для домашней птицы и свиней. Добавление \(L\)-валина может придать косметическим средствам увлажняющую функцию и стимулировать синтез коллагена. В фармацевтической промышленности \(L\)-валин широко используется в качестве компонента для инфузий аминокислот третьего поколения и обладает высокой устойчивостью к синтезу и разложению мышечного белка; он играет важную роль в фармакологических питательных веществах для пациентов с хроническими заболеваниями печени.
Валин (принимать Валин / ВАЛИН).
Среди перечисленных реакций выберите ту, с помощью которой можно отличать растворы пептидов от растворов аминокислот:
- нингидриновая;
- биуретовая;
- ксантопротеиновая;
- цистеиновая.
В ответе укажите только номер реакции.
Фрагмент белка, то есть пептид, можно обнаружить с помощью биуретовой реакции — качественной реакции на пептидную связь.
2.

Осмотическим давлением называют величину избыточного давления на раствор, отделенный от чистого растворителя полупроницаемой мембраной, при котором прекращается осмос, то есть диффузия растворителя через мембрану. Голландский химик Якоб Хендрик Вант-Гофф установил, что для разбавленных растворов осмотическое давление прямо пропорционально молярной концентрации частиц (молекул, ионов) растворенного вещества: \[\pi=CRT,\] где \(\pi\) — осмотическое давление, кПа; \(C\) — молярная концентрация частиц (молекул, ионов) растворенного вещества, моль/л; \(R\) — универсальная газовая постоянная, 8,314 Дж/(моль\(\cdot\)К); \(T\) — температура, К. Это открытие было отмечено первой Нобелевской премией по химии.
Мембраны всех живых клеток используют осмос для контроля поглощения необходимых веществ, поэтому он играет очень важную роль в медицине, биотехнологии и агротехнологии, особенно в гидропонике. Осмос помогает растениям расти и всасывать воду корневой системой — поскольку в клеточном соке концентрация солей и сахаров выше, чем в почвенном растворе. Это важно учитывать при внесении удобрений — если осмотическое давление почвенного раствора станет слишком большим, поступление воды в растение прекратится, и оно погибнет (например, как в засоленных почвах).
Рассчитайте осмотическое давление раствора удобрения (380 г мочевины в 15 л воды) при температуре 22 °C. Ответ выразите в килопаскалях (кПа) с точностью до целых.
Количество вещества мочевины: \[n(\ce{NH_2CONH_2})=\frac{m(\ce{NH_2CONH_2})}M=\frac{380}{16\cdot 2+28}=6{,}3\text{ моль,}\] соответственно молярная концентрация раствора \[C(\ce{NH_2CONH_2})=\frac{n(\ce{NH_2CONH_2})}V=\frac{6{,}3}{15}=0{,}42\text{ моль/л.}\]
Осмотическое давление \(\pi=CRT=0{,}42\cdot 8{,}314\cdot (273+22)=1030\) кПа.
1030. Диапазон 1015–1045.
В медицине при внутривенном введении используют гипертонические растворы — растворы, осмотическое давление которых превышает давление плазмы крови — в такой среде вода выходит через мембрану из клетки, и клетка сжимается.
Гипертонический раствор хлорида натрия применяют для снятия отека в офтальмологии, как осмотический диуретик, для коррекции состояния систем организма при операциях и в реанимационных целях.

Рассчитаем концентрацию частиц в растворе исходя из величины осмотического давления: \[C=\frac{\pi}{RT}=\frac {6661 }{8{,}314\cdot (273+37)}=2{,}58\text{~моль/л.}\]
Хлорид натрия — электролит, диссоциирующий в растворе на ионы \(\ce{Na^+}\) и \(\ce{Cl^-}\). Поскольку точная степень диссоциации в информации не указана, а раствор является разбавленным, ее можно принять равной 100%.
Тогда концентрация хлорида натрия составляет: \[C(\ce{NaCl})=\frac C2=\frac {2{,}58}2=1{,}29\text{~моль/л,}\] а масса соли в 1 л раствора: \[m(\ce{NaCl})=n(\ce{NaCl})\cdot M=C(\ce{NaCl})\cdot V\cdot M=1{,}29\cdot 1\cdot (23+35{,}5)=75{,}47\text{~г}.\]
Массовая доля в растворе \[\omega=\frac{m(\ce{NaCl})}{m_\text{р-ра}}=\frac{75{,}47}{1\cdot 1050}\cdot 100=7{,}2 \%.\]
7,2. Диапазон 7,0–7,4.
Измерение осмотического давления является одним из распространенных методов определения молекулярной массы полимера, влияющей на его свойства. Например, поливинилацетат с высокой молекулярной массой обладает более высокой твердостью и температурой стеклования, при меньшей растворимости в органических растворителях. Мембранный осмометр основан на измерении разности давлений — например, по разности высот в капиллярах раствора и растворителя, поскольку гидростатическое давление уравновешивает осмотическое.
Установите молекулярную массу поливинилхлорида, если разность высот жидкости в осмометре для его раствора в ацетоне, содержащего 0,2 г в 100 мл раствора, составляет 8,1 см при 25 °С. Ответ запишите в килограммах на моль (кг/моль) с точностью до десятых. Плотность ацетона и раствора 791 \(\text{кг/м}^3\).
Гидростатическое давление столба жидкости уравновешивает осмотическое давление, для удобства расчета используем единицы измерения системы СИ:
\[\pi=CRT=\rho g \Delta h=791\cdot 9{,}8\cdot (8{,}1\cdot 10^{-2})=627{,}9\text{~Па.}\]
Молярная концентрация раствора полимера составляет \[C=\frac {\pi}{RT}=\frac {627{,}9}{8{,}314\cdot (273+25)}=0{,}253\text{~моль/м}^3,\] то есть количество вещества полимера \[n=CV=0{,}253\cdot \frac{0{,}1}{1000}=0{,}025\text{~ммоль.}\]
Тогда молекулярная масса \[M=\frac mn=\frac {0{,}2}{0{,}025}=7{,}9\text{~кг/моль.}\]
7,9. Диапазон 7,5–8,3.
Ортофосфорная кислота используется в самых разных областях — в производстве удобрений и чистящих средств, для деревообработки и очистки металла от ржавчины, в стоматологии для реставрации зубов и в ювелирном деле при пайке. Также она зарегистрирована в качестве пищевой добавки E338, которую можно встретить в составе мармеладов, сиропов и напитков, хлебобулочных изделий, сыров и плавленых сырков.
Пищевую фосфорную кислоту производят термическим способом, позволяющим получить концентрированный продукт с меньшим содержанием примесей — для этого белый фосфор сжигают в воздухе и подвергают образующийся оксид фосфора (V) гидратации.
При нормальных условиях рассчитайте объем воздуха, который необходимо подавать в башню (камеру сжигания) в 1 ч для сжигания фосфора, если известно, что расход образующегося в башне 80%-го раствора фосфорной кислоты составляет 4500 кг/ч. Ответ выразите в кубических метрах с точностью до целых. Учтите, что для предотвращения образования оксида фосфора (III) в башню подают двукратный избыток воздуха по сравнению с расчетным количеством.
Запишем уравнения происходящих реакций: \[\begin{gather} \ce{P4 + 5O2 -> P4O10};\\ \ce{P4O10 + 6H2O -> 4H3PO4}. \end{gather}\] Масса фосфорной кислоты: \[m(\ce{H_3PO_4})=m_\text{р-ра}\omega_{\ce{H_3PO_4}}={4500}\cdot 0{,}80=3600 \text{~кг/ч.}\]
Количество вещества фосфорной кислоты: \[n(\ce{H_3PO_4})=\frac{m(\ce{H_3PO_4})}{M}=\frac{{3600}}{3+31+16\cdot 4}=36{,}73 \text{~кмоль/ч},\] что соответствует расчетному количеству вещества кислорода \[\begin{gather} n_\text{теор}(\ce{O2})=\frac 54n(\ce{H_3PO_4})=45,92\text{~кмоль/ч};\\ n_\text{практ}(\ce{O2})=2n_\text{теор}(\ce{O2})=2\cdot 45,92 =91,84 \text{~кмоль/ч}. \end{gather}\] Объем кислорода \[V(\ce{O2})=n_\text{практ}(\ce{O2})V_0=91{,}84\cdot 1000\cdot 22{,}4=2 057 143\text{ л,}\] объем воздуха \[V_\text{возд}=\frac {V(\ce{O2})}{\chi(\ce{O2})}= \frac {2057143}{0{,}21\cdot 1000} =9796 \text{~м}^3.\]
9796. Диапазон 9000–10600.
Использование теплоты, выделяющейся при сгорании фосфора, позволяет значительно увеличить энергоэффективность проведения процесса. При стандартных условиях рассчитайте теплоту, которая выделяется в ходе проходящих реакций при образовании указанного в подзадаче № 1 количества фосфорной кислоты. Используйте данные таблицы, ответ запишите в мегаджоулях (МДж).
| Вещество | \(\ce{P4O10}\)\(_\text{(тв)}\) | \(\ce{H3PO4}\)\(_\text{(ж)}\) | \(\ce{H2O}\)\(_\text{(ж)}\) |
|---|---|---|---|
| Теплота образования, кДж/моль | 2984,03 | 1266,90 | 285,83 |
В соответствии со следствием из закона Г. И. Гесса, теплоту каждой протекающей реакции можно выразить как разность между суммами теплот образования продуктов и реагентов с учетом стехиометрических коэффициентов: \[\begin{gather} \Delta_rQ=\Sigma n_i Q_f(\text{прод})-\Sigma n_j Q_f(\text{реаг});\\ \Delta_{r1}Q=Q_f(\ce{P_4 O_{10(\text{тв})}})-Q_f(\ce{P_{4(\text{тв})}})-5Q_f(\ce{O_{2(\text{г})}});\\ \Delta_{r2}Q=4Q_f(\ce{H_3PO_{4(\text{ж})}})-6Q_f(\ce{H_2 O_{(\text{ж})}})-Q_f(\ce{P_4 O_{10 (\text{тв})}}). \end{gather}\] С учетом того, что теплоты образования простых веществ равны нулю, получим: \[\begin{gather} \Delta_{r1}Q=2984,03\text{~кДж/моль};\\ \Delta_{r2}Q=4\cdot 1266,90-6\cdot 285,83-2984,03=368,59\text{~кДж/моль.} \end{gather}\] В расчете на 4 моль фосфорной кислоты \[Q_R=\Delta_{r1}Q+\Delta_{r2}Q=3352{,62}~\text{кДж/моль}.\]
Тогда \[Q=Q_R\cdot \displaystyle\frac{n(\ce{H_3PO_4})}4=3352{,62}\cdot \displaystyle\frac{36{,}73}4=30785~\text{МДж}.\]
30785. Диапазон 30700–30870.
В качестве пищевой добавки ортофосфорная кислота выступает регулятором кислотности и консервантом: кислая среда препятствует размножению микроорганизмов и порче продукта.

Именно наличие фосфорной кислоты в составе обуславливает способность газированных напитков растворять ржавчину и очищать бытовые поверхности, о которой снято много интернет-роликов. Впрочем, имеются сведения о стимулировании фосфорной кислотой вымывания кальция из организма и ее негативном влиянии на зубную эмаль при чрезмерном употреблении.
Рассчитайте \(pH\) 0,75 моль/л раствора фосфорной кислоты, если известно, что константа диссоциации кислоты по первой ступени составляет \(7{,}52\cdot 10^{-3}\), а диссоциацией по второй и третьей ступени можно пренебречь. Ответ приведите в моль на литр (моль/л).
Запишем уравнение диссоциации фосфорной кислоты по первой ступени: \[\ce{H3PO4 <--> H+ + H2PO4-}.\]
Выражение для константы диссоциации: \[K_I=\frac {[\ce{H2PO4-}][\ce{H+}]}{[\ce{H3PO4}]},\] где в квадратных скобках указаны равновесные концентрации.
Тогда \[\begin{gather} [\ce{H2PO4-}]=[\ce{H+}], [\ce{H3PO4}]=\ce{C0}-[\ce{H+}];\\ K_I=\frac{[\ce{H+}]^2}{\ce{C0}-[\ce{H+}]}=7,52\cdot 10^{-3}. \end{gather}\] Решение уравнения при \(C_0=0{,}75\) моль/л позволяет найти \[[\ce{H+}]=0{,}071\text{~моль/л,}\] откуда \(pH=-lg ([\ce{H+}])\approx 1{,}1.\)
1,1.
В стенах Казанского университета, где начинал свой путь будущий ученый, царила атмосфера, далекая от современного представления о химической лаборатории. Два рабочих стола, калильные печи, одна большая печь и песчаная баня без тяги — вот и весь скромный арсенал для проведения экспериментов. Опыты, требующие вытяжной вентиляции, проводились прямо на улице, независимо от времени года. Холодная зима или палящее солнце — наука не знала границ. В 1853 году отец ученого, желая обеспечить сыну более стабильное будущее, уговаривал его сменить направление деятельности и отказал во всяческой материальной поддержке. Но, вопреки всем уговорам, юноша, движимый неугасимой жаждой познания, твердо решил посвятить себя науке. В 1844 году он поступил в Петербургский университет, но уже через три года перешел в Казанский, где стал учеником знаменитого российского химика-органика Николая Николаевича Зинина. Казалось бы, естественным продолжением было бы изучение органической химии, следуя по стопам своего учителя. Однако молодой ученый, не ограничиваясь рамками одного направления, увлекся физической химией, тогда еще только формирующейся областью знания. И хотя немцы утверждают, что приоритет в развитии физической химии принадлежит Вильгельму Оствальду, наш ученый уже в 1865 году, когда Оствальд был еще ребенком, читал студентам систематический курс по этой дисциплине.
Важным фактором, способствовавшим его успехам, была не только страсть к науке, но и способность использовать подручные средства для достижения поставленных задач. Так, исследуя явление алюминотермии, он прибегнул к изогнутому ружейному стволу в качестве реакционного сосуда. Ученый также изучал восстановительные способности других металлов, что позволило ему разработать «вытеснительный ряд металлов». Этот ряд, составленный по возрастанию активности металлов, стал неотъемлемой частью химии, помогая прогнозировать и анализировать химические реакции.
По мнению И. А. Каблукова, имя этого ученого «будет стоять в истории науки рядом с именами Д. И. Менделеева и А. М. Бутлерова и будет занесено золотыми буквами в историю науки в России».
Назовите этого ученого:
- Федор Федорович Бейльштейн;
- Николай Николаевич Бекетов;
- Александр Порфирьевич Бородин;
- Владимир Иванович Вернадский;
- Александр Абрамович Воскресенский;
- Николай Дмитриевич Зелинский;
- Сергей Васильевич Лебедев;
- Юрий Анатольевич Овчинников;
- Игорь Михайлович Скурихин;
- Алексей Евграфович Фаворский.
B.
Освоение космоса имеет невероятную актуальность в наши дни, и тому есть объективные причины. Так, космонавтика позволяет развивать различные технологии, такие как системы навигации, спутниковая связь, наблюдение за погодой. В условиях изоляции и невесомости проводят биологические и медицинские исследования. Большой интерес изучение космоса вызывает у ученых как перспектива колонизация других планет или спутников в Солнечной системе, а также добыча ресурсов на астероидах.
Первостепенной задачей в обеспечении жизнедеятельности в космических аппаратах является поддержание необходимого химического состава атмосферы. В условиях замкнутого пространства уровень углекислого газа может быстро нарастать, что приводит к ухудшению самочувствия экипажа и в конечном итоге может стать причиной гибели. Поэтому регулярная очистка воздуха от углекислого газа является жизненно важной. Ранее в пилотируемых космических аппаратах для удаления углекислого газа использовались физико-химические методы — на американских космических кораблях применялись контейнеры с гидроксидом лития, а на советских — с надпероксидом калия, оба эти вещества связывают углекислый газ.Современные технологии, используемые на борту Международной космической станции (МКС) и ранее на космической станции «Мир», используют многоразовые цеолитовые поглотители углекислоты. Цеолиты представляют собой пористые минералы, которые способны эффективно поглощать молекулы углекислого газа. Регенерация цеолитов проводится в особых аппаратах, где под воздействием высоких температур они высвобождают накопленный углекислый газ в забортное пространство.
Используемый для регенерации воздуха в замкнутом пространстве надпероксид калия массой 35,5 г поместили в герметичную камеру, наполненную углекислым газом. После завершения процесса твердый остаток растворили в 100 мл воды и добавили 200 мл 15%-го раствора хлорида кальция (плотность 1,11 г/мл), в результате чего наблюдали выпадение белого осадка.
При нормальных условиях определите объем поглощенного в камере углекислого газа. Ответ, выраженный в литрах, округлите до десятых.
Составим уравнения протекающих реакций: \[\ce{4KO2 + 2CO2 -> 2K2CO3 + 3O2 }, \label{ch89_040101}\] \[\ce{K2CO3 + CaCl2 -> CaCO3 v + 2 KCl}. \label{ch89_040102}\] Определяем количество вещества надпероксида калия: \[n(\ce{KO2}) = \frac{35{,}5}{71} = 0{,}5\text{ моль.}\]
По уравнению реакции \eqref{ch89_040101} определяем количество вещества углекислого газа, а затем его объем: \[\begin{gather} n(\ce{CO2}) = \frac 12 n(\ce{K2O2}) = \frac{0,5}2 = 0,25\text{ моль};\\ V(\ce{CO2}) = n \cdot V_m = 0,25 \cdot 22,4 = 5,6\text{ л.} \end{gather}\]
5,6. Диапазон 5,5–5,6.
При нормальных условиях определите объем выделившегося кислорода. Ответ, выраженный в литрах, округлите до десятых.
По уравнению реакции \eqref{ch89_040101} определяем количество вещества кислорода: \[\begin{gather} n(\ce{O2}) = \frac 34 n(\ce{KO2}) = \frac{3 \cdot 0,5}4 = 0,375\text{ моль};\\ V(\ce{O2}) = n \cdot V_m = 0,375 \cdot 22,4 = 8,4\text{ л.} \end{gather}\]
8,4. Диапазон 8,3–8,5.
Определите в граммах массу осадка, выпавшего из раствора (ответ округлите до целых).
Белый осадок, выпавший из раствора, — это карбонат кальция.
Для того чтобы рассчитать его массу, предварительно нужно определить избыток/недостаток реагирующих веществ. \[\begin{gather} n(\ce{K2CO3}) = n(\ce{CO2}) = 0,25\text{ моль};\\ m(\text{р-ра} \ce{CaCl2}) = V \cdot \rho = 200 \cdot 1,11 = 222\text{ г};\\ m(\ce{CaCl2}) = 222 \cdot 0,15 = 33,3\text{ г};\\ n(\ce{CaCl2}) = \frac mM = \frac{33,3}{111} = 0,3\text{ моль};\\ \ce{K2CO3}- \text{в~недостатке}. \end{gather}\] По уравнениям реакций \eqref{ch89_040101} и \eqref{ch89_040102} количество вещества карбоната кальция составляет: \[\begin{gather} n(\ce{CaCO3}) = n(\ce{K2CO3}) = 0,25\text{ моль};\\ m (\ce{CaCO3}) = n \cdot M = 0,25 \cdot 100 = 25\text{ г.} \end{gather}\]
25.
Определите в процентах массовую долю хлорида калия в полученном растворе (ответ округлите до десятых).
\[\begin{gather} n (\ce{KCl}) = 2 \cdot n(\ce{K2CO3}) = 0,25 \cdot 2 = 0,5\text{ моль};\\ m (\ce{KCl}) = n \cdot M = 0,5\cdot 74,5 = 37,25\text{ г};\\ m(\text{р-ра}) = m(\ce{H2O}) + m(\ce{K2CO3}) + m(\text{р-ра}\ce{CaCl2}) - m(\ce{CaCO3}) =\\ = 100 + 0,25\cdot 138 + 222 - 25 = 331,5\text{ г};\\ \omega (\ce{KCl}) = \frac{37,25 \cdot 100}{331,5} = 11,2368 \approx 11,2 \%. \end{gather}\]
11,2. Диапазон 11–11,3.
Раствор для гидропоники представляет собой специальную жидкость, предназначенную для полноценного питания растений, в которую входят минеральные соли и другие необходимые компоненты. В традиционном земледелии растения получают все необходимые для роста вещества из почвы, но гидропоника позволяет обходиться без нее, обеспечивая растения питательными веществами непосредственно через корневую систему в водной среде. Это особенно полезно в условиях ограниченного пространства или неблагоприятных почвенных условий. При создании питательного раствора для гидропоники важно учитывать специфику каждой культуры, так как разные растения требуют различных соотношений макро- и микроэлементов. Для достижения оптимального результата в гидропонике необходимо не только правильно подбирать компоненты, но и следить за их концентрацией. Неправильные пропорции могут привести к дефициту или избытку полезных веществ, что негативно скажется на здоровье растений. На протяжении многих лет различные ученые и агрономы разработали множество формул для питательных растворов, адаптированных для разных систем гидропоники. Например, известны формулы, такие как формула Туманова, Кнопа, Кидсона, Пюрдье, Шварца, Пильгрима и другие, каждая из которых имеет свои особенности и преимущества. Эти формулы учитывают не только потребности конкретных культур, но и условия их выращивания: температура, влажность и освещение
Таким образом, раствор для гидропоники — это не просто смесь, а целая наука, требующая глубоких знаний о потребностях растений и условиях их роста.
Один из растворов для гидропоники — раствор Шварца — предполагает следующее содержание катионов в 1 л раствора, см. таблицу ниже.
| Катион | \(\ce{K+}\) | \(\ce{Ca^{2+}}\) | \(\ce{Mg^{2+}}\) | \(\ce{NH4+}\) |
|---|---|---|---|---|
| мг/л | 200 | 160 | 48 | 15 |
Рассчитайте массы солей калиевой селитры, двойного суперфосфата, кристаллического сернокислого магния, аммиачной селитры, необходимых для приготовления 1 л раствора с данным содержанием катионов.
Вычислите в миллиграммах массу калийной селитры, необходимую для приготовления 1 л раствора Шварца. Ответ округлите до целых.
Для определения массы \(\ce{KNO3}\) определим количество калия: \[\begin{gather} n (\ce{K+}) = \frac{200}{39} = 5,1282\text{ ммоль} \approx 5,13\text{ ммоль};\\ n (\ce{KNO3}) = n (\ce{K+}) = m (\ce{KNO3}) = n \cdot M = 5,13 \cdot 101 = 518\text{ мг.} \end{gather}\]
518. Диапазон 505–518.
Вычислите в миллиграммах массу двойного суперфосфата \(\ce{Ca(H2PO4)2}~\times~\ce{H2O}\), необходимую для приготовления 1 л раствора Шварца. Ответ округлите до целых.
Для определения массы двойного суперфосфата \(\ce{Ca(H2PO4)2}~\times~\ce{H2O}\) определим количество кальция: \[\begin{gather} n (\ce{Ca^{2+}}) = \frac{160}{40} = 4\text{ ммоль};\\ n (\ce{Ca(H2PO4)2}~\times~\ce{H2O}) = n (\ce{Ca^{2+}}) = 4\text{ ммоль};\\ m (\ce{Ca(H2PO4)2}~\times~\ce{H2O}) = n \cdot M = 4234 = 936\text{ мг.} \end{gather}\]
936.
Вычислите в миллиграммах массу кристаллического сернокислого магния \(\ce{MgSO4} \times \ce{7H2O}\), необходимую для приготовления 1 л раствора Шварца. Ответ округлите до целых.
Для определения массы сернокислого магния \(\ce{MgSO4} \times \ce{7H2O}\) определим количество магния: \[\begin{gather} n (\ce{Mg^{2+}}) =\frac {48}{24} = 2\text{ ммоль};\\ n (\ce{MgSO4} \times \ce{7H2O}) = n (\ce{Mg^{2+}}) = 2\text{ ммоль};\\ m (\ce{MgSO4} \times \ce{7H2O}) = n \cdot M = 2246 = 492\text{ мг.} \end{gather}\]
492.
Вычислите массу аммиачной селитры, необходимую для приготовления 1 л раствора Шварца. Ответ выразите в миллиграммах (мг) и округлите до целых.
Для определения массы \(\ce{NH4NO3}\) определим количество ионов аммония \(\ce{NH4+}\): \[\begin{gather} n (\ce{NH4+}) = \frac {15}{18} = 0,8333\text{ ммоль} \approx 0,83\text{ ммоль};\\ n (\ce{NH4NO3}) = n (\ce{NH4+}) = 0,83\text{ ммоль};\\ m (\ce{KNO3}) = n \cdot M = 0,83333 \cdot 80 = 67\text{ мг (без округления)};\\ m (\ce{KNO3}) = n \cdot M = 0,83333 \cdot 80 = 66\text{ мг (с округлением).} \end{gather}\]
\(66{,}5 \pm 0{,}5\).
Рассмотрим такую систему: мембрана, по разные стороны от которой расположены растворы с разным содержанием растворенного вещества. Поры полупроницаемой мембраны пропускают молекулы растворителя, но не молекулы растворенного вещества. Из-за того, что концентрации растворов различны, растворитель (например, вода) начнет диффундировать (перетекать) из более разбавленного раствора в более концентрированный и разбавлять его до тех пор, пока концентрация не станет равной по обе стороны мембраны. Это явление называют осмосом.

Мембраны всех живых клеток используют осмос для контроля поглощения необходимых веществ, поэтому он играет очень важную роль в медицине, биотехнологии и агротехнологии, особенно в гидропонике. Но осмос значим и в быту: с древности с его помощью консервировали пищу — в соленой среде вода вытекает из клеток, что приводит к сморщиванию (весь материал внутри клетки отслаивается от клеточной стенки) и потере жизнедеятельности микроорганизмов (этот процесс называют плазмолизом).
Рассчитайте массу поваренной соли, необходимую для приготовления 1,25 л рассола для засаливания огурцов (плотность \(\rho=1061\) г/л), массовая доля соли в котором составляет 8,5%. Ответ приведите в граммах с точностью до десятых.
Рассчитаем массу раствора \(m_{\text{р-ра}}=\rho V=1061\cdot 1{,}25=1326\) г.
Масса соли составляет: \[m(\ce{NaCl})=m_{\text{р-ра}}\omega (\ce{NaCl})=1326\cdot 0{,}085=112{,}7\text{~г.}\]
112,7. Диапазон 112–113.
Осмотическим давлением называют величину избыточного давления на раствор, отделенный от чистого растворителя полупроницаемой мембраной, при котором прекращается осмос, то есть диффузия растворителя через мембрану. Голландский химик Якоб Хендрик Вант-Гофф установил, что для разбавленных растворов осмотическое давление прямо пропорционально молярной концентрации частиц (молекул, ионов) растворенного вещества: \[\pi=CRT,\] где \(\pi\) — осмотическое давление, кПа; \(C\) — молярная концентрация частиц (молекул, ионов) растворенного вещества, моль/л; \(R\) — универсальная газовая постоянная, 8,314 Дж/(моль\(\cdot\)К); \(T\) — температура, К.
Это открытие было отмечено первой Нобелевской премией по химии.
В терапевтических целях иногда используют гипертонические растворы — растворы, осмотическое давление которых превышает давление плазмы крови — в такой среде вода выходит через мембрану из клетки, и клетка сжимается. Гипертонический 40%-й раствор глюкозы вводят при гипогликемии в качестве источника углеводов.

Рассчитайте величину осмотического давления 40%-го водного раствора глюкозы (\(\ce{C6H12O6}\)) при температуре 20 °С (плотность \(\rho=1172\) г/л). Ответ выразите в килопаскалях (кПа) с точностью до целых.
Рассчитаем массу 1 л раствора: \[m_{\text{р-ра}}=\rho V=1172\cdot 1{,}0=1172\text{ г.}\]
Масса глюкозы составляет: \[m(\ce{C6H12O6})=m_{\text{р-ра}}\omega (\ce{C6H12O6})=1172\cdot 0{,}40=468{,}8\text{ г.}\]
Количество вещества глюкозы: \[n(\ce{C6H12O6})=\frac{m(\ce{C6H12O6})}{M(\ce{C6H12O6})}=\frac{468{,}8}{6\cdot 12+12+6\cdot 16}=2{,}6\text{ моль,}\] соответственно молярная концентрация раствора
\[C(\ce{C6H12O6})=\frac{n(\ce{C6H12O6})}V=\frac{2{,}6}1=2{,}6\text{ моль/л.}\]
Осмотическое давление \(\pi =CRT=2{,}6\cdot 8{,}314\cdot (273+20)=6333{,6}\) кПа.
6334. Диапазон 6314–6354.
Водные растворы полимера полиэтиленгликоля (препарат «Полиоксидин») оказывают плазмозамещающее, антиагрегантное, противошоковое действие, их вводят внутривенно при острой кровопотере, посттравматическом и послеоперационном шоке. Препарат уменьшает вязкость крови за счет уменьшения вязкости плазмы и оказывает дезагрегирующее действие на форменные элементы крови, восстанавливает периферическое кровообращение, улучшает транспорт кислорода к тканям. Осмотическое давление раствора полимера мало, поэтому в состав также включают неорганические соли, чтобы сделать раствор препарата изотоничным крови.
Установите молярную массу полиэтиленгликоля, если осмотическое давление раствора, содержащего 7,5 г полимера в 0,5 л раствора, составляет 1,813 кПа при 25 °С. Ответ запишите в граммах на моль (г/моль) с точностью до целых.
Молярная концентрация раствора полимера: \[C=\frac{\pi}{RT}=\frac{1{,}813}{8{,}314\cdot (273+25)}=0{,}73\text{ ммоль/л},\] то есть количество вещества полимера \(n=CV=0{,}73\cdot 0{,}5=0{,}365\) ммоль.
Тогда молярная масса \[M=\frac mn=\frac{7{,}5}{0{,}365}\cdot 1000=20548\text{ г/моль.}\]
20548. Диапазон 20348–20748.
Ортофосфорная кислота используется в самых разных областях — в производстве удобрений и чистящих средств, для деревообработки и очистки металла от ржавчины, в стоматологии для реставрации зубов и в ювелирном деле при пайке. Также она зарегистрирована в качестве пищевой добавки E338, которую можно встретить в составе мармеладов, сиропов и напитков, хлебобулочных изделий, сыров и плавленых сырков.
Пищевую фосфорную кислоту производят термическим способом, позволяющим получить концентрированный продукт с меньшим содержанием примесей — для этого расплавленный белый фосфор сжигают в воздухе и подвергают образующийся оксид фосфора (V) гидратации.
Этот процесс упрощенно можно описать следующими реакциями: \[\begin{gather} \ce{4P + 5O2 -> 2P2O5};\\ \ce{P2O5 + 3H2O -> 2H3PO4}. \end{gather}\]
При нормальных условиях рассчитайте объем воздуха, который необходимо подавать в башню (камеру сжигания) в 1 ч для сжигания фосфора, содержащего 0,7% негорючих примесей (расход фосфора 2800 кг/ч). Ответ выразите в кубических метрах. Учтите, что для предотвращения образования оксида фосфора (III) в башню подают двукратный избыток воздуха по сравнению с расчетным количеством.
В расчете на один час количество вещества фосфора составляет \[n(P)=\frac mM=\frac{2800\cdot 0{,}993}{31}=89{,}69\text{~кмоль},\]
тогда \[\begin{gather} n_\text{теор}(\ce{O_2})=\frac 54n(\ce{P})=112,11\text{~кмоль};\\ n_\text{практ}(\ce{O_2})=2n_\text{теор}(\ce{O_2})=2\cdot 112,11=224,22\text{~кмоль}. \end{gather}\]
Объем кислорода: \[V(\ce{O_2})=n_\text{практ}(\ce{O_2})V_0=224{,}22\cdot 1000\cdot 22{,}4=5022658\text{~л,}\] объем воздуха \[V_\text{возд}=\frac{V(\ce{O_2})}{\chi(\ce{O_2})}=\frac {5022658}{0{,}21\cdot 1000}=23917\text{~м}^3.\]
23917. Диапазон 22240–25590.
Рассчитайте массу 70%-го раствора фосфорной кислоты, образующегося в башне. Ответ выразите в килограммах в час (кг/ч) с точностью до целых.
Количество вещества фосфорной кислоты соответствует количеству фосфора \(n(\ce{H_3PO_4})=n(P)=89{,}69\) кмоль/ч, тогда: \[\begin{gather} m(\ce{H_3PO_4})=n(\ce{H_3PO_4})M=89,69\cdot (3+31+16\cdot 4)=8789,62 \text{~кг/ч};\\ m_\text{р-ра}(\ce{H_3PO_4})=\frac{m(\ce{H_3PO_4})}{\omega(\ce{H_3PO_4})}=\frac{8789,62}{0,70}=12557\text{~кг/ч.} \end{gather}\]
12557. Диапазон 12553–12561.
Использование теплоты, выделяющейся при сгорании фосфора, позволяет значительно увеличить энергоэффективность проведения процесса. Рассчитайте массу угля, содержащего 10% негорючих примесей, которую удастся сэкономить при полном использовании тепла сгорания фосфора. Теплота сгорания белого фосфора в указанных условиях составляет 1764 кДж/моль, углерода — 394 кДж/моль. Ответ запишите в килограммах в час (кг/ч) с точностью до целых.
Количество теплоты, выделяющейся при сгорании фосфора, составляет \[Q=Q_Pn(P)=89{,}69\cdot 1764=158213~\text{МДж/ч},\] тогда \[\begin{gather} n(C)=\frac Q{Q_C}=\frac{158213\cdot 1000}{394}=401556\text{~моль/ч};\\ m(C)=n(C)M=401556\cdot 12=4819\text{~кг/ч};\\ m_\text{уголь}=\frac{m(C)}{\omega(C)}=\frac{4819}{0,90}=5354\text{~кг/ч.} \end{gather}\]
5354. Диапазон 5350–5358.
В качестве пищевой добавки ортофосфорная кислота выступает регулятором кислотности и консервантом: кислая среда препятствует размножению микроорганизмов и порче продукта. Именно наличие фосфорной кислоты в составе обуславливает способность газированных напитков растворять ржавчину и очищать бытовые поверхности, о которой снято много интернет-роликов. Впрочем, имеются сведения о стимулировании фосфорной кислотой вымывания кальция из организма и ее негативном влиянии на зубную эмаль при чрезмерном употреблении.

Рассчитайте концентрацию ионов водорода в 0,02 моль/л растворе фосфорной кислоты, если известно, что степень диссоциации кислоты по первой ступени составляет 46%, а диссоциацией по второй и третьей ступени можно пренебречь. Ответ приведите в миллимоль на литр (ммоль/л) с точностью до десятых.
Запишем уравнение диссоциации фосфорной кислоты по первой ступени: \[\ce{H3PO4 <--> H+ + H2PO4-}.\]
Степень диссоциации представляет собой отношение количества вещества, распавшегося на ионы, к общему количеству растворенного вещества: \[\alpha_I=\frac{n(\ce{H_2PO_4^-})}{n_0(\ce{H_3PO_4}) }.\]
В расчете на 1 л раствора \(n_0(\ce{H_3PO_4})=CV=0{,}02\cdot 1=0{,}02\) моль, \[\begin{gather} n(\ce{H^+})=n(\ce{H_2PO_4^-})=\alpha_In_0(\ce{H_3PO_4})=0,46\cdot 0,02=\\ =0,0092\text{~моль} =9,2\text{~ммоль.} \end{gather}\]
9,2.
Этого выдающегося ученого однажды спросили, кто такой исследователь. «В Солнечной системе, затерянной в спиралях одной из миллионов галактик, на одной из десятков миллионов планет стоит существо и пытается слабым взором охватить Вселенную. Почему ему это удается? В чем сила этого слабого обитателя затерянной в мироздании планеты? Я думаю, в вечном беспокойстве», — ответил академик. Пожалуй, только такой «беспокойный» человек мог охватить так много — от био- и геохимии до химии космоса. В начале карьеры этот ученый работал военным врачом и даже учился в двух университетах одновременно: в Военно-медицинской академии и на химфаке Ленинградского университета. Позднее он станет химиком, ядерщиком и даже планетологом.
Под руководством своего наставника В. Вернадского ученый начнет первое в мире исследование химического состава морских организмов. Он заложит биостанцию в Мурманске и проведет экспедицию по Баренцеву и Белому морям — в результате чего покажет, что живые организмы являются необходимым этапом круговорота элементов. Позднее он изучит влияние эволюции на изменение состава организмов и обоснует биогеохимический метод поиска полезных ископаемых.
Впоследствии он займется разработкой аналитических методов определения следов химических элементов в миллионных долях процента и меньше. Исследователь станет участником атомного проекта под руководством И. Курчатова, анализируя уран, тяжелую воду и другие материалы. Этот ученый станет основателем первой в России кафедры геохимии, организатором и первым директором Института геохимии и аналитической химии. Здесь он будет заниматься геохимией редких элементов, определит средние составы главных пород Земли, а после станет основоположником космохимии. Под его руководством определят состав лунного грунта, доставленного автоматическими станциями «Луна-16» и «Луна-20», а также состав атмосферы Венеры.
Имя этого ученого присвоено Институту геохимии, горному массиву на Луне и кратеру на Марсе, а также в его честь назван минерал, найденный на Кольском полуострове.
Назовите этого ученого:
- Сергей Васильевич Лебедев;
- Владимир Васильевич Марковников;
- Александр Павлович Виноградов;
- Александр Михайлович Зайцев;
- Николай Дмитриевич Зелинский;
- Карл Карлович Клаус;
- Николай Александрович Меншуткин;
- Николай Николаевич Зинин;
- Дмитрий Иванович Менделеев;
- Алексей Евграфович Фаворский.
C.
Освоение космоса имеет невероятную актуальность в наши дни, и тому есть объективные причины. Так, космонавтика позволяет развивать различные технологии, такие как системы навигации, спутниковая связь, наблюдение за погодой. В условиях изоляции и невесомости проводят биологические и медицинские исследования. Большой интерес изучение космоса вызывает у ученых как перспектива колонизация других планет или спутников в Солнечной системе, а также добыча ресурсов на астероидах.
Первостепенной задачей в обеспечении жизнедеятельности в космических аппаратах является поддержание необходимого химического состава атмосферы. В условиях замкнутого пространства уровень углекислого газа может быстро нарастать, что приводит к ухудшению самочувствия экипажа и в конечном итоге может стать причиной гибели. Поэтому регулярная очистка воздуха от углекислого газа является жизненно важной. Ранее в пилотируемых космических аппаратах для удаления углекислого газа использовались физико-химические методы — на американских космических кораблях применялись контейнеры с гидроксидом лития, а на советских — с надпероксидом калия, оба эти вещества связывают углекислый газ.
Современные технологии, используемые на борту Международной космической станции (МКС) и ранее на космической станции «Мир», используют многоразовые цеолитовые поглотители углекислоты. Цеолиты представляют собой пористые минералы, которые способны эффективно поглощать молекулы углекислого газа. Регенерация цеолитов проводится в особых аппаратах, где под воздействием высоких температур они высвобождают накопленный углекислый газ в забортное пространство.
Для получения надпероксида калия, используемого для регенерации воздуха в замкнутом пространстве, расплавленный калий сожгли в атмосфере с избытком кислорода. Оказалось, что в результате реакции кроме надпероксида калия образовался и пероксид калия. В образце смеси пероксида и надпероксида калия число атомов калия составило \(7{,}224 \cdot 10^{23}\), а атомов кислорода — \(1{,}204 \cdot 10^{24}\).
Определите массовую долю (в процентах) надпероксида калия в смеси с пероксидом (ответ округлите до целых).
Определим количество вещества атомов калия и кислорода: \[\begin{gather} n (K) = \frac{7,224 \cdot10^{23}}{6,02 \cdot10^{23}} = 1,2\text{ моль};\\ n (O) = \frac{1,204 \cdot10^{24}}{6,02 \cdot10^{23}} = 2\text{ моль.} \end{gather}\] Пусть \(n(\ce{KO2}) = x\) моль, а \(n(\ce{K2O2}) = y\) моль, тогда: \[\left\{\begin{aligned} &x + 2y = 1{,}2, \\ &2x + 2y = 2, \end{aligned}\right.\] \(x=0{,}8\) моль, \(y = 0{,}2\) моль. \[\begin{gather} m_{\ce{KO2}} = n \cdot M = 0,8 \cdot 71 = 56,8\text{ г};\\ m_{\ce{K2O2}} = n \cdot M = 0,2 \cdot 110= 22\text{ г};\\ m_\text{смеси} = 56,8 + 22 = 78,8\text{ г};\\ \omega_{\ce{KO2}} = \frac{56,8}{78,8} = 0,7208\text{ или }72\%. \end{gather}\]
72. Диапазон 71–73.
Определите, какой объем углекислого газа (в литрах) может поглотиться смесью надпероксида калия и пероксида калия массой 62,3 г при стандартных условиях. Массовая доля надпероксида калия в смеси с пероксидом составляет 91,2% (ответ округлите до целого числа).
Определяем массы и количества надпероксида калия и пероксида калия в смеси: \[\begin{gather} m({\ce{KO2}}) = 62,3 \cdot 0,912 = 56,8176\approx 56,8\text{ г};\\ m({\ce{K2O2}}) = 62,3 - 56,8176 = 5,4824\approx 5,5\text{ г};\\ n (\ce{KO2}) = \frac mM = \frac{56,8}{71} = 0,8\text{ моль};\\ n (\ce{K2O2}) = \frac mM = \frac{5,5}{110} = 0,05\text{ моль.} \end{gather}\] Составим уравнения протекающих реакций: \[\label{ch1011_0401} \ce{4KO2 + 2CO2 -> 2K2CO3 + 3O2};\] \[\label{ch1011_0402} \ce{2 K2O2 + 2 CO2 -> 2K2CO3 + O2}.\] По уравнениям реакций \eqref{ch1011_0401}, \eqref{ch1011_0402} определяем количество вещества углекислого газа, а затем его объем при нормальных условиях.
По уравнению \eqref{ch1011_0401}: \[n(\ce{CO2}) = \frac 12 n(\ce{KO2}) = \frac{0{,}8}2 = 0{,}4\text{ моль}.\]
По уравнению \eqref{ch1011_0402}: \[\begin{gather} n(\ce{CO2}) = n(\ce{K2O2}) = 0,05\text{ моль};\\ V(\ce{CO2}) = n \cdot V_m = (0,4 + 0,05) \cdot 22,4 = 10,08\text{ л.} \end{gather}\] В пересчете на стандартные условия (298 К) это составит: \[V(\ce{CO2}) = \frac{V_0 \cdot T_1}{T_0} = \frac{10{,}08\cdot 298}{273} = 11\text{ л.}\]
11.
Какая минимальная масса гидроксида лития может поглотить 11,2 л углекислого газа (н. у.) (ответ округлите до целых).
Взаимодействие гидроксида лития с углекислым газом при недостатке гидроксида лития описывается уравнением: \[\ce{LiOH + CO2 -> LiHCO3}.\]
Определяем количества углекислого газа: \[n (\ce{CO2}) = \frac V{V_m} = \frac{11{,}2}{22{,}4} = 0{,}5\text{ моль.}\] При соотношении веществ \(1 : 1\) имеем: \[\begin{gather} n (\ce{LiOH}) = n (\ce{CO2}) = 0,5\text{ моль};\\ m (\ce{LiOH}) = n \cdot M = 0,5 \cdot 24 = 12\text{ г.} \end{gather}\]
12. Диапазон 11–13.
Супероксид калия массой 85,2 г прореагировал с избытком углекислого газа. После завершения процесса образовавшееся твердое вещество растворили в 200 мл воды и добавили 300 мл 20%-го раствора хлорида кальция плотностью 1,181 г/мл. Определите массовую долю хлорида калия (в процентах) в полученном растворе (ответ округлите до десятых).
Составим уравнения протекающих реакций: \[\label{ch1011_0403} \ce{4KO2 + 2CO2 -> 2K2CO3 + 3O2};\] \[\label{ch1011_0404} \ce{K2CO3 + CaCl2 -> CaCO3 v + 2 KCl}.\] \[n (\ce{KO2}) =\frac mM =\frac{85{,}2}{71} = 1{,}2\text{ моль.}\]
Для того чтобы рассчитать массы хлорида калия и карбоната кальция, выпадающего в виде белого осадка, предварительно нужно определить избыток/недостаток реагирующих веществ. \[\begin{gather} n(\ce{K2CO3}) = \frac 12n (\ce{KO2}) =\frac{1,2}2 = 0,6\text{ моль};\\ m(\text{р-ра}\ce{CaCl2}) = V \cdot \rho = 300 \cdot 1,181 = 354,3\text{ г};\\ m(\ce{CaCl2}) = 354,3 \cdot 0,2 = 70,86\text{ г};\\ n(\ce{CaCl2}) = \frac mM = \frac{70,86}{111} = 0,638~ \text{моль} - \text{избыток};\\ A \ce{K2CO3} - \text{в~недостатке}. \end{gather}\] Количество вещества карбоната кальция, выпавшего в осадок, по уравнению реакции составляет: \[\begin{gather} n (\ce{CaCO3}) = n(\ce{K2CO3}) = 0,6 ~\text{моль};\\ m (\ce{CaCO3}) = n \cdot M = 0,6 \cdot 100 = 60~ \text{г};\\ n (\ce{KCl}) = 2 \cdot n(\ce{K2CO3}) = 0,6 \cdot 2 = 1,2 ~\text{моль};\\ m (\ce{KCl}) = n \cdot M = 1,2 \cdot 74,5 = 89,4 ~\text{г}. \end{gather}\] Определяем массу и массовую долю раствора: \[\begin{gather} m(\text{р-ра}) = m(\ce{H2O}) + m(\ce{K2CO3}) + m(\text{р-ра} \ce{CaCl2}) - m(\ce{CaCO3}) =\\ = 200 + 0,6 \cdot 138 + 354,3\text{ г} - 60 = 577,1\text{ г};\\ \omega (\ce{KCl}) = 15,49\approx 15,5\%. \end{gather}\]
15,5. Диапазон 15,2–15,8.
Одним из интересных аспектов аминокислот является их способность повышать внутриклеточное осмотическое давление, что позволяет клеткам адаптироваться к высоким концентрациям солей в окружающей среде. Эти свойства делают аминокислоты незаменимыми в биотехнологии, особенно когда речь идет о стабилизации белков.
Стабилизация белков — это важная задача, поскольку многие белки теряют свою активность при изменении условий окружающей среды, а добавление аминокислот помогает сохранить активную форму белков, предотвращая их денатурацию.
Таким образом, аминокислоты становятся неотъемлемой частью современных биотехнологий. Их применение охватывает широкий спектр областей, включая производство вакцин, терапевтических белков и других биофармацевтических препаратов. Исследования в этой области продолжаются, и, вероятно, в будущем мы увидим новые применения аминокислот, которые откроют дополнительные горизонты в биотехнологии и фармацевтике.
В процессе исследования некоторая аминокислота массой 17,4 г была подвергнута термическому разложению. Продукты сгорания были направлены последовательно через слой пентаоксида фосфора, в результате масса твердого вещества увеличилась на 12,6 г. Оставшиеся газообразные продукты были пропущены через избыток известковой воды. В результате образовался осадок, масса которого составила 60 г и 4,48 л газа (н. у.), образовавшегося в процессе горения, не поглотилась. Определите аминокислоту.
Определите молекулярную формулу аминокислоты. Запишите ее в формате \(\ce{C1H2O3N4}\).
Определим количества веществ, образующихся в результате термического разложения аминокислоты и количества элементов, входящих в ее состав.
В процессе термического разложения аминокислот образуется углекислый газ, вода, а для серосодержащих аминокислот еще и сероводород. При пропускании газообразной смеси над пентаоксидом фосфора с ним реагирует вода с образованием фосфорной кислоты, следовательно, увеличение массы твердого вещества обусловлено водой: \[\begin{gather} \ce{P2O5 + 3 H2O -> 2 H3PO4};\\ n (\ce{H2O}) = \frac{12,6}{18} = 0,7\text{ моль;}\\ n (H) = 2\cdot n (\ce{H2O}) = 2\cdot 0,7 = 1,4\text{ моль;}\\ m (H) = n\cdot M = 1\cdot 1 = 1,4\text{ г.} \end{gather}\] Известковая вода, представляющая собой раствор гидроксида кальция, связывает углекислый газ в нерастворимый карбонат кальция: \[\begin{gather} \ce{Ca(OH)2 + CO2 -> CaCO3 v + H2O};\\ n (\ce{CaCO3}) = \frac{60}{100}= 0,6\text{ моль};\\ n (\ce{CO2}) = n (\ce{CaCO3}) = 0,6\text{ моль};\\ m (\ce{C}) = n\cdot M = 0,6\cdot 12 = 7,2\text{ г.} \end{gather}\] Непоглотившийся известковой водой газ — это инертный азот, его количество составляет: \[\begin{gather} n (\ce{N2}) = \frac{4,48}{22,4} = 0,2\text{ моль};\\ n (\ce{N}) = 2\cdot n (\ce{N2}) = 2\cdot 0,2 = 0,4\text{ моль};\\ m (\ce{N}) = n\cdot M = 0,4\cdot 14 = 5,6\text{ г.} \end{gather}\] В аминокислотах содержится кислород, определяем его массу: \[\begin{gather} m (\ce{O}) =17,4 - 7,2 - 1,4 - 5,6 = 3,2\text{ г};\\ n (\ce{O}) = \frac{3,2}{16} = 0,2\text{ моль};\\ n (\ce{C}) : n (\ce{H}) : n (\ce{O}) : n (\ce{N}) = 0,6 : 1,4 : 0,2 : 0,4 = 3 : 7 : 1 : 2 ~(\times 2). \end{gather}\] Элементарная формула — \(\ce{C3H7ON2}\) — такой аминокислоты не существует, \[\begin{gather} n (\ce{C}) : n (\ce{H}) : n (\ce{O}) : n (\ce{N}) = 3 : 7 : 1 : 2~(\times 2);\\ n (\ce{C}) : n (\ce{H}) : n (\ce{O}) : n (\ce{N}) = 6 : 14 : 2 : 4. \end{gather}\] Молекулярная формула аминокислоты — \(\ce{C6H14O2N4}\).
\(\ce{C6H14O2N4}\).
Запишите тривиальное название данной аминокислоты.
Аминокислота, имеющая брутто-формулу \(\ce{C6H14O2N4}\) — аргинин.
Аргинин интересен тем, что это аминокислота, которая является эффективным реагентом для рефолдинга рекомбинантных белков. Этот процесс, в котором белки возвращаются к своей вторичной и третичной структуре после денатурации. Аргинин способствует этому процессу, подавляя агрегацию белков и тем самым повышая эффективность рефолдинга. Уникальные свойства делают его ценным инструментом в исследованиях и разработке новых белков, особенно в фармацевтическом контексте. Кроме того, аргинин способствует солюбилизации белков, которые находятся в рыхлых телах включения, что значительно упрощает процесс получения активных белков. Это особенно важно для разработки терапевтических белков.
Аргинин.
Какой является данная аминокислота с точки зрения синтеза в организме человека:
- заменимой,
- незаменимой.
В ответе укажите только цифру.
По значению для организма человека аминокислоты разделяют на заменимые и незаменимые. Заменимые аминокислоты — это те, которые организм может производить самостоятельно из других аминокислот и веществ, поступающих в организм. Незаменимые аминокислоты — необходимые аминокислоты, которые не могут быть синтезированы в организме. Для человека незаменимыми являются: валин, лейцин, изолейцин, метионин, триптофан, фенилаланин, треонин, лизин и гистидин.
Аргинин — заменимая аминокислота для организма человека.
1.
Рассмотрим такую систему: мембрана, по разные стороны от которой расположены растворы с разным содержанием растворенного вещества. Поры полупроницаемой мембраны пропускают молекулы растворителя, но не молекулы растворенного вещества. Из-за того, что концентрации растворов различны, растворитель (например, вода) начнет диффундировать (перетекать) из более разбавленного раствора в более концентрированный и разбавлять его до тех пор, пока концентрация не станет равной по обе стороны мембраны. Это явление называют осмосом.

Осмотическим давлением называют величину избыточного давления на раствор, отделенный от чистого растворителя полупроницаемой мембраной, при котором прекращается осмос, то есть диффузия растворителя через мембрану. Голландский химик Якоб Хендрик Вант-Гофф установил, что для разбавленных растворов осмотическое давление прямо пропорционально молярной концентрации частиц (молекул, ионов) растворенного вещества: \[\pi=CRT,\] где \(\pi\) — осмотическое давление, кПа; \(C\) — молярная концентрация частиц (молекул, ионов) растворенного вещества, моль/л; \(R\) — универсальная газовая постоянная, 8,314 Дж/(моль\(\cdot\)К); \(T\) — температура, К. Это открытие было отмечено первой Нобелевской премией по химии.
Мембраны всех живых клеток используют осмос для контроля поглощения необходимых веществ, поэтому он играет очень важную роль в медицине, биотехнологии и агротехнологии, особенно в гидропонике. Осмос помогает растениям расти и всасывать воду корневой системой — поскольку в клеточном соке концентрация солей и сахаров выше, чем в почвенном растворе. Это важно учитывать при внесении удобрений — если осмотическое давление почвенного раствора станет слишком большим, поступление воды в растение прекратится, и оно погибнет (например, как в засоленных почвах).
При температуре 25 °C рассчитайте осмотическое давление раствора удобрения (250 г мочевины в 7,5 л воды). Ответ запишите в килопаскалях (кПа) с точностью до целых.
Количество вещества мочевины: \[n(\ce{NH_2CONH_2})=\frac{m(\ce{NH_2CONH_2})}M=\frac{250}{16\cdot 2+28}=4{,}17\text{ моль,}\] соответственно молярная концентрация раствора \[C(\ce{NH_2CONH_2})=\frac{n(\ce{NH_2CONH_2})}V=\frac{4{,}17}{7{,}5}=0{,}56\text{ моль/л.}\]
Осмотическое давление \(\pi=CRT=0{,}56\cdot 8{,}314\cdot (273+25)=1387\) кПа.
1387. Диапазон 1350–1400.
В медицине при внутривенном введении используют изотонические растворы — растворы, осмотическое давление которых соответствует давлению плазмы крови — в такой среде вода не поступает в клетку и не выводится из клетки, что предотвращает от повреждения эритроциты. Изотонический раствор хлорида натрия применяют как дезинтоксикационное средство, для коррекции состояния систем организма в случае обезвоживания и как растворитель других лекарственных препаратов.

Рассчитайте массовую долю хлорида натрия в разбавленном растворе, осмотическое давление которого при температуре 37 °С составляет 5199 кПа (плотность примите \(\rho=1035\) г/л). Ответ запишите в процентах с точностью до сотых.
Рассчитаем концентрацию частиц в растворе, исходя из величины осмотического давления: \[C=\frac{\pi}{RT}=\frac {5199 }{8{,}314\cdot (273+37)}=2{,}02\text{~моль/л.}\]
Хлорид натрия — электролит, диссоциирующий в растворе на ионы \(\ce{Na^+}\) и \(\ce{Cl^-}\). Поскольку точная степень диссоциации в информации не указана, а раствор является разбавленным, ее можно принять равной 100%.
Тогда концентрация хлорида натрия составляет: \[C(\ce{NaCl})=\frac C2=\frac {2{,}02}2=1{,}01\text{~моль/л,}\] а масса соли в 1 л раствора: \[m(\ce{NaCl})=n(\ce{NaCl})\cdot M=C(\ce{NaCl})\cdot V\cdot M=1{,}01\cdot 1\cdot (23+35{,}5)=59{,}09\text{~г}.\]
Массовая доля в растворе \[\omega=\frac{m\ce{NaCl}}{m_\text{р-ра}}=\frac{59{,}09}{1\cdot 1035}\cdot 100=5{,}7 \%.\]
5,7. Диапазон 5,5–5,9.
Измерение осмотического давления является одним из распространенных методов определения молекулярной массы полимера, влияющей на его свойства. Например, полипропилен с высокой молекулярной массой обладает более высокими показателями предела прочности при растяжении, относительного удлинения при разрыве, ударной вязкости при изгибе и растяжении. Мембранный осмометр основан на измерении разности давлений — например, по разности высот в капиллярах раствора и растворителя, поскольку гидростатическое давление уравновешивает осмотическое.
Установите молекулярную массу полипропилена, если разность высот жидкости в осмометре для его раствора в тетралине, содержащего 2,5 г в 250 мл раствора, составляет 2,1 см при 20 °С. Ответ выразите в килограммах на моль (кг/моль) с точностью до целых. Плотность тетралина и раствора 973 \(\text{кг/м}^3\).
Гидростатическое давление столба жидкости уравновешивает осмотическое давление, для удобства расчета используем единицы измерения системы СИ: \[\pi=CRT=\rho g \Delta h=973\cdot 9{,}8\cdot (2{,}1\cdot 10^{-2})=200\text{~Па.}\]
Молярная концентрация раствора полимера составляет \[C=\frac {\pi}{RT}=\frac {200}{8{,}314\cdot (273+20)}=0{,}082\text{~моль/м}^3,\] то есть количество вещества полимера \[n=CV=0{,}082\cdot \frac{0{,}1}{1000}=0{,}008\text{~ммоль.}\]
Тогда молекулярная масса \[M=\frac mn=\frac {2{,}5}{0{,}008}=312{,}5\text{~кг/моль.}\]
312,5. Диапазон 290–320.
Ортофосфорная кислота используется в самых разных областях — в производстве удобрений и чистящих средств, для деревообработки и очистки металла от ржавчины, в стоматологии для реставрации зубов и в ювелирном деле при пайке. Также она зарегистрирована в качестве пищевой добавки E338, которую можно встретить в составе мармеладов, сиропов и напитков, хлебобулочных изделий, сыров и плавленых сырков.
Пищевую фосфорную кислоту производят термическим способом, позволяющим получить концентрированный продукт с меньшим содержанием примесей — для этого белый фосфор сжигают в воздухе и подвергают образующийся оксид фосфора (V) гидратации.
При нормальных условиях рассчитайте объем воздуха, который необходимо подавать в башню (камеру сжигания) в 1 ч для сжигания фосфора, если известно, что расход образующегося в башне 70%-го раствора фосфорной кислоты составляет 2200 кг/ч. Ответ приведите в кубических метрах с точностью до целых. Учтите, что для предотвращения образования оксида фосфора (III) в башню подают двукратный избыток воздуха по сравнению с расчетным количеством.
Запишем уравнения происходящих реакций: \[\begin{gather} \ce{P4 + 5O2 -> P4O10};\\ \ce{P4O10 + 6H2O -> 4H3PO4}. \end{gather}\]
Масса фосфорной кислоты: \[m(\ce{H_3PO_4})=m_\text{р-ра}\omega_{\ce{H_3PO_4}}=2200\cdot 0{,}70=1540 \text{~кг/ч.}\]
Количество вещества фосфорной кислоты: \[n(\ce{H_3PO_4})=\frac{m(\ce{H_3PO_4})}{M}=\frac{1540}{3+31+16\cdot 4}=15{,}71 \text{~кмоль/ч},\] что соответствует расчетному количеству вещества кислорода \[\begin{gather} n_\text{теор}(\ce{O2})=\frac 54n(\ce{H_3PO_4})=19,64\text{~кмоль/ч};\\ n_\text{практ}(\ce{O2})=2n_\text{теор}(\ce{O2})=2\cdot 19,64 =39,28 \text{~кмоль/ч}. \end{gather}\] Объем кислорода \[V(\ce{O2})=n_\text{практ}(\ce{O2})V_0=39{,}28\cdot 1000\cdot 22{,}4=880000\text{ л,}\] объем воздуха \[V_\text{возд}=\frac {V(\ce{O2})}{\chi(\ce{O2})}=\frac {880000}{0{,}21\cdot 1000}=4190 \text{~м}^3.\]
4190. Диапазон 3890–4490.
Использование теплоты, выделяющейся при сгорании фосфора, позволяет значительно увеличить энергоэффективность проведения процесса. При стандартных условиях рассчитайте теплоту, которая выделяется в ходе проходящих реакций при образовании указанного в подзадаче № 1 количества фосфорной кислоты. Используйте данные таблицы, ответ приведите в мегаджоулях (МДж) с точностью до целых.
| Вещество | \(\ce{P4O10}\)\(_\text{(тв)}\) | \(\ce{H3PO4}\)\(_\text{(ж)}\) | \(\ce{H2O}\)\(_\text{(ж)}\) |
|---|---|---|---|
| Теплота образования, кДж/моль | 2984,03 | 1266,90 | 285,83 |
В соответствии со следствием из закона Г. И. Гесса теплоту каждой из протекающей реакции можно выразить как разность между суммами теплот образования продуктов и реагентов с учетом стехиометрических коэффициентов: \[\begin{gather} \Delta_rQ=\Sigma n_i Q_f(\text{прод})-\Sigma n_j Q_f(\text{реаг});\\ \Delta_{r1}Q=Q_f(\ce{P_4 O_{10(\text{тв})}})-Q_f(\ce{P_{4(\text{тв})}})-5Q_f(\ce{O_{2(\text{г})}});\\ \Delta_{r2}Q=4Q_f(\ce{H_3PO_{4(\text{ж})}})-6Q_f(\ce{H_2 O_{(\text{ж})}})-Q_f(\ce{P_4 O_{10 (\text{тв})}}). \end{gather}\] С учетом того, что теплоты образования простых веществ равны нулю, получим: \[\begin{gather} \Delta_{r1}Q=2984,03\text{~кДж/моль};\\ \Delta_{r2}Q=4\cdot 1266,90-6\cdot 285,83-2984,03=368,59\text{~кДж/моль.} \end{gather}\] В расчете на 4 моль фосфорной кислоты \[Q_R=\Delta_{r1}Q+\Delta_{r2}Q=3352{,62}~\text{кДж/моль}.\]
Тогда \[Q=Q_R\cdot \displaystyle\frac{n(\ce{H_3PO_4})}4=3352{,62}\cdot \displaystyle\frac{15{,}71}4=13167~\text{МДж}.\]
13167. Диапазон 13080–13250.
В качестве пищевой добавки ортофосфорная кислота выступает регулятором кислотности и консервантом: кислая среда препятствует размножению микроорганизмов и порче продукта. Именно наличие фосфорной кислоты в составе обуславливает способность газированных напитков растворять ржавчину и очищать бытовые поверхности, о которой снято много интернет-роликов. Впрочем, имеются сведения о стимулировании фосфорной кислотой вымывания кальция из организма и ее негативном влиянии на зубную эмаль при чрезмерном употреблении.

Рассчитайте \(pH\) 0,35 моль/л раствора фосфорной кислоты с точностью до десятых, если известно, что константа диссоциации кислоты по первой ступени составляет \(7{,}52\cdot 10^{-3}\), а диссоциацией по второй и третьей ступени можно пренебречь.
Запишем уравнение диссоциации фосфорной кислоты по первой ступени: \[\ce{H3PO4 <--> H+ + H2PO4-}.\]
Выражение для константы диссоциации: \[K_I=\frac {[\ce{H2PO4-}][\ce{H+}]}{[\ce{H3PO4}]},\] где в квадратных скобках указаны равновесные концентрации.
Тогда \[\begin{gather} [\ce{H2PO4-}]=[\ce{H+}], [\ce{H3PO4}]=\ce{C0}-[\ce{H+}];\\ K_I=\frac{[\ce{H+}]^2}{\ce{C0}-[\ce{H+}]}=7,52\cdot 10^{-3}. \end{gather}\] Решение уравнения при \(C_0=0{,}35\) моль/л позволяет найти \[[\ce{H+}]=0{,}051\text{~моль/л,}\] откуда \(pH=-lg ([\ce{H+}])\approx 1{,}3.\)
1,3.
Этого выдающегося ученого однажды спросили, кто такой исследователь. «В Солнечной системе, затерянной в спиралях одной из миллионов галактик, на одной из десятков миллионов планет стоит существо и пытается слабым взором охватить Вселенную. Почему ему это удается? В чем сила этого слабого обитателя затерянной в мироздании планеты? Я думаю, в вечном беспокойстве», — ответил академик. Пожалуй, только такой «беспокойный» человек мог охватить так много — от био- и геохимии до химии космоса. В начале карьеры этот ученый работал военным врачом и даже учился в двух университетах одновременно: в Военно-медицинской академии и на химфаке Ленинградского университета. Позднее он станет химиком, ядерщиком и даже планетологом.
Под руководством своего наставника В. Вернадского ученый начнет первое в мире исследование химического состава морских организмов. Он заложит биостанцию в Мурманске и проведет экспедицию по Баренцеву и Белому морям — в результате чего покажет, что живые организмы являются необходимым этапом круговорота элементов. Позднее он изучит влияние эволюции на изменение состава организмов и обоснует биогеохимический метод поиска полезных ископаемых.
Впоследствии он займется разработкой аналитических методов определения следов химических элементов в миллионных долях процента и меньше. Исследователь станет участником атомного проекта под руководством И. Курчатова, анализируя уран, тяжелую воду и другие материалы. Этот ученый станет основателем первой в России кафедры геохимии, организатором и первым директором Института геохимии и аналитической химии. Здесь он будет заниматься геохимией редких элементов, определит средние составы главных пород Земли, а после станет основоположником космохимии. Под его руководством определят состав лунного грунта, доставленного автоматическими станциями «Луна-16» и «Луна-20», а также состав атмосферы Венеры.
Имя этого ученого присвоено Институту геохимии, горному массиву на Луне и кратеру на Марсе, а также в его честь назван минерал, найденный на Кольском полуострове.
Назовите этого ученого:
- Сергей Васильевич Лебедев;
- Владимир Васильевич Марковников;
- Александр Павлович Виноградов;
- Александр Михайлович Зайцев;
- Николай Дмитриевич Зелинский;
- Карл Карлович Клаус;
- Николай Александрович Меншуткин;
- Николай Николаевич Зинин;
- Дмитрий Иванович Менделеев;
- Алексей Евграфович Фаворский.
C.