Предметный тур. Математика. 3 этап

  \[\begin{gather} 7^4 = 49 \cdot 49 \equiv 1 \ (\mathrm{mod}\ {10});\\ 2024\, \vdots\, 4 \Rightarrow 7^{2024} \equiv 1\ (\mathrm{mod}\ {10});\\ 2025 \equiv 5 \ (\mathrm{mod}\ {10}) \Rightarrow 2025^7 \equiv 5\ (\mathrm{mod}\ {10});\\ 3^{2026} = 3^{2024} \cdot 3^2 = (3^4)^{506} \cdot 9 \equiv 9\ (\mathrm{mod}\ {10}) \Rightarrow\\ \Rightarrow 7^{2024} + 2025^7 - 3^{2026} \equiv 7\ (\mathrm{mod}\ {10}). \end{gather}\]

1. \(y = 0\) или \(y = 1 \Rightarrow y! = 1 \Rightarrow x^2 = 1 \Leftrightarrow x = \pm 1\).
2. \(y = 2 \Rightarrow \begin{cases} x^2 = 3, \\ x \in \mathbb{Z}. \end{cases} \Rightarrow x \in \varnothing\).
3. \(y = 3 \Rightarrow \begin{cases} x^2 = 11, \\ x \in \mathbb{Z}. \end{cases} \Rightarrow x \in \varnothing\).
4. \(y \geqslant 3 \Rightarrow y!\, \vdots \,3\), \(x^2 + 1 = 2 \cdot y!\). Но \(x^2\) при делении на 3 дает только остатки 0 или 1, следовательно, \(x^2 + 1\) не делится на 3.

1. 14 различных треугольников:

   • 1, 1, 1;
   • 1, 5, 5;
   • 1, 6, 6;
   • 1, 7, 7;
   • 5, 5, 5;
   • 5, 5, 6;
   • 5, 5, 7;
   • 5, 6, 6;
   • 5, 7, 7;
   • 5, 6, 7;
   • 6, 6, 6;
   • 6, 6, 7;
   • 6, 7, 7;
   • 7, 7, 7.

   \(\sum_{i=1}^{14} P_i = 222\).

2. Девять равнобедренных треугольников:

   • 1, 5, 5;
   • 1, 6, 6;
   • 1, 7, 7;
   • 5, 5, 6;
   • 5, 5, 7;
   • 5, 6, 6;
   • 5, 7, 7;
   • 6, 6, 7;
   • 6, 7, 7.

   Четыре равносторонних треугольника:

   • 1, 1, 1;
   • 5, 5, 5;
   • 6, 6, 6;
   • 7, 7, 7.

1. Пусть \(TP\) — средняя линия трапеции, \(EF\) — высота трапеции, проходящая через точку \(O\). \(EF \cap TP = K\).
2. \(TP = \dfrac{BC + AD}{2} = 16\), \(KP = 8\).
3. \(\triangle OPK\) прямоугольный, \(OK = 6\).
4. \(\triangle BEO \sim \triangle DFO\) по двум углам: \(\angle BOE = \angle DOF\) (вертикальные), \(\angle EBO = \angle FDO\) (внутренние накрест лежащие при \(AD \parallel BC\) и секущей \(BD\)). Отсюда следует: \(\dfrac{BE}{FD} = \dfrac{1}{3} = \dfrac{EO}{OF}\).
5. \(EO = \dfrac{1}{4} EF\), \(EK = \dfrac{1}{2} EF \Rightarrow OK = \dfrac{1}{4} EF = 6 \Rightarrow EF = 24\).
6. \(S_{ABCD} = 16 \cdot 24 = 384\).

1. \(\dfrac{(x + 3)^3}{\sqrt{x + 5}} = x + 5 \Rightarrow \begin{cases} (x + 3)^3 = (\sqrt{x + 5})^3, \\ x \neq -5. \end{cases}\)
2. \(f(t) = t^3\) — монотонная функция \(\Rightarrow x + 3 = \sqrt{x + 5}\).
3. \(\begin{cases} x^2 + 6x + 9 = x + 5, \\ x > -3. \end{cases} \Rightarrow \begin{cases} x^2 + 5x + 4 = 0, \\ x > -3. \end{cases} \Rightarrow \begin{cases} x = -4 \text{ или } x = -1, \\ x > -3. \end{cases} \Rightarrow x = -1\).

  \[\begin{gather} 7^4 = 49 \cdot 49 \equiv 1 \ (\mathrm{mod}\ {10});\\ 7^{2025} = (7^4)^{506} \cdot 7 \equiv 7 \ (\mathrm{mod}\ {10}); \\ 2024^7 \equiv 4^6 \cdot 4 \equiv 6 \cdot 4 \equiv 4 \ (\mathrm{mod}\ {10}); \\ 12^{2026} = (3^4)^{506} \cdot 3^2 \cdot (4^2)^{1013} \equiv 1 \cdot 9 \cdot 6 \equiv 4 \ (\mathrm{mod}\ {10}); \\ 7^{2025} - 2024^7 - 12^{2026} < 0; \\ 7^{2025} - 2024^7 - 12^{2026} \equiv 7 - 4 - 4 = -1. \end{gather}\] Число оканчивается на 1.

1. \(y = 0\) или \(y = 1 \Rightarrow y! = 1 \Rightarrow x^2 = 4 \Leftrightarrow x = \pm 2\).
2. \(y = 2 \Rightarrow \begin{cases} x^2 = 5 \\ x \in \mathbb{Z} \end{cases} \Rightarrow x \in \varnothing\).
3. \(y = 3 \Rightarrow \begin{cases} x^2 = 9 \\ x \in \mathbb{Z} \end{cases} \Rightarrow x = \pm 3\).
4. \(y \geqslant 4 \Rightarrow y! \,\vdots\, 4\), \(y! + 3 \equiv 3 \ (\mathrm{mod}\ {4})\). Но \(x^2\) при делении на 4 дает только остатки 0 или 1.

1. \(2025 ~\vdots~ 3\).

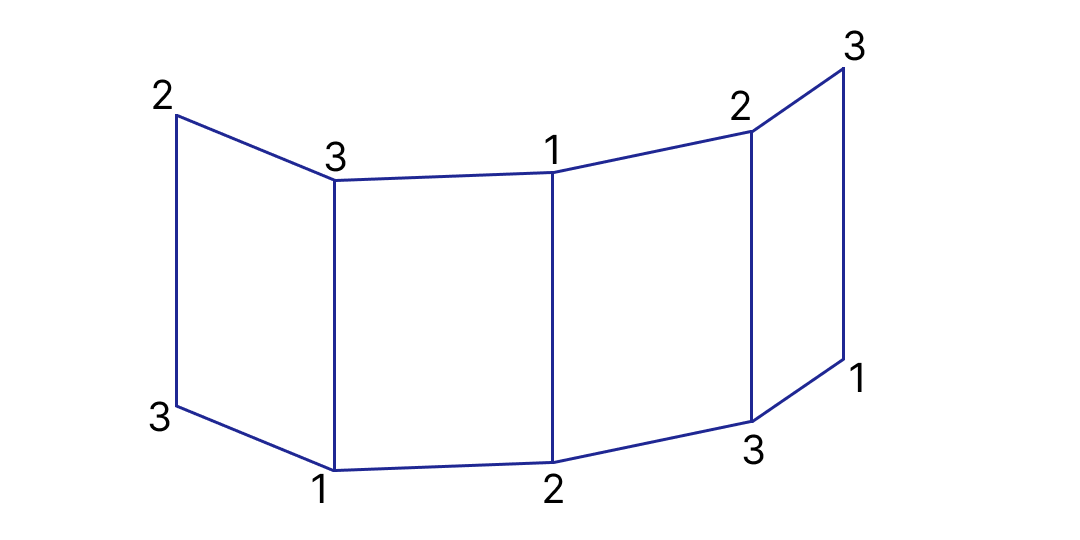
   Занумеруем все вершины на одном из оснований 1, 2, 3, 1, 2, 3…и в том же направлении — на другом со сдвигом на одно ребро.

   
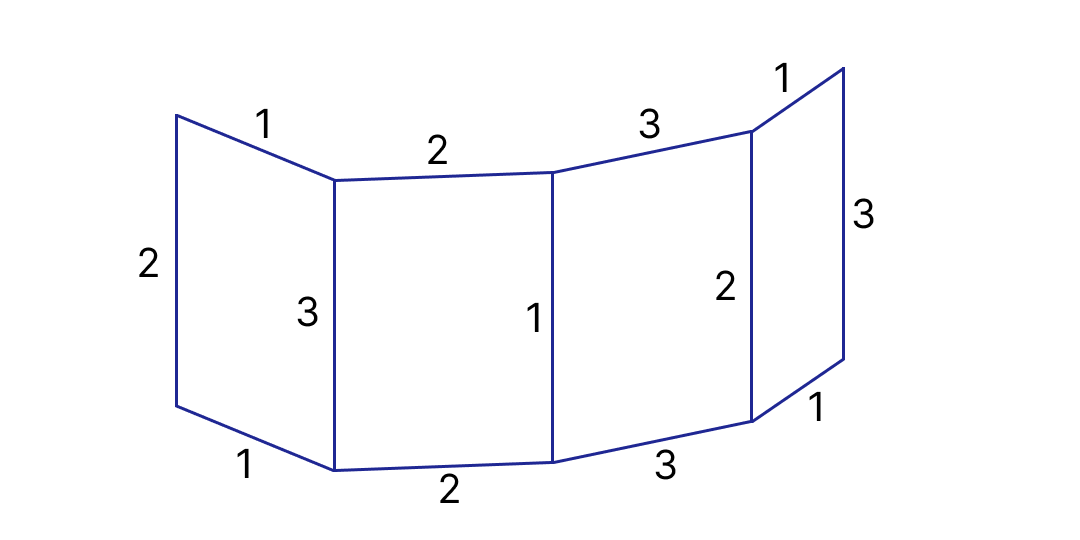
   Рис. 2.1.

2. Достаточно привести подтверждающий пример, см. рис. 2.2.

   
   Рис. 2.2.

1. 16 различных треугольников:

   • 2, 2, 2;
   • 2, 4, 4;
   • 2, 4, 5;
   • 2, 5, 5;
   • 2, 5, 6;
   • 2, 6, 6;
   • 4, 4, 4;
   • 4, 4, 5;
   • 4, 4, 6;
   • 4, 5, 5;
   • 4, 5, 6;
   • 4, 6, 6;
   • 5, 5, 5;
   • 5, 5, 6;
   • 5, 6, 6;
   • 6, 6, 6.

   \(\sum_{i=1}^{16} P_i = 216\).

2. 9 равнобедренных треугольников:

   • 2, 4, 4;
   • 2, 5, 5;
   • 2, 6, 6;
   • 4, 4, 5;
   • 4, 4, 6;
   • 4, 5, 5;
   • 4, 6, 6;
   • 5, 5, 6;
   • 5, 6, 6.

   \(P = \dfrac{9}{16}\).

   4 равносторонних треугольника:

   • 2, 2, 2;
   • 4, 4, 4;
   • 5, 5, 5;
   • 6, 6, 6.

   \(P = \dfrac{13}{16}\).

1. \(AM = MC\), \(\angle AMK = \angle CMB\) (вертикальные), \(\angle BCM = \angle MAK\) (внутренние накрест лежащие при \(AD \parallel BC\) и секущей \(AC\)).

   Отсюда: \(\triangle AMK = \triangle CMB\) по стороне и двум прилежащим углам. Значит, \(AK = BC \Rightarrow \dfrac{BC}{AD} = \dfrac{1}{3}\).

2. \(\dfrac{S_{BCD}}{S_{ABD}} = \dfrac{1}{3}\), \(S_{BCD} = \dfrac{1}{4} S_{ABCD} = 12\).

3. \(\triangle BTC \sim \triangle DTK\) по двум углам: \(\angle BTC = \angle DTK\) (вертикальные), \(\angle BCT = \angle TKD\) (внутренние накрест лежащие при \(AD \parallel BC\) и секущей \(KC\)).

   Отсюда следует, что \(\dfrac{BT}{TC} = \dfrac{BC}{KD} = \dfrac{1}{2}\), а значит, \(S_{BTC} = \dfrac{1}{3} S_{BCD} = 4\).