Предметный тур. Информатика. 3 этап
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 3 с.
Ограничение по памяти: 256 Мбайт.
Android-разработчик Егор Алексеев пытался продвинуть в МИФИ стартап по разработке собственных зарядных станций и пауэрбанков «ЯдерБанки». Поскольку один из членов комиссии по обсуждению актуальности стартапа недавно попал в невыгодную ситуацию, при которой во время перехода из одного учебного корпуса в другой у него сел телефон, а зарядка осталась в первом из них, было принято решение стартовать разработку прототипа мобильного приложения для данной задачи.
В зданиях университета есть \(count_d\) «ЯдерБанков», каждый из которых имеет свой начальный уровень заряда. Однако для клиентов важно, чтобы уровень заряда определенного «ЯдерБанка» был не меньше некоторого минимума к моменту, когда они им воспользуются.
Чтобы повысить уровень заряда этих «ЯдерБанков», сервис проводит \(count_s\) «этапов пополнения». На каждом этапе выбираются параметры \(first,\, last,\, a,\, b\). Затем выполняется серия действий по рядам устройств, пронумерованных подряд от 1 до \(N\):
- «ЯдерБанку» с номером \(first\) добавляется \(a\) единиц заряда.
- «ЯдерБанку» с номером \(first + 1\) добавляется \(a + b\) единиц заряда.
- «ЯдерБанку» с номером \(first + 2\) добавляется \(a + 2 \cdot b\) единиц заряда.
- «ЯдерБанку» с номером \(last\) добавляется \(a + (last - first) \cdot b\) единиц заряда.
Таким образом, по каждому устройству в диапазоне \(\left[first;\, last\right]\) распределяется дополнительный заряд, который растет линейно с каждым следующим устройством.
Для заданного «ЯдерБанка» необходимо определить номер первого этапа, после которого его заряд окажется не меньше требуемой величины.
Формат входных данных
В первой строке задано целое число \(count_d\, (1 \leqslant count_d \leqslant 10^5)\) — количество «ЯдерБанков».
Во второй строке заданы \(count_d\) целых чисел \(device_{i}\, (0 \leqslant device_{i} \leqslant 10^9)\) — начальное количество заряда в пауэрбанке с соответствующим ему индексом.
В третьей строке заданы \(count_d\) целых чисел \(charge_{i}\, (0 \leqslant charge_{i} \leqslant 10^9)\) — необходимое минимальное количество заряда в ЯдерБанке с соответствующим ему индексом.
В четвертой строке задано число \(count_s\, (0 \leqslant count_s \leqslant 10^5)\) — количество этапов увеличения единиц заряда в «ЯдерБанках».
В следующих \(count_s\) строках записаны сами этапы по порядку при помощи чисел \(first,\, last,\, a,\, b\ (1 \leqslant first \leqslant last \leqslant count_d,\, 0 \leqslant a, b \leqslant 10^5)\).
Формат выходных данных
Выведите \(count_d\) чисел, где для каждого «ЯдерБанка» с индексом \(i\) значение равняется 0, если исходного заряда было достаточно уже в самом начале; номер первого этапа от одного до \(count_s\), после которого уровень заряда впервые достиг или превысил требуемое значение; (\(-1\)) — если даже после всех \(count_s\) пополнений необходимый уровень заряда так и не был достигнут.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
5 5 4 4 2 1 7 7 4 7 7 3 1 2 2 0 2 5 1 1 3 4 2 2 |
1 2 0 3 -1 |
В задаче требуется для каждого из \(n\) устройств с начальными зарядами \(a_i\) и целевыми уровнями \(b_i\) определить номер первой из \(m\) операций, после которых заряд этого устройства достигнет или превысит \(b_i\). Каждая операция на отрезке \([l, r]\) добавляет линейно возрастающую последовательность (начальное значение \(x\), приращение \(y\)). Прямое применение каждой операции к каждому элементу отрезка и проверка всех устройств после каждой операции дают время \(\mathcal{O}(mn)\), что при \(n, m\leqslant10^5\) слишком медленно.
Чтобы обойти это, будем обрабатывать операции блоками по размеру \(S\) (например, \(S \approx 450\)). Внутри каждого блока операции накапливаются в разностных массивах с отложенными (ленивыми) обновлениями: один массив аккумулирует константную часть прибавок на отрезке, второй — коэффициент при индексе, а вспомогательный массив устраняет влияние линейного роста за пределами отрезка.
Пример программы-решения
Ниже представлено решение на языке Java.
import java.io.*;
import java.util.*;
public class Main {
private static final int SZ = 450;
static int n, m;
static long[] a, b;
static int[] ans;
static long[] sumX, sumY, sub;
static int[] l, r, x, y, num;
static int k = 0;
private static void doLazyUpdate() {
for (int i = 1; i <= k; i++) {
sumX[l[i]] += x[i];
sumX[r[i] + 1] -= x[i];
sumY[l[i] + 1] += y[i];
sumY[r[i] + 1] -= y[i];
sub[r[i] + 1] += 1L * y[i] * (r[i] - l[i]);
}
long add = 0;
for (int i = 1; i <= n; i++) {
sumX[i] += sumX[i - 1];
long initialValue = a[i];
a[i] += sumX[i];
sumY[i] += sumY[i - 1];
add += sumY[i] - sub[i];
a[i] += add;
if (ans[i] == -1 && a[i] >= b[i]) {
long value = initialValue;
for (int j = 1; j <= k; j++) {
if (l[j] > i || r[j] < i) continue;
value += x[j];
value += 1L * y[j] * (i - l[j]);
if (value >= b[i]) {
ans[i] = num[j];
break;
}
}
}
sumX[i - 1] = 0;
sumY[i - 1] = 0;
sub[i - 1] = 0;
}
sumX[n] = 0;
sumY[n] = 0;
sub[n] = 0;
k = 0;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
a = new long[n + 5];
b = new long[n + 5];
ans = new int[n + 5];
sumX = new long[n + 5];
sumY = new long[n + 5];
sub = new long[n + 5];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
a[i] = Long.parseLong(st.nextToken());
}
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
b[i] = Long.parseLong(st.nextToken());
ans[i] = (a[i] >= b[i] ? 0 : -1);
}
st = new StringTokenizer(br.readLine());
m = Integer.parseInt(st.nextToken());
l = new int[m + 5];
r = new int[m + 5];
x = new int[m + 5];
y = new int[m + 5];
num = new int[m + 5];
for (int i = 1; i <= m; i++) {
st = new StringTokenizer(br.readLine());
l[++k] = Integer.parseInt(st.nextToken());
r[k] = Integer.parseInt(st.nextToken());
x[k] = Integer.parseInt(st.nextToken());
y[k] = Integer.parseInt(st.nextToken());
num[k] = i;
if (k == SZ) {
doLazyUpdate();
}
}
if (k > 0) {
doLazyUpdate();
}
for (int i = 1; i <= n; i++) {
out.print(ans[i] + (i < n ? " " : "\n"));
}
out.flush();
}
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 3 с.
Ограничение по памяти: 256 Мбайт.
Анастасия — организатор Некоторой Технологической Олимпиады по профилю «Разработка некоторых приложений». Ей было поручено организовать уборку некоторых помещений МИФИ, для чего она обратилась к услугам некоторой клининговой компании. Анастасия, недолго думая, выбрала уборку при помощи роботов-пылесосов фирмы Circleaning, которые убирают помещение по окружности с центром в точке, откуда стартовал данный пылесос, с некоторым заданным пользователем радиусом. Чтобы все успеть к открытию профиля, Анастасия заказала сразу два пылесоса для круговой уборки.
Известны координаты в двухмерном пространстве каждого из пылесосов — центр окружности их движения, а также радиус действия пылесосов. Кроме того, известно, что данные окружности пылесосов могут пересекаться. Помогите Анастасии определить общую площадь, которую приберут пылесосы.
Формат входных данных
В одной строке через пробел даны пять целых положительных чисел \(first_x\), \(first_y\), \(second_x\), \(second_y\) — координаты точки старта по \(Oxy\) первого и второго пылесоса, а также \(radius\) — радиус действия для обоих пылесосов. Все пять чисел не превышают 100.
Формат выходных данных
Выведите одно вещественное число с точностью не менее трех знаков после запятой — общую площадь, которую приберут пылесосы.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1 2 3 4 2 |
22.84955592153876 |
В этой задаче необходимо найти площадь объединения двух кругов радиуса \(r\) с центрами в точках \((x_1, y_1)\) и \((x_2, y_2)\). Обозначим квадрат расстояния между центрами через \[d^2 = (x_1 - x_2)^2 + (y_1 - y_2)^2,\] а само расстояние через \(d = \sqrt{d^2}\). Если \(d \geqslant 2r\), круги не пересекаются и ответ равен \(2\pi r^2.\) Если \(d = 0\), круги полностью совпадают и ответ равен \(\pi r^2.\) В остальных случаях площадь пересечения двух одинаковых кругов задается формулой \[A_{\cap} \;=\; 2r^2\arccos\left(\frac{d}{2r}\right)\;-\;\frac{d}{2}\,\sqrt{4r^2 - d^2},\] и искомая площадь объединения равна \[2\pi r^2 \;-\; A_{\cap}.\]
Алгоритм требует лишь константного числа операций (вычисление корня и арккосинуса) и работает за \(\mathcal{O}(1)\) времени, используя \(\mathcal{O}(1)\) памяти.
Пример программы-решения
Ниже представлено решение на языке Java.
import java.io.*;
import java.util.*;
public class light_is implements Runnable {
private static final String FILENAME = "circleaning";
File inFile = new File(FILENAME + ".in");
PrintWriter out;
BufferedReader in;
private StringTokenizer st;
light_is() {
try {
in = new BufferedReader(new FileReader(inFile));
st = new StringTokenizer(in.readLine());
out = new PrintWriter(new File(FILENAME + ".out"));
} catch (IOException e) {
e.printStackTrace();
System.exit(239);
}
}
int nextInt() throws IOException {
if (!st.hasMoreTokens()) {
st = new StringTokenizer(in.readLine());
}
return Integer.parseInt(st.nextToken());
}
public void run() {
try {
int x1 = nextInt();
int y1 = nextInt();
int x2 = nextInt();
int y2 = nextInt();
int r = nextInt();
int d = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
double a;
if (d > 4 * r * r) {
a = 0;
} else if (d == 0) {
a = Math.PI / 2;
} else {
a = Math.acos(0.5 * Math.sqrt(d) / r);
}
out.println(2 * (Math.PI * r * r - 2 * (0.5 * a * r * r - 0.5 * (0.5 * Math.sqrt(d)) * (r * Math.sin(a)))));
} catch (IOException e) {
e.printStackTrace();
} finally {
out.close();
}
}
public static void main(String[] args) {
new Thread(new light_is()).start();
}
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 3 с.
Ограничение по памяти: 256 Мбайт.
Во время экспедиции к дальним звездным системам ученые из НИЯУ МИФИ решили создать подробные космические карты планет и астероидных поясов. Экземпляр карты — сетка размера \(2^h \times 2^h\), где каждая ячейка может быть заполнена либо космической пылью dust, либо оставаться пустотой void. В будущем эти карты будут использоваться для прокладки гиперпространственных маршрутов и постройки космических станций.
Для автоматизации процесса был написан специальный генератор космических топонимов. Он оперирует шаблонами template, которые описывают фрагмент будущей карты определенного размера. В самом начале доступны два базовых шаблона:
Dust(1)— ячейка, занятая пылью;Void(0)— ячейка, представляющая собой пустоту.
Каждый из этих шаблонов является единичным квадратом. Далее в генераторе задаются теги вида:
<NewTemplate>=<SubTemplate1>, <SubTemplate2>, <SubTemplate3>, <SubTemplate4>где <SubTemplate1>, <SubTemplate2>, <SubTemplate3>, <SubTemplate4> — ранее объявленные шаблоны размера \(h \times h\). По правилам они «склеиваются» в квадраты \(2h \times 2h\), образуя новый шаблон с именем <NewTemplate>. Схематично это можно представить как на рис. 1.1.
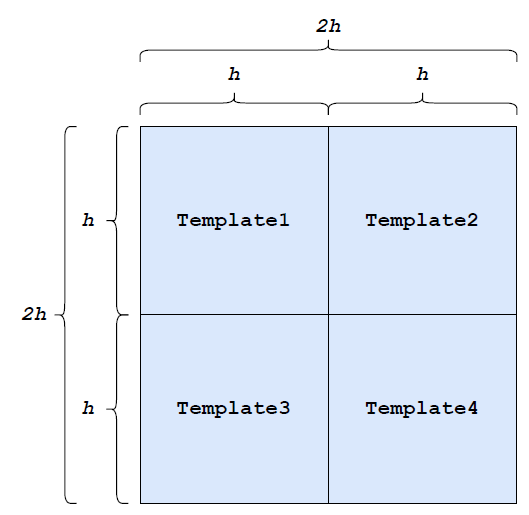
В итоге после обработки всех правил получается главный шаблон Map, который и описывает итоговую космическую карту размером \(2^h \times 2^h\). В случае, если ячейки карты имеют общую сторону, они считаются связными.
Найдите количество связных островов космической пыли на итоговой карте.
Формат входных данных
Сначала идет набор правил, задающих новые шаблоны. Каждый шаблон имеет уникальное имя, состоящее из латинских букв и цифр (прописные и строчные буквы различаются). Длина имени не превышает 20 символов.
Максимальный размер шаблона не превосходит \(2^{16}\) для каждой из сторон, а количество шаблонов не более 200.
Завершающий шаблон, имеющий специальное имя Map, описывается последним. Его размер и будет размером итоговой карты.
Из этих данных формируется итоговая космическая карта.
Формат выходных данных
Требуется вывести одно число — количество связных островов космической пыли на итоговой карте.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
A=0,1,1,0 X=1,1,1,1 B=A,A,A,X C=B,B,B,B Map=C,C,C,C |
56 |
В этой задаче каждый шаблон квадрата размера \(2^h\times2^h\) представляем в виде трех «метрик»: во-первых, число полностью «внутренних» островов пыли, которые не касаются границы шаблона; во-вторых, массив маркировок компонент вдоль периметра (с обходом по часовой стрелке) — каждая граница разбивается на непрерывные отрезки «пыль» или «пусто»; в-третьих, число «открытых» компонент, которые доходят до границы.
При объединении четырех квадрантов в новый шаблон, размер которого вдвое больше, их просто склеивают по периметрам: по внутренним стыкам соседних квадрантов соединяют смежные «пылевые» отрезки (DSU по меткам на границе), одновременно уменьшая число внешних компонентов, которые слились друг с другом, и добавляя к «внутренним» тем, что замкнулись полностью внутри. Таким образом, на каждом шаге сведение четырех шаблонов к новому занимает время, пропорциональное суммарному числу сегментов на их границах.
В итоге главный шаблон Map строится за суммарное время \(\mathcal{O}\bigl(\sum_{\text{шаблоны}} \text{периметр}_i\bigr)\), что при ограничении числа правил до 200 и максимальном размере \(2^{16}\times2^{16}\) остается вполне приемлемо.
Пример программы-решения
Ниже представлено решение на языке Java.
import java.io.*;
import java.util.*;
public class map_as {
Map<String, Pattern> patterns;
class DSU {
int n;
int[] p;
int[] r;
public DSU(int n) {
this.n = n;
p = new int[n];
r = new int[n];
for (int i = 0; i < n; i++) {
p[i] = i;
}
}
public int get(int x) {
if (p[x] != x) {
p[x] = get(p[x]);
}
return p[x];
}
public void union(int x, int y) {
x = get(x);
y = get(y);
if (r[x] == r[y]) {
r[x]++;
}
if (r[x] > r[y]) {
p[y] = x;
} else {
p[x] = y;
}
}
}
class Pattern {
Pattern[] parts;
int size;
long inside;
int ncol;
int[] col;
public Pattern(int w) {
size = 1;
inside = 0;
if (w == 0) {
ncol = 0;
col = new int[1];
col[0] = -1;
} else {
ncol = 1;
col = new int[1];
col[0] = 0;
}
}
public Pattern(Pattern[] parts) {
this.parts = parts;
int s = parts[0].size;
size = s * 2;
inside = 0;
for (int i = 0; i < 4; i++) {
inside += parts[i].inside;
}
int r = 4 * s - 4;
if (r == 0) {
r = 1;
}
int[] ost = new int[]{3 * s - 3, 0, s - 1, 2 * s - 2};
int[] oen = new int[]{s % r, (2 * s - 1) % r, (3 * s - 2) % r, 1 % r};
col = new int[4 * size - 4];
boolean[] existc = new boolean[4 * r];
int p = 0;
int q = 0;
for (int i = 0; i < 4 * size - 4; i++) {
col[i] = parts[p].col[q];
if (col[i] != -1) {
col[i] += p * r;
existc[col[i]] = true;
}
q = (q + 1) % r;
if (q == oen[p]) {
p = (p + 1) % 4;
q = ost[p];
}
}
DSU comps = new DSU(4 * r);
for (int i = 0; i < 4 * size - 4; i++) {
if (i % (size - 1) == s - 1) {
if (col[i] != -1 && col[(i + 1) % (4 * size - 4)] != -1) {
comps.union(col[i], col[(i + 1) % (4 * size - 4)]);
}
}
}
for (int i = 0; i < 4; i++) {
for (int j = oen[i] % r; j != (oen[i] + (s - 1)) % r; j = (j + 1) % r) {
int k = ((j - 2 * (j - (oen[i] - 1)) - (s - 1)) % r + r) % r;
int c1 = parts[i].col[j];
int c2 = parts[(i + 1) % 4].col[k];
if (c1 != -1) {
c1 += i * r;
existc[c1] = true;
}
if (c2 != -1) {
c2 += ((i + 1) % 4) * r;
existc[c2] = true;
}
if (c1 != -1 && c2 != -1) {
comps.union(c1, c2);
}
}
}
int[] nc = new int[4 * r];
Arrays.fill(nc, -1);
ncol = 0;
for (int i = 0; i < 4 * size - 4; i++) {
if (col[i] != -1) {
int c = comps.get(col[i]);
if (nc[c] == -1) {
nc[c] = ncol++;
}
col[i] = nc[c];
}
}
for (int i = 0; i < 4 * r; i++) {
if (existc[i]) {
int c = comps.get(i);
if (nc[c] == -1) {
nc[c] = ncol;
inside++;
}
}
}
}
}
public void run() throws IOException {
Scanner in = new Scanner(new File("space.in"));
PrintWriter out = new PrintWriter(new File("space.out"));
patterns = new HashMap<String, Pattern>();
Pattern one = new Pattern(1);
patterns.put("1", one);
Pattern zero = new Pattern(0);
patterns.put("0", zero);
while (in.hasNext()) {
StringTokenizer st = new StringTokenizer(in.next(), "=,");
String name = st.nextToken();
Pattern[] pp = new Pattern[4];
for (int i = 0; i < 4; i++) {
String p = st.nextToken();
pp[i] = patterns.get(p);
}
Pattern tmp = pp[2]; pp[2] = pp[3]; pp[3] = tmp;
Pattern pat = new Pattern(pp);
patterns.put(name, pat);
}
Pattern map = patterns.get("Map");
out.println(map.inside + map.ncol);
in.close();
out.close();
}
public static void main(String[] arg) throws IOException {
new map_as().run();
}
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 3 с.
Ограничение по памяти: 256 Мбайт.
В рамках одной из некоторых программ цифровизации в некотором институте НИЯУ МИФИ начали разработку мобильного приложения, автоматизирующего передачу экспериментальных данных в профильные лаборатории и внешние запросы на некоторые научные исследования. Команда молодого Android-разработчика Никиты сильна в реализации как бэкенда, так и фронтенда, но как только касается разного рода интеграций, так все идет не по плану.
Назовем научным исследованием последовательность базовых экспериментов, каждый из которых имеет свою стоимость, складывающуюся из энергозатрат и стоимости обслуживания установки. При запросе исследования от сотрудников или студентов НИЯУ МИФИ применяется скидка, покрывающая только энергозатраты при экспериментах.
Исходное исследование можно разбить на ряд подзадач, выполняющихся менее энергозатратно. Для каждой произвольной подгруппы экспериментов стоимость энергозатрат считается как сумма затрат на все эксперименты подгруппы без \(\left\lfloor \dfrac{count_e}{accuracy_h} \right\rfloor\) минимальных по стоимости экспериментов подгруппы, где \(count_e\) — количество экспериментов подгруппы, а \(accuracy_h\) — заданный заранее уровень точности результатов экспериментов. Например, для подгруппы \([1, 1, 3, 9, 4]\) и \(accuracy_h=2\) энергозатраты составят \(3+9+4=16\). Стоимость исследования со скидкой — минимальная сумма энергозатрат всех таких подгрупп.
Подсчитайте для заданной последовательности затрат на все эксперименты минимально возможную стоимость исследования для сотрудников МИФИ с оптимальным разбиением экспериментов на подгруппы. Исключать отдельные эксперименты или переставлять их между собой не разрешается.
Формат входных данных
В первой строке через пробел даны два целых числа \(n,\, accuracy_h\) — количество экспериментов исследования и необходимый уровень точности результатов \((1 \leqslant n, accuracy_h \leqslant 100000)\).
Во второй строке заданы \(n\) целых чисел \(experiment_i\) \((1 \leqslant experiment_i \leqslant 10^9)\) — стоимость каждого эксперимента в исследовании.
Формат выходных данных
Выведите единственное целое число — минимальную стоимость исследования со скидкой.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 5 1 2 3 |
6 |
2 |
12 10 1 1 10 10 10 10 10 10 9 10 10 10 |
92 |
3 |
7 2 2 3 6 4 5 7 1 |
17 |
4 |
8 4 1 3 4 5 5 3 4 1 |
23 |
Примечание
Например, в третьем примере эксперименты можно разбить на подгруппы \([2, 3]\), \([6, 4, 5, 7]\), \([1, 1]\), стоимость энергозатрат которых соответственно равна 3, 13 и 1, а итоговая стоимость исследования равна 17.
В задаче вводится одномерная последовательность затрат \(a_1, \ldots, a_n\) и целый параметр \(k\). Требуется разбить эту последовательность на непрерывные подгруппы так, чтобы суммарная стоимость \[\sum_{\text{группа }[l..r]}\left(\sum_{i=l}^r a_i \;-\;\sum_{\substack{\text{минимальные}\\\lfloor (r-l+1)/k\rfloor\text{ элемента}}}a_j\right)\] была минимальна.
Опишем оптимальное разбиение динамическим программированием по префиксам. Обозначим \[S[i]=\sum_{j=1}^i a_j, \qquad m(i, j)=\min_{\,i\leqslant t\leqslant j}a_t.\] Тогда для \(i < k\) очевидно \(dp[i]=S[i]\), а для \(i\geqslant k\) получаем \[dp[i] =\min\left\{ dp[i-1]+a_i,\; dp[i-k]+\bigl(S[i]-S[i-k]\bigr)-m(i-k+1, i) \right\}.\]
Будем поддерживать на скользящем окне длины \(k\) минимум и префиксные суммы.
Пример программы-решения
Ниже представлено решение на языке Java.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(reader.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
long[] a = new long[n + 1];
long[] dp = new long[n + 1];
long[] mn = new long[n + 1];
long[] sum = new long[n + 1];
TreeMap<Long, Integer> s = new TreeMap<>();
st = new StringTokenizer(reader.readLine());
for (int i = 1; i <= n; i++) {
a[i] = Long.parseLong(st.nextToken());
s.put(a[i], s.getOrDefault(a[i], 0) + 1);
if (i > k) {
long x = a[i - k];
int c = s.get(x);
if (c == 1) {
s.remove(x);
} else {
s.put(x, c - 1);
}
}
if (i >= k) {
mn[i] = s.firstKey();
}
}
for (int i = 1; i <= n; i++) {
dp[i] = dp[i - 1] + a[i];
sum[i] = sum[i - 1] + a[i];
if (i >= k) {
long candidate = dp[i - k] + sum[i] - sum[i - k] - mn[i];
if (candidate < dp[i]) {
dp[i] = candidate;
}
}
}
System.out.println(dp[n]);
}
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 3 с.
Ограничение по памяти: 256 Мбайт.
Арслан талантлив во всем. Из-за того, что в детстве и подростковом возрасте он часто ломал свои смартфоны по причине неуклюжести, в будущем он решил стать инженером микросхем. И поскольку он талантлив во всем, в качестве очередной практики своих навыков он пошел в лабораторию по ремонту и диагностике микросхем смартфонов в некотором университете.
Каждая микросхема содержит ровно \(count_p\) контактных площадок (пинов), пронумерованных от 1 до \(count_p\). Между некоторыми парами пинов \(first\) и \(second\) может существовать односторонняя цепочка (как провод или дорожка на плате), позволяющая протекать сигналу только в одном направлении: от \(first\) к \(second\). Если такая цепочка есть, то больше никаких параллельных дублей от \(first\) к \(second\) быть не может (то есть не может существовать двух разных проводов между той же парой пинов в одном направлении).
Назовем микросхему безопасной в том случае, если при уходе сигнала с любого пина вернуться на тот же пин уже невозможно. Другими словами, в схеме не должно быть замкнутых контуров: по проводам нельзя попасть из контактной площадки обратно к ней же самой.
Лаборатория собирает только безопасные микросхемы, и при этом все микросхемы должны отличаться друг от друга. Две микросхемы считаются различными, если существует хотя бы одна пара пинов \(\left\langle first, second\right\rangle\), для которой в одной схеме есть цепочка от \(first\) к \(second\), а в другой схеме такой цепочки нет (или наоборот).
Найдите максимально возможное число таких различных безопасных микросхем, которое может собрать лаборатория, если в каждой из них ровно \(count_p\) контактных площадок.
Формат входных данных
Система передачи данных к плате передает всего одно число \(count_p\) — количество контактных площадок на микросхеме (\(1 \leqslant counts_p \leqslant 6500\)).
Формат выходных данных
Необходимо вычислить максимальное возможное число различных безопасных микросхем при данном количестве пинов и вывести это число по модулю \(10^9+7\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 |
25 |
Задача сводится к подсчету количества ориентированных ациклических графов (DAG) на \(n\) пронумерованных вершинах. Вершины соответствуют пинам, а ориентированное ребро \(u\to v\) моделирует одностороннюю цепочку от \(u\) к \(v\). Условие «сигнал не может вернуться на тот же пин» эквивалентно отсутствию ориентированных циклов. Две микросхемы различны, если существует пара пинов, для которой наличие пути отличается, — значит, нужно посчитать именно число DAG, а не их транзитивных замыканий.
Классическая формула включений–исключений для количества пронумерованных DAG имеет вид \[A_0=1,\qquad A_n=\sum_{k=1}^{n}(-1)^{k-1}\binom{n}{k}\,2^{k(n-k)}\,A_{\,n-k}\quad(n\geqslant1).\] Выбирается \(k\) «ранних» вершин, запрещаются циклы внутри них, а все ребра из этих \(k\) во внешние \(n-k\) вершины задаются произвольно (\(2^{k(n-k)}\) вариантов); знак \((-1)^{k-1}\) появляется из принципа включений-исключений.
Решение данной задачи сводится к эффективной реализации данного рекуррентного соотношения с условиями ограничений по времени и памяти.
Пример программы-решения
Ниже представлено решение на языке Java.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
PrintWriter out = new PrintWriter(System.out);
int n = Integer.parseInt(br.readLine());
n++;
final long MOD = 1000000007;
long[] a = new long[n + 1];
long[] pow2 = new long[n + 1];
long[] cpow = new long[n + 1];
long[][] c = new long[2][n + 1];
int f = 0;
int ff = 1;
pow2[0] = 1;
a[0] = 1;
a[1] = 1;
for (int i = 1; i <= n; i++) {
pow2[i] = (pow2[i - 1] * 2) % MOD;
cpow[i] = 1;
}
c[1][0] = 1;
c[1][1] = 1;
cpow[0] = 1;
for (int i = 2; i < n; i++) {
c[f][0] = 1;
for (int j = 1; j < i; j++) {
c[f][j] = c[ff][j] + c[ff][j - 1];
if (c[f][j] > MOD) {
c[f][j] -= MOD;
}
cpow[j] = (cpow[j] * pow2[j]) % MOD;
}
c[f][i] = 1;
for (int k = 1; k <= i; k++) {
long tmp = a[i - k] * c[f][k] % MOD;
tmp = tmp * cpow[k] % MOD;
if ((k & 1) == 1) {
a[i] = (a[i] + tmp) % MOD;
} else {
a[i] = (a[i] - tmp + MOD) % MOD;
}
}
f = 1 - f;
ff = 1 - ff;
}
out.println(a[n - 1]);
out.flush();
}
}





