Предметный тур. Математика. 1 этап
Оля в каждую клетку таблицы \(3 \times 3\) записала по некоторому числу и с удивлением заметила, что сумма чисел в каждой строке и в каждом столбце таблицы равна 23. Внимательный же одноклассник Витя к ее размышлениям добавил информацию, что сумма чисел в каждом получившемся квадрате \(2\times 2\) равна 32. Какое число Оля записала в центральную клетку таблицы?
Проанализируем исходную таблицу и увидим, что при построении всех возможных квадратов \(2\times2\):
- числа, стоящие в угловых клетках исходной таблицы, входят по одному разу;
- числа, стоящие во второй строке и во втором столбце — по два раза;
- центральное число — четыре раза.
Тогда если найдем сумму чисел во всех квадратах \(2 \times 2\) и из нее вычтем сумму чисел всей таблицы, а также сумму чисел, стоящих во втором столбце и второй строке, то найдем центральное число, то есть \(32\cdot 4-23\cdot 3-23\cdot 2=13\).
13.
Нечетное восьмизначное число назовем «интересным», если оно состоит из простых цифр и одинаковые цифры не стоят рядом. Сколько существует таких «интересных чисел»?
Простые цифры — это 2, 3, 5 и 7. Тогда так как «интересное» число должно быть нечетным, то в разряде его единиц может стоять только 3, 5 или 7, то есть три варианта. В разряде десятков также может стоять только три варианта, т. к. одинаковые цифры не могут стоять рядом, и т. д. Таким образом, общее количество «интересных» чисел равно \(3^8=6561\).
6561.
В остроугольном треугольнике \(ABC\) провели высоты \(AA_1\) и \(CC_1\). Точки \(E\) и \(F\) — середины отрезков \(AC\) и \(A_1C_1\) соответственно.
Найдите длину отрезка \(EF\), если известно, что \(AC=30\) и \(A_1C_1=24\).
В прямоугольном треугольнике \(AC_1C\) с гипотенузой \(AC\): \(C_1E=\dfrac 12 AC=15\). Аналогично в треугольнике \(A_1C\): \(A_1E=\dfrac 12 AC=15\).
Таким образом, треугольник \(A_1C_1E\) является равнобедренным, и его медиана \(EF\) является также и высотой.
Тогда по теореме Пифагора: \(EF^2=A_1E^2-A_1F^2=15^2-12^2=81\), \(EF=9\).
9.
Найдите значение выражения \(x+y+3z\), если известно, что числа \(x\), \(y\), \(z\) удовлетворяют равенству: \[5x^2 +4y^2 +9z^2 +12z+13=4xy+12x.\]
Преобразуем равенство следующим образом: \[(x^2-4xy+4y^2)+(4x^2-12x+9)+(9z^2+12z+4)=0,\] то есть \[(x-2y)^2+(2x-3)^2+(3z+2)^2=0.\] Данное равенство будет выполняться при условии, что каждое слагаемое равно 0.
Отсюда получаем систему \[\left\{\begin{aligned} & x-2y=0, \\ & 2x-3=0, \\ & 3z+2=0, \end{aligned}\right.\] единственным решением которой будет \[x=\frac 32;~ y=\frac 34;~ z=-\frac 23.\]
Тогда \[x+y+3z=\frac 32+\frac 34+3\cdot \left(-\frac 23\right)=\frac 14=0{,}25.\]
0,25.
Шестизначное число будем называть «замечательным», если оно составлено из цифр 1, 2, 3, 4, 5, 6 (каждая цифра используется в числе по одному разу) и кратно 12. Какая вероятность, что сгенерированное компьютером шестизначное число будет «замечательным»?
Ответ выразите в долях и округлите его до четвертого знака после запятой.
Для того чтобы «замечательное» число делилось на 12, оно должно делиться на три и на четыре. Заметим, что все рассматриваемые числа кратны трем, так как сумма их цифр равна 21.
Для того же чтобы число было кратно четырем, необходимо, чтобы две его последние цифры образовывали число, кратное четырем. В нашем случае это могут быть варианты: 12, 16, 24, 32, 36, 52, 56, 64, всего их восемь. К каждому из них нужно приписать впереди четырехзначное число, составленное из остальных четырех цифр, таких чисел \(4!=24\). Значит, всего «интересных» чисел \(24\cdot 8=192\).
Всего же шестизначных чисел \(9\cdot 10^5=900000\).
Тогда вероятность, что сгенерированное компьютером число будет являться «замечательным», будет равна \(\dfrac {192}{900000} \approx 0{,}0002\).
0,0002.
Первый поезд мимо телеграфного столба проезжает за 9 с, второй поезд мимо этого же столба — за 14 с, а, двигаясь навстречу мимо друг друга, они проезжают за 10 с (с момента, когда поравнялись их начала, и до момента, когда разминулись концы).
Во сколько раз скорость первого поезда больше скорости второго?
Пусть \(x\) м/с — скорость первого поезда, тогда из условия задачи его длина \(9\) м. Аналогично, если \(y\) м/с — скорость второго поезда, то его длина равна \(14y\) м. Зная, что, двигаясь навстречу мимо друг друга, они проезжают за 10 с, составим уравнение: \[\frac {9x+14y}{x+y}=10.\]
Решив это уравнение, получим \(x=4y\). То есть скорость первого поезда в четыре раза больше скорости второго.
4.
Вася и Петя играют в разведчиков и для этого придумали свой язык шифрования, в котором используются только пять символов. При этом все «слова» в их сообщениях непустые, то есть содержат хотя бы один знак, и длиной не более пяти знаков.
Сколько различных «слов» они имеют в своем арсенале, чтобы передавать друг другу информацию?
«Слова», которые могут составлять Вася и Петя на своем языке, могут состоять из 1, 2, 3, 4 и 5 символов.
Тогда общее количество слов будет равно \(5^1+5^2+5^3+5^4+5^5=3905.\)
3905.
В треугольнике \(ABC\) длина биссектрисы \(AD\) равна длине отрезка \(DC\) и \(AC=2AB\). Найдите \(\angle ABC\).
В равнобедренном треугольнике \(ADC\) из точки \(D\) проведем медиану \(DE\) на сторону \(AC\), которая также будет являться и высотой.
Тогда \(AE=\dfrac 12 AC=AB\). Треугольники \(AED\) и \(ABD\) равны по двум сторонам и углу между ними: \(AE=AB\), \(AD\) — общая сторона и \(\angle DAE=\angle DAB\).
Следовательно, \(\angle ABC=\angle ABD=\angle AED=90°\).
90°.
В натуральном двузначном числе \(a\) цифры поменяли местами и получили двузначное число \(b\). Оказалось, что сумма чисел \(a\) и \(b\) делится на 5, а их разность — на 27.
Найдите все возможные значения числа \(a\). В ответ запишите сумму всех полученных чисел.
Пусть \(a=\overline{xy}=10x+y\) и \(b=\overline{yx}=10y+x\).
Тогда \[a+b=11x+y=11(x+y).\]
Так как по условию \(a+b=11(x+y)\,\vdots\, 5\) и числа 5 и 11 взаимно просты, то \[(x+y)\,\vdots\, 5. \label{math89-01}\]
Далее из второго условия \(a-b=9x-9y=9(x-y)\,\vdots\, 27\), следует, что \[(x-y)\,\vdots\, 3. \label{math89-02}\]
Осталось перебрать все возможные значения цифр \(x\) и \(y\), удовлетворяющих условиям \eqref{math89-01} и \eqref{math89-02}. Непосредственной проверкой можно убедиться, что этим условиям удовлетворяют пары (1; 4), (2; 8), (4; 1), (5; 5), (6; 9), (8; 2) и (9; 6).
Таким образом, получаем пять чисел, сумма которых равна \(14+28+41+55+69+82+96=385\).
385.
Команда «Математики» за последние три года, согласно протоколам, приняла участие в 111 матчах по мини-футболу (в это число вошли и игры, которые были отменены по техническим причинам). При анализе результатов было замечено:
- сколько-то игр было выиграно;
- ничьи составляют 45% от всех игр, в которых не были одержаны победы;
- количество матчей, в которых были допущены поражения, к количеству отмененных игр относится как \(1:2\).
Какое количество матчей «Математики» проиграли?
Пусть было одержано \(x\) побед. Тогда количество игр, которые были сыграны вничью, проиграны или были отменены, равно \(111-x\).
Тогда \(\dfrac 9{20}(111-x)\) — количество игр, сыгранных вничью.
Найдем количество игр, которые были проиграны, или отменены: \[(111-x)-\frac 9{20}(111-x)=\frac{1221-11x}{20}.\]
Тогда количество игр, в которых были поражения, равно \[y=\frac{1221-11x}{60},~y\in Z.\]
Получили диофантово уравнение \[11x+60y=1221.\]
Выразим \(x\): \[x=111-60\cdot \frac y{11}.\]
Таким образом, \(y\,\vdots\, 11\) и \(y>0\).
Рассмотрим различные случаи относительно \(y\):
- \(y=11\). Тогда \(x=111-60=51\).
- \(y=22\). Тогда \(x=111-120=-9\). Количество игр не может быть отрицательным числом. Следовательно, данный случай, как и все последующие, не подходит.
Таким образом, количество игр, в которых были получены поражения, равно 11.
11.
Начинающий предприниматель Петров закупил 1000 единиц некоторого товара и попытался его продать с наценкой 20% за единицу продукции. Однако ожидания предпринимателя не совпали с реальностью, и он смог продать только 40% от своего объема, после чего вынужден был снизить цену на товар на 10%. В результате снижения единица товара стала стоить 5832 руб. за штуку.
Какую чистую прибыль, то есть разность между деньгами, полученными за продажу товара и затратами на его закупку, получил Петров?
Пусть \(x\) руб. — цена за единицу товара, по которой совершена закупка предпринимателем Петровым. Тогда он первоначально планировал осуществить продажи по цене \[x+0{,}2x=1{,}2x.\]
После снижения же цены товар стал стоить \[1{,}2x-0{,}1\cdot 1{,}2x=1{,}08x.\]
Так как известно, что после снижения единица товара стала стоить 5832 руб. за штуку, то \[1{,}08x=5832x=5400.\]
Таким образом, товар был закуплен 5400 руб. за штуку, и общие затраты на его покупку составили 5400000 руб.
Согласно условию задачи 400 единиц товара было продано по цене \(1{,}2\cdot 5400=6480\) руб., и всего было получено за них \(6480\cdot 400=2592000\) руб.
Оставшиеся же 600 единиц были проданы по цене 5832 руб. и получено за них \(5832\cdot 600=3499200\) руб.
Тогда чистая прибыль предпринимателя Петрова будет равна \[2592000+3499200-5400000=691200~ \text{руб}.\]
691200.
Сколько существует нечетных пятизначных чисел, в которых есть хотя бы одна цифра 5?
Для того чтобы найти количество требуемых чисел, достаточно из общего количества пятизначных нечетных чисел вычесть количество чисел, в которых отсутствует цифра 5.
В десятичной записи нечетного пятизначного числа на последнюю позицию претендует пять вариантов (цифры 1, 3, 5, 7 и 9), на первую — девять вариантов (все цифры, кроме нуля), а на все остальные позиции — по 10 вариантов. Тогда общее количество пятизначных нечетных чисел будет равно \[9\cdot 10\cdot 10\cdot 10\cdot 5=45000.\]
Для записи нечетного пятизначного числа, в десятичной записи которого отсутствует цифра 5, на каждую соответствующую позицию будет на один вариант меньше, тогда общее количество таких чисел будет равно \[8\cdot 9\cdot 9\cdot 9\cdot 4=23328.\]
Тогда количество пятизначных нечетных чисел, в которых присутствует хотя бы одна цифра 5, равно \[45000-23328=21672.\]
21672.
Наблюдательный Витя для некоторых двух различных чисел заметил интересную особенность: первое число, увеличенное на 4, будет равно квадрату второго числа, уменьшенного на 2; и наоборот, если ко второму числу прибавить 4, то результат будет равен квадрату первого числа, уменьшенного на 2. Найдите сумму квадратов данных двух чисел.
Пусть \(x\), \(y\) — два исходных различных числа. Тогда согласно условиям задачи будем иметь систему уравнений:
\[\left\{\begin{aligned} &x+4=(y-2)^2, \\ &y+4=(x-2)^2. \end{aligned}\right.\]
Вычитая из первого равенства второе, получим: \[x-y=(y-2)^2-(x-2)^2=(y-x)(x+y-4).\]
Так как числа \(x\), \(y\) различны, то отсюда получаем, что \(x+y=3\).
Складывая же уравнения полученной системы, получим \[x+y+8=(y-2)^2+(x-2)^2=y^2-4y+4+x^2-4x+4.\]
Из последнего равенства получаем, что \[x^2+y^2=5(x+y)=15.\]
15.
Петя записал на доске три числа 391, 604, 888 и задумчиво сказал Васе: «Если я сейчас эти три числа разделю на одно и то же натуральное число, отличное от единицы, то в результате получу один и тот же остаток».
На какое натуральное число Петя планирует произвести деление исходных чисел?
Обозначим число, на которое производится деление, через \(x\), а остаток через \(y\).
Тогда каждое из записанных Петей чисел можно представить в виде: \[\begin{aligned} 391&=xm+y, \\ 604&=xk+y, \\ 888&=xn+y, \end{aligned}\]
где \(m\), \(k\) и \(n\) — неполные частные, возникающие при делении.
Вычитая из третьего равенства второе, а из второго — первое, получим: \[\begin{aligned} 284&=x(n-k), \\ 213&=x(k-m). \end{aligned}\]
Вычтем из верхнего равенства нижнее: \[71=x(n-2k+m).\]
Так как 71 — это простое число, то \(71=71\cdot 1\), и, по условию задачи \(x\ne 1\), то единственный возможный вариант для делителя Пети равен 71.
71.
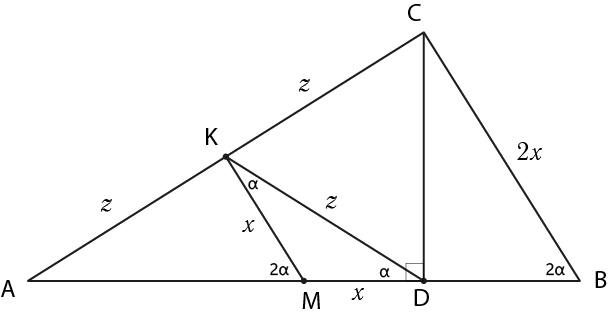
\(CD\) — высота остроугольного треугольника \(ABC\), \(M\) — середина стороны \(AB\) и \(\angle ABC=2\angle BAC\). Найдите отношение \(BC:MD\).
На стороне \(AC\) отметим ее середину — точку \(K\).
Тогда \(AK=KC\) и \(AM=MB\) (по условию задачи), следовательно, \(MK\) — средняя линия треугольника \(ABC\) и \(BC=2MK\).
Докажем, что \(MK=MD\).
По свойству медианы прямоугольного треугольника, проведенной из вершины прямого угла, в треугольнике \(ADC\): \(DK=\dfrac 12AC=AK\).
Таким образом, треугольник \(AKD\) — равнобедренный и \(\angle KAD=\angle KDA\) как углы при основании \(KD\).
Так как \(MK\) — средняя линия треугольника \(ABC\), то \(MK\parallel BC\) и \(\angle AMK=\angle ABC=2\angle BAC=2\angle KAD=2\angle KDA=2\angle KDM\).
По теореме о внешнем угле для треугольника \(MKD\) \[\angle AMK=\angle KDM+\angle MKD.\]
Тогда из последних двух равенств следует, что \(\angle KDM=\angle MKD\) и треугольник \(MKD\) — равнобедренный.
Следовательно, \(MK=MD\), и так как \(BC=2MK=2MD\), то \(BC:MD=2:1\).
2.
На доске записано число 202420252026. Танечка хочет убрать несколько цифр из исходного числа так, чтобы получившийся результат делился на 45 и являлся наибольшим из всех возможных. Какое число запишет на доске Танечка?
Для того чтобы число Танечки было бы кратно 45, необходимо выполнение условий делимости на 5 и 9. Следовательно, число должно заканчиваться на 0 или на 5. В данном случае первым делом Танечка должна убрать последние две цифры и получить 2024202520.
Для выполнения условия делимости на 9 необходимо, чтобы сумма цифр числа была бы 9. Сумма цифр сейчас равна 19. Ближайшая сумма, кратная 9, равна 18, но 1 в числе нет, следовательно, следующий вариант — 9. Для этого из оставшегося числа ей нужно вычеркнуть цифры, дающие в сумме 10. Тогда наибольшее число, которое может получить Танечка, — 202050.
202050.
Найдите все трехзначные натуральные числа \(\overline{abc}\), удовлетворяющие условию \[\overline{abc}=\overline{ab}+\overline{bc}+\overline{ca}.\]
В ответ запишите сумму всех найденных чисел.
Распишем равенство, заданное в условии задач \[\begin{gather} \overline{abc}=\overline{ab}+\overline{bc}+\overline{ca};\\ 100a+10b+c=10a+b+10b+c+10c+a;\\ 100a+10b+c=11a+11b+11c;\\ 89a=10c+b. \end{gather}\] Так как \(a\), \(b\), \(c\) — цифры, то единственным решением данного уравнения является набор \(a=1\), \(b=9\), \(c=8\). Следовательно, единственное число, удовлетворяющее условию задачи, это 198.
198.
Найдите количество значений параметра \(b\), при которых все корни уравнения \(x^2+bx+2026=0\) целые.
Пусть \(x_1\) и \(x_2\) — целые корни данного уравнения. Тогда согласно теореме Виета: \[x_1\cdot x_2=2026.\]
Так как 2026 раскладывается на множители \[2026=1\cdot 2026=2\cdot 1013,\] то получаем четыре набора для значений корней \[(1;2026),~ (-1; -2026),~ (2;1013),~ (-2; -1013).\]
Зная значения корней, также по теореме Виета найдем значения параметра \(b\): \[b=-(x_1+x_2).\]
Таким образом, всего существует четыре значения параметра \(b=\{-2027\); \(2027\); \(-2015\); \(2015\}\), при каждом из которых уравнение имеет целые корни.
4.
В треугольнике \(ABC\) на биссектрисе \(BD\) отмечена точка \(E\) так, что \(BE=ED\). Найти вероятность, что точка, брошенная в треугольник \(ABC\), попадет в треугольник \(AED\), если \(AB=3\) и \(BC=5\).
Ответ выразите в долях и при необходимости округлите его до четвертого знака после запятой.
Согласно определению геометрической вероятности, требуемая вероятность будет равна отношению площадей треугольников \(AED\) и \(ABC\). \(AE\) — медиана треугольника \(ABE\), следовательно, \(S_{ABD}=2S_{AED}\).
Площади треугольников \(ABD\) и \(BDC\) относятся как длины их оснований \(AD\) и \(DC\), то есть \[\frac{S_{ABD}} {S_{BDC}}=\frac{AD} {DC}=\frac{AB}{BC}=\frac 35.\]
Последнее равенство выполняется согласно свойству биссектрисы \(BD\) в треугольнике \(ABC\). Тогда \[S_{ABC}=S_{ABD}+S_{BDC}=S_{ABD}+\frac 53S_{ABD}=\frac 83S_{ABD}=\frac{16}3S_{AED}.\]
Из последнего равенства следует отношение \[\frac{S_{AED}}{S_{ABC}}=\frac 3{16}=0{,}1875.\]
Таким образом, вероятность того, что точка брошенная в треугольник \(ABC\), попадет в треугольник \(AED\), равна 0,1875.
0,1875.
При каком значении числа \(a\) сумма квадратов чисел \(x\) и \(y\) будет принимать наибольшее значение, если известно, что сумма этих чисел равна \(2a+1\), а произведение равно \(4a^2+8a-4\)?
По условию задачи \(x+y=2a+1\) и \(xy=4a^2+8a-4\).
Воспользуемся формулой квадрата суммы двух чисел \[(x+y)^2=x^2+2xy+y^2.\]
Отсюда \[x^2+y^2=(x+y)^2-2xy=(2a+1)^2-2(4a^2+8a-4)=4a^2+4a+1-8a^2-16a+8=\] \[=-4a^2-12a+9=-(4a^2+12a+9)+18=-(2a+3)^2+18.\]
В полученном выражении первое слагаемое принимает неположительные значения при любом \(a\). Следовательно, сумма квадратов чисел \(x\) и \(y\) будет максимальной при \(2a+3=0\) или \(a=-1{,}5.\)
Проверим, что при данном значении параметрам \(a=-1{,}5\) числа \(x\) и \(y\) действительно существуют. В этом случае \(x+y=-2\) и \(xy=-7\).
Выразив из первого равенства \(y=-x-2\) и подставив его во второе, после преобразований получим уравнение \(x^2+2x-7=0\). Дискриминант данного уравнения равен 32, следовательно, корни уравнения существуют, по которым однозначным образом восстанавливаются решения построенной системы. Откуда и следует существования чисел \(x\) и \(y\), заданных в условии задачи.
\(-1{,}5\).
Двузначное число назовем подходящим, если оно состоит из четных цифр, расположенных по возрастанию (например, 26). Сколько существует таких подходящих чисел?
Число не может начинаться с нуля, так что можно использовать только цифры 2, 4, 6, 8. Выпишем все подходящие: 24, 26, 28, 46, 48, 68.
6.
На Марсе планируется разместить колонию в 100 тысяч человек. Разные колонисты будут заняты на разных работах и важно, чтобы каждый вид работы выполняли группы из минимального количества человек. Одна из важных задач — обеспечение колонистов сбалансированным питанием. Нормы здорового рациона были рассчитаны таким образом, чтобы обеспечить для каждого человека 350 г картофеля в день. Полный цикл производства картофеля от посадки и до сбора составляет 60 дней, каждые 60 дней часть собранного урожая используется для выращивания нового. В той технологии, которую используют космонавты, с 1 га можно вырастить 250 т картофеля, а для посадки нужно 5 т/га. Специальная обработка почвы позволяет добиться сохранения постоянного уровня урожайности, причем можно засадить и обрабатывать произвольную долю гектара. Чтобы полностью обслуживать один гектар в условиях теплиц на Марсе, требуется труд четырех человек.
Какое минимальное количество человек должны трудиться на выращивании картофеля?
Один человек за 60 дней по плану должен съедать \(60\cdot 0{,}35 = 21\) кг картофеля. Следовательно, 100 тысяч человек по плану за это время съедят 2100000 кг.
С одного гектара получаем 250 т, но при этом из них 2 т нужно использовать для посадки. Это значит, что с каждого гектара люди получат в свой рацион 245 т картофеля. Если разделить количество картофеля, которое съест по плану колония за 60 дней, на количество картофеля, которое попадет к ним с 1 га, то получится, что требуется приблизительно 8,571 га. Так как каждый гектар должны обрабатывать четыре человека, то для обработки 8,571 га потребуется труд 34,286 человек. Это значит, что 34 человек недостаточно, требуется запланировать труд 35 человек.
35.
Две параболы с различными вершинами пересекаются таким образом, что первая парабола проходит через вершину второй параболы, а вторая — проходит через вершину первой. Уравнение первой параболы имеет вид \(y=x^2\), второй \(y= a\cdot x^2 + b \cdot x + c\). Найдите, чему равна величина \(10\cdot a+c\).
Координаты вершины первой параболы имеют вид \((0; 0)\), следовательно, коэффициент \(c=0\). Координаты вершины второй параболы имеют вид \[\begin{gather} x=-\frac b{2a};\\ y= -\frac{b^2}{4a}. \end{gather}\]
Тогда, подставив их в уравнение первой параболы, получаем:
\[-\frac {b^2}{4a}=\frac {b^2}{2a}.\]
Отсюда \(a=-1\).
\(-10\).
В 6:00 со дна океана, находящегося на глубине 2000 м, на поверхность, двигаясь с постоянной скоростью вертикально вверх, начала всплывать подводная лодка. Когда она поднялась до глубины 400 м, капитан заметил, что мимо них вниз плывет глубоководный батискаф. Ему что-то показалось странным. Когда подводная лодка поднялась на поверхность, капитан понял, что на оболочке батискафа были признаки повреждения. Чтобы предотвратить возможную трагедию, в тот же самый момент с подводной лодки вниз спустили спасательный глубоководный аппарат, который спускался с некоторой постоянной скоростью. Когда до дна оставалось 800 м, этот аппарат поравнялся с батискафом. Если бы спасательный аппарат не перехватил батискаф, то спасательный аппарат достиг бы дна к 11:00. Предполагая, что спасательный аппарат все время движения двигался равномерно, определите, в какой момент времени батискаф достиг бы дна, если бы он продолжил движение с той же постоянной скорость. Ответ введите в виде двух целых чисел, записанных подряд — количество часов и количество минут.
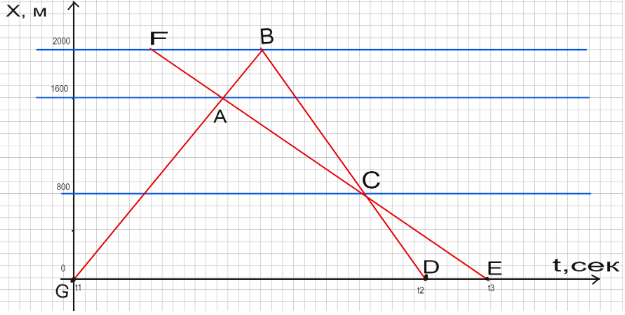
Самое изящное решение получается графическим методом.
Здесь данные из условия задачи можно обозначить следующим образом:
\(h_1=2000-400=1600\), \(h(2 )=800\), \(H=2000\), \(t_1= 6\), \(t_2=12\).
По теореме Менелая получаем: \[\frac{GA}{AB}\cdot \frac{BC}{CD}\cdot \frac{DE}{GE}=1.\]
Выразим эти отношения из разных пар подобных треугольников:
\[\begin{gather} \frac{GA}{AB}=\frac{h_1}{H-h_1} ;\\ \frac{BC}{CD}=\frac{H-h_2}{h_2} ;\\ \frac{DE}{GE}= \frac{t_3- t_2}{t_3- t_1} ;\\ \frac{h_1}{H-h_1}\cdot \frac{H-h_2}{h_2}\cdot \frac{t_3- t_2}{t_3- t_1}=1. \end{gather}\] Подставим числа: \[\begin{gather} \frac{1600}{400}\cdot \frac{1200}{800}\cdot \frac{t_3- 11}{t_3- 6}=1;\\ 6\cdot (t_3- 11)=t_3- 6;\\ 5\cdot t_3=60;\\ t_3=12\text{~ч.} \end{gather}\]
12.
Инженер-исследователь работает над созданием новой системы гиперпространственной навигации для космических кораблей, которая потребует меньших вычислительных ресурсов. Часть измерений гиперпространства скрыта от нас и устроена не так, как мы привыкли, а именно — являются дискретными (с конечным количеством позиций), позиции в которых следуют друг за другом циклически. Например, если это измерение, в котором 5 позиций, то их можно занумеровать числами от 0 до 4 так, что космический корабль, при прямолинейном движении вдоль этого измерения, будет пролетать позиции \(0-1-2-3-4-0-\ldots\) (конечно, корабль в любой момент может изменить направление своего движения на обратное или начать/продолжить изменять позиции и по другим измерениям гиперпространства).
Оказалось, что в гиперпространстве возможна быстрая (но не мгновенная) телепортация: для такого перемещения требуется особая последовательность перемещений в дискретных подпространствах с остановками лишь в выделенные моменты времени. Ранее для хранения таких сложных гипермаршрутов использовалась технология сплошного хранения всех промежуточных опорных точек пути. Однако из-за воздействия агрессивной космической радиации устройства хранения информации часто выходят из строя, что делает сплошное хранение информации очень дорогим, так как требует многократного резервного копирования,
Инженер корабля предложил хранить не сами последовательности позиций, а формулы для их вычисления (что хранить гораздо дешевле и надежнее). В частности, ему удалось запрограммировать движение в одном из измерений с 13 позициями следующим образом: начальное положение обозначается числом 0 и дальнейшие позиции для остановки вычисляются по формуле: \(x_{n+1}\) равно остатку от деления \((x_n^5 +2)\) на 13.
Переход корабля из одной позиции в соседнюю по прямому или обратному ходу занимает 1 единицу времени, которую называют таймом. Корабль, используя эту формулу, прошел полный цикл по остановкам и вернулся в позицию с номером 0.
Какое минимальное количество таймов могло занимать все его движение между остановками в ходе этого цикла?
Запишем последовательность позиций, в которых останавливается корабль:
\[0 - 2 - 8 - 10 - 6 - 4 - 12 - 1 - 3 - 11 - 9 - 5 - 7 - 0.\]
Между каждыми двумя позициями корабль может двигаться либо прямым ходом, либо обратным. Нужно выбирать кратчайший из двух.
Тогда общая длительность промежутков будет:
\[T=2+6+2+4+2+5+2+2+5+2+4+2+6=44.\]
44.
Прямоугольный параллелепипед имеет объем, равный 30. Его рассекли на две части, проведя плоскость через точку пересечения всех трех его диагоналей.
Чему равно максимальное значение объема одной из этих двух частей?
При центральной симметрии плоскости переходят в параллельные им плоскости, а прямые — в параллельные им прямые. Диагонали параллелепипеда делятся точкой пересечения пополам, поэтому он имеет центр симметрии. При центральной симметрии любая точка параллелепипеда, не находящаяся на секущей плоскости, перейдет в точку, которая находится с другой стороны от любой плоскости, проходящей через этот центр, так как эти две точки и центр симметрии находятся на одной прямой, которая пересекает эту плоскость.
Таким образом, плоскость делит параллелепипед на две части, которые переходят друг в друга при центральной симметрии. Следовательно, их объемы должны быть равны. Это означает, что часть параллелепипеда имеет объем, равный половине объема параллелепипеда
15.
Путешественник достал древнюю карту спрятанных сокровищ на острове Пасхи. Путь к пещере, в которой пиратами был закопан клад, был зашифрован с помощью квадратного уравнения. К сожалению, с течением времени запись одного из коэффициентов стерлась, и поэтому путешественник не смог его точно восстановить.
Оказалось, что оно имеет следующий вид: \(x^2 +6x+a=0\).
Здесь буквой \(a\) обозначен неизвестный коэффициент.
Уравнение использовалось для того, чтобы можно было разделить инструкцию по поиску сокровища на несколько частей таким образом, чтобы совершенно невозможно было бы понять, что и где искать, если хотя бы одной части недостает.
У путешественника были все части инструкции, поэтому он смог понять, что нужно от нужной точки на побережье идти ровно \(P\) км на юг вдоль единственной тропы, затем \(Q = \dfrac P2\) км на запад, а потом повернуться на северо-восток и идти прямо, пока вершина вулкана Теревака, кратер Рано-Арои, не станет виден под углом ровно \(10R°\) над уровнем горизонта. Рядом с этим местом и находится пещера. Здесь \(P\), \(Q\) — корни данного квадратного уравнения, упорядоченные по возрастанию, \(R = 2P + Q\).
Может ли путешественник, исходя из данных условий, однозначно найти два этих корня?
Если может, напишите в ответ число \(R\). Если не может, напишите в ответ число 0.
Запишем теорему Виета для квадратного уравнения: \[\left\{\begin{aligned} &P+Q=- 6,\\ &PQ=a. \end{aligned}\right.\]
В условии указано, что \(Q = \dfrac P2\). Подставив в первое уравнение, получаем, что \(P = -4\), \(Q = -2\).
\(-10\).
Исследователи выращивают экспериментальную культуру грибов. Эти грибы размножаются почкованием. Гриб порождает два новых гриба каждые 4 ч. Только что появившийся гриб слишком маленький, и поэтому он должен еще 6 ч расти, прежде чем размножаться, таким образом, первое потомство от нового гриба возникает лишь через 10 ч после его появления из почки.
Сколько грибов, включая только что появившихся, будет в лаборатории через 28 ч, если изначально там был один гриб, который породит два новых гриба только через 4 ч.
Самый первый гриб за 28 ч успеет породить только три поколения грибов, так как для появления четвертого поколения нужно 30 ч. Поэтому чтобы ответить на вопрос задачи, нужно посчитать, сколько грибов успеют отпочковаться от грибов, которые породил первый гриб, а потом посчитать также третье поколение.
Первые два гриба, отпочковавшиеся через 4 ч, создадут еще четыре гриба в 14 ч, еще четыре — в 18 ч, еще четыре — в 22 ч и еще четыре в — 26 ч. Всего они породят 16 грибов.
Вторые два гриба, появившиеся через 8 ч, создадут еще четыре гриба в 18 ч, еще четыре — в 22 ч и еще четыре гриба — в 26 ч. Всего они породят 12 грибов.
Третьи два гриба, появившиеся через 12 ч, создадут еще четыре гриба в 22 ч, и еще четыре гриба — в 26 ч. Всего они породят восемь грибов.
Четвертые два гриба, появившиеся через 16 ч, создадут еще четыре гриба в 26 ч.
Пятые два гриба — в 20 ч, шестые два гриба — в 24 ч, а седьмые два гриба в 28 ч не успеют породить никаких новых грибов — это еще шесть грибов.
Таким образом, можно посчитать количество грибов первого и второго поколения:
\[N_1=7\cdot 2=14;\] \[N_2=16+12+8+4=40.\]
Осталось посчитать третье поколение. Оно образуется в 24 ч и 28 ч из первых четырех грибов из первых двух грибов, в 28 ч из вторых четырех грибов из первых двух грибов и в 28 ч из первых четырех грибов из вторых двух грибов. То есть еще восемь грибов:
\[N_3=2\cdot 2\cdot 2+2\cdot 2\cdot 2 +2\cdot 2\cdot 2 +2\cdot 2\cdot 2 =32.\]
Суммарно получаем:
\[N=1+N_1+N_2+N_3=1+14+40+32=87.\]
87.
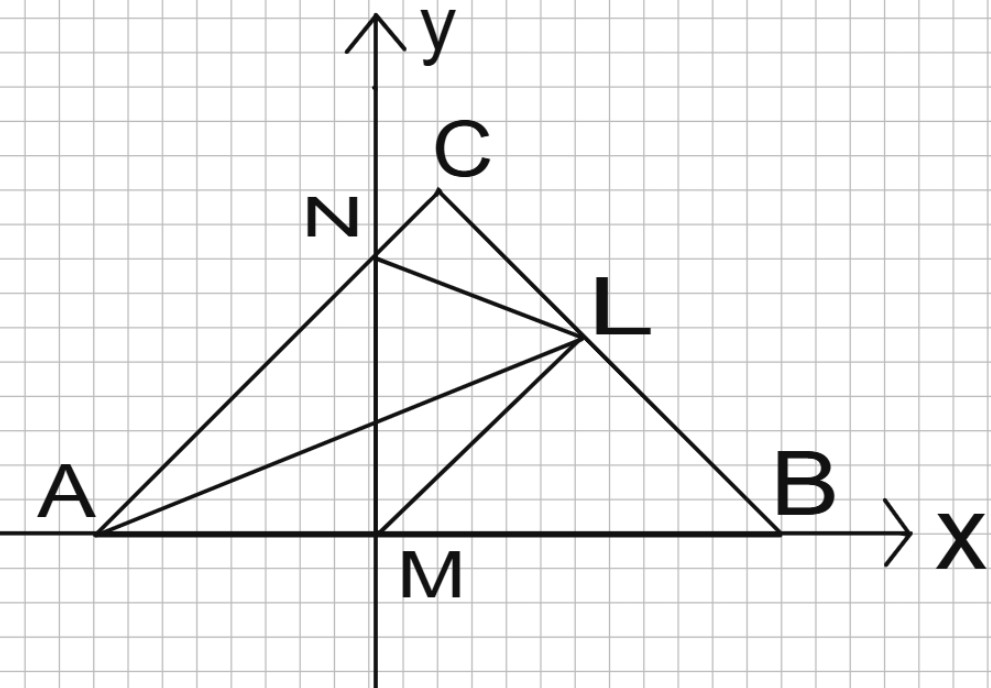
В прямоугольном равнобедренном треугольнике \(ABC\) с прямым углом \(C\) проведена биссектриса \(AL\). Из точки \(L\) к стороне \(BC\) проведен перпендикуляр, который пересек сторону \(AB\) в точке \(M\). Перпендикуляр, построенный к стороне \(AB\) в точке \(M\), пересекает сторону \(AC\) в точке \(N\).
Чему равен угол \(ANL\)? Ответ приведите в градусах.
\(MN = AM\), значит, угол \(ANM\) тоже равен 45° и \(NM\) перпендикулярно \(AB\).
Тогда углы \(NML\) и \(BML\) тоже равны по 45°.
Пусть \(AM = 1\) (в условии никаких длин нет, поэтому можем за единицу длины взять любой отрезок). Тогда \[AN= \sqrt{2};\] \[AL=2\cdot AM\cdot \cos{22{,}5}°=2\cdot \sqrt{\frac {\sqrt{2}+2}4}=\sqrt{\sqrt{2}+2}.\]
Чтобы найти \(NL\), используем метод координат. Проведем горизонтальную ось через \(AB\), вертикальную ось через \(MN\). Тогда точка \(N\) имеет координаты (0; 1). Что же касается точки \(L\), то ее координаты \(x\) и \(y\) совпадают, а длина \(ML\) равна 1. Следовательно, они равны \(L\left(\dfrac {\sqrt{2}}2;\dfrac {\sqrt{2}}2\right)\).
Используя формулу расстояния между двумя точками, получаем: \[NL^2=\frac 12+ \left(1-\frac{\sqrt{2}}2\right)^2=2-\sqrt{2}.\]
Обозначив угол \(ALN\) за \(x\), применим теорему косинусов: \[2=2-\sqrt{2}+\sqrt{2}+2-2\cdot \sqrt{\sqrt{2}+2}\cdot \sqrt{2-\sqrt{2}}\cdot \cos{x}.\]
Отсюда получаем, что: \[\cos{x}= \frac{\sqrt{2}}2\text{,~} x=45°.\]
Тогда угол \(ANL\) равен 180° минус угол \(ALN\) и угол \(NAL\): \[ANL=180-45-22{,}5=112{,}5.\]
112,5.
Для разработки оптической системы на основе параболических отражателей света потребовалось исследовать оптические свойства парабол. Пусть парабола задана уравнением \(y= 16x^2\). Требуется на плоскости найти такую точку \(O\), что все проекции этой точки на касательные к параболе лежат на оси абсцисс. Найдите координаты точки \(O\) и запишите их в ответ.
Уравнение касательной прямой к параболе (в заданной точке (\(x_0, y_0\))) однозначно устанавливается как уравнение невертикальной прямой, проходящей через (\(x_0, y_0\)) и имеющей единственную точку пересечения с параболой.
Рассмотрим точку с абсциссой \(x_0\) на параболе. Уравнение прямой, проходящей через эту точку, в общем виде имеет вид: \[y=a\cdot (x-x_0)+16\cdot (x_0)^2.\]
Приравняем его к уравнению параболы и найдем, при каком значении \(a\) они будут иметь ровно одну точку пересечения: \[16\cdot x^2=a\cdot (x-x_0)+16\cdot (x_0)^2;\] \[16\cdot x^2-a\cdot x+x_0\cdot a- 16\cdot (x_0)^2=0;\] \[D= a^2-4\cdot 16\cdot (x_0\cdot a- 16\cdot x_0^2)= (a-32\cdot x_0)^2=0;\] \[a=32\cdot x_0.\]
Итак, запишем уравнение касательной в этой точке к параболе в виде
\[y=32\cdot x_0\cdot (x-x_0)+16\cdot (x_0)^2.\]
Эта прямая пересечет ось абсцисс в точке с координатой \(x_1=\dfrac{x_0}2.\)
Уравнение прямой, проходящей через эту точку перпендикулярно касательной: \[y=-\frac{2\cdot x- x_0}{64\cdot x_0}.\]
Эта прямая пересечет ось ординат в точке с координатами \((0 ; 0{,}015625)\). Координаты этой точки не зависят от значения \(x_0\), а значит, все такие прямые пройдут через эту точку.
\((0 ; 0{,}015625)\).
Известно, что выпуклая фигура \(\Phi\) на плоскости устроена таким образом, что она симметрична относительно любой прямой, которая проходит через точку \(O\) на этой плоскости. Самое большое расстояние между двумя точками, принадлежащими фигуре \(\Phi\), равно дроби, в числителе которой шесть, а в знаменателе квадратный корень из числа \(\pi\).
Чему равна площадь фигуры \(\Phi\)?
Докажем, что все точки на границе фигуры равноудалены от центра симметрии \(O\).
- Возьмем на границе фигуры произвольную точку \(A\). Пусть расстояние \(OA=R\).
- Возьмем любую другую точку \(B\) на границе фигуры.
- Построим прямую \(I\), проходящую через точку \(O\) и являющуюся биссектрисой угла \(AOB\).
- По свойству осевой симметрии, точка \(A^\prime\), симметричная точке \(A\) относительно прямой \(I\), также принадлежит фигуре \(\Phi\).
- Поскольку \(I\) — биссектриса, точка \(A^\prime\) попадет на луч \(OB\). Так как при симметрии расстояние до центра сохраняется (\(OA^\prime = OA =R\)), точка \(A^\prime\) совпадет с точкой \(B\) только если \(OB=R\).
- Предположим, что \(OB >R\). Тогда точка \(A\) лежит внутри отрезка \(OB\). Но поскольку фигура выпуклая, весь отрезок \(OB\) должен принадлежать фигуре, а значит, и точка \(A\) не может быть граничной. Пришли к противоречию.
- Предположим, что \(OB < R\). Тогда точка \(B\) лежит внутри отрезка \(OA\). Это также противоречит тому, что \(B\) — граничная точка.
- Следовательно, единственно возможный вариант — \(OB=R\).
- Поскольку точка \(B\) была выбрана на границе произвольно, получается, что все точки границы фигуры \(\Phi\) находятся на одинаковом расстоянии \(R\) от точки \(O\). По определению, это окружность.
- Так как границей является окружность, то сама фигура — круг.
- Используя данное в условии значение диаметра (\(6/\sqrt\pi\)), находим радиус (\(3/\sqrt\pi\)) и вычисляем площадь, которая равна 9.
9.
Находясь на борту космического корабля, главный двигатель за первый час израсходовал \(40\%\) всего запаса анобтаниума, а вспомогательные двигатели вместе за это же время израсходовали лишь 300 г анобтаниума. За следующий час главный двигатель израсходовал \(80\%\) оставшегося топлива, а вспомогательные двигатели израсходовали 100 г топлива на двоих. В итоге на борту корабля осталось 800 г топлива. Сколько килограммов фантастического топлива было на борту до начала полета?
Найдем массу анобтаниума, оставшегося к концу первого часа.
Не было израсходовано главным двигателем к этому моменту \(100+ 800= 900\text{~г}.\)
Это составляет \(100 - 80 = 20\%\).
Составим пропорцию и решим ее: \[\begin{aligned} 20\% & ~-~ 900,\\ 100\% & ~-~ ? \end{aligned}\]
Значит, к концу первого часа оставалось \(900:0{,}2 = 4500\text{~г}\) анобтаниума.
Найдем массу топлива к началу первого часа.
Не было израсходовано главным двигателем к этому моменту \(4500+ 300= 4800\) г, что составляет \(100 - 40 = 60\%\).
Составим пропорцию и решим ее: \[\begin{aligned} 60\% & ~-~ 4800,\\ 100\% & ~-~ ? \end{aligned}\]
Значит, к началу первого часа было \(4800: 0{,}6 = 8000\text{~г}\), что составляет 8 кг.
8.
Известно, что три различные точки \(A(2; 4)\), \(B(x; 6)\), \(C(6; y)\) расположены на координатной плоскости таким образом, что через них нельзя провести параболу с вертикальной осью. При этом также известно, что \(x\) — минимальное натуральное подходящее число, неравное единице.
Найдите величину \(x+y\).
Через три точки нельзя провести параболу тогда и только тогда, когда они расположены на одной прямой. Действительно, прямая не может пересекать параболу в трех точках, так как квадратное уравнение имеет не больше двух корней. С другой стороны, если три точки не лежат на одной прямой, то через них всегда можно провести параболу. Покажем это.
Пусть на числовой прямой есть три точки с координатами \((x_1, y_1)\), \((x_2, y_2)\), \((x_3, y_3)\). Запишем уравнение параболы в следующем виде: \[y=y_1\frac{(x-x_2)\cdot (x-x_3)}{(x_1-x_2)\cdot (x_1-x_3)}+ y_2\frac{(x-x_1)\cdot (x-x_3)}{(x_2-x_1)\cdot (x_2-x_3)}+y_3\frac{(x-x_1)\cdot (x-x_2)}{(x_3-x_1)\cdot (x_3-x_2)}.\]
Первое слагаемое равно нулю во второй и третьей точке, и равно \(y_1\) в первой, аналогичным образом устроены второе и третье слагаемые, так что это уравнение задает функцию, проходящую через три точки. Однако надо еще проверить, что уравнение задает именно параболу. Для этого нужно, чтобы коэффициент при \(x_2\) не равнялся нулю. \[\begin{gather} \frac{y_1}{(x_1-x_2)\cdot (x_1-x_3)}+ \frac{y_2}{(x_2-x_1)\cdot (x_2-x_3)}+ \frac{y_3}{(x_3-x_1)\cdot (x_3-x_2)}\not = 0;\\ y_1\cdot (x_2-x_3)-y_2\cdot (x_1-x_3)+y_3\cdot (x_1-x_2)\not = 0. \end{gather}\] Можно убедиться, что это условие означает, что три точки не лежат на одной прямой. А именно, нахождение трех точек на одной прямой можно записать следующим образом: \[\begin{gather} \frac{y_1-y_2}{x_1-x_2}=\frac{y_1-y_3}{x_1-x_3};\\ (y_1-y_2)\cdot (x_1-x_3)=(y_1-y_3)\cdot (x_1-x_2);\\ y_1\cdot (x_1-x_3)-y_1\cdot (x_1-x_2)=y_2\cdot (x_1-x_3)-y_3\cdot (x_1-x_2);\\ y_1\cdot (x_2-x_3)+y_3\cdot (x_1-x_2)-y_2\cdot (x_1-x_3)=0. \end{gather}\] Таким образом, если это условие выполнено, то через три точки проходит прямая, и не проходит никакая парабола. А если оно не выполнено, то проходит единственная парабола, и нельзя провести никакую прямую.
Тогда выразим угловой коэффициент этой прямой тремя разными способами: \[k=\frac 2{x-2}=\frac {y-6}{6-x}=\frac{y-4}4.\]
Отсюда получаем, что \[y=\frac{4\cdot x}{x-2}.\]
Минимальное натуральное \(x\), не равное единице, которое подходит — это \(x = 3\). Тогда \(y = 12\).
Значит, \(x + y = 15\).
15.
Три прямые дороги образуют треугольник с равными сторонами, длина которых равна 1000 м. У этих дорог стоят четыре человека, каждый на обочине одной из трех дорог. Иван и Александр стоят возле одной дороги в 500 м друг от друга. Сергей и Петр стоят у обочин двух других дорог. Сергею идти до Ивана 1500 м по дорогам кратчайшим путем, Александру до Петра тоже. Между дорогами расположено поле. Какая величина получится, если к расстоянию от Сергея до Ивана по прямой (то есть по полю, а не по дорогам) добавить половину расстояния от Ивана до Александра вдоль дороги, возле которой они стоят, и вычесть расстояние от Александра до Петра по прямой (по полю)?
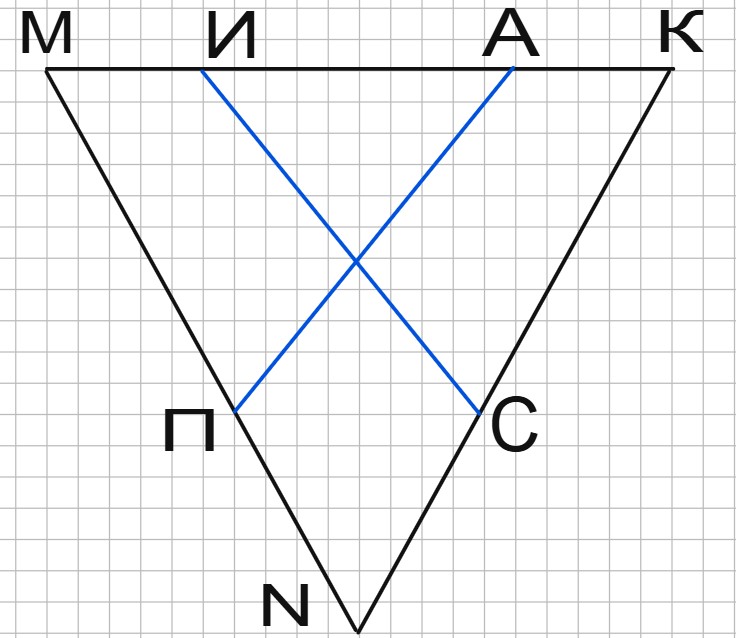
Нарисуем расположение всех этих четырех человек. Расположение Сергея и Петра здесь определяется из того условия, что путь до Ивана и Александра соответственно должен занимать 1500 м, в то время как расстояние по одной стороне не больше 1000 м, а по другой не больше 500 м.
Используя указанные расстояния, можем записать:
\(\text{MA} + \text{MП }= \text{KИ} + \text{KC}\), а значит, \(\text{MИ} + \text{MП} = \text{KA} + \text{KC} = 1000\) м.
\(\text{MИ} + \text{KA} = \text{ИA} = 500\) м. Кроме того, длина \(\text{KM}\) равна 1000 м.
Отсюда выходит, что \(\text{KA} = 1000 - \text{KC} = 1000 - \text{MA}\), а значит, \(\text{KC} = \text{MA}\). Аналогично выходит, что \(\text{KИ}= \text{МП}\).
Тогда треугольники \(\text{KИC}\) и \(\text{MПA}\) равны друг другу по двум сторонам и углу между ними.
Следовательно, \(\text{AП} = \text{CИ}\), а значит, \(\text{AП} - \text{СИ} + 0{,}5\cdot \text{ИА} = 250\) м.
250.
Количество четных делителей натурального числа в 5 раз больше всех остальных его делителей (рассматриваются все делители, включая само число и единицу). Третья часть всех делителей не делится на 3. Половина четных делителей делится на 5. Само число при этом не превосходит 10000. Напишите в ответ максимальное число, которое подходит под этим условия.
Количество четных делителей натурального числа в 5 раз больше всех остальных его делителей.
Это значит, что оно делится на \(2^5\) степени, но не делится на \(2^6\).
Третья часть всех делителей не делится на 3.
Это значит, что оно делится на \(3^2\), но не делится на \(3^3\).
Половина четных делителей делится на 5.
Это значит, что оно делится на 5, но не делится на 25.
Если перемножим \(2^5\) на \(3^2\) и на 5, то получим 1440. Минимальное число, подходящее под условия выше, но большее этого числа, равно \(7\cdot 1440 = 10080 > 10000\).
Следовательно, под все условия подходит только число 1440.
1440.
Склад находится в месте, отмеченном на карте точкой \(A\). Нужно проложить дорогу до берега реки, затем построить мост, перпендикулярный течению реки, и от другого берега проложить дорогу до деревни, отмеченной на карте точкой \(B\). Пример подобного построения на рисунке.
Берега реки здесь нарисованы как параллельные прямые.
Координатная ось \(Ox\) на рисунке отсчитывает положения моста относительно реки в километрах. В примере, приведенном на рисунке, мост проходит через метку 1 км.
Через какую метку должен проходить мост, чтобы сумма длин пути от склада \(A\) до реки по дороге и от противоположного берега реки до деревни \(B\) была наименьшей? Ответ дайте в километрах.
Если вырезать с карты реку и соединить точки \(A\) и \(B\) прямой, то это и будет кратчайший путь, их соединяющий. Чтобы получить путь до реки, нужно после этого вновь вставить реку. Продемонстрируем эти операции с помощью рис. 8.2–8.3.
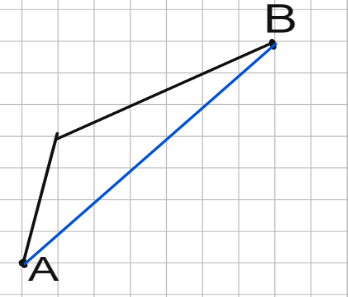
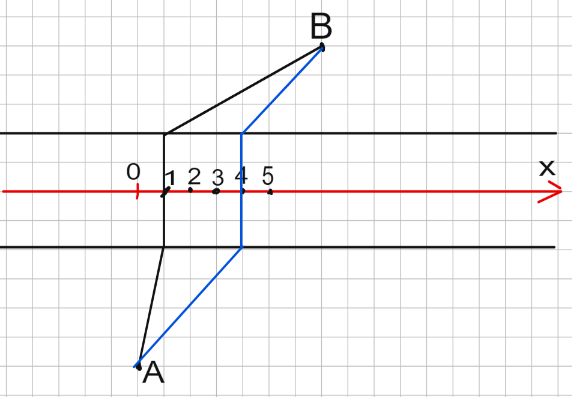
4.
Два космических корабля стартуют одновременно с одной планеты и направляются к Альфе Центавра, расстояние до которой составляет 4,37 св. лет. Один корабль движется со скоростью 0,1 св. год в год, а другой — со скоростью 0,2 св. год в год.
Через сколько лет расстояние до Альфы Центавра для более быстрого корабля будет в три раза меньше, чем для более медленного корабля? Ответ приведите с точностью до сотых.
Обозначим время, прошедшее с начала пути, как \(t\) лет.
Расстояние, пройденное медленным кораблем, равно \(0{,}1t\) св. год, и оставшееся расстояние до Альфы Центавра для медленного корабля \(4{,}37-0{,}1t\) св. год.
Расстояние, пройденное быстрым кораблем, равно \(0{,}2t\) св. год, и оставшееся расстояние до Альфы Центавра для быстрого корабля \(4{,}37-0{,}2t\) св. год.
По условию задачи, остаток пути для быстрого корабля в 3 раза меньше, чем остаток пути для медленного корабля: \[4{,}37-0{,}2t=\frac 13(4{,}37-0{,}1t).\]
Умножим обе стороны на 3: \[3(4{,}37-0{,}2t)=4{,}37-0{,}1t;\] \[13{,}11-0{,}6t=4{,}37-0{,}1t.\]
Переносим все \(t\) в одну сторону и постоянные в другую: \[13{,}11-4{,}37=0{,}6t-0{,}1t;\] \[8{,}74=0{,}5t.\]
Делим обе стороны на \(0{,}5\): \[t=\frac{8{,}74}{0{,}5}={17{,}48}.\]
Таким образом, искомое время равно 17,48 лет.
17,48.
Функция \(f(x)\) является квадратным трехчленом и может быть описана следующим образом: \[f(x)=(f(1)+f(-1)+f(0))\cdot x^2+(f(1)+2\cdot f(0))\cdot x-1.\]
В то же время квадратный трехчлен в общем виде может быть записан так: \[f(x)=a\cdot x^2+b\cdot x+c.\]
Найдите минимальное значение величины \(a^2 + 2b^2 + 3c^2\) при данных условиях.
Подставим \(f(x)\) в общем виде в первую формулу из условия: \[a\cdot x^2+b\cdot x+c= (a+b+c+a-b+c+c)\cdot x^2+(a+b+c+2\cdot c)\cdot x-1;\] \[\left\{\begin{aligned} &a=2\cdot a+3\cdot c,\\ &b=a+b+3\cdot c, \\ &c= -1. \end{aligned}\right.\]
Отсюда получаем, что \(a = 3\), \(c = -1\). Чтобы искомая величина была минимальной, нужно, чтобы коэффициент \(b = 0\).
12.
Произведение всех делителей числа 1000, включая само это число и единицу, равно \(10^k\).
Чему равно \(k\)?
\[1000 = 2^3\cdot 5^3.\]
Комбинируя все возможные способы выбрать степень двойки и степень пятерки, входящие в делитель, получаем все \((3+1) \cdot (3+1) = 16\) вариантов, каждый из которых соответствует делителю числа. При этом эти 16 делителей можно разбить на пары, произведение в каждой дает 1000: \[1000 = 1\cdot 1000 = 2\cdot 500 = 4\cdot 250 = 8\cdot 125 = 5\cdot 200 = 10\cdot 100 = 20\cdot 50 = 25\cdot 40.\]
Тогда выходит, что это будет число \(1000^8\), а значит, \(10^{24}\).
24.
Дан квадрат \(ABCD\). На сторонах \(CB\) и \(CD\) отмечены точки \(L\) и K соответственно такие, что \(CL = CK\). Из точки \(C\) на отрезок \(LD\) опущен перпендикуляр в точку \(E\).
Пусть \(AE = 60\), \(EK = 91\). Найдите длину \(AK\).
Сделаем рис. 8.4.
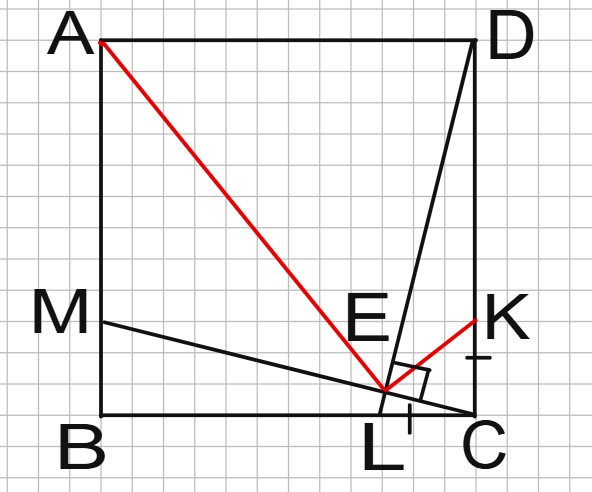
Одно из возможных решений заключается в использовании метода координат. Обозначим длину квадрата за единицу, а \(CL = LK = x\).
Тогда \[L(1-x;0);~K(1;x);~\overrightarrow{LD}=(x;1);~\overrightarrow{CE}=t\cdot (1;-x);~E(1+t; -x\cdot t);~\overrightarrow{LE}=(t+x; -x\cdot t).\]
Так как вектора \(LE\) и \(LD\) должны быть сонаправлены, то \[\frac{t+x}{x} =-x\cdot t;~t= -\frac x{1+x^2};~E(1-\frac x{1+x^2};~1-\frac 1{1+x^2});\] \[\overrightarrow{AE}=(1-\frac x{1+x^2};~-\frac 1{1+x^2});~ \overrightarrow{EK}=(\frac x{1+x^2};~x-\frac{x^2}{1+x^2}).\]
Посчитаем скалярное произведение: \(\overrightarrow{AE}\cdot \overrightarrow{EK}=0.\) Это значит, что треугольник \(AEK\) прямоугольный.
Тогда \(AK\) можно найти по теореме Пифагора: \(60^2+91^2=109^2\).
109.