Предметный тур. Математика. 3 этап
Пусть \(2 < a < b\). Найдите наибольшее значение \(b\), при котором верно неравенство \[a^{2}b - ab^{2} - 2(a^{2} - b^{2}) - 3a^{2} + 3ab + 10a - 10b \geqslant 0.\]
Разложим левую часть неравенства на множители. Имеем \[\begin{aligned} &a^{2}b - ab^{2} - 2(a^{2} - b^{2}) - 3a^{2} + 3ab + 10a - 10b = \\ &= ab(a - b) - 2(a - b)(a + b) - 3a(a - b) + 10(a - b) = \\ &= (a - b)(ab - 2a - 2b - 3a + 10) = \\ &= (a - b)(ab - 5a - 2b + 10) \\ &= (a - b)(a(b - 5) - 2(b - 5)) = (a - b)(a - 2)(b - 5) = (b - a)(a - 2)(5 - b). \end{aligned}\] Так как \(b > a > 2\), то первые два множителя положительны. Следовательно, требуется найти такое \(b\), что \(5 - b \geqslant 0\). Тогда наибольшее такое \(b\) равно числу 5.
5.
Числа 1765, 1950, 1543 дают одинаковый остаток при делении на некоторое натуральное число \(k\), где \(k \geqslant 2\). Найдите этот остаток.
Так как данные числа при делении на \(k\) дают одинаковый остаток, то разность любых двух из них делится на \(k\). Имеем \[\begin{aligned} &1765 - 1543 = 222, \\ &1950 - 1765 = 185. \end{aligned}\] Числа 222 и 185 делятся на \(k\), следовательно, их разность, равная \(222-185=37\), тоже делится на \(k\). Так как 37 — простое число, то \(k=37\).
Разделив, например, 1543 на 37, получим искомый остаток 26.
26.
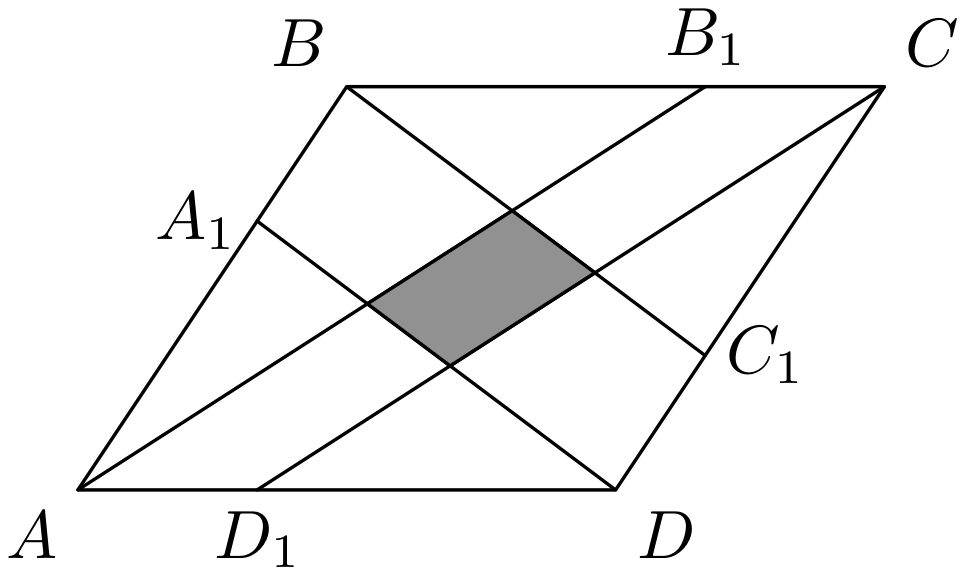
На сторонах параллелограмма \(ABCD\) отмечены точки \(A_{1}\), \(B_{1}\), \(C_{1}\), \(D_{1}\) так, что \(AA_{1}:A_{1}B = BB_{1}:B_{1}C=CC_{1}:C_{1}D=DD_{1}:D_{1}A = 2:1\). Найдите отношение площади параллелограмма \(ABCD\) к площади закрашенной фигуры (см. рис. 1.1).
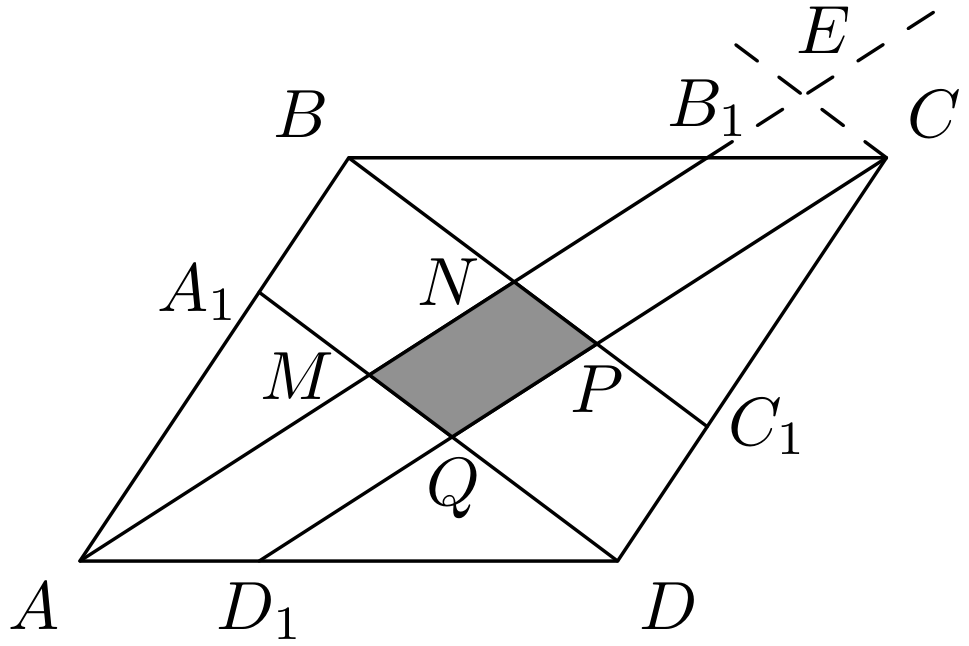
Пусть \(MNPQ\) — закрашенный четырехугольник (см. рис. 1.2).
Треугольники \(ABB_{1}\) и \(CDD_{1}\) равны, так как \(AB = CD\) (противоположные стороны параллелограмма), \(BB_{1} = DD_{1}\) (составляют одинаковую часть от противоположных сторон параллелограмма), \(\angle ABC = \angle CDA\) (свойство параллелограмма).
Тогда \(\angle BB_{1}A = \angle CD_{1}D\).
Так как \(BC \parallel AD\), то \(AB_{1} \parallel CD_{1}\).
Аналогично \(BC_{1} \parallel DA_{1}\). Следовательно, \(MNPQ\) — параллелограмм.
Проведем через точку \(C\) прямую, параллельную \(BC_{1}\). Пусть \(E\) — точка пересечения построенной прямой и прямой \(AB_{1}\).
Треугольники \(BB_{1}N\) и \(CB_{1}E\) подобны по двум углам (\(\angle BB_{1}N = \angle EB_{1}C\), \(\angle NBB_{1} = \angle ECB_{1}\)), коэффициент подобия равен \(BB_{1}:B_{1}C = 2\). Тогда их площади отличаются в 4 раза. Пусть \(S_{CB_{1}E} = x\). Тогда \(S_{BB_{1}N} = 4x\).
Треугольники \(BCP\) и \(BB_{1}N\) подобны по двум углам (\(\angle PBC\) общий, \(\angle BCP = \angle BB_{1}N\)), коэффициент подобия равен \(BC:BB_{1} = 3:2\). Тогда их площади отличаются в \(\dfrac{9}{4}\) раза. Следовательно, \(S_{PNB_{1}C} = 5x\).
Параллелограммы \(MNPQ\) и \(PNEC\) имеют одинаковую высоту, опущенную из точки \(N\) на прямую \(D_{1}C\). Тогда их площади относятся как основания \(CP\) и \(PQ\). По теореме Фалеса \(CP:PQ = CC_{1}:C_{1}D = 2\). Поскольку \[S_{PNEC} = S_{PNB_{1}C} + S_{CB_{1}E} = 5x + x = 6x,\] получаем, что \(S_{MNPQ} = 3x\). То есть \(S_{BCP} = 9x = 3S_{MNPQ}\).
Аналогично \(S_{CDQ} = S_{DAM} = S_{ABN} = 3S_{MNPQ}\). Тогда \[\frac{S_{ABCD}}{S_{MNPQ}} = \frac{S_{MNPQ} + S_{ABN} + S_{BCP} + S_{CDQ} + S_{DAM}}{S_{MNPQ}} = 1 + 4\cdot 3 = 13.\]
13.
Найдите наибольший корень уравнения \[4x^{2} + 2x - 8 = 3 \sqrt{x^{4} - x^{2} + 4}.\]
Попробуем найти положительные корни (если они есть, то неположительные нас уже не интересуют). Вынесем за скобку \(4x\) в левой части, а в правой под корнем вынесем величину \(x^{2}\), которую затем вынесем из-под корня. Имеем \[4x\left( x - \frac{2}{x} + \frac{1}{2} \right) = 3x\sqrt{x^{2} + \frac{4}{x^{2}} - 1}.\]
Разделив обе части на \(x > 0\), получаем \[4\left( x - \frac{2}{x} + \frac{1}{2} \right) = 3\sqrt{x^{2} + \frac{4}{x^{2}} - 1}.\]
Положим \(t = x - \frac{2}{x}\). Тогда \(t^{2} = x^{2} + \frac{4}{x^{2}} - 4\). Следовательно, \(x^{2} + \frac{4}{x^{2}} = t^{2} + 4\). Тогда уравнение равносильно \[4\left( t + \frac{1}{2} \right) = 3\sqrt{t^{2} + 3}. \label{eq:FinTex89_3_1}\] Возведя обе части уравнения в квадрат, находим \[16t^{2} + 16t + 4 = 9t^{2} + 27.\] То есть \[7t^{2} + 16t - 23 = 0.\]
Корень \(t = - \frac{23}{7}\) не обращает уравнение \eqref{eq:FinTex89_3_1} в верное равенство, а корень \(t = 1\) подходит. Значит, \[x - \frac{2}{x} = 1 \quad \iff \quad x^{2} - x - 2 = 0.\]
Из корней \(x = -1\), \(x = 2\) нам подходит только положительный. Таким образом, \(x = 2\).
2.
В сообществе некоторой социальной сети, состоящем из двадцати человек, сложилась следующая ситуация. У девяти членов этого сообщества оказалось ровно по три друга, также входящих в это сообщество. А у остальных оказалось ровно по \(n\) друзей, также входящих в это сообщество. Определите наибольшее возможное значение \(n\).
Представим сообщество в виде графа, вершины которого соответствуют членам сообщества, а ребра — дружбе между ними.
Разобьем вершины на два класса: «группа девяти» — вершины, имеющие степень 3, и «группа одиннадцати» — вершины, имеющие степень \(n\).
Докажем, что \(n < 13\). Пусть число \(n\) принимает значение хотя бы 13. Рассмотрим одну вершину из «группы одиннадцати». Эта вершина может быть соединена максимум с десятью вершинами «группы одиннадцати». Значит, эта вершина соединена хотя бы с тремя вершинами из «группы девяти». Следовательно, вершины «группы одиннадцати» добавляют к общей сумме степеней вершин «группы девяти» хотя бы \(11 \cdot 3 = 33\). Но сумма степеней вершин «группы девяти» равна \(9 \cdot 3 = 27\). Получили противоречие.
Так как каждое ребро графа добавляет к общей сумме степеней вершин двойку, то общая сумма степеней четна. Тогда число \(n\) не может быть равным 12, поскольку иначе сумма степеней будет равна нечетному числу \(11 \cdot 12 + 9\cdot 3\). Таким образом, \(n \leqslant 11\).
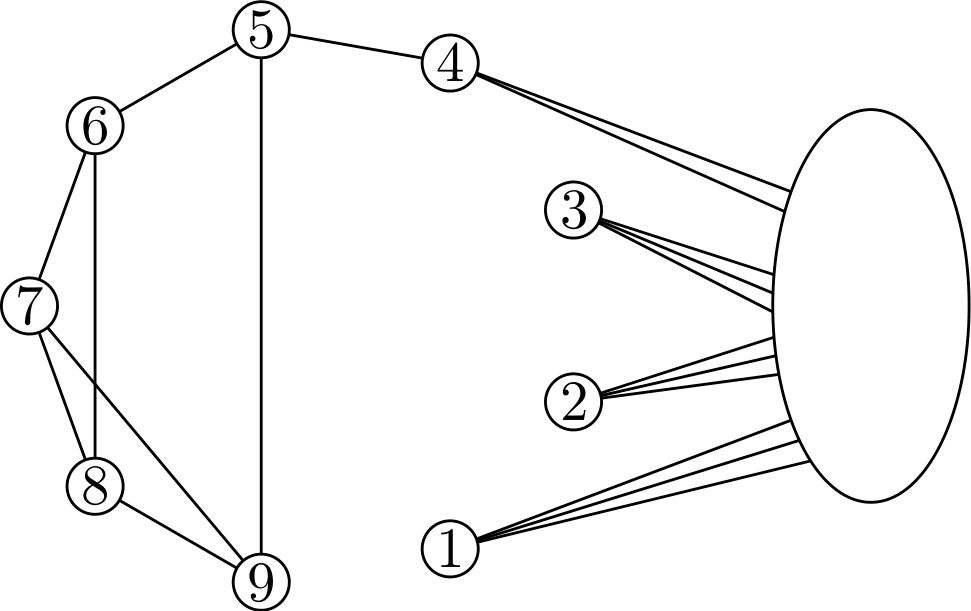
Приведем пример, когда \(n = 11\). «Группа одиннадцати» обозначена на рисунке овалом, а вершины «группы девяти» отмечены пронумерованными кругами.
Пусть «группа одиннадцати» образует полный подграф. При этом каждая вершина «группы одиннадцати» смежна ровно с одной вершиной «группы девяти». Вершины 1, 2 и 3 соединены только с «группой одиннадцати». Вершина 4 имеет две смежных в «группе одиннадцати». Тогда степени вершин «группы девяти» равны трем, а степени вершин «группы одиннадцати» равны 11.
11.
Семизначное число \(*\)20\(*\)25\(*\) (звездочки обозначают некоторые цифры) делится на 2475. Какое это число?
Поскольку \[2475 = 9 \cdot 25 \cdot 11,\] то искомое число делится на 9, 25 и 11.
Из делимости на 25 следует, что последняя цифра равна нулю. То есть искомое число равно \[\overline{a20b250}.\]
Из делимости на 9 следует, что сумма всех цифр делится на 9. Следовательно, \(a + b~ \vdots~ 9\). Так как \(a \neq 0\), то возможные варианты для \((a, b): (1, 8)\), \((2, 7)\), …, \((9, 0)\), а также \((9, 9)\).
Из делимости на 11 следует, что разность между суммами цифр на четных и на нечетных позициях делится на 11. То есть \[(a + 0 + 2 + 0) - (2 + b + 5) = a - b - 5~ \vdots~ 11.\] Из перечисленных выше вариантов пар \((a, b)\) подходит лишь один: \(a = 7\), \(b = 2\) (проверяется непосредственным перебором).
7202250.
Ваня решил обновить мышь и клавиатуру на своем рабочем месте. То же самое решила сделать и Таня. Ваня готов заплатить за клавиатуру не более 2000 руб., а за мышь не более \(r\) руб. Таня, наоборот, готова заплатить за клавиатуру не более \(r\) руб., а за мышь не более 2000 руб. Ваня и Таня непременно покупают товар, если он стоит не более, чем они готовы за него заплатить, а при большей стоимости — не покупают. Сотрудники магазина «Вся электроника» устанавливают цены на товары, зная о ценовых предпочтениях своих клиентов. Поразмыслив, сотрудники сообразили: если продавать мышь и клавиатуру только в комплекте, то наибольшая возможная выручка от продажи товаров Ване и Тане будет на \(p\%\) больше, чем наибольшая возможная выручка при продаже товаров по отдельности (Ваня или Таня купит комплект, если его стоимость не более \(2000 + r\) руб.). При каком наименьшем значении \(r\) величина \(p\) будет наибольшей?
При продаже клавиатуры и мыши в комплекте магазину необходимо установить цену \(2000 + r\) руб. за комплект (при меньшей стоимости выручка будет меньше, а при большей — и вовсе равна нулю). Тогда наибольшая выручка при продаже товаров Ване и Тане в комплекте равна \[A = 2 \cdot (2000 + r) = 4000 + 2r ~ \text{руб.}\]
Теперь определим наибольшую возможную выручку при продаже товаров по отдельности. Заметим, что нет смысла устанавливать цены на клавиатуру и мышь, отличные от \(2000\) или \(r\). Поясним это утверждение. Пусть \(m = \min\left\{2000, r\right\}\), \(M = \max\left\{2000, r\right\}\), \(c\) — цена на товар. Если \(c < m\), то товар купят все, а цену можно повысить до \(m\), увеличив выручку. Если \(m < c < M\), то товар купит кто-то один, а цену можно поднять до \(M\), увеличив выручку. Если \(c > M\), то товар никто не купит, следовательно, можно увеличить выручку, положив, например, \(c = m\).
Если \(r = 2000\) руб., то нет разницы между продажей товаров в комплекте и по отдельности, то есть \(p = 0\%\).
Рассмотрим случай, когда \(r < 2000\).
Если клавиатура и мышь стоят одинаково по 2000 руб., то Ваня купит только клавиатуру, а Таня — только мышь. Суммарная выручка магазина равна 4000 руб.
Если клавиатура и мышь стоят одинаково по \(r\) руб., то все купят все товары. Суммарная выручка магазина составит \(4r\) руб.
Если клавиатура и мышь стоят по-разному, то один из покупателей купит и клавиатуру, и мышь, а второй — только тот товар, который стоит \(r\) руб. Суммарная выручка магазина в этом случае равна \(2000 + 2r\) руб.
Если \(r \leqslant 1000\), то \[4r \leqslant 2000 + 2r \leqslant 4000,\] следовательно, наибольшая выручка равна \(4000\). Отношение \[\frac{A}{4000} = 1 + \frac{2r}{4000}\] принимает наибольшее значение \(3/2\) при \(r = 1000\).
Если же \(1000 < r < 2000\), то \[4000 < 2000 + 2r < 4r,\] следовательно, наибольшая выручка равна \(4r\). Имеем \[\frac{A}{4r} = \frac{1000}{r} + \frac{1}{2} < \frac{3}{2}.\]
Таким образом, в случае \(r < 2000\) наибольшее значение \(p = 50\%\) достигается при \(r = 1000\).
Рассмотрим случай, когда \(r > 2000\).
Если клавиатура и мышь стоят одинаково по \(2000\) руб., то все купят все товары. Суммарная выручка магазина составит \(8000\) руб.
Если клавиатура и мышь стоят одинаково по \(r\) руб., то Ваня купит только мышь, а Таня — только клавиатуру. Суммарная выручка равна \(2r\) руб.
Если клавиатура и мышь стоят по-разному, то один из покупателей купит и клавиатуру, и мышь, а второй — только тот товар, который стоит 2000 руб. Выручка магазина — \(4000 + r\) руб.
Если \(r \leqslant 4000\), то \[2r \leqslant 4000 + r \leqslant 8000,\] следовательно, наибольшая выручка равна 8000. Отношение \[\frac{A}{8000} = \frac{1}{2} + \frac{r}{4000}\] достигает наибольшего значения \(\frac{3}{2}\) при \(r = 4000\).
Если \(r > 4000\), то \[8000 < 4000 + r < 2r.\] Тогда наибольшая выручка равна \(2r\), \[\frac{A}{2r} = \frac{2000}{r} + 1 < \frac{3}{2}.\]
Таким образом, в случае \(r > 2000\) наибольшее значение \(p = 50\%\) достигается при \(r = 4000\).
Отсюда делаем вывод, что наименьшее значение \(r\), при котором величина \(p\) принимает наибольшее значение \(50\%\), равно \(1000\) руб.
1000.
Внутри тетраэдра \(ABCD\) выбрана точка \(Z\), обладающая свойством: \[\overrightarrow{AZ} = 2\overrightarrow{ZB} + 3\overrightarrow{ZC} + 4\overrightarrow{ZD}.\] Прямая \(DZ\) пересекает основание \(ABC\) в точке \(E\). Чему равно отношение \(\dfrac{DZ}{ZE}\)?
Первый способ. Разместим в точках \(A\), \(B\), \(C\) и \(D\) массы \(1\), \(2\), \(3\) и \(4\). Поскольку выполняется равенство \[\overrightarrow{ZA} + 2\overrightarrow{ZB} + 3\overrightarrow{ZC} + 4\overrightarrow{ZD} = \overrightarrow{0},\] то точка \(Z\) — центр масс вершин тетраэдра. Центр масс не изменится, если заменить вершины основания \(ABC\) на точку \(M\) массы \(1 + 2 + 3 = 6\) — центр масс точек \(A, B, C\).
Точка \(Z\) лежит на отрезке \(DM\), следовательно, точка \(M\) лежит на прямой \(DZ\). В то же время, точка \(M\) лежит в плоскости \(ABC\). Следовательно, \(E = M\).
По свойству центра масс (архимедово правило рычага) имеем \(\dfrac{DZ}{ZE} = \dfrac{6}{4} = 1{,}5\).
Второй способ. В данном в условии равенстве \[\overrightarrow{AZ} = 2\overrightarrow{ZB} + 3\overrightarrow{ZC} + 4\overrightarrow{ZD}\] каждый вектор \(\overrightarrow{XY}\) представим как сумму \(\overrightarrow{XE} + \overrightarrow{EY}\). Имеем \[\overrightarrow{AE} + \overrightarrow{EZ} = 2(\overrightarrow{ZE} + \overrightarrow{EB}) + 3(\overrightarrow{ZE} + \overrightarrow{EC}) + 4(\overrightarrow{ZE} + \overrightarrow{ED}).\] Раскрывая скобки и приводя подобные слагаемые, получаем \[\overrightarrow{AE} + 2\overrightarrow{BE} + 3\overrightarrow{CE} = 10\overrightarrow{ZE} + 4\overrightarrow{ED}.\]
Заметим, что в левой части складываются векторы, принадлежащие плоскости \(ABC\), следовательно, и вся сумма будет лежать в плоскости \(ABC\). Сумма в правой части — вектор, коллинеарный прямой \(DE\). Поскольку прямая \(DE\) не лежит в плоскости \(ABC\), то полученное равенство возможно лишь в случае, когда левая и правая части равны нулевому вектору. Тогда \[\frac{|\overrightarrow{ZE}|}{|\overrightarrow{ED}|} = \frac{4}{10} = \frac{2}{5}.\] Следовательно, \(\dfrac{DZ}{ZE} = \dfrac{3}{2} = 1{,}5\).
1,5.
Найдите наименьший корень уравнения \[\log_{3}(\operatorname{tg}^{2}x + 2\operatorname{tg} x + 2) + \log_{9}\left(2\sin^{2}x + \cos^{2}x - \sqrt{2}\sin x + \frac{1}{2}\right) = 0\] на отрезке \([-\pi, \pi]\).
Имеем \[\operatorname{tg}^{2}x + 2\operatorname{tg} x + 2 = (\operatorname{tg} x + 1)^{2} + 1 \geqslant 1,\] следовательно, первое слагаемое в левой части уравнения неотрицательно.
Аргумент второго логарифма равен \[\sin^{2}x + (\sin^{2}x + \cos^{2}x) - \sqrt{2}\sin x + \frac{1}{2} = 1 + \left(\sin x - \frac{1}{\sqrt{2}}\right)^{2} \geqslant 1.\] Значит, второе слагаемое левой части уравнения также неотрицательно.
Сумма двух неотрицательных слагаемых равна нулю лишь в случае, когда оба этих слагаемых равны нулю. Тогда уравнение равносильно системе \[\begin{cases} \log_{3}((\operatorname{tg} x + 1)^{2} + 1) = 0,\\ \log_{9}(1 + \left(\sin x - \frac{1}{\sqrt{2}}\right)^{2}) = 0 \end{cases} \quad \iff \quad \begin{cases} \operatorname{tg} x = -1,\\ \sin x = \frac{1}{\sqrt{2}}. \end{cases}\] На отрезке \([-\pi, \pi]\) имеется единственный корень \(x = \dfrac{3\pi}{4}\), удовлетворяющий этой системе.
\(\dfrac{3\pi}{4}\).
Петя готовит блюда, и у него есть 9 ингредиентов на выбор с разными вкусами. Он руководствуется правилом: «1 блюдо = 3 вкуса». В процессе кулинарных экспериментов у Пети получилось сделать так, что любые два блюда имеют разные наборы вкусов. При этом для любых трех блюд есть вкус, который не входит ни в какое из них. Какое наибольшее число блюд мог приготовить Петя?
Оценка. Рассмотрим максимальный набор \(M\) блюд, который мог приготовить Петя. Дополним этот набор множеством \(A\) блюд так, чтобы новый набор \(M \cup A\) был максимальным, обладающим свойствами: «1 блюдо = 3 вкуса», и любые два блюда имеют разные наборы вкусов. Всего в наборе \(M \cup A\) будет \(C_{9}^{3} = 84\) блюда.
Из блюд множества \(M \cup A\) можно составить тройки, содержащие в совокупности все 9 вкусов. Назовем такие тройки «плохими». Всего имеется \(\dfrac{C_9^3 \cdot C_6^3 \cdot C_3^3}{3!}=280\) «плохих» троек. Будем убирать из множества \(M \cup A\) по одному блюда, входящие в набор \(A\), пока не получим множество \(M\). В конце этой процедуры все «плохие» тройки разрушатся. С одним блюдом можно составить \(\dfrac{C_{6}^{3}C_{3}^{3}}{2!} = 10\) «плохих» троек, поэтому, убрав одно блюдо, мы разрушим не более 10 «плохих» троек. Следовательно, для количества блюд \(|A|\) в множестве \(A\) верно неравенство \(|A| \cdot 10 \geqslant 280\). То есть \(|A| \geqslant 28\). Поскольку \(|M \cup A| = 84\), то \(|M| \leqslant 84 - 28 = 56\).
Пример. Если Петя приготовил всевозможные различные блюда из трех ингредиентов, не используя девятый, то он получил как раз \(C_{8}^{3} = 56\) блюд.
56.