Предметный тур. Информатика. 3 этап
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 256 Мбайт.
При разработке новых материалов учитываются комбинации различных свойств, таких как прочность, плотность, устойчивость к температуре, токсичность и так далее. Так, в новом исследовании рассматриваются некоторые \(n\) свойств новых материалов.
В результате экспериментов были получены \(m\) образцов новых материалов. Для каждого образца были измерены каждое из \(n\) свойств и записаны в виде \(n\) целых чисел.
Для применения на практике некоторые свойства полученных материалов более важны, чем другие, а некоторые вообще нежелательны. Поэтому для каждого из них были введены весовые коэффициенты. Для \(i\)-го свойства коэффициент равен целому числу \(c_i\). Чем коэффициент больше, тем более важно соответствующее свойство. Для нежелательных свойств коэффициенты \(c_i\) отрицательные.
Теперь ученым нужно выбрать лучший образец. Общая полезность материала вычисляется следующим образом: значение каждого свойства умножается на соответствующий ему коэффициент, а затем все полученные числа складываются. Например, если для некоторого материала измеренные значения свойств равны \(a_1, a_2, \ldots, a_n\), то общая полезность равна \(c_1a_1 + c_2a_2 + \cdots + c_na_n\). Лучшим материалом считается тот, который имеет максимальную общую полезность.
Напишите программу, которая определяет, какой из материалов самый лучший.
Формат входных данных
В первой строке дано целое число \(n\) — количество свойств, \(1 \leqslant n \leqslant 10\).
Во второй строке дано \(n\) целых чисел — коэффициенты свойств. \(i\)-е из них равно \(c_i\), \(-100 \leqslant c_i \leqslant 100\), \(1 \leqslant i \leqslant n\).
В третьей строке дано одно целое число \(m\) — количество образцов, \(1 \leqslant m \leqslant 100\).
Далее идут \(m\) строк, в которых даны измеренные значения свойств. В \(j\)-й из этих строк дано \(n\) целых чисел, \(i\)-е из этих чисел \(a_{ji}\) равно измеренному значению \(i\)-го свойства \(j\)-го образца. \(0 \leqslant a_{ji} \leqslant 100\), \(1 \leqslant j \leqslant m\), \(1 \leqslant i \leqslant n\).
Гарантируется, что максимальную общую полезность среди всех данных на входе имеет только один образец.
Формат выходных данных
Выведите одно целое число от \(1\) до \(m\) — номер образца с максимальной общей полезностью.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 1 4 -3 3 5 2 1 0 3 5 2 3 1 |
3 |
Примечания
В примере образцы имеют следующие общие полезности: \(10\), \(-3\) и \(11\). Третий образец самый лучший.
Нужно аккуратно реализовать то, что написано в условии задачи.
Единственный подводный камень, из-за которого решение могло набирать не полный балл: у всех образцов суммарная полезность может быть отрицательной.
Пример программы-решения
Ниже представлено решение на языке Python.
n = int(input())
C = list(map(int, input().split()))
m = int(input())
best,best_cost = -1,-10000000
for j in range(m):
A = list(map(int, input().split()))
cost = 0
for i in range(n):
cost += C[i]*A[i]
if cost > best_cost:
best_cost = cost
best = j+1
print( best )Программа проверяется на 10 скрытых тестах. Прохождение каждого теста оценивается в 1 балл. Пример из условия задачи оцениваются в 0 баллов.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 256 Мбайт.
В честь юбилея со дня открытия Берляндского института Исследования Материалов было решено создать скульптуру в виде гигантской молекулы. Главный дизайнер проекта уже продумал художественную составляющую в виде схемы. Теперь нужно подобрать подходящий материал, чтобы воплощенная в реальность конструкция не рухнула под тяжестью собственного веса.
Согласно схеме, скульптура состоит из \(n\) узлов, соединенных \(m\) балками. Все узлы находятся на разной высоте и пронумерованы сверху вниз целыми числами от \(1\) до \(n\). \(i\)-я балка соединяет узлы с номерами \(a_i\) и \(b_i\), причем \(a_i < b_i\). Вес каждой балки равен 1 условной единице, весом узлов в данной задаче пренебрегаем и полагаем равным 0.
Нагрузка на каждый узел рассчитывается как сумма нагрузок на балки, которые опираются на данный узел, плюс вес самих этих балок. Например, если на узел \(x\) опирается \(k\) балок (все те балки, для которых \(b_i = x\)), и нагрузка на \(j\)-ю из этих балок равна \(E_j\), то нагрузка \(N_x\) на узел \(x\) равна \(N_x = E_1 + E_2 + \ldots + E_k + k\). Если на узел не опирается ни одна из балок, то нагрузка на данный узел равна 0.
Нагрузка на каждую из балок рассчитывается следующим образом. Пусть балка \(y\) подпирает снизу узел \(x\) (по определению \(x = a_i\)). Нагрузка на узел \(x\) (рассчитанная согласно абзацу выше) распределяется равномерно на все подпирающие его балки.
Так, если нагрузка на узел \(x\) равна \(N_x\), и узел \(x\) подпирают \(k\) балок, то нагрузка на каждую из этих балок рассчитывается как \(\displaystyle\frac{N_x}{k}\). В том числе \(E_y = \displaystyle\frac{N_x}{k}\).
Задача — определить максимальную нагрузку по всем узлам и по всем балкам. С этой информацией инженеры института подберут для узлов и балок подходящие материалы.
Формат входных данных
В первой строке даны два целых числа \(n\) и \(m\) — количество узлов и количество балок соответственно, \(2 \leqslant n \leqslant 10^5\), \(1 \leqslant m \leqslant 10^5\).
Далее идут \(m\) строк, описывающих балки. \(i\)-я из этих строк содержит два целых числа \(a_i\) и \(b_i\) — номера узлов, которые соединяет \(i\)-я балка, \(1 \leqslant a_i < b_i \leqslant n\), \(1 \leqslant i \leqslant n\).
Гарантируется, что любые два узла соединяет не более одной балки.
Формат выходных данных
В первой строке выведите одно вещественное число — максимальную нагрузку по всем узлам.
Во второй строке выведите одно вещественное число — максимальную нагрузку по всем балкам.
Ответ будет засчитан, если будет отличаться от ответа жюри не более, чем на \(10^{-6}\) по абсолютному или по относительному значению.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
7 10 1 3 3 6 4 5 1 4 4 7 3 4 5 6 2 4 3 5 5 7 |
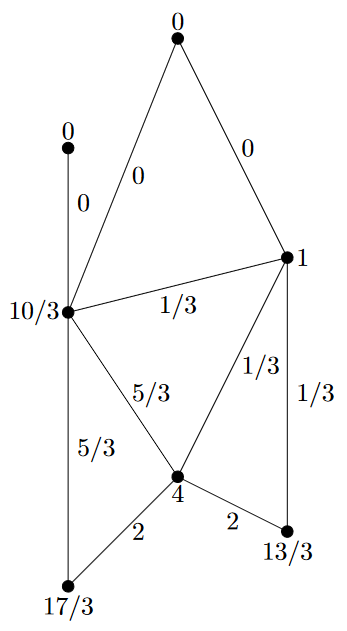
5.666666666666667 2.0 |
Примечания
На рис. 1.1 показана нагрузка на каждый из элементов конструкции из примера.
Для решения задачи следует идти по всем узлам в порядке возрастания номеров. Для каждого узла: сначала следует рассчитать нагрузку на текущий узел, а затем рассчитать нагрузку на каждую исходящую из данного узла балку.
Частичное решение за \(\mathcal{O}(nm)\) предполагает, что для каждого узла входящие и исходящие балки ищутся полным проходом по списку балок.
Пример программы-решения
Ниже представлено решение на языке Python.
n,m = map(int, input().split())
N = [0] * n #нагрузка на узлы
E = [0] * m #нагрузка на балки
AB = [] #список всех балок
for i in range(m):
a,b = map(int, input().split())
AB.append( [a-1,b-1] )
for i in range(n):
for j in range(m):
if AB[j][1]==i:
N[i] += E[j]+1
cnt = 0 #количество исходящих балок
for j in range(m):
if AB[j][0]==i:
cnt += 1
for j in range(m):
if AB[j][0]==i:
E[j] = N[i] / cnt
print( max(N) )
print( max(E) )
Решение можно ускорить до \(\mathcal{O}(n+m)\), если для каждого узла заранее сформировать списки входящих и исходящих балок.
Пример программы-решения
Ниже представлено решение на языке Python.
n,m = map(int, input().split())
In = [ [] for _ in range(n) ]
Out = [ [] for _ in range(n) ]
N = [0] * n
E = [0] * m
for i in range(m):
a,b = map(int, input().split())
In[b-1].append( i )
Out[a-1].append( i )
for i in range(n):
N[i] = len(In[i])
for j in In[i]:
N[i] += E[j]
for j in Out[i]:
E[j] = N[i] / len(Out[i])
print( max(N) )
print( max(E) )Программа проверяется на 16 скрытых тестах. Прохождение каждого теста оценивается в 1 балл. Пример из условия задачи оцениваются в 0 баллов.
В первых восьми тестах ограничения \(n \leqslant 100\), \(m \leqslant 200\).
В следующих восьми тестах ограничения полные \(n \leqslant 10^5\), \(m \leqslant 10^5\).
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 256 Мбайт.
Рассмотрим соединения, записываемые формулой \(\ce{C_nH_{2n+1}Cl}\). Эти соединения представляют собой алканы, в которых один из атомов водорода заменен на атом хлора.
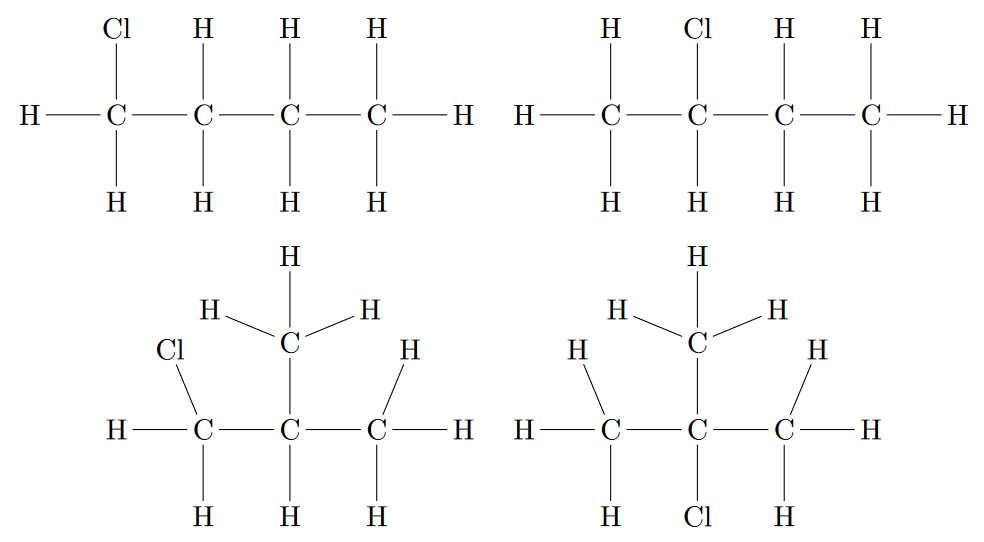
Для одной и той же формулы \(\ce{C_nH_{2n+1}Cl}\) молекула вещества может иметь разную структуру. Например, для \(n=4\) имеется четыре варианта построения молекулы, как показано на рис. 1.2. Такие варианты называются изомерами.
Дано число \(n\). Задача — для данного \(n\) посчитать количество попарно различных изомеров с формулой \(\ce{C_nH_{2n+1}Cl}\). Формально должны быть выполнены следующие условия:
- Молекула должна быть связной.
- Каждый атом углерода должен быть соединен связями с четырьмя другими различными атомами.
- Каждый атом водорода и атом хлора должны быть соединены с одним атомом углерода.
Две молекулы считаются одинаковыми, если можно каждому атому из первой молекулы поставить в соответствие атом из второй молекулы так, чтобы:
- каждый атом второй молекулы соответствовал какому-то одному атому первой молекулы (взаимно-однозначное соответствие);
- соответствующие атомы были одного элемента;
- если какие-то два атома соединены связью в первой молекуле, то соответствующие им атомы во второй молекуле также должны быть соединены связью; и наоборот — если связи между двумя атомами в первой молекуле нет, то ее нет и между соответствующими атомами во второй молекуле.
- Молекулы, которые неодинаковы (соответствия атомов нет) — считаются различными.
Так как ответ может получиться очень большим — выведите остаток от его деления на \(10^9+7\).
Формат входных данных
Дано целое число \(n\), \(1 \leqslant n \leqslant 500\).
Формат выходных данных
Выведите одно целое число — остаток от деления на \(10^9+7\) количества попарно различных изомеров с формулой \(\ce{C_nH_{2n+1}Cl}\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1 |
1 |
2 |
4 |
4 |
3 |
8 |
89 |
Примечания
При \(n \leqslant 45\) количество изомеров не превышает \(10^{18}\). Можно использовать этот факт при написании решения на языке C++ (однако выводить в ответ все равно нужно остаток от деления на \(10^9+7\)).
В последних семи тестах ограничение \(46 \leqslant n \leqslant 500\).
n = int(input())
print( [1,1,1,2,4,8,17,39,89][n] )Для решения второй и третьей группы нужно воспользоваться методом динамического программирования.
Рассмотрим атом углерода в молекуле, который соединен с атомом хлора. Пусть данный атом углерода будет «корневым». Теперь оставим в молекуле только атомы углерода, а остальные атомы «выкинем». У нас получится некоторое дерево, которое подвесим за «корневой» атом углерода. Понятно, что из данного подвешенного дерева всегда можно однозначно восстановить молекулу обратно. Задача свелась к следующей: нужно посчитать количество подвешенных деревьев из \(n\) вершин, причем каждая вершина дерева может иметь не более трех дочерних (непосредственно висящих на ней) вершин.
Пусть \(dp[i]\) — количество таких деревьев из \(i\) вершин. Полагаем, что \(dp[0] = 1\). Чтобы посчитать значение \(dp[i]\), нужно всеми способами разбить \(i\) в сумму \(i = 1+a+b+c\), где \(1\) — это корневая вершина, а \(a\), \(b\) и \(c\) — это количества вершин в каждом из трех поддеревьев. Тогда данное разбиение даст \(dp[a] \cdot dp[b] \cdot dp[c]\) способов. Если у вершины меньше трех поддеревьев, то какие-то из значений \(a\), \(b\), \(c\) равны \(0\).
Однако нужно учесть, что перестановка поддеревьев местами иногда может дать повторяющиеся способы. Чтобы их избежать, рассматриваем только варианты, когда \(a \leqslant b \leqslant c\). Причем если \(a < b = c\) или \(a = b < c\), то количество вариантов будет равно \(dp[a] \cdot dp[b] \cdot (dp[b]+1) / 2\) и \(dp[a] \cdot (dp[a]+1) \cdot dp[c] / 2\) соответственно, а если \(a = b = c\), то число вариантов будет равно \(dp[a] \cdot (dp[a]+1) \cdot (dp[a]+2) / 6\).
В зависимости от сложности реализации (за \(\mathcal{O}(n^4)\) или за \(\mathcal{O}(n^3)\)) решение получает \(16\) или \(23\) балла.
Ниже представлен пример решения за \(\mathcal{O}(n^4)\) на языке Python 3.
n = int(input())
dp = [1,1,1]
for i in range(3,n+1):
dp.append(0)
for a in range(0,i):
for b in range(a,i):
for c in range(b,i):
if a+b+c == i-1:
if a < b < c: dp[i] += dp[a] * dp[b] * dp[c]
elif a == b == c: dp[i] += dp[a] * (dp[a]+1) * (dp[a]+2) // 6
elif a == b: dp[i] += dp[a] * (dp[a]+1) * dp[c] // 2
elif b == c: dp[i] += dp[a] * dp[b] * (dp[b]+1) // 2
print( dp[n] % (10**9+7) )Ниже представлен пример решения за \(\mathcal{O}(n^3)\) на языке Python 3.
n = int(input())
dp = [1,1,1]
for i in range(3,n+1):
dp.append(0)
for a in range(0,i):
for b in range(a,i):
c = i-a-b-1
if c >= b:
if a < b < c: dp[i] += dp[a] * dp[b] * dp[c]
elif a == b == c: dp[i] += dp[a] * (dp[a]+1) * (dp[a]+2) // 6
elif a == b: dp[i] += dp[a] * (dp[a]+1) * dp[c] // 2
elif b == c: dp[i] += dp[a] * dp[b] * (dp[b]+1) // 2
print( dp[n] % (10**9+7) )Для решения задачи на полный балл на языке C++ без использования длинной арифметики нужно уметь находить обратные числа по простому модулю для чисел \(2\) и \(6\). К счастью, при \(p = 10^9+7\) число \(p+1 = 10^9+8\) делится и на \(2\), и на \(6\). Поэтому \[\dfrac{1}{2} \equiv \dfrac{10^9+7+1}{2} \equiv 500000004 \pmod{10^9+7},\] \[\dfrac{1}{6} \equiv \dfrac{10^9+7+1}{6} \equiv 166666668 \pmod{10^9+7}.\]
Ниже представлен пример решения на языке C++.
#include <iostream>
using namespace std;
#define LL long long
LL MOD = 1'000'000'007;
LL inv2 = (MOD+1)/2, inv6 = (MOD+1)/6;
LL dp[1000];
void F( LL & res, LL a, LL b, LL c, LL d )
{
LL tmp = (((a * b) % MOD *c) % MOD * d) % MOD;
res = (res + tmp) % MOD;
}
int main()
{
int n;
cin >> n;
dp[0] = dp[1] = dp[2] = 1;
for (int i=3; i<=n; i++)
for (int a=0; a<n; a++)
for (int b=a; b<n; b++)
{
int c = i-a-b-1;
if (c >= b)
{
if (a==b && b==c) F(dp[i], dp[a], dp[a]+1, dp[a]+2, inv6);
else if (a==b) F(dp[i], dp[a], dp[a]+1, dp[c], inv2);
else if (b==c) F(dp[i], dp[a], dp[b], dp[b]+1, inv2);
else F(dp[i], dp[a], dp[b], dp[c], 1);
}
}
cout << dp[n] << "\n";
return 0;
}Программа проверяется на \(23\) скрытых тестах. Прохождение каждого теста оценивается в \(1\) балл. Примеры из условия задачи оцениваются в \(0\) баллов.
В первых \(5\) тестах ограничение \(1 \leqslant n \leqslant 7\).
В следующих \(11\) тестах ограничение \(8 \leqslant n \leqslant 45\). Примечание: при \(n \leqslant 45\) количество изомеров не превышает \(10^{18}\). Можно использовать этот факт при написании решения на языке C++ (однако выводить в ответ все равно нужно остаток от деления на \(10^9+7\)).
В последних \(7\) тестах ограничение \(46 \leqslant n \leqslant 500\).
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 256 Мбайт.
При помощи различного порядка наложения горизонтальных и вертикальных нитей можно менять такие свойства ткани, как, например, плотность, мягкость, фактуру, даже используя один и тот же материал для нитей.
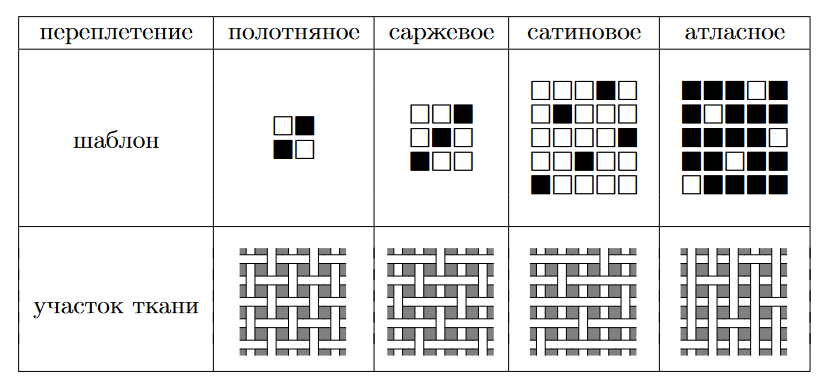
Порядок переплетения задается в виде шаблона размера \(n \times n\), каждый элемент которого указывает, какая из нитей в соответствующем пересечении идет поверх другой — горизонтальная или вертикальная. После этого шаблон копируется на все полотно ткани. На рис. 1.3 приведены примеры самых распространенных шаблонов переплетения.
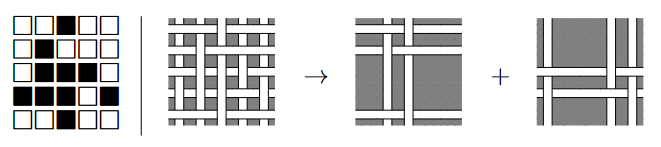
Ученые-ткачи из Берляндского Текстильного Института разрабатывают новые типы тканей. Они собираются сгенерировать несколько случайных шаблонов переплетения нитей, а затем проанализировать свойства получившейся ткани при помощи машинного обучения. Однако не любой шаблон будет задавать корректное переплетение. Например, для следующего шаблона получается ткань, которая распадается на независимые слои, рис. 1.4.
Ткань расслаивается тогда и только тогда, когда можно разделить нити на две непустые группы \(A\) и \(B\) так, что любая нить из \(A\) идет поверх любой нити из \(B\), если они пересекаются. Будем называть шаблон корректным, если в итоге расслоения ткани не происходит. Иначе, если ткань расслаивается, шаблон считается некорректным.
Анализ шаблонов занимает много времени. Чтобы ускорить исследования, ученые хотят отсеять те шаблоны, которые являются некорректными. Напишите программу, которая по заданному шаблону переплетения определяет, корректный он или нет.
Формат входных данных
В первой строке дано целое число \(n\) — размер шаблона, \(1 \leqslant n \leqslant 450\).
В следующих \(n\) строках дано по \(n\) символов в каждой — описание шаблона. Каждый символ — либо «|», либо «-». Если \(j\)-й символ \(i\)-й строки равен «|», то \(j\)-я вертикальная нить идет поверх \(i\)-й горизонтальной. Иначе, если \(j\)-й символ \(i\)-й строки равен «-», то \(i\)-я горизонтальная нить идет поверх \(j\)-й вертикальной.
Формат выходных данных
Выведите YES, если шаблон корректный, или NO, если шаблон некорректный.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
2 -| |- |
YES |
2 |
5 ---|- -|--- ----| --|-- |---- |
YES |
3 |
5 --|-- -|--- -|||- |||-| --|-- |
NO |
Решение на 8 баллов «в лоб» подразумевает перебор всех разделений нитей на две группы \(A\) и \(B\) с последующей проверкой: расслаивается ткань или нет.
Ниже представлен пример такого решения за \(\mathcal{O}(2^{2n}n^2)\) на языке Python 3.
n = int(input())
A = [input() for _ in range(n)]
B = [[0] * (2*n) for _ in range(2*n)]
for i in range(n):
for j in range(n):
if A[i][j]=='-': B[i][n+j] = 1
else: B[n+j][i] = 1
ans = True
for mask in range(1,2**(2*n)-1):
flag = True
for i in range(2*n):
for j in range(2*n):
if ((mask>>i)&1)==1 and ((mask>>j)&1)==0:
if B[j][i]:
flag = False
if flag: ans = False
if ans: print( "YES" )
else: print( "NO" )Решение следующих двух подгрупп тестов предполагает переформулировать задачу в терминах графов. Пусть в графе на \(2n\) вершин каждая вершина соответствует какой-то нити. Проведем ориентированное ребро из вершины \(u\) в вершину \(v\) для всех таких \(u\) и \(v\), что нить, соответствующая \(u\), накрывает нить, соответствующую \(v\). В решении выше уже строится подобный граф в виде матрицы смежности B.
Разбиение нитей на группы \(A\) и \(B\) из условия задачи — это такое разбиение множества вершин на два множества \(A\) и \(B\), что ребра графа могут вести только из \(A\) в \(B\), но не из \(B\) в \(A\). Тогда если разбиение на \(A\) и \(B\) существует, то в графе есть такая вершина \(v\) (любая из \(B\)), что из данной вершины достижимы не все вершины графа (например, вершины множества \(A\), так как все ребра ведут из нее).
Решение на 16 баллов за \(\mathcal{O}(n^3)\) предполагает, что перебираются все вершины из графе в качестве потенциальной вершины \(v\) и запускается из нее поиск в глубину (или поиск в ширину). Если хотя бы из одной вершины графа достижимы не все остальные — ответ NO, иначе — ответ YES.
Ниже представлен пример такого решения на языке Python 3.
n = int(input())
A = [input() for _ in range(n)]
B = [[0] * (2*n) for _ in range(2*n)]
for i in range(n):
for j in range(n):
if A[i][j]=='-': B[i][n+j] = 1
else: B[n+j][i] = 1
def dfs( v, F ):
F[v] = 1
for u in range(2*n):
if B[v][u] and not F[u]:
dfs( u, F )
for i in range(2*n):
F = [0] * (2*n)
dfs( i, F )
if sum(F)!=2*n:
print("NO")
exit(0)
print("YES")Решение на полный балл выглядит следующим образом. Предположим, что разделение вершин на множества \(A\) и \(B\) существует (которые заранее неизвестны). Возьмем произвольную вершину \(v\). Если она попала в множество \(B\), то тогда из нее достижимы не все вершины графа. Если она попала в \(A\), то тогда не все вершины достижимы в графе, который получен из изначального разворотом всех ребер в обратную сторону. В качестве \(A\) или \(B\) в соответствующих случаях можно взять все те вершины, до которых удалось добраться из \(v\), все остальные вершины отнести в другое множество. Таким образом, если разделения на \(A\) и \(B\) нет, то в обоих случаях из \(v\) можно добраться до всех вершин графа.
Таким образом, для решения задачи достаточно запустить по одному поиску в глубину (или в ширину) из одной произвольной вершины графа в изначальном графе и в «развернутом» графе.
Ниже представлен пример такого решения за \(\mathcal{O}(n^2)\) на языке Python 3.
n = int(input())
A = [input() for _ in range(n)]
B = [[0] * (2*n) for _ in range(2*n)]
for i in range(n):
for j in range(n):
if A[i][j]=='-': B[i][n+j] = 1
else: B[n+j][i] = 1
def dfs( v, F ):
F[v] = 1
for u in range(2*n):
if B[v][u] and not F[u]:
dfs( u, F )
F1 = [0] * (2*n)
dfs( 0, F1 )
for i in range(2*n):
for j in range(i+1,2*n):
B[i][j],B[j][i] = B[j][i],B[i][j]
F2 = [0] * (2*n)
dfs( 0, F2 )
if sum(F1)==2*n and sum(F2)==2*n: print("YES")
else: print("NO")Программа проверяется на трех группах скрытых тестов. Прохождение каждой группы оценивается в 8 баллов. Группа считается пройденной, если пройдены все тесты в данной группе. Примеры из условия задачи не входят в группы и оцениваются в 0 баллов.
В первой группе ограничение \(n \leqslant 7\).
Во второй группе ограничение \(n \leqslant 100\).
В третьей группе полные ограничения \(n \leqslant 450\).
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 3 с.
Ограничение по памяти: 256 Мбайт.
Для нужд военных требуется разработать новый материал для снарядов. Снаряд должен иметь фиксированный объем 1 дм\(^3\), чтобы им можно было стрелять из стандартных орудий. Для обеспечения бронебойных свойств снаряд должен быть достаточно тяжелым, а также дешев в производстве.
Имеется \(n\) видов металлов. \(i\)-й из них имеет массу \(m_i\) на 1 дм\(^3\) объема, а 1 дм\(^3\) \(i\)-го вида металла имеет стоимость \(c_i\).
Предлагается сделать снаряд из сплава данных металлов. А именно, каждый \(i\)-й металл берется в объеме \(v_i\) дм\(^3\) (при этом считаем, что \(0 \leqslant v_i \leqslant 1\) для каждого \(i\), а сумма всех \(v_i\) равна \(1\)). Тогда масса снаряда будет равна \(m = v_1m_1 + v_2m_2 \cdots + v_nm_n\) при суммарной стоимости сырья \(c = v_1c_1 + v_2c_2 + \cdots + v_nc_n\).
У военных есть информация о \(q\) видах брони противника. \(j\)-й вид брони можно пробить, только если масса снаряда будет не меньше \(x_j\).
Определите для каждого вида брони минимальную стоимость сырья, из которого можно произвести \(1\) снаряд с массой не меньше необходимой.
Формат входных данных
В первой строке дано одно целое число \(n\), \(1 \leqslant n \leqslant 10^5\).
Во второй строке даны \(n\) целых чисел, разделенные пробелом — массы \(1\) дм\(^3\) каждого из металлов. \(i\)-е из этих чисел равно \(m_i\). \(1 \leqslant m_i \leqslant 10^9\), \(1 \leqslant i \leqslant n\).
В третьей строке даны \(n\) целых чисел, разделенные пробелом — стоимости \(1\) дм\(^3\) каждого из металлов. \(i\)-е из этих чисел равно \(c_i\). \(1 \leqslant c_i \leqslant 10^9\), \(1 \leqslant i \leqslant n\).
В четвертой строке дано одно целое число \(q\), \(1 \leqslant q \leqslant 10^5\).
В пятой строке даны \(q\) целых чисел, разделенных пробелом — информация о видах брони. \(j\)-е из этих чисел равно \(x_j\), \(1 \leqslant x_j \leqslant 10^9\), \(1 \leqslant j \leqslant q\).
Формат выходных данных
Выведите \(q\) вещественных чисел по одному в строке. \(j\)-е из этих чисел должно быть равно минимальной стоимости сырья для производства 1 снаряда, который пробивает \(j\)-й вид брони. Если для какого-либо вида брони произвести снаряд нужной массы из имеющихся металлов невозможно — выводите \(-1\).
Ответ будет засчитан, если будет отличаться от ответа жюри не более, чем на \(10^{-6}\) по абсолютному или по относительному значению.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 3 5 8 5 2 3 3 4 6 9 |
2 2.3333333333333335 -1 |
Примечания
Для первого вида брони выгодно делать снаряды полностью из металла 2. Для второго вида брони следует делать снаряды из сплава металлов 2 и 3, сплавленных в пропорции \(2 : 1\). Для третьего вида брони снаряд необходимой массы произвести невозможно.
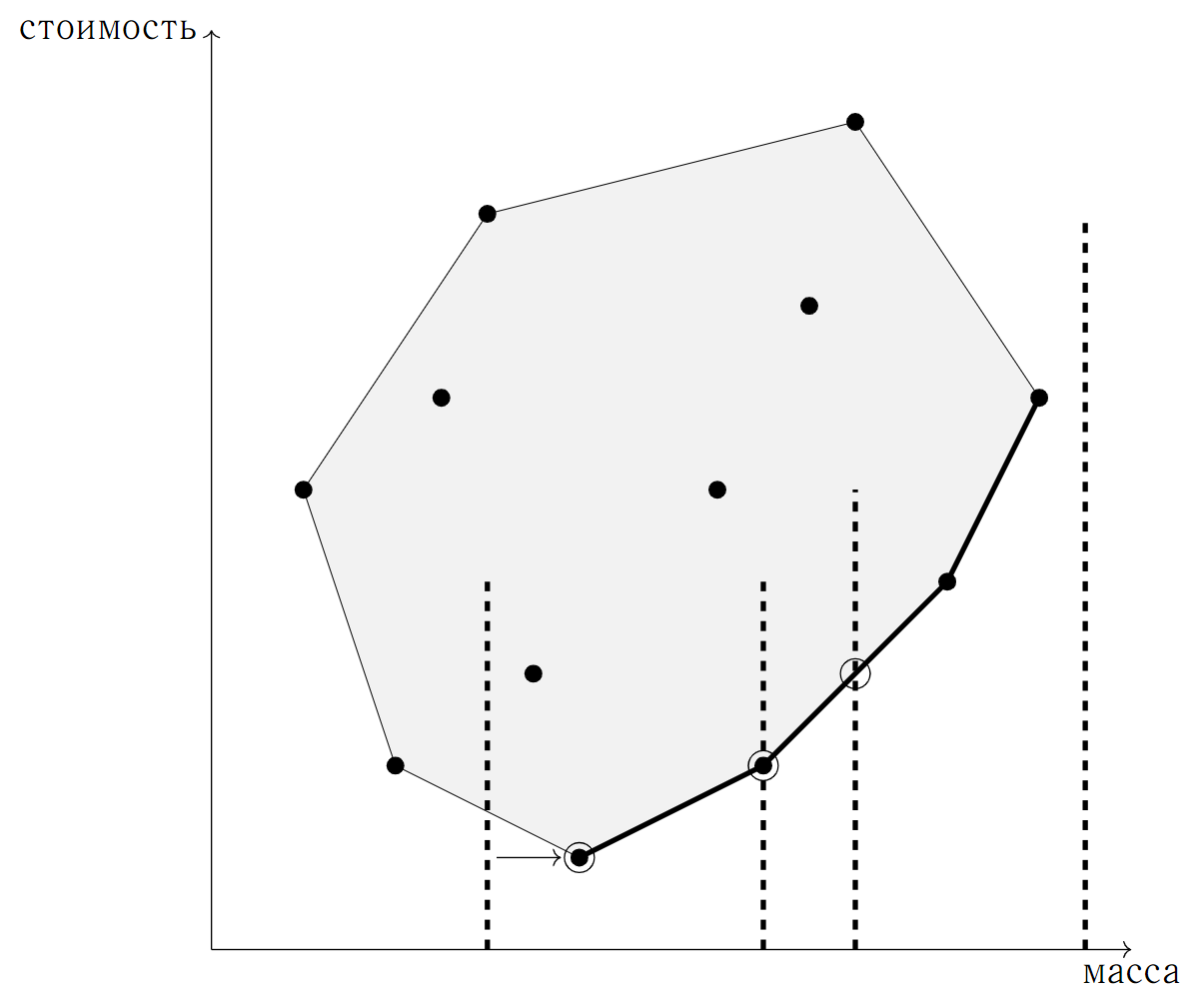
Каждый металл можно изобразить в виде точки на плоскости с координатами \((m_i, c_i)\). Тогда всевозможные сплавы, которые можно получить, соответствуют точкам внутри или на границе выпуклой оболочки, построенной на данном множестве точек.
Каждый запрос представляет собой вертикальную линию, и ответом на данный запрос будет высота самой нижней точки, принадлежащая многоугольнику, которая находится на данной линии или правее. На рис. 1.5 показаны ответы для каждого запроса пустыми кружочками, ответ на самый правый запрос — (\(-1\)).
Из данной интерпретации задачи понятно, что ответ всегда будет находиться на границе многоугольника, а точнее — на той линии, что выделена на рисунке жирным. Из этого, в частности, следует, что в любом оптимальном сплаве нужно использовать не более двух металлов.
Для решения задачи на 9 баллов достаточно перебрать все точки по одной (для сплавов из одного металла), а также для каждой пары точек найти пересечение вертикальной прямой и отрезка, соединяющего данные точки. В итоге получается решение за \(\mathcal{O}(qn^2)\).
Ниже представлен пример такого решения на языке Python 3.
n = int(input())
mass = list(map(int, input().split()))
cost = list(map(int, input().split()))
_ = int(input())
queries = list(map(int, input().split()))
for q in queries:
best_cost = 10**10
for i in range(n):
if mass[i] >= q:
best_cost = min( best_cost, cost[i] )
for i in range(n):
for j in range(n):
if mass[i] < q < mass[j]:
c = cost[i] + (cost[j]-cost[i]) * (q-mass[i]) / (mass[j]-mass[i])
best_cost = min( best_cost, c )
if best_cost == 10**10: best_cost = -1
print( best_cost )Для решения задачи на 18 баллов нужно найти все точки на «жирной» линии следующим образом. Сначала находим самую нижнюю точку (если таких несколько — берем самую правую). Назовем ее текущей. После этого перебираем все точки правее текущей и находим ту, для которой отрезок, соединяющий ее и текущую, имеет наименьший угол наклона. Это дает первый сегмент «жирной» ломаной. Теперь выбранную точку назначаем текущей и повторяем процесс, пока для текущей точки справа больше не будет точек. В полученной ломаной будет \(\mathcal{O}(n)\) точек, на запросы отвечаем проходом по всем отрезкам данной ломаной за \(\mathcal{O}(n)\). В итоге получаем решение за \(\mathcal{O}(n^2+qn)\).
Ниже представлен пример такого решения на языке Python 3.
from fractions import Fraction
n = int(input())
mass = list(map(int, input().split()))
cost = list(map(int, input().split()))
points = list(zip( mass, cost ))
chain = []
cur = points[0]
for p in points:
if p[1]<cur[1] or (p[1]==cur[1] and p[0]>cur[0]):
cur = p
chain.append(cur)
def a(o,x):
return Fraction(x[1]-o[1],x[0]-o[0])
while True:
nxt = 0
for p in points:
if p[0]>cur[0]:
if nxt==0 or a(cur,p) < a(cur,nxt):
nxt = p
if nxt==0: break
cur = nxt
chain.append( cur )
_ = int(input())
queries = list(map(int, input().split()))
for q in queries:
best_cost = 10**10
for p in chain:
if p[0]>=q:
best_cost = min( best_cost, p[1] )
for i in range(len(chain)-1):
p1,p2 = chain[i],chain[i+1]
if p1[0] < q < p2[0]:
c = p1[1] + a(p1,p2) * (q-p1[0])
best_cost = min( best_cost, c )
if best_cost == 10**10: best_cost = -1
print( float(best_cost) )На самом деле предложенное решение работает чуть быстрее — за \(\mathcal{O}(nh+qh)\), где \(h \leqslant n\) — количество точек на «жирной» ломаной, поэтому набирает чуть больше 18 баллов.
Для решения на полный балл предлагает использовать алгоритм Грэхема для построения выпуклой оболочки, а на запросы затем отвечать при помощи двоичного поиска. В итоге получается решение со сложностью \(\mathcal{O}((n+q)\log n)\).
Ниже представлен пример такого решения на языке Python 3.
import sys
input = sys.stdin.readline
from fractions import Fraction
n = int(input())
mass = list(map(int, input().split()))
cost = list(map(int, input().split()))
points = list(zip( mass, cost ))
def a(o,x):
return Fraction(x[1]-o[1],x[0]-o[0])
pivot = points[0]
for p in points:
if p[1]<pivot[1] or (p[1]==pivot[1] and p[0]>pivot[0]):
pivot = p
points = list( filter( lambda x: x[0]>pivot[0], points ) )
points.sort( key = lambda x: a(pivot, x) )
chain = [pivot]
if len(points)>0:
chain.append( points[0] )
for p in points[1:]:
if p[0] <= chain[-1][0]:
continue
while a(chain[-2],chain[-1]) > a(chain[-1],p):
chain.pop()
chain.append( p )
_ = int(input())
queries = list(map(int, input().split()))
for q in queries:
best_cost = -1
if q <= chain[0][0]:
best_cost = chain[0][1]
elif q <= chain[-1][0]:
L, R = 0, len(chain)-1
while L+1 < R:
S = (L+R) // 2
if chain[S][0]<q: L = S
else: R = S
p1,p2 = chain[L],chain[R]
best_cost = float( p1[1] + a(p1,p2) * (q-p1[0]) )
print( best_cost )Программа проверяется на 27 скрытых тестах. Прохождение каждого теста оценивается в 1 балл. Пример из условия задачи оценивается в 0 баллов.
Первые 9 тестов имеют ограничения \(n \leqslant 100\) и \(q \leqslant 100\).
Следующие 9 тестов имеют ограничения \(n \leqslant 10^3\) и \(q \leqslant 10^3\).
Последние 9 тестов имеют полные ограничения — \(n \leqslant 10^5\) и \(q \leqslant 10^5\).