Предметный тур. Физика. 3 этап
Грузовой дрон представляет собой небольшой летающий беспилотник, несущий груз также небольших геометрических размеров, прикрепленный к нему снизу на легком нерастяжимом тросе длиной \(l = 6\textrm{\,м}\). Беспилотник движется по прямолинейному горизонтальному участку своего маршрута поступательно с постоянной скоростью. В некоторый момент ему поступает сигнал от пункта управления, и беспилотник практически мгновенно снижает свою скорость в \(n = 2\) раза, сохраняя ее направление, в результате чего закрепленный на конце троса груз, качнувшись на тросе подобно маятнику, поднимается на максимальную высоту \(h = l/4\) от своего прежнего равновесного положения. Определите начальную скорость беспилотника. Ускорение свободного падения \(g = 9{,}8\textrm{\,м/с}^2\). Влиянием сопротивления воздуха пренебречь.
Без учета влияния воздуха на груз, подвешенный на тросе, действуют только две силы: тяжести и натяжения троса. Пока беспилотник движется по прямой с постоянной скоростью \(v\), так же движется и груз, значит, его ускорение оказывается равно нулю, а трос натянут вертикально, чтобы скомпенсировать действие силы тяжести.
После резкого замедления груза задачу удобнее решать в системе отсчета, связанной с беспилотником. Начальная скорость груза в этой системе равна \(v_0 = v(1-1/n)\), а начальную высоту удобно считать нулевой. Поскольку за исключением однократного быстрого изменения скорости эта система инерциальна, а сопротивление воздуха мало, движение груза после замедления подчиняется закону сохранения механической энергии: \[\frac{mv_0^2}{2} + 0 = 0 + mgh \Rightarrow v_0 = \sqrt{2gh}.\] Чтобы получить ответ на вопрос задачи, эту скорость остается разделить на \((1-1/n)\): \[v = \frac{v_0}{1-1/n} = \frac{n}{n-1}\sqrt{2gh} = \frac{n}{n-1}\sqrt{\frac{gl}{2}} \approx 10{,}8 \textrm{\,м/с}.\]
\[v = \frac{n}{n-1}\sqrt{\frac{gl}{2}} \approx 10{,}8 \textrm{\,м/с}.\]
| Верно записан закон сохранения механической энергии | 5 баллов |
| Возможность применения ЗСМЭ на том интервале времени и в той системе отсчета, в которой он записан, обоснована | 5 баллов |
| Получен правильный ответ | 6 баллов |
| Всего | 16 баллов |
В управляющей цепи дрона используется нелинейный электрический элемент, вольт-амперная характеристика которого изображена на рис. 1.1: при напряжениях \(U\) меньше некоторого значения \(U_0\) ток через этот элемент не протекает вовсе, а при напряжениях \(U > U_0\) сила тока оказывается прямо пропорциональна разности \(U-U_0\). Известно, что при приложении к нему напряжения \(3U_0\) через элемент протекает ток \(I_1 = 4\textrm{\,мА}\), а при приложении очень больших (много больше \(U_0\)) напряжений нелинейный элемент ведет себя как резистор с сопротивлением \(R_1 = 3\textrm{\,кОм}\). Найдите \(U_0\).
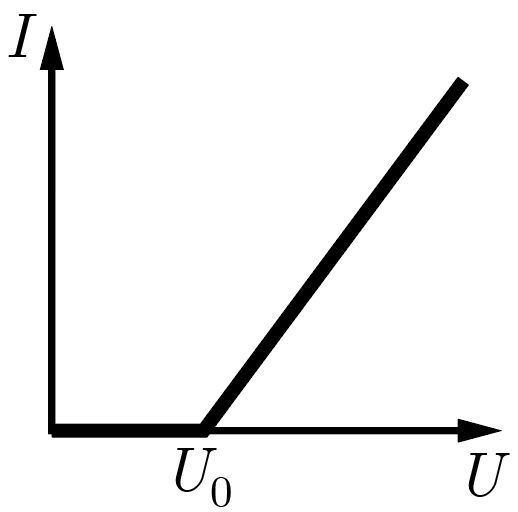
Согласно условиям, при \(U > U_0\) сила тока \(I\) через нелинейный элемент прямо пропорциональна разности \(U-U_0\). Обозначим коэффициент этой пропорциональности \(k\): \[I(U) = k(U-U_0).\] Электрическое сопротивление \(R\) элемента — это отношение напряжения на его концах к силе протекающего через него тока, поэтому зависимость \(R(U)\) принимает вид \[R(U) = \frac{U}{I(U)} = \frac{U}{k(U-U_0)}.\] Легко видеть, что при \(U \gg U_0\) знаменатель этого выражения становится близок к \(U\), а значит, сопротивление нелинейного элемента приближается к величине \(1/k\), следовательно \[k = \frac{1}{R_1}.\] Подставив найденное значение коэффициента в выражение для силы тока при напряжении \(3U_0\), получим: \[I_1 = I(3U_0) = \frac{3U_0-U_0}{R_1} = \frac{2U_0}{R_1} \Rightarrow U_0 = \frac{I_1 R_1}{2} = 6\textrm{\,В}.\]
\[U_0 = \frac{I_1 R_1}{2} = 6\textrm{\,В}.\]
| Верно записан закон Ома для участка цепи | 4 балла |
| Составлено уравнение, отражающее прямую пропорциональность тока разнице \(U-U_0\) | 4 балла |
| Найден коэффициент этой пропорциональности. | 5 баллов |
| Получен правильный ответ | 5 баллов |
| Всего | 18 баллов |
Благодаря уникальному климату и составу далекой планеты, ее атмосфера имеет два слоя с достаточно четкими границами, в пределах каждого из которых ее плотность практически постоянна, и столь же резкую верхнюю границу с пустотой космоса в верхней части второго слоя. При этом нижний слой атмосферы в два раза тоньше ее верхнего слоя. Два абсолютно одинаковых аэростата с жесткими оболочками висят неподвижно в серединах соответствующих слоев. Один из них удерживается в атмосфере без груза, второй — с грузом, масса которого равна массе самого аэростата. При этом барометр первого показывает давление \(p_1 = 12\textrm{\,кПа}\). Какое давление показывает барометр второго?
Очевидным следствием закона Архимеда является то, что слой с меньшей плотностью (обозначим ее \(\rho_1\)) находится выше слоя с большей (обозначим ее \(\rho_2\)).
Для каждого аэростата сила Архимеда \(\rho g V\), где \(\rho\) — плотность атмосферного слоя, в котором он находится, \(g\) — ускорение свободного падения планеты, а \(V\) — объем аэростата, должна в точности компенсировать силу тяжести, действующую на аэростат с грузом. Объем \(V\) не зависит от внешнего давления, поскольку по условиям оболочки аэростатов жесткие. Обозначив массу пустого аэростата \(m\), условия их равновесия запишем в виде \[\left\{\begin{aligned} &\rho_1 g V = m g, \\ &\rho_2 g V = 2 mg. \end{aligned}\right.\] Из этой системы элементарно следует \[\rho_2 = 2\rho_1.\] Обозначив \(h\) толщину верхнего слоя, запишем теперь выражения для давлений, действующих на барометры каждого из аэростатов. На каждый из них давление оказывает половина воздушного слоя, в котором он находится, и вышележащий слой, если такой есть: \[\left\{\begin{aligned} &p_1 = \frac{\rho_1 h}{2} g, \\ &p_2 = \left(\rho_1 h + \frac{\rho_2 2h}{2}\right) g = (\rho_1 + \rho_2)gh. \end{aligned}\right.\] Подставляя в последнее уравнение полученное выражение для \(\rho_2\), приведем его к виду \[p_2 = 3 \rho_1gh = 3p_1 = 36\textrm{\,кПа}.\]
\[p_2 = 3p_1 = 36\textrm{\,кПа}.\]
| Верно записаны условия равновесия аэростатов | по 3 балла за аэростат |
| Верно записаны выражения для гидростатических давлений, действующих на аэростаты | по 3 балла за аэростат |
| Получен правильный ответ | 6 баллов |
| Всего | 18 баллов |
Поисковый дрон снабжен прожектором, состоящим из мощного точечного источника света и плоской линзы с оптической силой \(D = 2\textrm{\,дптр}\), жестко закрепленной так, что когда дрон зависает над зоной спасательной операции, плоскость линзы оказывается параллельна земле. Источник света может перемещаться относительно линзы. В начальный момент источник находился в главном фокусе линзы, в результате чего дрон, висящий на высоте \(H = 15\textrm{\,м}\) над равнинной местностью, создавал на земле круглое световое пятно. Определите, на какое расстояние должен сдвинуться вниз вдоль главной оптической оси линзы источник света, чтобы площадь светового пятна увеличилась в четыре раза.
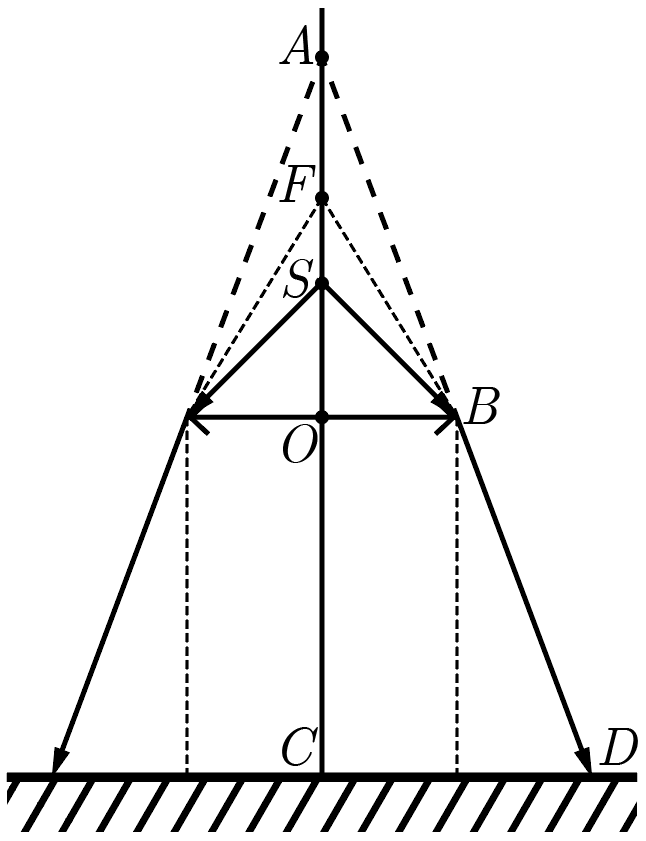
Когда источник света находится строго в фокусе линзы, прожектор создает пучок лучей, параллельных главной оптической оси и перпендикулярных экрану (поверхности Земли), а значит, независимо от высоты дрона, радиус светового пятна равен радиусу линзы. Чтобы увеличить площадь светового пятна в четыре раза, его радиус необходимо увеличить в два раза. Поскольку по условиям источник сдвигается вниз (ближе к линзе), линза сформирует его мнимое изображение. Изобразим ход лучей в этом случае на чертеже (рис. 1.2). На нем \(O\) — оптический центр линзы, \(F\) — ее фокус, \(S\) — источник после смещения, \(A\) — мнимое изображение источника в линзе, \(B\) — край линзы, \(C\) — центр светового пятна, \(D\) — его край. Сплошные стрелки изображают реальный ход световых лучшей, редкий пунктир — их продолжения, частый тонкий пунктир — ход лучей до сдвига источника.
Из чертежа легко видеть, что треугольники \(\triangle ABO\) и \(\triangle ADC\) подобны (по двум углам), а значит, \[\frac{AC}{AO} = \frac{CD}{OB} = 2.\] При этом длина отрезка \(AO\) — есть расстояние \(f\) от мнимого изображения до плоскости линзы, а длина отрезка \(OC\) — высота зависания дрона. С учетом этого перепишем отношение в виде \[\frac{f+H}{f} = 2 \Rightarrow f = H\] и применим данный результат в формуле тонкой линзы: \[D = \frac{1}{d} -\frac{1}{H} \Rightarrow d = \left(D+\frac{1}{H}\right)^{-1} = \frac{H}{DH+1},\] где \(d\) — расстояние от линзы до источника (длина отрезка \(OS\) на рисунке). Чтобы окончательно дать ответ на вопрос задачи, вычтем новое значение \(d\) из прежнего, равного фокусному расстоянию \(1/D\): \[b = \frac{1}{D} - d = \frac{1}{D} - \frac{H}{DH +1} \approx 1{,}6\textrm{\,см}.\]
\[b = \frac{1}{D} - \frac{H}{DH +1} \approx 1{,}6\textrm{\,см}.\]
| Качественно правильно изображен ход лучей | 4 балла |
| Определено, что изначальный радиус светового пятна равен радиусу линзы | 2 балла |
| Определено, что конечный радиус светового пятна в два раза больше начального | 3 балла |
| Верно найдено положение мнимого изображения | 3 балла |
| Верно записана формула тонкой линзы | 4 балла |
| Получен правильный ответ | 4 балла |
| Всего | 20 баллов |
Роботизированный самолет снабжен электродвигателем, контроллер которого поддерживает на нем постоянное напряжение \(U\). Сила сопротивления воздуха, которую приходится преодолевать электродвигателю для горизонтального движения с постоянной скоростью \(v\), прямо пропорциональна квадрату этой скорости, а КПД \(\eta\) двигателя зависит от этой скорости по закону \(\displaystyle \eta(v) = \frac{3v(2v_0-v)}{4v_0^2}\), где \(v_0 = 150\textrm{\,м/с}\). В штатных условиях самолет движется с крейсерской скоростью, при которой КПД его двигателя максимален, а в режиме форсажа — в \(k = 1{,}5\) раз быстрее. Определите, во сколько раз необходимо повысить силу протекающего через двигатель тока, чтобы перейти с крейсерской скорости в этот режим.
Прежде всего проанализируем характер зависимости \(\eta(v)\). Раскрыв скобки, легко видеть, что функция \[\eta(v) = -\frac{3}{4v_0^2}v^2 + \frac{3}{2v_0}v\] квадратичная, причем коэффициент перед ее старшим слагаемым отрицательный. Это значит, что ее график представляет собой параболу ветвями вниз.
Из исходного вида этой функции очень легко видеть, что она имеет два корня: \(\eta(v)\) равна нулю либо когда \(v = 0\), либо когда \(v = 2v_0\), откуда следует, что вершина параболы лежит ровно в середине между этими двумя корнями: в точке \(v = v_0\). Подставив это значение, получим \[\eta_{max} = \eta(v_0) = \frac{3v_0(2v_0-v_0)}{4v_0^2} = \frac{3}{4}.\] Это и есть КПД двигателя на крейсерской скорости \(v_0\). Найдем теперь КПД \(\eta_f\) двигателя в режиме форсажа: \[\eta_f = \eta\left(\frac{3}{2}v_0\right) = \frac{3\frac{3}{2}v_0(2v_0-\frac{3}{2}v_0)}{4v_0^2} = \frac{9}{16}.\]
Полезная мощность \(P\), которую необходимо развивать двигателю для преодоления силы сопротивления \(F\), определяется по формуле \(P = vF\), а потребляемая им мощность \(P_0\) равна, соответственно, \(P_0 = vF/\eta\). В то же время из раздела Электричество известно, что эта последняя равна \(UI\). Тогда сила тока в любом режиме может быть выражена как \[I = \frac{v F}{\eta U}.\]
Чтобы ответить на вопрос задачи, составим пропорцию между силами тока \(I_0\) в крейсерском и \(I_f\) в форсажном режиме: \[\frac{I_f}{I_0} = \frac{v_f F_f}{\eta_f \cancel{U}} \cdot \frac{\eta_{max} \cancel{U}}{v_0 F_0} = \frac{v_f}{v_0} \cdot \frac{F_f}{F_0} \cdot \frac{3}{4}\cdot\frac{16}{9},\] где индексы \(0\) и \(f\) также используются для обозначения величин, относящихся к крейсерскому и форсажному режимам соответственно.
Согласно условиям задачи \(v_f/v_0 = k\), а соответствующее увеличение силы сопротивления воздуха \(F_f/F_0 = (v_f/v_0)^2 = k^2\). Тогда окончательно \[\frac{I_f}{I_0} = k^3\frac{4}{3} = \frac{9}{2}.\]
\[\frac{I_f}{I_0} = \frac{9}{2} = 4{,}5.\]
| Верно записана связь мощности со скоростью и силой сопротивления | 3 балла |
| Верно записана связь мощности с напряжением и силой тока | 3 балла |
| Продемонстрировано понимание того, что зависимость КПД от скорости квадратичная и имеет один максимум | 5 баллов |
| Показано, что крейсерская скорость равна \(v_0\) | 4 балла |
| Верно найден максимальный КПД двигателя | 3 балла |
| Верно найден КПД двигателя при форсаже | 4 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 28 баллов |
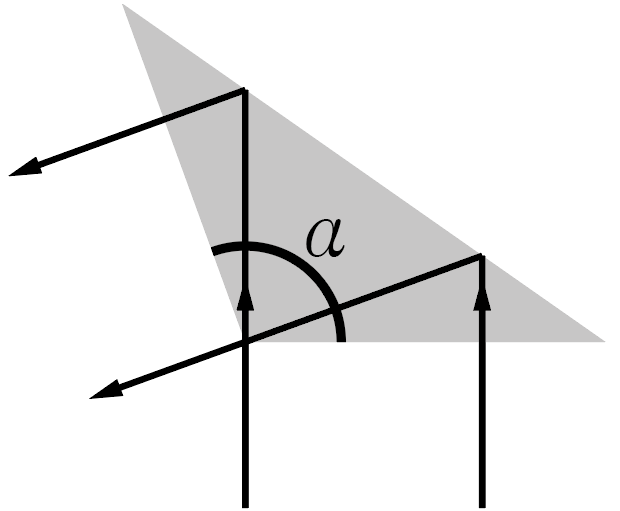
В оптической системе наблюдательного самолета используется поворотная призма с основанием в виде равнобедренного тупоугольного треугольника, тупой угол которого обозначен \(\alpha\). Пучок световых лучей попадает на призму через одну из ее меньших прямоугольных граней, падая на эту грань вдоль ее нормали (см. рис. 2.1).
Из-за требований к обтекаемости прибора угол \(\alpha\) требуется сделать как можно больше. Определите, при каком максимальном значении \(\alpha\) свет испытает полное внутреннее отражение, если оптическое стекло, из которого изготовлена призма, имеет абсолютный показатель преломления \(n = 1{,}7\), а снаружи от нее находится воздух, достаточно разреженный, чтобы считать его показатель преломления единицей.
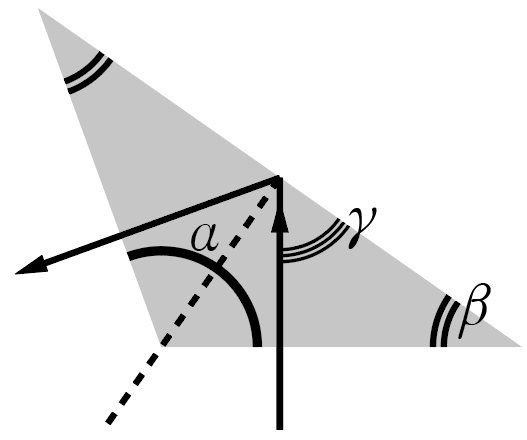
Изобразим ход одного луча в призме (рис. 2.2). В силу симметрии, лучи выходят из призмы по нормали к ее границе раздела, поэтому полное внутреннее отражение возможно только на самой широкой стороне призмы. Найдем угол падения света на эту границу. Угол \(\beta\) при основании призмы легко найти, опираясь на сумму углов треугольника и равенство углов при основании равнобедренного треугольника: \[\alpha + 2\beta = 180° \Rightarrow \beta = 90°-\frac{\alpha}{2}.\] Угол \(\gamma\), который падающий луч составляет с широкой гранью призмы, можно найти, опираясь на сумму углов в треугольнике, образованном этим лучем и двумя гранями призмы. Поскольку первое падение по условиям задачи происходит по нормали (под углом \(90°\) к границе раздела), а угол между гранями равен \(\beta\), справедливо равенство \[\gamma + \beta + 90° = 180° \Rightarrow \gamma = 90° - \beta = \frac{\alpha}{2}.\] Наконец, угол падения луча \(\phi\) по определению является углом между падающим лучом и нормалью к границе раздела; следовательно, он равен \[\phi = 90° - \gamma = 90° - \frac{\alpha}{2}.\] Согласно закону Снеллиуса, критический угол \(\phi_\textrm{кр}\) полного внутреннего отражения достигается тогда, когда синус угла падения оказывается равен относительному показателю преломления сред: \[\frac{1}{n} = \sin \phi_\textrm{кр} = \cos \frac{\alpha_\textrm{кр}}{2}.\] При меньших углах падения (и, следовательно, больших углах \(\alpha\)) явление полного внутреннего отражения наблюдаться не будет. Отсюда \[\alpha_\textrm{кр} = 2\arccos\left(\frac{1}{n}\right) \approx 108°.\]
\[\alpha_\textrm{кр} = 2\arccos\left(\frac{1}{n}\right) \approx 108°.\]
| Верно записан закон Снеллиуса или условие ПВО | 4 балла |
| Верно записана связь между углом \(\alpha\) и углом падения луча на широкую границу раздела | 3 балла |
| Указанная взаимосвязь геометрически обоснована | 3 балла |
| Получен правильный ответ | 5 баллов |
| Всего | 15 баллов |
В сравнительных испытаниях принимают участие два дрона. К характеристикам дрона — рабочей массе и запасу хода — предъявляются суровые требования, поэтому каждый из них способен развивать свое максимальное ускорение \(a\) (одинаковое для обоих дронов) довольно недолго. В ходе испытаний дронам предстоит преодолеть по прямой одинаковое расстояние \(S\) в спокойном воздухе. Первый дрон двигался с ускорением \(a\) на протяжении некоторого времени \(t_1\) а затем, из-за разрядки аккумуляторов, был вынужден снизить ускорение до \(a/2\) и, двигаясь с ним на протяжении такого же времени, достиг финиша. Второй дрон, напротив, взял запас и на протяжении некоторого времени \(t_2\) двигался с ускорением \(a/2\), а уже по прошествии этого времени, обнаружив, что запас хода достаточен, поднял ускорение до \(a\) и, двигаясь на протяжении такого же времени с ним, дошел до конца маршрута. Какой дрон пришел к финишу первым? Во сколько раз меньшее время занял у него маршрут? Начальные скорости обоих дронов равнялись нулю.
Рассмотрим движение первого дрона. На первом участке пути \(S_1\) он движется без начальной скорости с постоянным ускорением \(a\), поэтому для этой половины закон движения имеет вид \[S_1 = \frac{a t_1^2}{2}.\] На втором участке пути \(S_1^\prime\) дрон движется с меньшим ускорением, но обладает начальной скоростью \(v_1 = a t_1\), поэтому его закон движения принимает вид \[S_1^\prime = v_1 t_1 + \frac{a t_1^2}{4} = \frac{5}{4}at_1^2.\] Таким образом, общий путь \(S_1\) дрона связан с его временем в движении выражением \[S = S_1 + S_1^\prime = \frac{7}{4}at_1^2.\] Аналогичные рассуждения для второго дрона (все величины с индексом \(2\) вместо \(1\)) имеют вид \[S_2 = \frac{a t_2^2}{4}; \qquad v_2 = \frac{at_2}{2},\] \[S_2^\prime = v_2 t_2 + \frac{a t_2^2}{2} = at_2^2,\] \[S = S_2 + S_2^\prime = \frac{5}{4}at_2^2.\] Приравнивая эти совокупные пути, получим \[\frac{7\cancel{a} t_1^2}{\cancel{4}} = \frac{5\cancel{a} t_2^2}{\cancel{4}} \Rightarrow \frac{t_2}{t_1} = \sqrt{\frac{5}{7}} \approx 1{,}18.\]
Первый дрон прибудет к финишу быстрее в \(\displaystyle \sqrt{\frac{7}{5}} \approx 1{,}18\) раза.
| Верно записан хотя бы один закон равноускоренного движения без начальной скорости | 3 балла |
| Верно записан хотя бы один закон равноускоренного движения с учетом правильной начальной скорости на втором участке | 5 баллов |
| Верно выражены пути обоих дронов через \(a\) и \(t_{1{,}2}\) | 3 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 17 баллов |
Спускаемый аппарат разрабатывается для работы в условиях атмосферы неизведанной планеты, состоящей из сложной смеси одноатомных, двухатомных и многоатомных газов, которая, однако, ведет себя как достаточно близкий к идеальному газ. Аппарат будет приводиться в движение тепловым двигателем, рабочий цикл которого состоит из двух изохор и двух изобар. При этом максимальное давление газа в цикле в \(m = 2\) раза выше минимального, а максимальный объем — в \(n = 3\) раз выше минимального. В качестве рабочего тела в двигателе выступает забортная атмосфера. Измерения показали, что работающий так двигатель обладает коэффициентом полезного действия \(\eta = 1/8\). Найдите молярную теплоемкость атмосферы неизведанной планеты в изохорном процессе. Универсальная газовая постоянная \(R = 8{,}31\) Дж/моль\(\cdot\)К.
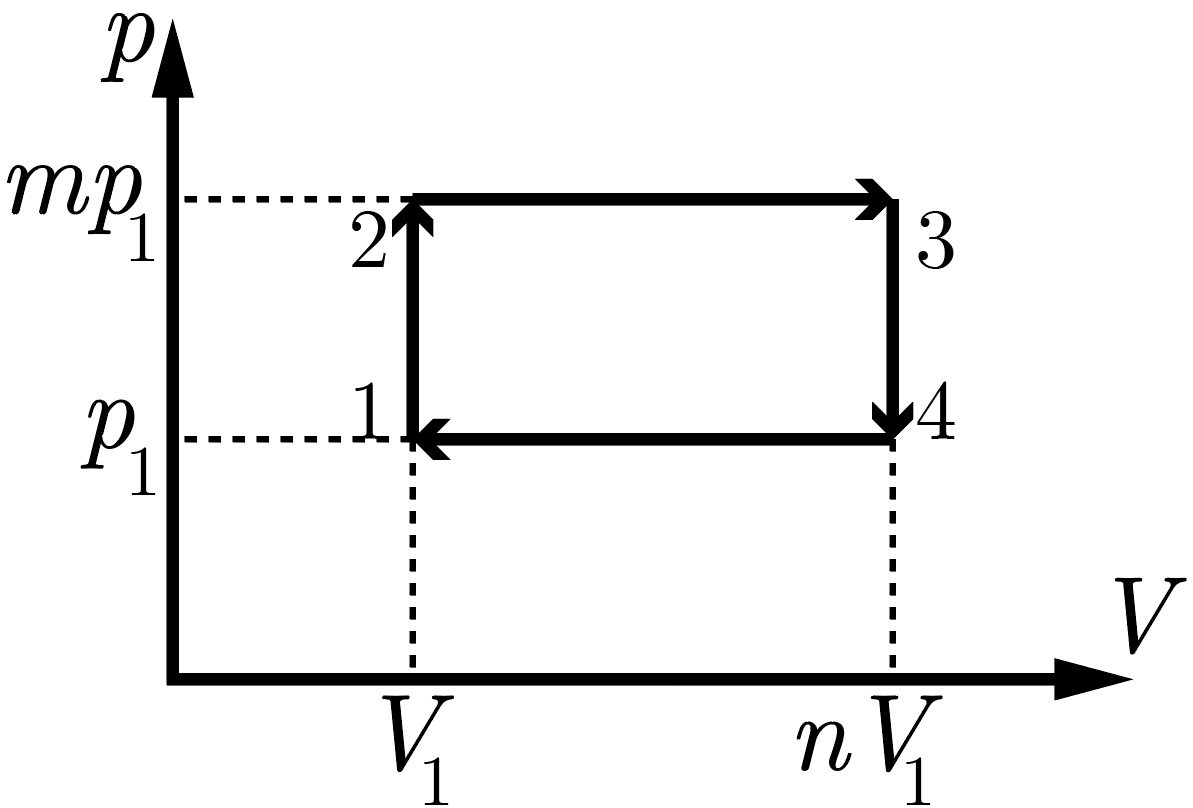
Изобразим цикл на \(pV\)-координатах: он имеет вид прямоугольника (рис. 2.3). Легко заметить, что площадь внутри этого прямоугольника (работа за цикл) \[A = (m-1)(n-1)p_1V_1.\]
Обозначим искомую молярную теплоемкость \(C_V\). Процесс 1–2 изохорный, поэтому газ получает на нем теплоту в количестве, полностью определяемом этой величиной: \[Q_{12} = C_V \nu (T_2 - T_1),\]
где \(\nu\) — количество вещества рабочего газа, а \(T_{1{,}2}\) — абсолютные температуры газа в точках \(1\) и \(2\) соответственно. Газ также получает теплоту на изобарном процессе 2–3, где количество этой теплоты можно выразить при помощи первого начала термодинамики: \[Q_{23} = C_V \nu (T_3 - T_2) + mp_1 (n-1)V_1,\] где \(T_3\) — абсолютная температура газа в точке \(T_3\).
Таким образом, КПД цикла определяется соотношением \[\eta = \frac{A}{Q_{12} + Q_{23}} = \frac{(m -1)(n -1)p_1V_1}{C_V\nu (T_3-T_1) + m(n-1)p_1V_1}.\] Поскольку рабочее тело ведет себя как идеальный газ, к нему применимо уравнение Менделеева – Клапейрона, из которого следует \[\nu T_1 = \frac{p_1 V_1}{R}; \qquad \nu T_3 = \frac{mnp_1 V_1}{R}.\] С учетом этих соотношений выражение для КПД принимает вид \[\eta = \frac{(m -1)(n -1)\cancel{p_1V_1}}{C_V/R(mn-1)\cancel{p_1V_1} + m(n-1)\cancel{p_1V_1}},\] откуда окончательно выразим \(C_V\): \[\begin{aligned} C_V = \frac{(m-1)(n-1)}{\eta (mn-1)}R - \frac{m(n-1)}{mn-1}R = \frac{(n-1)(m-m\eta-1)}{\eta (mn-1)}R=\\ =\frac{12}{5} R \approx 20\textrm{\,Дж/(моль$\cdot$К)}. \end{aligned}\]
\[C_V = \frac{(n-1)(m-m\eta-1)}{\eta (mn-1)} =\frac{12}{5} R \approx 20\textrm{\,Дж/(моль $\cdot$ К)}.\]
Примечание: хотя полное решение было представлено в общем виде, оно будет значительно короче, если переменные \(m\) и \(n\) сразу заменить их численными значениями. Снижать оценку за подобную подстановку не следует.
| Верно записано уравнение Менделеева – Клапейрона | 3 балла |
| Верно указано, на каких участках цикла газ получает и теряет тепло | 3 балла |
| Верно найдена работа газа за цикл | 3 балла |
| Верно записано первое начало термодинамики | 3 балла |
| Продемонстрировано понимание термина «молярная теплоемкость в изохорном процессе» | 3 балла |
| Получен правильный ответ | 5 баллов |
| Всего | 20 баллов |
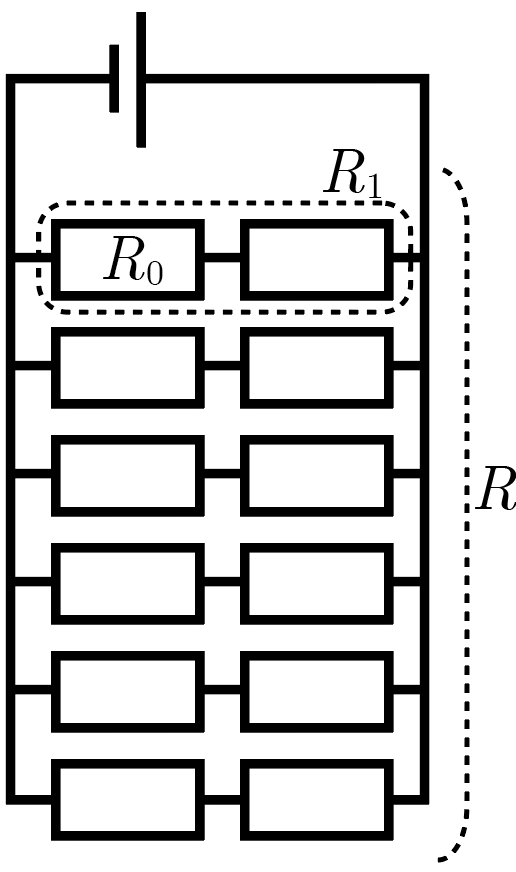
Двенадцать двигателей дрона должны были питаться от единого источника с пренебрежимо малым внутренним сопротивлением и ЭДС \(\mathcal{E}_0 = 240\textrm{\,В}\). Но очутившись с презентацией на технической выставке, команда разработчиков обнаружила, что вместо заявленного, организаторы предоставили им источник тока с ЭДС \(\mathcal{E} = 600\textrm{\,В}\), а вдобавок — имеющий не столь малое внутреннее сопротивление \(r = 2\textrm{\,Ом}\). Команда разработчиков ненадолго пришла в замешательство: прежняя схема подключения вывела бы двигатели из строя; но вскоре один из инженеров обнаружил, что, разбив двигатели на несколько одинаковых групп, внутри каждой из которых они будут соединены последовательно, а затем уже эти группы параллельно друг другу соединив с источником, можно добиться того, что через каждый двигатель будет протекать строго номинальная сила тока \(I_0\). Найдите \(I_0\).
Напряжение на двигателях, подключенных параллельно к идеальному источнику, будет равно ЭДС \(\mathcal{E}_0\) этого источника. Напряжение на любой группе двигателей, подключенных к неидеальному источнику, не может превышать ЭДС источника, а значит, на каждом из двигателей оно не будет превышать \(\mathcal{E}/n\), где \(n\) — число двигателей в группе. Для протекания через отдельный двигатель номинальной силы тока напряжение на двигателе также должно быть номинальным. Но учитывая известные значения \(\mathcal{E}\) и \(\mathcal{E}_0\), легко видеть, что \(\mathcal{E}_0 < \mathcal{E}/n\) только при \(n = 1\) и \(n = 2\). Первый вариант невозможен, поскольку в этом случае двигатели остаются фактически подключены по прежней схеме, а по условиям такое подключение выведет их из строя. Значит, в каждой группе последовательно соединенных элементов по два двигателя.
Обозначим сопротивление одного двигателя \(R_0\). Тогда эквивалентное сопротивление одной группы двигателей \(R_1 = 2R_0\), а шести таких групп, соединенных параллельно: \[R = \frac{R_1}{6} = \frac{R_0}{3}.\] По закону Ома для полной цепи через эту батарею будет протекать ток \[I = \frac{\mathcal{E}}{R + r} = \frac{\mathcal{E}}{R_0/3 + r},\] а значит, через каждый двигатель будет протекать ток, равный \[I_0 = \frac{I}{6} = \frac{\mathcal{E}}{2R_0 + 6r}.\] В то же время, при подключении двигателей по изначальному плану, эта сила тока составила бы \[I_0 = \frac{\mathcal{E}_0}{R_0}.\] Приравнивая эти два выражения, получим \[\frac{\mathcal{E}_0}{R_0} = \frac{\mathcal{E}}{2R_0 + 6r} \Rightarrow R_0 = \frac{6 r \mathcal{E}_0}{\mathcal{E} - 2\mathcal{E}_0}.\] Используя последние два соотношения, находим окончательно ответ на вопрос задачи: \[I_0 = \frac{\mathcal{E}_0}{R_0} = \frac{\mathcal{E}-2\mathcal{E}_0}{6r} = 10\textrm{\,А}.\]
\[I_0 = \frac{\mathcal{E}-2\mathcal{E}_0}{6r} = 10\textrm{\,А}.\]
| Указано, что при соединении по изначальной схеме напряжение на каждом двигателе равно ЭДС источника | 3 балла |
| Обосновано, что двигателей в группе может быть только два | 3 балла |
| Найдено эквивалентное сопротивление смешанного соединения двигателей | 3 балла |
| Верно записан закон Ома для полной цепи | 3 балла |
| Получено выражение для силы тока или напряжения на одном двигателе при смешанном соединении | 5 баллов |
| Получен правильный ответ | 6 баллов |
| Всего | 23 балла |
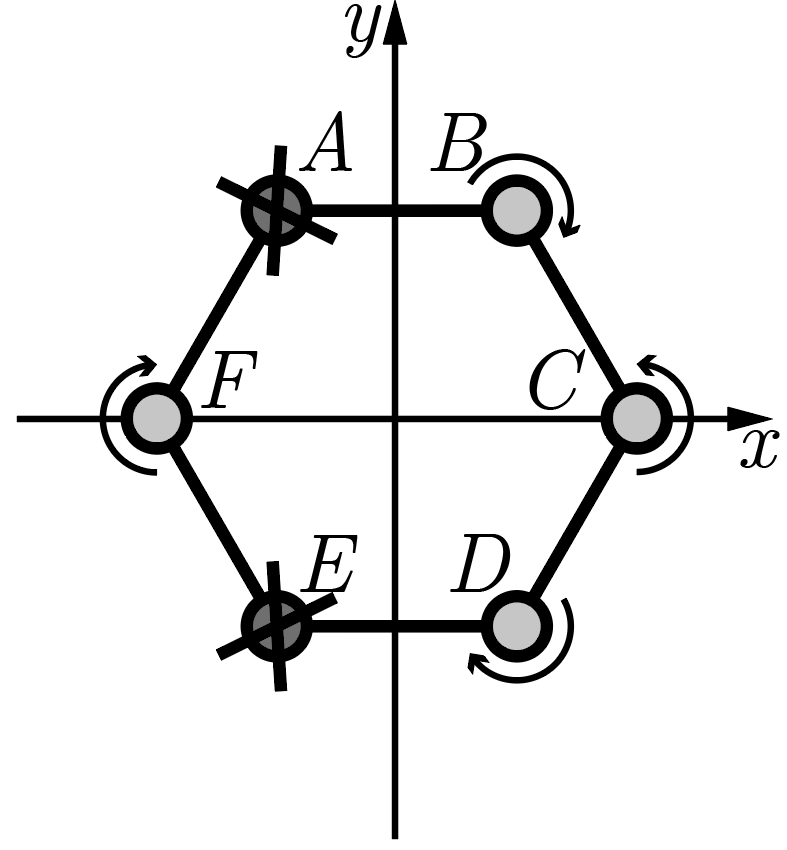
Мультикоптер удерживается в спокойном воздухе неподвижно благодаря одновременной работе шести одинаковых электродвигателей, расположенных в вершинах правильного шестиугольника \(ABCDEF\), в центре которого находится центр масс коптера. Лопасти каждого из двигателей вращаются с одинаковой угловой скоростью \(\omega_0\), при этом лопасти двигателей, расположенных в вершинах \(A\), \(C\) и \(E\), имеют такую форму, чтобы создавать подъемную силу при вращении в одном направлении, а расположенных в вершинах \(B\), \(D\) и \(F\) — в противоположном. В остальном они идентичны. Подъемная сила, создаваемая каждым из двигателей, прямо пропорциональна скорости его вращения, и также прямо пропорционален ей момент силы, вращающей лопасти относительно оси двигателя. В некоторый момент двигатели в вершинах \(A\) и \(E\) одновременно отказали и остановились. Бортовой компьютер быстро вычислил, каким образом необходимо поменять скорости вращения каждого из оставшихся исправными двигателей, чтобы коптер остался неподвижен. Найдите эти скорости.
Прежде всего введем систему обозначений. Обозначим искомые скорости вращения уцелевших двигателей \(\omega_{B,C,D,F}\). Аналогично эти же индексы будем использовать для других величин, связанных с двигателем в соответствующей вершине. Величины, касающиеся работы двигателей до поломки, будем помечать индексом \(0\). Введем систему координат так, как это изображено на рис. 2.5: ось \(0x\) проведем через вершины \(F\) и \(C\), а \(0y\) — перпендикулярно ей. Начало системы координат поместим в центр масс мультикоптера. Сторону шестиугольника обозначим \(a\).
Для того чтобы коптер остался в равновесии, должны выполниться четыре условия. Первое из них достаточно очевидно: сумма подъемных сил \(F\), действующих на коптер, должна остаться неизменной, так как не изменился вес коптера: \[F_B + F_C + F_D + F_F = 6F_0.\] Второе условие: суммарный момент подъемных сил относительно \(0x\) должен остаться равен нулю. Относительно этой оси плечи подъемных сил в вершинах \(F\) и \(C\), а также плечо силы тяжести равны нулю. Плечи подъемных сил в вершинах \(B\) и \(D\) одинаковы и равны \(\sqrt{3}a/2\), при этом эти вершины находятся по разные стороны от оси. Следовательно, уравнение моментов принимает вид \[F_B \cancel{\frac{\sqrt{3}a}{2}} = F_D \cancel{\frac{\sqrt{3}a}{2}}.\] Третье условие: суммарный момент подъемных сил относительно \(0y\) должен остаться равен нулю. Относительно этой оси плечи подъемных сил в вершинах \(F\) и \(C\) одинаковы и равны \(a\). Плечи подъемных сил в вершинах \(B\) и \(D\) одинаковы и равны \(a/2\). Плечо силы тяжести вновь равно нулю. С учетом направлений действия соответствующих сил, уравнение моментов принимает вид \[F_F \cancel{a} = F_C \cancel{a} + (F_B + F_D)\frac{\cancel{a}}{2}.\] Последнее условие предотвращает вращение мультикоптера в плоскости рисунка. Каждый двигатель, вращая свои лопасти и действуя на них с некоторым моментом \(M\), создает момент \(-M\), действующий на коптер в противоположную сторону (по третьему закону Ньютона). Это значит, что суммарный момент сил относительно осей двигателей для всех двигателей, вращающихся в одну сторону (в вершинах \(F\), \(B\) и \(D\)), должен равняться суммарному моменту двигателей, вращающихся в другую сторону (только в вершине \(C\) из уцелевших): \[M_C = M_B+M_D+M_F.\] Во всех четырех составленных уравнениях учтем пропорциональность сил и моментов соответствующим угловым скоростям, и перепишем систему через эти скорости (коэффициенты пропорциональности во всех уравнениях ниже сразу сократим): \[\left\{\begin{aligned} &\omega_B + \omega_C + \omega_D + \omega_F = 6\omega_0,\\ &\omega_B = \omega_D, \\ &\omega_F = \omega_C + \frac{\omega_B + \omega_D}{2},\\ &\omega_C = \omega_B+\omega_D+\omega_F. \end{aligned}\right.\] Эта система имеет единственное решение: \[\left\{\begin{aligned} &\omega_B = \omega_D = 0, \\ &\omega_F = \omega_C = 3\omega_0. \\ \end{aligned}\right.\] Такое равновесие, разумеется, является неустойчивым и не может удерживаться без контроля со стороны электроники коптера.
| Верно составлено первое условие равновесия (сумма сил) | 4 балла |
| Верно составлено второе условие равновесия (сумма моментов относительно \(0x\)) | 5 баллов |
| Верно составлено третье условие равновесия (сумма моментов относительно \(0y\)) | 5 баллов |
| Верно составлено четвертое условие равновесия (сумма моментов в плоскости коптера) | 6 баллов |
| Получен правильный ответ | 5 баллов |
| Всего | 25 баллов |