Предметный тур. Физика. 3 этап
Место на печатных платах лабораторного оборудования бывает весьма ограничено, и размещать на них элементы порой приходится в непривычном порядке. На некоторой плате собрана схема (см. рис. 1.1), состоящая из четырех приборов, которые при расчете цепи можно считать резисторами, и трех миниатюрных, но идеальных вольтметров, изображенная на рисунке. Определите показания этих вольтметров при подключении клемм цепи к источнику постоянного напряжения \(U = 12\) В.
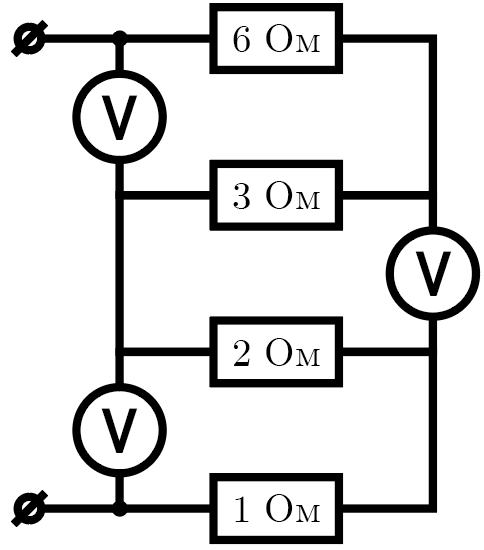
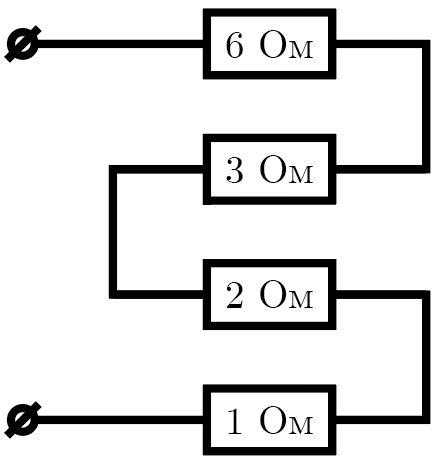
Соединение резисторов может показаться параллельным, смешанным или даже коротким замыканием, если забыть, что сопротивление идеального вольтметра не очень мало, а, напротив, очень велико. Если же об этом помнить — можно элементарно изобразить эквивалентную схему, заменив вольтметры, через которые не может протекать ток, на разрывы цепи (см. рис. 1.2). После этого легко видеть, что соединение на самом деле является последовательным.
Тогда эффективное сопротивление \(R\) всей цепи равно сумме сопротивлений отдельных резисторов: \[R = R_1 + R_2 + R_3 + R_4,\] сила тока в цепи определяется по закону Ома: \[I = \frac{U}{R} = \frac{U}{R_1 + R_2 + R_3 + R_4},\] а напряжение на каждом резисторе, следуя тому же закону, равно произведению его сопротивления на эту силу тока: \[U_i = I R_i = \frac{U R_i}{R_1 + R_2 + R_3 + R_4},\] где индекс \(i\) принимает значения от \(1\) до \(4\) и означает номер резистора.
Наконец, каждый из вольтметров показывает сумму напряжений на двух резисторах, находящихся между его клеммами. Пронумеровав вольтметры \(1, 2, 3\) сверху вниз и обозначив их показания \(V_{1, 2, 3}\) соответственно, получим \[V_1 = U_1 + U_2 = U \frac{R_1 + R_2}{R_1 + R_2 + R_3 + R_4} = 9\textrm{\,В} \qquad\] и аналогично \[V_2 = U \frac{R_2 + R_3}{R_1 + R_2 + R_3 + R_4} = 5\textrm{\,В}; \qquad V_3 = U \frac{R_3 + R_4}{R_1 + R_2 + R_3 + R_4} = 3\textrm{\,В}. \qquad\]
Показания вольтметров сверху вниз \(V_1 = 9\textrm{\,В}\), \(V_2 = 5\textrm{\,В}\), \(V_3 = 3\textrm{\,В}\).
| Верно записан закон Ома для любого участка цепи | 2 балла |
| Продемонстрировано понимание того, что идеальный вольтметр имеет бесконечное сопротивление | 3 балла |
| Изображена эквивалентная цепь или словами описано, что соединение можно считать последовательным | 3 балла |
| Найдена сила тока в цепи или записана верная пропорция между напряжениями на последовательно соединенных элементах | 3 балла |
| Получен правильный ответ | 5 баллов |
| Всего | 16 баллов |
Центральным компонентом твердотельных лазеров является кристалл, в котором создается так называемая инверсная населенность — особое состояние вещества, делающее возможной генерацию когерентного (лазерного) излучения. Для этого веществу необходимо передать большое количество энергии, что достигается обычно за счет освещения кристалла мощной, но не когерентной (естественного света) лампой. Этот процесс называют накачкой лазера. К сожалению, эффективность преобразования энергии в этом процессе не бывает велика, и большая часть изначально переданной кристаллу световой энергии переходит в тепло, а не в энергию последующего лазерного импульса. Чтобы отводить это тепло и тем самым минимизировать тепловые деформации тонко настроенной оптики, кристалл помещают в воду, непрерывно омывающую его и лампу накачки.
Рубиновый лазер генерирует импульсы излучения, обладающие энергией \(W = 3\textrm{\,Дж}\) каждый и следующие друг за другом с частотой \(\nu = 0{,}8\textrm{\,Гц}\). Для охлаждения лазера через него приходится прокачивать воду с объемным расходом \(v = 11\textrm{\,л/мин}\), при этом температура воды на выходе из лазера оказывается на \(\Delta t = 3\textrm{\,° С}\) выше, чем на входе. Определите КПД преобразования энергии лампы накачки в энергию лазерного излучения. Удельная теплоемкость воды \(c = 4200\) Дж/(кг\(\cdot\)°C), ее плотность \(\rho = 1000\) кг/м\(^3\).
Из описания принципов работы лазера можем заключить, что изначальная мощность \(P_0\), используемая для накачки лазера, переходит в процессе его работы в мощность \(P_\textrm{л}\) лазерных импульсов и тепловую мощность \(P_\textrm{т}\), отводимую системой охлаждения. Очевидно, полезным является первый из этих видов мощности, так что коэффициент полезного действия задается формулой \[\eta = \frac{P_\textrm{л}}{P_0} = \frac{P}{P_\textrm{л}+P_\textrm{т}}.\] Чтобы определить среднюю полезную мощность лазерного излучения, достаточно умножить энергию одного импульса на частоту их следования: \[P_\textrm{л} = \nu W.\] Для нахождения тепловой мощности найдем количество теплоты \(Q\), уносимое водой за время \(\tau\). Оно, как хорошо известно из термодинамики, задается выражением \[Q = c m \Delta t,\] где \(m\) — масса воды, протекающей за это время через систему охлаждения. Зная объемный расход жидкости, найти ее также можно тривиально: \[m = \rho v \tau \Rightarrow Q = c \rho v \tau \Delta t.\] Тепловая мощность есть отношение этой теплоты ко времени: \[P_\textrm{т} = \frac{Q}{\tau} = c \rho v \Delta t.\] Остается окончательно подставить мощности в определение КПД и получить ответ (не забывая перевести литры в кубические метры и минуты в секунды): \[\eta = \frac{P}{P_\textrm{л}+P_\textrm{т}} = \frac{\nu W}{\nu W + c \rho v \Delta t} \approx 0{,}1\%.\]
К сожалению, эффективность преобразования световой энергии в большинстве твердотельных лазеров действительно имеет настолько малый порядок. Тем не менее качественные отличия когерентного света лазера от естественного света лампы делают и устройства со столь низким КПД весьма полезными.
\[\eta \frac{\nu W}{\nu W + c \rho v \Delta t} \approx 0{,}1\%.\]
| Верно определено, какие мощности или энергии следует отнести друг другу для нахождения КПД лазера | 4 балла |
| Найдена средняя полезная мощность или частота верно использована для определения промежутка времени между двумя импульсами | 3 балла |
| Верно записана связь теплоты с массой и удельной теплоемкостью | 3 балла |
| Верно найдена тепловая мощность или теплота, отводимая от лазера за время между двумя последовательными импульсами | 4 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 20 баллов |
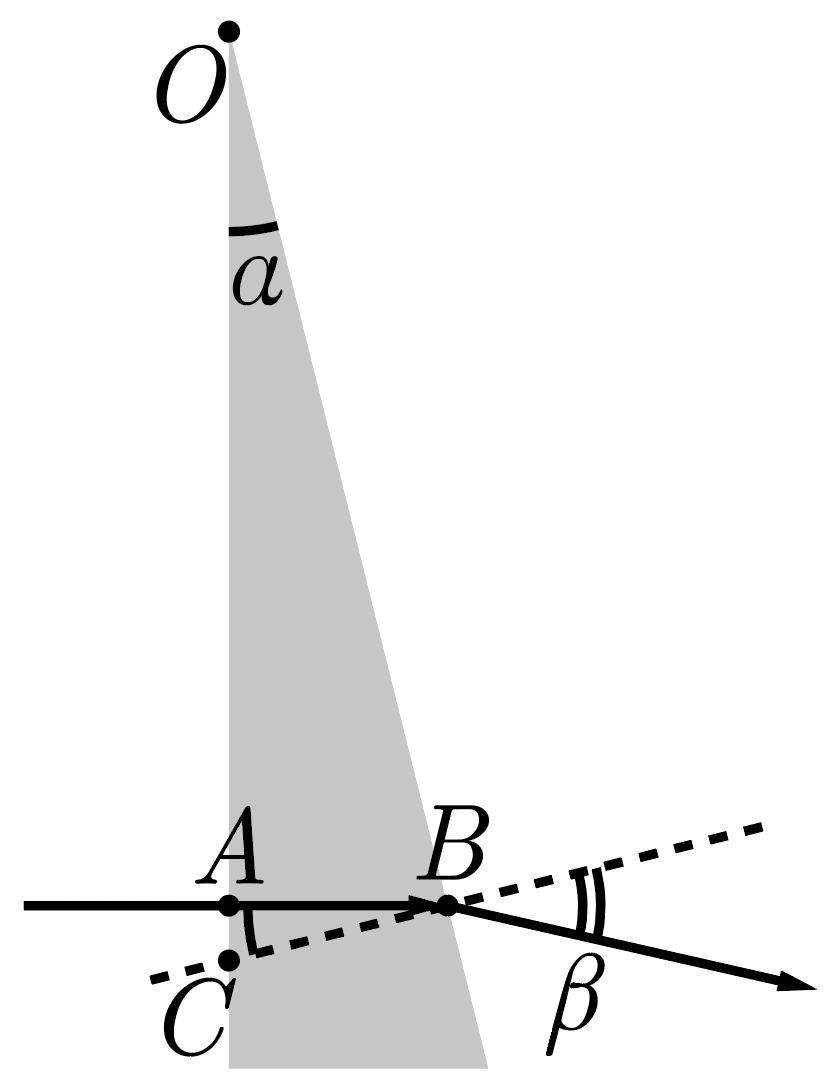
Для оптического эксперимента из легкого стекла с показателем преломления \(n\) изготовлена треугольная призма в виде тонкого клина с очень острым углом между ребрами. На одно из ребер клина нормально падает из воздуха луч света и, пройдя сквозь призму, отклоняется на угол \(\phi_1 = 5°\) от своего изначального направления распространения. Затем клин полностью погружают в плотную оптическую смолу с показателем преломления \(n_0 = 1{,}75\), в результате чего луч света, также нормально падающий на одно из ребер клина, начинает отклоняться на угол \(\phi_2 = 2°\), но в обратную сторону. Найдите \(n\). Указание: для малых углов справедливо приближенное равенство \(\sin \alpha \approx \alpha\) (в радианах).
Изобразим ход лучей при падении их на клин из воздуха. На рис. 1.3 сплошными линиями изображен ход лучей, пунктиром построена нормаль ко второй границе раздела сред.
Поскольку падение луча на первую границу нормальное, ни при каких показателях преломления луч на этой границе не отклоняется. Тогда треугольники \(\triangle OBC\) и \(\triangle OAB\) являются прямоугольными и имеют общий угол при вершине \(O\). Следствием этого подобия становится равенство \[\angle OCB = \angle OBA = 90° - \alpha,\] где \(\alpha\) — угол при вершине клина. Но так как угол падения \(\angle ABC\) луча на вторую границу раздела равен \(90° - \angle ABO\), то он также равен \(\alpha\).
Тогда из закона Снеллиуса легко выразим угол преломления \(\beta\): \[\sin \beta = n \sin \alpha \Rightarrow \beta \approx n \alpha.\] Применимость приближения малых углов обоснована тем, что по условиям клин является тонким, то есть имеет малый угол раствора, а также малыми (по сравнению с \(1\textrm{\,рад}\)) значениями углов \(\phi_{1{,}2}\).
Теперь остается заметить, что угол \(\phi_1\), на который луч отклонился от своего изначального направления распространения, равен \[\phi_1 = \beta - \alpha \approx \alpha (n-1).\]
При проведении аналогичных рассуждений во втором случае (клин в оптически плотной смоле) следует сделать два изменения. Во-первых, роль показателя преломления \(n\) в законе Снеллиуса будет выполнять относительный показатель преломления двух сред \(n/n_0\). Во-вторых, поскольку отклонение луча по условиям происходит в другую сторону, \(\phi_2\) имеет противоположный знак: \[\phi_2 = \alpha - \beta_2 \approx \alpha \left(1 - \frac{n}{n_0}\right).\] Решая полученную систему из двух уравнений, найдем ответ на вопрос задачи: \[n = n_0 \frac{\phi_1 + \phi_2}{\phi_2 n_0 + \phi_1} \approx 1{,}44.\]
\[n = n_0 \frac{\phi_1 + \phi_2}{\phi_2 n_0 + \phi_1} \approx 1{,}44.\]
| Верно изображен или детально описан ход лучей | 5 баллов |
| Верно записан закон Снеллиуса для одного случая | 3 балла |
| Верно записан закон Снеллиуса для второго случая | 2 балла |
| Верно найдено соотношение между углами падения, преломления и отклонения луча для одного случая | 3 балла |
| То же для второго случая | 2 балла |
| Получен правильный ответ | 5 баллов |
| Всего | 20 баллов |
В квантовой физике почти никогда не говорят о скоростях частиц, вместо этого используя термины импульса и энергии. Еще не привыкший к этому лаборант нашел запись в лабораторном журнале, согласно которой некоторая частица, обладавшая изначальным импульсом \(p_0\), за время \(t\) пролетела через область сильного электромагнитного поля, в которой на нее действовала постоянная сила, равная \(0{,}6 p_0 / t\). В следующей записи было указано, что начальная кинетическая энергия этой частицы равнялась \(K_0\), а после пролета через поле окна оказалась равна \(K_1 = 0{,}64 K_0\). Сначала эти же записи показались лаборанту взаимно исключающими, но чуть позже он понял их и даже вычислил, на какой угол отклонилась частица от начального направления своего движения. Найдите и вы этот угол.
Обозначим массу частицы \(m\), а ее начальную и конечную скорости \(v_0\) и \(v_1\) соответственно. Из известного изменения кинетической энергии легко вычислить отношение между этими скоростями. Будет удобнее записать его в виде простой дроби: \[K = \frac{mv^2}{2} \Rightarrow v = \sqrt{\frac{2K}{m}} \Rightarrow \frac{v_1}{v_0} = \sqrt{\frac{K_1}{K_0}} = \sqrt{0{,}64} = \frac{4}{5}.\] В то же время приращение \(\Delta v\) скорости легко вычислить, зная величину действовавшей на частицу силы \(F\): \[\Delta v = at =\frac{Ft}{m} = \frac{0{,}6 p_0\cancel{t}}{m \cancel{t}} = \frac{3}{5}v_0,\] где \(a\) обозначено ускорение частицы. То же можно доказать при помощи понятия импульса силы.
Изменение скорости на величину \(3/5 v_0\) и конечное значение этой скорости, равное \(4/5\) от начального, можно принять за противоречие, но оно легко снимется, если учесть, что сила направлена к начальной и конечной скоростям под некоторыми углами. Эти углы можно напрямую вычислить из теоремы косинусов, но гораздо проще узнать в числах \(3, 4, 5\) египетский треугольник: \[v_1^2 + \Delta v^2 = \left(\frac{4}{5} v_0\right)^2 + \left(\frac{3}{5} v_0\right)^2 = v_0^2.\]
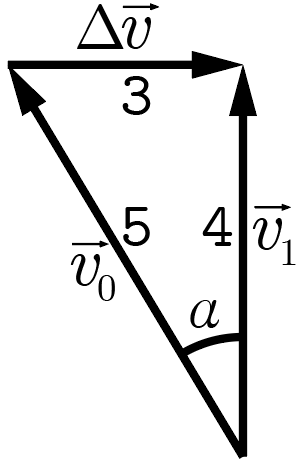
Тогда становится очевидно, что конечная скорость \(\vec{v}_1\) и приращение скорости \(\Delta \vec{v}\) перпендикулярны друг другу (см. рис. 1.4). На рисунке модули векторов указаны в единицах \(v_0/5\), а отмеченный угол \(\alpha\) является искомым в задаче. Найдем его, используя тригонометрию: \[\alpha = \arccos \frac{4}{5} = \arcsin \frac{3}{5} \approx 36{,}8°.\]
\[\alpha = \arccos \frac{4}{5} = \arcsin \frac{3}{5} \approx 36{,}8°.\]
| Верно найдено отношение модуля конечного значения скорости или импульса к начальному | 4 балла |
| Верно найдено отношение приращения скорости или импульса к начальному или конечному | 4 балла |
| Верно изображена или описана процедура векторного сложения скоростей или импульсов | 3 балла |
| Определено, что треугольник, образованный скоростями или импульсами и их приращениями, прямоугольный, или правильно записана теорема косинусов | 3 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 20 баллов |
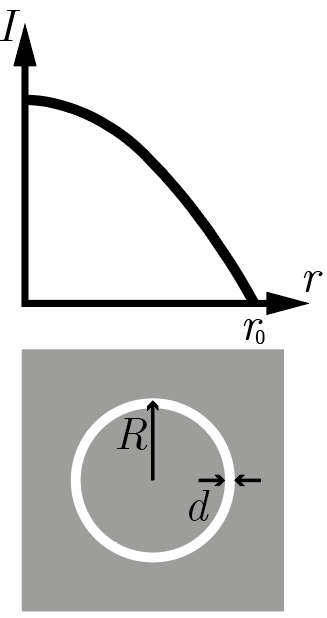
Интенсивностью \(I\) излучения называется отношение мощности этого излучения, попадающей на некоторую площадку, к площади этой площадки. Интенсивность световых пучков, как правило, максимальна вблизи их оси и уменьшается к краям.
В эксперименте получен лазерный пучок радиусом \(r_0 = 10\textrm{\,см}\), имеющий параболический профиль зависимости интенсивности от расстояния \(r\) до оси пучка (см. рис. 1.5, верхнее изображение) и не зависящий от других координат. Этот пучок падает нормально на непрозрачный экран, в котором вытравлены различные кольцевые маски — участки с радиусом \(R\) и толщиной \(d \ll R\), прозрачные для излучения лазера (см. рис. 1.5, нижнее изображение). В результате эксперимента было установлено, что сквозь кольцо радиусом \(R_1 = 6\textrm{\,см}\) проходит излучение с общей мощностью \(P_1 = 4\textrm{\,мВт}\). Найдите мощность излучения, проходящего через кольцо радиусом \(R_2 = 8\textrm{\,см}\). Центр маски совпадает с центром пучка, а дифракционными явлениями можно пренебречь.
Прежде всего по данным задачи построим явно функцию зависимости \(I(r)\). Согласно условиям, этот график представляет собой параболу, поэтому зависимость следует искать в форме \[I(r) = a r^2 + br + c.\]
По графику хорошо видно, что парабола направлена ветвями вниз, значит, \(a < 0\), ее вершина, расположенная всегда в точке \(-b/(2a)\), находится в нуле, значит, \(b = 0\), а в точке \(r = r_0\) парабола пересекает ось абсцисс: \[I(r_0) = ar_0^2 + c = 0 \Rightarrow c = - ar_0^2.\]
Введем более физически обоснованные обозначения, переобозначив величину \(-a\) как \(I_0\) (интенсивность на оси пучка). Получим \[I(r) = I_0\left(1- \frac{r^2}{r_0^2}\right).\]
Поскольку по условиям толщина кольца мала в сравнении с его радиусом, а от полярного угла интенсивность пучка не зависит, в пределах всей кольцевой маски интенсивность можно считать постоянной и равной \(I(R)\).
Мощность \(P\) прошедшего через маску излучения по определению интенсивности необходимо искать как произведение этой интенсивности на площадь \(S\) маски. Последнюю, опять опираясь на приближение \(d \ll R\), легко найти как произведение толщины кольца на его длину окружности: \[S(R) \approx 2\pi R d.\] Тогда \[P \approx I(R)S(R) \approx 2\pi R d I_0\left(1- \frac{R^2}{r_0^2}\right).\] Подставляя в это выражение два радиуса из условий, получим \[\frac{P_2}{P_1} \approx \frac{\cancel{2\pi d I_0 r_0^2} R_2 (r_0^2 - R_2^2)}{\cancel{2\pi d I_0 r_0^2} R_1 (r_0^2 - R_1^2)} \Rightarrow P_2 \approx \frac{R_2 (r_0^2 - R_2^2)}{R_1 (r_0^2 - R_1^2)} P_1 = 3\textrm{\,мВт}.\]
\[P_2 \approx \frac{R_2 (r_0^2 - R_2^2)}{R_1 (r_0^2 - R_1^2)} P_1 = 3\textrm{\,мВт}.\]
| Верно составлено уравнение, описывающее зависимость \(I(r)\) | 6 баллов |
| Продемонстрировано понимание того, что мощность пучка равна произведению интенсивности на радиусе кольца на площадь этого кольца | 4 балла |
| Получено явное выражение для площади кольца: точное или в приближении \(d \ll R\) | 4 балла |
| Получено явное выражение для мощности прошедшего через маску пучка в зависимости от радиуса маски | 4 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 24 балла |
Для изучения самых крохотных частиц порой приходится использовать самые громадные установки. Инновационный рентгеновский лазер представляет собой трубу длиной \(L = 70\textrm{\,м}\) и массой \(M = 800\textrm{\,т}\), достаточно равномерно распределенной по длине трубы, которую требуется иметь возможность наклонять в вертикальной плоскости. К сожалению, из-за необходимости размещения на этой трубе большого количества сложного оборудования, подвижный шарнир пришлось закрепить на расстоянии \(x = 4\textrm{\,м}\) от центра тяжести лазера на его оси. Двигатель, управляющий наклоном всей установки, питается от постоянного напряжения \(U = 600\textrm{\,В}\) и имеет КПД \(\eta = 45\%\). Найдите величину заряда, который должен протечь через двигатель, чтобы повернуть лазер на \(\alpha = 5°\) в сторону подъема центра тяжести из изначально горизонтального положения. Ускорение свободного падения \(g = 9{,}8\textrm{\,м/с}^2\).
При повороте лазера на угол \(\alpha\) вокруг шарнира, расположенного на расстоянии \(x\) от его центра тяжести, последний смещается по вертикали на расстояние \(h = x\sin\alpha\). Полная длина лазера при этом не играет роли. Полезная механическая работа двигателя \(A_\textrm{мех}\) равна приращению потенциальной энергии лазера: \[A_\textrm{мех} = M g h = M g x \sin \alpha.\] Потребленная электроэнергия, сопутствующая этому повороту, окажется больше в \(1/\eta\) раз и будет равна, согласно определению напряжения, произведению искомого заряда \(q\) на напряжение между контактами двигателя: \[q U = \frac{A_\textrm{мех}}{\eta} = \frac{M g x \sin \alpha}{\eta}.\] Отсюда окончательно запишем ответ \[q = \frac{M g x \sin \alpha}{\eta U} \approx 10{,}1\textrm{\,кКл}.\]
\[q = \frac{M g x \sin \alpha}{\eta U} \approx 10{,}1\textrm{\,кКл}.\]
| Верно найдена высота подъема центра тяжести лазера | 3 балла |
| Верно записана связь механической работы с высотой подъема и массой лазера | 2 балла |
| Верно записана связь электрической работы с зарядом и напряжением | 3 балла |
| Верно записана связь двух работ с КПД | 2 балла |
| Получен правильный ответ | 3 балла |
| Всего | 13 баллов |
При расчете излучения колеблющейся молекулы используется ее компьютерная модель, состоящая из двух материальных точек с равными массами \(m\) и разноименными зарядами равной величины \(\pm q\), находящимися на некотором расстоянии \(l\) друг от друга. Материальные точки связаны химической связью, которая в рамках модели ведет себя как идеальная пружина, и совершают, благодаря ей, синхронные гармонические колебания вокруг своих равновесных положений с амплитудой \(l/6\) (каждая частица) так, что центр масс системы остается на месте. Другого взаимодействия между частицами в рамках этой модели нет. Определите, во сколько раз будут отличаться минимальная и максимальная напряженность электрического поля, создаваемого такой системой в точке, находящейся на одной прямой с частицами на расстоянии \(2l\) от ее центра масс. Дайте ответ с точностью до двух значащих цифр.
В описанной модели напряженность электрического поля \(E\) в точке наблюдения находится по принципу суперпозиции как сумма напряженностей, созданных в этой точке каждой из частиц по отдельности. В силу симметрии задачи модуль напряженности не зависит от того, с какой стороны от системы рассматривается точка наблюдения, поэтому будем для определенности считать, что она ближе к положительному заряду. В таком случае напряженность в этой точке равна \[E = kq\left(\frac{1}{x_+^2} - \frac{1}{x_-^2}\right),\] где \(x_\pm\) — расстояния до точки наблюдения от положительной и отрицательной частиц соответственно, \(k\) — коэффициент пропорциональности в законе Кулона.
Поскольку по условиям центр масс системы остается на месте, а частицы имеют одинаковые массы, в каждый момент колебаний одна частица приближается к точке наблюдения настолько же, насколько вторая отдаляется. Следовательно, напряженность электрического поля будет максимальна при максимальном растяжении связи, когда положительная частица ближе всего к точке наблюдения, а противодействующая ей отрицательная — дальше всего, и минимальна при ее максимальном сжатии.
В равновесии положительный заряд находится от точки наблюдения на расстоянии \[x_+ = 2l - \frac{1}{2}l = \frac{3}{2}l,\] а отрицательный — на расстоянии \[x_- = 2l + \frac{1}{2}l = \frac{5}{2}l.\] Вычислим теперь минимальные и максимальные расстояния от частиц до точки наблюдения: \[x_{+max} = \frac{3}{2}l + \frac{l}{6} = \frac{5}{3}l; \qquad x_{+min} = \frac{3}{2}l - \frac{l}{6} = \frac{4}{3}l;\] \[x_{-max} = \frac{5}{2}l + \frac{l}{6} = \frac{8}{3}l; \qquad x_{-min} = \frac{5}{2}l - \frac{l}{6} = \frac{7}{3}l.\] Остается подставить эти расстояния в приведенное выражение для напряженности: \[E_{max} = kq\left(\frac{9}{16 l^2} - \frac{9}{64 l^2}\right) = \frac{27}{64}\frac{k}{l^2} \approx 0{,}422 \frac{kq}{l^2},\] \[E_{min} = kq\left(\frac{9}{25 l^2} - \frac{9}{49 l^2}\right) = \frac{216}{1225}\frac{kq}{l^2} \approx 0{,}176 \frac{kq}{l^2}.\] Отсюда окончательно \[\frac{E_{max}}{E_{min}} = \frac{1225}{512} \approx 2{,}4.\]
\[\frac{E_{max}}{E_{min}} = \frac{1225}{512} \approx 2{,}4.\]
В условиях ограниченного времени можно прибегнуть к разумному промежуточному округлению и не давать ответа простой дробью.
| Записано верное выражение для напряженности электрического поля точечного заряда | 3 балла |
| Верно применен принцип суперпозиции электрических полей | 2 балла |
| Изображены на рисунке или описаны словами соображения, демонстрирующие понимание того, что удаления зарядов от центра системы одинаковы в каждый момент времени | 3 балла |
| Верно найдены минимальные и максимальные расстояния от зарядов до точки наблюдения (4 расстояния) | 4 балла |
| Получен правильный ответ | 5 баллов |
| Всего | 17 баллов |
Металлический сплав изготовлен из радиоактивного изотопа \(X\), имеющего период полураспада \(T\), радиоизотопа \(Y\), имеющего период полураспада \(2T\) и нескольких стабильных металлов. Ядро каждого из радиоизотопов, претерпев \(\beta\)-распад, образует ядро стабильного металла. Когда образец из этого сплава был привезен в лабораторию, масса радиоизотопа \(X\) в нем была вдвое выше массы радиоизотопа \(Y\), а общая масса стабильных металлов в образце совпадала с общей массой радиоизотопов. По прошествии месяца образец подвергли анализу и установили, что теперь уже масса радиоизотопа \(Y\) оказалась вдвое выше, чем масса радиоизотопа \(X\). Во сколько раз теперь отличаются общие массы стабильных и радиоактивных изотопов в образце?
За время \(2T\) распадается половина изотопа \(Y\) и три четверти изотопа \(X\) (как следует из определения периода полураспада). Следовательно, отношение этих двух изотопов изменяется в \(2\) раза (в сторону увеличения доли изотопа \(Y\)). За описанный в задаче месяц соотношение между этими изотопами изменилось в \(4\) раза, следовательно, прошло время \(4T\) — два периода полураспада для \(Y\) и четыре для \(X\).
Изначальную массу изотопа \(Y\) обозначим \(m_{0Y}\). Из условий задачи следует, что начальная масса изотопа \(X\) была равна \(m_{0X} = 2m_{0Y}\), а стабильных изотопов \(m_{0S} = m_{0X} + m_{0Y} = 3m_{0Y}\). По прошествии указанного времени масса изотопа \(X\) становится равна \(m_{1X} = m_{0X}/16 = m_{0Y}/8\), а масса изотопа \(Y\) — равна \(m_{1Y} = m_{0Y}/4\).
Поскольку при \(\beta\)-распаде нейтроны превращаются в протоны (\(\beta^-\)-распад) или наоборот (\(\beta^+\)-распад), масса ядер в этом процессе существенно не меняется, поэтому можно считать, что суммарная масса образца осталась прежней: \[m_{0X} + m_{0Y} + m_{0S} = m_{1X} + m_{1Y} + m_{1S},\] откуда легко найти конечную массу \(m_{1S}\) стабильных изотопов: \[m_{1S} = m_{0X} + m_{0Y} + m_{0S} - m_{1X} - m_{1Y} = \left(2 + 1 +3 - \frac{1}{8} -\frac{1}{4}\right) m_{0Y} = \frac{45}{8} m_{0Y}.\] Таким образом, \[\frac{m_{1R}}{m_{1S}} = \frac{m_{1X} + m_{1Y}}{m_{1S}} = \frac{3/8}{45/8} = \frac{1}{15},\] где \(m_{1R}\) обозначена конечная масса радиоактивных изотопов.
Масса стабильных изотопов в \(15\) раз выше массы радиоактивных.
| Хотя бы один раз верно записан формулой или описан словами закон радиоактивного распада или явно продемонстрировано его понимание | 3 балла |
| Вычислено, что прошедший месяц составляет \(4T\) | 4 балла |
| Верно найдено, во сколько раз за этот месяц изменились массы радиоизотопов | 3 балла |
| Указано, что после \(\beta-\) распада масса ядер-продуктов практически не отличается от массы ядер-реагентов | 3 балла |
| Получен правильный ответ | 7 баллов |
| Всего | 20 баллов |
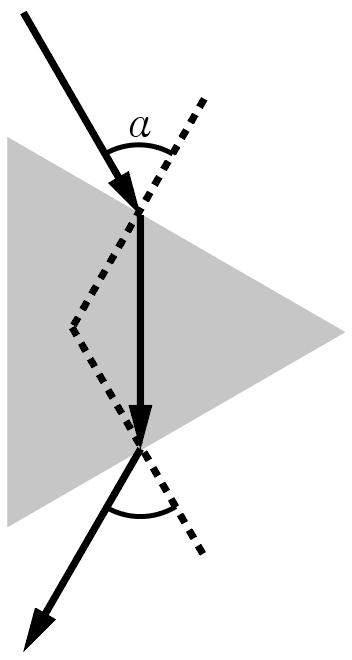
Как известно, свет оказывает крошечные силы давления на поверхности, на которых он поглощается, преломляется или отражается, причем сила этого давления зависит от того, что именно происходит со световым пучком. На треугольную призму, основание которой представляет собой правильный треугольник, падает лазерный луч так, что его угол падения на первую грань и его угол преломления на второй грани одинаковы и равны \(\alpha = 60°\) (см. рис. 2.1). Определите, во сколько раз изменится модуль силы светового давления на призму, если поверхность, на которую падает луч, посеребрить так, что она станет отражать \(R = 50\%\) падающей световой энергии? Считайте, что на непосеребренных поверхностях происходит только преломление, а поглощение во всех случаях весьма мало.
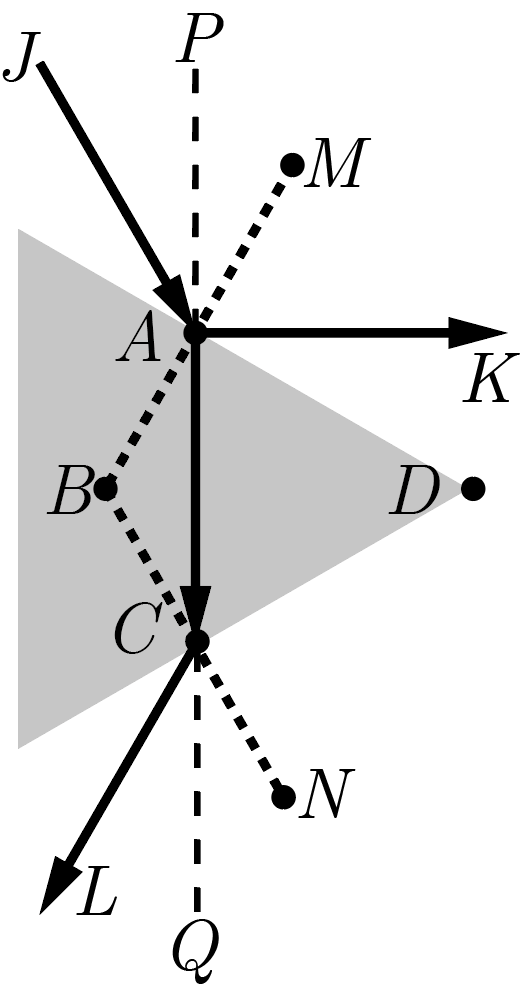
Изобразим падающий, преломленный и отраженный лучи и введем обозначения для удобства дальнейших рассуждений, как это показано на рис. 2.2. Сплошными линиями обозначен ход лучей, частым пунктиром — нормали к границам раздела, редким тонким пунктиром — продолжения лучей. Прежде всего следует заметить, что так как оба преломления происходят на границе одних и тех же сред, а угол первого падения \(\angle JAM\) равен углу второго преломления \(\angle LCN\) по условиям задачи, то углы первого преломления \(\angle BAC\) и второго падения \(\angle BCA\) также равны.
Из суммы углов в четырехугольнике \(ADCB\) легко найти угол \(\angle ABC = 120°\), а тогда, в силу доказанного выше равенства, и суммы углов в треугольнике \(\triangle ABC\), \(\angle LCN = \angle JAM = 30°\). Тогда углы \(\angle PAM\) и \(\angle QCN\) также равны \(30°\) как вертикальные, а следовательно, \(60°-30° = 30 °\) равны и углы \(\angle JAP = \angle LCQ\), которые падающий и преломленный луч составляют с прямой \(PQ\).
Последнее равенство позволяет утверждать, что дважды преломленный луч \(CL\) и падающий луч \(JA\) составляют друг с другом угол \(120°\). Существует и множество других способов доказать этот ключевой для дальнейшего решения результат. Отраженный луч \(AK\) также составляет угол \(2 \alpha = 120°\) с падающим: этот результат прямо следует из закона отражения. А значит, с дважды преломленным лучом \(CL\) он составляет такой же угол.
Теперь рассмотрим изменение импульса фотонов в результате преломлений и отражений на найденные углы. Обозначим \(\vec{j}\) единичный вектор, сонаправленный с направлением распространения падающего луча \(JA\), \(\vec{k}\) — единичный вектор, сонаправленный с направлением распространения отраженного луча \(AK\) и \(\vec{l}\) — единичный вектор, сонаправленный с направлением распространения дважды преломленного луча \(CL\). Также обозначим \(p_0\) модуль импульса одного фотона, падающего на призму, а \(n\) — число фотонов, падающих на нее в единицу времени.
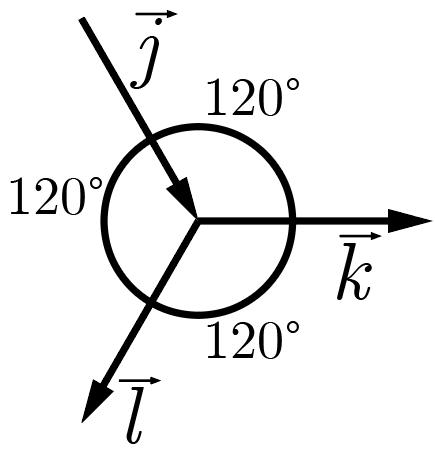
В этих обозначениях очень легко записать силы \(\vec{F}\) светового давления, всегда равные скорости изменения импульса света (с обратным знаком): \[\vec{F} = -\frac{\Delta \vec{p}_\textrm{св}}{\Delta t} = -n\Delta \vec{p}.\] В случае чистого преломления начальный импульс всех фотонов равен \(\vec{p}_0 = p_0 \vec{j}\), а конечный — равен \(\vec{p}_1 = p_0\vec{l}\). Сила светового давления в этом случае задается выражением \[\vec{F}_1 = np_0 (\vec{j} - \vec{l}) = np_0 \vec{k}.\] Последнее равенство цепочки обусловлено правилом треугольника для сложения векторов.
В случае частичного отражения половина (\(R\)) всех фотонов имеет тот же конечный импульс \(\vec{p}_1\), и половина — конечный импульс \(\vec{p}_2 = p_0\vec{k}\). Сила светового давления тогда задается выражением \[\vec{F}_2 = p_0 \left(n\vec{j} - (1-R)\vec{l} - R\vec{k}\right) = np_0 \left(\vec{j} - \frac{\vec{j}}{2}\right) = \frac{np_0}{2}\vec{j}.\] Учитывая, что векторы \(\vec{j}, \vec{k}, \vec{l}\) единичные, для ответа на вопрос о модулях сил их можно отбросить из окончательных выражений и получить \[\frac{F_2}{F_1} = \frac{1}{2}.\]
Сила светового давления уменьшится в \(2\) раза.
| Верно найдены углы между падающим, преломленным и отраженным лучами | 5 баллов |
| Предыдущий пункт подкреплен хорошими геометрическими рассуждениями | 5 баллов |
| Продемонстрировано понимание того, что сила светового давления пропорциональна изменению импульса фотона | 3 балла |
| Продемонстрировано понимание того, что это изменение необходимо искать с помощью векторной разности; записаны или изображены процедуры вычитания верных векторов | 5 баллов |
| Получен правильный ответ | 8 баллов |
| Всего | 26 баллов |
В эксперименте был получен лазерный пучок, интенсивность (плотность потока мощности) \(I\) которого зависит от расстояния \(r\) до оси пучка по закону \[\left\{\begin{aligned} &I(r) = I_0 (r_0 - r)/r_0 &&\textrm{при } r < r_0,\\ &I(r) = 0 &&\textrm{при } r \geqslant r_0, \end{aligned}\right.\] где \(I_0, r_0\) — известные постоянные. От других координат интенсивность пучка не зависит.
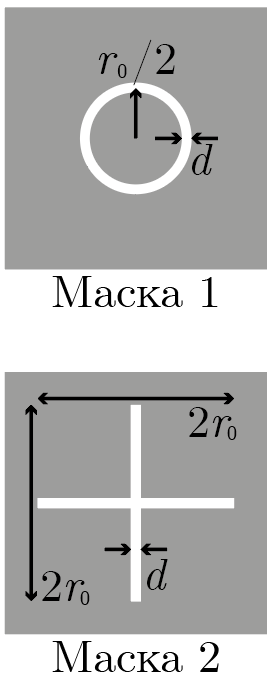
Лазерный пучок с этим профилем интенсивности падает нормально на непрозрачный экран, на котором вытравлены маски (участки, пропускающие излучение лазера) различной формы. Определите, во сколько раз отличаются мощности излучения, проходящего через две маски, изображенные на рис. 2.4, если их толщины \(d \ll r_0\), а дифракционными явлениями можно пренебречь.
Поскольку по условиям толщина масок существенно меньше радиуса пучка, для первой маски, имеющей вид кольца радиуса \(r_0/2\), можно считать, что интенсивность всего прошедшего через нее излучения одинакова и равна \[I_1 = I(r_0/2) = \frac{I_0}{2}.\] Тогда, чтобы найти общую прошедшую через нее мощность \(P_1\), достаточно умножить эту величину на площадь маски \(S_1\). Последняя опять-таки, в силу пренебрежимо малой толщины, может быть найдена как произведение длины маски на ее толщину: \[S_1 = \pi r_0 d \Rightarrow P_1 = \frac{\pi}{2} I_0 r_0 d.\]
Сложнее дело обстоит с крестообразной маской. Ее удобно представить как сумму четырех одинаковых отрезков, исходящих из центра пучка: область пересечения этих отрезков имеет пренебрежимо малую площадь \(\sim d^2\). В пределах каждого из этих лучей интенсивность снижается от оси пучка к краю линейно, поэтому общую мощность \(P_{20}\), прошедшую через каждый из лучей, необходимо искать как площадь под графиком \(I(r)\), дополнительно умноженную на ширину луча \(d\), как это изображено на рис. 2.5.
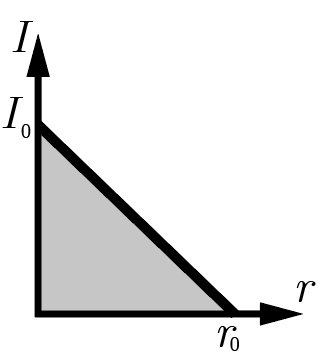
Таким образом, мощность \(P_{20}\) равна \[P_{20} = \frac{I_0r_0}{2}d,\] а мощность \(P_2\), прошедшая через всю маску, соответственно, в \(4\) раза больше: \[P_2 = 4P_{20} = 2I_0 r_0d.\]
Тогда окончательно \[\frac{P_2}{P_1} = \frac{4}{\pi}.\]
Другой допустимый способ рассуждения состоит в том, что на обеих этих масках средняя интенсивность излучения оказывается одинаковой, поэтому отношение полных мощностей фактически равно отношению площадей масок. Это решение тоже будет считаться верным, если его ключевое соображение убедительно обосновано.
Мощность излучения, прошедшего через вторую маску, больше в \(4/\pi \approx 1{,}27\) раза.
| Продемонстрировано понимание того, что интенсивность в пределах первой маски можно считать постоянной, а в пределах второй — нельзя | 5 баллов |
| Верно найдена интенсивность на уровне первой маски | 3 балла |
| Верно найдена (точно или в приближении \(d \ll r_0\)) площадь первой маски | 3 балла |
| Продемонстрировано понимание того, что на второй маске мощность можно вычислить через площадь под графиком, определенный интеграл или среднее значение | 6 баллов |
| Получен правильный ответ | 7 баллов |
| Всего | 24 балла |