Инженерный тур. 2 этап
Задачи второго отборочного этапа направлены на формирование у участников знаний и компетенций, необходимых для выполнения комплексной инженерной задачи заключительного этапа. Они разбиты на четыре блока:
- Излучение в оптоволоконной линии: набор задач этого блока знакомит участников с понятийным и вычислительным аппаратом, необходимым для описания лазерного импульса в оптоволоконной линии.
- Волоконный интерферометр: набор задач этого блока проверяет, насколько хорошо участники усвоили материал первого отборочного этапа, касающийся квантового состояния одиночного фотона в интерферометрической схеме, а также формирует представление о некоторых особенностях волоконного исполнения оптических схем.
- Распределение вероятностей: третий набор задач предлагает участникам освоить базовые понятия теории вероятностей, научиться применять математический аппарат к описанию дискретных и непрерывных физических величин.
- Тест на случайность: последний блок состоит из одной задачи, посвященной обработке данных и программированию. Участникам предстоит изучить различные виды тестов, позволяющих различать случайные и псевдослучайные последовательности, а также реализовать эти тесты в программном коде.
Командные задачи второго этапа инженерного тура открыты для решения. Соревнование доступно на платформе Яндекс.Контест: https://contest.yandex.ru/contest/69920/enter/.
Импульсный источник лазерного излучения подключен к оптоволоконной линии. Длина оптоволоконной линии — 5 км, ширина лазерного импульса по основанию — 2 нс. Определить, какую длину занимает импульс в волокне. Показатель преломления оптоволокна считать равным 1,47, скорость света в вакууме считать равной \(3 \cdot 10^8\) м/с. Ответ выразить в метрах и указать с точностью до сотых.
Длину импульса можно определить, умножив скорость распространения излучения в оптоволокне на ширину импульса (его длительность): \[l = \frac{c}{n} \cdot t = \frac{3 \cdot 10^8}{1{,}47} \cdot 2 \cdot 10^{-9} = 0{,}408 = 0{,}41 ~ \text{м}.\]
\(0{,}41\) м.
Импульсный источник лазерного излучения подключен к оптоволоконной линии. Длина оптоволоконной линии — 5 км, ширина лазерного импульса по основанию — 2 нс. Определить, какое количество импульсов поместится в волокне, если частота генерации импульсов 500 МГц. Показатель преломления оптоволокна считать равным 1,47, скорость света в вакууме считать равной \(3 \cdot 10^8\) м/с.
По заданной частоте генерации импульсов можно определить промежуток времени между двумя импульсами: \[t = \frac{1}{500 \cdot 10^6} = 2 \cdot 10^{-9} \, \text{с},\] то есть импульсы следуют сразу друг за другом. Тогда общее число импульсов можно определить простым делением: \[N = \frac{L}{l} = \frac{5000}{0{,}41} = 12195.\]
12195.
Импульсный источник лазерного излучения подключен к оптоволоконной линии. Длина оптоволоконной линии — 5 км, ширина лазерного импульса по основанию — 2 нс. Определить, какое количество импульсов поместится в волокне, если рабочий цикл равен 0,3. Показатель преломления оптоволокна считать равным 1,47.
Рабочий цикл: \[D = \frac{t}{T},\] где \(t\) — ширина импульса по основанию, \(T\) — период. Тогда количество импульсов, которые поместятся в оптическое волокно: \[N = \frac{L \cdot n \cdot D}{c \cdot t},\] где \(L\) — длина волоконной линии 5000 м, \(n\) — показатель преломления 1,47, \(c\) — скорость света \(3\cdot10^8\) м/с. \[N = \frac{5000 \cdot 1{,}47 \cdot 0{,}3}{3 \cdot 10^8 \cdot 2 \cdot 10^{-9}} = 3675.\]
3675.
На вход в волоконный интерферометр подается фотон в состоянии \(N(2 \ket{H} - \ket{V})\). Определить \(N\). Ответ привести с точностью до четвертого знака после запятой.
Коэффициент нормировки должен подбираться таким образом, чтобы сумма квадратов модулей коэффициентов при \(\ket{H}\) и \(\ket{V}\) была равна 1. Отсюда получаем уравнение: \[|N|^2 (4 + 1) = 1 \Rightarrow N = \frac{1}{\sqrt{5}} = 0{,}4472.\]
0,4472.
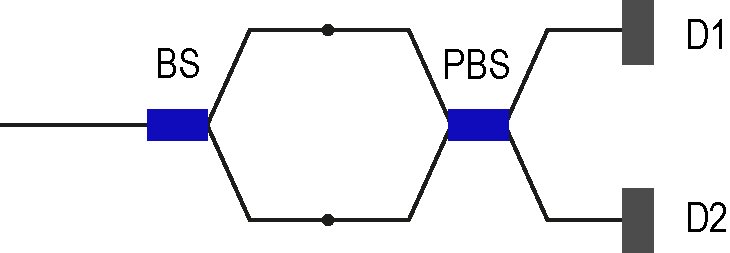
На вход в волоконный интерферометр подается фотон в состоянии \(N(2 \ket{H} - \ket{V}\) (\(N\) — из задания 1.4). BS — волоконный делитель 50/50, PBS — поляризационный делитель, организованный как призма с четырьмя коллиматорами. С какой вероятностью сработает детектор \(D1\)? Ответ привести с точностью до одного знака после запятой.
При прохождении фотона через волоконный делитель 50/50 происходит простое разделение вероятности прохождения по верхнему и нижнему плечу интерферометра, без скачка фазы. При подключении оптоволокна к PBS, реализованному указанным образом, для каждого из плеч интерферометра происходит разделение состояния фотона на вертикальное (со скачком фазы на \(\pi\)) и горизонтальное.
Таким образом, на детектор \(D1\) придет состояние: \[\begin{aligned} \ket{\psi} \rightarrow \frac{\ket{\psi}}{\sqrt{2}} (\text{верхний}) + \frac{\ket{\psi}}{\sqrt{2}} (\text{нижний}) \rightarrow\\ {}\rightarrow \frac{\ket{V}}{\sqrt{10}} (\text{с верхнего плеча}) + \frac{2\ket{H}}{\sqrt{10}} (\text{с нижнего плеча}). \end{aligned}\]
Отсюда получаем полную вероятность срабатывания детектора \(D1\) как: \[\left(\frac{1}{\sqrt{10}}\right)^2 + \left(\frac{2}{\sqrt{10}}\right)^2 = \frac{1}{10} + \frac{4}{10} = \frac{5}{10} = 0{,}5.\]
0,5.
На вход в волоконный интерферометр подается фотон в состоянии \(N(2 \ket{H} - \ket{V})\) (\(N\) — из задания 1.4). BS — волоконный делитель 50/50, PBS — поляризационный делитель, организованный как призма с четырьмя коллиматорами. С какой вероятностью на детектор \(D2\) придет фотон с вертикальной поляризацией? Ответ привести с точностью до одного знака после запятой.
При прохождении фотона через волоконный делитель 50/50 происходит простое разделение вероятности прохождения по верхнему и нижнему плечу интерферометра, без скачка фазы. При подключении оптоволокна к PBS, реализованному указанным образом, для каждого из плеч интерферометра происходит разделение состояния фотона на вертикальное (со скачком фазы на \(\pi\)) и горизонтальное.
Таким образом, на детектор \(D2\) придет состояние: \[\begin{aligned} \ket{\psi} \rightarrow \frac{\ket{\psi}}{\sqrt{2}} (\text{верхний}) + \frac{\ket{\psi}}{\sqrt{2}} (\text{нижний}) \rightarrow\\ {}\rightarrow -\frac{\ket{V}}{\sqrt{10}} (\text{с нижнего плеча}) + \frac{2\ket{H}}{\sqrt{10}} (\text{с верхнего плеча}). \end{aligned}\]
Отсюда получаем вероятность прихода фотона с вертикальной поляризацией на детектор \(D2\) как: \[\left(\frac{1}{\sqrt{10}}\right)^2 = \frac{1}{10} = 0{,}1\]
0,1.
Аттенюатор в лазерной системе настроен таким образом, что в одном лазерном импульсе содержится в среднем один фотон. Определить, в скольких импульсах из 100 будет содержаться ровно один фотон.
Случайные дискретные события описываются распределением Пуассона: \[P(n_p, \mu) = \frac{\mu^{n_p}}{n_p!} \cdot \exp(-\mu),\] где \(\exp(a)=e^a\).
Число однофотонных импульсов можно определить, зная вероятность \(P\) генерации импульса с \(n_p = 1\) фотоном при среднем числе фотонов в импульсе \(\mu = 1\): \[P = \frac{1^1}{1!} \cdot \exp(-1) = 0{,}37.\]
Значит, из 100 импульсов 37 будут однофотонными.
37.
Генератор случайных чисел выбирает целые числа на отрезке \([1, 10]\). Распределение вероятности генератора — равномерное. Какова вероятность того, что при запуске генератора выпадет число 4? Ответ дать с точностью до десятых.
При заданных условиях работы генератора возможно 10 равновероятных исходов его запуска. Поэтому для любого числа из заданного отрезка вероятность его выпадения будет равна: \[P = \frac{1}{10} = 0{,}1.\]
0,1.
Генератор случайных чисел выдает действительные числа на отрезке \([1, 10]\). Распределение вероятности генератора — равномерное. Какова вероятность того, что при запуске генератора выпадет число 4? Ответ дать с точностью до десятых.
При заданных условиях работы генератора возможно бесконечное число равновероятных исходов его запуска. Поэтому для любого конкретного числа из заданного отрезка вероятность его выпадения будет равна 0.
0,0.
Генератор случайных чисел выбирает действительные числа, сэмплируя распределение Гаусса со средним значением \(\mu = 0{,}5\) и дисперсией \(\sigma^2 = 4\). Определить, с какой вероятностью сгенерированное устройством число попадет в промежуток от \(3\sigma\) до \(3{,}5\sigma\)? Ответ привести с точностью до четырех знаков после запятой.
Распределение Гаусса задается выражением: \[p(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2 \sigma^2}\right),\] где \(\exp(a)=e^a\).
Вероятность сгенерировать число в заданном промежутке определяется выражением: \[P = \int_{3 \cdot 2}^{3{,}5 \cdot 2} \frac{1}{\sqrt{2 \pi \cdot 2^2}} \exp\left(-\frac{(x - 0{,}5)^2}{2 \cdot 2^2}\right) dx = 0{,}0024.\]
0,0024.
30 баллов — за 2 теста, 20 баллов — за 1 тест.
Даны 10 битовых последовательностей (строки из 0 и 1). Одна из них создана генератором истинных случайных чисел (TRNG) и имеет равномерное распределение битов, а остальные выбраны генераторами псевдослучайных чисел (PRNG) и имеют квазипериодическую структуру: https://disk.yandex.ru/d/zLMimECE7Li4MQ.
Задача — написать программу, которая определяет последовательность, выданную истинным генератором случайных чисел, без построения графиков. Необходимо использовать статистические методы для анализа последовательностей и определить, какая из них ближе всего к равномерному распределению.
Программа должна возвращать одно единственное число — номер последовательности, созданной генератором истинных случайных чисел.
Указание: для определения истинно случайной последовательности рекомендуется использовать не менее двух различных способов (тестов), так как оценка только по одному признаку может привести к неверному выводу.
Есть три простых варианта решения и еще множество сложных:
- прогонный тест,
- расчет параметра \(\chi^2\),
- расчет автокорреляционной функции — для равномерного распределения она будет иметь наименьшее значение.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chisquare
def read_binary_sequence(file_path):
with open(file_path, 'r') as file:
sequence = [int(bit) for bit in file.read().strip() if bit in '01']
return sequence
def runs_test(sequence):
"""Perform the Runs Test on a binary sequence."""
n = len(sequence)
if n == 0:
return 0, 0, 0
# Count the number of runs
runs = 1
for i in range(1, n):
if sequence[i] != sequence[i - 1]:
runs += 1
# Calculate proportions of 0s and 1s
p1 = np.sum(sequence) / n # Proportion of 1s
p0 = 1 - p1 # Proportion of 0s
# Calculate expected number of runs
expected_runs = (2 * p1 * p0 * n) / (p1 + p0) + 1
# Calculate variance of runs
variance_runs = (2 * p1 * p0 * (2 * p1 * p0 - n)) / (n**2 * (p1 + p0 - 1))
# Calculate Z-score
z = (runs - expected_runs) / np.sqrt(variance_runs) if variance_runs > 0 else 0
return runs, expected_runs, z
def chi_squared_test(sequence):
""" Chi-Squared test"""
observed = [np.sum(sequence), len(sequence) - np.sum(sequence)]
expected = [len(sequence) / 2, len(sequence) / 2]
chi2_stat, p_value = chisquare(observed, expected)
return chi2_stat, p_value
def autocorrelation_test(sequence, lag=1):
"""Autocorrelation"""
n = len(sequence)
if n <= lag:
return 0
mean = np.mean(sequence)
c0 = np.sum((sequence - mean) ** 2) / n
c1 = np.sum((sequence[:-lag] - mean) * (sequence[lag:] - mean)) / (n - lag)
return c1 / c0
file_paths = [
'pattern_sequence_1.txt',
'pattern_sequence_2.txt',
'pattern_sequence_3.txt',
'pattern_sequence_4.txt',
'pattern_sequence_5.txt',
'pattern_sequence_6.txt',
'pattern_sequence_7.txt',
'pattern_sequence_8.txt',
'lfsr_sequence_1.txt',
'true_random.txt'
]
results = []
for file_path in file_paths:
sequence = read_binary_sequence(file_path)
runs, expected_runs, z = runs_test(sequence)
chi2_stat, p_value = chi_squared_test(sequence)
autocorr = autocorrelation_test(sequence)
results.append({
'file_path': file_path,
'runs': runs,
'expected_runs': expected_runs,
'z': z,
'chi2_stat': chi2_stat,
'p_value': p_value,
'autocorr': autocorr
})
most_random_sequence = None
best_score = -np.inf
for result in results:
score = 0
score += 1 - abs(result['z'])
if result['p_value'] > 0.05:
score += 1
score += 1 - abs(result['autocorr'])
if score > best_score:
best_score = score
most_random_sequence = result['file_path']
for result in results:
print(f"Results for {result['file_path']}:")
print(f" Runs = {result['runs']}, Expected Runs = {result['expected_runs']:.2f}, Z-score = {result['z']:.2f}")
print(f" Chi2 Stat = {result['chi2_stat']:.2f}, p-value = {result['p_value']:.4f}")
print(f" Autocorrelation (lag=1) = {result['autocorr']:.4f}\n")
print(f"The most random sequence based on the criteria is: {most_random_sequence}")
Другие способы по желанию, но не обязательно.
Генератор Python проходит все три статистических теста, которые предлагаются здесь для решения, другие две последовательности — нет.
Таким образом, получаем упрощенную модель реального тестирования на случайность QRNG (квантовый генератор случайных чисел), где генератор Python выступает в качестве QRNG, а остальные варианты — как PRNG.
6.