Инженерный тур. 1 этап
Пусть состояние квантовой лампочки полностью описывается вектором состояния: \[\ket{\Psi} = -\frac{2}{\sqrt{5}} \ket{\text{on}} + \frac{1}{\sqrt{5}}\ket{\text{off}}.\]
Выбрать все верные утверждения:
- вероятность при измерении обнаружить лампочку включенной равна \(4/5\);
- возможны и другие, кроме
onиoff, результаты измерения состояния лампочки в этом базисе; - замена знака перед коэффициентом при \(\ket{\text{off}}\) не приведет к наблюдаемым последствиям при определении вероятности исходов
onиoff.
- Вероятность получить результат измерения «лампочка включена» определяется квадратом модуля коэффициента при состоянии \(\ket{\text{on}}\).
- В условии сказано, что состояние лампочки полностью описывается приведенным выражением, значит, здесь уже учтены все возможные результаты измерений и других быть не может.
- Поскольку вероятность сходов измерений определяется квадратом модуля соответствующих коэффициентов, знак в данном случае не играет роли.
A, C.
В ходе предварительных экспериментов физики обнаружили новую характеристику квантовой частицы, которая принимает строго одно из значений -1, 0, 1. Причем значение -1 получалось в 600 случаях из 1000, значение 0 — в 250 случаях из 1000, а 1 — в 150 случаях из 1000. Каким вектором состояния можно описать такую квантовую систему, если опираться только на эти данные?
- \(\ket{\Psi} = \sqrt{\frac{3}{5}} \ket{-1} + \frac{1}{2} \ket{0} + \sqrt{\frac{3}{20}} \ket{1}\).
- \(\ket{\Psi} = \frac{3}{5} \ket{-1} + \frac{1}{4} \ket{0} + \frac{3}{20} \ket{1}\).
- \(\ket{\Psi} = - \frac{3}{5} \ket{-1} - \frac{1}{4} \ket{0} + \frac{3}{20} \ket{1}\).
- \(\ket{\Psi} = - \sqrt{\frac{3}{5}} \ket{-1} - \frac{1}{2} \ket{0} - \sqrt{\frac{3}{20}} \ket{1}\).
- \(\ket{\Psi} = \sqrt{\frac{3}{5}} \ket{-1} - \frac{1}{2} \ket{0} + \sqrt{\frac{3}{20}} \ket{1}\).
- \(\ket{\Psi} = - \frac{3}{5} \ket{-1} + \frac{3}{20} \ket{1}\).
- \(\ket{\Psi} = \sqrt{\frac{3}{5}} \ket{-1} + \sqrt{\frac{3}{20}} \ket{1}\).
На основании предварительных экспериментов, приведенных в условии, можно сделать вывод о том, что вероятность получения -1 равна: \[\dfrac{600}{1000} = \dfrac{3}{5};\] вероятность получения 0 равна: \[\dfrac{250}{1000} = \dfrac{1}{4};\] вероятность получения 1 равна: \[\dfrac{150}{1000}=\dfrac{3}{20}.\]
Поскольку исследуемая характеристика квантовой частицы может принимать только эти значения, можно утверждать, что ее квантовое состояние описывается вектором с тремя компонентами, соответствующими {\(\ket{-1}\), \(\ket{0}\), \(\ket{1}\)}. Причем квадрат модуля этих компонент должен давать значение вероятности конкретного результата измерения. Этим требованиям отвечают варианты A, D, E.
A, D, E.
Нормировать вектор состояния: \[\ket{\Psi} = \sqrt{\frac{1}{10}} \ket{a = 1} + \frac{2}{3} \ket{a = 2} - \frac{1}{2} \ket{a = 3}+ \frac{13}{40} \ket{a = 4} - \frac{9}{11} \ket{a = 5}.\] В ответе указать нормировочный коэффициент с точностью до четвертого знака после запятой.
Сумма вероятностей всех возможных результатов измерения должна равняться единице, а вероятность отдельного исхода определяется квадратом модуля соответствующего числового коэффициента. Для приведенного вектора состояния сумма квадратов модулей числовых коэффициентов равна: \[P =\left(\sqrt{\frac{1}{10}}\right)^2+ \left(\frac{2}{3} \right)^2+\left(- \frac{1}{2}\right)^2+ \left(\frac{13}{40}\right)^2 + \left(- \frac{9}{11}\right)^2 =1{,}56951\neq 1.\] Чтобы \(P\) стало равно единице, состояние \(\ket{\Psi}\) необходимо домножить на величину: \[\frac{1}{\sqrt{P}} = 0{,}7982.\] Эта величина и является нормировочным коэффициентом.
0,7982.
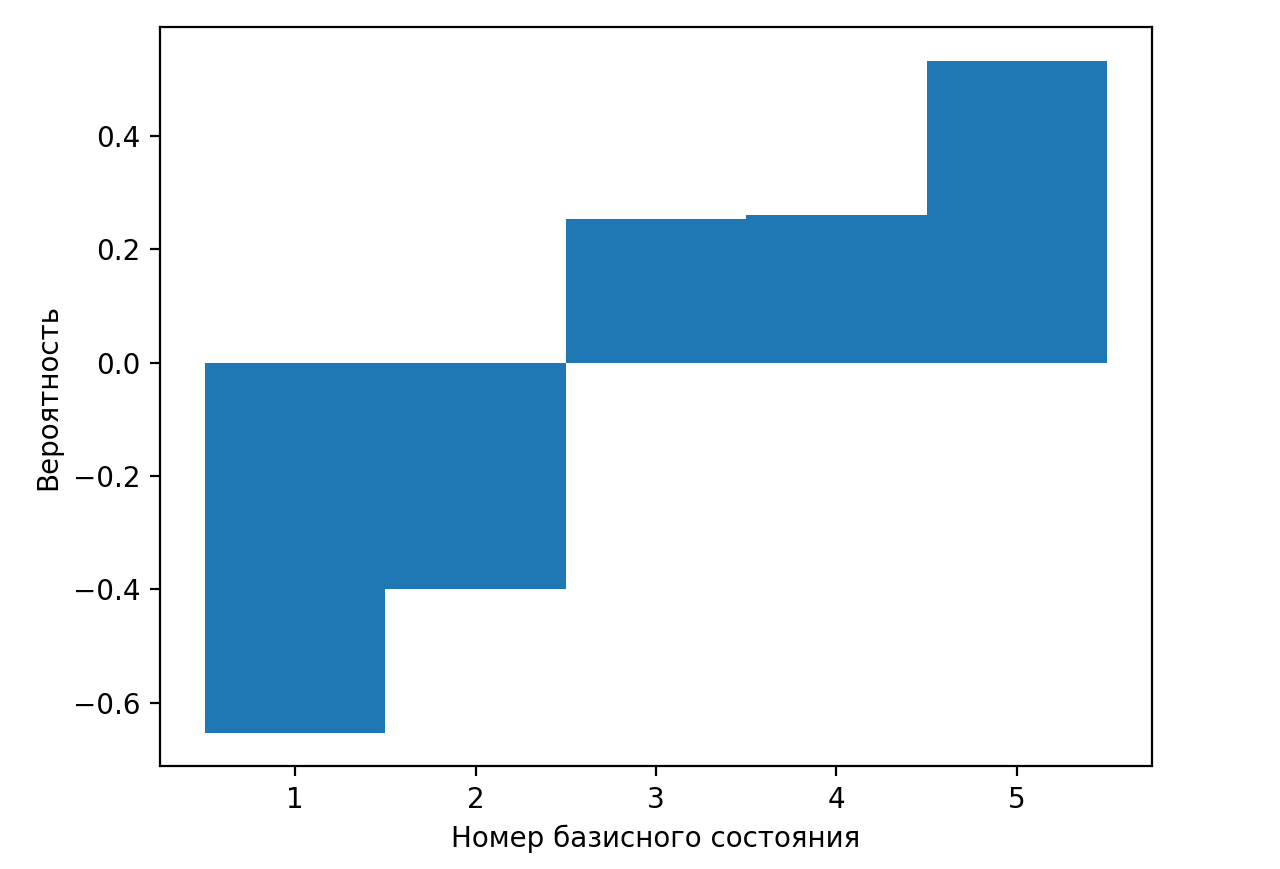
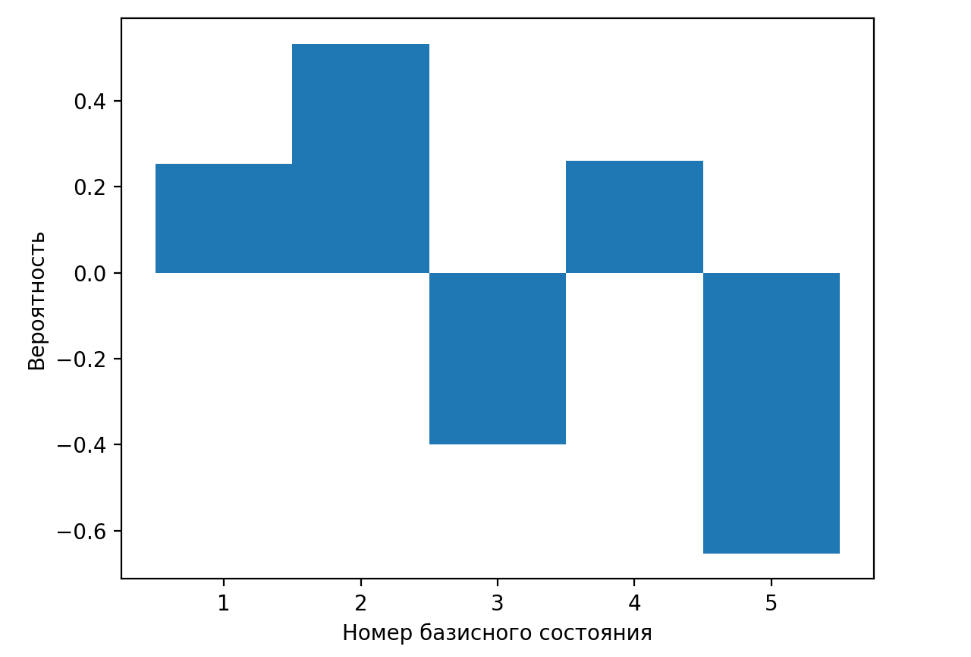
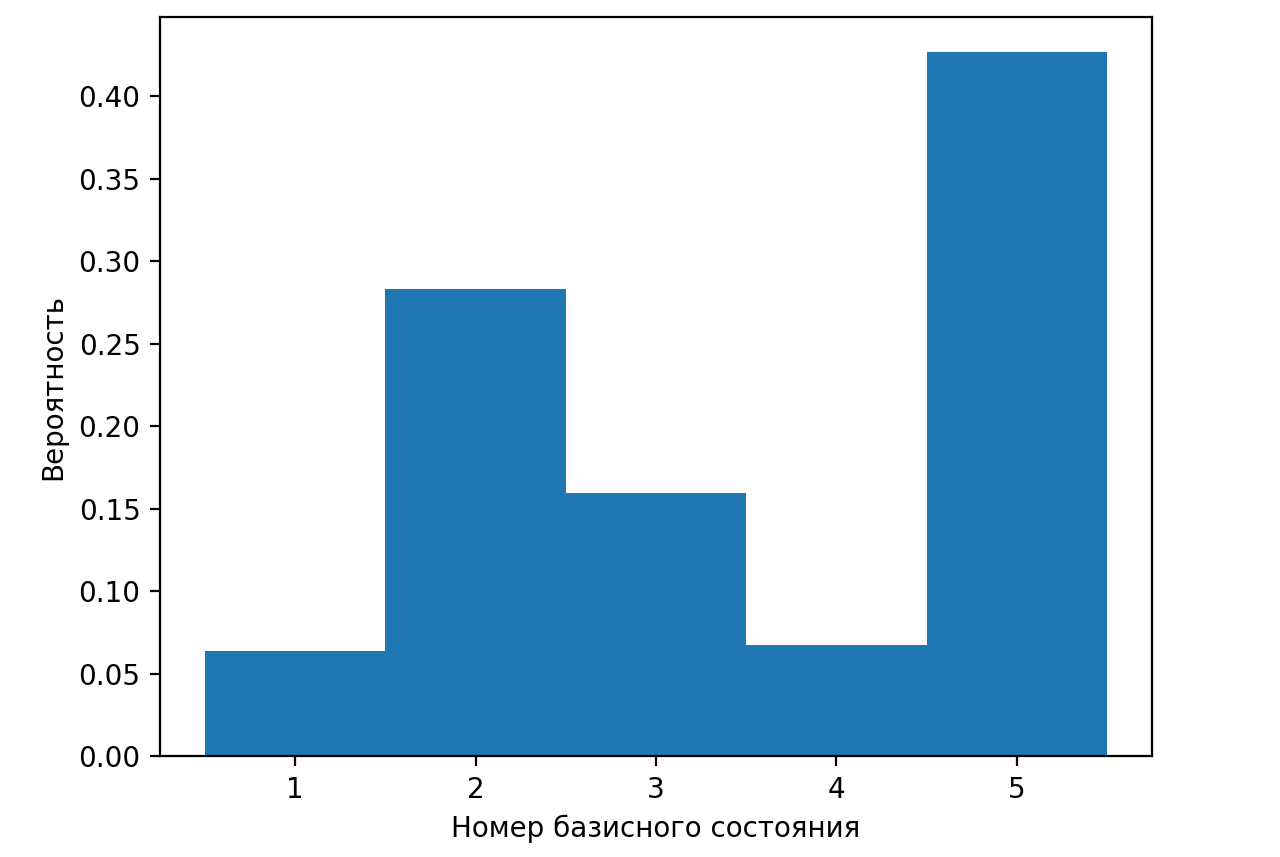
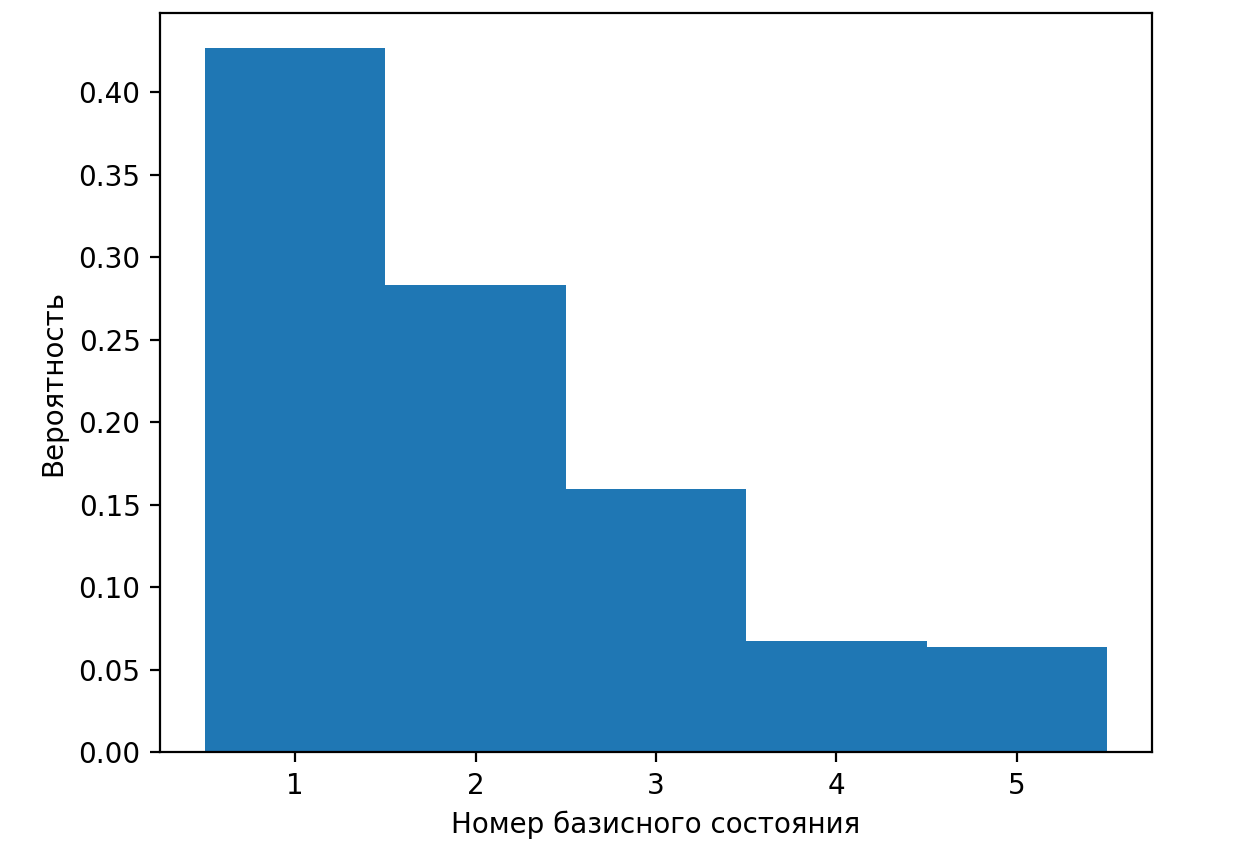
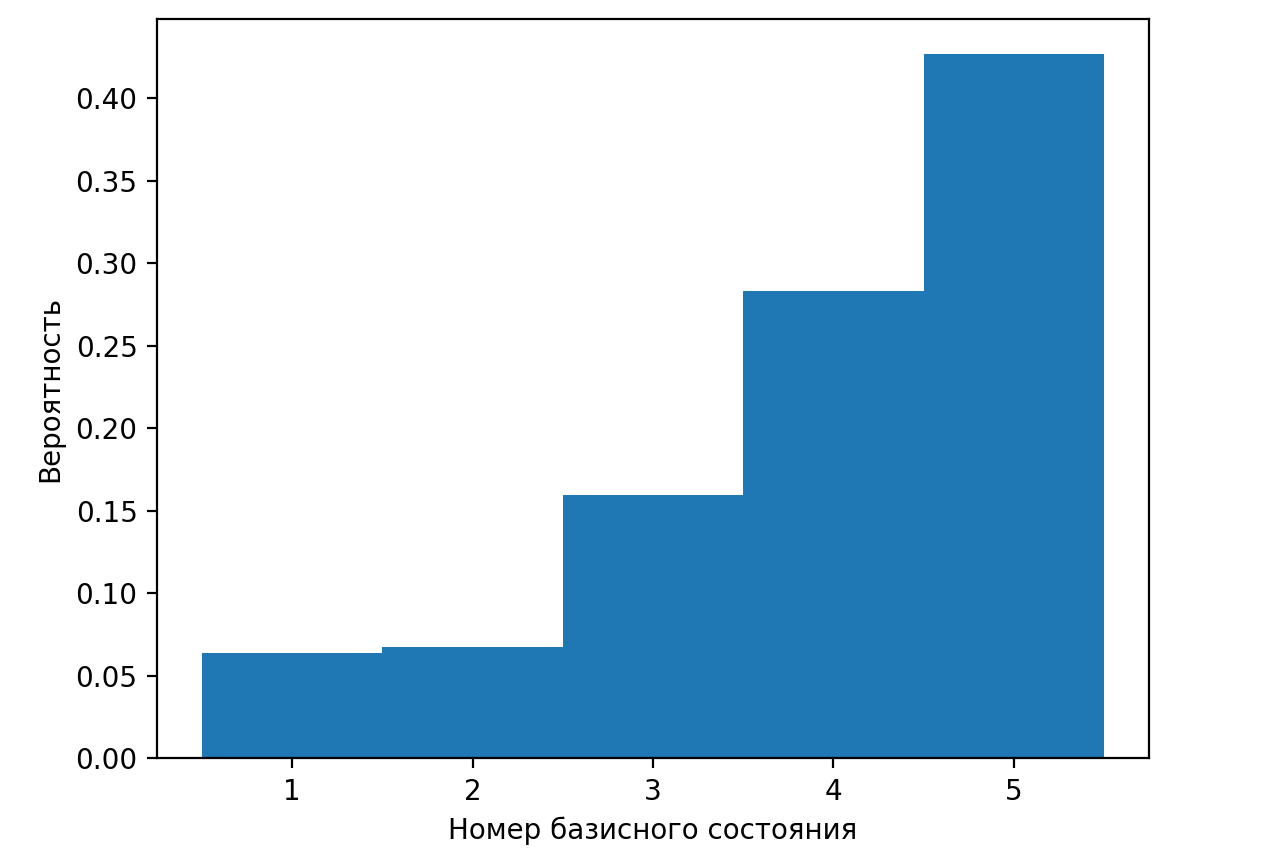
Выбрать гистограмму, верно описывающую вероятности получения различных результатов при измерении физической величины \(a\) в квантовом состоянии \(\ket{}\) из предыдущей задачи с учетом нормировки.
Вероятности получения различных результатов измерений можно представить в виде гистограммы, где положение столбца будет определять результат измерения, а высота — вероятность его получения. Этому правилу соответствует только картинка С.
C.
Пусть кошка Шредингера находится в квантовом состоянии \[\ket{\Psi} =\sqrt\frac{1}{5}\cdot (-2 \ket{\text{жива}} + \ket{\text{мертва}}).\]
Какова вероятность обнаружить кошку Шредингера в состоянии «призрак» при измерении ее в следующем базисе? \[\left\{ \begin{aligned} \ket{\text{зомби}} &=\sqrt\frac{1}{2} \ket{\text{жива}} + \sqrt\frac{1}{2}\ket{\text{мертва}},\\ \ket{\text{призрак}} &= \sqrt\frac{1}{2}\ket{\text{жива}} - \sqrt\frac{1}{2}\ket{\text{мертва}}. \end{aligned} \right.\]
Ответ записать в виде десятичной дроби.
Для определения вероятности обнаружить кошку в состоянии «призрак» необходимо переписать состояние \(\ket{\Psi}\) в базисе \(\{\ket{\text{зомби}}, \ket{\text{призрак}}\}\). Это можно сделать, выразив состояния \(\ket{\text{жива}}\) и \(\ket{\text{мертва}}\) через состояния \(\ket{\text{зомби}}\) и \(\ket{\text{призрак}}\) из приведенной в условии системы уравнений: \[\left\{ \begin{aligned} \ket{\text{жива}} &=\sqrt\frac{1}{2} \ket{\text{зомби}} +\sqrt\frac{1}{2} \ket{\text{призрак}},\\ \ket{\text{мертва}} &= \sqrt\frac{1}{2} \ket{\text{зомби}}-\sqrt\frac{1}{2} \ket{\text{призрак}}. \end{aligned} \right.\] Подставив это в выражение для \(\ket{\Psi}\), получим: \[\ket{\Psi} = - \sqrt\frac{1}{10} \ket{\text{зомби}} - \sqrt\frac{3}{10} \ket{\text{призрак}}.\] Отсюда следует, что вероятность обнаружения кошки Шредингера в состоянии «призрак» равна: \[p_{\text{призрак}} = \left(-\sqrt\frac{3}{10}\right)^2= 0{,}9.\]
0,9.
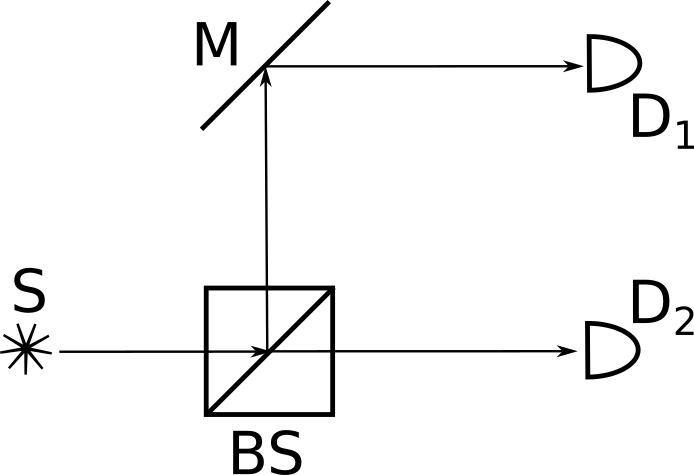
Источник S испустил одиночный фотон в квантовом состоянии: \[\ket{\Psi} =\sqrt\frac{1}{2} \ket{H} +\sqrt\frac{1}{2}\ket{V}.\] Чему равна вероятность срабатывания детектора \(D_1\)? Ответ привести в виде дроби.
Согласно оптической схеме (рис. 1.1), после испускания из источника фотон попадает на светоделитель \(BS\). При этом часть вектора состояния фотона проходит \(BS\) насквозь с коэффициентом \(\sqrt\frac{1}{2}\), она для данной задачи неинтересна. Другая часть — отражается и выходит из \(BS\) наверх, в результате чего приобретает коэффициент \(\left(-\sqrt\frac{1}{2}\right)\). Далее эта часть отражается от зеркала \(M\), приобретая дополнительный знак (\(-1\)). Таким образом, до детектора \(D_1\) доходит состояние фотона: \[\ket{\Psi_1}=\left(-\sqrt\frac{1}{2}\right)\cdot (-1)\cdot \left( \sqrt\frac{1}{2} \ket{H}+\sqrt\frac{1}{2} \ket{V}\right)=\sqrt\frac{1}{2} \cdot \left(\sqrt\frac{1}{2} \ket{H}+\sqrt\frac{1}{2} \ket{V}\right).\] Детектор сработает при попадании на него фотона с любой поляризацией, значит, необходимо найти полную вероятность прихода фотона на детектор \(D_1\): \[P_1 = \left(\sqrt\frac{1}{2} \cdot \sqrt\frac{1}{2}\right) ^2 + \left(\sqrt\frac{1}{2} \cdot \sqrt\frac{1}{2}\right)^2 = 0{,}5.\]
0,5.
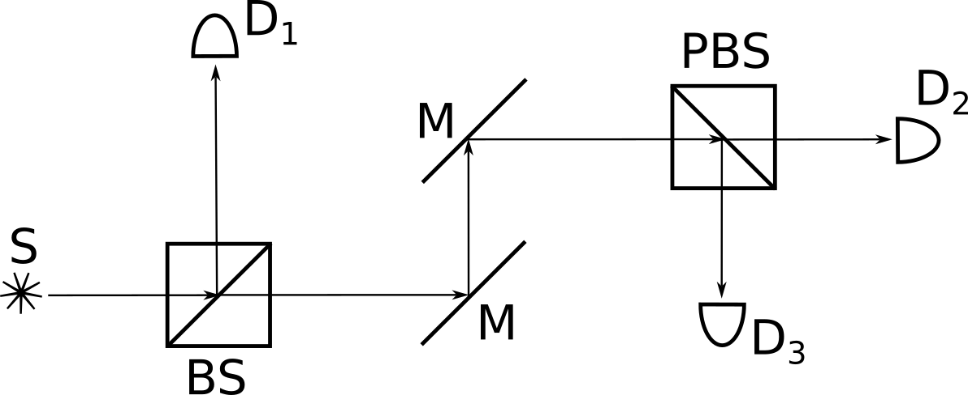
Источник S испустил одиночный фотон в квантовом состоянии: \[\ket{\Psi} =\sqrt\frac{1}{2} \ket{H} +\sqrt\frac{1}{2}\ket{V}.\] Определить числовой коэффициент при \(\ket{V}\) на входе в детектор \(D_2\) (рис. 1.2).
Проследим за изменениями квантового состояния фотона на пути от источника до детектора \(D_2\). При прохождении состояния \(\ket{\Psi}\) через первый светоделитель вызывает интерес та часть, которая пройдет горизонтально; она при этом приобретает коэффициент \(\sqrt\frac{1}{2}\). При каждом из двух отражений от зеркал M вектор состояния будет приобретать по (\(-1\)). Таким образом, до поляризационного светоделителя \(PBS\) дойдет состояние: \[\ket{\Psi'}=\sqrt\frac{1}{2} \cdot (-1) \cdot (-1) \ket{\Psi } = \frac{1}{2} \ket{H} - \frac{1}{2}\ket{V}.\] Поляризационный светоделитель отражает часть состояния с поляризацией \(V\) и пропускает часть с поляризацией \(H\). То есть до детектора \(D_2\) дойдет состояние: \[\ket{\Psi''} = \frac{1}{2} \ket{H}.\] Как видим, коэффициент при \(\ket{V}\) равен нулю.
0.
Источник S испустил одиночный фотон в квантовом состоянии: \[\ket{\Psi} =\sqrt\frac{1}{2} \ket{H} -\sqrt\frac{1}{2}\ket{V}.\] Определить числовой коэффициент при \(\ket{V}\) на входе в детектор \(D_3\) (рис. 1.3).
Проследим за изменениями квантового состояния фотона на пути от источника до детектора \(D_2\). При прохождении состояния \(\ket{\Psi}\) через первый светоделитель вызывает интерес та часть, которая пройдет горизонтально; она при этом приобретает коэффициент \(\sqrt\frac{1}{2}\). При каждом из двух отражений от зеркал \(M\) вектор состояния будет приобретать по (\(-1\)). Таким образом, до поляризационного светоделителя \(PBS\) дойдет состояние: \[\ket{\Psi'}=\sqrt\frac{1}{2} \cdot (-1) \cdot (-1) \ket{\Psi} = \frac{1}{2} \ket{H} - \frac{1}{2}\ket{V}.\] Поляризационный светоделитель отражает часть состояния с поляризацией \(V\) и пропускает часть с поляризацией \(H\). То есть до детектора \(D_3\) дойдет состояние: \[\ket{\Psi''} = \frac{1}{2} \ket{V}.\] Детектор срабатывает при попадании в него фотона с любой поляризацией, поэтому для нахождения следует возвести в квадрат модуль коэффициента при единственной оставшейся компоненте \(\ket{V}\), что даст \(1/4\).
0,25.