Предметный тур. Химия. 3 этап
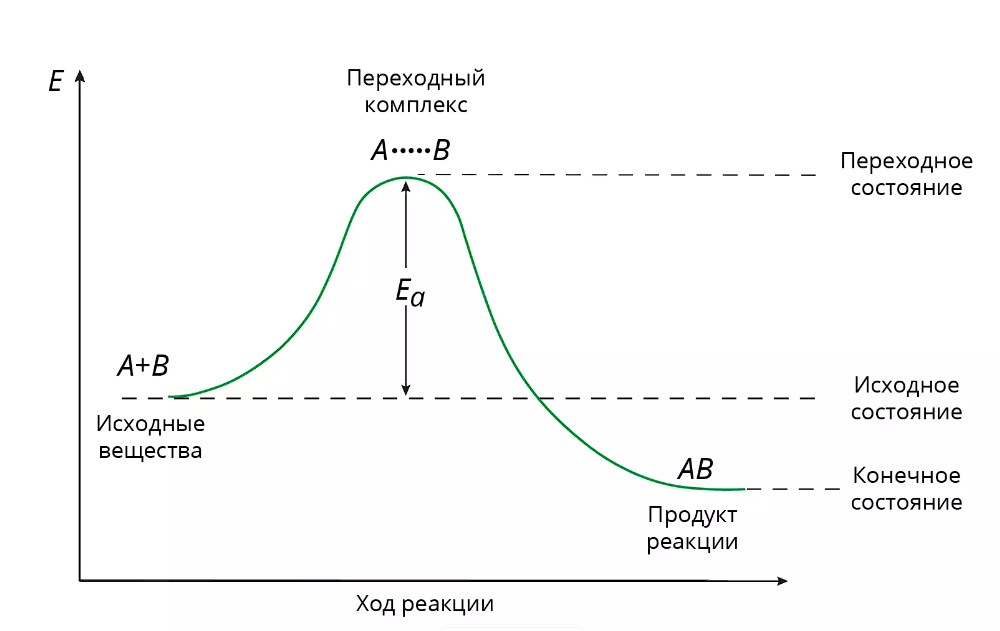
Энергия активации имеет несколько различных трактовок, однако общим остается представление о том, что в ходе элементарного акта химической реакции реагирующие частицы (молекулы, радикалы, ионы и т. д.) преодолевают энергетический барьер, высота которого является величиной энергии активации. Соотношение между энергией активации и температурой устанавливается уравнением Аррениуса: \[\ln\left(\frac{k_2}{k_1}\right) = \frac{E_a}{R} \left(\frac{1}{T_1} - \frac{1}{T_2}\right).\]
Химик-органик Влад пришел к своему другу химику-теоретику Дане и попросил помочь ему изучить кинетику одной реакции.
Энергия активации этой органической реакции равна 40 кДж/моль. Константа скорости этой реакции при температуре 40 °С равна \(2{,}5 \cdot 10^{-3}\) (моль/л)\(^{-1}\)мин\(^{-1}\). Какую температуру (в градусах Цельсия) химик Даня посоветовал выбрать для проведения реакции, чтобы скорость ее увеличилась в 200 раз? Считайте, что все остальные условия во всех опытах совпадают. Ответ укажите с округлением до целых.
Из уравнения Аррениуса выразим \(\Delta T\) и подставим значения \[\begin{gather} \ln(200) = \frac{40000}{8,314} \left( \frac{\Delta T}{313(313+\Delta T)}\right);\\ \Delta T = 164;\\ \Delta T = T_1 - T_2 = 164 = T_2 - 40;\\ T_2 = 204. \end{gather}\]
204 или 205.
Корректный ответ может быть 204 или 205. Разница в результатах обусловлена тем, какая точность для температуры 0 °С взята, а именно, 273 К или 273,15 К.
В результате разлива нефти в воду попало 250 м\(^3\) нефтепродуктов, которые стали быстро распространяться по поверхности.
- Рассчитайте площадь пятна нефти, если толщина слоя на старте аварии была 2 см. Ответ запишите в квадратных метрах и округлите до целых.
- Рассчитайте площадь пятна после размывания, если толщина пленки нефти составляет 100 молекул. Ответ запишите в квадратных километрах целым числом.
- Адсорбент способен поглощать или флоккулировать 15 г нефти на 1 г вещества. Сколько тонн адсорбента понадобится для удаления всей нефти? Введите целое число.
- Средняя формула разлитой нефти соответствует \(\ce{C10H22}\). Какова масса одной молекулы в пикограммах? Ответ округлите до десятых.
Считайте, что плотность нефти равна 0,9 г/мл, а молекулы можно представить, как шарики диаметром 2 нм (числа в степени следует вводить как \(5 \cdot 10^{-2}\)).
\[\begin{gather} S = V / h;\\ S = 250 / 0,02 = 12500;\\ h = 2 \cdot 100 \cdot 10^{-9} = 2 \cdot 10^{-7};\\ S = 250 / 2 \cdot 10^{-7} = 1,25 \cdot 10^9. \end{gather}\]
Переведем объем нефти в массу: 250 м\(^3\) = 250000000 мл. Тогда: \[250000000 \cdot 0{,}9 = 225 \text{ т}.\]
Масса адсорбента: \[\begin{gather} 225000000 / 15 = 15000000 \text{ г} = 15 \text{ т};\\ M(\ce{C10H22}) = 142;\\ m \text{~(одной~молекулы)}= 142 / 6,02 \cdot 10^{23} = 2,358 \cdot 10^{-22};\\ 1\text{ пг} = 10^{-12}\text{ г};\\ 2,358 \cdot 10^{-22} / 10^{-12} = 2,358 \cdot 10^{-10}. \end{gather}\] C учетом округления \(2{,}4 \cdot 10^{-10}\).
- 12500.
- 1250.
- 15.
- \(2{,}4 \cdot 10^{-10}\).
Если верно указаны три правильных ответа, задача оценивается в 10 баллов, если указано менее трех верных ответов, задача оценивается в 0 баллов. Если верно указаны все ответы, задача оценивается в 20 баллов.
В лаборатории исследовали аналог соединения А, используемого в аналитической химии для детектирования ионов железа (II). В результате молекулярного моделирования было выяснено, что ион Х представляет собой тетрагональную бипирамиду, состоящую из атома железа (3+) в центре, двух групп \(\ce{CN}\)(\(^{-}\)), двух анионов фтора и двух анионов хлора.
- Рассчитайте заряд иона Х.
- Какая молярная масса аниона будет у иона Y, полученного по реакции моля Х с двумя молями фторида натрия? Ответ округлите до целых.
- При замене всех лигандов железа на фтор образуется симметричная фигура. Как она называется?
Ион X представляет собой комплекс с ЦА \(\ce{Fe^{3+}}\) и лигандами \(\ce{2CN-}\), \(\ce{2F-}\), \(\ce{2Cl-}\).
Чтобы найти полный заряд комплекса, складываем заряды центрального атома и всех лигандов: \[+3 + (-2) + (-2) + (-2) = -3.\]
По условию в результате реакции комплекс X (с двумя \(\ce{Cl-}\)) взаимодействует с \(\ce{2NaF}\), при этом два \(\ce{Cl-}\) будут заменены на \(\ce{2F-}\). Получится комплекс вида: \(\ce{[Fe^{3+}(CN)2(F)4]^{3-}}\).
Рассчитаем массу: \(55{,}85 + 4 \cdot 19 + 2 \cdot 26 = 183{,}85\). С учетом округления — 184.
- Если в исходном или аналогичном комплексе \(\ce{Fe}\) окружен шестью идентичными лигандами (все \(\ce{F-}\)), то координационное число равно 6. Наиболее симметричная и распространенная структура для шести одинаковых лигандов вокруг центрального атома — это октаэдр (октаэдрическая геометрия).
- \(-3\) или \(3-\).
- 184.
- Октаэдр.
Если верно указаны два правильных ответа, задача оценивается в 5 баллов, если указано менее двух верных ответов, задача оценивается в 0 баллов. Если верно указаны все ответы, задача оценивается в 20 баллов.
Ответ к заданию 1 может быть указан \(-3\) или \(3-\).
В старом подвале городской гимназии, среди пыльных колб и рукописей дореволюционных времен, обнаружили емкость с неизвестным металлом X. Юные химики решили разгадать тайну этого металла и провели в лаборатории несколько опытов, чтобы установить его природу и выяснить, какие соединения можно из него получить.
Исследователи взяли 6,50 г неизвестного металла и поместили его в избыток соляной кислоты, началось энергичное выделение водорода. При нормальных условиях объем выделившегося водорода составил 2,24 л. Тот же металл нагрели в токе хлора, после остывания твердого продукта определили, что массовая доля хлора в этом соединении составляет 52,2%. Полученный хлорид растворили в воде и аккуратно добавляли к раствору гидроксид натрия. Сначала появился белый студенистый осадок, который, однако, растворялся при дальнейшем прибавлении избытка щелочи.
- Введите символ элемента.
- Определите точный состав хлорида металла X. Введите формулу. Ответ укажите на листочке.
- Напишите сумму коэффициентов в уравнении реакции металла X с газообразным хлором.
- Введите формулу иона, объясняющего растворение осадка в избытке щелочи. Укажите формулу и заряд иона на листочке.
- Из условия: \[\begin{gather} n(\ce{H2}) = 2,24 / 22,4 = 0,1;\\ n(X) = n(\ce{H2});\\ M_r(X) = m / n = 6,5 / 0,1 = 65 = \ce{Zn}. \end{gather}\]
- Цинк при обработке хлором дает только один возможный продукт \(\ce{Zn + Cl2 -> ZnCl2}\).
- \(\ce{Zn + Cl2 -> ZnCl2}\). Сумма коэффициентов равна 3.
При растворении цинка в щелочи происходит процесс: \[\ce{Zn + 2NaOH + 2H2O -> Na2[Zn(OH)4] + H2}.\]
Ион (то есть заряженная частица, ответственная за растворение) — \(\ce{[Zn(OH)4]}\) с зарядом \(2-\).
- \(\ce{Zn}\).
- \(\ce{ZnCl2}\).
- 3.
- \(\ce{[Zn(OH)4]^{2-}}\).
Если верно указаны три правильных ответа, задача оценивается в 10 баллов, если указано менее трех верных ответов, задача оценивается в 0 баллов. Если верно указаны все ответы, задача оценивается в 20 баллов.
В лаборатории при 20 °С в колбе под тягой стоял сосуд с серной кислотой. На этикетке стерлась надпись, в связи с этим лаборант взял пикнометр объемом 10 мл и взвесил на аналитических весах, поддерживающих постоянную температуру. Вес пикнометра составил 12,0567 г, а вес пикнометра с раствором серной кислоты был равен 23,0777 г. Пикнометр — стеклянный сосуд определенной вместимости, предназначенный для измерения плотности веществ в газообразном, жидком и твердом состояниях, так как позволяет отмерять определенный объем вещества.
- Какова массовая доля серной кислоты, если в справочнике при 20 °С плотность 14%-го раствора \(\ce{H2SO4}\) равна 1,0947 г/мл, а 16%-го раствора \(\ce{H2SO4}\) — 1,1094 г/мл. Ответ округлите до сотых. Каким еще способом можно определить концентрацию серной кислоты?
- Какова молярная и нормальная концентрация полученного раствора? Найдите моляльность и мольную долю полученного раствора серной кислоты. Ответ и расчеты округлите до тысячных долей и запишите на листочке.
- При какой температуре (в градусах Цельсия) замерзнет данный раствор, если криоскопическая константа воды равна 1,86, а изотонический коэффициент примите за 2. О чем говорит это значение изотонического коэффициента? Ответ запишите в градусах Цельсия, округлив до тысячных.
Пикнометр — стеклянный сосуд определенной вместимости, позволяющий отмерять заданный объем вещества. Он предназначен для измерения плотности веществ в газообразном, жидком и твердом состояниях. С помощью этого прибора найдем плотность раствора, а по плотности раствора — массовую долю кислоты. Кроме метода с использованием пикнометра концентрацию можно определить кислотно-основным титрованием. Существует и третий способ — с помощью ареометров найти плотность раствора, а затем — все параметры кислоты.
- Масса серной кислоты: \[\begin{split}m(\ce{H2SO4}) = m(\text{сосуда с кислотой}) - m(\text{пикнометра}) =\\= 23{,}0777 - 12{,}0567 = 11{,}021 \text{ г}.\end{split}\]
- Плотность раствора серной кислоты будет равна массе серной кислоты, деленной на объем пикнометра: \(11{,}021 / 10 = 1{,}1021\) г/мл.
По условию 14%-я серная кислота имеет плотность 1,0947 г/мл, а 16%-я — 1,1094 г/мл. Искомое значение как раз посередине, значит, можно их использовать. Для определения массовой доли раствора применим уравнение прямой, где за \(y\) обозначим плотность раствора, а за \(x\) — массовую долю.
Для этого можем использовать формулу \(y = kx + b\), создать на его основе систему уравнений, найти \(k\) и \(b\), а затем найти \(y\) по уравнению, приняв \(x = 1{,}021\) г/мл.
Воспользуемся общим уравнением для прямой: \[\begin{gather} \frac{x - x_1}{x_2 - x_1} = \frac{y - y_1}{y_2 - y_1};\\ \frac{1,1021 - 1,0947}{1,1094 - 1,0947} = \frac{y - 0,14}{0,16 - 0,14};\\ \frac{0,0074}{0,0147} = 50(y - 0,14) = 50y - 7;\\ 0,5034 = 50y - 7;\\ y = 0,1501. \end{gather}\] Округлив до сотых получаем, \(y = 0{,}150\) или \(y = 15{,}00\%\).
В пункте 1 найдено, что массовая доля серной кислоты в растворе равна 15%.
Найдем тогда молярную концентрацию полученного раствора: \[C_M (\ce{H2SO4}) = n(\ce{H2SO4}) / V(\ce{H2SO4}).\]
По условию задачи объем серной кислоты равен 10 мл. Переведем его в литры: \(V = 0{,}010\) л.
- Чтобы найти химическое количество серной кислоты, найдем массу серной кислоты в растворе (масса раствора дана в задаче): \[m (\ce{H2SO4}) = W (\ce{H2SO4})_{\text{р-ра}} \cdot m (\ce{H2SO4})_{\text{р-ра}} = 0{,}15 \cdot 11{,}021 = 1{,}654 \text{ г}.\]
- Тогда химическое количество серной кислоты будет равно: \[n(\ce{H2SO4}) = m(\ce{H2SO4}) / M(\ce{H2SO4}) = 1{,}654 / 98 = 0{,}017 \text{ моль}.\]
- На основании перечисленного выше введем общую формулу и рассчитаем концентрацию: \[\begin{split}C_M (\ce{H2SO4}) = \frac{W (\ce{H2SO4})_{\text{р-ра}} \cdot m (\ce{H2SO4})_{\text{р-ра}}}{V(\ce{H2SO4}) \cdot M (\ce{H2SO4})_{\text{р-ра}}} =\\= 0{,}017/0{,}010 = 1{,}700 \text{ моль/л}.\end{split}\]
Нормальная концентрация раствора серной кислоты может быть рассчитана из формулы: \[C_H = z \cdot C_M,\] где \(z\) — число эквивалентности, равная в случае кислот числу \(\ce{H+}\), которые образуются при диссоциации кислоты. \[C_H = z \cdot C_M = 2 \cdot 1{,}7 = 3{,}400 \text{ моль/л}.\]
Либо по общей формуле: \[\begin{split}C_H (\ce{H2SO4}) = \frac{W (\ce{H2SO4})_{\text{р-ра}} \cdot m (\ce{H2SO4})_{\text{р-ра}}}{V(\ce{H2SO4}) \cdot M_{\text{экв}} (\ce{H2SO4})_{\text{р-ра}}} =\\= \frac{0{,}150 \cdot 11{,}021}{0{,}010 \cdot 49} = 3{,}374 \text{ моль/л},\end{split}\] где \(M_{\text{экв}} = M / z = 98 / 2 = 49\) моль экв/л.
Мольная доля серной кислоты в растворе считается по формуле: \[\chi (\ce{H2SO4}) = \frac{n(\ce{H2SO4})} {n(\ce{H2SO4}) + n(\ce{H2O})},\] где \(n(\ce{H2SO4})\) и \(n(\ce{H2O})\) — химические количества серной кислоты и воды.
Найдем химическое количество воды: \[n(\ce{H2O}) = \frac{m(\ce{H2O})}{ M(\ce{H2O})}.\] В свою очередь, \(m(\ce{H2O}) = m(\ce{H2SO4})_{\text{р-ра}} - m(\ce{H2SO4})\), тогда общая формула будет:
\[\begin{split}n(\ce{H2O}) = \frac{m(\ce{H2SO4})_{\text{р-ра}} - m(\ce{H2SO4})} { M(\ce{H2O})} =\\= \frac{11{,}021 - 1{,}654}{18} = 0{,}520 \text{ моль};\end{split}\]
\[\begin{split}\chi (\ce{H2SO4}) = \frac{n(\ce{H2SO4}) }{ n(\ce{H2SO4}) + n(\ce{H2O})} =\\=\frac{ 0{,}017 }{0{,}017 + 0{,}520} = \frac{0{,}017}{0{,}537} = 0{,}032.\end{split}\]
- Найдем моляльность серной кислоты по формуле: \[b(\ce{H2SO4}) = \frac{n(\ce{H2SO4})} {m(\ce{H2O}) }=\frac{ 0{,}017 }{ 0{,}009367} = 1{,}815 \text{ моль/кг}.\]
Изотонический коэффициент (обозначается \(i\)) — безразмерный параметр, характеризующий поведение вещества в растворе. Он рассчитывается по формуле: \[i = \frac{N - N \cdot \alpha + N \cdot \alpha \cdot n}{N} = \frac{N(1 - \alpha + \alpha \cdot n)}{N} = 1 + \alpha(n - 1),\] где \(\alpha\) — степень диссоциации вещества, а \(n\) — число компонентов, на которые распадается вещество. Серная кислота является сильной кислотой, поэтому \(\alpha = 1\). Тогда получается, что \(i = 2 = 1 + 1(n-1) = 1 + n - 1 = n\). Следовательно, серная кислота распадается на две части при диссоциации, а значит, она идет по первой ступени: \[\ce{H2SO4 -> H+ + HSO4-}.\]
Рассчитаем, при какой температуре замерзнет раствор по формуле: \[\Delta T = i K b,\] где \(K = 1{,}86\) — криоскопическая постоянная, \(i\) — изотонический коэффициент, \(b\) — моляльность. \[\Delta T = i K b = 2 \cdot 1{,}86 \cdot 1{,}815 = 6{,}752.\] Температура замерзания воды равна \(0~°\)С, тогда: \[\Delta T = T_0 - T_{\text{р-ра}} = 0 - T_{\text{р-ра}} = 6{,}752.\] \[T_{\text{р-ра}} = -6{,}752~°\text{С}.\]
- \(W (\ce{H2SO4}) = 15{,}00\%\).
- \(C_M (\ce{H2SO4}) = 1{,}700\) моль/л; \(C_H (\ce{H2SO4}) = 3{,}400\) моль/л или 3,374 моль/л; \(\chi (\ce{H2SO4}) = 0{,}032\); \(b(\ce{H2SO4}) = 1{,}815\) моль/кг.
- Диссоциация идет по первой ступени: \(\ce{H2SO4 = H+ + HSO4-}\), \(T_{\text{р-ра}} = -6{,}752~°\)С.
Ответ в задании 2: \(C_H (\ce{H2SO4}) = 3{,}400\) моль/л или 3,374 моль/л, результат зависит от способа расчета.
Если верно указаны два правильных ответа, задача оценивается в 15 баллов, если указано менее двух верных ответов, задача оценивается в 0 баллов. Если верно указаны все ответы, задача оценивается в 25 баллов.
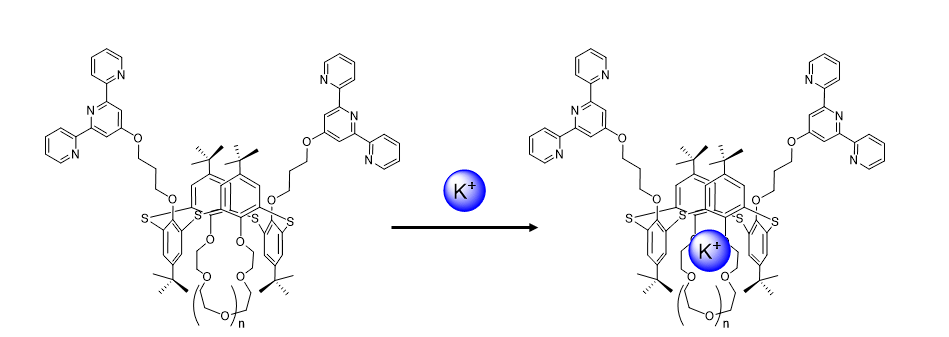
Каликсарены — продукты циклической олигомеризации фенола с формальдегидом. Название происходит от латинского слова calix (chalice) «чаша», что отображает особенную форму молекулы, и слова «арен» (arene) указывающее на ароматический строительный блок данного соединения.
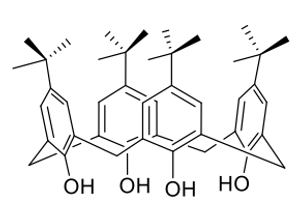
Ученые НОЦ Инфохимии исследуют каликсарены в качестве супрамолекулярных сборок для детекции ионов металлов. Этот процесс схематически отображен на рис. 2.2.
Для изучения связывания иона металла (в нашем случае \(\ce{K+}\)) в комплекс «Каликсарен-Металл» используют комплексонометрическое титрование с использованием натрий-тетрафенилбората \(\ce{NaB(C6H5)4}\).
По результатам титрования установлено, что это реакция первого порядка, и получены данные, приведенные в таблице 1.1.
| \(T\), мин | 0 | 3 | 5 | 7 | 12 | 20 |
|---|---|---|---|---|---|---|
| \(C\), моль/м\(^3\) | 100 | 63,8 | 47,2 | 35 | 16,5 | 5,0 |
Определите:
- Концентрацию вещества через 10 мин реакции (округлите до десятых).
- Константу скорости реакции (округлите до сотых).
- Время полупревращения (округлите до десятых).
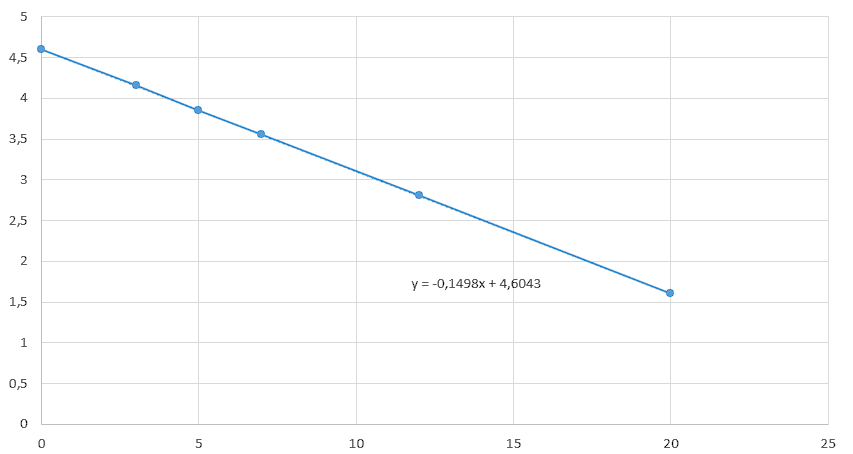
Строим график в координатах \(\ln(C)\) от \(T\) (рис. 2.3). Находим уравнение прямой.
Откуда 0,1498 — коэффициент \(k\). Подставим \(t = 10\) в это уравнение: \[\begin{gather} \ln(C) = -0,1498 \cdot 10 + 4,6043;\\ \ln(C) = 3,1;\\ C = e^{3,1} = 22,2 \text{ моль/м}^3. \end{gather}\] Чтобы определить константу скорости для первого порядка, воспользуемся уравнением прямой от \(t\): \[\ln(C) = \ln(C_0) - k \cdot t,\] где \(k\) — угловой коэффициент.
Соответственно, 0,1498 и есть константа скорости, с учетом округления получим 0,15.
Также это значение можно получить аналитически. Возьмем начальную и конечную точки и подставим в уравнение реакции первого порядка: \[\begin{gather} \ln\frac{C(0)}{C(t)} = kt;\\ k = \frac{\ln(C(0)/C(t))}{t}. \end{gather}\] При \(t = 0\) мин, \(C_0 = 100\) моль/м\(^3\) и \(t = 20\) мин, \(C(20) = 5\) моль/м\(^3\); \[k = \frac{\ln(100/5)}{20} = 0{,}1498 \text{ (с учетом округления 0{,}15 мин$^{-1}$)}.\]
Время полупревращения: \[t_{1/2} = \frac{\ln(2)}{k} = \frac{\ln(2)}{0{,}1498} = 4{,}6 \text{ мин}.\]
- 22,2 моль/м\(^3\cdot\)мин.
- 0,15 мин\(^{-1}\).
- 4,6 мин.
Если верно указаны два правильных ответа, задача оценивается в 10 баллов, если указано менее двух верных ответов, задача оценивается в 0 баллов. Если верно указаны все ответы, задача оценивается в 20 баллов.
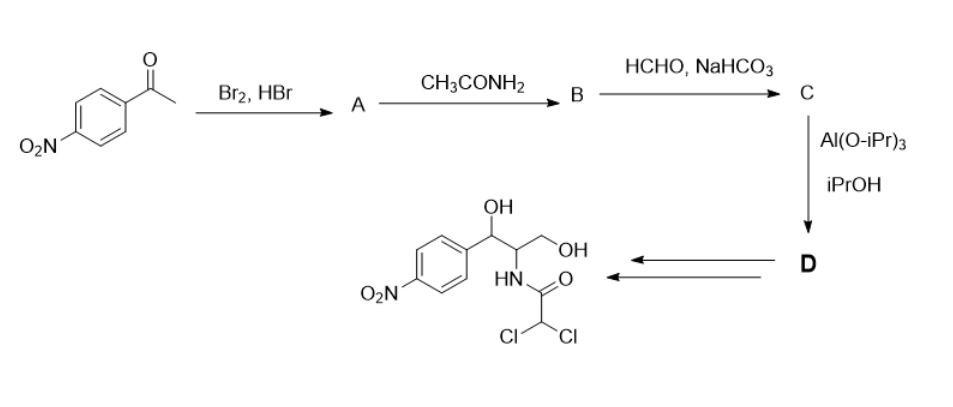
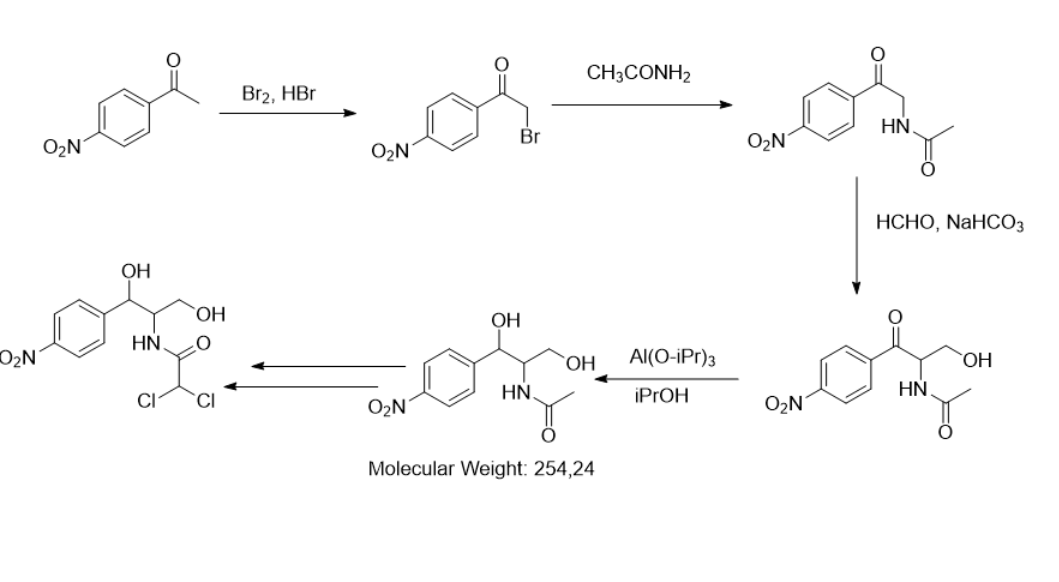
Одним из направлений органического синтеза является разработка методик синтеза и очистки медицинских субстанций, например, создание хлорамфеникола — антибиотика, который используется в том числе при лечении конъюнктивита или менингита. Ниже представлена часть существующей методики синтеза данного препарата. В ответе укажите молярную массу продукта D в граммах, деленных на моль (г/моль), с точностью до целых.
254.
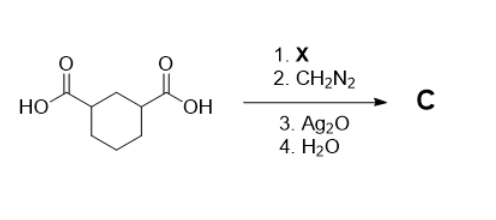
Селективное получение хлор-производных и хлорангидридов является важной задачей для современной промышленной и лабораторной химии в самых разных ее отраслях — от фундаментальных исследований до фармации. Одним из самых популярных и легкодоступных реагентов для этого является вещество X. Для получения 14,875 г вещества Х проводят реакцию между 2,8 л трехатомного газа А (50% кислорода по массе) и 26,1 г галогенида фосфора (массовая доля фосфора 14,87%). Предполагается, что выход реакции 100%. Примером использования вещества Х является реакция гомологизации, представленная на схеме. Определите вещество Х и расшифруйте схему. В ответе укажите:
- геометрическую форму вещества Х (например, пентагональная пирамида);
- молярную массу соединения С (округлите до целых).
Трехатомный газ с 50% кислорода по массе — \(\ce{SO2}\).
Галогенид фосфора с массовой долей P = 14,87 это \(\ce{PCl5}\) \(\left(\dfrac{31}{31+5\cdot 35{,}5} = 14{,}9\right)\).
В результате их взаимодействия получается широко известный «хлорирующий» реагент, применяемый для превращения карбоновых кислот в хлорангидриды. Таким X-веществом является тионилхлорид \(\ce{SOCl2}\).
У серы в \(\ce{SOCl2}\) формально четыре области электронной плотности: двойная связь S=O и две связи S–Cl, плюс неподеленная пара электронов на S. Такая конфигурация дает тригональную пирамиду с вершиной в атоме серы.
На рис. 2.6 показана циклическая дикарбоновая кислота (1,4-дизамещенный циклогексан с двумя карбоксилами). Далее идут стадии:
- Обработка \(\ce{SOCl2}\): каждая \(\ce{COOH}\)-группа превращается в хлорангидрид \(\ce{COCl}\).
- Реакция хлорангидрида с диазометаном \(\ce{CH2N2}\) дает соответствующие дикарбен.
- Действие \(\ce{Ag2O}\) и последующий гидролиз приводит к гомологизации (Арндт – Эйстерт), то есть каждая \(\ce{COOH}\)-группа удлиняется на один \(\ce{CH2}\)-фрагмент.
Итоговый продукт — это 1,4-бис (карбоксиметил) циклогексан (\(\ce{C10H16O4}\)). \[M_r = 10 \cdot 12 + 16 + 4 \cdot 16 = 200.\]
- Тригональная пирамида.
- 200.
Если верно указан один правильный ответ, задача оценивается в 10 баллов. Если верно указаны все ответы, задача оценивается в 20 баллов.
Графит состоит из параллельных слоев углеродных атомов, в каждом из которых атомы расположены в гексагональной (шестигранной) сетке. Пусть ковалентный радиус углерода равен \(r = 0{,}0709\) нм, и в плоскостях атомы связаны, образуя длину связи \(2r\). Плотность графита равна 2,267 г/см\(^3\). Предполагая, что объем, приходящийся на один атом, равен произведению площади, занимаемой этим атомом в слое, на расстояние \(d\) между соседними углеродными слоями. Вычислите расстояние \(d\). Ответ запишите в нанометрах (нм), округлив до сотых.
Примечание: плотность выражайте в граммах на кубический нанометр (г/нм\(^3\)). Для гексагональной упаковки используйте формулу \(S = \frac{3\sqrt{3}}{2}l^2\) (на две атомные позиции), где \(S\) — площадь, а \(l\) — отражает характерный межатомный параметр в плоскости.
Найдем объем на один атом: \[\begin{gather} 1 \text{ см}^3 = 10^{21} \text{ нм}^3;\\ \rho = 2,267 \text{ г/см}^3 = 2,267 \cdot 10^{-21} \text{ г/нм}^3;\\ \frac{m}{\rho} = \frac{1,99 \cdot 10^{-23}}{2,267 \cdot 10^{-21}} \approx 8,77 \cdot 10^{-3} \text{ нм}^3. \end{gather}\] Площадь ячейки равна: \[S = \frac{3\sqrt{3}}{2} l^2.\]
На 1 атом получаем: \[\begin{gather} l = 2 \cdot r = 2 \cdot 0,0709 = 0,1418 \text{ нм};\\ S = \frac{3\sqrt{3}}{2} \cdot \frac{0,1418^2}{2} = 0,0261 \text{ нм}^2;\\ V_{\text{атом}} = \frac{m}{\rho} = \frac{1,99 \cdot 10^{-23}}{2,267 \cdot 10^{-21}} \approx 8,77\cdot 10^{-3}= 0,0088 \text{ нм}^3;\\ S_{\text{атом}} \cdot d = 0,0088;\\ d = \frac{0,0088}{0,0261} = 0,337 \approx 0,34 \text{ нм}. \end{gather}\]
0,34.
Корректный ответ может быть 0,34 или 0,33, в зависимости от калькулятора, с помощью которого выполнен расчет.
При взаимодействии 1 г простого вещества X с избытком водного раствора гидроксида калия выделилось 0,487 л водорода (при н. у.). Укажите элемент X (введите символ элемента).
После того как будет выполнен перебор самых очевидных вариантов \(\ce{P}\), \(\ce{Zn}\), \(\ce{Al}\), \(\ce{Pb}\) и т. д., следует вспомнить, что водный раствор \(\ce{KOH}\) содержит воду, а значит, с металлами первой и второй группы он будет реагировать с выделением водорода (не сам \(\ce{KOH}\), а вода из раствора): \[\begin{gather} \ce{2X + 2H2O -> 2XOH + H2};\\ n(\ce{H2}) = \frac{0,487}{22,4} = 0,02 \text{ моль};\\ n(X) = 2 \cdot n(\ce{H2}) = 0,04 \text{ моль};\\ M_r(X) = \frac{1}{0,04} = 22,9 \Rightarrow \ce{Na}. \end{gather}\]
Na.