Инженерный тур. 3 этап
Основная задача заключительного этапа — разработка подхода (пайплайна), включающего модели машинного обучения и/или искусственных нейронных сетей, который позволит предсказывать целевой параметр масла на основе представленных теоретических (расчетных) и экспериментальных данных.
Подход должен работать как при подаче только нескольких SMILES (как компонентов), так и при подаче параметров, похожих на свойства компонентов, как в данных (модель должна сама восполнить пропуски в них, если они будут).
Современные смазочные материалы представляют собой сложные многокомпонентные системы, состоящие из базовых масел и различных присадок. Оптимизация их состава требует:
- глубокого анализа химических свойств компонентов;
- влияния компонентов на ключевые эксплуатационные характеристики продукта;
- большого количества экспериментальных исследований.
Участникам необходимо разработать и реализовать пайплайн для предсказания параметров многокомпонентных рецептур масел с использованием данных об отдельных компонентах рецептуры. Компоненты нужно представлять с использованием дескрипторов для отражения их химической природы, структуры (SMILES), геометрии (координаты атомов) и т. д. в машиночитаемом виде.
Основной проблемой в создании алгоритма является разное число компонентов и их свойств в рецептурах масел. Для этого используются современные алгоритмы, например, графовые нейронные сети, трансформеры, LSTM и другие. В частности, для работы с формами представления молекул особенно полезны графовые нейронные сети.
Работа с различным набором входных данных, в соответствии с количеством компонентов в масле, а также их разнообразие может потребовать разработку универсального конвейера (пайплайна), который применяется для предсказания других свойств многокомпонентных смесей.
Участникам представлены два вида данных:
- расчетные данные (открытые) — молекулы компонентов масла в формате SMILES; участники могут извлекать любые признаки из SMILES (дескрипторы, графовую репрезентацию и т. д.);
- экспериментальные данные (обезличенные) предоставляются участникам на момент проведения заключительного этапа в зашифрованном виде.
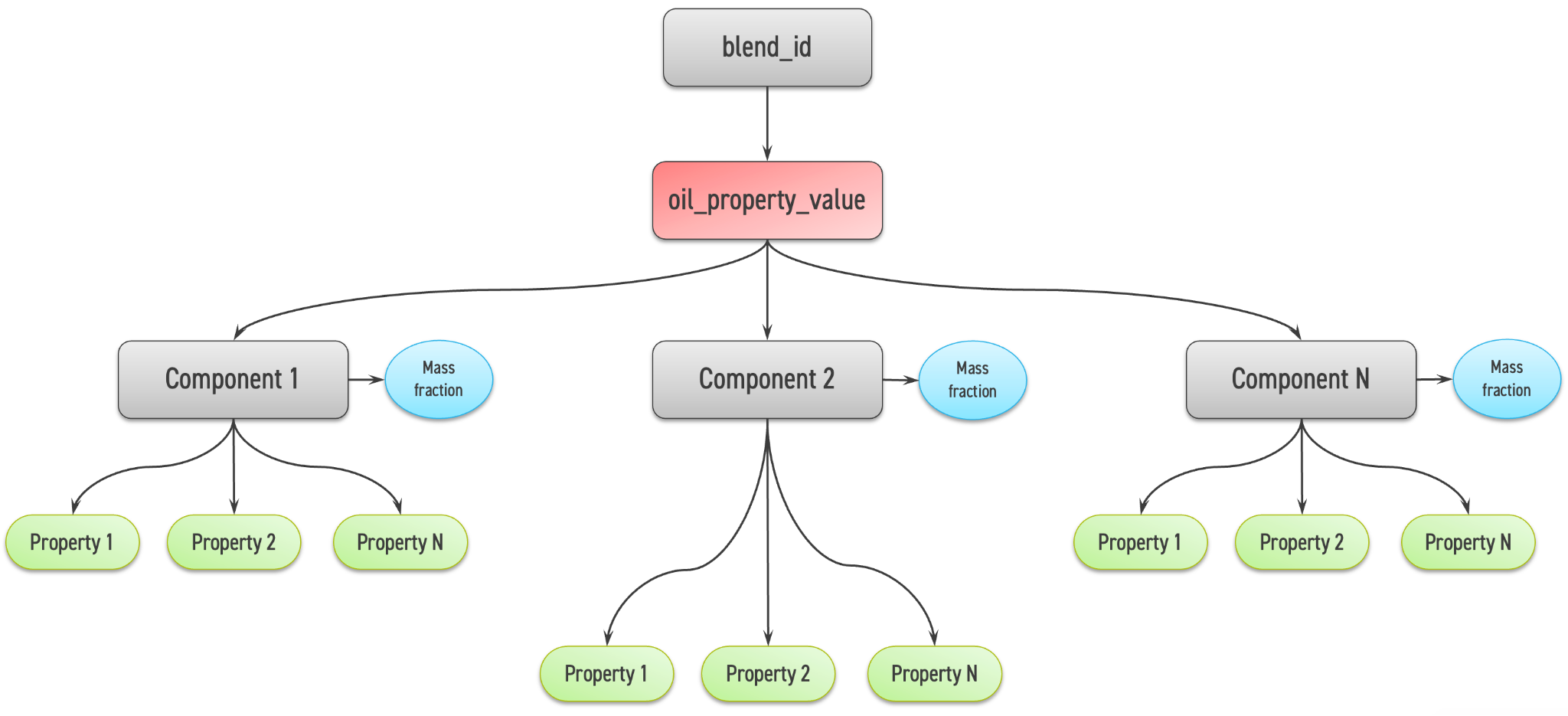
На рис. 2.1 приведена схема распределения данных. Зеленым цветом отмечены признаки, которые можно использовать для обучения, красным — признак, который нужно предсказать.
Представленные экспериментальные данные имеют пропуски, участники могут воспользоваться любым доступным способом. Однако не рекомендуется применять исключительно восстановленные данные для обучения, а изначально полные данные для валидации, так как модель может себя неправильно повести на скрытой выборке.
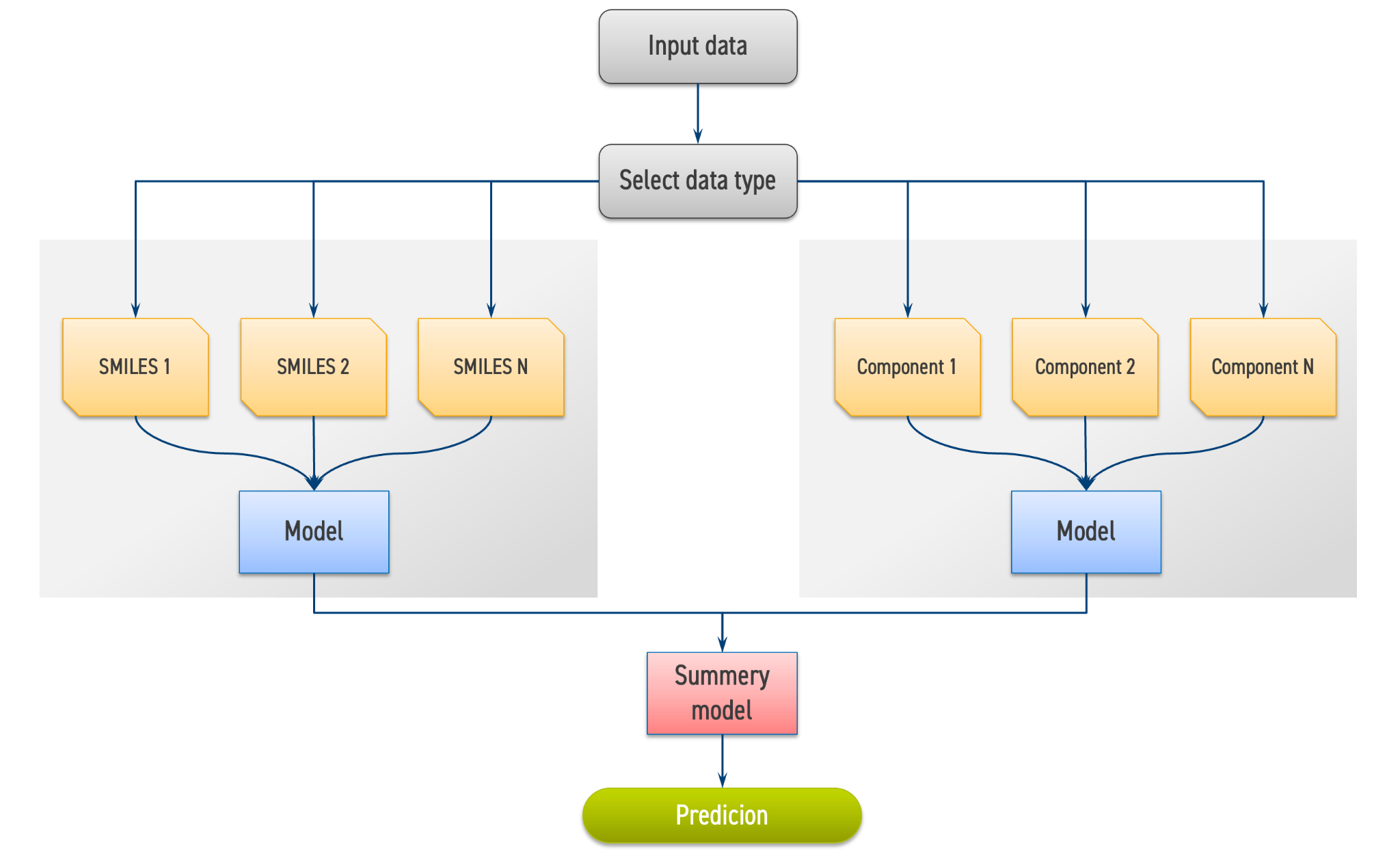
Образ финального решения должен состоять из модели(-ей), способной(-ых) предсказывать исследуемый параметр смазочного масла с произвольным количеством компонентов как для компонентов, представленных с помощью SMILES, так и для известных компонентов, представленных экспериментальными параметрами из приватного обезличенного датасета. На рис. 2.2 приведен примерный образ финального решения.
Задание разбито на отдельные задачи, которые необходимо распределить между участниками команды в соответствии с их ролями. Теоретические задачи и задачи на программирование выполняются участниками стандартным образом, ответы предоставляются в виде текстовых файлов и кодов программ, формат которых задан в требованиях к выполнению заданий.
Количество участников в команде: 2–4 человека.
Компетенции, которыми должны обладать члены команды:
- Химик — анализ химических свойств многокомпонентных рецептур масел, выбор дескрипторов для представления молекул, работа с химическими структурами (SMILES).
- Программист по машинному обучению — анализ и обработка данных многокомпонентных рецептур масел, разработка и построение пайплайнов для предсказания параметров масел, работа с алгоритмами машинного обучения и искусственного интеллекта.
- Программист-математик — решение задач по математической обработке многокомпонентных рецептур и построение базы данных, анализ корреляций, визуализация и исследование распределений данных, подготовка данных для моделирования.
Для создания модели используется язык программирования Python 3.8 и выше, менеджер пакетов Conda, фреймворк Pytorch и командная оболочка Jupyter Notebook:
- Python 3.7 и выше (https://www.python.org/);
- Conda (https://www.anaconda.com/);
- Pytorch (https://pytorch.org/);
- Jupyter Notebook (https://jupyter.org/).
На данном этапе участникам необходимо выполнить литературный обзор, обобщить современные исследования и методы анализа многокомпонентных рецептур масел, а именно:
- описать химические компоненты;
- оценить функциональное взаимодействие компонентов;
- объяснить влияние компонентов на ключевые физико-химические параметры;
- выявить проблемы и предложить подходы для оптимизации состава с учетом возможностей математического моделирования и методов машинного обучения.
Порядок работы:
- Проанализируйте, какие типы компонентов включаются в многокомпонентные рецептуры масел. Опишите, как каждый класс (например, базовые масла, присадки, антиокислители, модификаторы вязкости и т. д.) влияют на технологические и эксплуатационные свойства конечного продукта.
- Ответьте на вопрос: «Какие компоненты оказывают максимальное влияние на ключевые свойства многокомпонентных рецептур масел (например, вязкость, термостабильность, окислительная стабильность и т. д.)?»
- Используя примеры из научных публикаций, оцените, как изменение пропорций компонентов может приводить к изменению свойств масла, и обсудите возможные механизмы этих влияний.
- Проанализируйте, каким образом современные методы машинного обучения могут быть задействованы для прогнозирования физико-химических свойств масел и оптимизации состава рецептуры.
- Рассмотрите существующие исследования или кейсы, где машинное обучение уже использовалось для оптимизации рецептур.
Формат ответа: текстовый файл с ответами на вопросы в формате .pdf, поместить в корень проекта.
Основная роль: химик.
Вспомогательные роли: программист по машинному обучению, программист математик.
Количество попыток: 1.
Максимальное количество баллов за задачу — 10.
За полный ответ на вопросы №№ 1, 2, 3, 4, 5 ставится по 2 балла.
Эталонное решение команды участников.
Базовые масла являются основой любого смазочного материала и играют решающую роль в определении его ключевых физико-химических свойств, таких как вязкость, температурная стабильность, окислительная стойкость и многих других.
Классификация базовых масел традиционно включает три основные категории:
- минеральные,
- синтетические,
- растительные.
Минеральные масла, получаемые путем глубокой переработки нефти, остаются наиболее распространенными и экономически выгодными, обеспечивая при этом достаточно широкий диапазон эксплуатационных свойств для многих областей применения.
Синтетические масла представляют собой более высокотехнологичную альтернативу, демонстрируя превосходные характеристики, особенно в экстремальных температурных режимах и при повышенных нагрузках. К наиболее известным классам синтетических базовых масел относятся полиальфаолефины (ПАО), эстеры (сложные эфиры), алкилированные нафталины и силиконы. Каждый представитель данной группы обладает уникальным набором свойств и преимуществ.
Растительные масла, получаемые из возобновляемых природных источников, привлекают все большее внимание в контексте устойчивого развития и экологической безопасности. Однако их использование в качестве базовых масел пока ограничено рядом факторов, включая недостаточную окислительную и термическую стабильность, а также несколько худшие низкотемпературные характеристики по сравнению с синтетическими аналогами.
Присадки являются неотъемлемой частью современных смазочных масел, представляя собой разнообразный класс химических соединений, которые добавляются в базовые масла в относительно небольших концентрациях с целью модификации и улучшения их эксплуатационных свойств. Многообразие присадок обусловлено широким спектром требований, предъявляемых к смазочным материалам в различных отраслях промышленности и техники. Среди основных категорий присадок, наиболее часто используемых в многокомпонентных маслах, можно выделить следующие:
- Антиокислители: предназначены для замедления процессов окисления масла под воздействием высоких температур и кислорода, что позволяет предотвратить образование отложений, увеличение вязкости и ухудшение смазывающих свойств, тем самым продлевая срок службы масла.
- Модификаторы вязкости: известны как загустители или улучшители вязкостного индекса; представляют собой полимерные соединения, которые минимизируют зависимость вязкости масла от температуры, обеспечивая стабильную работу смазочной системы в широком температурном диапазоне.
- Противоизносные присадки: играют ключевую роль в защите поверхностей трения от износа, особенно в условиях граничного трения, когда прямой контакт металлических поверхностей становится весьма вероятным; формируют защитные пленки на поверхностях трения, снижая интенсивность износа и продлевая срок службы механизмов.
- Антикоррозионные присадки: обеспечивают защиту металлических элементов смазочной системы от коррозионного воздействия влаги, кислот и других агрессивных сред, предотвращая разрушение и обеспечивая надежную работу оборудования.
- Диспергаторы и детергенты: выполняют важную функцию по поддержанию чистоты двигателя и других механизмов, предотвращая образование и накопление отложений, нагара, лаковых пленок и других загрязнений на рабочих поверхностях, что способствует более эффективной работе и увеличению срока службы оборудования.
Помимо перечисленных категорий, существует множество других специализированных присадок, таких как противозадирные, антипенные, депрессорные, эмульгирующие и многие другие, каждая из которых вносит свой вклад в оптимизацию эксплуатационных характеристик многокомпонентных масел для конкретных применений
В многокомпонентных смазочных маслах компоненты не действуют изолированно, а вступают в сложные взаимодействия, которые могут проявляться как положительными эффектами синергии, так и отрицательными эффектами антагонизма.
Синергия наблюдается в тех случаях, когда комбинированное действие двух или более присадок превосходит простую сумму их индивидуальных эффектов, что позволяет достичь более высокой эффективности смазочного материала в целом. Например, весьма распространенным является синергетический эффект, наблюдаемый при сочетании различных типов антиокислителей, таких как фенольные и аминные антиоксиданты, которые в комбинации обеспечивают более эффективную защиту масла от окисления, чем каждый из них по отдельности.
Антагонизм, напротив, проявляется в снижении эффективности одной присадки в присутствии другой, что может привести к ухудшению эксплуатационных характеристик масла. Например, некоторые детергенты могут оказывать негативное влияние на эффективность противоизносных присадок типа диалкилдитиофосфатов цинка (ZDDP), снижая их способность формировать защитные пленки на поверхностях трения.
Глубокое понимание и тщательный учет эффектов взаимодействия компонентов является абсолютно необходимым условием для рациональной разработки многокомпонентных масел с оптимальными свойствами и максимальной эффективностью в конкретных условиях применения. Почему именно эти компоненты? Они обеспечивают баланс между стоимостью, производительностью и стабильностью. Например, ZDDP сочетает противоизносные и антиокислительные свойства, а синтетические базовые масла (ПАО) позволяют работать в широком температурном диапазоне.
Компонентный состав многокомпонентного масла оказывает прямое и существенное влияние на его эксплуатационные характеристики. Изменение пропорций даже одного из них способно привести к заметным изменениям вязкости, окислительной стабильности, износостойкости, температурных свойств и многих других важных показателей. Например, увеличение концентрации модификатора вязкости обычно приводит к повышению вязкостного индекса, что улучшает вязкостно температурные характеристики масла, но при этом может также негативно сказаться на окислительной стабильности или других свойствах.
Экспериментальные исследования неоднократно подтверждали, что даже незначительные корректировки в компонентном составе многокомпонентных масел могут вызывать значительные изменения в их эксплуатационных характеристиках, что подчеркивает важность точного контроля состава и тщательной оптимизации рецептур для достижения заданных свойств.
Прогнозирование влияния состава на свойства многокомпонентных масел представляет собой весьма сложную задачу из-за нелинейного характера зависимостей и комплексного взаимодействия компонентов, что требует применения современных методов моделирования и анализа данных.
Ключевые компоненты и их влияние на свойства масел:
- Вязкость: базовое масло (основа) + модификаторы вязкости (например, полиизобутилены).
- Термоокислительная стабильность: антиокислители (фенольные/аминные) + синтетические базовые масла (ПАО).
- Износостойкость: ZDDP, MoDTC.
- Совместимость и стабильность: детергенты (сульфонаты) предотвращают выпадение осадка.
В ряде исследований комбинация фенольного (Irganox L135) и аминного (Vanlube 81) антиокислителей показала синергетический эффект, увеличивая срок службы масла на 30% по сравнению с их раздельным использованием.
Разработка эффективных многокомпонентных масел сопряжена с рядом значительных технологических и научных вызовов. Одной из ключевых проблем является обеспечение совместимости компонентов в составе масла.
Несовместимость различных присадок или присадок с базовым маслом может привести к нежелательным явлениям, таким как:
- выпадение осадка,
- расслоение смеси,
- помутнение масла,
- снижение эксплуатационных характеристик масла.
Стабильность многокомпонентных масел при длительном хранении и в условиях высоких температур также представляет собой серьезную проблему, требующую тщательного подбора компонентов и введения специальных стабилизирующих добавок, которые предотвращают деградацию масла и сохраняют его свойства в течение всего срока службы.
Кроме того, как уже упоминалось ранее, синергетические и антагонистические эффекты взаимодействия компонентов существенно усложняют процесс оптимизации рецептур, требуя проведения обширных экспериментальных исследований и применения сложных методов математического моделирования для прогнозирования свойств и поведения многокомпонентных смесей.
Решение определенных проблем:
Антагонизм ZDDP и детергентов: сульфонаты кальция могут снижать эффективность ZDDP из-за конкуренции за поверхность металла.
Решение: оптимизация концентраций (например, снижение доли сульфонатов) или использование альтернативных противоизносных присадок (например, беззольных).
Выпадение осадка при смешивании минеральных и синтетических масел:
Решение: добавление совместителей (например, сложных эфиров) или предварительное тестирование смесей.
Можно создать модель машинного обучения, которая на основании полученных из SMILES дескрипторов и массовых долей всех соединений, входящих в смесь, будет предсказывать важные физические свойства смазывающих масел, такие как:
- вязкость,
- температура вспышки в закрытом тигле,
- термоокислительная устойчивость,
- текучесть при низких температурах,
- примерный диапазон температур, при которых можно использовать данную смазку,
- степень повышение коррозионной устойчивости металла,
- окислительная стойкость,
- другие параметры.
Это существенно сократит временные и денежные затраты на разработку новых рецептур, так как можно будет сразу предупредить проблемы, описанные в п. 3.
Примеры:
«Газпромнефть»
Компания запустила первую в России цифровую систему «Алхимик» для разработки рецептур моторных масел с использованием ИИ. Эта система сокращает процесс создания и запуска новых продуктов с полугода до 1–2 месяцев. Пользователь вводит параметры будущего масла, такие как вязкость, плотность и щелочное число, а также спецификации оборудования, на котором будет использоваться продукт. «Алхимик», используя алгоритмы машинного обучения и 15-летнюю базу исследований, анализирует данные и предлагает оптимальные сочетания смазочных материалов и присадок.
PETRONAS
Инженеры PETRONAS разработали систему на основе МО для моделирования и оптимизации интегрированного комплекса по производству базовых масел. Были исследованы пять моделей МО: регрессия на основе дерева решений, векторное регрессирование поддержки, искусственные нейронные сети, случайный лес и градиентный бустинг (XGBoost). Модель XGBoost показала наилучшие результаты и была использована в сочетании с байесовской оптимизацией и методом дифференциальной эволюции. В результате удалось повысить выход базового масла на 5,24% и 4,48% для двух случаев оптимизации индекса вязкости соответственно.
Beyond Limits
Компания внедрила когнитивную систему искусственного интеллекта для ускорения процесса разработки новых смазочных материалов. Система анализирует обширные наборы данных о базовых маслах, присадках и характеристиках производительности, позволяя предсказывать оптимальные рецептуры быстрее традиционных методов исследований и разработок. Это способствует сокращению времени вывода продукта на рынок и снижению затрат на разработку.
На данном этапе участникам необходимо выполнить поиск и анализ научной литературы, а также преобразовать химические структуры (SMILES) в машиночитаемый вид с использованием дескрипторов. Необходимо выполнить несколько заданий и ответить на следующие вопросы:
- Что такое SMILES? Опишите основные принципы построения и ключевые особенности при работе с ними.
- Какие преимущества и ограничения имеет использование SMILES?
- Опишите существующие подходы для преобразования SMILES в числовые представления (например, фингерпринты, молекулярные дескрипторы и т. п.).
- Изучите, какие дескрипторы могут быть наиболее полезны для предсказания свойств рецептур масел. Обоснуйте выбор дескрипторов, опираясь на публикации и теоретические исследования.
- Определите, по каким критериям можно оценивать эффективность выбранных дескрипторов для моделирования.
После выполненного анализа участникам следует:
- изучить возможности библиотеки RDKit для извлечения молекулярных дескрипторов из SMILES;
- написать скрипт, производящий генерацию выбранных и обоснованных дескрипторов (на основании вопросов 4, 5) из представленных теоретических данных SMILES в отдельную таблицу (пример — см. таблицу 1.1).
| SMILES | MolWt | MaxAbsPartialCharge | NumValenceElectrons |
|---|---|---|---|
| CN=C=O | |||
| CC[C@H](O1)CC[C@@]12CCCO2 | |||
| … |
Справочные материалы: библиотека языка программирования Python RDKit, Pandas.
Основные роли: химик, программист-математик.
Формат ответа: анализ литературы следует представить в виде текстового файла формата .pdf названного по форме (Задание_2_анализ_дескрипторов_ФИО.pdf). В файле должен быть реализован скрипт для генерации выбранных дескрипторов из SMILES формата .py, названного по форме (descriptors_gen_ФИО.py) на языке программирования Python версии 3.7 или выше, файл необходимо поместить в корень проекта. Таблицу со сгенерированными дескрипторами необходимо сохранить в формате .csv и поместить в папку output_data.
Количество попыток: 1.
- Полный ответ на вопросы №№ 1, 2, 3, 4, 5 — по 1 баллу.
- Скрипт на языке программирования Python версии 3.7 или выше, выполняющий задачу в соответствии с условием — 5 баллов.
- Суммарно за задание — 10 баллов.
- При невозможности запуска скрипта, несоблюдения формата выходных данных, а также за необоснованный выбор дескрипторов — 0.
Эталонное решение команды участников приведено ниже.
1. Основные принципы построения и ключевые особенности при работе со SMILES.
SMILES (Simplified Molecular Input Line Entry System) — это текстовый формат для однозначного описания структуры химических соединений с использованием строки ASCII-символов. Ключевые принципы построения:
- Атомы: обозначаются символами элементов (например, C — углерод, O — кислород). Водород обычно не указывается (неявно считается присоединенным к атомам). Обозначение атомов в квадратных скобках используется для явного указания на определенные атомы (например, неорганические элементы), обозначения изотопов, задания зарядов и изменения количества присоединенных водородов.
Связи:
- одинарная связь — не указывается (по умолчанию),
- двойная — =,
- тройная — #,
- разветвления — элементы боковых цепей обозначаются в скобках.
Пример: CC(C)O — изопропанол. Циклы: нумеруются цифрами. Одна и та же цифра сигнализирует о первом и последнем атоме цикла. Пример: C1CCCCC1 — циклогексан.
- Ароматичность: атомы в ароматических циклах пишутся строчными буквами. Пример: c1ccccc1 — бензол.
- Стереохимия: конфигурация двойных связей: / (цис) и \ (транс) (например, C/C=C/C — транс-бутен). Хиральность: @ (S) и @@ (R) (например, CC@HCO — L-молочная кислота).
2. Преимущества и ограничения использования SMILES.
Преимущества:
- Компактность: сложные молекулы описываются короткими строками (например, кофеин — CN1C=NC2C1C(=O)N(C)C(=O)N2C).
- Легкость в прочтении: химики могут визуализировать простые структуры по SMILES.
- Универсальность: поддержка большинством хемоинформатических инструментов (RDKit, OpenBabel).
- Стандартизация: существуют алгоритмы канонизации SMILES для устранения неоднозначностей.
Ограничения:
- Неоднозначность: одна молекула может иметь несколько валидных SMILES (например, CCO и OCC — оба обозначают этанол).
- Сложные структуры: проблемы с описанием металлоорганических соединений (например, ферроцен).
- Ограниченная поддержка стереохимии для высокосимметричных молекул.
- Нековалентные взаимодействия: не описываются водородные связи или \(\pi\)-стэкинг, неудобно работать с ионной связью.
3. Подходы для преобразования SMILES в числовые представления:
- Молекулярные фингерпринты — биты, отражающие наличие структурных фрагментов. Примеры: MACCS Keys: 166 бит, кодирующих наличие/отсутствие предопределенных структур. Morgan Fingerprints: на основе окружения атомов (радиус = 2–3).
- Молекулярные дескрипторы.
- Фрагментные дескрипторы: отражают наличие или количество определенных подструктур (фрагментов) в молекуле. Бывают бинарными (показывают присутствие фрагмента) и целочисленными (указывают число вхождений фрагмента).
- Физико-химические дескрипторы: основаны на измеряемых физико-химических свойствах молекул, таких как липофильность (LogP), молярная рефракция (MR), молекулярный вес (MW), поляризуемость и другие.
- Квантово-химические дескрипторы: получаются в результате квантово-химических расчетов и включают энергии граничных молекулярных орбиталей (ВЗМО и НСМО), частичные заряды на атомах, индексы реакционной способности и другие параметры.
- Дескрипторы молекулярных полей: аппроксимируют значения молекулярных полей путем вычисления энергии взаимодействия пробного атома, помещенного в узел решетки, с рассматриваемой молекулой. Используются в методах 3D-QSAR, таких как CoMFA.
- Фармакофорные дескрипторы: показывают, могут ли простейшие фармакофоры, состоящие из пар или троек фармакофорных центров с определенным расстоянием между ними, содержаться внутри анализируемой молекулы.
4. Дескрипторы, которые могут быть максимально полезны для предсказания свойств рецептур масел
С помощью выбранных дескрипторов будут предсказываться свойства смазывающих смесей. Для того чтобы выбрать нужные дескрипторы, необходимо определиться с важными свойствами смесей.
Как сказано в условии задачи, интересующий параметр — вязкость, поэтому рассмотрим дескрипторы, которые будут влиять именно на нее. Нужно понимать, что вязкость очень по-разному зависит от молекулярных дескрипторов в смесях разного состава. Например, вязкость водных растворов будет определяться взаимодействием растворенных веществ с водой, а значит, ее будут задавать такие дескрипторы, как: TPSA, дипольный момент, липофильность.
Кроме этого, с увеличением объема молекулы будет увеличиваться вязкость ее раствора, так как большим молекулам тяжело перемещаться внутри раствора, поэтому важны такие дескрипторы, как: молекулярный объем, молярная масса (ее выбор может показаться необоснованным, однако здесь она выступает скорее как второй дескриптор, задающий размер молекулы), количество атомов.
Если более детально изучить все SMILES всех молекул, то можно разбить вещества на базовые масла и присадки. Почти все присадки не влияют на вязкость соединения, поэтому главный интерес представляют только базовые масла, которые в данном наборе все являются углеводородами.
Для предсказания вязкости смесей углеводородов такие дескрипторы, как TPSA, дипольный момент и липофильность становятся ненужными, так как в них нет воды, и с ней невозможно взаимодействовать. Сами углеводороды имеют нулевой дипольный момент. Здесь на первый план выходят дескрипторы, задающие размер молекулы, а также дескрипторы, задающие подвижность соединений и описывающие взаимодействие с присадками, так как некоторые присадки способны изменять вязкость.
Первая группа уже описана, ко второй группе можно отнести: долю кратных связей, степень разветвленности молекулы, площадь поверхности, энергию межмолекулярного взаимодействия (последние два описывают то, на сколько сильно молекулы смеси будут связаны между собой, что определяет подвижность).
Третья группа дескрипторов включает в себя: площадь поверхности, дипольный момент, поляризуемость, энергия межмолекулярного взаимодействия, TPSA. Эти дескрипторы смогут описать взаимодействие молекул базового масла с присадками:
- Молекулярный объем — влияет на вязкость. Это видно из уравнений вязкости Эринга и Бачинского. На самом деле рассчитать молекулярный объем для органических молекул непросто, так как органические молекулы обладают большим количеством конформаций, каждая из которых обладает уникальным объемом. Поэтому нужно считать средний молекулярный объем. Однако и это очень сложно, и для заданных целей будет достаточно расчета Ван-дер-Ваальсового объема. В приложенном файле можно найти алгоритм.
- Площадь поверхности молекул — характеризует энергию межмолекулярного взаимодействия как молекул базового масла между собой, так и молекул базового масла с присадками. В данном случае реализована площадь поверхности за счет дескриптора аппроксимированной площади поверхности LabuteASA, который есть в библиотеке RDKit.
- Дипольный момент — важный дескриптор для определения силы межмолекулярного взаимодействия. Известно, что для молекул с ненулевым значением дипольного момента доступно диполь – дипольное взаимодействие, сила которого больше силы Ван-дер-Вальсового взаимодействия и определяется величиной дипольного момента.
- Поляризуемость — еще один значимый дескриптор для определения силы межмолекулярного взаимодействия. Известно, что поляризуемость определяет силу взаимодействия диполь – наведенный диполь, которое реализуется между поляризующимися молекулами и диполями. Поляризуемость реализовна с помощью дескриптора «Молярная рефракция» (Molar Refractivity, MolMR), который есть в библиотеке RDKit. Это не совсем поляризуемость, но величина, связаная с ней.
- Энергия межмолекулярного взаимодействия. Для описания энергии дескриптор пока не подобран. Однако можно это сделать для улучшения модели.
- Молярная масса полимера характеризует размер молекулы и напрямую влияет на вязкость его растворов. Увеличение молярной массы молекулы симпатично увеличению ее объема, а следовательно, можно использовать данный дескриптор. Молярная масса была реализована с помощью одноименного дескриптора molar weight (MolWt), который есть в библиотеке RDKit.
- Степень разветвленности влияет на средний объем молекулы и на способность молекулы к свободному перемещению, а значит, вязкость зависит от нее. Степень разветвленности была реализована за счет дескриптора индекс Балабана (BalabaJ), который можно найти в библиотеке RDKit.
- TPSA (суммарная площадь поверхности полярных фрагментов) — довольно значимый параметр молекулы для определения взаимодействия между компонентами смеси. Особенно это важно при предсказании вязкости растворов в полярных растворителях. В решении рассматривается другой тип смесей, и в данном случае TPSA характеризует скорее взаимодействия между компонентами. TPSA была реализована за счет дескриптора TPSA, который есть в библиотеке RDKit.
- Доля кратных связей — наличие двойных или тройных связей может влиять на поляризуемость и способность молекулы менять свою форму, что, в свою очередь, отражается на ее подвижности, а значит, и на вязкости.
- Количество атомов — влияет на размер молекул, а значит, и на вязкость. Количество атомов было реализовано за счет дескриптора количество атомов в соединении (GetNumAtoms), который есть в библиотеке RDKit.
- Липофильность — не самый ключевой параметр, связанный с полярностью соединения, что важно при рассмотрении вязкости водных растворов и взаимодействий между присадками. Липофильность была реализована за счет дескриптора липофильность (LogP), который есть в библиотеке RDKit.
5. Критерии, по которым можно оценивать эффективность выбранных дескрипторов для моделирования:
- Физико-химическая значимость: дескрипторы должны иметь четкую физико-химическую интерпретацию и быть тесно связаны с молекулярными свойствами, влияющими на вязкость. Например, молекулярный объем, площадь поверхности и молярная масса непосредственно влияют на вязкость.
- Корреляция с экспериментальными данными: эффективность дескрипторов оценивается через их способность коррелировать с экспериментально измеренной вязкостью; высокая корреляция указывает на значимость дескриптора для предсказания вязкости.
- Независимость дескрипторов: важно, чтобы дескрипторы были статистически независимы друг от друга, чтобы избежать мультиколлинеарности в моделях — это обеспечивает стабильность и надежность предсказаний.
- Простота вычисления: дескрипторы должны быть легко вычисляемыми, предпочтительно с использованием доступных программных инструментов, таких как RDKit, для обеспечения практической применимости.
- Обобщающая способность модели: дескрипторы должны обеспечивать создание моделей, которые хорошо обобщаются на новые, ранее не виденные молекулы, предотвращая переобучение.
Пример программы-решения
Ниже представлено решение на языке Python.
import pandas as pd
import numpy as np
from math import pi
from typing import Optional, List
from numpy import ndarray
from rdkit import Chem
from rdkit.Chem import AllChem, Descriptors, rdMolDescriptors, MolSurf, rdPartialCharges, GraphDescriptors
from rdkit.Chem.rdchem import Mol
class Smiles2Descriptors:
"""
Класс для вычисления дескрипторов молекул на основе SMILES-строки
"""
def __init__(self, smiles: str) -> None:
self.smiles: str = smiles
self.molecule: Mol = Chem.MolFromSmiles(smiles)
if self.molecule is None:
raise ValueError("Неверный SMILES")
# Молекула с водородом
self.mol_with_h: Mol = Chem.AddHs(self.molecule)
# Генерация 3D конформации для расчета дипольного момента
AllChem.EmbedMolecule(self.mol_with_h)
AllChem.MMFFOptimizeMolecule(self.mol_with_h)
# Основные дескрипторы
self.logp: float = Descriptors.MolLogP(self.molecule) # липофильность
self.tpsa: float = rdMolDescriptors.CalcTPSA(self.molecule) # площадь поверхности полярных участков
self.molwt: float = Descriptors.MolWt(self.molecule) # молярная масса
# Характеристики связей
self.num_bonds: int = self.molecule.GetNumBonds()
self.num_rotatable_bonds: int = rdMolDescriptors.CalcNumRotatableBonds(self.mol_with_h)
self.num_non_rotatable_bonds: int = self.num_bonds - self.num_rotatable_bonds
self.fraction_non_rotatable_bonds: float = (self.num_non_rotatable_bonds / self.num_bonds) if self.num_bonds > 0 else 0.0
# Объем по Ван-дер-Ваальсу
self.vdw_volume: float = self._calculate_vdw_volume(self.mol_with_h)
self.num_atoms: int = self._find_atomic_number(self.mol_with_h)
# Степень разветвленности
self.degree_of_branching: float = GraphDescriptors.BalabanJ(self.molecule)
# Дипольный момент
self.dipole_moment: Optional[float] = self._calculate_dipole()
# Дополнительные дескрипторы
self.labute_asa: float = MolSurf.LabuteASA(self.molecule)
self.mol_mr: float = Descriptors.MolMR(self.molecule)
@staticmethod
def _calculate_vdw_volume(mol: Mol) -> float:
"""Вычисляет объем по Ван-дер-Ваальсу"""
volume: float = 0.0
periodic_table = Chem.GetPeriodicTable()
for atom in mol.GetAtoms():
atomic_number: int = atom.GetAtomicNum()
radius: float = periodic_table.GetRvdw(atomic_number)
volume += (4 / 3) * pi * (radius ** 3)
return volume
@staticmethod
def _find_atomic_number(mol: Mol) -> int:
"""Возвращает количество атомов в молекуле"""
return mol.GetNumAtoms() if mol is not None else 0
def _calculate_dipole(self) -> Optional[float]:
"""Вычисляет дипольный момент в Дебаях"""
try:
rdPartialCharges.ComputeGasteigerCharges(self.mol_with_h)
conf = self.mol_with_h.GetConformer()
dipole = np.zeros(3)
for atom in self.mol_with_h.GetAtoms():
charge = atom.GetDoubleProp("_GasteigerCharge")
pos = conf.GetAtomPosition(atom.GetIdx())
# Конвертация в Дебаи
dipole += charge * np.array([pos.x, pos.y, pos.z]) * 4.803
return np.linalg.norm(dipole)
except Exception as e:
print(f"Ошибка расчета дипольного момента: {str(e)}")
return None
def as_vector(self) -> ndarray:
"""Возвращает дескрипторы в виде вектора numpy"""
return np.array([
self.logp,
self.tpsa,
self.molwt,
self.vdw_volume,
self.fraction_non_rotatable_bonds,
self.num_atoms,
self.degree_of_branching,
self.dipole_moment if self.dipole_moment is not None else np.nan,
self.labute_asa,
self.mol_mr
])
def __descript__(self) -> str:
return (
f"SMILES: {self.smiles}\n"
f"Descriptors:\n"
f" LogP: {self.logp:.2f}\n"
f" TPSA: {self.tpsa:.2f}\n"
f" Molecular Weight: {self.molwt:.2f}\n"
f" Van der Waals Volume: {self.vdw_volume:.2f}\n"
f" Rotatable Bonds: {self.num_rotatable_bonds}\n"
f" Fraction of non-rotatable bonds: {self.fraction_non_rotatable_bonds:.2f}\n"
f" Number of atoms: {self.num_atoms}\n"
f" Degree of branching: {self.degree_of_branching:.2f}\n"
f" Dipole Moment: {self.dipole_moment:.2f} D\n"
f" Labute ASA: {self.labute_asa:.2f}\n"
f" Molar Refractivity: {self.mol_mr:.2f}"
)
def calculate_descriptors(smiles: str) -> Optional[List[float]]:
"""Вычисляет дескрипторы для одной молекулы"""
try:
descriptor = Smiles2Descriptors(smiles)
return descriptor.as_vector().tolist()
except ValueError as e:
print(f"Ошибка при обработке {smiles}: {e}")
return None
except Exception as e:
print(f"Неизвестная ошибка для {smiles}: {e}")
return None
if __name__ == "__main__":
input_df = pd.read_csv("./input_data/NTO_smiles.csv")
# Список дескрипторов
descriptor_labels = [
"LogP",
"TPSA",
"MolWt",
"Van_Der_Waals_volume",
"Fraction_non_rotatable_bonds",
"num_atoms",
"Degree_of_branching",
"Dipole_Moment",
"Labute_asa",
"Mol_mr"
]
# Вычисление дескрипторов
descriptors_data = []
for smiles in input_df['smiles']:
desc = calculate_descriptors(smiles)
descriptors_data.append(desc if desc is not None else [np.nan]*len(descriptor_labels))
result_df = pd.DataFrame(descriptors_data, columns=descriptor_labels)
result_df.insert(0, 'SMILES', input_df['smiles'])
# Сохранение результатов
result_df.to_csv("./output_data/smiles_desc.csv", index=False)На данном этапе участникам необходимо провести комплексный анализ набора данных, используя современные методы обработки, статистической оценки и визуализации. Основная цель — детально изучить распределение признаков, их взаимосвязи с целевой переменной, а также выявить аномалии и системные закономерности, которые помогут в дальнейшем построении модели.
Порядок работы:
- Идентифицируйте пропущенные значения, выберите и обоснуйте оптимальные методы для их заполнения или, при необходимости, удалите такие записи.
- Используя статистические методы (например, z-score, IQR) и визуальные инструменты (ящики с усами, диаграммы рассеяния и т. д.), проанализируйте нерегулярные наблюдений. Если потребуется, то удалите такие наблюдения.
- При необходимости обоснуйте и примените методы масштабирования (стандартизация, нормализация и др.) для обеспечения сопоставимости данных (разрешается использовать преобразования (например, логарифмическое, Box-Cox и др.) для приведения распределений к нормальному виду).
- Постройте корреляционные матрицы для выявления линейных и нелинейных взаимосвязей между признаками и целевой переменной. Проведите анализ мультиколлинеарности с применением методов факторного анализа или кластеризации признаков.
- Примените статистические тесты (например, тесты Пирсона или Спирмена) для оценки значимости обнаруженных корреляций.
- Проведите обоснованный отбор признаков (feature selection) с использованием методов оценки значимости, чтобы снизить размерность и улучшить качество модели (разрешается использовать различные методы извлечение признаков (feature extraction)).
Справочные материалы: библиотека языка программирования Python Pandas, Seaborn, Matplotlib.
Основные роли: программист-математик, программист по машинному обучению, химик.
Формат ответа: анализ данных необходимо выполнить в Jupyter Notebook с использованием библиотеки Pandas и др., в котором каждая стадия работы расположена в отдельной ячейке, а также снабжена комментариями, визуализациями и аргументированными выводами. Блокнот необходимо сохранить в корне проекта с расширением .ipynb и названного по форме (Задание_3_анализ_данных_ФИО.ipynb).
Обработка данных должна быть реализованы в виде отдельного скрипта, сохраненного в файле с расширением .py и названного по форме (data_preper_ФИО.py). Файл необходимо поместить в корень проекта. Исходные данные должны лежать в папке input_data, а финальные, обработанные и очищенные данные, сохранены в формате .csv и помещены в папку output_data. Используемая версия языка Python — 3.7 или выше.
Количество попыток: 1.
Код на языке программирования Python версии 3.7 или выше, выполненный в Jupyter Notebook, с решенными задачами в соответствии с условием:
- При соблюдении формата ответа за задачи №№ 1, 2, 3, 4, 5 — по 4 балла.
- Задача № 6 — 5 баллов.
- Максимально — 25 баллов.
- При невозможности запуска кода, несоблюдения форматов выходных данных, а также отсутствия обоснования в задачах — 0.
Пример Jupyter Notebook с анализом данных:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math
from scipy.stats import zscore
from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from phik import phik_matrix
df = pd.read_csv('./input_data/NTO_exp_encoded.csv')Задание № 1
Перед выполнением анализа данных необходимо добавить данные SMILES в общий датасет. Поскольку данные имеют своеобразный формат, легче всего это будет сделать преобразованием датафрейма, где все свойства компонентов будут в колонках, добавить свойства смайлс и сделать обратное преобразование.
df = df.pivot_table(
index=[
'blend_id',
'oil_property_value',
'component_type_title',
'component_name',
'mass_fraction'
],
columns='component_param_title',
values='component_param_value',
aggfunc="first"
).reset_index()
smiles = pd.read_csv("./input_data/NTO_smiles_encoded.csv")
desript = pd.read_csv("./output_data/smiles_desc.csv")
smiles_des = smiles.merge(desript, how='left', on='SMILES')
df = df.merge(smiles_des, how='left', on='component_name').drop(columns=['SMILES'])
df = df.melt(
id_vars=[
'blend_id',
'oil_property_value',
'component_type_title',
'component_name',
'mass_fraction'
],
value_vars=df.columns[5:],
var_name='component_param_title',
value_name='component_param_value'
)df.isna().sum()Пропуски содержатся в колонке component_param_value. Согласно структуре данных в колонке component_param_value содержатся значения свойств, которые относятся к компонентам.
Обратим внимание на количество уникальных свойств (component_param_title).
len(df['component_param_title'].unique())Всего имеется 66 уникальных свойств. Как говорилось ранее, у каждого компонента — определенный набор количества свойств. В данном случае заполнение пропусков свойств является ошибочным. Например, у одного соединения есть свойства, которые характеризуют вязкость. Однако существуют твердые компоненты, для которых измерение вязкости невозможно. При заполнении пропусков можно исказить данные, в результате чего предсказание модели будет неправильным.
df_n = df[~df['component_param_value'].isna()].reset_index(drop=True)
print(f"Общие потери смесей: {len(df['blend_id'].unique()) - len(df_n['blend_id'].unique())}")
print(f"Общие потери компонентов: {len(df['component_name'].unique()) - len(df_n['component_name'].unique())}")Таким образом, при удалении пропусков количество смесей и компонентов осталось неизменным.
Задание № 2
В первую очередь стоит рассмотреть распределения свойств компонентов. Для этого создадим таблицу с именами компонентов, свойств компонентов, а также значений свойств.
df_p = df_n[['component_name', 'component_param_title', 'component_param_value']].drop_duplicates(subset=['component_name', 'component_param_title']).reset_index(drop=True)unique_titles = df_p['component_param_title'].unique()
n = len(unique_titles)
cols = 5
rows = math.ceil(n / cols)
fig, axes = plt.subplots(rows, cols, figsize=(cols * 4, rows * 3))
axes = axes.flatten()
for idx, title in enumerate(unique_titles):
subset = df_p[df_p['component_param_title'] == title]
sns.histplot(subset['component_param_value'], ax=axes[idx], kde=False)
axes[idx].set_title(f"Свойство: {title}", fontsize=10)
axes[idx].tick_params(axis='x', rotation=45)
for j in range(idx + 1, len(axes)):
fig.delaxes(axes[j])
plt.tight_layout()
plt.show()Видно, что довольно обширная часть компонентов содержит выбросы — удалим их. Существует множество методов удаления выбросов, но в данном случае в качестве демонстрации выбран z-score из-за его простоты и удобства.
df_p['zscore'] = df_p.groupby('component_param_title')['component_param_value'].transform(
lambda x: zscore(x, nan_policy='omit')
)
threshold = 3
df_clean = df_p[df_p['zscore'].abs() < threshold].drop(columns='zscore')blends = df_n[['blend_id', 'component_name', 'mass_fraction', 'component_type_title', 'oil_property_value']].drop_duplicates(subset=['blend_id', 'component_name', 'mass_fraction']).reset_index(drop=True)
new_data = blends.merge(df_clean, how='left', on='component_name')Задание № 3
В данном случае необходимо использовать масштабирование, поскольку, как видно из анализа выше, каждое свойство и каждая переменная находятся в разных числовых диапазонах.
Использовать стандартизацию и другие методы, основанные на ней, нецелесообразно, поскольку распределения в большинстве своем нерегулярные, разреженные, поэтому применим нормировку.
def normalize_group(group):
scaler = MinMaxScaler()
group['component_param_value'] = scaler.fit_transform(group[['component_param_value']])
return group
df_scal = new_data.groupby('component_param_title', group_keys=False).apply(normalize_group)Задания №№ 4, 5
Для удобства преобразуем таблицу, где свойства компонентов будут трансформированы в колонки.
df_cor_o = df_scal.pivot_table(
index=[
'blend_id',
'oil_property_value',
'component_type_title',
'component_name',
'mass_fraction'
],
columns='component_param_title',
values='component_param_value',
aggfunc="first"
).reset_index()
df_cor_o = df_cor_o.drop(columns=['blend_id', 'component_name', 'component_type_title', 'component_name', 'mass_fraction'])Проведем классический линейный корреляционный анализ с использованием коэффициента Пирсона.
cor = df_cor_o.fillna(0).corr()
lower = cor.where(np.tril(np.ones(cor.shape), k=-1).astype(np.bool))
plt.figure(figsize=(30, 24))
heatmap = sns.heatmap(cor, annot=True, fmt=".2f", cmap="coolwarm")
plt.title("Корреляционная матрица", fontsize=16)
plt.xticks(rotation=45)
plt.yticks(rotation=0)
plt.tight_layout()
plt.show()Заметим, что факторы мало влияют на целевую переменную. Это не значит, что признаки незначительны, а лишь показывает, что признаки не влияют линейно на целевую переменную.
Кроме того, здесь наблюдается сильная мультиколлинеарность между некоторыми признаками (коэф. кор > 0,85). Для улучшения качества будущей модели и для предотвращения искажения результатов удалим сильно коррелирующие признаки.
Проведем нелинейный корреляционный анализ с использованием корреляции Фи, который определяет нелинейные связи лучше, чем корреляция Спирмана.
plt.figure(figsize=(30, 24))
heatmap = sns.heatmap(phik_matrix(df_cor_o.fillna(0)), annot=True, fmt=".2f", cmap="coolwarm")
plt.title("Корреляционная матрица", fontsize=16)
plt.xticks(rotation=45)
plt.yticks(rotation=0)
plt.tight_layout()
plt.show()Наблюдаем иную ситуацию, нежели при классической линейной корреляции. Признаки в большей степени коррелируют нелинейно. С целевой переменной все также не наблюдается нелинейной корреляции, однако это не означает, что корреляция отсутствует. Вероятнее всего, зависимость сложнее (https://www.sciencedirect.com/science/article/abs/pii/S0167947320301341).
Задание № 6
Данные предоставлены в зашифрованном виде, поэтому выполним отбор признаков посредством удаления сильно коррелирующих признаков.
high_corr = [
column for column in lower.columns if any((lower[column] > 0.85)|(lower[column] < -0.85))
]
new_df = df_scal[~df_scal['component_param_title'].isin(high_corr)].reset_index(drop=True)Свойства component_name, component_type_title и component_param_title представлены в виде категориальных значений. Необходимо их также перевести в численные значения. Использование One-Hot в данном случае будет нецелесообразно, поскольку свойства нерегулярные, кроме того, количество уникальных значений велико. В данном случае лучше всего использовать Label-кодирование.
le_comp = LabelEncoder()
le_comp_type = LabelEncoder()
le_comp_prop = LabelEncoder()
new_df['component_name'] = le_comp.fit_transform(new_df['component_name'])
new_df['component_type_title'] = le_comp_type.fit_transform(new_df['component_type_title'])
new_df['component_param_title'] = le_comp_prop.fit_transform(new_df['component_param_title'])
le_comp_prop.transform(['TPSA', 'Fraction_non_rotatable_bonds', 'num_atoms', 'Degree_of_branching', 'Dipole_Moment'])
new_df.reset_index(drop=True).to_csv('./output_data/prepared_data.csv', index=False)Таким образом, в результате анализа и обработки данных была выполнена подготовка данных к использованию для обучения моделей. Обнаруженные пропуски в целевых переменных были удалены, поскольку их невозможно восполнить. Аналогичным образом поступили и с пропусками внутри свойств: их заполнение может вызвать появление ошибок в данных, например, одно из свойств может являться вязкостью. При заполнении пропусков можно внести значения для свойств компонентов, которые по природе являются твердыми и не могут иметь вязкость.
Существует множество причин появления экстремальных значений в свойства компонентах: ошибка при формировании данных, ошибка при выполнении эксперимента и т. д. С помощью метода z-score были удалены все выбросы, что позволило сделать данные более регулярными.
Кроме того, свойства существуют в разных единицах измерениях, что может негативным образом сказаться при обучении модели. Применение методов стандартизации нежелательно из-за нерегулярности и разреженности данных, поэтому была использована нормализация, что позволило перевести все свойства в диапазон от 0 до 1.
Корреляционный анализ показал наличие мультиколлинеарности между признаками, что может негативно повлиять на качество итоговой модели. Выполнено удаление таких признаков. Кроме того, в случае линейной и нелинейной корреляции не было обнаружено зависимости свойств и целевой переменной. Ненайденная корреляция не означает полного отсутствия зависимости — результаты открывают дорогу к использованию нейросетевых подходов, которые позволяют работать с сильно нелинейными зависимостями.
На данном этапе участникам необходимо разработать и обосновать три различных последовательных подхода (пайплайна), которые решают поставленную задачу с применением двух или более предсказательных моделей. Пайплайны должны быть структурированы в виде нескольких логически взаимосвязанных этапов, где результаты одного шага служат отправной точкой для следующего.
Каждый подход должен содержать минимум две предсказательные модели:
- Первая часть модели, способная предсказывать необходимый параметр по SMILES. Количество SMILES для одного масла может быть произвольным.
- Вторая часть модели, предсказывающая нужный параметр по приватным обезличенным данным. При этом модель должна уметь работать с пропусками в данных, если таковые имеются.
Каждый из предложенных подходов должен включать:
- подробное описание используемых алгоритмов и методов обработки данных (в реализации каждого пайплайна можно использовать разные методы обработки данных);
- обоснование выбора конкретных техник с точки зрения их эффективности, надежности и применимости к исходным данным.
Важно указать преимущества и потенциальные ограничения каждого подхода, оценить сложность реализации и выделить ключевые этапы для достижения оптимального результата. Необходимо обеспечить достаточную детализацию каждого подхода, чтобы продемонстрировать глубокое понимание проблемы и обоснованность выбранных методов.
Основные роли: программист по машинному обучению, программист-математик, химик.
Формат ответа: pdf-файл, содержащий детальное объяснение каждого из трех предложенных подходов. Документ должен включать:
- подробное описание каждого подхода с теоретическим обоснованием;
- блок-схемы, иллюстрирующие основные этапы и логику реализации каждого подхода.
Pdf-файл необходимо оформить по форме (выбор_пайплайнов_ФИО) и поместить в корень проекта.
Количество попыток: 1.
За полное выполнение задачи с сохранением формата ответа можно получить максимум 15 баллов, в том числе:
- полнота и логическая последовательность описанных пайплайнов, сопровождающаяся блок-схемами и ссылками на научную литературу — максимально 5 баллов;
- обоснованность выбора алгоритмов для работы со SMILES — максимально 3 балла и экспериментальными данными — максимально 3 балла;
- качество обоснования преимуществ и ограничений каждого подхода, включая план валидации и контроль качества — максимально 2 балла;
- инновационность подхода и практическую применимость решения — максимально 2 балла.
Представленные данные имеют сложную многоуровневую структуру, что затрудняет использование классических алгоритмов машинного обучения. Кроме того, согласно проведенному анализу, данные являются нерегулярными и разреженными. Большое количество пропусков и различное количество компонентов и свойств компонентов накладывают дополнительные ограничения при выборе моделей и построении пайплайнов.
Использование графовых нейронных сетей (ГНН) позволяет учитывать разное количество компонентов и свойств благодаря следующим ключевым механизмам:
- ГНН обрабатывают данные без предварительного преобразования в вектор, сохраняя топологические связи между узлами. Каждый узел обновляет свое состояние, агрегируя информацию от соседей через функцию сообщений и комбинируя ее с собственными признаками. Этот процесс итеративно распространяет информацию по графу, охватывая локальные и глобальные зависимости (https://journalofbigdata.springeropen.com/articles/10.1186/s40537-023-00876-4).
- К сожалению, традиционные нейросети требуют данных в виде регулярных сеток, что в данном случае невозможно из-за разного количество компонентов в смесях. Графовые сети наоборот, работают с неевклидовыми пространствами, где расстояния и связи определяются топологией графа (https://www.sciencedirect.com/science/article/abs/pii/S0020025523000579).
Таким образом, в данной реализации будут использоваться графовые нейронные сети. Выбрана структура графа, где в центральных узлах расположены типы компонентов, а от них — названия компонентов и их свойств. Данный подход обусловлен тем, что при разработке смесей важно учитывать роль компонента в данной системе. Кроме того, это позволит учесть возможность наличия нескольких компонентов одного типа в рамках данной системы.
Пайплайн №1
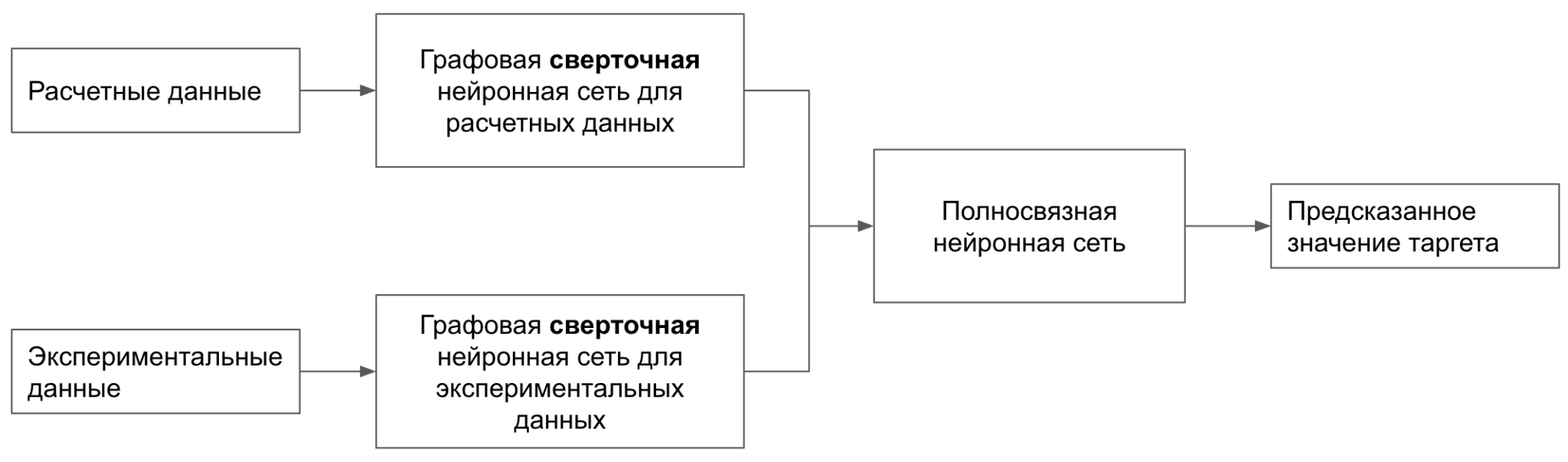
В данном подходе применяется двухголовая графовая сверточная нейронная сеть, предназначенная для использования как расчетных, так и экспериментальных данных с целью предсказания целевого параметра масла. Такой архитектурный выбор обусловлен необходимостью объединения различных источников информации для более точного моделирования свойств химических соединений.
Первая голова сети обрабатывает расчетные данные, полученные из SMILES, которые представляют собой текстовое описание молекулярной структуры. Эти строки преобразуются в графовые представления, где узлы соответствуют атомам, а ребра — химическим связям. Для извлечения информативных признаков из этих графов используется механизм передачи сообщений, позволяющий учитывать как локальные, так и глобальные структурные особенности молекул. Подобный подход продемонстрировал высокую эффективность в задачах предсказания свойств молекул, таких как токсичность и активность.
Вторая голова сети предназначена для обработки экспериментальных данных. Эти данные проходят через отдельную ветвь графовой нейронной сети, что позволяет учитывать дополнительные аспекты, не отраженные в структурных дескрипторах. Такой подход обеспечивает более полное представление о молекуле, учитывая как теоретические, так и практические данные.
На выходе обеих голов формируются эмбеддинги — векторные представления, отражающие ключевые характеристики масел и молекул с разных точек зрения. Они объединяются и подаются на полносвязную нейронную сеть, которая выполняет окончательное предсказание целевого параметра, будь то биологическая активность, токсичность или другие свойства. Использование подобной архитектуры позволяет эффективно интегрировать разнородные данные, что способствует повышению точности и надежности предсказаний.
Преимущества:
- Объединение расчетных и экспериментальных данных позволяет модели учитывать как теоретические, так и эмпирические аспекты молекул. Кроме того, инвариантность к входному графу позволяет предсказывать значение на смесях с разным количестве компонентов.
- Архитектура может быть адаптирована под различные задачи, включая классификацию, регрессию и другие.
Ограничения:
- Необходимость в большом объеме качественных данных для обучения модели.
- Требовательность к вычислительным мощностям, а также сложность технической реализации.
Пайплайн №2
Данный подход основан практически на тех же принципах, что и первый пайплайн. Однако в данном случае графовые сверточные нейронные сети заменяются на графовые сети с механизмом внимания. В обычных графовых слоях все соседние узлы вносят одинаковый вклад при агрегации информации, что может приводить к потере значимых деталей.
Графовые сети с механизмом внимания, напротив, использует механизм внимания, позволяющий присваивать различную важность каждому соседу на основе их признаков. Кроме того, данные нейронные сети эффективно справляются с объектами, содержащими разнообразные подструктуры и иерархии, благодаря способности фокусироваться на наиболее информативных частях графа. Это позволяет модели учитывать сложные взаимосвязи внутри молекулы, что критично для точного моделирования ее свойств.
Преимущества:
- Благодаря способности присваивать разные веса соседним узлам, данная архитектура демонстрирует повышенную устойчивость к структурному шуму в графе, что особенно важно при работе с реальными молекулярными данными, содержащими погрешности.
- Механизм внимания предоставляет возможность визуализировать, какие части компонентов масел наиболее влияют на предсказание, что может быть полезно для последующего анализа и разработки новых смесей.
Ограничения:
- Необходимость в большом объеме качественных данных для обучения модели.
- Механизм внимания требует еще больше дополнительных вычислений для определения весов между узлами, что может привести к увеличению времени обучения и потребности в вычислительных ресурсах, особенно на больших графах.
- При увеличении числа слоев GAT может столкнуться с проблемой over-squashing, когда информация из удаленных узлов становится искаженной или теряется, что ограничивает способность модели захватывать долгосрочные зависимости в графе.
Пайплайн №3
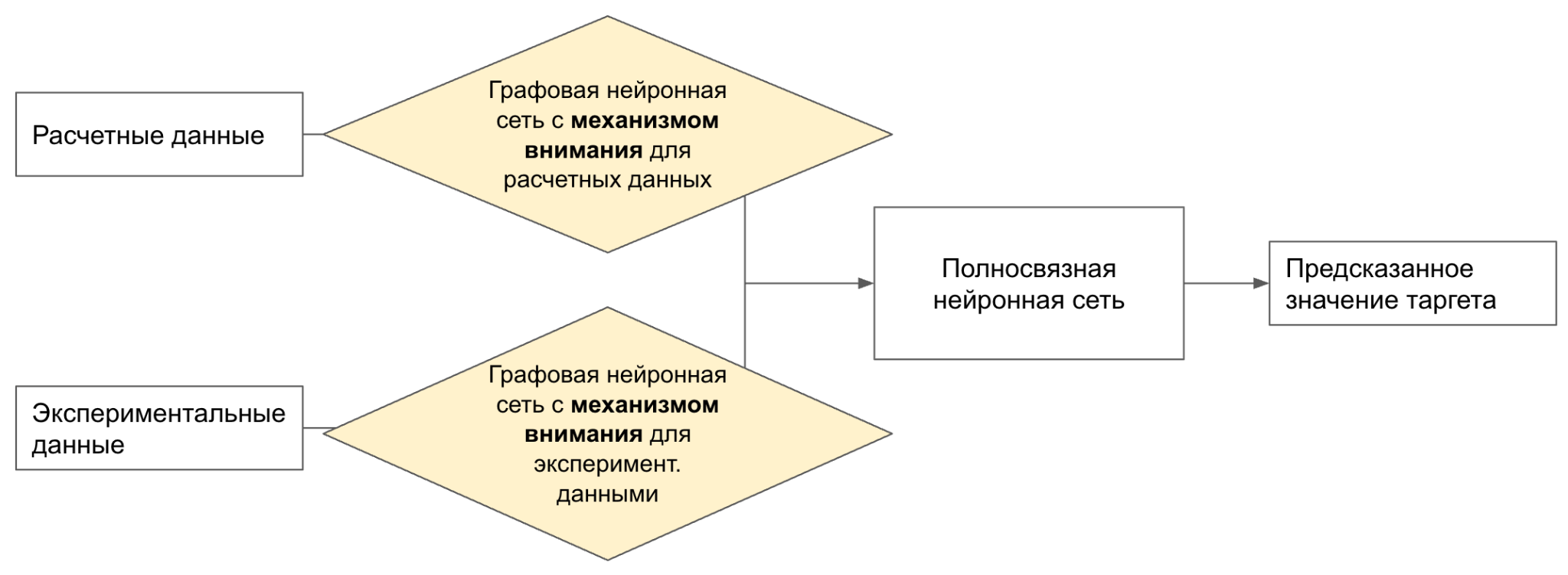
На вход модели одновременно подаются расчетные и экспериментальные данные. Эти данные конвертируются в графовую форму.
Далее информация поступает в графовую нейронную сеть с механизмом внимания. Здесь происходит агрегация признаков от соседних узлов с учетом их значимости. В отличие от классических графовых сверточных сетей, где все соседи имеют равный вес, механизм внимания позволяет адаптивно вычислять вклад каждого узла, что особенно важно в случае молекул со сложной структурой. Такой подход позволяет точнее учитывать контекст, локальные особенности и влиятельные фрагменты молекулы.
После этого из графовой сети извлекаются эмбеддинги и подаются на полносвязную нейронную сеть, задача которой — интерпретировать полученные признаки и выполнить окончательное предсказание.
На последнем этапе формируется предсказанное значение таргета — целевого параметра, который может представлять собой, например, эффективность соединения, его токсичность, сродство к рецептору или иной значимый молекулярный показатель.
По сравнению с предыдущими подходами, представленная на схеме архитектура отличается более интегрированной и унифицированной структурой. Если в первом и втором варианте использовалась двухголовая архитектура, где одна ветка обрабатывала расчетные данные, а другая — экспериментальные, то здесь оба типа данных объединены уже на входе и подаются в одну графовую нейронную сеть с механизмом внимания. Это делает модель более компактной и потенциально более устойчивой за счет одновременного обучения на смешанном источнике признаков.
Вместо того чтобы разделять потоки информации, как в первом пайплайне, или фокусироваться исключительно на структурной информации, как во втором, текущий подход предлагает целостное представление молекулы, где внимание внутри графа динамически адаптируется как к структуре, так и к дополнительным эмпирическим данным. Это позволяет модели гибко учитывать взаимосвязь между химической структурой и реальными физико-химическими характеристиками соединения.
Преимущества:
- Требуется гораздо меньше вычислительных ресурсов по сравнению с предыдущими реализациями.
- Наличие механизма внимания.
- Не требуется оптимизация двух отдельных голов.
Ограничения:
- Все также необходимы большие объемы данных.
- Смещение внимания на другие признаки.
На данном этапе участникам необходимо реализовать и протестировать все три ранее разработанных подхода для предсказания целевого параметра на подготовленных данных (этапы 2 и 3). Для каждого подхода требуется:
- Создать модель или набор моделей, использующих выбранные алгоритмы и методы обработки данных, адаптированные для работы с SMILES и экспериментальными данными.
- Обучить разработанные модели с проведением настройки гиперпараметров, используя тренировочные и валидационные выборки. Основным критерием оценки является средняя абсолютная ошибка (MAE). Участникам следует обеспечить корректность обучения, реализовать контроль переобучения и задокументировать динамику обучения.
- Провести детальный экспериментальный анализ с визуализацией результатов. В этом разделе необходимо представить и проанализировать графики динамики обучения (графики изменения MAE на обучающем и валидационном наборах).
После реализации и обучения моделей необходимо сформулировать следующие выводы в виде текстового отчета:
- Определить, какой из подходов продемонстрировал наилучшую точность по заданной метрике, и обосновать возможные причины его превосходства (например, особенности архитектуры, методы предобработки данных, эффективность оптимизации гиперпараметров).
- Провести сравнительный анализ всех реализованных подходов, выделив их ключевые преимущества и недостатки, а также оценить сложность реализации каждого из них.
Справочные материалы: библиотеки машинного обучения (например, scikit-learn, TensorFlow, PyTorch), Pandas, seaborn, matplotlib.
Основные роли: программист по машинному обучению, программист-математик.
Вспомогательные роли: химик.
Формат ответа: скрипты пайплайнов формата .py, названные по форме (pipeline_*номер пайплайна*_ФИО.py) на языке программирования Python версии 3.7 или выше. Скрипты должны быть сохранены в папке pipelines. Также необходимо сохранить веса модели в соответствующем формате для последующего импорта и оценки. Текстовый файл с отчетом в формате .pdf, расположенный в корне проекта.
Количество попыток: 1.
- Скрипт написан на Python версии 3.7 или выше, корректно выполняется и соблюдается заданный формат входных и выходных данных — 5 баллов, при несоблюдении условий баллы не начисляются.
- За каждую рассчитанную и оптимизированную модель, адаптированную для работы с SMILES и экспериментальными данными — 2 балла (максимум 6 моделей, то есть до 12 баллов) с учетом контроля переобучения; если при обучении используются тренировочные, валидационные и/или тестовые датасеты с целью достижения минимума ошибки (или максимума точности), за задание баллы не засчитываются.
- Подробный экспериментальный анализ — до 5 баллов.
- Текстовый отчет согласно заданию — до 2 баллов.
- При невозможности воспроизвести результаты моделей и/или пайплайна за задание — 0 баллов.
- Максимальное количество возможных баллов — 25.
Пример решения задачи.
В данном эксперименте реализованы три подхода для предсказания целевого параметра масла с использованием графовых нейронных сетей. Все модели используют различные архитектурные особенности и способы интеграции расчетных и экспериментальных данных.
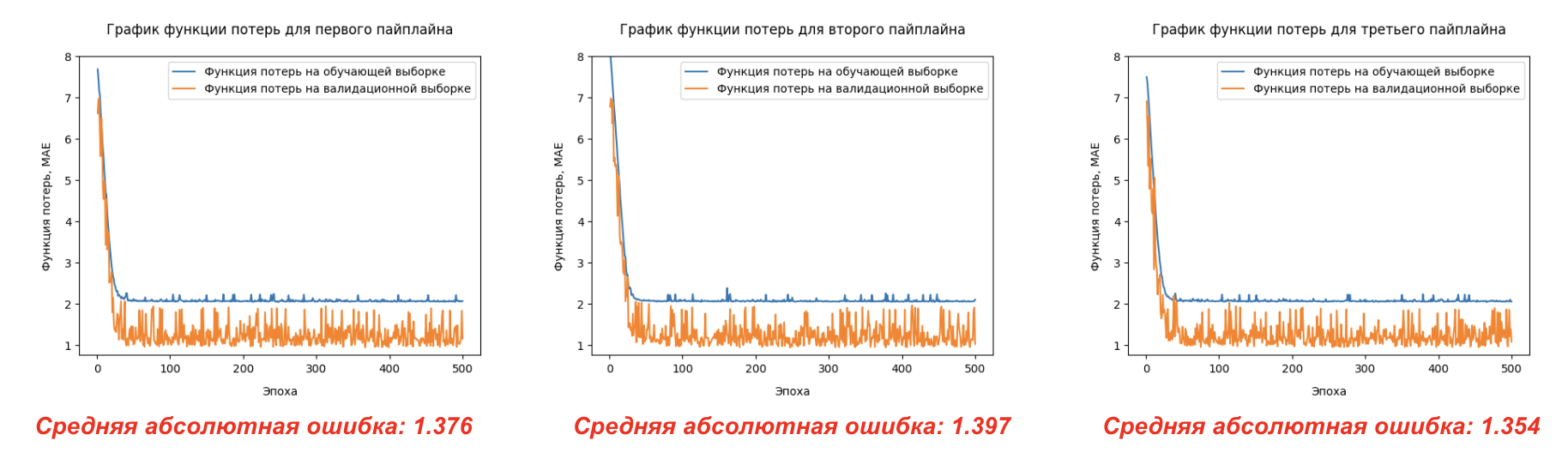
Основной метрикой для оценки работы моделей была выбрана средняя абсолютная ошибка (MAE), которая позволяет измерить отклонение предсказанных значений от реальных на тестовой выборке. На графиках зависимости функции потерь от количества эпох для каждого из пайплайна видно, что все пайплайны демонстрируют примерно схожую тендцию сходимости, а также примерно одинаковую среднюю абсолютную ошибку.
Лучшим оказался пайплайн № 3, что указывает на хорошую способность модели учитывать как теоретические, так и экспериментальные данные одновременно. Графики динамики MAE на обучающем и валидационном наборах данных показывают стабильное снижение ошибки без явных признаков переобучения.
Такие результаты, вероятнее всего, связаны с одинаковой структурой данных. Вместо того чтобы обрабатывать данные в отдельных потоках (как в двухголовой архитектуре первого пайплайна), модель сразу получает комбинированную информацию, что упрощает структуру модели и позволяет более эффективно учитывать взаимосвязи между расчетными и экспериментальными данными.
Кроме того, одновременная работа с обоими типами данных на входе позволяет модели более точно учитывать все аспекты молекулы как теоретические (структурные), так и эмпирические (физико-химические). Это способствует улучшению точности предсказания целевых параметров.
Пример программы-решения
Пайплайн №1
Ниже представлено решение на языке Python.
import pandas as pd
import numpy as np
import torch
from sklearn.model_selection import train_test_split
from torch import nn
from torch_geometric.data import Data
from torch_geometric.loader import DataLoader
from torch_geometric.nn import GATv2Conv, GCNConv, global_mean_pool
def csv_to_json(df):
possible_targets = ['oil_property_value']
target_cols = [col for col in possible_targets if col in df.columns]
blends = []
grouped_blends = df.groupby('blend_id', sort=False)
for blend_id, blend_group in grouped_blends:
unique_targets = blend_group.drop_duplicates(subset=target_cols)
if len(unique_targets) != 1:
raise ValueError(f"Для blend_id {blend_id} найдено несколько уникальных значений целевых переменных.")
target_values = unique_targets.iloc[0][target_cols].to_dict()
grouped_components = blend_group.groupby(
['component_name', 'component_type_title', 'mass_fraction'], sort=False
)
components = []
for (component_name, component_type_title, mass_fraction), component_group in grouped_components:
component_properties = []
for _, prop_row in component_group.iterrows():
property_dict = {
"param_title": int(prop_row['component_param_title']),
"value": float(prop_row['component_param_value'])
}
component_properties.append(property_dict)
component_dict = {
"component_name": int(component_name),
"component_type_title": int(component_type_title),
"component_mass_fraction": float(mass_fraction),
"component_properties": component_properties
}
components.append(component_dict)
blend_dict = {
"blend_id": str(blend_id),
"components": components
}
for key, value in target_values.items():
blend_dict[key] = float(value)
blends.append(blend_dict)
json_structure = {
"blends": blends
}
return json_structure
class Universal_Dataset:
def __init__(self, data):
self.data = data
self.graphs = []
self.excluded_params = {19, 18, 33, 16, 17} # Исключенные param_title
for blend in self.data:
# Контейнеры для двух графов
main_data = {"x": [], "edges": [], "y": blend.get('oil_property_value')}
excluded_data = {"x": [], "edges": [], "y": blend.get('oil_property_value')}
# Базовые узлы для обоих графов
for component in blend["components"]:
# Добавляем базовые узлы (type, id, mass) в оба графа
base_nodes = [
[int(component["component_type_title"])],
[int(component["component_name"])],
[float(component["component_mass_fraction"])]
]
# Индексы базовых узлов
type_idx_main = len(main_data["x"])
main_data["x"].extend(base_nodes)
type_idx_excl = len(excluded_data["x"])
excluded_data["x"].extend(base_nodes)
# Связи между базовыми узлами
main_data["edges"] += [
(type_idx_main, type_idx_main + 1),
(type_idx_main, type_idx_main + 2)
]
excluded_data["edges"] += [
(type_idx_excl, type_idx_excl + 1),
(type_idx_excl, type_idx_excl + 2)
]
# Обработка параметров компонента
for param in component["component_properties"]:
value = param["value"]
param_title = param["param_title"]
if np.isnan(value):
continue
# Выбираем целевой граф
if param_title in self.excluded_params:
target = excluded_data
type_idx = type_idx_excl
else:
target = main_data
type_idx = type_idx_main
# Добавляем узлы параметра
value_idx = len(target["x"])
target["x"].append([value])
target["x"].append([param_title])
# Связи: component_type -> value -> param_title
target["edges"] += [
(type_idx, value_idx),
(value_idx, value_idx + 1)
]
# Создаем объекты Data
main_graph = Data(
x=torch.tensor(main_data["x"], dtype=torch.float),
edge_index=torch.tensor(main_data["edges"], dtype=torch.long).t().contiguous(),
y=torch.tensor([main_data["y"]], dtype=torch.float),
mixture=blend['blend_id']
)
excluded_graph = Data(
x=torch.tensor(excluded_data["x"], dtype=torch.float),
edge_index=torch.tensor(excluded_data["edges"], dtype=torch.long).t().contiguous(),
y=torch.tensor([excluded_data["y"]], dtype=torch.float),
mixture=blend['blend_id']
)
self.graphs.append({
"theoretical": main_graph,
"experimental": excluded_graph
})
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.graphs[idx]
class Pipeline1GCN(torch.nn.Module):
def __init__(self):
super(Pipeline1GCN, self).__init__()
# ТЕОРЕТИЧЕСКИЕ ДАННЫЕ
input_size = 1
self.num_gcn_layers = 2
self.num_linear_layers = 3
self.hidden_size = 64
self.gcn_layers_theor = nn.ModuleList()
for index in range(self.num_gcn_layers):
self.gcn_layers_theor.append(
GCNConv(input_size, self.hidden_size)
)
self.gcn_layers_theor.append(nn.LeakyReLU())
input_size = self.hidden_size
self.hidden_size *= 2
# ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
input_size = 1
self.hidden_size = 64
self.gcn_layers_exp = nn.ModuleList()
for index in range(self.num_gcn_layers):
self.gcn_layers_exp.append(
GCNConv(input_size, self.hidden_size)
)
self.gcn_layers_exp.append(nn.LeakyReLU())
input_size = self.hidden_size
self.hidden_size *= 2
# Полносвязные слои
self.layers = nn.ModuleList()
for index in range(self.num_linear_layers):
output_size = max(1, 2 ** (int(np.log2(self.hidden_size)) - index))
self.layers.append(nn.LazyLinear(output_size))
self.layers.append(nn.BatchNorm1d(output_size))
self.layers.append(nn.LeakyReLU())
self.hidden_size = output_size
if self.hidden_size > 1:
self.layers.append(nn.LazyLinear(1))
def forward(self, x_t, x_e):
x_t, edge_index, batch = x_t.x, x_t.edge_index, x_t.batch
for layer in self.gcn_layers_theor:
if isinstance(layer, nn.LeakyReLU):
x_t = layer(x_t)
else:
x_t = layer(x_t, edge_index)
x_t = global_mean_pool(x_t, batch)
x_e, edge_index, batch = x_e.x, x_e.edge_index, x_e.batch
for layer in self.gcn_layers_exp:
if isinstance(layer, nn.LeakyReLU):
x_e = layer(x_e)
else:
x_e = layer(x_e, edge_index)
x_e = global_mean_pool(x_e, batch)
x = torch.cat((x_t, x_e), dim=1)
for layer in self.layers:
x = layer(x)
return x
df_exp = pd.read_csv('./output_data/prepared_data.csv')
df_exp_json = csv_to_json(df_exp)['blends']
train, test = train_test_split(df_exp_json, test_size=0.1, shuffle=True, random_state=23)
train_exp_dataset = Universal_Dataset(train)
test_exp_dataset = Universal_Dataset(test)
train_exp_dataloader = DataLoader(train_exp_dataset, batch_size=16, shuffle=True)
val_exp_dataloader = DataLoader(test_exp_dataset, batch_size=16, shuffle=True)
model = Pipeline1GCN()
device = "cuda" if torch.cuda.is_available() else "cpu"
model.to(device)
criterion = nn.L1Loss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
scheduler = torch.optim.lr_scheduler.CyclicLR(
optimizer, base_lr=0.0001, max_lr=0.001, step_size_down=15, step_size_up=15
)
metrics = {
'epoch': [],
'train_loss': [],
'val_loss': [],
'lr': []
}
best_val_loss = float('inf')
# Training loop
for epoch in range(500):
# Training phase
model.train()
train_loss = 0.0
train_preds = []
train_targets = []
for batch in train_exp_dataloader:
exp = batch["experimental"].to(device)
theor = batch["theoretical"].to(device)
optimizer.zero_grad()
outputs = model(theor, exp)
loss = criterion(outputs, exp.y)
loss.backward()
optimizer.step()
train_loss += loss.item()
train_preds.extend(outputs.detach().cpu().numpy())
train_targets.extend(exp.y.detach().cpu().numpy())
avg_train_loss = train_loss / len(train_exp_dataloader)
# Validation phase
model.eval()
val_loss = 0.0
val_preds = []
val_targets = []
with torch.no_grad():
for batch in val_exp_dataloader:
exp = batch["experimental"].to(device)
theor = batch["theoretical"].to(device)
outputs = model(theor, exp)
loss = criterion(outputs, exp.y)
val_loss += loss.item()
val_preds.extend(outputs.cpu().numpy())
val_targets.extend(exp.y.cpu().numpy())
avg_val_loss = val_loss / len(val_exp_dataloader)
# Update scheduler
scheduler.step(avg_val_loss)
# Store metrics
metrics['epoch'].append(epoch + 1)
metrics['train_loss'].append(avg_train_loss)
metrics['val_loss'].append(avg_val_loss)
metrics['lr'].append(optimizer.param_groups[0]['lr'])
# Print progress
print(f'Epoch {epoch+1}/{500}')
print(f'Train Loss: {avg_train_loss:.4f} | Val Loss: {avg_val_loss:.4f}')
print(f'Learning Rate: {optimizer.param_groups[0]["lr"]:.6f}')
print('-' * 50)
# Save metrics
pd.DataFrame(metrics).to_csv('pipe_1_training_metrics.csv', index=False)
# Save best model
if avg_val_loss < best_val_loss:
best_val_loss = avg_val_loss
torch.save(model.state_dict(), 'pipe_1_best_model.pth')Пайплайн №2
Ниже представлено решение на языке Python.
class Universal_Dataset:
def __init__(self, data):
self.data = data
self.graphs = []
self.excluded_params = {19, 18, 33, 16, 17} # Исключенные param_title
for blend in self.data:
# Контейнеры для двух графов
main_data = {"x": [], "edges": [], "y": blend.get('oil_property_value')}
excluded_data = {"x": [], "edges": [], "y": blend.get('oil_property_value')}
# Базовые узлы для обоих графов
for component in blend["components"]:
# Добавляем базовые узлы (type, id, mass) в оба графа
base_nodes = [
[int(component["component_type_title"])],
[int(component["component_name"])],
[float(component["component_mass_fraction"])]
]
# Индексы базовых узлов
type_idx_main = len(main_data["x"])
main_data["x"].extend(base_nodes)
type_idx_excl = len(excluded_data["x"])
excluded_data["x"].extend(base_nodes)
# Связи между базовыми узлами
main_data["edges"] += [
(type_idx_main, type_idx_main + 1),
(type_idx_main, type_idx_main + 2)
]
excluded_data["edges"] += [
(type_idx_excl, type_idx_excl + 1),
(type_idx_excl, type_idx_excl + 2)
]
# Обработка параметров компонента
for param in component["component_properties"]:
value = param["value"]
param_title = param["param_title"]
if np.isnan(value):
continue
# Выбираем целевой граф
if param_title in self.excluded_params:
target = excluded_data
type_idx = type_idx_excl
else:
target = main_data
type_idx = type_idx_main
# Добавляем узлы параметра
value_idx = len(target["x"])
target["x"].append([value])
target["x"].append([param_title])
# Связи: component_type -> value -> param_title
target["edges"] += [
(type_idx, value_idx),
(value_idx, value_idx + 1)
]
# Создаем объекты Data
main_graph = Data(
x=torch.tensor(main_data["x"], dtype=torch.float),
edge_index=torch.tensor(main_data["edges"], dtype=torch.long).t().contiguous(),
y=torch.tensor([main_data["y"]], dtype=torch.float),
mixture=blend['blend_id']
)
excluded_graph = Data(
x=torch.tensor(excluded_data["x"], dtype=torch.float),
edge_index=torch.tensor(excluded_data["edges"], dtype=torch.long).t().contiguous(),
y=torch.tensor([excluded_data["y"]], dtype=torch.float),
mixture=blend['blend_id']
)
self.graphs.append({
"theoretical": main_graph,
"experimental": excluded_graph
})
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.graphs[idx]
class Pipeline2GAT(torch.nn.Module):
def __init__(self):
super(Pipeline2GAT, self).__init__()
# ТЕОРЕТИЧЕСКИЕ ДАННЫЕ
input_size = 1
self.num_gat_layers = 2
self.num_linear_layers = 3
self.hidden_size = 64
self.gat_layers_theor = nn.ModuleList()
for index, _ in enumerate(range(self.num_gat_layers)):
if index + 1 == self.num_gat_layers:
concat = True
else:
concat = False
self.gat_layers_theor.append(
GATv2Conv(
input_size,
self.hidden_size,
heads=20,
concat=concat,
dropout=0.2,
)
)
self.gat_layers_theor.append(nn.LeakyReLU())
input_size = self.hidden_size
self.hidden_size *= 2
# ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
input_size = 1
self.num_gat_layers = 2
self.num_linear_layers = 3
self.hidden_size = 64
self.gat_layers_exp = nn.ModuleList()
for index, _ in enumerate(range(self.num_gat_layers)):
if index + 1 == self.num_gat_layers:
concat = True
else:
concat = False
self.gat_layers_exp.append(
GATv2Conv(
input_size,
self.hidden_size,
heads=20,
concat=concat,
dropout=0.2,
)
)
self.gat_layers_exp.append(nn.LeakyReLU())
input_size = self.hidden_size
self.hidden_size *= 2
self.layers = nn.ModuleList()
for index, _ in enumerate(range(self.num_linear_layers)):
output_size = max(1, 2 ** (int(np.log2(self.hidden_size)) - index))
self.layers.append(nn.LazyLinear(output_size))
self.layers.append(nn.BatchNorm1d(output_size))
self.layers.append(nn.LeakyReLU())
self.hidden_size = output_size
if self.hidden_size > 1:
self.layers.append(nn.LazyLinear(1))
def forward(self, x_t, x_e):
x_t, edge_index, batch = x_t.x, x_t.edge_index, x_t.batch
for layer in self.gat_layers_theor:
if isinstance(layer, nn.LeakyReLU):
x_t = layer(x_t)
else:
x_t = layer(x_t, edge_index)
x_t = global_mean_pool(x_t, batch)
x_e, edge_index, batch = x_e.x, x_e.edge_index, x_e.batch
for layer in self.gat_layers_exp:
if isinstance(layer, nn.LeakyReLU):
x_e = layer(x_e)
else:
x_e = layer(x_e, edge_index)
x_e = global_mean_pool(x_e, batch)
x = torch.cat((x_t, x_e), dim=1)
for layer in self.layers:
x = layer(x)
return x
df = pd.read_csv('./output_data/prepared_data.csv')
df_json = csv_to_json(df)['blends']
train, test = train_test_split(df_json, test_size=0.1, shuffle=True, random_state=23)
train_exp_dataset = Universal_Dataset(train)
test_exp_dataset = Universal_Dataset(test)
train_exp_dataloader = DataLoader(train_exp_dataset, batch_size=16, shuffle=True)
val_exp_dataloader = DataLoader(test_exp_dataset, batch_size=16, shuffle=True)
model = Pipeline2GAT()
device = "cuda" if torch.cuda.is_available() else "cpu"
model.to(device)
criterion = nn.L1Loss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
scheduler = torch.optim.lr_scheduler.CyclicLR(
optimizer, base_lr=0.0001, max_lr=0.001, step_size_down=15, step_size_up=15
)
# Initialize metrics tracking
metrics = {
'epoch': [],
'train_loss': [],
'val_loss': [],
'lr': []
}
best_val_loss = float('inf')
# Training loop
for epoch in range(500):
# Training phase
model.train()
train_loss = 0.0
train_preds = []
train_targets = []
for batch in train_exp_dataloader:
exp = batch["experimental"].to(device)
theor = batch["theoretical"].to(device)
optimizer.zero_grad()
outputs = model(theor, exp)
loss = criterion(outputs, exp.y)
loss.backward()
optimizer.step()
train_loss += loss.item()
train_preds.extend(outputs.detach().cpu().numpy())
train_targets.extend(exp.y.detach().cpu().numpy())
avg_train_loss = train_loss / len(train_exp_dataloader)
# Validation phase
model.eval()
val_loss = 0.0
val_preds = []
val_targets = []
with torch.no_grad():
for batch in val_exp_dataloader:
exp = batch["experimental"].to(device)
theor = batch["theoretical"].to(device)
outputs = model(theor, exp)
loss = criterion(outputs, exp.y)
val_loss += loss.item()
val_preds.extend(outputs.cpu().numpy())
val_targets.extend(exp.y.cpu().numpy())
avg_val_loss = val_loss / len(val_exp_dataloader)
# Update scheduler
scheduler.step(avg_val_loss)
# Store metrics
metrics['epoch'].append(epoch + 1)
metrics['train_loss'].append(avg_train_loss)
metrics['val_loss'].append(avg_val_loss)
metrics['lr'].append(optimizer.param_groups[0]['lr'])
# Print progress
print(f'Epoch {epoch+1}/{500}')
print(f'Train Loss: {avg_train_loss:.4f} | Val Loss: {avg_val_loss:.4f}')
print(f'Learning Rate: {optimizer.param_groups[0]["lr"]:.6f}')
print('-' * 50)
# Save metrics
pd.DataFrame(metrics).to_csv('pipe_2_training_metrics.csv', index=False)
# Save best model
if avg_val_loss < best_val_loss:
best_val_loss = avg_val_loss
torch.save(model.state_dict(), 'pipe_2_best_model.pth')Пайплайн №3
Ниже представлено решение на языке Python.
class Universal_Dataset:
def __init__(self, data):
self.data = data
self.graphs = []
for idx in range(len(self)):
blend = self.data[idx]
edges = []
target = blend.get('oil_property_value')
last_index = -1
component_values = []
component_ids = []
for component in blend["components"]:
mass = component["component_mass_fraction"]
component_id = component["component_name"]
component_type = component["component_type_title"]
component_values.append([int(component_type)])
component_values.append([int(component_id)])
component_values.append([float(mass)])
component_type_index = last_index + 1
component_id_index = last_index + 2
mass_index = last_index + 3
last_index += 3
edges.append((component_type_index, component_id_index))
edges.append((component_type_index, mass_index))
component_ids.append(component_id_index)
all_properties = component["component_properties"]
for param in all_properties:
value = param["value"]
if np.isnan(value):
continue
else:
param_title = param["param_title"]
index_property = last_index + 1
component_values.append([value])
edges.append((component_type_index, index_property))
index_param_title = last_index + 2
component_values.append([param_title])
edges.append((index_property, index_param_title))
last_index += 2
for i in range(len(component_ids)):
for j in range(i + 1, len(component_ids)):
edges.append((component_ids[i], component_ids[j]))
edge_index = torch.tensor(edges, dtype=torch.long).t().contiguous()
x = torch.tensor(np.array(component_values), dtype=torch.float)
y = torch.tensor([target], dtype=torch.float)
self.graphs.append(Data(x=x, edge_index=edge_index, y=y, mixture=blend['blend_id']))
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.graphs[idx]
class Pipeline3GAT(torch.nn.Module):
def __init__(self):
super(Pipeline3GAT, self).__init__()
input_size = 1
self.num_gat_layers = 2
self.num_linear_layers = 3
self.hidden_size = 64
self.gat_layers = nn.ModuleList()
self.layers = nn.ModuleList()
for index, _ in enumerate(range(self.num_gat_layers)):
if index + 1 == self.num_gat_layers:
concat = True
else:
concat = False
self.gat_layers.append(
GATv2Conv(
input_size,
self.hidden_size,
heads=20,
concat=concat,
dropout=0.2,
)
)
self.gat_layers.append(nn.LeakyReLU())
input_size = self.hidden_size
self.hidden_size *= 2
for index, _ in enumerate(range(self.num_linear_layers)):
output_size = max(1, 2 ** (int(np.log2(self.hidden_size)) - index))
self.layers.append(nn.LazyLinear(output_size))
self.layers.append(nn.BatchNorm1d(output_size))
self.layers.append(nn.LeakyReLU())
self.hidden_size = output_size
if self.hidden_size > 1:
self.layers.append(nn.LazyLinear(1))
def forward(self, x):
x, edge_index, batch = x.x, x.edge_index, x.batch
for layer in self.gat_layers:
if isinstance(layer, nn.LeakyReLU):
x = layer(x)
else:
x = layer(x, edge_index)
x = global_mean_pool(x, batch)
for layer in self.layers:
x = layer(x)
return x
df_exp = pd.read_csv('./output_data/prepared_data.csv')
df_exp_json = csv_to_json(df_exp)['blends']
train, test = train_test_split(df_exp_json, test_size=0.1, shuffle=True, random_state=23)
train_exp_dataset = Universal_Dataset(train)
test_exp_dataset = Universal_Dataset(test)
train_exp_dataloader = DataLoader(train_exp_dataset, batch_size=16, shuffle=True)
val_exp_dataloader = DataLoader(test_exp_dataset, batch_size=16, shuffle=True)
model = Pipeline3GAT()
device = "cuda" if torch.cuda.is_available() else "cpu"
model.to(device)
criterion = nn.L1Loss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
scheduler = torch.optim.lr_scheduler.CyclicLR(
optimizer, base_lr=0.0001, max_lr=0.001, step_size_down=15, step_size_up=15
)
# Initialize metrics tracking
metrics = {
'epoch': [],
'train_loss': [],
'val_loss': [],
'lr': []
}
best_val_loss = float('inf')
# Training loop
for epoch in range(500):
# Training phase
model.train()
train_loss = 0.0
train_preds = []
train_targets = []
for batch in train_exp_dataloader:
batch = batch.to(device)
optimizer.zero_grad()
outputs = model(batch)
loss = criterion(outputs, batch.y)
loss.backward()
optimizer.step()
train_loss += loss.item()
train_preds.extend(outputs.detach().cpu().numpy())
train_targets.extend(batch.y.detach().cpu().numpy())
avg_train_loss = train_loss / len(train_exp_dataloader)
# Validation phase
model.eval()
val_loss = 0.0
val_preds = []
val_targets = []
with torch.no_grad():
for batch in val_exp_dataloader:
batch = batch.to(device)
outputs = model(batch)
loss = criterion(outputs, batch.y)
val_loss += loss.item()
val_preds.extend(outputs.cpu().numpy())
val_targets.extend(batch.y.cpu().numpy())
avg_val_loss = val_loss / len(val_exp_dataloader)
# Update scheduler
scheduler.step(avg_val_loss)
# Store metrics
metrics['epoch'].append(epoch + 1)
metrics['train_loss'].append(avg_train_loss)
metrics['val_loss'].append(avg_val_loss)
metrics['lr'].append(optimizer.param_groups[0]['lr'])
# Print progress
print(f'Epoch {epoch+1}/{500}')
print(f'Train Loss: {avg_train_loss:.4f} | Val Loss: {avg_val_loss:.4f}')
print(f'Learning Rate: {optimizer.param_groups[0]["lr"]:.6f}')
print('-' * 50)
# Save metrics
pd.DataFrame(metrics).to_csv('pipe_3_training_metrics.csv', index=False)
# Save best model
if avg_val_loss < best_val_loss:
best_val_loss = avg_val_loss
torch.save(model.state_dict(), 'pipe_3_best_model.pth')После реализации всех трех подходов и их предварительного анализа на предыдущем шаге участникам необходимо выбрать наиболее эффективный подход среди трех опробованных и провести детальную оптимизацию гиперпараметров у моделей.
В конце участникам необходимо сформировать итоговый текстовый отчет по этапам №№ 5 и 6, в котором следует:
- Описать выбранный подход.
- Привести финальные метрики качества, а также сравнительную характеристику с результатами предыдущих экспериментов и подходов (пайплайнов).
- Указать ограничения и потенциальные сценарии применения (что произойдет с моделью, если входные данные сильно изменятся; насколько устойчив подход к шуму и другим искажениям).
- Сформировать рекомендации по дальнейшему развитию системы (возможность дообучения на более обширном наборе данных, интеграция дополнительных функций, использование ансамблей и т. д.).
Основные роли: программист по машинному обучению, программист-математик, химик.
Формат ответа: скрипты финального пайплайна формата .py, названного по форме (final_pipeline_*номер пайплайна*_ФИО.py) на языке программирования Python версии 3.7 или выше. Скрипт должны быть сохранен в папке pipelines. Также необходимо сохранить веса модели в соответствующем формате для последующего импорта и оценки. Текстовый файл с отчетом в формате .pdf, расположенный в корне проекта.
Количество попыток: 1.
- Максимальное количество баллов за задание — 15.
- За полный ответ на пункты №№ 2, 3, 4 — по 3 балла.
- За полный ответ на пункт № 1 — 2 балла; если при обучении/или оптимизации финального пайплайна используются тренировочные, валидационные и/или тестовые датасеты с целью достижения минимума ошибки (или максимума точности), то баллы не засчитываются.
- Оптимизированная модель вместе с кодом — 5 баллов.
- Текстовый отчет согласно заданию — до 2 баллов.
- Невозможность воспроизвести результаты моделей и/или пайплайна — 0 баллов.
Пример решения задачи.
На основании анализа средних абсолютных ошибок (MAE), а также с учетом устойчивости к шуму и вычислительной эффективности наиболее эффективным оказался пайплайн № 3. При оптимизации гиперпараметров удалось получить среднюю абсолютную ошибку 0,982, что является минимумом среди всех подходов. Его архитектура позволяет более полно интегрировать информацию, избегая дублирования и переобучения, при этом сохраняя интерпретируемость за счет attention-механизма.
Ограничения:
- Требовательность к объему данных: при недостатке данных возможна переадаптация под обучающую выборку.
- Смещение внимания: Attention может давать избыточный вес незначимым признакам, особенно в разреженных графах.
- Неустойчивость к радикальным изменениям структуры входных графов: модель обучена на текущем распределении данных и может быть чувствительна к новым типам компонентов/свойств.
Сценарии изменений
Если значительно изменится структура входных данных (например, появятся новые типы компонентов или значимо другие графы) — потребуется дообучение или полное переобучение модели на расширенном датасете. За счет механизма внимания и объединенной архитектуры модель устойчива к умеренным искажением и пропускам, особенно если они затрагивают менее значимые узлы.
Рекомендации по улучшению системы
Главное, что стоит сделать — увеличить размер выборки. Разработанные подходы имеют высокий потенциал для роста, в частности, при повышении качества и размера выборки будет также увеличиваться точность модели. Кроме того, важным фактором может стать разработка дополнительных подходов для умного заполнения пропусков, что, несомненно, повысит точность.
Пример программы-решения
Ниже представлено решение на языке Python.
import optuna
from optuna.trial import Trial
from optuna.samplers import TPESampler
from optuna.pruners import MedianPruner
import pandas as pd
import numpy as np
import torch
from sklearn.model_selection import train_test_split
from torch import nn
from torch_geometric.data import Data
from torch_geometric.loader import DataLoader
from torch_geometric.nn import GATv2Conv, global_mean_pool
def csv_to_json(df):
possible_targets = ['oil_property_value']
target_cols = [col for col in possible_targets if col in df.columns]
blends = []
grouped_blends = df.groupby('blend_id', sort=False)
for blend_id, blend_group in grouped_blends:
unique_targets = blend_group.drop_duplicates(subset=target_cols)
if len(unique_targets) != 1:
raise ValueError(f"Для blend_id {blend_id} найдено несколько уникальных значений целевых переменных.")
target_values = unique_targets.iloc[0][target_cols].to_dict()
grouped_components = blend_group.groupby(
['component_name', 'component_type_title', 'mass_fraction'], sort=False
)
components = []
for (component_name, component_type_title, mass_fraction), component_group in grouped_components:
component_properties = []
for _, prop_row in component_group.iterrows():
property_dict = {
"param_title": int(prop_row['component_param_title']),
"value": float(prop_row['component_param_value'])
}
component_properties.append(property_dict)
component_dict = {
"component_name": int(component_name),
"component_type_title": int(component_type_title),
"component_mass_fraction": float(mass_fraction),
"component_properties": component_properties
}
components.append(component_dict)
blend_dict = {
"blend_id": str(blend_id),
"components": components
}
for key, value in target_values.items():
blend_dict[key] = float(value)
blends.append(blend_dict)
json_structure = {
"blends": blends
}
return json_structure
class Universal_Dataset:
def __init__(self, data):
self.data = data
self.graphs = []
for idx in range(len(self)):
blend = self.data[idx]
edges = []
target = blend.get('oil_property_value')
last_index = -1
component_values = []
component_ids = []
for component in blend["components"]:
mass = component["component_mass_fraction"]
component_id = component["component_name"]
component_type = component["component_type_title"]
component_values.append([int(component_type)])
component_values.append([int(component_id)])
component_values.append([float(mass)])
component_type_index = last_index + 1
component_id_index = last_index + 2
mass_index = last_index + 3
last_index += 3
edges.append((component_type_index, component_id_index))
edges.append((component_type_index, mass_index))
component_ids.append(component_id_index)
all_properties = component["component_properties"]
for param in all_properties:
value = param["value"]
if np.isnan(value):
continue
else:
param_title = param["param_title"]
index_property = last_index + 1
component_values.append([value])
edges.append((component_type_index, index_property))
index_param_title = last_index + 2
component_values.append([param_title])
edges.append((index_property, index_param_title))
last_index += 2
for i in range(len(component_ids)):
for j in range(i + 1, len(component_ids)):
edges.append((component_ids[i], component_ids[j]))
edge_index = torch.tensor(edges, dtype=torch.long).t().contiguous()
x = torch.tensor(np.array(component_values), dtype=torch.float)
y = torch.tensor([target], dtype=torch.float)
self.graphs.append(Data(x=x, edge_index=edge_index, y=y, mixture=blend['blend_id']))
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.graphs[idx]
# Модифицированная модель для поддержки гиперпараметров из Optuna
class Pipeline3GAT(torch.nn.Module):
def __init__(self, trial: Trial = None):
super(Pipeline3GAT, self).__init__()
# Гиперпараметры по умолчанию
default_params = {
'num_gat_layers': 2,
'num_linear_layers': 3,
'hidden_size': 64,
'gat_heads': 20,
'gat_dropout': 0.2,
'use_batch_norm': True,
'activation': 'LeakyReLU'
}
# Если trial передан, выбираем гиперпараметры из Optuna
if trial is not None:
self.num_gat_layers = trial.suggest_int('num_gat_layers', 1, 4)
self.num_linear_layers = trial.suggest_int('num_linear_layers', 1, 5)
self.hidden_size = trial.suggest_categorical('hidden_size', [32, 64, 128, 256])
self.gat_heads = trial.suggest_int('gat_heads', 4, 32, step=4)
self.gat_dropout = trial.suggest_float('gat_dropout', 0.0, 0.5, step=0.1)
self.use_batch_norm = trial.suggest_categorical('use_batch_norm', [True, False])
self.activation = trial.suggest_categorical('activation', ['LeakyReLU', 'ReLU', 'ELU'])
else:
# Используем значения по умолчанию
for param, value in default_params.items():
setattr(self, param, value)
input_size = 1
self.gat_layers = nn.ModuleList()
self.layers = nn.ModuleList()
# GAT слои
for index in range(self.num_gat_layers):
if index + 1 == self.num_gat_layers:
concat = True
else:
concat = False
self.gat_layers.append(
GATv2Conv(
input_size,
self.hidden_size,
heads=self.gat_heads,
concat=concat,
dropout=self.gat_dropout,
)
)
# Добавляем функцию активации
if self.activation == 'LeakyReLU':
self.gat_layers.append(nn.LeakyReLU())
elif self.activation == 'ReLU':
self.gat_layers.append(nn.ReLU())
else: # ELU
self.gat_layers.append(nn.ELU())
input_size = self.hidden_size
self.hidden_size *= 2
# Линейные слои
for index in range(self.num_linear_layers):
output_size = max(1, 2 ** (int(np.log2(self.hidden_size)) - index))
self.layers.append(nn.LazyLinear(output_size))
if self.use_batch_norm:
self.layers.append(nn.BatchNorm1d(output_size))
# Функция активации
if self.activation == 'LeakyReLU':
self.layers.append(nn.LeakyReLU())
elif self.activation == 'ReLU':
self.layers.append(nn.ReLU())
else: # ELU
self.layers.append(nn.ELU())
self.hidden_size = output_size
if self.hidden_size > 1:
self.layers.append(nn.LazyLinear(1))
def forward(self, x):
x, edge_index, batch = x.x, x.edge_index, x.batch
for layer in self.gat_layers:
if isinstance(layer, (nn.LeakyReLU, nn.ReLU, nn.ELU)):
x = layer(x)
else:
x = layer(x, edge_index)
x = global_mean_pool(x, batch)
for layer in self.layers:
x = layer(x)
return x
# Функция для обучения модели
def train_model(model, train_loader, val_loader, optimizer, criterion, scheduler, device, epochs):
best_val_loss = float('inf')
for epoch in range(epochs):
model.train()
train_loss = 0.0
for batch in train_loader:
batch = batch.to(device)
optimizer.zero_grad()
outputs = model(batch)
loss = criterion(outputs, batch.y)
loss.backward()
optimizer.step()
train_loss += loss.item()
avg_train_loss = train_loss / len(train_loader)
# Валидация
model.eval()
val_loss = 0.0
with torch.no_grad():
for batch in val_loader:
batch = batch.to(device)
outputs = model(batch)
loss = criterion(outputs, batch.y)
val_loss += loss.item()
avg_val_loss = val_loss / len(val_loader)
# Обновление scheduler
if scheduler is not None:
scheduler.step(avg_val_loss)
# Сохранение лучшей модели
if avg_val_loss < best_val_loss:
best_val_loss = avg_val_loss
return best_val_loss
# Функция objective для Optuna
def objective(trial):
# Загрузка данных
df_exp = pd.read_csv('./output_data/prepared_data.csv')
df_exp_json = csv_to_json(df_exp)['blends']
train, test = train_test_split(df_exp_json, test_size=0.1, shuffle=True, random_state=23)
train_dataset = Universal_Dataset(train)
test_dataset = Universal_Dataset(test)
# Гиперпараметры для DataLoader
batch_size = trial.suggest_categorical('batch_size', [8, 16, 32, 64])
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
val_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=True)
# Создание модели с гиперпараметрами из Optuna
device = "cuda" if torch.cuda.is_available() else "cpu"
model = Pipeline3GAT(trial).to(device)
# Оптимизатор и его параметры
optimizer_name = trial.suggest_categorical('optimizer', ['Adam', 'AdamW', 'RMSprop', 'SGD'])
lr = trial.suggest_float('lr', 1e-5, 1e-2, log=True)
weight_decay = trial.suggest_float('weight_decay', 1e-6, 1e-2, log=True)
if optimizer_name == 'Adam':
optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=weight_decay)
elif optimizer_name == 'AdamW':
optimizer = torch.optim.AdamW(model.parameters(), lr=lr, weight_decay=weight_decay)
elif optimizer_name == 'RMSprop':
optimizer = torch.optim.RMSprop(model.parameters(), lr=lr, weight_decay=weight_decay)
else: # SGD
momentum = trial.suggest_float('momentum', 0.1, 0.9)
optimizer = torch.optim.SGD(model.parameters(), lr=lr, momentum=momentum, weight_decay=weight_decay)
# Scheduler
use_scheduler = trial.suggest_categorical('use_scheduler', [True, False])
if use_scheduler:
scheduler_type = trial.suggest_categorical('scheduler_type', ['ReduceLROnPlateau', 'CyclicLR'])
if scheduler_type == 'ReduceLROnPlateau':
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(
optimizer, mode='min', factor=0.5, patience=5
)
else: # CyclicLR
base_lr = trial.suggest_float('base_lr', 1e-6, 1e-4, log=True)
max_lr = trial.suggest_float('max_lr', 1e-4, 1e-2, log=True)
scheduler = torch.optim.lr_scheduler.CyclicLR(
optimizer, base_lr=base_lr, max_lr=max_lr, step_size_up=15, step_size_down=15
)
else:
scheduler = None
# Функция потерь
criterion = nn.L1Loss()
# Количество эпох для оптимизации (можно уменьшить для ускорения)
epochs = trial.suggest_int('epochs', 50, 200, step=50)
# Обучение модели
val_loss = train_model(model, train_loader, val_loader, optimizer, criterion, scheduler, device, epochs)
return val_loss
# Основная функция для оптимизации
def optimize_hyperparameters(n_trials=100):
# Создаем study для Optuna
sampler = TPESampler(seed=42)
pruner = MedianPruner(n_warmup_steps=10)
study = optuna.create_study(
direction='minimize',
sampler=sampler,
pruner=pruner
)
# Запускаем оптимизацию
study.optimize(objective, n_trials=n_trials)
# Выводим результаты
print("Number of finished trials: ", len(study.trials))
print("Best trial:")
trial = study.best_trial
print(" Value: ", trial.value)
print(" Params: ")
for key, value in trial.params.items():
print(f" {key}: {value}")
# Сохраняем лучшие параметры
best_params = trial.params
pd.DataFrame([best_params]).to_csv('best_hyperparameters.csv', index=False)
return best_params
# Запуск оптимизации
if __name__ == "__main__":
best_params = optimize_hyperparameters(n_trials=50)
# После оптимизации можно обучить финальную модель с лучшими параметрами
df_exp = pd.read_csv('./output_data/prepared_data.csv')
df_exp_json = csv_to_json(df_exp)['blends']
train, test = train_test_split(df_exp_json, test_size=0.1, shuffle=True, random_state=23)
train_dataset = Universal_Dataset(train)
test_dataset = Universal_Dataset(test)
train_loader = DataLoader(train_dataset, batch_size=best_params['batch_size'], shuffle=True)
val_loader = DataLoader(test_dataset, batch_size=best_params['batch_size'], shuffle=True)
device = "cuda" if torch.cuda.is_available() else "cpu"
model = Pipeline3GAT().to(device) # Используем значения по умолчанию, так как trial=None
# Настраиваем оптимизатор с лучшими параметрами
if best_params['optimizer'] == 'Adam':
optimizer = torch.optim.Adam(model.parameters(), lr=best_params['lr'], weight_decay=best_params['weight_decay'])
elif best_params['optimizer'] == 'AdamW':
optimizer = torch.optim.AdamW(model.parameters(), lr=best_params['lr'], weight_decay=best_params['weight_decay'])
elif best_params['optimizer'] == 'RMSprop':
optimizer = torch.optim.RMSprop(model.parameters(), lr=best_params['lr'], weight_decay=best_params['weight_decay'])
else: # SGD
optimizer = torch.optim.SGD(
model.parameters(),
lr=best_params['lr'],
momentum=best_params.get('momentum', 0.9),
weight_decay=best_params['weight_decay']
)
# Настраиваем scheduler с лучшими параметрами
if best_params['use_scheduler']:
if best_params['scheduler_type'] == 'ReduceLROnPlateau':
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(
optimizer, mode='min', factor=0.5, patience=5
)
else: # CyclicLR
scheduler = torch.optim.lr_scheduler.CyclicLR(
optimizer,
base_lr=best_params['base_lr'],
max_lr=best_params['max_lr'],
step_size_up=15,
step_size_down=15
)
else:
scheduler = None
criterion = nn.L1Loss()
# Обучаем финальную модель
final_val_loss = train_model(
model, train_loader, val_loader,
optimizer, criterion, scheduler,
device, epochs=500 # Больше эпох для финального обучения
)
print(f"Final validation loss: {final_val_loss:.4f}")
torch.save(model.state_dict(), 'final_best_model.pth')Максимальное количество баллов за задачу инженерного тура — 100. На каждом этапе оцениваются задачи №№ 1–6 согласно указанным критериям. Максимальное количество баллов за каждую задачу, количество попыток на задачу и рекомендуемые роли приведены в таблице ниже.
Команда-победитель определяется по наибольшей сумме баллов за задачи командного этапа. При одинаковом количестве баллов более высокий рейтинг будет у той команды, которая по итогам очного представления результатов работы набрала больше баллов от членов жюри, оценивающих самостоятельность участников (максимально 10 баллов) и качество ответов на вопросы членов жюри (максимально 10 баллов).
| Номер задачи | Количество баллов | Количество попыток | Рекомендованные роли |
|---|---|---|---|
| 1 | 10 | 1 | Основная роль: химик. Вспомогательные роли: программист по машинному обучению, программист математик. |
| 2 | 10 | 1 | Основные роли: химик, программист математик. |
| 3 | 25 | 1 | Основные роли: программист математик, программист по машинному обучению, химик |
| 4 | 15 | 1 | Основные роли: программист по машинному обучению, программист математик, химик |
| 5 | 25 | 1 | Основные роли: программист по машинному обучению, программист математик. Вспомогательные роли: химик |
| 6 | 15 | 1 | Основные роли: программист по машинному обучению, программист математик, химик. |