Предметный тур. Математика. 3 этап
Четверо друзей собираются купить подарок своему товарищу на день рождения, разделив стоимость подарка поровну. Ребята подсчитали расходы и сошлись во мнении, что было бы гораздо лучше, если бы взнос каждого оказался хотя бы на 30% меньше. Какое наименьшее число друзей следует еще позвать для покупки подарка?
Пусть стоимость подарка равна \(S\) руб. Тогда изначально друзья должны скинуться по \(S/4\) руб., но хотели бы не более, чем по \(\dfrac{S}{4} - 0{,}3 \cdot \dfrac{S}{4} = \dfrac{0{,}7S}{4}\) руб.
Обозначим через \(n\) количество друзей, которых нужно для этого позвать. Тогда должно выполняться неравенство \[(4 + n) \cdot \frac{0{,}7S}{4} \geqslant S.\] Отсюда \[n \geqslant \frac{4}{0{,}7} - 4 = \frac{12}{7}.\] Так как \(n\) — целое, то нужно позвать еще хотя бы двух друзей.
2.
Есть два натуральных числа \(x\) и \(y\). Известно, что их произведение равно \(66000\). Какое максимальное значение может принимать НОД этих чисел?
Представим произведение чисел \(x\) и \(y\) в виде произведения простых множителей: \[x\cdot y = 66000 = 2^4\cdot 3\cdot 5^3\cdot 11.\] Наибольший общий делитель чисел \(x\) и \(y\) не может содержать \(3\) и \(11\), так как они не могут быть одновременно делителями и \(x\), и \(y\). Число \(2\) может входить в НОД максимум во второй степени, число \(5\) — в первой. Таким образом, наибольшее значение \(\text{НОД}(x, y) = 2^2\cdot 5 = 20.\)
20.
Решить неравенство \[\sqrt{5-x} - \sqrt{3 + x} \geqslant x^2 + 6x - 7.\]
Заметим, что левая часть \[f(x) = \sqrt{5-x} - \sqrt{3 + x}\] определена при \(x \in [-3, 5]\) и убывает на области определения, причем \(f(1) = 0\). Правая часть неравенства может быть переписана в виде \[g(x) = (x + 3)^2 - 16,\] откуда видно, что она возрастает при \(x \in [-3, 5]\) и \(g(1) = 0\). Значит, ответом служит промежуток \([-3, 1]\).
\([-3, 1]\).
\(A, B, C\) — точки плоскости, не лежащие на одной прямой. Окружность с диаметром \(AB\) пересекает отрезки \(AC\) и \(BC\) в точках \(D\) и \(E\) соответственно. Найти площадь четырехугольника \(ABED\), если известно, что \(AC=5\), \(BC=8\), а угол между ними \(\angle C = 45°\).
Имеем \[S_{ABC} = \frac{1}{2}\cdot AC \cdot BC \cdot \sin C = \frac{1}{2} \cdot 5 \cdot 8 \cdot \frac{\sqrt{2}}{2} = 10 \sqrt{2}.\]
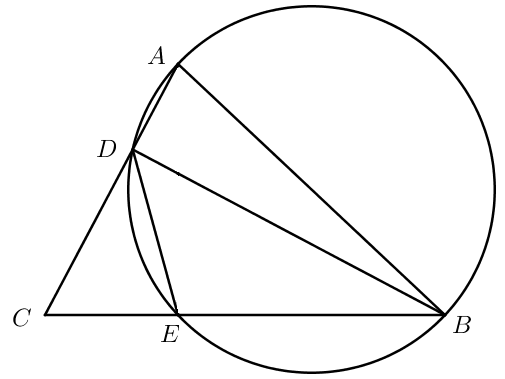
Четырехугольник \(ABED\) вписанный, значит, \(\angle ADE + \angle ABE = 180°\). Сумма смежных углов \(\angle ADE + \angle CDE = 180°\). Следовательно, \(\angle ABE = \angle CDE\). Тогда треугольники \(ABC\) и \(EDC\) подобны по двум углам (\(\angle ABE = \angle CDE\), угол \(\angle{C}\) — общий).
Проведем отрезок \(DB\). Угол \(\angle{ADB}\) опирается на диаметр, поэтому \(\angle ADB = 90°\), значит, смежный с ним \(\angle CDB = 90°\).
Треугольник \(CDB\) прямоугольный, поэтому \[\cos C = \frac{CD}{BC} = \cos 45° = \frac{\sqrt{2}}{2}.\]
Таким образом, треугольники \(EDC\) и \(ABC\) подобны с коэффициентом подобия \(\dfrac{CD}{BC} = \dfrac{\sqrt{2}}{2}\). Следовательно, \[\frac{S_{EDC}}{S_{ABC}} = \left(\frac{\sqrt{2}}{2}\right)^{2} = \frac{1}{2}.\]
Значит, \(S_{EDC} = \frac{1}{2} S_{ABC} = 5 \sqrt{2}\), \(S_{ABED} = S_{ABC} - S_{EDC} = 5 \sqrt{2}\).
\(5 \sqrt{2} \approx 7{,}07\).
Пусть на окружности некоторого радиуса случайным образом выбраны \(5\) точек. Сколько существует различных способов построить ровно \(4\) отрезка с концами в этих точках так, чтобы из любой точки можно было попасть в любую другую точку (возможно, проходя через другие точки)?
Всего существует \[C_{5}^2 = 10\] способов выбрать пару точек для проведения отрезка между ними. Значит, всего существует \[C_{10}^{4} = 210\] способов выбрать \(4\) пары точек для соединения. Осталось вычленить плохие соединения. Они бывают двух типов. Первый тип — точка оказалась изолированной, то есть она не соединена ни с одной из оставшихся точек. Способов выбрать эту точку оказывается \(5\), остальные точки можно соединять произвольно: количество способов выбрать \(2\) точки из \(4\) равно \[C_{4}^2 = 6,\] количество способов организовать \(4\) связи тогда равно \[C_{6}^{4} = 15,\] а значит, всего способов организовать такое соединение \[5 \cdot 15 = 75.\] Второй тип — ситуация, когда есть ровно 2 связные структуры — 2 точки соединены отрезком, а остальные — какой-то ломаной. Количество способов выбрать 2 точки для соединения отрезком равно \[C_{5}^2 = 10,\] и остается соединить оставшиеся \(3\) точки при помощи трех отрезков. Итого искомое число равно \[210 - 75 - 10 = 125.\]
125.
Известно, что \[11 \ldots 1_{2} = 100 \ldots 0_{1024} - 1,\] где число в левой части записано в двоичной системе счисления и содержит только единицы, а первое число в правой части записано в 1024-ичной системе счисления и содержит одну единицу и 2025 нулей. Сколько единиц содержит число в левой части?
Пусть число слева содержит \(n\) единиц. Тогда данное в условии уравнение равносильно \[2^{n} - 1 = 1024^{2025} - 1.\] Значит, \(2^{n} = 2^{10\cdot 2025}\), то есть \(n = 20250\).
20250.
Решить неравенство \[\log_3(7 - x) - \log_6(x - 5) \leqslant x^2 - 10x + 24.\]
Заметим, что левая часть \[f(x) = \log_3(7 - x) - \log_6(x - 5)\] определена при \(x \in (5, 7)\) и убывает на области определения, причем \(f(6) = 0\). Правая часть неравенства может быть переписана в виде \[g(x) = (x - 5)^2 - 1,\] откуда видно, что она возрастает при \(x \in (5, 7)\) и \(g(6) = 0\). Значит, ответом служит промежуток \([6, 7)\).
\([6, 7)\).
Два менеджера обрабатывают заявки клиентов на подключение к интернету. В понедельник вместе они обработали все заявки за 3 ч. Во вторник первый работал 2 ч, а второй — 1,5, в сумме они обработали 36 заявок. В среду первый обработал в пять раз больше заявок, чем второй в понедельник, а второй — в три раза больше, чем первый во вторник. При этом в среду первый работал на 1 ч дольше второго. Сколько заявок в 1 ч обрабатывает каждый менеджер?
Обозначим через \(v_{1}\) и \(v_{2}\) количество заявок в 1 ч, обрабатываемых первым и вторым менеджером соответственно.
Предложение из условия, касающееся вторника, можно записать в виде уравнения так: \[2 v_{1} + 1{,}5v_{2} = 36. \label{eq:IRS10-11text-1}\]
В среду первый менеджер обработал \(5 (3v_{2})\) заявок, а второй — \(3 (2v_{1})\). Тогда информация о среде формулируется в виде уравнения следующим образом: \[\frac{5(3v_{2})}{v_{1}} - \frac{3(2v_{1})}{v_{2}} = 1.\] Положим \(x = \dfrac{v_{2}}{v_{1}}\). Тогда \[15x - \frac{6}{x} = 1,\] что равносильно \[15x^{2} - x - 6 = 0.\] Это уравнение имеет два корня, один из которых отрицательный и не подходит по смыслу, а второй равен \(2/3\).
Подставляя \(v_{2} = \dfrac{2}{3}v_{1}\) в уравнение \eqref{eq:IRS10-11text-1}, получаем \(v_{1} = 12\). Следовательно, \(v_{2} = 8\).
12 и 8.
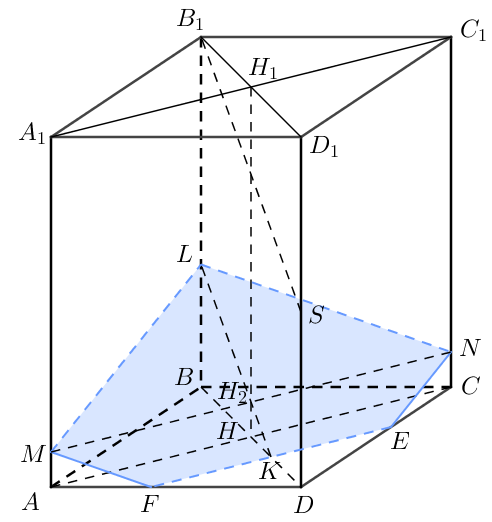
В правильной призме \(ABCDA_{1}B_{1}C_{1}D_{1}\) боковые ребра равны \(10 \sqrt{2}\), а стороны основания — 5. Точка \(E\) принадлежит \(DC\), а точка \(F\) принадлежит \(AD\), причем \(AF = EC = 2\). Точка \(S\) — середина ребра \(DD_{1}\). Найти площадь сечения призмы, проходящего через точки \(F\) и \(E\) параллельно прямой \(SB_{1}\).
Сначала построим сечение, площадь которого требуется вычислить.
- \(FE \cap BD = K\).
- \(KL \parallel SB_{1}\), \(L = KL \cap BB_{1}\), \(H_{2} = KL \cap HH_{1}\).
- Искомая плоскость содержит \(FE \parallel AC\), значит, сама параллельна \(AC\).
- \(H_{2} \in MN\), \(MN \parallel AC\), \(M = MN \cap AA_{1}\), \(N = MN \cap CC_{1}\).
- \(FMLNE\) — искомое сечение.
Теперь вычислим площадь сечения.
- Найдем косинус угла между построенной плоскостью и плоскостью основания. \(FE\) — ребро двугранного угла. \(FE \perp BK\), т. к. \(FE \parallel AC\), а \(AC \perp BK\) (диагонали квадрата). \(FE \perp LK\) (теорема о трех перепендикулярах). Далее \[\angle(FML, ABC) = \angle(LK, BK) = \angle BKL = \alpha.\] \(B_{1}D_{1} = 5 \sqrt{2}\), следовательно, треугольник \(B_{1}D_{1}S\) равнобедренный, \[\angle BKL = \angle SB_{1}D_{1} = 45° \quad \Rightarrow \quad \cos \alpha = \frac{\sqrt{2}}{2}.\]
\(FABCE\) — проекция \(FMLNE\) на плоскость основания.
\(AC = 5 \sqrt{2}\), \(FE = 3 \sqrt{2}\), \(KH = \dfrac{2}{5}\cdot \dfrac{1}{2} \cdot 5 \sqrt{2} = \sqrt{2}\).
Найдем \[S_{FABCE} = S_{ABC} + S_{ACEF} = \frac{25}{2} + \frac{5 \sqrt{2} + 3 \sqrt{2}}{2} \cdot \sqrt{2} = \frac{41}{2}.\]
- \[S_{FMLNE} = \frac{S_{FABCE}}{\cos \alpha} = \frac{41 \cdot 2}{2 \cdot \sqrt{2}} = \frac{41 \sqrt{2}}{2}.\]
\(\dfrac{41 \sqrt{2}}{2} \approx 29\).
Пусть на окружности некоторого радиуса случайным образом выбраны \(2025\) точек. Сколько существует способов выбрать из них два раза по две различные точки так, чтобы отрезки, соединяющие выбранные две точки соответственно не пересекались? Порядок выбора точек считать неважным.
Подсчет будем вести следующим образом: искомое число — это разность общего количества возможных отрезков и количества пересекающихся отрезков. Последнее число распадается на два слагаемых: первое отвечает количеству пар пересекающихся отрезков с точкой пересечения во внутренней точке для каждого из отрезков, а второе — количество пар пересекающихся отрезков с точкой пересечения на границе (обоих) отрезков — количество пар отрезков, выходящих из одной точки. Проведем подсчеты.
Не учитывая порядок, всего можем провести \[C_{2025}^2 = \frac{2025 \cdot 2024}{2} = 2025 \cdot 1012\] отрезков. Значит, не учитывая порядок, всего существует \[C_{2025 \cdot 1012}^2\] пар отрезков. Заметим, что любым четырем точкам из условия соответствует ровно одна конфигурация проведенных отрезков с внутренней точкой пересечения и наоборот. Значит, число пар пересекающихся отрезков с точкой пересечения во внутренней точке равно \[C_{2025}^4.\] Осталось вычислить число «смежных» отрезков. Из каждой точки можно провести \(C_{2024}^2\) пар отрезков, а значит, всего таких пар \[2025 \cdot C_{2024}^2.\] Итого, искомое число равно \[C_{2025 \cdot 1012}^2 - C_{2025}^4 - 2025 \cdot C_{2024}^2 = 1397112324300.\]
\(1397112324300\).






