Инженерный тур. 2 этап

Рассматривается мобильный робот с дифференциальной платформой и карта местности со статичными препятствиями. Требуется написать программу для планирования пути для посещения целевых точек (в правильном порядке), при этом избегая столкновений с препятствиями. Целевые точки задаются в виде координат на изображении карты местности в системе координат OpenCV (ось \(x\) смотрит вправо, ось — \(y\) вниз), положительный угол отсчитывается против часовой стрелки относительно оси \(x\).

В этой задаче рассматривается только форма робота, без учета его кинематики. Принимается, что в точках найденного пути робот может поворачиваться, а между ними он движется прямолинейно. Считается, что по пути передвигается центр масс маски робота (имеется в виду центр масс, определяемый по изображению маски робота), и вокруг нее происходит вращение робота при повороте на месте. Найденный путь должен проходить через заданные целевые точки.

Для обеспечения безопасного движения по пути требуется, чтобы расстояние от робота до препятствий было не менее трех пикселей. Причем в точках пути робот должен быть способен выполнить полный оборот.

Карта местности, где требуется построить маршрут, и форма робота (вид сверху) задаются в виде черно-белых изображений. Целевые точки задаются в виде координат на изображении карты местности. Порядок прохождения точек имеет значение.

Гарантируется, что:

• при расположении центра масс робота в ключевой точке столкновения с препятствиями отсутствуют, в том числе при выполнении полного оборота;
• путь до каждой целевой точки существует.

На рис. 1.1 приведен пример сегментированной карты местности.

Формат входных данных

• Первая строка содержит два числа \(N\) и \(M\) — ширина и высота изображения сегментированной карты.
• Вторая строка содержит изображение заранее сегментированной карты пространства (черным цветом обозначены препятствия, белым — пространство, где можно двигаться) в виде \(N\times M\) элементов, разделенных пробелами (сначала элементы первой строки, далее второй и т. д.).
• Третья строка содержит два числа \(K\) и \(L\) — ширина и высота изображения маски робота.
• Четвертая строка содержит изображение маски робота (черным цветом обозначен фон, белым цветом — сам робот) в виде \(K\times L\) элементов, разделенных пробелами (сначала элементы первой строки, далее — второй и т. д.).
• Пятая строка содержит два целых числа, соответствующие начальному положению робота \(XY\).
• Шестая строка содержит начальную ориентацию робота.
• Следующие строки содержат координаты целевых точек в формате \(XY\), то есть два целых числа, разделенных пробелом. Обратите внимание, что порядок прохождения заданных точек важен!

Формат выходных данных

• Первая строка содержит целое число \(C\) — количество точек в найденном пути.
• Следующие строки содержат координаты маршрута в формате \(XY\), то есть два целых числа, разделенных пробелом.

Тестовые данные

Строки, соответствующие изображениям, слишком велики, поэтому вместо примеров ввода и вывода предлагаем скачать файлы, содержащие один из тестов, для тестирования на вашем ПК.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/1/input.1.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/1/output.1.txt.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/1/input.2.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/1/output.2.txt.

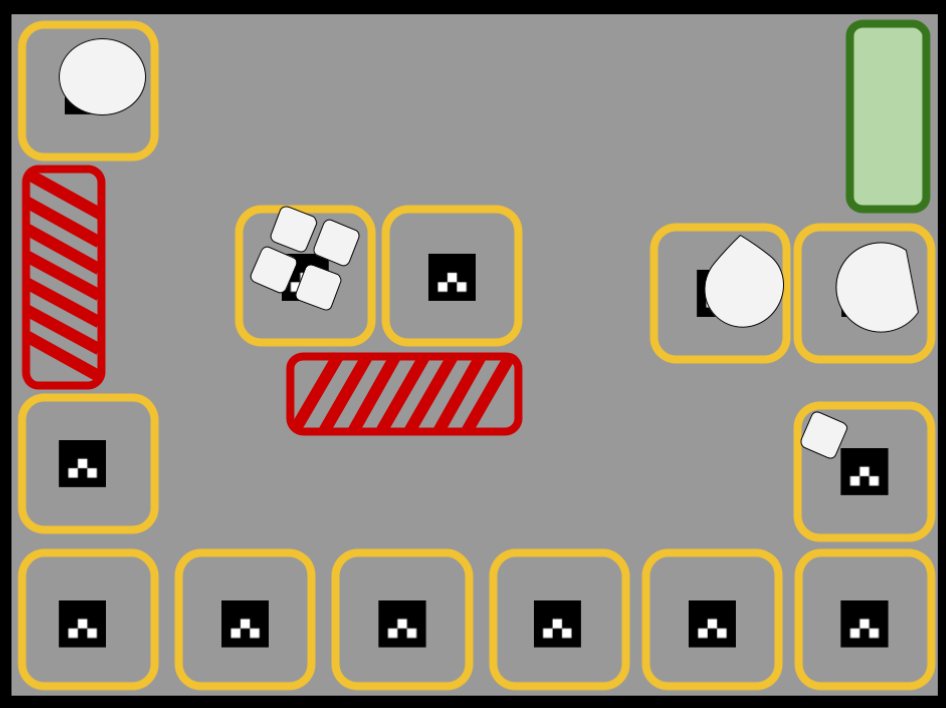
Рассматривается задача сегментации изображения складского помещения. Пример такого изображения представлен на рис. 1.2. На исследуемом изображении можно найти:

• карту-схему складского помещения;
• техническую зону для роботов (обозначена зеленым цветом с заполнением);
• запрещенные зоны, на которых роботу нельзя находиться (обозначены красным цветом со штрихом);
• зоны хранения (обозначены желтым цветом без заполнения, но с ArUco-маркером в центре);
• хранящиеся на складе грузы (обозначены светлыми фигурами).

Необходимо написать программу, которая по полученному изображению будет производить сегментацию складского помещения:

• на техническую зону;
• на зоны со свободными местами хранения;
• на зоны, где робот может передвигаться.

Также требуется определить массив идентификаторов ArUco-маркеров свободных мест и координаты центров масс каждого груза. Форма грузов может быть произвольной, как и цвет, но при этом цвет груза не совпадает с цветами зон, и расположение груза находится в пределах зон хранения. Площадь груза не менее девятой части площади зоны хранения. Если в зоне хранения расположен груз, то эта зона будет считаться запрещенной для перемещения робота. По пустым зонам хранения передвигаться можно. Зоны хранения могут иметь различные размеры. Возможная вариация расцветок зон не отличается в открытой и закрытой части тестов.

Более точный пример можно найти в формате ввода.

Формат входных данных

• Первая строка содержит два числа \(N\) и \(M\) — ширина и высота изображения сегментированной карты.
• Следующие три строки содержат BGR-каналы изображения, которое нужно сегментировать, в виде \(N \times M\) элементов, разделенных пробелами (сначала идут элементы первой строки, далее второй и т. д.).

Формат выходных данных

• Первая строка содержит маску технической зоны.
• Вторая строка содержит маску зоны, где робот может передвигаться.
• Третья строка содержит маску мест свободных зон хранения.
• Четвертая строка содержит словарь, в котором в качестве ключей содержатся ID ArUco-маркеров свободных зон хранения, значения которых будут содержать центр соответствующей зоны хранения.
• Пятая строка содержит двумерный массив центров масс каждого из грузов.

Тестовые данные

Поскольку строки, соответствующие изображениям, слишком велики, вместо первого примера ввода и вывода предлагаем скачать файлы, содержащие один из тестов, для тестирования на вашем ПК.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/2/input.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/2/output.txt.

1

1280 720
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
,[30,30],[150,50],[50,150]]

0 0 0 0 … 0 0
0 0 0 0 … 0 0
0 0 0 0 … 0 0
"27": [110, 250], "51": [660, 351]

В этой задаче рассматривается мобильный робот с дифференциальной платформой, которому необходимо посещать целевые точки в пространстве со статичными препятствиями, избегая столкновений с ними. Напишите программу для расчета требуемых скоростей колес робота с заданной частотой дискретизации, при которых робот посетит все целевые точки, избегая столкновений с препятствиями. Кинематическая модель робота описывается следующими уравнениями: \[\dot{p} = \begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{bmatrix} = \begin{bmatrix} v \cos \theta \\ -v \sin \theta \\ \omega \end{bmatrix},\] \[v = \frac{(w_r + w_l) r}{2} \cdot \frac{\pi}{180},\] \[\omega = \frac{(w_r - w_l) r}{b},\] где

• \(r\) — радиус колес,
• \(b\) — расстояние между колесами,
• \(w_r\) и \(w_l\) — угловые скорости правого и левого колес соответственно (град/c),
• \(x, y\) — координаты центра робота относительно неподвижной системы отсчета,
• \(\theta\) — ориентация робота (град, угол поворота относительно оси \(x\)).

Положительное вращение робота соответствует правилу правой руки (против часовой стрелки), отрицательное — по часовой стрелке.

Шаг времени при генерации требуемых угловых скоростей колес должен быть равен 0,01 с. При проверке предоставленного решения дифференциальные уравнения кинематики робота будут решаться с использованием метода Коши (см. задание 1.2 инженерного тура отборочного этапа). Робот должен посетить все целевые точки не более, чем за 100 с. Для обеспечения безопасного движения по пути требуется, чтобы расстояние от робота до препятствий было не менее трех пикселей.

Целевая точка считается пройденной, если центр робота прошел не дальше, чем три пикселя от точки. Порядок прохождения точек имеет значение.

Формат входных данных

• Первая строка содержит два числа \(N\) и \(M\) — ширина и высота изображения сегментированной карты.
• Вторая строка содержит изображение заранее сегментированной карты пространства (черным цветом обозначены препятствия, белым — пространство, где можно двигаться) в виде \(N \times M\) элементов, разделенных пробелами (сначала элементы первой строки, далее — второй и т. д.).
• Третья строка содержит два числа \(K\) и \(L\) — ширина и высота изображения маски робота.
• Четвертая строка содержит изображение маски робота в виде \(K \times L\) элементов, разделенных пробелами (сначала элементы первой строки, далее — второй и т. д.). Робот имеет круглую форму с центром в середине, однако его размеры четко не определены.

• Следующая строка содержит словарь, который будет содержать следующие поля:

  • init — массив из трех чисел, которые обозначают начальное положение и ориентацию робота \([x, y, \theta]\).
  • params — массив, содержащий параметры робота \([r, b, \text{max\_speed}]\), где \(\text{max\_speed}\) — максимальная угловая скорость колес.
  • points — массив целевых точек в формате \([x, y]\), которые робот должен посетить.

Формат выходных данных

• Первая строка содержит целое число \(C\) — количество точек траектории.
• Следующие строки содержат временную метку (время задания скоростей), а также задаваемые угловые скорости для левого и правого колеса в формате \(\langle t, \omega_l, \omega_r \rangle\).

Тестовые данные

Строки, соответствующие изображениям, слишком велики, поэтому вместо примеров ввода и вывода предлагаем скачать файлы, содержащие один из тестов, для тестирования на вашем ПК.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/3/input.1.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/3/output.1.txt.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/3/input.2.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/3/output.2.txt.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/3/input.3.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/3/output.3.txt.

Задача является продолжением задачи «Траекторное управление» 1.3. Рассматривается команда мобильных роботов с дифференциальной платформой, которым необходимо посещать целевые точки в пространстве со статичными препятствиями. Напишите программу для расчета требуемых скоростей колес для каждого из роботов с заданной частотой дискретизации, при которых они посетят все целевые точки, избегая столкновений с препятствиями и другими роботами.

Кинематическая модель робота описывается следующими уравнениями: \[\dot{p} = \begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{bmatrix} = \begin{bmatrix} v \cos \theta \\ -v \sin \theta \\ \omega \end{bmatrix},\] \[v = \frac{(w_r + w_l) r}{2} \cdot \frac{\pi}{180},\] \[\omega = \frac{(w_r - w_l) r}{b},\] где

• \(r\) — радиус колес,
• \(b\) — расстояние между колесами,
• \(w_r\) и \(w_l\) — угловые скорости правого и левого колес соответственно (град/c),
• \(x, y\) — координаты центра робота относительно неподвижной системы отсчета,
• \(\theta\) — ориентация робота (град, угол поворота относительно оси \(x\)).

Положительное вращение робота соответствует правилу правой руки (против часовой стрелки), отрицательное — по часовой стрелке.

Шаг времени при генерации требуемых угловых скоростей колес должен быть равен 0,01 с. При проверке предоставленного решения дифференциальные уравнения кинематики робота будут решаться с использованием метода Коши (см. задание 1.2 инженерного тура отборочного этапа). Роботы должны посетить все целевые точки не более, чем за 100 с.

Целевая точка отмечается как пройденная, если центр робота прошел не дальше, чем два пикселя от точки. Порядок прохождения точек имеет значение. Для обеспечения безопасного движения по пути требуется, чтобы расстояние от робота до препятствий и других роботов было не менее трех пикселей.

Формат входных данных

• Первая строка содержит два числа \(N\) и \(M\) — ширина и высота изображения сегментированной карты.
• Вторая строка содержит изображение заранее сегментированной карты пространства (черным цветом обозначены препятствия, белым — пространство, где можно двигаться) в виде \(N \times M\) элементов, разделенных пробелами (сначала элементы первой строки, далее — второй и т. д.).
• Третья строка содержит два числа \(K\) и \(L\) — ширина и высота изображения маски робота.
• Четвертая строка содержит изображение маски робота в виде \(K \times L\) элементов, разделенных пробелами (сначала элементы первой строки, далее — второй и т. д.). Робот имеет круглую форму с центром в середине, однако его размеры четко не определены.

• Следующая строка содержит словарь, который будет содержать следующие поля:

  • init — массив из трех чисел, которые обозначают начальное положение и ориентацию робота \([x, y, \theta]\).
  • params — массив, содержащий параметры робота \([r, b, \text{max\_speed}]\), где \(\text{max\_speed}\) — максимальная угловая скорость колес.
  • points — массив целевых точек в формате \([x, y]\), которые робот должен посетить.

Формат выходных данных

• Первая строка содержит целое число \(C\) — количество точек траектории.
• Следующие строки содержат временную метку (время задания скоростей), а также задаваемые угловые скорости для левого и правого колеса в формате \(\langle t, \omega_l, \omega_r \rangle\).

Тестовые данные

Строки, соответствующие изображениям, слишком велики, поэтому вместо примеров ввода и вывода предлагаем скачать файлы, содержащие один из тестов, для тестирования на вашем ПК.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/4/input.1.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/4/output.1.txt.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/4/input.2.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/4/output.2.txt.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/4/input.3.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/4/output.3.txt.

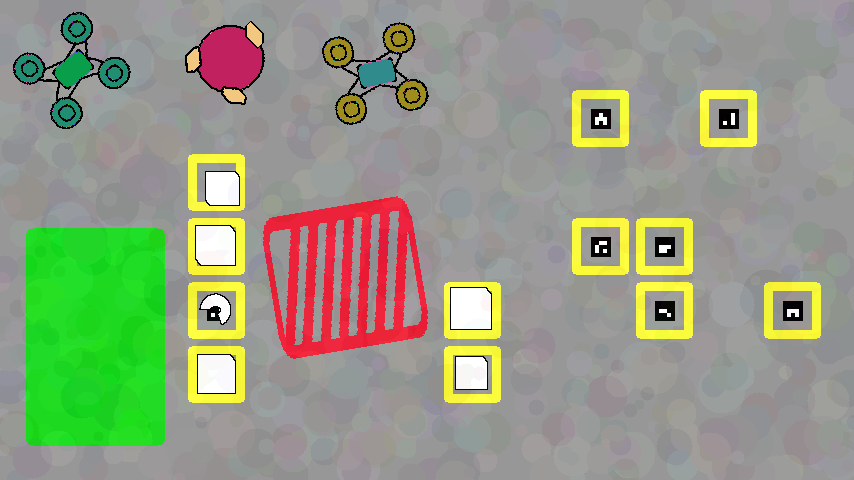
Рассматривается несколько последовательных изображений складского помещения (вид сверху), на которых помимо статических объектов также присутствуют роботы, которые передвигаются от кадра к кадру. Требуется написать программу для детекции и отслеживания перемещений роботов. Для первого кадра положения роботов известны. Для всех остальных кадров необходимо определить положение центра (центра масс маски робота). Всего дано не менее трех кадров в каждом тесте. На рис. 1.3 представлен пример одного кадра.

Раскраска роботов заранее неизвестна и является случайной, однако она отличается у разных роботов в рамках одного теста. Форма роботов является произвольной и может совпадать у разных роботов в рамках одного теста. Отдельно отметим, что робот явно виден на фоне, то есть исключено наличие случаев частичного перекрытия или слияния робота с окружением. Все остальные элементы, кроме роботов, на всех кадрах статичны, то есть не изменяются от кадра к кадру, а роботы между последовательными кадрами передвигаются. Кроме того, никакие два робота во время своего движения не сталкивались, то есть отсутствуют кадры, где изображения роботов бы перекрывались.

Формат входных данных

• Первая строка содержит два целых числа \(N\) и \(M\) — ширина и высота изображения сегментированной карты в пикселях.
• Следующие строки содержат последовательные изображения карты с роботами в виде \(N \times M\) элементов, разделенных пробелами (сначала идут элементы первой строки, далее — второй и т. д.). Каждый кадр представлен тремя строками, в которых последовательно содержатся три канала изображения BGR.
• Последняя строка содержит положения роботов на первом кадре в виде двумерного массива, см. примеры.

Формат выходных данных

• Для каждого робота на отдельной строке должны быть выведены координаты положений роботов, соответствующих порядку последовательных изображений, в виде целых чисел, разделенных пробелами. Например, для трех кадров строка будет иметь вид \(\langle X1\ Y1\ X2\ Y2\ X3\ Y3 \rangle\), и так для каждого робота.
• Порядок вывода, то есть в какой строке координаты какого робота, неважен.
• Координаты рекомендуется округлить до целых чисел, и выводить сначала координату по оси \(OX\), потом \(OY\).

Примечания

В примере ниже приведены три последовательных кадра, на которых изображены четыре робота.

1

640 480
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
0 0 0 0 ... 0 0
, [316, 464], [344, 239], [420, 334]]

231 105 150 444 150 444
316 464 50 72 400 410
344 239 151 63 344 237
420 334 321 321 211 312

Поскольку строки, соответствующие изображениям, слишком велики, полные примеры входных данных можно найти по ссылкам ниже. Только один из примеров содержится в тестах.

Тестовые данные

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/5/input.1.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/5/output.1.txt.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/5/input.2.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/5/output.2.txt.

Стандартный ввод: https://disk.yandex.ru/d/oAF6TMss93XjJg/5/input.3.txt.

Стандартный вывод: https://disk.yandex.ru/d/oAF6TMss93XjJg/5/output.3.txt.

Рассматривается мультиагентная система из \(S\) (\(S\leqslant 7\)) одинаковых круглых роботов на омниплатформе (роботы могут двигаться в любом направлении), расположенная на некоторой плоской местности. На местности присутствует одно круглое препятствие.

Задача роботов: из произвольных начальных положений образовать формацию, описываемую графом расстояний между каждым роботом и всеми остальными. Это значит, что для каждого робота заданы желаемые расстояния до всех других роботов.

Формация должна быть образована не более, чем за 1000 с, при этом расстояния между роботами должны отличаться от желаемых не более, чем на 5%. Гарантируется, что желаемые расстояния между роботами строго больше их диаметра, кроме того, формирование указанной формации возможно.

Напишите одну программу-регулятор, которая будет исполняться на каждом из роботов (на всех роботах будет одновременно запущена одна и та же программа), и формировать сигнал управления, обеспечивающий решение задачи, так что роботы не будут сталкиваться между собой и с препятствием, не будут выезжать за границы карты. Сигналом управления для каждого из роботов являются проекции линейной скорости, то есть модель \(i\)-го робота выглядит следующим образом: \[\left\{ \begin{aligned} \dot{x}_i (t)&=u_{x,i} (t),\\ \dot{y}_i (t)&=u_{y,i} (t), \end{aligned} \right.\] где \(u_{x,i} (t)\) и \(u_{y,i} (t)\) — проекции желаемой скорости на соответствующие оси. Решение этих дифференциальных уравнений производится методом Эйлера.

За основу решения задачи возьмите следующий пропорциональный регулятор, в котором специальным образом определен сигнал ошибки, на основе координат роботов и желаемых расстояний. Очевидно, что ошибку можно посчитать, например, как \[e_d=d_{ij}^2-m_{ij}^2,\] где \(d_{ij}\) — фактическое расстояние между \(i\)-м и \(j\)-м роботом, а \(m_{ij}\) — желаемое расстояние между ними. Однако из разницы между расстояниями или квадратами расстояний непонятно, в каком направлении следует двигаться на плоскости, поэтому предлагается рассмотреть модифицированную ошибку, которая может быть рассчитана по каждой из осей: \[\left\{ \begin{aligned} e_{x,ij}&=(d_{ij}^2-m_{ij}^2 )(x_j-x_i ),\\ e_{y,ij }&=(d_{ij}^2-m_{ij}^2 )(y_j-y_i ), \end{aligned} \right.\] где \(x_i\) и \(x_j\) — координаты \(i\)-го и \(j\)-го роботов по оси \(OX\) соответственно, \(y_i\) и \(y_j\) — координаты \(i\)-го и \(j\)-го роботов по оси \(OY\) соответственно.

Тогда управление для \(i\)-го робота с помощью пропорционального регулятора можно рассчитать, как сумму модифицированных ошибок по расстоянию между \(i\)-м роботом и всеми остальными, умноженную на некоторый коэффициент: \[\left\{ \begin{aligned} u_{x,i} (t)=\alpha\sum_{j=1,j\neq i}^S e_{x,ij },\\ u_{y,i} (t)=\alpha\sum_{j=1,j\neq i}^S e_{y,ij}, \end{aligned} \right.\] где \(\alpha>0\) — коэффициент регулятора, \(u_{x,i} (t)\) и \(u_{y,i} (t)\) — элементы вектора управления для \(i\)-го робота.

Если у всех роботов реализовать такой регулятор, то гарантируется сходимость расстояний между роботами к желаемым значениям. Однако он не учитывает препятствия, возможные столкновения между роботами, не предотвращает выезд робота за пределы местности. Внесите модификацию, чтобы решить эту проблему. Кроме того, можно реализовать любой другой регулятор.

Формат входных данных

def controller(robot_position, other_robot_positions, target_distances, map_image, robot_mask, max_velocity, data):
    ...
    return velocity, data

где

• robot_position — положение робота на карте в системе координат OpenCV (list с двумя числами типа float).
• other_robot_positions — положения остальных роботов на карте в системе координат OpenCV (list из list-ов, которые аналогичны robot_position).
• target_distances — желаемые расстояния до роботов. Порядок соответствует порядку координат в other_robot_positions.
• map_image — изображение карты.
• robot_mask — маска робота.
• max_velocity — максимальная скорость по одной из осей.
• data — словарь, куда можно сохранять то, что нужно участнику. Он будет передаваться от цикла к циклу. У каждого робота свой словарь.

Так как данная задача является интерактивной, то простой набор входных и выходных данных отсутствует. Однако примеры задач можно найти в папке по ссылке: https://disk.yandex.ru/d/oAF6TMss93XjJg/6/input/.

Здесь:

• первая строка содержит два числа \(N\) и \(M\) — ширина и высота изображения местности;
• вторая строка содержит изображение местности (черным цветом обозначено препятствие, белым — пространство, где можно двигаться) в виде \(N \times M\) элементов, разделенных пробелами (сначала элементы первой строки, далее — второй и т. д.);
• третья строка содержит два числа \(K\) и \(L\) — ширина и высота изображения маски робота;
• четвертая строка содержит изображение маски робота в виде \(K \times L\) элементов, разделенных пробелами (сначала элементы первой строки, далее — второй и т. д.), робот имеет круглую форму с центром в середине, однако его размеры четко не определены;
• следующая строка содержит двумерный массив, представляющий собой list начальных положений роботов в системе координат OpenCV, сами начальные положения тоже представляют собой list, содержащий два числа типа float.

Задав желаемые расстояния между роботами, можно провести тестирование своей программы.

Формат выходных данных

Ожидается, что функция участника вернет рассчитанную скорость для робота в системе координат OpenCV в виде массива с двумя числами типа float и словарь data.