Инженерный тур. 1 этап
Рассмотрим мобильного робота с дифференциальной платформой. У него есть два колеса (левое и правое), соединенные с двигателем.
Кинематическая модель робота описывается следующим уравнением: \[\begin{gather} \dot{p} = [\dot{x} \quad \dot{y} \quad \dot{\theta}]^T = [-\nu \sin\theta \quad \nu \cos\theta \quad \omega]^T;\\ \nu = \frac{(\omega_r + \omega_l)r}{2};\\ \omega = \frac{(\omega_r + \omega_l)r}{b}, \end{gather}\] где \(r > 0\) и \(b > 0\) — радиус колес и база (расстояние между колесами); \(\omega_l\), \(\omega_r\) — скорость вращения колес (левого и правого); \(x\), \(y\) — координаты центра робота относительно неподвижной системы отсчета; \(\theta\) — ориентация робота (угол поворота относительно оси \(x\)). Положительное вращение робота соответствует правилу правой руки (положительное направление — против часовой стрелки, отрицательное — по часовой стрелке).
На практике возникает проблема с тем, что параметры робота (радиус колес и расстояние между колесами) оказываются не равны измеренным, например, с помощью штангенциркуля или линейки. В первую очередь это справедливо для роботов, чьи колеса не слишком узкие и имеют мягкое покрытие. В результате возникает задача калибровки параметров одометрии, а именно, по измеренным данным о положении робота и колес определить параметры \(r\) и \(b\). Это и требуется сделать в задании.
Платформа двигается из известного начального положения \(x(t_0)\), \(y(t_0)\), \(\theta(t_0)\), а углы двигателей в начальный момент времени были равны \(\varphi_l(t_0)\), \(\varphi_r(t_0)\). С постоянным шагом по времени \(h\) поступают значения положений робота \(x(t_i)\), \(y(t_i)\) и углы на двигателях робота \(\varphi_l(t_i)\), \(\varphi_r(t_i)\), здесь \(t_i = t_0 + h \cdot i\), \(i \in \mathbb{N}\). Требуется определить радиус колес робота \(r\) и расстояние между колесами \(b\).
Формат входных данных
- Первая строка содержит значение \(0 < h < 0{,}1\).
- Вторая строка содержит положение \(-100 < x(t_0), y(t_0) < 100\) и ориентацию \(-100 < \theta(t_0) < 100\) робота, углы поворота колес \(-\pi < \varphi_l(t_0), \varphi_r(t_0) < \pi\) в начальный момент времени, значения разделены пробелом.
- Третья строка содержит значение \(5 < n < 10000\) количества измерений \(x(t_i)\), \(y(t_i)\), \(\varphi_l(t_i)\), \(\varphi_r(t_i)\).
- Следующие \(n\) строк хранят значения \(-10000 < x(t_i), y(t_i), \varphi_l(t_i), \varphi_r(t_i) < 10000\), разделенные пробелом.
Все величины указаны в единицах СИ.
Формат выходных данных
- Первая строка содержит значение параметра \(r\) и \(b\), разделенные пробелом.
При выводе округлите значения до шести знаков после запятой.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3.859787684798448e-05 0.000000 0.000000 1.000000 0.000000 0.000000 10 0.000000 0.000000 1.000000 0.000000 0.000000 -0.009552 0.006135 0.999688 0.001930 0.000000 -0.019102 0.012274 0.999375 0.003860 0.000000 -0.028651 0.018415 0.999063 0.005790 0.000000 -0.038197 0.024560 0.998750 0.007720 0.000000 -0.047741 0.030707 0.998438 0.009649 0.000000 -0.057284 0.036857 0.998125 0.011579 0.000000 -0.066825 0.043011 0.997813 0.013509 0.000000 -0.076363 0.049167 0.997500 0.015439 0.000000 -0.085900 0.055327 0.997188 0.017369 0.000000 |
11.765247 72.667897 |
2 |
3.859787684798448e-05 0.000000 0.000000 0.000000 0.000000 0.000000 30 0.000000 0.000000 0.000000 0.000000 0.000000 -0.000002 0.013623 0.000250 0.000386 0.001930 -0.000007 0.027247 0.000500 0.000772 0.003860 -0.000015 0.040870 0.000750 0.001158 0.005790 -0.000027 0.054494 0.001000 0.001544 0.007720 -0.000043 0.068117 0.001250 0.001930 0.009649 -0.000061 0.081740 0.001500 0.002316 0.011579 -0.000083 0.095364 0.001750 0.002702 0.013509 -0.000109 0.108987 0.002000 0.003088 0.015439 -0.000138 0.122611 0.002250 0.003474 0.017369 -0.000170 0.136234 0.002500 0.003860 0.019299 -0.000206 0.149857 0.002750 0.004246 0.021229 -0.000245 0.163481 0.003000 0.004632 0.023159 -0.000288 0.177104 0.003250 0.005018 0.025089 -0.000334 0.190727 0.003500 0.005404 0.027019 -0.000383 0.204351 0.003749 0.005790 0.028948 -0.000436 0.217974 0.003999 0.006176 0.030878 -0.000492 0.231597 0.004249 0.006562 0.032808 -0.000552 0.245220 0.004499 0.006948 0.034738 -0.000615 0.258844 0.004749 0.007334 0.036668 -0.000681 0.272467 0.004999 0.007720 0.038598 -0.000751 0.286090 0.005249 0.008106 0.040528 -0.000824 0.299713 0.005499 0.008492 0.042458 -0.000901 0.313337 0.005749 0.008878 0.044388 -0.000981 0.326960 0.005999 0.009263 0.046317 -0.001064 0.340583 0.006249 0.009649 0.048247 -0.001151 0.354206 0.006499 0.010035 0.050177 -0.001241 0.367829 0.006749 0.010421 0.052107 -0.001335 0.381452 0.006999 0.010807 0.054037 -0.001432 0.395075 0.007249 0.011193 0.055967 |
11.765247 72.667897 |
3 |
3.859787684798448e-05 0.000000 0.000000 0.000000 0.000000 0.000000 30 0.000000 0.000000 0.000000 0.000000 0.000000 0.000002 -0.013623 0.000250 -0.001930 -0.000386 0.000007 -0.027247 0.000500 -0.003860 -0.000772 0.000015 -0.040870 0.000750 -0.005790 -0.001158 0.000027 -0.054494 0.001000 -0.007720 -0.001544 0.000043 -0.068117 0.001250 -0.009649 -0.001930 0.000061 -0.081740 0.001500 -0.011579 -0.002316 0.000083 -0.095364 0.001750 -0.013509 -0.002702 0.000109 -0.108987 0.002000 -0.015439 -0.003088 0.000138 -0.122611 0.002250 -0.017369 -0.003474 0.000170 -0.136234 0.002500 -0.019299 -0.003860 0.000206 -0.149857 0.002750 -0.021229 -0.004246 0.000245 -0.163481 0.003000 -0.023159 -0.004632 0.000288 -0.177104 0.003250 -0.025089 -0.005018 0.000334 -0.190727 0.003500 -0.027019 -0.005404 0.000383 -0.204351 0.003749 -0.028948 -0.005790 0.000436 -0.217974 0.003999 -0.030878 -0.006176 0.000492 -0.231597 0.004249 -0.032808 -0.006562 0.000552 -0.245220 0.004499 -0.034738 -0.006948 0.000615 -0.258844 0.004749 -0.036668 -0.007334 0.000681 -0.272467 0.004999 -0.038598 -0.007720 0.000751 -0.286090 0.005249 -0.040528 -0.008106 0.000824 -0.299713 0.005499 -0.042458 -0.008492 0.000901 -0.313337 0.005749 -0.044388 -0.008878 0.000981 -0.326960 0.005999 -0.046317 -0.009263 0.001064 -0.340583 0.006249 -0.048247 -0.009649 0.001151 -0.354206 0.006499 -0.050177 -0.010035 0.001241 -0.367829 0.006749 -0.052107 -0.010421 0.001335 -0.381452 0.006999 -0.054037 -0.010807 0.001432 -0.395075 0.007249 -0.055967 -0.011193 |
11.765247 72.667897 |
- Рассчитать линейную и угловую скорости по осям координат (первую производную положений \(x\) и \(y\)), численно продифференцировав измерения положений \(x\) и \(y\).
- Из кинематической модели рассчитать линейную скорость и угловое положение робота, использовав значение \(\theta(t_0)\).
- Рассчитать угловую скорость, численно продифференцировав полученные значения ориентации \(\theta(t)\).
- Рассчитать угловые скорости колес робота, численно \(\omega_l(t)\) и \(\omega_r(t)\), продифференцировав измерения их угловых положений \(\varphi_l(t)\), \(\varphi_r(t)\).
- С помощью выражения \(r = \frac{2\nu}{(\omega_r + \omega_l)}\) и полученных значений \(\omega_l(t)\) и \(\omega_r(t)\) получить оценку радиуса колес.
- Из выражения \(b = \frac{(\omega_r + \omega_l)r}{\omega}\), используя оценку \(r\), найти значение \(b\).
Реализация описанного алгоритма на языке программирования Python представлена в файле https://disk.yandex.ru/d/xhgXxuKfe7QhEQ/solution_1.py.
Реальные технические и физические системы на макроуровне отличаются тем, что все сигналы в них непрерывны. При построении их моделей естественным образом возникают производные. Например, скорость — это первая производная положения, а ускорение является его второй производной, через операцию дифференцирования связаны ток в катушке индуктивности и падение напряжения на ней.
В результате математические модели для описания таких систем и их функционирования состоят из дифференциальных уравнений. В этих уравнениях, в отличие от алгебраических, решением является не какое-то значение переменной, а функция.
Например, решением дифференциального уравнения \[\ddot{y}(t) + y(t) = 0,\] где точка над символом означает взятие производной по времени, а две точки — вторую производную, является функция \(y(t) = a \sin(t + b)\), здесь \(a\) и \(b\) — некоторые параметры, которые определяются начальными условиями. Например, если \(y(0) = 1\), \(\dot{y}(0) = 0\), тогда подставив в найденное решение и его первую производную \(t = 0\), получим \[\begin{gather} 1 = a \sin(b),\\ 0 = a \cos(b), \end{gather}\] откуда можно найти, что \(a = 1\), \(b = \pi/2\).
Для проверки найдем вторую производную и подставим в уравнение: \[\begin{gather} \dot{y}(t) = a \cos(t + b);\\ \ddot{y}(t) = -a \sin(t + b);\\ -a \sin(t + b) + a \sin(t + b) = 0;\\ 0 = 0 - \text{верно}. \end{gather}\]
Далее, имея математическую модель, можно провести численное моделирование и проанализировать ее поведение. Для того чтобы проводить моделирование таких динамических моделей, применяются численные методы решения дифференциальных уравнений.
Самым простым из них является метод Эйлера. Для общности рассмотрим модель следующего вида: \[\dot{y}(t) = f(t, y(t), u(t)),\] где \(t\) — время, а \(u\) — некоторый измеряемый входной сигнал, то есть его значение в текущий момент времени известно, например, это может быть сигнал управления.
Для численного решения дифференциального уравнения нужно взять некоторое начальное условие \(y(0)\) и определить шаг интегрирования \(h\). Тогда можно рассчитать значение функции \(y(t)\) в момент времени \(h\) следующим образом: \[y(h) = y(0) + h f(0, y(0), u(0)).\] Затем можно последовательно рассчитывать значение функции \(y(t)\) в следующие моменты времени с шагом \(h\): \[\begin{gather} y(2h) = y(h) + h f(h, y(h), u(h));\\ y(3h) = y(2h) + h f(2h, y(2h), u(2h));\\ \ldots\\ y(kh + h) = y(kh) + h f(kh, y(kh), u(kh)). \end{gather}\]
Суть метода: предполагается, что в течение периода времени в \(h\) секунд (это могут быть и доли секунды, например, \(0{,}0001\) с) среднее значение производной будет равно значению производной в начале шаге. Это равносильно предположению, что достаточно точно можно аппроксимировать функцию на этом шаге прямым отрезком, а в данном случае следующее значение функции может быть рассчитано как сумма текущего значения функции и значения производной функции, умноженной на временной шаг \(h\).
При использовании достаточно малого \(h\) это допущение можно считать вполне оправданным. Другое дело, что в общем случае шаг должен быть очень малым, иначе данный метод может давать значительную ошибку, но это увеличивает количество вычислений при моделировании одного и того же периода времени работы системы.
Более точным является метод Коши или метод средней точки. Идея заключается в том, что можно получить более высокую точность, если в качестве некоторого среднего значения производной возьмем значение не из начала шага, а из его середины. Действительно, в общем случае можно ожидать, что значение производной в конце шага скорее будет ближе к значению производной в середине шага, чем к значению в его начале.
Проблема состоит в том, что невозможно рассчитать значение производной в середине шага, так как для этого требуется знать значение функции в середине шага \(y(t + h/2)\): \[\dot{y}(t) = f(t, y(t), u(t)),\] а значит, \[\dot{y}(t + h/2) = f(t + h/2, y(t + h/2), u(t + h/2)).\] Эту проблему можно решить, используя метод Эйлера: \[y(t + h/2) = y(t) + \frac{h}{2} f(t, y(t), u(t)).\] Заметим, что в этом случае шаг для метода Эйлера составляет \(h/2\), а не \(h\), что положительно сказывается на точности решения. Теперь можно рассчитать значение в момент времени \(y(t + h)\): \[y(t + h) = y(t) + h f(t + h/2, y(t + h/2), u(t + h/2)).\]
Напишите программу, выполняющую численное решение дифференциального уравнения методом Коши с постоянным шагом по времени \(h\) для заданного начального условия \(y(0)\): \[\dot{y}(t) = \frac{a y(t) + b t^2 + c}{d t + e} + f,\] где \(a\), \(b\), \(c\), \(d\), \(e\), \(f\) — параметры системы.
Формат входных данных
- Первая строка хранит параметры системы \(a\), \(b\), \(c\), \(d\), \(e\), \(f\), разделенные пробелом в виде вещественных чисел в диапазоне \([-100; 100]\). Гарантируется, что параметры являются корректными и решение дифференциального уравнения существует.
- Вторая строка хранит начальное условия для интегрирования \(y(0)\).
- Третья строка хранит шаг интегрирования \(0 < h < 1\), размер \(5 < n < 100000\) — сколько шагов при численном решении требуется сделать, разделенных пробелом.
Все величины указаны в единицах СИ.
Формат выходных данных
- Первая строка содержит число \(s = n + 1\) с результатами вычислений задания.
- Далее идут \(s\) строк со значениями \(y(i h)\), где \(i = 0, 1, 2, \ldots, n\).
При выводе округлите значения до шести знаков после запятой.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1.0 1.0 -2.0 1.0 1.0 0.0 2.0 0.1 9 |
10 2.000000 2.001818 2.016480 2.053692 2.120697 2.223114 2.365425 2.551294 2.783768 3.065426 |
2 |
1.228789 3.391090 -8.000000 3.000000 4.000000 0.000000 4.923386 0.695078 9 |
10 4.923386 4.682327 4.818577 5.451902 6.641021 8.419785 10.809752 13.825631 17.477967 21.774620 |
3 |
6.240544 6.747381 5.000000 2.000000 1.000000 0.000000 8.437533 0.637444 9 |
10 8.437533 75.791111 273.755572 684.289592 1394.034051 2492.819850 4072.940261 6228.718086 9056.214864 12653.019828 |
- Реализовать метод Коши согласно выражению \(\dot{y}(t) = \frac{a y(t) + b t^2 + c}{d t + e} + f\).
- Подставить начальное условие и все параметры в выражение для производной.
- Далее в цикле вычислять решение системы на основе реализации метода (см. пункт 1).
Реализация описанного алгоритма на языке программирования Python представлена в файле https://disk.yandex.ru/d/xhgXxuKfe7QhEQ/solution_2.py.
Положение равновесия динамической системы — это такое положение, в котором система не двигается, все скорости, ускорения и более старшие производные выходной переменной равны нулю. Например, модель маятника имеет два положения равновесия: верхнее и нижнее.
Положения равновесия могут быть устойчивыми и неустойчивыми. В устойчивое положение равновесия система возвращается, если находилась в некоторой его окрестности, например, после прекращения внешнего воздействия. У маятника верхнее положение является неустойчивым, а нижнее — устойчивым.
У некоторых систем только одно положение равновесия, в таком случае часто говорят об устойчивости самой системы. Если это единственное положение равновесия устойчиво, то система будет в него возвращаться из любого начального положения при отсутствии внешнего воздействия. В противном случае это будет происходить только из некоторой окрестности положения равновесия.
Есть несколько разных способов рассмотрения устойчивости динамических систем, и в этом задании рассмотрим устойчивость системы по выходу, т. е. как изменяется ее выходная переменная. В этом случае, кроме устойчивых и неустойчивых систем (или положений равновесия), выделяют системы, находящиеся на границе устойчивости. То есть такие системы, которые при отклонении от положения равновесия хоть и не возвращаются в него, но и не отдаляются, а так и продолжают находиться в его окрестности. Система при этом может колебаться в этой окрестности или находится неподвижно.
Например, нижнее положение маятника без трения находится на границе устойчивости (колебательной). Если отклонить маятник от него, то он начнет бесконечно колебаться относительно нижнего положения, так как трение отсутствует. Здесь важно заметить, что верхнее положение неустойчиво, оно находится на границе устойчивости. Маятник хоть и не может бесконечно далеко отклониться от него, но он будет колебаться в области, которая не включает верхнее положение равновесия, в отличие от нижнего.
Среди систем, приведенных ниже, требуется определить систему, чье положение равновесия \([x_1,~x_2] = [0,~0]\) находится на границе устойчивости.
В обозначениях ниже точка над буквой означает производную, т. е. \(\dot{x}\) — это производная \(x\).
- Простое решение — численными методами решить систему и посмотреть на то, как меняется выходная переменная при различных начальных условиях из окрестности нулевого положения равновесия. Если она сходится к нулю, значит, нулевое положение равновесия устойчиво.
- Если участник знаком с теорией устойчивости, то для линейных систем он может проверить один из критериев устойчивости. Например, найти собственные числа матрицы. В случае, если они чисто мнимые, можно сделать вывод, что система находится на (колебательной) границе устойчивости.
- Неустойчивая: \[\left\{ \begin{aligned} \dot{x}_1 = x_1 + 2x_2 + u,\\ \dot{x}_2 = 3x_1 + 4x_2 + u. \end{aligned}\right.\]
- На границе устойчивости: \[\left\{ \begin{aligned} \dot{x}_1 = x_2 + u,\\ \dot{x}_2 = -2x_1 + u. \end{aligned}\right.\]
- На границе устойчивости: \[\left\{ \begin{aligned} \dot{x}_1 = u,\\ \dot{x}_2 = u. \end{aligned}\right.\]
- Неустойчивая: \[\left\{ \begin{aligned} \dot{x}_1 = x_1 + 2x_2 + u,\\ \dot{x}_2 = 2x_1 + x_2 + u. \end{aligned}\right.\]
- Устойчивая: \[\left\{ \begin{aligned} \dot{x}_1 = -x_1 + 2x_2 + u,\\ \dot{x}_2 = -2x_1 - x_2 + u. \end{aligned}\right.\]
Ограничение: TL — 10 с, ML — 64 МБ.
Задана карта в виде двумерного массива размером \(N \times M\), \(1 \leqslant N, M \leqslant 100\). Каждая клетка задается парой чисел \((i, j)\), где \(i\) (\(1 \leqslant i \leqslant N\)) — номер строки, \(j\) (\(1 \leqslant j \leqslant M\)) — номер столбца. В каждой клетке лежат целые числа в диапазоне от 0 до 255, назовем это число стоимостью клетки, означающей получаемую награду роботом.
Робот Саша хочет добраться из клетки \(S\) с координатами \((x_s, y_s)\) в клетку \(F\) с координатами \((x_f, y_f)\), проходя только по клеткам с наградой. Саша занимает собой одну клетку, а двигаться может только в соседние клетки (соседние по ребрам клетки, а не по диагонали), причем робот не будет вставать на клетку, которая не содержит награду (то есть в клетку со стоимостью 0), а также не может посещать уже пройденные клетки, ведь там не осталось награды.
Помогите найти Саше путь из точки \(S\) в точке \(F\) такой, что минимальная полученная по пути награда является максимальной. Обращаем внимание, что имеется ввиду не сумма наград по пути, а величина самой маленькой награды по пути, полученная в одной из клеток.
Сумму наград по пути будем называть стоимостью пути, его тоже надо будет посчитать, но задача робота — максимизировать самую маленькую награду, которая встретится на пути.
Награда в начальной точке не рассматривается, она не должна входить в рассчитываемую стоимость пути и не должна рассматриваться при определении минимальной награды на пути.
Формат входных данных
- В первой строке заданы два целых числа: \(N\) и \(M\).
- Далее идут четыре целых числа: \(x_s\), \(y_s\), \(x_f\), \(y_f\) — координаты точек \(S\) и \(F\) соответственно.
- Далее задана карта в виде двумерного массива размером \(N \times M\) в виде таблицы из \(N\) строк и \(M\) столбцов с целыми числами от 0 до 255.
Формат выходных данных
- В первой строке выведите три числа: \(k\) — количество клеток в пути, \(S\) — стоимость пути, \(D\) — минимальная полученная по пути награда.
- В следующих \(k\) строках выведите координаты вершин \((i, j)\) в пути в порядке обхода, по одной вершине в строке (начальная и конечная вершины тоже считаются).
- В случае, если построить путь без пустых клеток нельзя, вывести
-1.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1 4 1 1 1 4 1 1 1 1 |
4 4 1 1 1 1 2 1 3 1 4 |
2 |
3 3 3 1 1 3 255 0 255 255 0 255 255 0 255 |
-1 |
- Представить исходную карту в виде ориентированного графа. Таким образом, стоимость вершины будет отождествляться со стоимостью ребра. Если стоимость вершины равна 0, то данная вершина не имеет ребер (как из нее, так и в нее).
- Для поиска требуемого пути можно модифицировать алгоритм Дейкстры так, чтобы сохранять не кратчайший путь до вершины, а вес минимального ребра в этом пути, а при релаксации отдавать предпочтение ребрам с большим весом.
Реализация описанного алгоритма на языке программирования Python представлена в файле https://disk.yandex.ru/d/xhgXxuKfe7QhEQ/solution_4.py.
Ограничение: TL — 10 с, ML — 488,3 МБ.
Дано поле размером \(N \times M\), \(1 \leqslant N, M \leqslant 100\) квадратных единиц, по которому ездит круглый робот Саша. Диаметр робота Саши равен \(D\). Саша начинает путь из точки \((x_s, y_s)\).
Саше известно, что на поле расположены \(K\) препятствий, которые являются прямоугольниками и задаются двумя точками \((p_1, p_2)\) (это диагонально противоположные точки). Гарантируется, что все препятствия находятся в пределах поля, а также гарантируется, что координаты вершин препятствий являются целыми числами. Саше известна конечная точка \((x_f, y_f)\), до которой ему нужно доехать. Задача: составить граф на поле так, чтобы робот мог перемещаться по вершинам и ребрам, не сталкиваясь с препятствиями. Таким образом, каждая вершина графа будет задаваться своими координатами \((x_i, y_i)\), кроме того, начальная и конечная точки также должны быть в графе. Количество ребер и вершин в графе может быть любым, с учетом ограничений задачи.
В ответ необходимо вывести координаты вершин, по которым нужно пройти роботу, чтобы добраться из своей стартовой точки до конечной, не сталкиваясь с препятствиями.
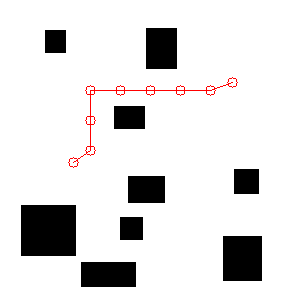
- Робот Саша очень осторожен и остановится, если расстояние по любой из осей до препятствия от его центра станет равным или меньше его радиуса, то есть робот не поедет в точку \((1;1)\), если в точке \((2;2)\) есть препятствие, несмотря на то, что расстояние между этими точками \(\sqrt{2}\).
- Робот может ездить по границе поля.
Формат входных данных
- В первой строке заданы четыре числа: \(N \in \mathbb{N}\), \(M \in \mathbb{N}\), \(K \in \mathbb{N}\), \(D \in \mathbb{R}_+\) такие, что \(1 \leqslant N, M \leqslant 100\), \(1 \leqslant K \leqslant 10\), \(1 \leqslant D \leqslant 50\).
- Далее идут четыре вещественных числа: \(x_s\), \(y_s\), \(x_f\), \(y_f\) — координаты точек \(S\) и \(F\) соответственно.
- Далее идут \(K\) строк, в каждой описаны четыре точки (каждая задается двумя вещественными числами), задающие препятствия-прямоугольники.
Формат выходных данных
- В первой строке выведите одно число \(C\) — количество вершин в пути.
- В следующих \(C\) строках выведите координаты вершин \((x_i, y_i)\) в пути в порядке обхода, по одной вершине в строке (начальная и конечная вершины тоже считаются).
- Заметьте, не требуется найти минимальный путь — достаточно найти любой путь.
- В случае, если построить путь без пересечения препятствия нельзя, в том числе из-за того, что начальная или конечная точка слишком близко к препятствию, вывести
-1.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
8 8 1 1 7.0 1.0 1.0 7.0 1.0 1.0 4.0 4.0 |
15 7 1 6 1 6 2 6 3 6 4 6 5 6 6 5 6 4 6 3 6 2 6 1 6 1 7 |
Один из способов решения данной задачи заключается в инициализации графа карты с учетом размера робота и препятствиями.
- Чтобы учесть границы препятствий и размеры робота, нужно сделать следующее преобразование. В качестве радиуса робота использовать нулевое значение, а все линейные размеры препятствий увеличить на величину, равную половине радиуса робота.
- Задать матрицу для представления пространства, где будут отмечены свободные ячейки и ячейки, занятые препятствиями.
- Убедиться, что после преобразования из предыдущего пункта начальная и конечная точки не оказались в пределах препятствий.
- Полученную матрицу представить в виде графа: на исходное поле натягивается сетка. Вершины сетки соответствуют точкам, в которые робот может переходить, а ребра соединяют возможные перемещения.
- Задать шаг, на который робот будет перемещаться. С учетом шага инициализировать новый граф смежности, в котором две вершины будут смежными в том случае, если обе вершины свободны и расстояние между ними равно одному шагу.
- Для каждой полученной вершины проверить, что существует путь к начальной точке и к конечной точке без пересечения препятствий. Тем самым формируется конечный граф, учитывающий заданный шаг робота, а также свободное и занятое пространство.
- С помощью алгоритма Дейкстры найти путь от начальной точки к конечной в графе из пункта 6. Повторять шаги 5–7, уменьшая шаг, пока не будет найден путь, или шаг не станет меньше единицы.
Реализация описанного алгоритма на языке программирования Python представлена в файле https://disk.yandex.ru/d/xhgXxuKfe7QhEQ/solution_5.py.
TL — 25 с, ML — 320 МБ.
Беспилотный автономный роботизированный вертолет «Изобретательность», выполняющий исследовательскую миссию на Марсе, после очередного полета сделал снимок местности вокруг точки его приземления.
Требуется написать программу для определения расположения препятствий на полученном от марсианского вертолета изображении песчаной местности. Само изображение было обработано внутренней программой вертолета для поиска препятствий: убрано большинство лишних деталей и изображение бинаризировано (есть только черные и белые пиксели).
К сожалению, несмотря на обработку изображения, на нем, кроме препятствий, остались отдельные следы песчинок. Препятствием для последующей посадки вертолета являются камни, представляющие собой группу окрашенных в черный цвет пикселей размером не меньше, чем \(2 \times 2\) пикселя.
В качестве ответа для каждого препятствия нужно вывести координаты его центра масс. В данном случае центром масс камня будем считать среднее по всем положениям пикселей, принадлежащих данному камню. Центр массы камня считается найденным правильно, если полученный ответ отличается от истинного не более, чем на 1 пиксель в каждую сторону или по диагонали. Гарантируется, что пиксели, представляющие собой песок, не являются соседними, в том числе по диагонали, и не граничат с камнями.
Формат входных данных
- В первой строке заданы два числа \(W\) и \(H\) — ширина и высота изображения.
- Далее следующие \(H\) строк построчно поступает бинаризованное изображение в виде двумерного массива, элементы строки разделены пробелами.
Формат выходных данных
- В первой строке поступает количество камней \(0 \leqslant n \leqslant 50\) на изображении.
- Далее в отдельных строках поступают по два числа, задающих координаты центра масс для соответствующего препятствия.
Примечания
При использовании компилятора (make) Python 3.12.3 будут доступны для использования Python пакеты scipy, sklearn, numpy и cv2.
Обратите внимание на то, что направление осей отличается от направления осей, принятого при работе с изображениями на компьютере. В качестве положительного направления осей используйте направление осей Opencv (ось \(x\) смотрит вправо, ось \(y\) вниз).
Строки, соответствующие изображениям слишком велики, поэтому вместо примера ввода предлагаем скачать файл по ссылке https://disk.yandex.ru/d/l62rd_j5CR013A, содержащий один из тестов, для тестирования на вашем ПК.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
2048 2048 255 255 255 255 ... 255 0 255 255 ... 255 255 255 0 ... 255 255 255 255 ... ... |
2 251 109 357 152 |
В качестве рекомендуемого способа решения данной задачи предлагается использовать метод DBSCAN библиотеки sklearn.
- Методом DBSCAN обнаружить кластеры, группы пикселей, которые будут соответствовать профилю камней. В качестве признаков для кластеризации необходимо использовать положения пикселей, а минимальное расстояние между кластерами задать как 1 пиксель.
- Для каждого кластера найти центр масс.
В качестве альтернативного решения можно использовать подход, основанный на операции эрозии.
- Применить метод эрозии к изображению (использовать функцию
cv2.erodeиз библиотеки OpenCV). Другим способом избавления от шумов является применение медианного фильтра с ядром \(3\times 3\). - Осуществить сегментацию изображения. Можно применить такие методы, как K-Means или методы для выделения контуров.
- Анализ объектов: после сегментации можно вычислить центры оставшихся объектов аналогично тому, как это делалось в предыдущем способе решения.
Реализация описанного алгоритма на языке программирования Python представлена в файле https://disk.yandex.ru/d/xhgXxuKfe7QhEQ/solution_6.py.
TL — 25 с, ML — 320 МБ.
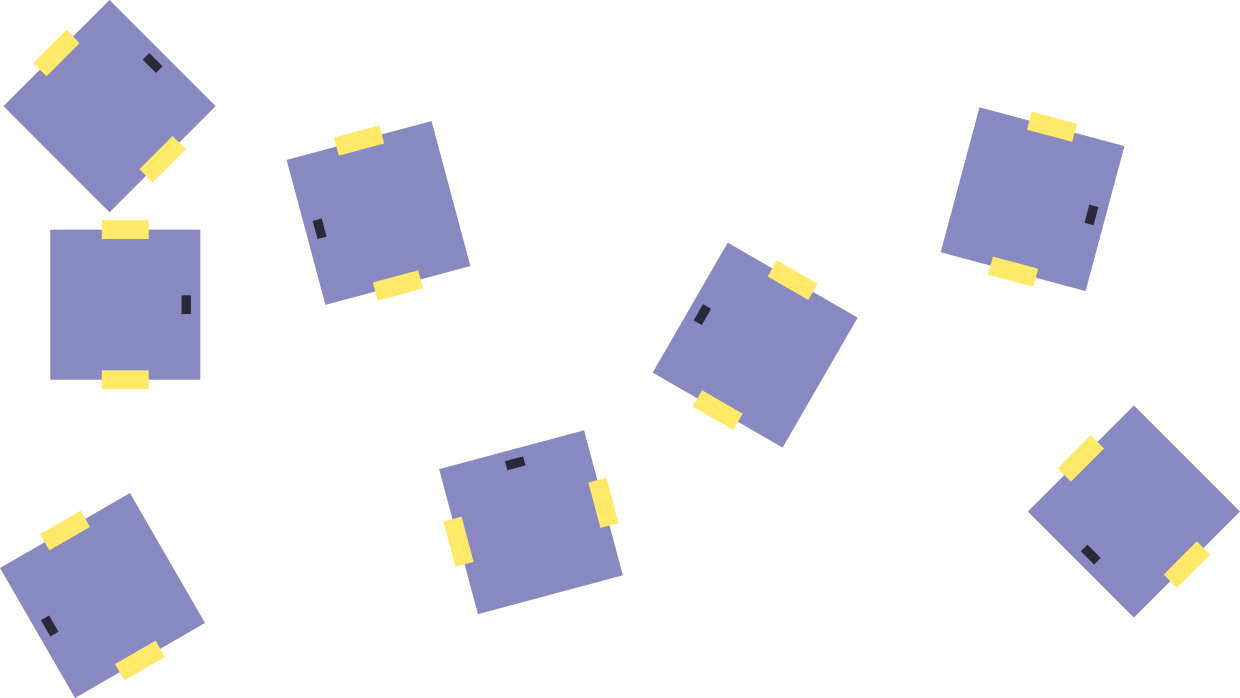
Рассмотрим мобильного робота с дифференциальной платформой. У него есть два колеса (левое и правое), соединенных с мотором. У робота есть передняя и задняя часть (ось \(y\) направлена на переднюю часть), его корпус имеет форму квадрата.
Представим, что таких роботов много, они двигаются по полю, имеют разные координаты \(x\), \(y\) центра робота и разную ориентацию \(\theta\).
Задание. По изображению необходимо определить, какие из роботов столкнулись, и вывести центры \((x, y)\) всех роботов, которые не столкнулись ни с одним другим роботом. Считается, что роботы столкнулись, если расстояние между ними менее двух пикселей, либо их изображения пересекаются. Кроме того, известно, что хотя бы один робот на изображении не пересекается ни с каким другим роботом, а также, что площадь общей части двух пересекающихся роботов не превышает 20% от площади робота. На изображении может находиться от 0 до 50 роботов.
В данной задаче рекомендуется использовать исключительно язык Python и компилятор/окружение (make) Python 3.12.3, где будут доступны для использования Python-пакеты scipy, sklearn, numpy и cv2.
Изображения предоставляются в сериализованном виде. Пример сериализации в Python:
import cv2
import base64
import numpy as np
buffer = cv2.imencode('.jpg', img)
jpgBufferText = base64.b64encode(buffer)
imageString = jptBufferText.decode('utf-8')Пример десериализации. Здесь обратно преобразуем изображение из строки:
import cv2
import base64
import numpy as np
buffer = base64.b64decode(imageString)
array = np.frombuffer(buffer, dtype=np.uint8)
img = cv2.imdecode(array, flags=1)Формат входных данных
- В первой строке заданы два числа \(N\) и \(M\) — ширина и высота изображения.
- Во второй строке передается преобразованное к строке изображение.
Значения элементов массива изображения лежат в диапазоне от 0 до 255 и имеют тип uint8.
Обратите внимание, что каждая ячейка изображения в OpenCV хранит три числа: B, G, R. Соответственно, img[0, 0] = [B, G, R]. В качестве положительного направления осей используйте направление осей OpenCV (ось \(x\) смотрит вправо, ось \(y\) — вниз) — положительный угол отсчитывается по часовой стрелке.
Формат выходных данных
- В первой строке поступает количество роботов \(0 \leqslant n \leqslant 50\) на изображении, которые не столкнулись с другими роботами.
- Далее в отдельных строках поступают координаты центра каждого такого робота, разделенные пробелом. Координаты центра должны быть целыми числами.
Тестовые данные
Пример входных данных приведен в файле https://disk.yandex.ru/d/xhgXxuKfe7QhEQ/input_problem_7.txt
Пример выходных данных:
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
4 344 345 340 225 114 168 249 154 |
- Преобразовать изображение к двум цветам так, чтобы черный цвет означал, что этот пиксель является частью какого-то робота, а белый цвет — что пиксель не является частью какого-либо робота.
- Применить операцию эрозии к изображению на два пикселя, чтобы заполнить пространство между роботами, которые находятся на расстоянии до двух пикселей включительно.
- Определить все контуры на изображении с помощью
canny. - Посчитать площадь каждого контура, если все роботы на изображении одинаковы, и гарантируется, что есть робот, который ни с кем не столкнулся, то контур с наименьшей площадью и есть такой робот.
- Найти другие контуры, площади которых превышают минимальную площадь не более, чем на 80%.
- Определить центр квадрата каждого подходящего робота с помощью поиска контуров
cannyи вывести ответ.
Реализация описанного алгоритма на языке программирования Python представлена в файле https://disk.yandex.ru/d/xhgXxuKfe7QhEQ/solution_7.py.
TL — 20 с, ML — 64 МБ.
По конвейеру движется кубическая деталь в случайной ориентации. Рядом с конвейером работает робот-манипулятор, и ему необходимо следить, чтобы деталь имела заданную ориентацию (рис. 1.8).
Робот должен повернуть деталь, если ее исходная ориентация будет отличаться от заданной. В качестве обратной связи используется камера, расположенная на конвейере.
Внешний вид детали можно представить в виде развертки (так как деталь имеет кубическую форму), причем каждая из граней может быть раскрашена в сплошной цвет, либо содержать нанесенную метку (ArUco-маркер). Пример развертки представлен на рис. 1.9 на левом изображении. На правом изображении представлен порядок граней на развертке (он понадобится позже).
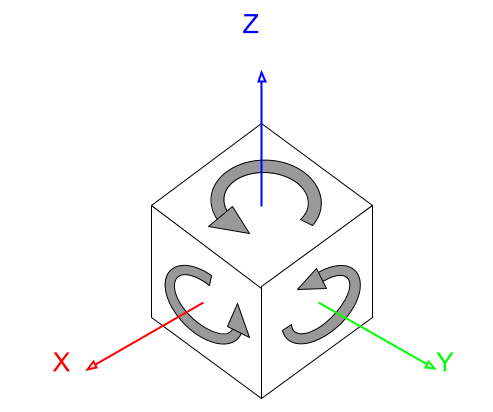
Вращение детали осуществляется вокруг осей на 90°, как показано на рис. 1.10. Набор возможных команд ограничивается шестью командами и обозначает ось вращения и направление («+X», «-X», «+Y», «-Y», «+Z», «-Z»).
Примеры вращений представлен в таблице 1.
| Команда | До | После |
|---|---|---|
«+X» |
 |
 |
«-X» |
 |
 |
«+Y» |
 |
 |
«-Y» |
 |
 |
«+Z» |
 |
 |
«-Z» |
 |
 |
Задание. Требуется на основе исходного и заданного изображений определить набор команд, при помощи которых робот-манипулятор сможет переложить деталь в заданную ориентацию. Максимально разрешенное количество команд равно 30.
Формат входных данных
- В первой строке задается развертка детали в виде массива, содержащего шесть элементов. Номер элемента соответствует порядковому номеру грани развертки, которые были представлены ранее. Если грань содержит сплошной цвет, то она будет описываться словарем, содержащим ключ
colorи значение в виде массива чиселint, задающие цвет согласно цветовой модели RGB, например,{"color": [R, G, B]}. Если грань содержит метку, то она будет описываться словарем, содержащим ключmarker\idи значениеint, которое соответствуетIDзначению маркера, например,{"marker_id": 173}. - Вторая строка содержит два целых числа \(N\) и \(M\) — ширина и высота изображения.
- В следующих трех строках содержатся RGB-каналы исходного изображения соответственно в виде \(N\times M\) элементов, разделенных пробелами (сначала идут элементы первой строки, далее — второй и т. д.).
- В следующих трех строках содержатся RGB-каналы заданного изображения соответственно в виде \(N\times M\) элементов, разделенных пробелами (сначала идут элементы первой строки, далее — второй и т. д.).
Формат выходных данных
Выходными данными служит одна строка, содержащая в себе команды (описаны ранее в таблице), разделенные пробелами. Всего не более тридцати команд.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
[’color’: [ 0, 0, 255],’marker_id’: 173, ... 640 480 255 255 255 255 ... 255 255 255 255 255 255 ... 255 255 255 255 255 255 ... 255 255 255 255 255 255 ... 255 255 255 255 255 255 ... 255 255 255 255 255 255 ... 255 255 |
+X +X +Y -Z -Z |
- Сначала ведется поиск видимых вершин кубов (деталей) на двух изображениях. Для каждой из граней, согласно известной развертке, надо определить или ее цвет, или ArUco-метку, а также ее центр.
- По координатам центров граней определить, какая грань находится сверху, какая — слева, а какая — справа на каждом изображении, из чего определить текущую и заданную ориентацию куба.
- Выбрать две смежные грани куба, представляющего желаемую ориентацию, на основе которых будет производиться поиск последовательности команд. Последующие пункты описывают последовательность при выборе левой и правой граней.
- Убедиться, что грань, которая должна оказаться в левом положении, не находится на верхней или нижней грани. В противном случае с помощью поворотов вокруг оси \(Y\) перевести грань в центральное положение (т. е. такое положение, при котором она не находится ни сверху, ни снизу).
- Окончательно за счет поворотов вокруг оси \(Z\) привести грань из предыдущего пункта в левое положение.
- С помощью поворотов вокруг оси \(X\) выставить необходимую грань в правое положение. Заметим, что вместе с тем будет выставлена и верхняя грань в нужное положение.
Реализация описанного алгоритма на языке программирования Python представлена в файле https://disk.yandex.ru/d/xhgXxuKfe7QhEQ/solution_8.py.