Предметный тур. Математика. 3 этап
Даны три натуральных числа \(a\), \(b\), \(c\), удовлетворяющие следующим условиям:
- \(a>1\),
- \(ab\) — простое число,
- \(bc\) — произведение двух простых чисел,
- \(abc\) не кратно квадратам простых чисел,
- \(abc \leqslant 42\).
Найдите все тройки чисел \((a, b, c)\), удовлетворяющих указанным условиям.
Так как \(a>1\), \(ab\) — простое, то \(b=1\) и \(a\) — простое.
Из третьего условия \(bc=1\cdot c=c\). Значит, \(c\) — это произведение двух различных простых чисел \(p_1\cdot p_2\), так как если \(p_1= p_2=p\), то \(abc\) делится на \(p^2\), что недопустимо по условию. Тогда можно считать, что \(abc\) — это произведение трех различных простых чисел \(abc=p_1 \cdot p_2 \cdot p_3\).
Заметим, что наименьшие произведения дают тройки \(2\cdot 3\cdot 5=30\), \(2\cdot 3\ \cdot 7 =42\). Все остальные произведения трех простых чисел будут больше 42. Тогда возможны следующие наборы чисел \((a, b, c)\): (2, 1, 15), (3, 1, 10), (5, 1, 6), (2, 1, 21), (3, 1, 14), (7, 1, 6).
(2, 1, 15), (3, 1, 10), (5, 1, 6), (2, 1, 21), (3, 1, 14), (7, 1, 6).
Приведен только верный ответ без объяснений — 5 баллов.
Потеряна одна из серий решений, то есть получено только 3 ответа — 7 баллов.
Нет объяснений, почему простые числа должны быть различными, хотя это подразумевается в решении — снять 2 балла.
Потерян один из ответов при верном решении — 12 баллов.
Отсутствуют объяснения, что нет других подходящих троек простых чисел, кроме 2, 3, 5 и 2, 3, 7 — баллы не снижать.
Пусть множество \(S\) является наименьшим набором натуральных чисел, удовлетворяющих следующим свойствам:
- число \(2\) принадлежит \(S\),
- если \(n^2\) принадлежит \(S\), то \(n\) также принадлежит \(S\),
- если \(n\) принадлежит \(S\), то \((n+5)^2\) также принадлежит \(S\).
- Верно ли, что число \(4\underbrace{0\dots0}_{2025}4\) принадлежит \(S\)? (в этом числе 2025 нулей).
- Найдите все числа \(n \geqslant 10000\), которые принадлежат \(S\).
Если \(n \in S\), то \((n+5)^2 \in S \Longrightarrow{ n+5 \in S}\), тогда для любого натурального \(k\) верно: \(n+5k \in S\).
Так как \(2 \in S \Longrightarrow (2+5)^2=49 \in S\), кроме того, \(5k+2 \in S\) для любого целого \(k\geqslant 0\).
Из того, что \(49 \in S\) следует, что все числа вида \(5k+4 \in S,\) где \(k\geqslant 9\).
Отсюда сразу получаем решение для п.1, так как число \(4\underbrace{0\dots0}_{2025}4\) имеет вид \(5k+4.\)
Из того, что \(49 \in S \Longrightarrow (49+5)^2=54^2=2916 \in S\), значит, все числа вида \(5k+1 \in S\), где \(k\geqslant 583\).
Так как \(54 \in S \Longrightarrow 54+2\cdot 5 =64 \in S \Longrightarrow 8 \in S\), значит, все числа вида \(5k+3 \in S\), где \(k\geqslant 1\).
В итоге получили, что все числа \(n\geqslant 10000\), дающие остатки 1, 2, 3, 4 при делении на 5, содержатся в \(S\).
Покажем теперь, что никакое число, кратное 5, не может содержаться в \(S\). Действительно, \(n^2\) делится на 5 тогда и только тогда, когда \(n\) делится на 5. А также \((n+5)^2\) делится на 5 тогда и только тогда, когда \(n\) делится на 5. Но изначально в множестве \(S\) есть только число 2, которое не делится на 5, поэтому нельзя получить никакое число, кратное 5.
Замечание. Можно доказать более общее утверждение: в \(S\) содержатся все натуральные числа, кроме 1 и чисел, кратных 5.
Так как \(54=49+5 \in S \Longrightarrow 54^2 \in S\). Заметим, что числа вида \((5k+4)^2\equiv 1 \pmod{5}\), значит, все числа вида \(5k+1\), большие \(54^2\), содержатся в \(S\). Значит, \(256^2 \in S\). Отсюда получаем, что \(256 \in S\), \(16=\sqrt{256} \in S, 4=\sqrt{16} \in S\). Следовательно, любое число вида \(5k+4 \in S\).
Далее \(4 \in S \Longrightarrow 4+5=9 \in S \Longrightarrow 3 \in S\). Поэтому любое число вида \(5k+3 \in S\).
Так как \(16 \in S\), то \(16+5\cdot 4=36 \in S \Longrightarrow 6 \in S\). Значит, все числа вида \(5k+1\), начиная с 6, содержатся в \(S\).
Осталось показать, что 1 не может содержаться в \(S\). Это следует из того, что \(1=1^2\), а значит, 1 нельзя получить из чисел, больших 1.
1. Да. 2. Все натуральные числа, кроме кратных 5.
Приведен только ответ в пункте 1 — 0 баллов.
Приведен только ответ в пункте 2 — 1 балл.
Доказано, что все числа вида \(5k+i \geqslant 10000\) содержатся в \(S\) — добавить 2 балла для каждого \(i\).
Доказано, что числа, кратные 5, не содержатся в \(S\) — 5 баллов.
Верно решен пункт 1 — 7 баллов.
При решении пункта 2 доказано, что любое число \(n\geqslant 10000\), некратное 5, подходит — 8 баллов.
Заданы целые числа \(m > n \geqslant 3\). Рамкой прямоугольника \(m \times n\) называется фигура, состоящая из \(2m +2n-4\) граничных квадратов этого прямоугольника. На рис. 1.1 показана рамка размером \(4\times 7\) в качестве примера.
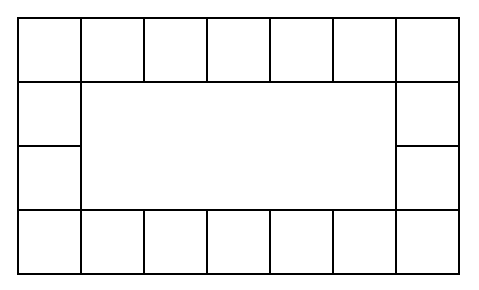
На рамке размера \(m\times n\), все клетки которой первоначально белые, играют робот А и робот Б. Ходят по очереди, первый ход делает А. За один ход нужно выбрать полностью белый прямоугольник \(1\times k\), \(k\geqslant 1\) и перекрасить все его клетки в черный цвет так, чтобы оставшиеся белые клетки образовывали связную фигуру (клетки, имеющие лишь общую вершину, связными не являются). Выиграет игрок, сделавший последний ход.
Найдите все пары \((m, n)\), для которых у робота А есть выигрышная стратегия, позволяющая ему победить вне зависимости от ходов противника.
Пусть для определенности левая и правая границы рамки состоят из \(n\) клеток, а верхняя и нижняя — из \(m\) клеток.
Приведем выигрышную стратегию робота А и покажем, что он всегда может ее придерживаться.
Робот А первым своим ходом закрашивает нижнюю границу рамки (прямоугольник \(1\times m\)).
Теперь у робота Б есть возможность закрасить клетки только на левой или правой границе. Следующими ходами робот А закрашивает столько же клеток, сколько закрасил Б, но на противоположной границе. Например, Б закрасил \(k\) клеток на левой границе, тогда А закрашивает \(k\) клеток на правой. Так продолжается до тех пор, пока одна из границ не будет полностью закрашена. Заметим, что это обязательно произойдет после хода робота Б. Пусть теперь осталось \(s\) незакрашенных клеток на боковой границе и \(t\) на верхней (одна угловая клетка общая). Причем \(t > s\), так как боковая граница содержит меньше клеток, чем верхняя. Теперь робот А закрашивает клетки на верхней границе так, чтобы количества оставшихся клеток на верхней и боковой границах было одинаковым. Далее робот А повторяет ходы робота Б симметрично незакрашенной угловой клетке до тех пор, пока незакрашенная фигура не является прямоугольником. В силу симметрии незакрашенная фигура станет прямоугольником после хода робота Б. После этого робот А закрасит оставшийся прямоугольник и выиграет.
Робот А выигрывает для любых \(m\), \(n\).
Указано, что робот А всегда выигрывает без объяснений — 0 баллов.
Приведена верная стратегия робота А, однако не доказано, что ее всегда можно реализовать — 15 баллов.
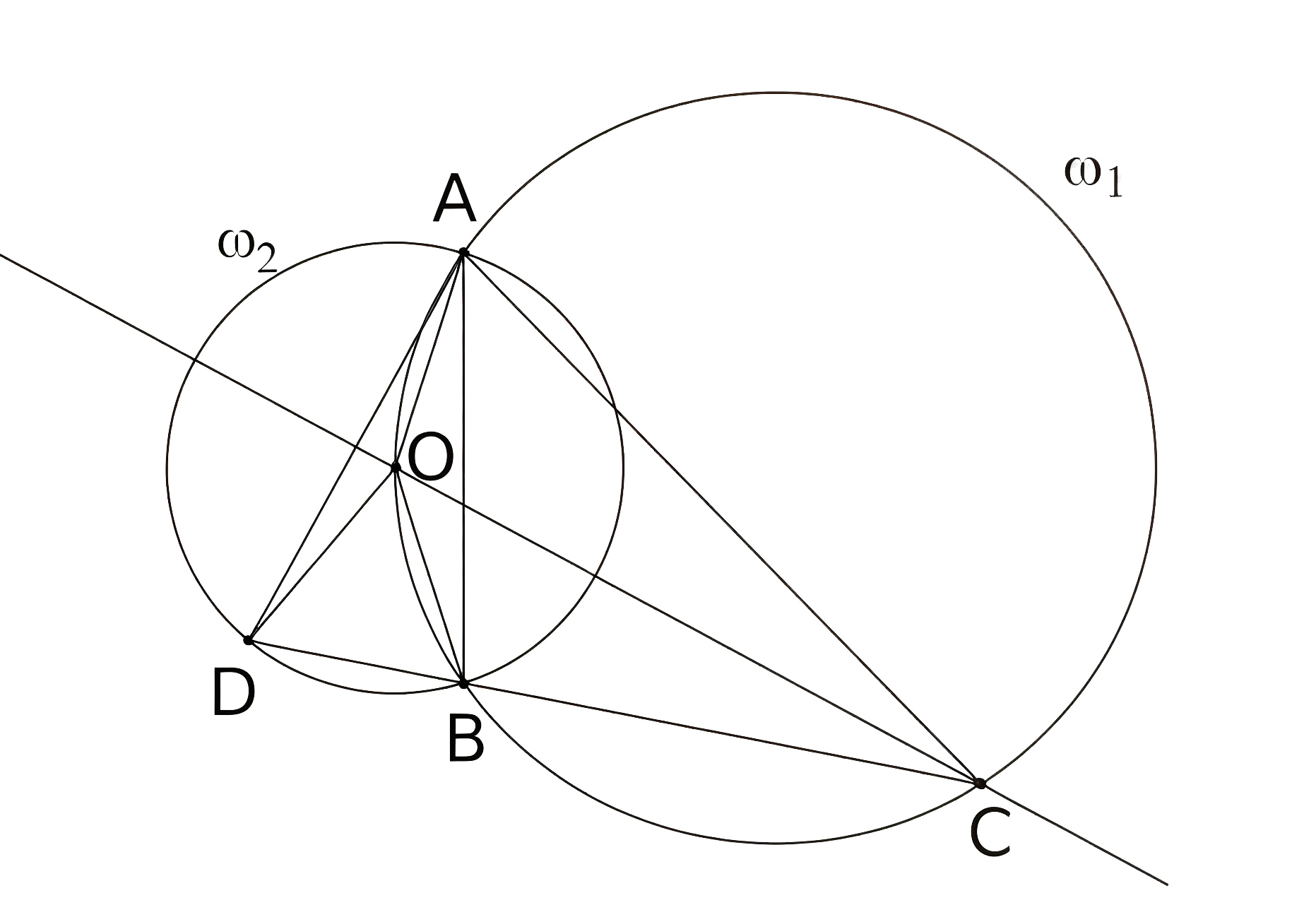
Две окружности \(\omega_1\) и \(\omega_2\) пересекаются в двух различных точках \(A\) и \(B\). Прямая, проходящая через \(B\), снова пересекает \(\omega_1\) и \(\omega_2\) в точках \(C\) и \(D\) соответственно. Докажите, что если \(CA = CD\), то центр \(\omega_2\) лежит на окружности \(\omega_1\).
Проведем перпендикуляр из точки \(C\) на \(AD\). Он пересечет \(\omega_1\) в некоторой точке \(O\). Поскольку \(CA = CD\), то \(CO\) является серединным перпендикуляром к \(AD\), а также биссектрисой угла \(\angle ACD\). Тогда треугольники \(AOC\) и \(DOC\) равны, значит, \(OA = OD\). Так \(\angle OCB = \angle OAB\) как вписанные углы, опирающиеся на дугу \(\overset{\frown}{OB}\), а \(\angle ACO = \angle ABO\) как вписанные углы, опирающиеся на дугу \(\overset{\frown}{AO}\), то треугольник \(AOB\) — равнобедренный.
Таким образом, получаем \(OA = OB = OD\). Это означает, что \(O\) равноудалена от вершин \(A\), \(B\), \(D\) и является центром описанной окружности треугольника \(ADB\), а значит, и центром окружности \(\omega_2\).
Сформулирована идея выбора точки \(O\) на биссектрисе угла \(C\) — 5 баллов.
Доказано, что \(OA=OD\) при выборе точки \(O\) на биссектрисе — 10 баллов.
Доказано, что \(OA=OB\) при выборе точки \(O\) на биссектрисе — 10 баллов.
Пусть \(P(x) = x^2 + ax + b\) — квадратный трехчлен. Известно, что числа \(P(-1)^2\), \(P(0)^2\), \(P(1)^2\), являются целыми и в указанном порядке образуют арифметическую прогрессию. Докажите, что \(a\) и \(b\) — целые числа.
Так как \(P(-1)=1-a+b\), \(P(0)=b\), \(P(1)=1+a+b\), то по свойству арифметической прогрессии \(2b^2 = (1 - a + b)^2 + (1 + a + b)^2 = 2 + 4b + 2b^2 + 2a^2\). Следовательно, \(a^2 + 2b + 1 = 0\).
Заметим, что \(1 + a^2 + b^2 + 2a + 2b + 2ab = (1 + a + b)^2 \in \mathbb{Z}\). Так как \(1, b^2, a^2 + 2b\) — целые числа, то \(2a+2ab=2a(1+b)\) тоже целое, значит, \(4a^2(1 + b)^2\) — целое. Но \(a^2 = -(2b + 1)\), поэтому \(4(2b + 1)(1 + b)^2\) тоже целое.
Так как \(4(2b + 1)(1 + b)^2 = 4(1 + 4b + 5b^2 + 2b^3)=4b(4+2b^2)+4+20b^2\), то \(4b(4 + 2b^2)\) — целое число. Если \(b=0\), то \(b\) — целое, иначе оно рационально, но так как \(b^2\) целое, а квадрат рационального нецелого не может быть целым, значит, \(b\) может быть только целым.
Так как \(a^2 = -(2b + 1)\), то \(a^2\) — целое. Далее, так как \(2a(1 + b)\) — целое, то если \(b \ne -1\), получим, что \(a\) рациональное, а значит, целое. Если \(b = -1\), то \(P(-1) = -a\), \(P(0) = b = -1\) и \(P(1) = a\). Поэтому числа \(a^2, 1, a^2\) должны образовывать арифметическую прогрессию. Это означает, что \(a^2 = 1\), \(a = \pm1\).
Во всех случаях получаем, что \(a, b\) являются целыми числами.
Доказано, что \(b\) — целое — 15 баллов.
Доказано, что \(b\) — рациональное — 10 баллов.
Доказано, что \(b\) — целое и \(a^2\) — целое — 20 баллов.
Упущены случаи такие как, \(b=0, b=-1\) — снять 5 баллов.
Нейросеть получила на выходе упорядоченный по возрастанию список четырехзначных чисел, каждое из которых удовлетворяет следующим условиям:
- в списке только четные числа;
- у каждого числа ровно 3 нечетные цифры и все они различны;
- сумма цифр каждого числа равна 23.
Ответьте на вопросы:
- Какое первое число записано в списке?
- Сколько всего чисел в списке?
Обратите внимание: единственная четная цифра стоит на четвертом месте, так как число четное.
Заметим, что 1598 удовлетворяет указанным условиям. Предположим, что есть меньшее число. Его первая цифра не может быть меньше 1. Предположим, что его вторая цифра меньше 5, тогда его первые две цифры — 13. Следовательно, сумма всех его цифр не больше \(1+3+8+9 = 21\) (8 и 9 — максимально возможные цифры). Противоречие.
Следовательно, первые две цифры данного числа — 15 (иначе число больше 1598). Заметим, что \(23-1-5=17\), следовательно, последние две цифры нашего числа — 8 и 9, причем 8 стоит на четвертом месте.
Рассмотрим какое-нибудь четырехзначное число, удовлетворяющее указанным условиям. Обозначим через \(d\) его последнюю цифру.
Максимальная сумма трех различных нечетных цифр равна \(9+7+5=21\), поэтому \(d\geqslant 2\).
Рассмотрим теперь возможные значения \(d\):
- Если \(d=2\), то сумма трех других цифр равна 21. Единственная возможность 5, 7, 9.
- Если \(d=4\), то сумма трех других цифр равна 19. Единственная возможность 3, 7, 9.
- Если \(d=6\), то сумма трех других цифр равна 17. Возможности 1, 7, 9 или 3, 5, 9.
- Если \(d=8\), то сумма трех других цифр равна 15. Возможности 3, 5, 7 или 1, 5, 9.
Получаем 6 вариантов. В каждом варианте первые три цифры можно переставлять местами \(3!\) способами. Окончательно получаем \(6\cdot 3! = 36\) чисел.
1. 1598, 2. 36.
Ответ в пункте 1, возможно, без обоснования — 5 баллов.
Верное решение пункта 2 — 10 баллов.
Упущен один из 6 случаев троек нечетных цифр — 5 баллов за пункт 2.
Неверно посчитали число перестановок из трех нечетных цифр (например, 3, вместо \(3!\)) — 5 баллов за пункт 2.
В таблице \(N\times N\) каждая из клеток раскрашена в черный или белый цвет. Оказалось, что для любой пары столбцов и любой пары строк среди четырех клеток на их пересечении встречаются хотя бы одна черная и хотя бы одна белая. Какое наибольшее значение может принимать число \(N\)?
Пусть \(N\geqslant 5\). Выделим квадрат \(5\times 5\). Если его столбец содержит хотя бы три черные клетки, то назовем его черным, в противном случае — белым. Из пяти столбцов хотя бы три — одного цвета. Рассмотрим эти три столбца. Без ограничения общности будем считать их черными. Обозначим строки \(a, b, c, d, e\) в каком-либо порядке. Пусть в первом столбце черные клетки стоят в строках \(a, b, c\). Тогда во втором и третьем столбцах максимум по одной черной клетке в этих строках. Значит, во втором и третьем столбцах черные клетки точно стоят в строках \(d\) и \(e\), и найдена пара строк \(d, e\) и пара столбцов \(2, 3\), в пересечении которых все клетки черные. Противоречие.
Пример для \(N=4\) приведен на рис. 2.1.

\(N=4\).
Только верный ответ — 0 баллов.
Дан верный ответ и приведен пример — 5 баллов.
Доказано, что \(N\geqslant 5\) не подходит — 15 баллов.
Баллы, указанные в критериях выше, складываются.
Вместо \(N\geqslant 5\) рассматривается лишь случай \(N=5\) — баллы не снимать.
Найдите все тройки целых чисел \(a, b, c\) для которых выполняются оба равенства \(a^2=bc+4\), \(b^2=ac+4\).
Пусть \(a=b\), тогда \(a^2=ac+4\) или \(a(a-c)=4\). Получаем, что \(a\) равно одному из чисел \(\pm 4, \pm 2, \pm 1\). Рассматривая каждый случай, получаем решения \((4, 4, 3)\), \((-4, -4, -3)\), \((2, 2, 0)\), \((-2, -2, 0)\), \((1, 1, -3)\), \((-1, -1, 3)\).
Пусть \(a\neq b\). Вычтем из первого уравнения второе \(a^2-b^2=c(b-a)\). Разделим обе части уравнения на \(b-a\) и получим \(-a-b=c\). Подставим в первое уравнение \(a^2=-ab-b^2+4\). Откуда \(2a^2+2b^2+2ab=8\). Следовательно, \((a+b)^2+a^2+b^2=8\).
Число 8 раскладывается в сумму трех квадратов единственным образом \(8=0+4+4\), поэтому пара \((a,b)\) может быть равна \((2, -2)\), \((-2, 2)\), \((2, 0)\), \((-2, 0)\), \((0, 2)\), \((0, -2)\). Учитывая, что \(c=-a-b\), получим тройки \((2, -2, 0)\), \((-2, 2, 0)\), \((2, 0, -2)\), \((-2, 0, 2)\), \((0, 2, -2)\), \((0, -2, 2)\).
\((4, 4, 3)\), \((-4, -4, -3)\), \((2, 2, 0)\), \((-2, -2, 0)\), \((1, 1, -3)\), \((-1, -1, 3)\), \((2, -2, 0)\), \((-2, 2, 0)\), \((2, 0, -2)\), \((-2, 0, 2)\), \((0, 2, -2)\), \((0, -2, 2)\).
Рассмотрен случай \(a=b\) — 5 баллов.
Рассмотрен случай \(a\neq b\) — 15 баллов.
В случае \(a\neq b\) доказано лишь, что \(a+b+c=0\) — 5 баллов.
За потерю каждого из ответов снимать 1 балл.
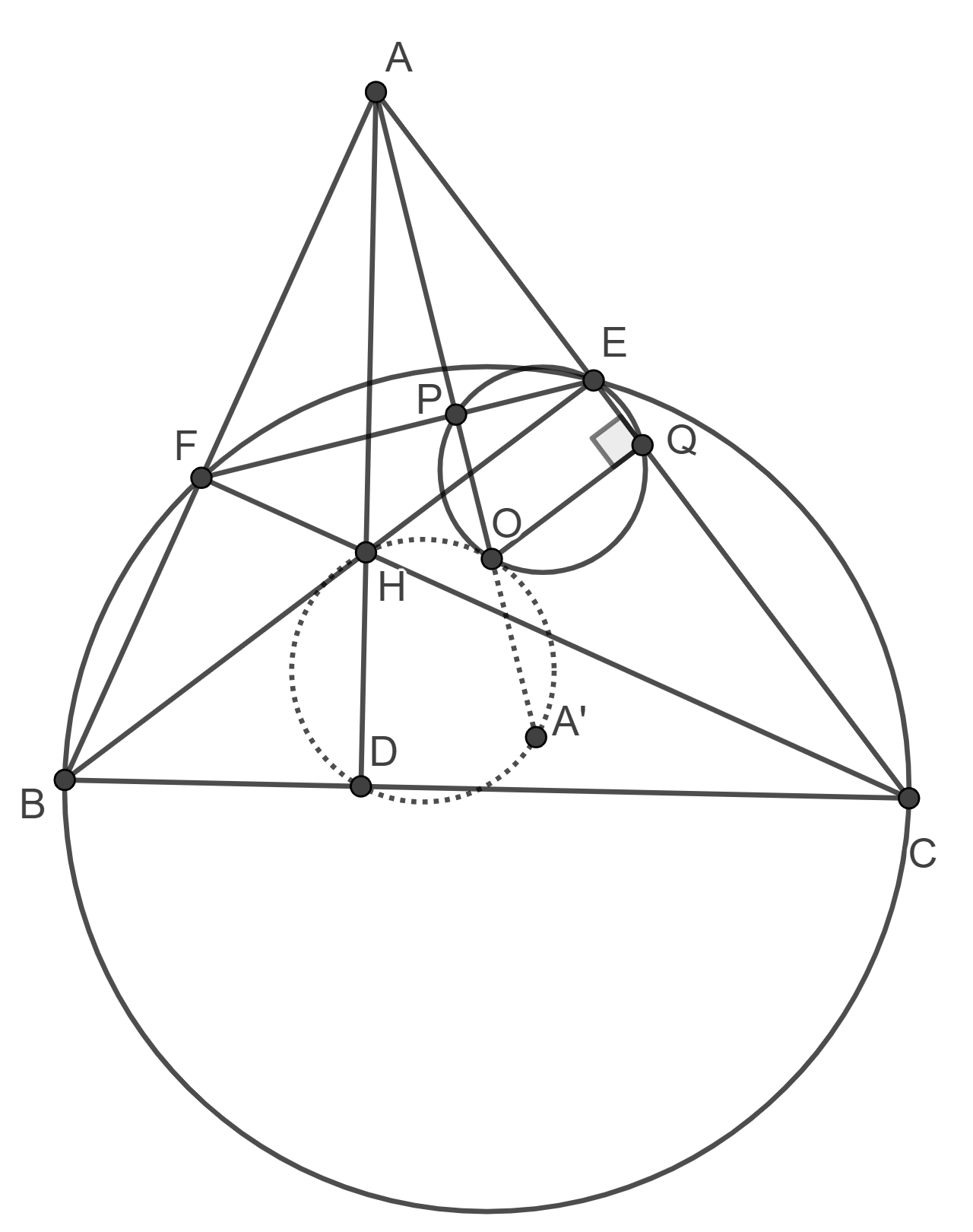
Пусть \(ABC\) треугольник, в котором \(O\) — центр описанной окружности и \(H\) — точка пересечения высот. Пусть \(AD\), \(BE\) и \(FC\) — высоты треугольника \(ABC\). Обозначим через \(A'\) точку, симметричную точке \(A\) относительно прямой \(EF\). Докажите, что \(HOA'D\) — вписанный четырехугольник.
Докажем, что \(A\), \(O\), \(A'\) лежат на одной прямой.
Пусть \(AO\) пересекает \(EF\) в точке \(P\).
Заметим, что \(\angle AOC\) — центральный, поэтому \(\angle AOC = 2\angle B\). Кроме того, \(AO=OC\), поэтому \(\angle OAC=\angle OCA=(180^\circ-2\angle B)/2=90^\circ - \angle B\).
Тогда \[\angle OAC = 90^\circ - \angle B = \angle DAF.\] Из вписанности четырехугольника \(BCEF\) \[\angle AEP = \angle B.\] Тогда треугольники \(PEA\) и \(DBA\) подобны и \(\angle APE = \angle ADB = 90^\circ\). Получаем \[AO \perp EF,\] и точки \(A\), \(O\), \(P\), \(A'\) лежат на одной прямой.
Пусть \(Q\) середина \(AC\). Тогда \(OQEP\) вписанный.
Имеем \[AO \cdot AP = AQ \cdot AE.\]
Умножим обе части на 2 \[AO \cdot (2AP) = (2AQ) \cdot AE.\]
Так как \(2AP = AA'\) и \(2AQ = AC\), то \[AO \cdot AA' = AC \cdot AE = AD \cdot AH \quad (\text{так как } DHEC \text{ вписанный}).\]
Следовательно, \(DHOA'\) — вписанный.
Доказано, что \(AO \perp EF\) — 5 баллов.
Доказано, что точки \(A, O, A'\) лежат на одной прямой — 5 баллов.
Найдите все функции \(f: \mathbb{R} \to \mathbb{R}\) такие, что \[f(yf(x)-x) + f(xy-y) + f(x+y) = 2xy\] для всех \(x, y \in \mathbb{R}\). \(f: \mathbb{R} \to \mathbb{R}\) означает, что аргумент и значение функции \(f\) принадлежат множеству всех действительных чисел \(\mathbb{R}\).
- Подставим \(x=y=0\). Получим, \(3f(0)=0\), откуда \(f(0)=0\).
- Подставим \(y=0\). Получим \(f(-x)+f(x)=0\). Т. е. \(f(-x)=-f(x)\) для всех \(x \in \mathbb{R}\).
- Подставим \(y=-1\). Получим \(f(-f(x)-x)+f(1-x)+f(x-1)=-2x\). Откуда \(f(x+f(x))=2x\). Обозначим \(k=-\frac12 +f(-\frac12)\). Тогда при \(x=-1/2\) получим \(f(k)=-1\).
Подставим вместо \(x\) число \(k\), а вместо \(y\) подставим \(x\). Получим \(f(xf(k)-k)+f(kx-x)+f(k+x)=2kx\). Тогда \(f(x(k-1))=2kx\).
Если \(k=1\), то \(f(0)=2x\) и \(0=2x\) для всех \(x \in \mathbb{R}\). Противоречие.
Если \(k\neq 1\), то, обозначив, \(z=x(k-1)\), получим \(f(z)=\dfrac{2k}{k-1}z\). Поэтому \(f(x)=cx\), для некоторого \(c\).
Подставим теперь в исходное уравнение \(c(ycx-x)+c(xy-y)+c(x+y)=2xy\) или \(cxy(c+1)=2xy\) для всех \(x, y \in \mathbb{R}\). Откуда \(c(c+1)=2\). Решая уравнение, находим \(c=1\) или \(c=-2\).
\(f(x)=x\), \(f(x)=-2x\).
Приведен один из ответов и проверено, что он подходит — 2 балла.
Приведены оба ответа и проверено, что они подходят — 5 баллов.
Баллы за указанные выше критерии не складываются.
Получено условие \(f(-x)=-f(x)\) — 5 баллов.
Получено \(f(x)=cx\) — 10 баллов.
Баллы за указанные продвижения складываются.