Предметный тур. Информатика. 3 этап
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Одним из развлечений для любого разума является нахождение красивых математических объектов. Один ИИ решил строить пифагоровы треугольники, состоящие из двух других пифагоровых треугольников.
Напомним, что тройка натуральных чисел \(a\), \(b\), \(c\) называется пифагоровой, если \(a^2 + b^2 = c^2\). Если нарисовать треугольник со сторонами \(a, b, c\), то он получится прямоугольным с гипотенузой длины \(c\) и катетами \(a\) и \(b\). Самый известный пифагоров треугольник имеет стороны \(3,~4,~5\).
В пифагоровом треугольнике можно провести высоту из прямого угла на его гипотенузу и получить разбиение на два других прямоугольных треугольника, однако далеко не всегда эти два треугольника будут пифагоровыми. Вот ИИ и задался вопросом: существует ли некоторый пифагоров треугольник, который можно раз- бить таким образом на два других пифагорова треугольника? И ответ обнадеживает: такие треугольники есть. Пример одного такого треугольника представлен на рис. 1.1.
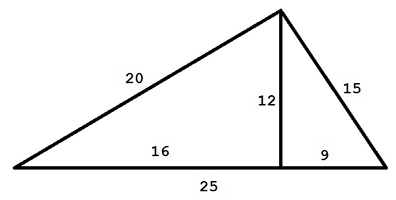
Можно видеть, что для всех трех треугольников на этом рисунке выполняются требуемые равенства: \(15^2 + 20^2 = 25^2\), \(12^2 + 16^2 = 20^2\), \(9^2 + 12^2 = 15^2\).
Обозначим стороны самого маленького из трех треугольников в разбиении через \(a_1, b_1, c_1\), стороны среднего — через \(a_2,~b_2,~c_2\), а стороны самого большого, того, который разбивается на два меньших — через \(a_3, b_3, c_3\). Всегда выполняется \(a_i~<~b_i~<~c_i\). В примере на рисунке \(a_1=9,~b_1=12,~c_1=15,~a_2=12,~b_2=16,~c_2=20,~a_3=15,~b_3=20,~c_3=25\).
Теперь ИИ хочет познакомить со своей коллекцией таких треугольников. Необходимо по заданным \(a_3, b_3, c_ 3\) разбить предлагаемый пифагоров треугольник на два меньших. Гарантируется, что для заданных трех чисел ответ всегда существует.
Формат входных данных
В одну строку через пробел задаются три натуральных числа \(a_3, b_3, c_3\) — стороны большого пифагорова треугольника. Гарантируется, что его можно разбить на два меньших пифагорова треугольника, если провести высоту из прямого угла на его гипотенузу.
\(1 \leqslant a_3 < b_ 3 < c_3 \leqslant 10^9\).
Формат выходных данных
Вывести в две строки стороны двух пифагоровых треугольников, на которые разбивается заданный на входе. В первую строку вывести через пробел стороны \(a_1, b_1, c_1\) самого маленького треугольника разбиения, а во вторую сторону — стороны среднего. Всегда должно выполняться \(a_i < b_i < c_i\) и \(a_1 < a_2, b_1 < b_2, c_1 < c_2\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
15 20 25 |
9 12 15 12 16 20 |
Пример программы-решения
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main(){
int a3, b3, c3;
cin >> a3 >> b3 >> c3;
int a1 = a3 * a3 / c3;
int b1 = a3 * b3 / c3;
int c1 = a3;
int a2 = b1;
int b2 = b3 * b3 / c3;
int c2 = b3;
cout << a1 <<' '<< b1<<' '<< c1<< endl;
cout << a2 <<' '<< b2<<' '<< c2<< endl;
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Рассмотрим следующую задачу из области криптографии.
Алиса посылает Бобу сообщение, которое состоит из \(n\) положительных целых чисел \(a_i\) (\(i\) от 1 до \(n\)). Злоумышленница Мэллори перехватывает эти числа и каждое \(a_i\) преобразует в какое-то также положительное целое число \(t_i\) по следующему правилу: изначально у Мэллори есть число \(t_0 = 0\). Далее, перехватив очередное число Алисы \(a_i\), Мэллори из него получает число \(t_i\). Если \(a_i \leqslant t_{i-1}\), то \(t_i = a_i + t_{i-1}\), если же \(a_i > t_{i-1}\), то Мэллори может случайным образом выбрать \(t_i\) из двух вариантов \(t_i = a_i + t_{i-1}\) или \(t_i = a_i - t_{i-1}\). После этого полученное \(t_i\) отправляется Бобу, а также используется для получения следующего \(t_{i + 1.}\)
Допустим, если Алиса хочет переслать числа \(2, 6, 5, 8, 11, 1\), то Мэллори может сделать, например, следующее преобразование (в суммах первое число — это \(a_i\), второе число \(t_{i-1}\)) — \(t_1 = 2 + 0 = 2\), \(t_2 = 6 - 2 = 4\), \(t_3 = 5 - 4 = 1\), \(t_4 = 8 + 1 = 9\), \(t_5 = 11 - 9 = 2\), \(t_6 = 1 + 2 = 3\). После этого Боб получит сообщение \(2, 4, 1, 9, 2, 3\).
Алиса, зная, что при передаче сообщения возможны взломы, решила продублировать его два раза подряд, то есть Мэллори, не зная этого, будет преобразовывать удвоенное сообщение. Боб, получив сообщение и зная проделки Мэллори, хочет восстановить исходное сообщение Алисы, для чего использует ИИ.
В решении задачи нужно не отстать от ИИ и написать программу, которая восстановит исходное сообщение Алисы вне зависимости от зловредных действий Мэллори. Можно показать, что при указанным условиях любое удвоенное сообщение можно восстановить однозначно.
Для лучшего понимания условия рекомендуем разобрать тесты из условия, которые получились из одного и того же сообщения Алисы, и иллюстрируют разные варианты выбора Мэллори в тех случаях, когда она может как складывать, так и вычитать.
Формат входных данных
В первой строке подается одно целое число \(n\) — количество чисел в исходном сообщении Алисы (до того, как она его удвоила), \(1 \leqslant n \leqslant 10^5\).
Во второй строке через пробел приведены \(2\cdot n\) чисел \(t_i\) — те, что сгенерировала Мэллори и получил Боб, \(1 \leqslant t_i \leqslant 10^9\). Гарантируется, что эти \(2 \cdot n\) чисел \(t_i\) получены из некоторого удвоенного исходного набора Алисы по правилам из условия.
Формат выходных данных
Вывести \(n\) чисел — восстановленное сообщение, исходно созданное Алисой до того, как она его удвоила.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
6 2 4 1 9 2 3 5 1 6 2 9 10 |
2 6 5 8 11 1 |
2 |
6 2 4 1 7 4 5 7 13 18 26 37 38 |
2 6 5 8 11 1 |
3 |
6 2 8 13 21 32 33 35 41 46 54 65 66 |
2 6 5 8 11 1 |
Пример программы-решения
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;
signed main(){
int n;
cin >> n;
vi v(2 * n);
for0(i, 2 * n){
cin >> v[i];
}
int t = 0;
vector<pii> tmp(2 * n, {0, 0});
for0(i, 2 * n){
tmp[i].x = v[i] + t;
if(v[i] > t){
tmp[i].y = v[i] - t;
}
t = v[i];
}
for0(i, n){
int tans;
if(tmp[i].x == tmp[i + n].x || tmp[i].x == tmp[i + n].y){
tans = tmp[i].x;
}
else{
tans = tmp[i].y;
}
cout << tans <<' ';
}
cou
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
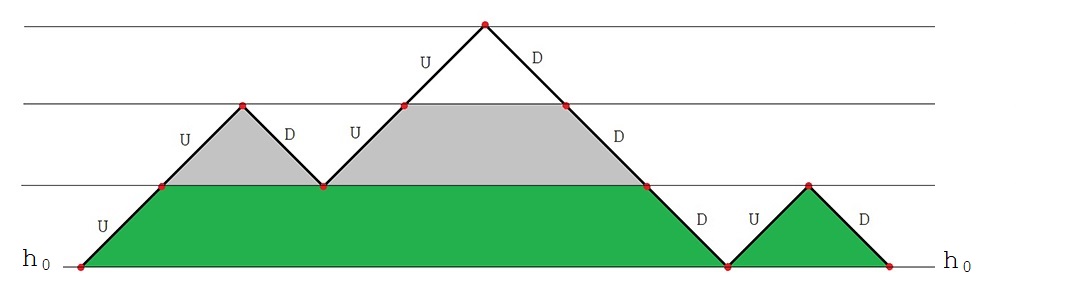
Группа биологов и ботаников исследует малоизвестный горный район. Каждый день они перемещаются по склону горного массива, фотографируют, описывают, проводят исследования и т. п. За один день группа либо поднимается на один дневной переход вверх, либо опускается также на один дневной переход вниз. Упрощенно можно считать, что расстояния, проходимые группой в течение любого дня, одинаковы, а угол к горизонту, под которым группа поднимается или опускается, равен \(45°\).
Исследователями был подмечен следующий факт: каждый раз место остановки группы на ночлег находилось как раз на границе зоны высотной поясности. Например, в первый день они поднимались по тропическому лесу, во второй — прошли пояс хвойных лесов, в третий — поднялись в пояс альпийских лугов, в четвертый — снова спустились в пояс хвойных лесов и т. д. В итоге группа последним переходом спустилась точно на ту же высоту \(h_0\), с которой начала маршрут. Помимо этого, известно, что во время прохождения маршрута группа не опускалась ниже высоты \(h_0\), но в промежуточных точках могла останавливаться на этой высоте.
Пришло время обрабатывать результаты. В числе прочих руководитель экспедиции хочет начертить двумерную диаграмму, схематично представляющую пройденный маршрут, и по ней оценить площадь каждого пояса горного рельефа, пройденного группой.
По описанию пройденного группой маршрута вывести площадь каждого пояса на полученной двумерной диаграмме.
Формат входных данных
В первой строке приведено целое четное число \(n\) — количество дневных переходов, сделанных группой, \(2 \leqslant n \leqslant 2 \cdot 10^5\).
Во второй строке содержится набор из \(n\) символов \(U\) и \(D\), описывающий характер движения группы в каждый из дней. Символ \(U\) означает, что в соответствующий день группа поднималась, а символ \(D\) означает, что в этот день группа опускалась. Гарантируется, что для этого маршрута выполняются все условия, приведенные в описании задачи.
Формат выходных данных
В первой строке следует вывести число \(k\) — количество высотных поясов, которые посетила группа.
В следующей строке вывести \(k\) чисел через пробел — площади каждого пояса на двумерной диаграмме маршрута. Пояса нумеруются с самого нижнего до самого верхнего по возрастанию высот.
В качестве единицы измерения следует использовать проекцию одного дневного перехода на горизонтальную ось и считать, что длина одного дневного перехода равна \(\sqrt{2}\). Можно показать, что площадь любого пояса в такой системе будет целым числом.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
10 UUDUUDDDUD |
3 8 4 1 |
Пример программы-решения
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
typedef vector<double> vd;
typedef vector<vd> vvd;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;
signed main(){
int n;
cin >> n;
string s;
cin >> s;
vi st;
vi ans;
for0(i, n){
if(s[i] == 'U'){
st.pb(i);
if(sz(ans) < sz(st)){
ans.pb(0);
}
continue;
}
int d = i - st.back();
ans[sz(st) - 1] += d;
st.pop_back();
}
cout << sz(ans) << endl;
for0(i, sz(ans)){
cout << ans[i] <<' ';
}
cout << endl;
}Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 128 Мбайт.
Иван Иванович купил электромобиль и хочет поехать на нем в путешествие по прямой. Емкость аккумулятора его электромобиля 100 кВтч. На один километр его машина тратит 1 кВтч. Так как электромобиль произведен неизвестным широкой публике производителем, есть небольшое условие: его аккумулятор может за одну зарядку увеличить запас только на количество киловатт-часов, равное квадрату натурального числа, то есть на 1, 4, 9, 16, 25, 36, 49, 64, 81 или 100 кВтч, при условии, что эта добавка не превысит общую емкость аккумулятора в 100 кВтч.
Например, если в момент начала зарядки аккумулятор хранил 60 кВтч, то после зарядки он может содержать 61, 64, 69, 76, 85, или 96 кВтч.
Иван Иванович знает, что по пути он встретит \(n\) электрозаправочных станций. До каждой из этих станций известно расстояние в километрах от начала маршрута, равное \(d_i\). Иван Иванович может как угодно действовать в рамках описанных выше ограничений: пропустить заправку вообще, либо заправить на ней любое разрешенное условием квадратное число киловатт-часов. На каждой станции он может заряжать автомобиль только один раз. Исходно аккумулятор его электромобиля был полностью заряжен.
Иван Иванович поставил ИИ, управляющему электромобилем, задание составить режим дозаправок по этим данным так, чтобы проехать максимальное расстояние от начала маршрута. Если в момент приезда на заправку аккумулятор опустошается и содержит 0 кВтч, то Иван Иванович может заправить любое количество, равное квадрату натурального числа от 1 до 100 кВтч и продолжать двигаться далее. В конце маршрута Иван Иванович планирует вызвать эвакуатор, поэтому будет продолжать движение до тех пор, пока не опустеет аккумулятор.
Формат входных данных
В первой строке содержится одно число \(n\) — количество электрозаправок на пути Ивана Ивановича, \(0 \leqslant n \leqslant 10^5\).
В следующей строке содержатся \(n\) целых чисел \(d_i\) через пробел — расстояние от точки старта до \(i\)-й заправки, \(1 \leqslant d_i \leqslant 10^7\). Заправки описаны в порядке увеличения расстояния от точки старта, то есть \(d_1 < d_2< \ldots < d_n\). Никакие две заправки не находятся в одной точке.
Формат выходных данных
Вывести одно число — максимальное расстояние, на которое сможет уехать Иван Иванович от точки старта.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
4 45 101 196 224 |
318 |
Примечания
В примере из условия одна из оптимальных стратегий следующая:
- Проехать от точки старта до первой заправки 45 км, останется заряд 55 кВтч. На первой заправке заправить 1 кВтч, теперь заряд 56 кВтч.
- Проехать от первой заправки до второй заправки 56 км, останется заряд 0 кВтч. На второй заправке заправить 100 кВтч, теперь заряд 100 кВтч.
- Проехать от второй заправки до третьей заправки 95 км, останется заряд 5 кВтч. На третьей заправке заправить 36 кВтч, теперь заряд 41 кВтч.
- Проехать от третьей заправки до четвертой заправки 28 км, останется заряд 13 кВтч. На четвертой заправке заправить 81 кВтч, теперь заряд 94 кВтч.
- Проехать от четвертой заправки до конца маршрута 94 километра, заряд 0 кВтч.
Окончание маршрута в точке 318 км. Можно показать, что это наилучший возможный для первого примера результат.
Пример программы-решения
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#pragma GCC target("popcnt")
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;
signed main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n;
cin >> n;
if(n == 0){
cout << 100 << endl;
return 0;
}
vector<bitset<101> > sq(101);
for0(i, 101){
for1(j, 10){
if(i + j * j <= 100){
sq[i][i + j * j] = 1;
}
}
}
bitset<101> u = sq[99];
int ans = 0;
if(u.count() != 0){
for(int j = 100; j >= 0; j--){
if(u[j]){
ans = max(ans, j);
break;
}
}
}
int p = 0;
for0(i, n){
int d;
cin >> d;
u = (u >> (d - p));
p = d;
bitset<101> dp = 0;
for0(j, 101){
if(u[j]){
dp |= sq[j];
}
}
u |= dp;
if(u.count() != 0){
for(int j = 100; j >= 0; j--){
if(u[j]){
ans = max(ans, d + j);
break;
}
}
}
}
cout << ans << endl;
}
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 256 Мбайт.
На далекой планете был открыт гигантский архипелаг, заселенный исключительно кузнечиками. Исследователи заметили, что эти кузнечики были \(p\) различных видов. На каждом острове архипелага проживал ровно один вид кузнечиков, при этом некоторые их виды захватили множество островов. Помимо естественной возможности передвигаться обычным образом по своему острову, кузнечики обладали сверхспособностью совершать гигантские суперпрыжки с острова на остров. Для этого они пользовались направлениями магнитного поля, которое на этой планете позволяло делать прыжки строго в меридиональном направлении (север-юг или юг-север), или строго в направлении параллели (запад-восток или восток-запад) и никак иначе.
Кузнечики могут передвигаться обычным образом по суше внутри любого единичного квадрата и между двумя рядом расположенными единичными квадратами, имеющими общую сторону. Если два единичных квадрата расположены рядом, но по диагонали и между ними нет пути через клетки с общими сторонами, это два различных острова, напрямую между ними передвижение невозможно.
Для исследования вопроса происхождения и расселения этих видов и объяснения возникшей ситуации был подключен ИИ, который сделал предположение, что изначально каждый вид кузнечиков зародился на своем острове и потом они, пользуясь своей способностью к суперпрыжкам, расселились по всему архипелагу. Если у двух островов есть единичные квадраты, расположенные в одном столбце или строке, то между ними возможно передвижение при помощи суперпрыжка, поэтому на данных двух островах обязательно проживают кузнечики одного вида.
Теперь у ученых возник новый вопрос: для каждого вида они хотят знать минимальную необходимую длину суперпрыжка, обладая которой, этот вид смог расселиться по островам, которые сейчас заселяет.
По заданной карте архипелага требуется определить число видов кузнечиков, обитающих на архипелаге, и вывести для каждого вида минимальную длину суперпрыжка, при помощи которого этот вид смог заселить свои острова. Расстояние суперпрыжка между двумя единичными клетками вычисляется как расстояние между центрами этих клеток.
Формат входных данных
В первой строке содержатся числа \(n\) и \(m\) — размеры архипелага, и далее в следующих \(n\) строках представлена карта архипелага в виде таблицы \(n \times m\), каждая ячейка которой либо принадлежит острову, и тогда в ней содержится \(1\), либо морю, тогда в ней содержится \(0\).
Числа \(n\) и \(m\) имеют следующие ограничения: \(5 \leqslant n, m \leqslant 500\).
Формат выходных данных
В первой строке следует вывести одно число \(p\) — количество видов кузнечиков.
В следующих строке требуется вывести \(p\) чисел через пробел. Для каждого вида нужно вывести его минимальную возможную длину суперпрыжка. Виды нумеруются и перечисляются по самой северной строке их обитания. Более строго, среди всех точек обитания вида находится самая северная (самая верхняя на карте). Так как в этой строке будут расположены только точки обитания этого вида кузнечиков, то каждый вид однозначно определяется по самой северной строке своего обитания. Из двух видов первым будет выведен ответ для того вида, у которого эта строка будет встречена первой при движении сверху вниз.
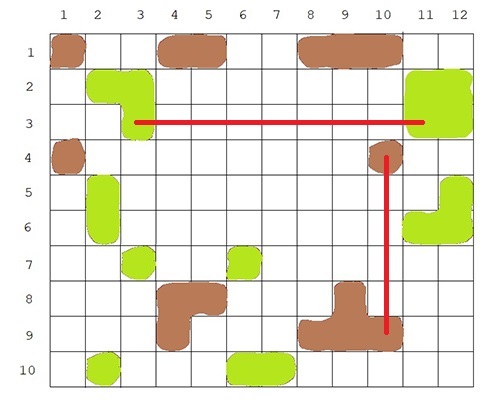
На рис. 1.3 приведена карта архипелага из примера № 1. Острова на ней уже раскрашены согласно обитающим на них видам кузнечиков. Можно видеть, что в данном случае возникло два вида кузнечиков. Первый из них, ареал обитания которого раскрашен коричневым, имеет самую северную точку обитания в строке \(1\) и должен обладать длиной суперпрыжка как минимум \(5\), а второй, ареал которого раскрашен зеленым, имеет самую северную точку обитания в строке \(2\) и должен обладать длиной суперпрыжка как минимум \(8\). Соответствующие прыжки указаны на рисунке.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
10 12 100110011100 011000000011 001000000011 100000000100 010000000001 010000000011 001001000000 000110001000 000100011100 010001100000 |
2 5 8 |
2 |
10 12 100111011100 011000000011 001000000011 100000000100 010000000001 010000000011 001001000000 000110001000 000100011100 010001100001 |
1 6 |
3 |
8 8 11100011 10000110 10000100 00010000 00001000 00000001 00000011 00100000 |
3 7 0 0 |
4 |
8 8 11100011 10000110 10000100 00011000 00011000 00000001 00000011 00100100 |
2 5 0 |
5 |
5 5 11111 10000 11111 00001 11111 |
1 0 |
Пример программы-решения
Ниже представлено решение на языке C++.
#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;
int n, m;
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
bool inside(int x, int y){
return (x >= 0 && y >= 0 && x < n && y < m);
}
vector<string> T;
vvi col;
vector<vector<pii> > G;
vector<pii> st1;
void nodfs1(int x, int y, int c){
col[x][y] = c;
st1.pb({x, y});
while(sz(st1) > 0){
pii top = st1.back();
st1.pop_back();
for0(i, 4){
int nx = top.x + dx[i];
int ny = top.y + dy[i];
if(inside(nx, ny) && T[nx][ny] == '1' && !col[nx][ny]){
st1.pb({nx, ny});
col[nx][ny] = c;
}
}
}
}
vi used;
vvi lst;
vi emp;
vi st2;
void nodfs2(int a){
st2.pb(a);
used[a] = 1;
lst.back().pb(a);
while(sz(st2) > 0){
int top = st2.back();
st2.pop_back();
for(auto to : G[top]){
if(!used[to.x]){
st2.pb(to.x);
used[to.x] = 1;
lst.back().pb(to.x);
}
}
}
}
vi dist;
int prim(int num){
int res = 0;
dist[lst[num][0]] = 0;
set<pii> que;
que.insert({0, lst[num][0]});
for(int i = 1; i < sz(lst[num]); i++){
que.insert({INF, lst[num][i]});
}
for(int u = 0; u < sz(lst[num]); u++){
pii top = *que.begin();
used[top.y] = 1;
que.erase(que.begin());
res = max(res, top.x);
for(auto to : G[top.y]){
if(used[to.x]){
continue;
}
que.erase({dist[to.x], to.x});
dist[to.x] = min(dist[to.x], to.y);
que.insert({dist[to.x], to.x});
}
}
return res;
}
signed main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n >> m;
T.resize(n);
col.resize(n, vi(m, 0));
for0(i, n){
cin >> T[i];
}
int z = 0;
for0(i, n){
for0(j, m){
if(T[i][j] == '1' && !col[i][j]){
z++;
nodfs1(i, j, z);
}
}
}
G.resize(z + 1);
for0(i, n){
int last = -1, d = 0;
for0(j, m){
if(last == -1){
if(col[i][j] != 0){
last = col[i][j];
}
continue;
}
if(col[i][j] == 0){
d++;
continue;
}
if(col[i][j] != 0){
if(last != col[i][j]){
G[last].pb({col[i][j], d + 1});
G[col[i][j]].pb({last, d + 1});
}
last = col[i][j];
d = 0;
}
}
}
for0(j, m){
int last = -1, d = 0;
for0(i, n){
if(last == -1){
if(col[i][j] != 0){
last = col[i][j];
}
continue;
}
if(col[i][j] == 0){
d++;
continue;
}
if(col[i][j] != 0){
if(last != col[i][j]){
G[last].pb({col[i][j], d + 1});
G[col[i][j]].pb({last, d + 1});
}
last = col[i][j];
d = 0;
}
}
}
for1(i, z){
sort(all(G[i]));
}
vector<pii> tmp;
for1(i, z){
tmp.resize(0);
tmp = G[i];
G[i].resize(0);
if(sz(tmp) > 0){
G[i].pb(tmp[0]);
for1(j, sz(tmp) - 1){
if(tmp[j].x != tmp[j - 1].x){
G[i].pb(tmp[j]);
}
}
}
}
used.resize(z + 1, 0);
for1(i, z){
if(!used[i]){
lst.pb(emp);
nodfs2(i);
}
}
dist.resize(z + 1, INF);
used.resize(0);
used.resize(z + 1, 0);
cout << sz(lst) << endl;
for0(i, sz(lst)){
cout << prim(i) << ' ';
}
cout << endl;
}