Предметный тур. Математика. 3 этап
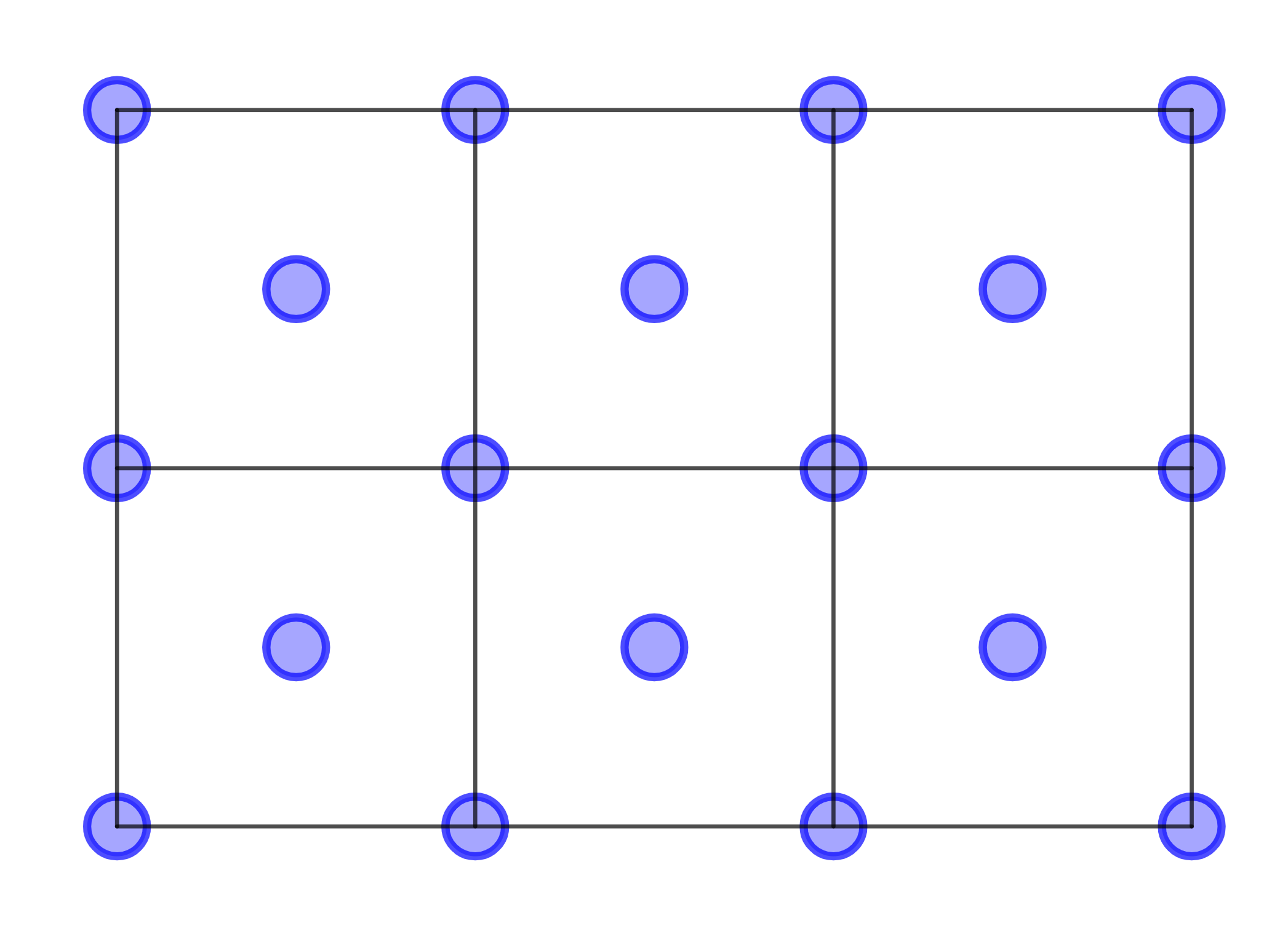
На сетке расставлены фишки следующим образом: по одной фишке в центре каждой из ячеек и по одной фишке — в каждом из узлов сетки.
Для примера на рис. 1.1 приведена сетка размером \(2 \times 3\), на которой 18 фишек (фишки отмечены синим цветом).
Найдите количество фишек на сетке размером \(25 \times 24\) ячейки.
Сетка содержит \(25 \times 24 = 600\) ячеек, таким образом, 600 фишек находятся в центрах ячеек.
Количество фишек в узлах \((25+1)\cdot(24+1)=650\), так как количество горизонтальных и вертикальных линий, ограничивающих ячейки, на единицу больше, чем число ячеек в строке или столбце.
Значит, всего фишек \(600+650=1250.\)
1250.
Только ответ без объяснения — 5 баллов.
Верно посчитано общее количество фишек в центрах ячеек — 5 баллов.
Верно посчитано общее количество фишек в узлах ячеек — 10 баллов.
Арифметическая ошибка при верной логике решения — 12 баллов.
Найдены 600 и 650, но не найдена сумма — баллы не снимаются.
В стране 20 городов, некоторые из которых соединены дорогами. Каждая дорога начинается в одном городе, заканчивается в другом и не проходит через остальные города. Дороги не пересекаются. Автолюбители Петя и Коля играют в следующую игру. Вначале Петя определяет два города, в первый из которых перемещается сам, а во второй перемещается Коля. Далее передвигаются по очереди, начинает Коля. За один ход игрок выбирает дорогу, ведущую из города, в котором он находится и едет по ней, попадая в другой город. Если после очередного хода оба игрока оказываются в одном городе, то сделавший ход игрок выигрывает. При каком наибольшем числе дорог может оказаться так, что у Пети есть выигрышная стратегия?
Оценка. Заметим, что наибольшее число дорог в стране будет в том случае, если каждый город соединен с каждым. В такой стране \(\frac{20\cdot 19}{2}=190\) дорог. Но если в стране 190 дорог, то Коля первым же своим ходом может приехать в город, в котором находится Петя (каждый город соединен с каждым). Следовательно, в этом случае у Пети нет выигрышной стратегии. Поэтому в стране меньше 190 дорог, т. е. не больше 189 дорог.
Пример. Рассмотрим страну, в которой соединены дорогами все пары городов, кроме пары \((A, B)\). В такой стране 189 дорог. Выигрышная стратегия Пети заключается в том, чтобы выбрать для себя город \(A\), для Коли — город \(B\). В таком случае Коля не сможет выиграть первым своим ходом, и в какой бы город \(D\) Коля ни поехал, Петя перейдет из \(A\) в \(D\) своим первым ходом и выиграет.
189.
Получен только ответ без рассуждений или с неверными рассуждениями — 5 баллов (баллы за этот пункт не складываются с баллами за следующие пункты).
Доказана «оценка», что городов не более 189 — 10 баллов.
Построен «пример» в котором 189 дорог и приведена стратегия за Петю — 10 баллов.
Построен «пример» в котором 189 дорог, но нет стратегии за Петю — 0 баллов.
На пальме растут 55 бананов, которые нужно распределить между девятью обезьянами так, чтобы любые две обезьяны получили в сумме хотя бы 9 бананов (некоторые обезьяны могут получить 0 бананов). Докажите, что по крайней мере три обезьяны получат одинаковое количество бананов.
Предположим противное, что одинаковое количество бананов могут получить не более двух обезьян. Теперь рассмотрим два случая.
- Каждая обезьяна получила хотя бы 5 бананов. Тогда по 5 бананов получили не более двух обезьян, по шесть бананов — не более двух обезьян и т. д. Поэтому все обезьяны получили не менее \(5\cdot 2+6\cdot 2+7\cdot 2+8\cdot 2+9=61\) банан. Противоречие.
- Хотя бы одна обезьяна получила менее 5 бананов. Обозначим эту обезьяну за \(A\), а за \(n\), \(n\leqslant 4\), обозначим количество полученных ею бананов. Рассматривая пары обезьян, одна из которых \(A\), получим, что каждая из оставшихся получила хотя бы \(9-n\) бананов. Действуя аналогично предыдущему случаю, получим, что все обезьяны получили в сумме хотя бы \(n+(9-n)\cdot 2+(10-n)\cdot 2+(11-n)\cdot 2+(12-n)\cdot 2 = 84-7n\) бананов. Учитывая, что \(n\leqslant 4\), получим \(84-7n \geqslant 84-28 = 56\). Противоречие.
Рассмотрен лишь первый случай или доказано, что есть обезьяна получившая не более 4 бананов — 5 баллов.
Рассмотрен лишь второй случай — 15 баллов.
Второй случай делается перебором возможных значений \(n\), т. е. \(n=4, 3, 2, 1, 0\). В этом переборе упущен или неверно рассмотрен один случай — 10 баллов за весь второй случай.
В этом переборе упущено более одного случая, при этом рассмотрен случай \(n=4\) — 5 баллов за весь второй случай.
Рассмотрен лишь случай \(n=4\) без попыток перебора — 5 баллов за весь второй случай.
В этом переборе упущено более одного случая, при этом не рассмотрен случай \(n=4\) — 0 баллов за весь второй случай.
Баллы за первый и второй случаи складываются.
Пусть \(\Omega\) — описанная окружность остроугольного треугольника \(ABC\). Биссектрисы углов \(A\), \(B\) и \(C\) пересекают \(\Omega\) в точках \(A_1\), \(B_1\) и \(C_1\) соответственно, а биссектрисы углов \(A_1\), \(B_1\) и \(C_1\) треугольника \(A_1B_1C_1\) пересекают \(\Omega\) в точках \(A_2\), \(B_2\) и \(C_2\) соответственно. Известно, что наименьший угол треугольника \(ABC\) равен \(40°\). Найдите наименьший угол треугольника \(A_2B_2C_2\).
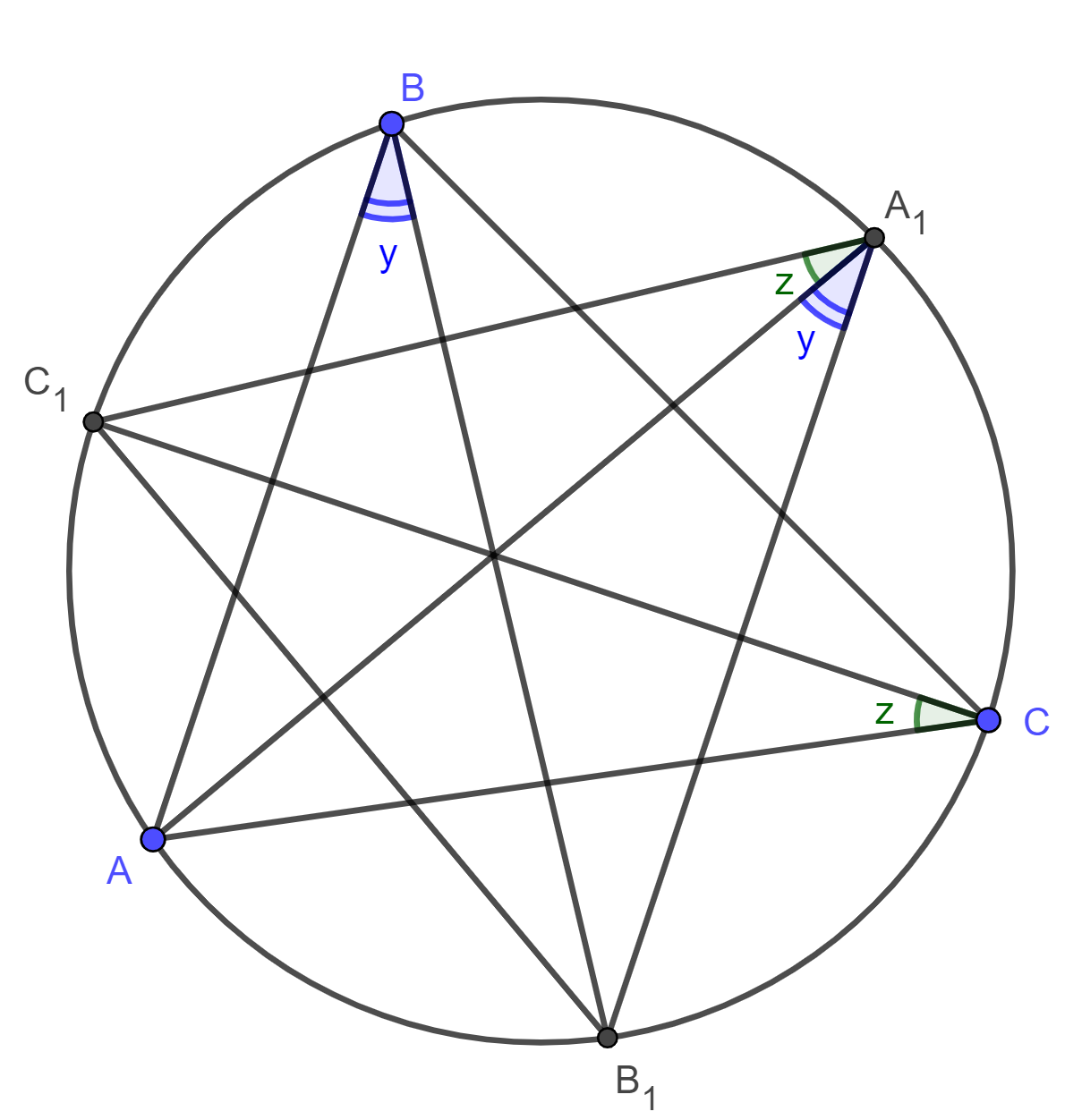
Утверждение. Пусть дан треугольник \(ABC\) с углами \(2x\), \(2y\), \(2z\), в котором его биссектрисы пересекают его описанную окружность в точках \(A_1, B_1, C_1\) соответственно. Тогда углы треугольника \(A_1B_1C_1\) равны \(x+y, y+z, z+x\).
Доказательство. Заметим, что \(\angle C_1A_1A=\angle C_1CA\) как опирающиеся на дугу \(C_1A\) (см. рис. 1.2). При этом \(\angle C_1A_1A=\dfrac 12 \angle ACB=z\). Аналогично \(\angle B_1A_1A = y\). Тогда \(\angle B_1A_1C_1 = y+z\). Аналогично для других углов треугольника \(A_1B_1C_1\). Утверждение доказано.
Обозначим теперь углы исходного треугольника \(4\alpha=40°, 4\beta, 4 \gamma\) (\(\alpha \leqslant \beta \leqslant \gamma\)). Применяя полученное выше утверждение для треугольника \(ABC\), получим, что углы треугольника \(A_1B_1C_1\) равны \(\dfrac{4\alpha}{2}+\dfrac{4\beta}{2}=2\alpha+2\beta\), \(\dfrac{4\beta}{2}+\dfrac{4\gamma}{2}=2\beta+2\gamma\) и \(\dfrac{4\gamma}{2}+\dfrac{4\alpha}{2}=2\gamma+2\alpha\).
Применяя теперь то же утверждение для треугольника \(A_1B_1C_1\) получим, что углы треугольника \(A_2B_2C_2\) равны \(\alpha+\beta+\beta+\gamma=\dfrac{4\alpha+4\beta+4\gamma}{4}+\beta = 45°+\beta\), \(45°+\gamma\), \(45°+\alpha\). Учитывая, что \(\alpha \leqslant \beta \leqslant \gamma\), получим \(45°+\alpha \leqslant 45°+\beta \leqslant 45°+\gamma\). Поэтому наименьший угол треугольника \(A_2B_2C_2\) равен \(45°+\alpha = 55°\).
\(55°\).
Дан только верный ответ — 1 балл.
При верном решении используется утверждение без доказательства — снимается 2 балла.
Сформулировано утверждение без дальнейших продвижений — 3 балла.
Сформулировано и доказано утверждение без дальнейших продвижений — 5 баллов.
Вычислены углы треугольника \(A_2B_2C_2\) через углы треугольника \(ABC\), ответ не получен — 10 баллов.
Вычислены углы треугольника \(A_2B_2C_2\) через углы треугольника \(ABC\) и посчитано значение одного из углов, равного \(55°\), но не доказано, что он наименьший — 15 баллов.
Найдите всевозможные тройки целых чисел \(a, b, c\), для которых выполняются равенства: \(a+b-c=1\) и \(a^2+b^2-c^2=-1.\)
Перепишем равенства в виде: \[\label{eq:math_rki_0501} a+b=c+1;\] \[\label{eq:math_rki_0502} a^2+b^2=c^2-1.\]
Равенство \eqref{eq:math_rki_0502} можно записать в виде \((a+b)^2-2ab=c^2-1\). Используя \eqref{eq:math_rki_0501}, получим \((c+1)^2-2ab=c^2-1\) или \(c^2+2c+1-2ab=c^2-1\), если привести подобные и разделить обе части равенства на 2, получим: \(c+1=ab\). Снова используя \eqref{eq:math_rki_0501}, получим \(a+b=ab \Leftrightarrow ab-a-b+1=1 \Leftrightarrow (a-1)(b-1)=1\). Последнее уравнение имеет два решения в целых числах:
- \(a-1=1\) и \(b-1=1\), тогда получим тройку \(a=2, b=2, c=3\);
- \(a-1=-1\) и \(b-1=-1\), тогда получим тройку \(a=0, b=0, c=-1\).
\((2, 2, 3), (0, 0, -1)\).
Найден только один ответ подбором и показано, что он подходит — 3 балла.
Найдены оба ответа подбором и показано, что они подходят — 5 баллов.
Получено равенство \(a+b=ab\) без дальнейших продвижений — 10 баллов.
Получено разложение \((a-1)(b-1)=1\) без дальнейших продвижений — 15 баллов.
Баллы за указанные выше продвижения и ответ (ответы) суммируются.
При решении уравнения в целых числах \((a-1)(b-1)=1\) потерян один из ответов, например, рассмотрен только случай \(a-1=1, b-1=1\) — 20 баллов.
Баллы за указанное выше продвижение и ответ (ответы) не суммируются.
Сколько должно быть слагаемых под знаком корня в выражении \[\sqrt[3]{tg^3\frac{\pi}{3}+...+tg^3\frac{\pi}{3}}=6\sqrt{3},\] чтобы равенство было верным?
Обозначим количество слагаемых под корнем через \(n\), тогда \(\sqrt[3]{n\cdot tg^3\dfrac{\pi}{3}}=6\sqrt{3}.\) Вынося тангенс из-под корня и учитывая, что \(tg\dfrac{\pi}{3}=\sqrt{3}\), получим \(\sqrt[3]{n}=6\). Отсюда \(n=6^3=216.\)
216.
Только ответ — 2 балла.
Записано уравнение, в котором неизвестным является количество слагаемых под корнем, например, \(\sqrt[3]{n\cdot tg^3\dfrac{\pi}{3}}=6\sqrt{3}\) — 5 баллов.
Арифметическая ошибка при логически верном рассуждении — 10 баллов.
На доске выписаны все натуральные числа от 1 до 999 включительно. Миша и Ян ходят по очереди, начинает Миша. За один ход игрок стирает с доски одно из чисел. Игра заканчивается, когда на доске останется два числа. Если их сумма равна кубу какого-либо целого числа, то выигрывает Миша, в противном случае выигрывает Ян. Кто из игроков имеет выигрышную стратегию, позволяющую ему победить вне зависимости от ходов противника?
Опишем выигрышную стратегию Миши. Первым ходом Миша стирает число 500, а оставшиеся числа мысленно делит на следующие пары: (1, 999), (2, 998), \(\ldots\), (499, 501). Далее, какое бы число ни вычеркнул Ян, своим очередным ходом Миша вычеркивает число из той же пары. После 997-го хода, который сделает Миша, останется два числа, причем оба будут входить в одну и ту же пару. Осталось заметить, что сумма чисел в каждой паре равна 1000, что является кубом целого числа.
Миша имеет выигрышную стратегию.
Верно указан Миша как игрок, имеющий выигрышную стратегию — 1 балл.
Показано, что последний ход делает Миша — 1 балл.
Приведено разбиение на 499 пар таких, что сумма чисел в каждой паре является кубом целого числа — 5 баллов.
Баллы, указанные в критериях выше, складываются. И не складываются с баллами в нижеследующих критериях.
Приведена выигрышная стратегия за Мишу, возможно, отличающаяся от стратегии, содержащейся в авторском решении, но не доказано, что стратегия выигрышная — 12 баллов.
Пусть \(x_1, x_2, x_3, x_4, x_5\) — последовательные натуральные числа (именно в таком порядке) такие, что \(x_1 + x_2 + x_3 + x_4 + x_5\) — точный куб, а \(x_2 + x_3 + x_4\) — точный квадрат. Найдите наименьшее возможное значение, которое может принимать \(x_3\).
Обозначим \(x_3\) через \(n\). Тогда \(x_1 + x_2 + x_3 + x_4 + x_5= 5n\) и \(x_2 + x_3 + x_4=3n.\)
Так как \(5n=m^3\) и 5 — простое число, то \(m\) делится на 5, \(m^3\) делится на \(5^3=125\), а значит, \(n\) делится на 25.
С другой стороны, \(3n=k^2\), значит, \(k\) делится на 3, значит, \(n\) делится на 3.
Так как \((5, 3)=1\) и \(5n=m^3\), то \(n\) делится на 27. Таким образом, \(n\) делится на \(25 \cdot 27=675\), поэтому \(n \geqslant 675\).
Убедимся, что \(n=675\) подходит: \(673+674+675+676+677=(3\cdot5)^3=15^3\), \(674+675+676=2025=45^2.\)
675.
Только ответ без объяснений — 0 баллов.
Ответ и проверка, что ответ подходит — 2 балла.
Доказано, что \(x_3\) делится на 3 — 3 балла.
Доказано, что \(x_3\) делится на 5 — 3 балла (суммируется с предыдущим).
Доказано, что \(x_3\) делится на 27 — 6 баллов.
Доказано, что \(x_3\) делится на 25 — 6 баллов (суммируется с предыдущим).
Доказано, что \(x_3\geqslant 675\) — 15 баллов.
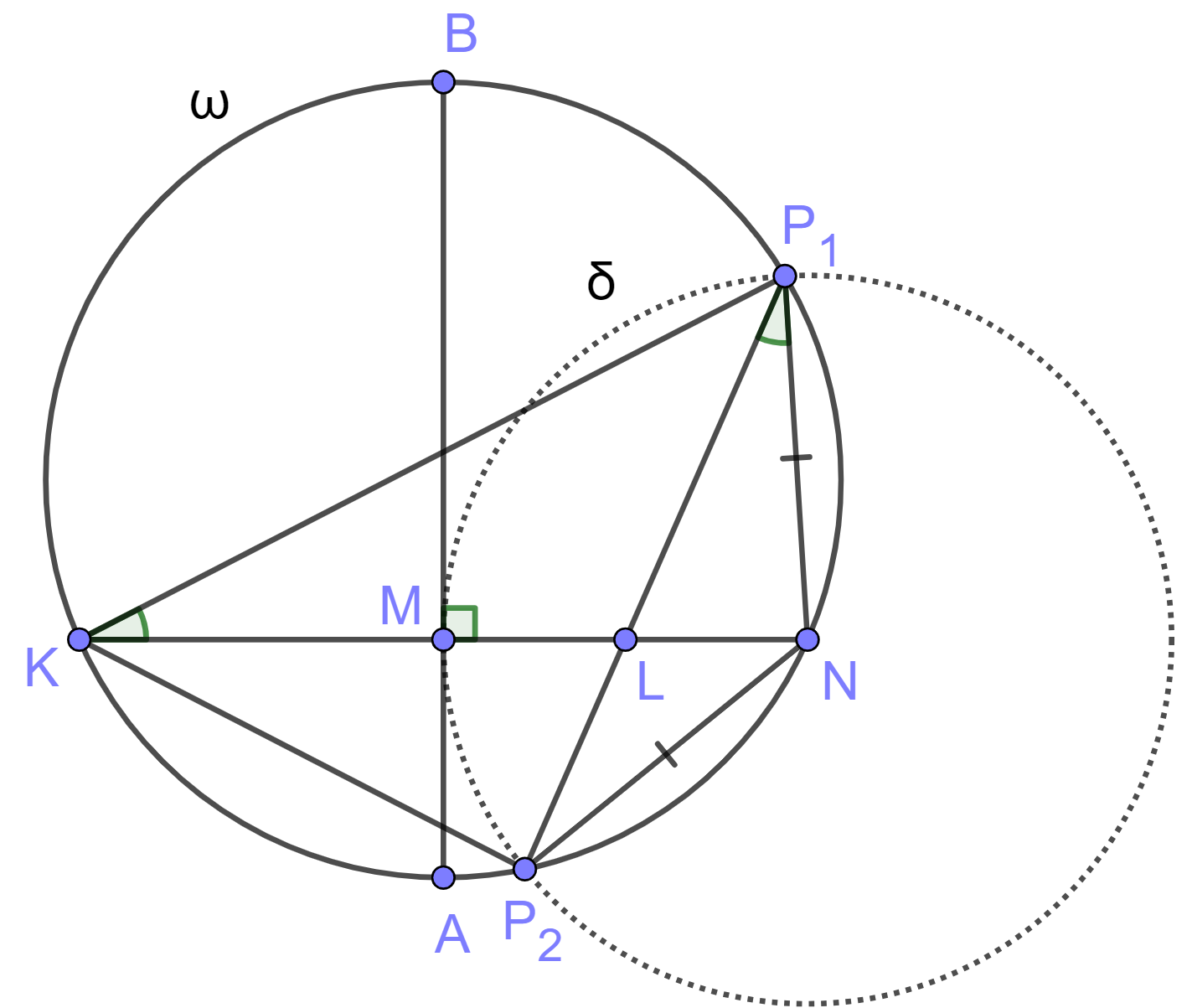
Дана окружность \(\omega\) с диаметром \(AB\). На окружности выбрана точка \(N\), отличная от точек \(A\) и \(B\). Перпендикуляр из \(N\) к \(AB\) пересекает \(AB\) в точке \(M\) и повторно пересекает \(\omega\) в точке \(K\). Окружность с центром \(N\) и радиусом \(NM\) пересекает \(\omega\) в точках \(P_1\) и \(P_2\). Точка \(L\) — точка пересечения \(P_1P_2\) с отрезком \(KN\). Докажите, что \(KP_1\) вдвое больше \(P_1L\).
Обозначим окружность с центром \(N\) и радиуса \(NM\) за \(\delta\).
Так как хорды \(P_1N\) и \(P_2N\) равны как радиусы окружности \(\delta\), то равны и дуги \(P_1N\) и \(P_2N\). Следовательно, равны углы \(\angle NKP_1 = \angle NP_1P_2\) как опирающиеся на равные дуги. Тогда треугольники \(NKP_1\) и \(NP_1L\) подобны по двум углам (\(\angle NKP_1=\angle NP_1L\) и \(\angle KNP_1\) — общий). Тогда \(\dfrac{KP_1}{P_1L}=\dfrac{NK}{NP_1}\). Заметим теперь, что \(NP_1=NM\) как радиусы окружности \(\delta\) и \(NM=MK\), так как диаметр делит перпендикулярную ему хорду пополам. Поэтому \(\dfrac{NK}{NP_1}=\dfrac{2NM}{NM}=2\), откуда \(\dfrac{KP_1}{P_1L}=2\).
Упоминается без доказательства, что диаметр делит перпендикулярную хорду пополам — баллы не снимаются.
Доказано, что треугольники \(NKP_1\) и \(NP_1L\) подобны — 10 баллов.
Дано натуральное \(n=p^k\), где \(p\) — простое, а \(k\) — нечетное. На доску выписали все натуральные делители \(n\) (в том числе 1 и само \(n\)). Юра разбил выписанные числа на пары, в каждой паре посчитал произведение чисел и все эти произведения выписал в тетрадку. Оказалось, что все числа в тетрадке имеют одинаковое количество натуральных делителей. Докажите, что у Юры есть ровно один способ такого разбиения делителей числа \(n\) на пары.
Обозначим \(d(x)\) — количество натуральных делителей числа \(x\).
Лемма. Количество делителей числа \(p^m\), где \(p\) — простое, равно \(m+1\).
Доказательство. Делители \(p^m\) — это числа \(1, p, p^2, \ldots, p^m\). Их ровно \(m+1\). Лемма доказана.
У числа \(n=p^k\) следующие делители: 1, \(p\), \(p^2\), \(\ldots\), \(p^k\).
Рассмотрим какой-нибудь способ разбиения Юрой делителей числа \(n\) на пары. Пусть \(p^x\) — делитель, попавший в пару с 1, а \(p^y\) — делитель, попавший в пару с \(p^k\). Тогда \(d(1\cdot p^x) = d(p^y \cdot p^k)\). Откуда \(d(p^x)=d(p^{y+k})\), значит, \(x+1=y+k+1\). Учитывая, что \(x\leqslant k\) и \(y\geqslant 0\), получим \(x=k\), \(y=0\). Т. е. 1 и \(p^k\) попали в одну пару. Следовательно, число делителей в каждой паре равно \(d(1\cdot p^k)=k+1\).
Рассмотрим делитель \(p^m\) числа \(n\). К нему в пару попадет такой делитель \(p^t\), что \(d(p^m\cdot p^t)=k+1\) или \(m+t+1=k+1\). Откуда \(t=k-m\). Учитывая, что \(k\) нечетное, получим, что \(t\) и \(m\) разной четности, и \(p^m \neq p^t\), а значит, \(p^t\) определяется однозначно.
Разбиение всех делителей на пары вида \(\left(d, \dfrac nd\right)\) удовлетворяет условию задачи, так как в этом случае равны все произведения чисел в парах, а значит, равны и их количества делителей.
Приводится разбиение на пары, удовлетворяющие условию задачи — 5 баллов.
Доказана лемма — 2 балла.
Доказано, что делитель 1 должно быть в паре с числом \(n\) — 6 баллов.
Доказано, что если пару составляют делители \(p^m\) и \(p^t\), то \(m+t=k\) — 12 баллов.
Баллы за указанные выше критерии складываются.
В верном решении не доказывается, что если пару составляют делители \(p^m\) и \(p^t\), то \(p^m \neq p^t\) — снять 5 баллов.
В решении не приводится разбиение на пары, удовлетворяющие условию задачи — снять 5 баллов.