Инженерный тур. 2 этап
Командная задача заключительного этапа представляет собой комплексную инженерную задачу и заключается в экономическом и энергетическом моделировании энергосистемы и конкуренции предложенных участниками решений. Участники разрабатывают экономические стратегии, работают с прогнозами погоды и потребления, пишут скрипты по управлению энергообъектами.
Подготовка к заключительному этапу проходит во время предыдущих этапов с постепенным увеличением сложности — во время инженерного тура первого этапа и во время второго этапа.
Второй этап — отборочный этап, задачи которого подобраны таким образом, чтобы объективно проверить индивидуальные знания участников и косвенно оценить личный вклад участников в результат командной работы. Второй тур является не только отборочным соревнованием, но прежде всего — введением в профиль. То есть его содержание (задачи, динамика) несет образовательную составляющую не только в рамках подготовки к заключительному этапу, но и для развития общих навыков (командное взаимодействие, работа со сложными моделями, информационный поиск и нестандартное мышление).
Второй этап включает в себя восемь командных задач. Для решения задач второго этапа необходимы не только школьные знания и умения программы, навыки использования школьных знаний для решения новых задач, но и факультативные знания в области программирования, математики и геометрии. Методические рекомендации к данному этапу позволяют очертить область знаний и навыков для самостоятельного изучения.
Кроме того, задачи второго этапа направлены на развитие элементов научного исследовательского подхода и навыков командной работы. Здесь участники формируют команды и загружают общее командное решение. Функций у этого этапа несколько:
- отбор команд из трех-пяти участников, способных решать сложные задачи;
- ознакомление участников с математическими и физическими концепциями, на которых будет построена задача заключительного этапа;
- предъявление командам требований к уровню программирования, идентичных тем, что будут предъявлены им на заключительном этапе.
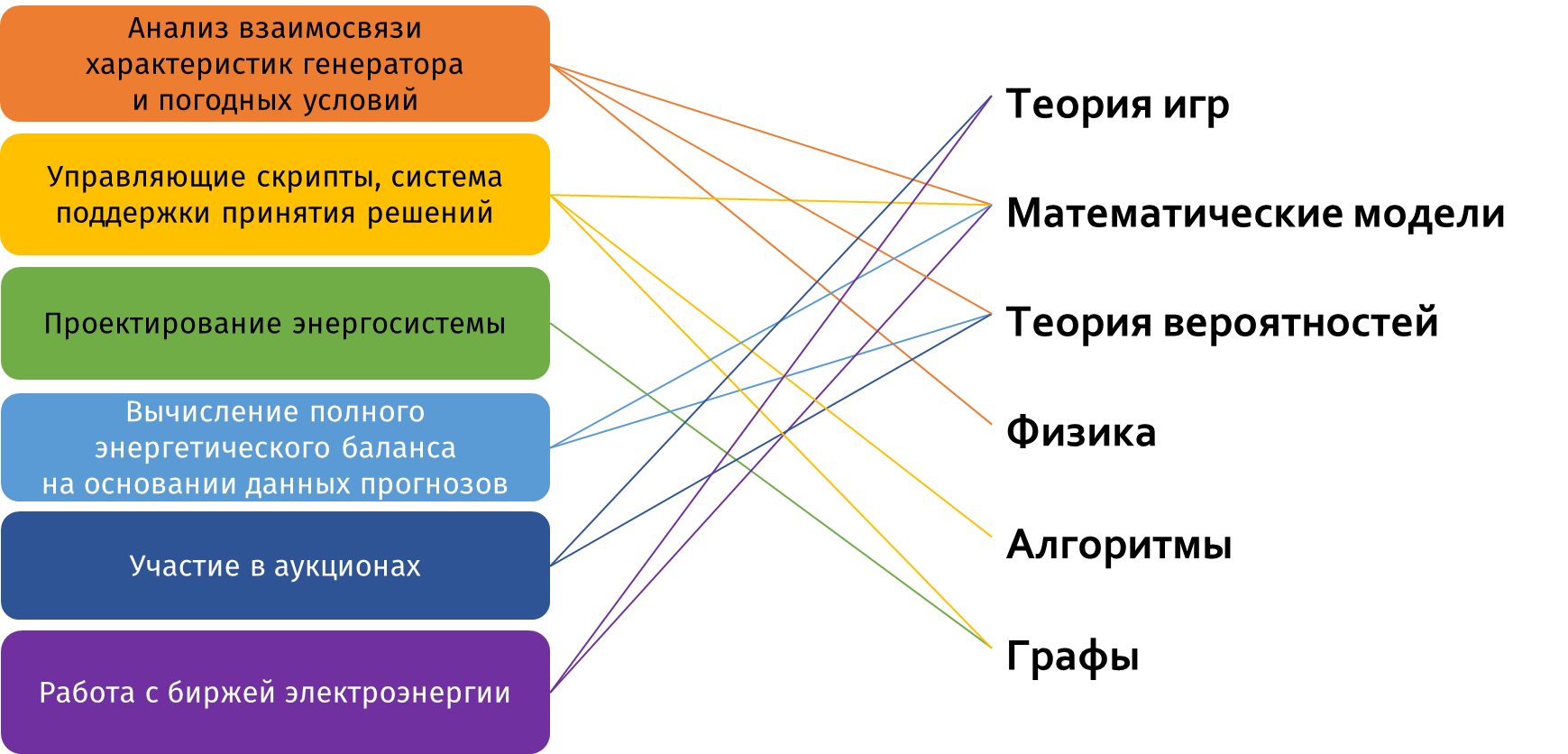
Во время второго отборочного этапа участники решают задачи, которые отражают часть большой командной задачи заключительного этапа, и знакомятся с базовыми концепциями — вероятностными прогнозами, графами, математическими моделями. На рис. 1.1 представлена схема связей тем задач второго тура и навыков, необходимых для решения задач заключительного этапа.
На заключительном этапе участникам предстоит на одном поле столкнуться с другими командами, и понимание основ теории игр позволит объективнее оценивать игровую ситуацию в условиях конкуренции за ресурсы.
Работа со сложными математическими моделями и системами — фундаментальный навык, в полной мере раскрывающийся при работе с комплексной инженерной задачей.
Мир сложен и неустойчив, и задача заключительного этапа моделирует это в полной мере. Лучше заранее подготовиться и научиться работать с вероятностями, для чего второй этап содержит достаточно много задач по теории вероятностей. При этом для полноценной работы не потребуется погружаться в нее с головой — достаточно знания основ математической статистики и распределений случайных величин.
В работе с энергетическими системами необходимо знать электротехнику, в частности, и физику в плане построения и работы с физическими моделями.
Задача заключительного этапа предполагает написание управляющего скрипта, и здесь важную роль играет навык разработки алгоритмов, равно как и поиска подходящих типовых. На проработку этих навыков и рассчитаны задачи раздела «Алгоритмы». При работе с ними важно делать акцент на информационном поиске и умении выявить типовую подзадачу.
Энергосети — это графы, и с ними нужно уметь работать. В работе с задачами этого раздела в первую очередь важно овладеть основным арсеналом — программные представления графов и базовые алгоритмы. Это может понадобиться при написании управляющего скрипта, не говоря уже о фундаментальном понимании сетей.
Все задачи второго отборочного этапа решаются на платформе Яндекс Контест. В заданное время всем участникам открывается доступ к очередному набору задач (их условиям и проверочной системе). Участники должны написать программу на языке Python 3.12 и загрузить ее текст на сервер. На сервере выполняется тестирование загруженной программы: ее ответы сверяются с ответами эталонного решения, составленного авторами задачи. Их решение требует наличия базовых навыков программирования, поскольку это является необходимой частью комплексной инженерной задачи. Случайные числа, используемые для генерации тестов, являются псевдослучайными. Все проверки программ всех участников производятся на одинаковых данных.
Командная работа начинается именно во время второго этапа. Помимо общих механизмов, здесь созданы условия для командного взаимодействия — ограниченное число попыток на каждую задачу для команды. Это приводит к необходимости уже на начальном этапе договариваться о стратегии сдачи решений общекомандно, и обозначать свою позицию по отношению к каждой задаче внутри команды — берешь ли ты ее на себя, пишешь варианты решений или передаешь ответственность за нее другим участникам команды. Так, задачи разделяются между участниками с учетом их сильных и слабых сторон, что создает предпосылки к формированию ролей в работе на заключительном этапе.
Учет общекомандных попыток ведется посредством внешнего бота, предоставляющего текущую информацию о командных баллах и оставшихся командных попытках. Бот оживляет и делает осмысленным соревнование во время второго тура — оно становится проявленным и работает на повышение мотивации. На протяжении всего второго тура на вебинарах поднимаются темы совместных ресурсов (Яндекс Диск, Github) для структурирования командной работы. Также на вебинарах не всегда возможно присутствие всех членов команды — и это порождает отдельный процесс по синхронизации информации и понимания. В конце второго тура командам предлагается совместная рефлексия с выявлением слабых и сильных сторон у каждого члена команды, определением белых пятен в знаниях и навыках у каждого и распределением нерешенных задач для дорешивания.
На заключительном этапе команды попадают в мир энергетических систем. Профиль посвящен энергетическим системам ближайшего будущего. Построение архитектуры Интернета энергии предполагает создание многочисленных надежных гибких энергосистем, способных в любой ситуации эффективно распределять электроэнергию, использовать альтернативные источники и взаимодействовать с рынком мощностей.
Прежде всего, второй этап — командный, поэтому оценивается общий результат. Главная задача второго этапа — формирование команды. Чем лучше выстроена командная работа на втором этапе, тем больше шансов на победу у команды в каждом из этапов. Общайтесь, учитесь эффективно распределять задачи, искать сильные стороны каждого участника вашей команды, наращивайте общекомандные навыки — и коммуникативные, и профессиональные. Решайте задачи максимально эффективно и результативно.
Во время второго этапа предлагаются задачи, которые отражают часть большой командной задачи заключительного этапа и знакомят участников с базовыми концепциями. В них затронуты следующие темы:
- теория игр;
- математические модели;
- теория вероятностей;
- графы;
- физика;
- алгоритмы.
Все задачи требуют написания программного кода на языке программирования Python 3.12. Для работы с этим языком достаточно редактора IDLE, входящего в стандартную поставку, но также можно работать с любой удобной IDE (Visual Studio Code, Spyder и т. д.) или онлайн-средой (Repl.it, Google Colab и т. д.). Следует учитывать, что платформа Яндекс Контест использует Python версии 3.12 без дополнительных библиотек.
Все дополнительные материалы к заданиям и исходные коды решений доступны по ссылке: https://disk.yandex.ru/d/ZJQRGmly59ubxA.
Командные задачи второго этапа инженерного тура открыты для решения. Соревнование доступно на платформе Яндекс.Контест: https://contest.yandex.ru/contest/69917/enter/.
Среди \(M\) участников проводятся торги за некоторый лот в формате аукциона второй цены. Лот имеет истинную ценность \(C\), но каждый из них оценивает его по-своему, и эта оценка выражается ставками (они гарантированно различаются).
При передаче проданного лота с победителя удерживается комиссия аукционного дома (10% от цены). Если после покупки лота участником выясняется, что истинная ценность лота меньше, чем он за него заплатил, он выставляет лот обратно на аукцион.
Определите номер участника, у которого в итоге окажется лот.
Формат входных данных
Два числа через пробел, \(M\) (натуральное), и \(C\) (вещественное). Далее \(M\) строк, в каждой вещественное число — ставка соответствующего участника.
Формат выходных данных
Единственное целое число, номер участника-владельца лота (нумерация с 0).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
203137 4133324.096959806 1868457.6938164262 5589981.056932577 1051762.38668823 4803039.491311131 ... 3513325.4824158354 |
156066 |
Тестовые данные
Выплата за лот складывается из второй ставки (следующей за выигрышной), к которой прибавляется 10%. Если эта сумма больше истинной ценности, лот выставляется повторно.
Оптимальное решение не требует итерационно моделировать аукцион второй цены. Достаточно отсортировать ставки по убыванию и определить первую ставку, которая будет меньше истинной ценности с наценкой 10%. Участник со ставкой выше этой и будет итоговым владельцем лота.
Авторское решение задачи приведено на языке Python 3.12.
from dataclasses import dataclass
@dataclass
class Item:
bet: float
participant: int
N, C = input().split()
N = int(N)
C = float(C)
items = []
for i in range(N):
elem = float(input())
items.append(Item(bet=elem, participant=i))
items.sort(key=lambda x: x.bet, reverse=True)
winner = -1
for i in range(1, len(items)):
cost = items[i].bet + items[i].bet * 0.1
if cost < C:
winner = items[i-1].participant
break
print(winner)Среди \(M\) участников проводятся торги за некоторый лот в формате аукциона второй цены. Лот имеет истинную ценность \(C\), но каждый участник оценивает его по-своему, и эта оценка выражается ставками (они гарантированно различаются). При передаче проданного лота с победителя удерживается комиссия аукционного дома (10% от цены). Если после покупки лота участником выясняется, что истинная ценность лота меньше, чем он за него заплатил, участник выставляет лот обратно на аукцион.
Какова будет прибыль аукционного дома?
Формат входных данных
Два числа через пробел, \(M\) (натуральное), и \(C\) (вещественное). Далее \(M\) строк, в каждой вещественное число — ставка соответствующего участника.
Формат выходных данных
Единственное вещественное число, прибыль аукционного дома.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
203137 4133324.096959806 1868457.6938164262 5589981.056932577 1051762.38668823 4803039.491311131 ... 3513325.4824158354 |
66669815647.2999 |
Тестовые данные
Это продолжение первой подзадачи. Имея отсортированный список ставок, достаточно просуммировать 10% комиссии от всех ставок, начиная со второй максимальной и заканчивая следующей за номером итогового владельца (который определяется в первой подзадаче).
Авторское решение задачи приведено на языке Python 3.12.
from dataclasses import dataclass
@dataclass
class Item:
bet: float
participant: int
N, C = input().split()
N = int(N)
C = float(C)
items = []
for i in range(N):
elem = float(input())
items.append(Item(bet=elem, participant=i))
items.sort(key=lambda x: x.bet, reverse=True)
winner = -1
profit = 0.0
for i in range(1, len(items)):
profit += items[i].bet * 0.1
cost = items[i].bet + items[i].bet * 0.1
if cost < C:
winner = items[i-1].participant
break
# print(winner)
print(f"{profit:.4f}")Решение принимается, если значение отличается от эталонного не более, чем на \(10^{-4}\).
Двустороннее шахматное поле шириной пять клеток и длиной \(L\) клеток свернули в ленту Мебиуса, а в ее середину поставили шахматного коня. После этого конь делает \(M\) случайных ходов по ленте. Какова вероятность, что в итоге конь окажется на клетке, из которой одним ходом можно вернуться в начальное положение?
Формат входных данных
Два натуральных числа через пробел, соответственно \(L\) и \(M\). Известно, что \(10 \leqslant L \leqslant 200\), \(50 \leqslant M \leqslant 300\).
Формат выходных данных
Единственное вещественное число, искомая вероятность.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
10 51 |
0.14306267857158905 |
Тестовые данные
Решение строится по принципу динамического программирования. Строим матрицу вероятностей для случая \(N = 0\) (какова вероятность, что конь следующим ходом придет в начальное положение?), после чего последовательно пересчитываем матрицу для случая на ход больше, пока не придем к \(N\). Для большей точности предлагается использовать библиотеку fractions. Чтобы решение уложилось в ограничение по времени выполнения, следует обратить внимание, что матрица вероятностей симметрична относительно начальной точки по линиям вдоль и поперек ленты. Таким образом, достаточно считать лишь четверть поля.
Авторское решение задачи приведено на языке Python 3.12.
# используем Fraction для большей точности
from fractions import Fraction as frac
L, N = map(int, input().split())
# оптимизация: число ходов должно быть нечётным
if N % 2 == 0:
print(0.0)
from sys import exit
exit()
W = 5
WM, L2 = W // 2, L * 2
WX, LX = WM + 1, L + 1 # размеры матрицы
s_col, s_row = WM, 0 # начальное положение
# матрицы для расчёта вероятностей
probs = [[frac(0) for _ in range(WX)]
for _ in range(LX)]
new_probs = [[frac(0) for _ in range(WX)]
for _ in range(LX)]
# смещения для хода коня
deltas = [
(-2, -1), (-2, +1), (+2, -1), (+2, +1),
(-1, -2), (-1, +2), (+1, -2), (+1, +2),
]
def wr(col, row, value): # запись в матрицу
if not 0 <= col < W: return
# оптимизация: симметрия вдоль ленты
if col > WM: col = W-1-col
# учитываем бесконечность ленты
row = row % L2
# оптимизация: симметрия от начальной точки
if row > L: row = 2*L-row
probs[row][col] = value
def get(col, row): # чтение из матрицы
if not 0 <= col < W: return frac(0), 0
if col > WM: col = W-1-col
row = row % L2
if row > L: row = 2*L-row
return probs[row][col], 1
# заполняем конечное положение
for dc, dr in deltas:
wr(s_col + dc, s_row + dr, frac(1))
# производим обратный расчёт
for mv in range(N):
for row in range(LX):
for col in range(WX):
a, b = map(sum, zip(
get(col+2, row+1), get(col+2, row-1),
get(col-2, row+1), get(col-2, row-1),
get(col+1, row+2), get(col+1, row-2),
get(col-1, row+2), get(col-1, row-2)
))
new_probs[row][col] = a / b
new_probs, probs = probs, new_probs
# выводим ответ
print(float(probs[s_row][s_col]))Решение оценивается по совокупности тестов. Тест засчитывается на 50%, если ответ отличается от эталонного не более, чем на \(10^{-5}\). Полный балл за тест засчитывается при погрешности не более, чем \(10^{-9}\).
Арсений Иголкин любит искусство, особенно непризнанное и малоизвестное. В каждом городе он ищет какой-нибудь авангардный или отдаленный музей и часами бродит по нему, разглядывая экспонаты. В очередной поездке у Арсения было совсем немного времени, поэтому из вариантов осталась только галерея современного искусства. Тогда Арсений решил найти в галерее самые непопулярные экспонаты и сосредоточиться на них.
Представим галерею в виде графа из экспонатов и двунаправленных переходов между ними. Вес перехода — это время, за которое от одного экспоната можно добраться до другого. Между двумя экспонатами может быть более одного перехода. Представим блуждающего посетителя, который, начиная от случайного экспоната, делает 100 случайных перемещений по галерее. При этом вероятность выбрать переход пропорциональна весу этого перехода (чтобы было время осмыслить увиденное).
Определите экспонат, который будет посещаться реже всего. Учитываются только посещения с переходов (то есть посещение в самом начале блуждания не рассматривается).
Формат входных данных
Два натуральных числа через пробел, число экспонатов \(N\) и число переходов \(M\). Далее идет \(M\) строк, в каждой три числа, первые два — целые номера экспонатов (нумерация с нуля) и вес перехода (вещественное ненулевое число).
Формат выходных данных
Единственное целое число, наименее популярный экспонат.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
5 21 0 1 69 1 2 65 2 3 20 3 4 56 ... 4 3 7 |
2 |
Тестовые данные
В задаче рассматривается произвольный граф, для которого необходимо рассчитать наименее проходимую вершину. Аналитическое решение имеет слишком высокую вычислительную сложность (для каждой вершины необходимо провести перебор на большую глубину). По этой причине предлагается использование метода Монте-Карло: моделирование достаточно большого числа блужданий, чтобы получить статистику по посещаемости всех вершин графа, после определения наиболее редкой вершины.
Авторское решение задачи приведено на языке Python 3.12.
import random
import sys
from typing import List, Tuple, DefaultDict, Dict
from dataclasses import dataclass
from collections import defaultdict
N = 25000
@dataclass
class Transition:
"""
Однонаправленный переход из одного узла в другой.
Двунаправленный переход состоит из двух однонаправленных.
"""
from_node: int # Откуда
to_node: int # Куда
weigth: int # Вес
probabilty: Tuple[float, float] = tuple([0., 0.]) # Вероятность пойти
class Node:
transitions: List[Transition]
def __init__(self):
# Каждый узел характеризуется списком исходящих переходов
self.transitions = []
def set_probabilities(self) -> None:
# Сумма всех весов исходящих переходов
weigth_sum = sum(transition.weigth for transition in self.transitions)
# Выставляем вероятности пойти по переходу в виде интервалов
# (например, [0.0, 0.15], [0.16, 1.0])
min_value = 0.0
for transition in self.transitions:
high_value = min_value + transition.weigth / weigth_sum
transition.probabilty = [min_value, high_value]
min_value = high_value
def get_transition(self) -> Transition:
# Получить случайный переход
prob = random.random()
for transition in self.transitions:
min_value, max_value = transition.probabilty
if prob > min_value and prob <= max_value:
return transition
raise Exception('No transitions!')
def walk(nodes: Dict[str, Node], N: int):
# По умолчанию для всех узлов количество переходов равно нулю
count: DefaultDict[str, int] = defaultdict(lambda: 0)
def get_random_node() -> Node:
nonlocal nodes
node = random.choice(list(nodes.values()))
return node
for i in range(N):
# начинаем в случайном узле
current_node = get_random_node()
for _ in range(100):
transition = current_node.get_transition()
count[transition.to_node] += 1
# Добавляем в счетчик, что мы посетили узел
current_node = nodes[transition.to_node]
return count
data = sys.stdin.readlines()[1:]
nodes: DefaultDict[str, Node] = defaultdict(lambda: Node())
# Считывание исходных данных
for unprocessed_transition in data:
from_node, to_node, weigth = map(int, unprocessed_transition.split())
# Так как переход двухнаправленный, добавляем
# переход в оба узла
nodes[from_node].transitions.append(
Transition(from_node, to_node, weigth))
nodes[to_node].transitions.append(
Transition(to_node, from_node, weigth))
# Приводим вероятности в виде интервалов для всех узлов
for node in nodes.values():
node.set_probabilities()
statistic = walk(nodes, N)
# Сортируем узлы по количеству переходов в них
sorted_nodes = sorted(statistic.keys(), key=lambda key: statistic[key])
print(sorted_nodes[0], flush=True)
Решение принимается, если выбранный экспонат является одним из трех наименее популярных, выбранных авторским решением.
У Марины есть детская мечта — стать капитаном корабля. Несколько лет она упорно трудилась: участвовала в НТО, чтобы уметь работать в команде и быть лидером, училась в специализированном институте, работала — и вскоре сможет осуществить свою мечту. Чтобы покрыть расходы на аренду корабля с экипажем, она решает заняться ловлей рыбы — будут и выходы в море, и прибыль.
В течение сезона Марина с командой может сделать 50 выходов в море. В каждый из выходов они могут ловить либо минтая, либо тунца. Улов минтая дает в среднем 15 тыс. у. е. дохода, улов тунца — 30 тыс. Вероятность выловить минтая и тунца отличается, во время выхода заранее неизвестна, но постоянна в течение сезона. Аренда судна с экипажем на сезон стоит 385 тыс. у. е.
Помогите морякам и запрограммируйте такую стратегию ловли, чтобы не выйти в минус, а лучше — максимизировать ожидаемую прибыль.
Формат входных данных
POLLOCK— выйти на минтая;TUNA— выйти на тунца.
В начале работы система ждет от вашего бота первое сообщение. Приняв последний ответ, ваше решение должно штатно завершиться.
Формат выходных данных
NO— рыба не поймана;YES— рыба поймана.
Тестовые данные
В авторском решении сначала производится по пять выходов на минтая и тунца, и рассчитывается статистика успешности каждого выхода. Цель следующих выходов выбирается, исходя из наибольшего математического ожидания прибыли (произведение текущей вероятности успеха и дохода за улов), и также дополняет статистику, влияя на дальнейший выбор.
Авторское решение задачи приведено на языке Python 3.12.
N = 50
REWARD_PO, REWARD_TU = 15, 30
CH_PO, CH_TU = 0, 1
WARMUP = 5
class Thinker:
def __init__(self):
self.time = 0
self.po_found = self.po_fail = 0
self.tu_found = self.tu_fail = 0
def think(self):
# пробные заходы
if self.time < WARMUP: return CH_TU
if self.time < WARMUP * 2: return CH_PO
# считаем вероятности успеха
po = self.po_found / (self.po_found + self.po_fail)
tu = self.tu_found / (self.tu_found + self.tu_fail)
# оцениваем выгоду и принимаем решение
is_pollock = po * REWARD_PO > tu * REWARD_TU
choice = CH_PO if is_pollock else CH_TU
return choice
def update(self, choice, result):
# обновление статистики
self.time += 1
if choice == CH_PO:
if result:
self.po_found += 1
else:
self.po_fail += 1
elif choice == CH_TU:
if result:
self.tu_found += 1
else:
self.tu_fail += 1
t = Thinker()
for _ in range(N):
# принятие и отправка решения
choice = t.think()
msg = "POLLOCK" if choice == CH_PO else "TUNA"
print(msg, flush=True)
# получение и обработка обратной связи
answer = input()
answer = 1 if answer == "YES" else 0
t.update(choice, answer)Это интерактивная задача, значит, программа взаимодействует с проверочной системой посредством стандартных потоков ввода и вывода. Иными словами, после отправки сообщения программа должна очистить буфер (выполнить flush) и считать ответ от системы (прочесть строку). В случае некорректного ответа проверка прерывается с вердиктом PE (Presentation Error).
Решение будет проверено 200 раз, и итоговая оценка будет рассматриваться по среднему полученному результату. За неотрицательный итог начисляется 50%. Максимальный балл присуждается, если результат достигает или обгоняет по прибыли авторское решение.
Кристина решила попытать счастья в мини-игре в своем любимом дачном симуляторе. Мини-игра представляет собой слепой турнир по игре в камень-ножницы-бумага. Суть в следующем: вы с соперником выкидываете по 300 жестов, но жесты друг друга вы не видите. Их видит арбитр, который молчаливо ведет счет и объявляет его в конце турнира. За победу в раунде присуждается 3 очка, за ничью — 1 очко, за проигрыш — 0.
Кристина очень хочет получить золотой наперсток, а для этого в турнире нужно набрать хотя бы 510 очков. Так как турнир играется раз в день, а хочется сейчас, Кристина сохранилась перед началом турнира, и после объявления результатов загружается обратно. Так она точно выяснила, что соперник будет постоянно выкидывать одни и те же жесты.
Кристина очень усидчивая, но ее терпения хватит только на 100 таких турниров. Помогите Кристине выиграть, реализовав бота для подбора победной комбинации.
Формат входных данных
В одной строке приводится набор, состоящий из слов ROCK, PAPER и SCISSORS через пробел. Количество слов соответствует длительности турнира. Чтобы завершить турнир досрочно и зафиксировать последний результат, отправьте CHEENAZES и завершите программу.
В начале работы ваша программа отправляет сообщение первой. Приняв завершающее сообщение, программа должна штатно завершиться.
Формат выходных данных
- 4 999 — турнир сыгран со счетом 4 очка в вашу пользу, осталось 999 тренировочных турниров;
- 12 1 — турнир сыгран со счетом 12 очков, сейчас будет последний турнир;
- 43
IMTIRED— последний турнир сыгран со счетом 43 очка, завершите программу.
Тестовые данные
Первая попытка состоит из случайного набора жестов. Результат этой попытки записывается как наилучший. Дальше производятся попытки улучшить результат путем замены случайного подотрезка другим набором жестов (по сути, максимизация результата по обратной связи). Когда остается последняя попытка, повторно отсылается наилучшее найденное решение.
Авторское решение задачи приведено на языке Python 3.12.
from random import randint
N, SEG_N = 300, 10
def encode(xs): # для формирования вывода
return ' '.join(['ROCK', 'PAPER', 'SCISSORS'][x] for x in xs)
# делаем случайное решение
base = [randint(0, 2) for _ in range(N)]
print(encode(base), flush=True)
# записываем его результат как лучший
r, _ = input().split()
best_res = int(r)
while True:
# улучшаем решение заменой случайного подотрезка
new = base.copy()
salt_i = randint(0, N-SEG_N-1)
new[salt_i:salt_i+SEG_N] = [randint(0, 2) for _ in range(SEG_N)]
print(encode(new), flush=True)
r, t = input().split()
# проверяем, улучшилось ли решение
res = int(r)
if res > best_res:
best_res, base = res, new
# прерываемся, если осталась одна попытка
if t == "1": break
# отправляем наилучшее решение
print(encode(base), flush=True)
_ = input()
Это интерактивная задача, значит, программа взаимодействует с проверочной системой посредством стандартных потоков ввода и вывода. Иными словами, после отправки сообщения программа должна очистить буфер (выполнить flush) и считать ответ от системы (прочесть строку). В случае некорректного ответа проверка прерывается с вердиктом PE (Presentation Error).
Решение будет проверено 200 раз, и итоговая оценка будет рассматриваться по среднему полученному результату. Результат проверки считается по последнему сыгранному турниру.
Правильное платоново тело \(B\) с ребром длиной \(L\) мкм, состоящее из дигидрида кислорода при температуре 273,15 К, с помощью тончайшего молекулярного скальпеля разделили на \(M\) одинаковых правильных платоновых тел (обусловимся, что такое разделение всегда возможно). Определите, насколько в итоге изменилась энергия льда. Диаметр молекулы воды примите за 0,28 нм, ее массу — за \(2{,}99\cdot 10^{-23}\) г, а удельную теплоту плавления воды — за 330 Дж/г.
Формат входных данных
В одну строку через пробел — \(B\) (английское название тела в нижнем регистре), \(L\) (вещественное число, в микрометрах) и \(M\) (натуральное). Названия тел единообразны.
Формат выходных данных
Единственное вещественное число, в наноджоулях.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
dodecahedron 1861.8616334625685 87842 |
249168.78412828103 |
Тестовые данные
- По типу многогранника и длине грани вычисляем площадь поверхности \(S\).
- По количеству новых тел \(m\) определяем площадь поверхности малого тела \(S_m\) (через объем или с помощью пропорции).
- Вычисляем площадь разрушенного слоя воды. Он составит половину разницы площадей, так как на две новые грани приходится один разрушенный слой: \[\vartriangle S = \frac{S - (S_m \cdot m)}{ 2}.\]
- Представим занимаемую молекулой воды площадь как круг диаметром 0,28 нм. Тогда количество расплавленных молекул составит отношение площади слоя к площади этого круга.
- Умножаем число молекул на массу молекулы воды и умножаем на удельную теплоту его плавления.
Таким образом получаем теплоту, выделенную при разделении многогранника на \(m\) подобных многогранников.
Авторское решение задачи приведено на языке Python 3.12.
from math import sqrt, pi
S_C = {
'tetrahedron': sqrt(3),
'hexahedron': 6,
'octahedron': 2 * sqrt(3),
'dodecahedron': 3 * sqrt(25 + 10 * sqrt(5)),
'icosahedron': 5 * sqrt(3),
}
lam = 330 # Дж/г
d_h2o = 0.28 # нм
S_h2o = ((d_h2o / 2) ** 2) * pi # нм2
m_h2o = 2.99e-23 # г (10^-23)
# подготавливаем входные данные
b, a, m = input.split()
a = float(a) * 1000 # um -> nm
m = int(m)
# считаем изменение площади поверхности
S = S_C[b] * a**2 # nm2
S_m = S / (m ** (2/3)) # nm2
dS = (S_m * m - S) / 2 # nm2
# пересчитываем в молекулы
n_h2o = dS / S_h2o # unit
# рассчитываем итоговую теплоту
p = n_h2o * m_h2o * lam / 1e-9 # nJ
print(p)Решение засчитывается, если ответ отличается от авторского не более, чем на 25%.
Разведовательный беспилотник «Фаина Клементьевна» совершал плановый облет местности на метеорите, имеющем форму тора, когда его застала сильная космическая буря с грозой. Удар молнии повредил ряд важных модулей, в том числе модуль геопозиционирования, а порыв ветра отнес беспилотник в неизвестную точку метеорита. К счастью, память не пострадала и сохранила точную посекторную карту метеорита с информацией о количестве ориентиров трех типов: холмы, кратеры и вкрапления руды.
Загруженная карта имеет один из двух форматов:
- формат 1 хранит информацию о количестве ориентиров всех типов в пределах данного сектора;
- формат 2 хранит информацию о группе ориентиров в северно-западном углу данного сектора. В данном случае подразумевается, что группы ориентиров расположены на угловых пересечениях секторов, при этом на каждом пересечении встречается произвольное количество ориентиров одного конкретного типа.
Запаса батареи «Фаины» хватит еще на 20 с. За 1 с беспилотник может переместиться в соседний сектор и сразу выполнить быстрое сканирование, в результате которого будет получена информация о примерном количестве ориентиров в текущем секторе. При быстром сканировании «Фаина» обнаруживает их по отдельности с вероятностью 80%, 70% и 60% соответственно.
Вместо очередного перемещения «Фаина» может передать сигнал бедствия в окрестности космоса. Но для успешного обнаружения беспилотник должен передать свои координаты с точностью до сектора.
Опишите стратегию, при которой «Фаина» сможет успешно сориентироваться и запросить помощь.
Формат входных данных
MAP 1 20 15— готовьтесь принять карту в формате 1 размером 15 строк с 20 ячейками в каждой.5;2;3 5;2;3 10;2;3 5;2;30 10;2;3— передается строка из пяти ячеек формата 1 с информацией об количествах ориентиров, разделенных точкой с запятой.0-20 1-25 2-13 1-23 0-2— передается строка из пяти ячеек формата 2 с информацией о типе (от 0 до 2) и количестве ориентиров, разделенных дефисом.10 23 10— в текущем секторе обнаружено такое количество ориентиров.YESилиNO— завершите программу.
Формат выходных данных
HELPME 0 5— передать сигнал помощи с координатами (0; 5), столбец и строка соответственно (нумерация координат с 0!).LEFT, RIGHT, UP, DOWN— переместиться по карте на соседний сектор и отсканировать его.
В самом начале проверочная система присылает вашей программе карту и результат первого сканирования согласно формату. После этого программа должна передать запрос, получить ответ и, если указано, штатно завершиться.
Тестовые данные
Авторское решение укладывается в ограничения задачи и работает путем обхода карты фиксированным циклическим набором команд. Результат каждого сканирования накладывается на считанную карту так, чтобы получить ячейки, на которых может находиться беспилотник. Число ориентиров на такой ячейке будет не меньше, чем обнаружено в ходе сканирования. Имея матрицу для предыдущего и текущего сканирования, а также смещение по матрице (на соседнюю ячейку), можно определить пары соседних ячеек, на которых мог находиться беспилотник, и тем самым отсеять часть вариантов. Таким образом, множество ячеек итерационно сводится к единственному варианту.
Авторское решение задачи на языке Python 3.12.
from copy import deepcopy
INF = float('inf')
MAP_N, MAP_M = 30, 30
N_ORIENT = 3
CMD_LEFT, CMD_RIGHT = "LEFT", "RIGHT"
CMD_UP, CMD_DOWN = "UP", "DOWN"
CMD_SOLVE = "HELPME"
DELTAS = {
CMD_LEFT: (-1, 0), CMD_RIGHT: (1, 0),
CMD_UP: (0, -1), CMD_DOWN: (0, 1),
}
def find_coord(f):
# поиск первого ненулевого элемента
for j in range(len(f)):
for i in range(len(f[j])):
if f[j][i]:
return (i, j)
return None
def filter_orient(m, sm):
# получить бинарную матрицу ячеек,
# где число ориентиров не меньше заданного
return [
[ all(x >= rx for (x, rx) in zip(c, sm))
for c in l
] for l in m
]
def filter_connected(rm1, rm2, delta):
# наложение бинарных матриц со сдвигом
dx, dy = delta
rm = deepcopy(rm2)
for j in range(len(rm)):
for i in range(len(rm[j])):
x = (i - dx) % len(rm[j])
y = (j - dy) % len(rm)
if not rm1[y][x]:
rm[j][i] = False
return rm
my_map = None
step_log = []
scan_log = []
filters = []
steps = [
CMD_DOWN,
CMD_RIGHT,
CMD_UP,
CMD_RIGHT,
]
move_idx = 0
def next_move() -> str:
global move_idx
move_idx = (move_idx + 1) % len(steps)
return steps[move_idx]
msg = input()
if msg[:3] == "MAP":
# чтение карты
toks = msg.split()
map_type, MAP_N, MAP_M = int(toks[1]), int(toks[2]), int(toks[3])
my_map = [[None for _ in range(MAP_N)] for _ in range(MAP_M)]
if map_type == 1:
# ориентиры помещаются в ячейку как есть
for j in range(MAP_M):
line = input().split()
for i in range(MAP_N):
c = line[i].split(";")
my_map[j][i] = tuple(int(c[k]) for k in range(N_ORIENT))
else: # map_type == 2
# сначала считываем карту
raw_map = [[None for _ in range(MAP_N)] for _ in range(MAP_M)]
for j in range(MAP_M):
line = input().split()
for i in range(MAP_N):
c = line[i].split("-")
raw_map[j][i] = tuple(int(k) for k in c)
# кладём ориентиры во все ячейки, граничащие с соответствующим углом
my_map = [[[0 for _ in range(N_ORIENT)] for _ in range(MAP_N)] for _ in range(MAP_M)]
for j in range(MAP_M):
for i in range(MAP_N):
for dx in (0, 1):
for dy in (0, 1):
cell = raw_map[(j+dy) % MAP_M][(i+dx) % MAP_N]
my_map[j][i][cell[0]] += cell[1]
else:
raise ValueError("Expected MAP")
while True:
# запрашиваем результат сканирования
msg = input().split()
if msg[0] == "YES" or msg[0] == "NO":
break # штатное завершение
msg = tuple(map(int, msg))
scan_log.append(msg)
# получаем вероятные ячейки
if filters:
filters.append(filter_connected(filters[-1], filter_orient(my_map, scan_log[-1]), step_log[-1]))
else:
filters.append(filter_orient(my_map, scan_log[-1]))
# положение определено однозначно?
if sum(1 for l in filters[-1] for c in l if c) == 1:
print("HELPME", *find_coord(filters[-1]), flush=True)
continue
# делаем следующий ход
move = next_move()
step_log.append(DELTAS[move])
print(move, flush=True)Это интерактивная задача, значит, программа взаимодействует с проверочной системой посредством стандартных потоков ввода и вывода. Иными словами, после отправки сообщения программа должна очистить буфер (выполнить flush) и считать ответ от системы (прочесть строку). В случае некорректного ответа проверка прерывается с вердиктом PE (Presentation Error).
Решение будет проверено 200 раз, и итоговая оценка будет рассматриваться по числу успешных обнаружений. Решение засчитывается на полный балл, если доля успешных испытаний составит не меньше 90%.