Инженерный тур. 1 этап
На аукционе с пятью участниками представлено десять лотов. Все участники являются покупателями. У каждого лота есть своя реальная стоимость, а каждый участник имеет свое представление о ней. Выгода участника заключается в разнице между реальной стоимостью лота и ставкой, которую заплатил за него участник. Каждый лот выставляется на аукцион по принципу «первой цены» на повышение ставки. Пусть участники делают ставки, равные их представлению о стоимости. Кто из участников получит наибольшую выгоду от участия в аукционе?
В ответ напишите только номер участника.
Ценности лотов: 1,5798; 1,6064; 1,9614; 1,8850; 1,1010; 1,8911; 1,0226; 1,3908; 1,2414; 1,4331.
Ставки:
- Участник 1: 1,4677; 1,6054; 2,1281; 2,0558; 1,0331; 1,9565; 1,0470; 1,3317; 1,1777; 1,3046.
- Участник 2: 1,7049; 1,5426; 1,8581; 1,9503; 1,2074; 1,8291; 1,0876; 1,5199; 1,2901; 1,5358.
- Участник 3: 1,6117; 1,5865; 2,1466; 2,0016; 1,0121; 2,0230; 0,9819; 1,3106; 1,3429; 1,3134.
- Участник 4: 1,6150; 1,7188; 1,7872; 1,7634; 1,1143; 1,9733; 1,0473; 1,3088; 1,3005; 1,4478.
- Участник 5: 1,5031; 1,4801; 1,9936; 2,0135; 1,0584; 1,7534; 1,0649; 1,3442; 1,1376; 1,5654.
Эта задача проверяет базовые знания теории аукционов, что потребуется на заключительном этапе.
Принцип аукциона «первой цены» прост: кто сделал максимальную ставку — тот и забирает лот. Следовательно, для каждого лота (столбца таблицы) определяем участника-победителя по наибольшей ставке и прибавляем ему выгоду как разницу между ценностью лота и ставкой победителя.
После вычисления всех лотов получаем следующие итоговые выгоды:
- Участник 1: \(-0{,}1708\).
- Участник 2: \(-0{,}4256\).
- Участник 3: \(-0{,}4186\).
- Участник 4: \(-0{,}1124\).
- Участник 5: \(-0{,}1322\).
Наибольшую выгоду (наименьший убыток) получил участник под номером 4.
4.
Дан куб, изображенный на рис. 1.1.
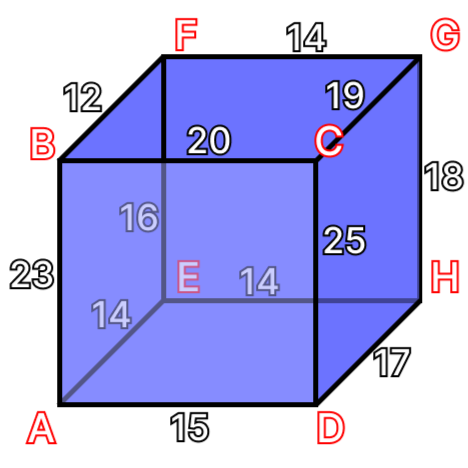
Каждое ребро куба, без диагоналей, обладает собственными фиксированными затратами на перемещение по ним. Найдите путь по ребрам из узла \(A\) в узел \(G\), требующий наименьших затрат. В ответе укажите число — суммарные затраты на этом пути. Задача проверяет навык работы с графовыми моделями, что является частью заключительного этапа.
Выпишем все возможные пути.
| Откуда | Куда | Затраты | Откуда | Куда | Затраты |
|---|---|---|---|---|---|
| \(A\) | \(B\) | 23 | \(D\) | \(H\) | 17 |
| \(B\) | \(F\) | 12 | \(D\) | \(C\) | 25 |
| \(F\) | \(G\) | 14 | \(C\) | \(B\) | 20 |
| \(A\) | \(E\) | 14 | \(C\) | \(G\) | 19 |
| \(E\) | \(H\) | 14 | \(F\) | \(E\) | 16 |
| \(A\) | \(D\) | 15 | \(G\) | \(H\) | 18 |
Решение имеет несколько способов, в том числе динамическое программирование (которое можно выполнить даже на бумаге) и реализацию алгоритма Дейкстры. Оптимальный путь, который по суммарным затратам равен 44, выглядит следующим образом: \(A \rightarrow E \rightarrow F \rightarrow G\).
44.
Роботы-уборщики А и Б исправно обслуживают марсианскую солнечную электростанцию уже так долго, что научились испытывать нечеловеческую скуку. В качестве одного из способов скрасить рутину А и Б подключаются к энергонакопителю и играют в разрядки. Правила просты: по очереди каждый робот разряжает накопитель на целое ненулевое число ампер-часов. Максимальную величину разряда за ход роботы определяют случайно перед каждой партией. Кто в свой ход остается без заряда — проиграл. После этого роботы возвращаются к работе, пока накопитель подзаряжается обратно.
Напишите бота для игры в разрядки. Бот должен сыграть 10 партий с проверочной системой. Балл за эту задачу составит отношение выигранных партий к их общему числу.
В каждой партии первый ход за вашей программой. Проверочная система играет идеально, и чтобы все было честно, в случае гарантированного поражения вы можете отказаться от партии в первый ход. Если это действительно так, отказ от партии засчитывается в качестве победы.
Это интерактивная задача, а значит, программа взаимодействует с проверочной системой посредством стандартных потоков ввода и вывода. Иными словами, после отправки сообщения программа должна очистить буфер (выполнить flush) и считать ответ от системы (прочесть строку). В случае некорректного ответа проверка прерывается с вердиктом PE (Presentation Error).
В начале работы система отправляет вашему боту очередное положение и ждет ответа.
Эта задача проверяет базовые навыки программирования и теории игр, что потребуется на заключительном этапе.
Примечания
- Каждое входящее и исходящее сообщение должно сопровождаться переносом строки.
- Очистка буфера делается функцией
sys.stdout.flush().
Формат входных данных
Строки, сообщения следующего вида:
START 15 3— начало партии, первое число — заряд накопителя (например, 15 А\(\cdot\)ч), далее максимальный разряд за ход;NEXT 12— очередной ход, числом передается текущий заряд накопителя;ISHOULDGO— игра окончена, завершите программу штатным образом;- остальные сообщения содержат сообщение об ошибке, и за ними следует вердикт
PE.
Формат выходных данных
Строки, сообщения следующего вида:
3— разрядить накопитель на указанное число ампер-часов (например, на 3);X(латинская «икс») — отказаться от партии (только в первый ход).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
15 3 16 3 9 5 100 9 100 10 500 101 150 7 27 8 39 4 40 2 |
3 3 3 3 X 3 5 X 1 10 ... |
Тестовые данные
Задача моделирует игру Баше, частный случай игры в Ним. Оптимальная стратегия без обращения к функции Шпрага – Гранди и в целом теории игры Ним сводится к простой формулировке: при максимальном разряде \(M\) разряжайте накопитель так, чтобы после вашего хода заряд был кратен (\(M+1\)). С другой стороны, если заряд уже в первый ход кратен \(M+1\), необходимо отказаться от партии.
Авторское решение задачи на языке Python 3.12 представлено в файле «Разрядки на подзарядке Решение.py» (https://disk.360.yandex.ru/d/2EzK88CZzHPP8A).
Развитие энергосистемы иногда сводится не к строительству новых объектов, а совсем наоборот. Чтобы развить что-то нужное, приходится избавляться от чего-то ненужного. И хорошо, если можно решить эту задачу однозначно.
Представлена энергосистема небольшого микрорайона. В файле https://disk.yandex.ru/d/P-tvXXZzsjFFFQ содержится аналитика по потребителям и генераторам этой системы за последние 10 суток. В первой строке приводятся типы объектов (C — потребитель, G — генератор), во второй строке — тариф в условных единицах, в следующих строках — влияние на энергобаланс в мегаваттах (положительное — генерация, отрицательное — потребление). Тариф потребителя — выплачивается участнику за каждый потребленный мегаватт, тариф генератора — выплачивает участник за каждые сутки. Недостающая или излишняя энергия в каждых сутках покупается или продается на внешнем рынке, тариф продажи — 2 у. е./МВт, тариф покупки — 5 у. е./МВт.
Определите, какой объект нужно убрать из системы, чтобы достичь максимального общего экономического баланса (доходы минус расходы, в условных единицах). В качестве ответа введите вещественное число — значение баланса после удаления объекта.
Обратите внимание на то, что в ответе в качестве разделителя используется точка. Ответ засчитывается, если отличается от эталонного не более, чем на \(10^{-2}\).
Задача проверяет навыки работы с данными и математическими моделями, что является частью заключительного этапа.
Заметим, что в модели отличаются цена покупки и продажи на внешнем рынке, а также характер влияния на экономику у обоих типов объектов (потребители платят пропорционально, генераторы — фиксировано). Следовательно, задачу нельзя решить «в лоб», посчитав индивидуальные экономические балансы и выбрав минимальный. Необходимо поочередно убирать каждый объект и пересчитывать энергетический и экономический балансы всей системы. Этот процесс можно ускорить применением Excel или программирования. Общий принцип следующий:
- Для каждых суток складываем потребление и генерацию, получая суточный энергобаланс. В зависимости от знака, умножаем на соответствующий тариф и получаем изменение экономического баланса. Суммируем все изменения и складываем в общий экономический баланс.
- Для каждого потребителя перемножаем суммарное потребление на его тариф и прибавляем к общему экономическому балансу.
- Для каждого генератора умножаем его тариф на 10 (число суток в данных) и вычитаем из общего экономического баланса.
Выполнив эти вычисления с поочередным удалением каждого объекта, получаем ряд значений, среди которых выбираем максимальный. Это и будет ответ.
Решение представлено в таблице: https://disk.yandex.ru/i/3F7YfUQ8VzL2cQ.
2741,83.
Энергоснабжение в отдаленных местностях, где не прокладывают линии электропередач, держится на собственных источниках электроэнергии. В том числе (как ни странно) теплоэнергоцентралях (ТЭЦ), использующих для работы газ, нефть, мазут и даже уголь. Своевременная поставка топлива, в отличие от погодных условий, более контролируема. Особенно если есть возможность обмениваться топливом с соседями. Только бы не запутаться во всех этих дорогах...
Дана сеть двусторонних дорог между населенными пунктами с расстояниям (в км) по каждому ребру, два населенных пункта, откуда и куда нужно перевезти грузовик с углем, а также фактический маршрут, по которому предлагается его отправить. Рассчитайте, насколько фактический маршрут отличается от кратчайшего.
Задача проверяет навык программной работы с графовыми моделями, что является частью заключительного этапа.
Формат входных данных
В первой строке два числа \(N\) (до 100) и \(M\) (до 200) — соответственно число населенных пунктов и дорог между ними. Далее идет \(M\) строк, в каждой три числа, первые два — соединяемые узлы (нумеруются с нуля!), третье вещественное число — расстояние между ними (до 50). В последней строке приводится предлагаемый маршрут как последовательность номеров узлов через пробел. Последовательность начинается и заканчивается соответственно искомыми начальным и конечными пунктами. Например.
5 5
0 1 10.123123
1 2 20.456456
2 3 30.789789
3 4 20.456456
4 0 10.123123
0 1 2 3Формат выходных данных
Единственное вещественное число — разница между длительностью фактического и кратчайшего маршрутов. Ответ засчитывается, если отличается от эталонного не более, чем на \(10^{-3}\) км.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
33 66 0 15 1.8048578387308658 0 12 27.827199865885426 0 4 11.087019215553134 0 28 2.8397283978530856 0 19 22.484731859522654 1 11 1.7776693647962352 1 8 47.0822317682757 1 27 21.764679873312986 2 32 6.532395422128161 ... |
37.952397149109274 |
Тестовые данные
Считаем расстояние фактического маршрута, после находим кратчайшее расстояние между двух точек (применяя, например, алгоритм Дейкстры), вычитаем первое из второго и приводим в качестве ответа.
Авторское решение задачи на языке Python 3.12 представлено в файле: https://disk.yandex.ru/d/q4-J-UicS38sgA.






