Предметный тур. Физика. 3 этап
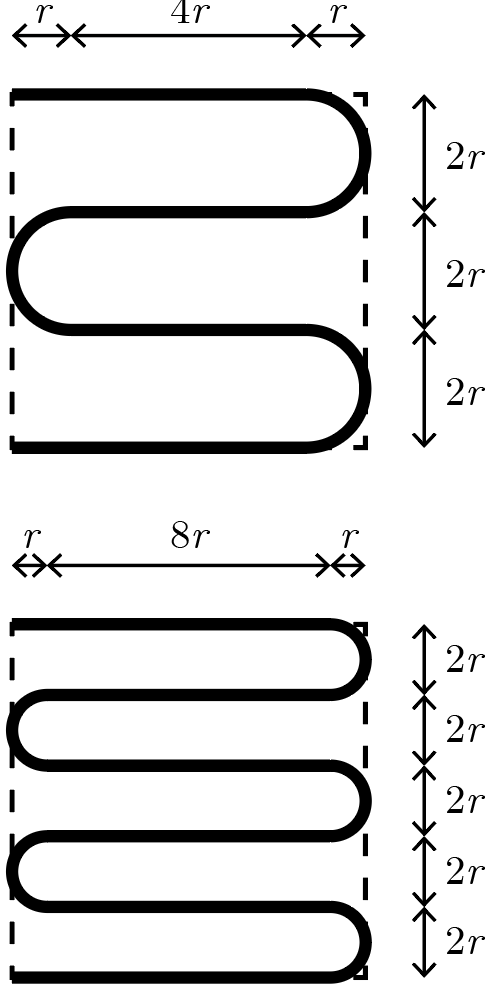
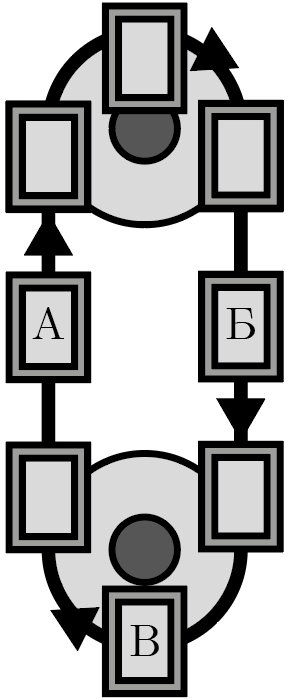
В квадратном помещении было решено изготовить электрический теплый пол, представляющий собой кабель постоянных толщины и материала, уложенный «змейкой», состоящей из прямолинейных и полукруглых участков, как это изображено на рис. 1.1, и точно вписывающейся своими границами в квадрат стен (пунктир на рис. 1.1). При этом были предложены две схемы укладки: с четырьмя либо восемью прямолинейными участками (на рис. 1.1 изображена только первая). В обеих схемах совпадают точки подключения пола (левые углы комнаты на рисунке). Определите мощность, выделяемую первой схемой, если при подключении к источнику тока одной и той же силы вторая схема отдает мощность на \(\Delta P\) выше.
Количество теплоты, выделяемое теплым полом за время \(t\), может быть найдено по закону Джоуля – Ленца: \[Q = I^2R t,\] где \(I\) — сила протекающего в кабеле тока, \(R\) — электрическое сопротивление кабеля, равное \[R = \frac{\rho l}{S},\] где \(\rho\) — удельное сопротивление материала кабеля, \(S\) — площадь поперечного сечения этого кабеля. Таким образом, мощность \[P = \frac{Q}{t} = I^2 \frac{\rho l}{S}\] прямо пропорциональна длине кабеля.
Обозначив сторону квадрата за \(a\), выразим ее через радиусы \(r_{1{,}2}\) скругления участков первой и второй схем. В формулах ниже первый множитель каждого слагаемого соответствует числу отрезков определенной длины, а второй — этой длине:
\[l_1 = 2\cdot 5r_1 + 2\cdot 4 r_1 + 3\cdot \pi r_1 = (18+3\pi)r_1,\] где \[r_1 = a/6 \Rightarrow l_1 = \frac{6+\pi}{2} a\] (см. верхний рисунок на рис. 1.2). Аналогично \[l_2 = 2\cdot 9r_2 + 4\cdot 8 r_2 + 5\cdot \pi r_2 = (50+5\pi)r_2,\] где \[r_2 = a/10 \Rightarrow l_2 = \frac{10+\pi}{2} a\] (см. нижний рисунок на рис. 1.2).
В результате мощности, выделяемые этими двумя схемами, относятся как \[\frac{N_2}{N_1} = \frac{l_2}{l_1} = \frac{10+\pi}{6+\pi}.\]
Дополняя эту пропорцию уравнением \(P_2 - P_1 = \Delta P\), получим систему двух линейных уравнений, имеющую решение \[P_1 = \frac{6+\pi}{4}\Delta P.\]
\[P_1 = \frac{6+\pi}{4}\Delta P.\]
| Верно записан закон Джоуля – Ленца | 2 балла |
| Верно записано выражение для сопротивления проводника известной геометрии | 3 балла |
| Верно вычислена длина кабеля в каждой схеме укладки | по 2 балла |
| Получен правильный ответ | 4 балла |
| Всего | 13 баллов |
Архитектурным проектом предусмотрен балкон, состоящий из железобетонной плиты перекрытия с массой \(M\) и длиной \(L = 9\textrm{\,м}\), установленной на две тонкие вертикальные колонны, разделенные расстоянием \(l = 6\textrm{\,м}\) (см. рис. 1.3). Поверх этих двух колонн установлен симметричный жилой модуль из легкого композита, обладающий массой \(m\), левый край которого совпадает с правой колонной, а правый — с правым краем плиты перекрытия (см. рис. 1.3). Найдите отношение масс \(M/m\), при котором обе колонны работают на сжатие, при этом одна из них испытывает вчетверо большую нагрузку, чем другая.
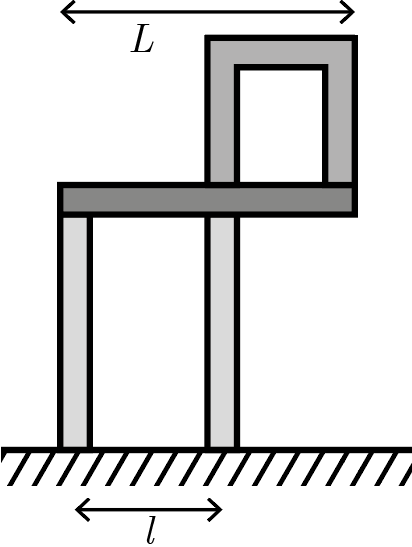
На плиту перекрытия действуют четыре силы. Вертикально вниз — сила ее собственной тяжести \(Mg\), приложенная к центру плиты, вес модуля \(mg\), приложенный к середине модуля (поскольку по условиям он симметричен), а также силы реакции двух колонн \(N\) (левой) и \(4N\) (правой). Легко показать из уравнения моментов, что именно правая колонна должна испытывать большую нагрузку, поскольку центр тяжести конструкции смещен в ее сторону.
Тогда первое условие равновесия (второй закон Ньютона) для этой плиты имеет вид \[N +4N = Mg + mg \Rightarrow N = \frac{(M+m)g}{5},\] а второе (уравнение моментов), записанное относительно левой колонны, \[Mg\frac{L}{2} + mg\frac{l + L}{2} = 4Nl = \frac{4(M+m)gl}{5}.\] Уравнение, полученное после проделанной подстановки, элементарно дает \[\frac{M}{m} = \frac{5L - 3L}{8l - 5L} = 9.\]
\[\frac{M}{m} = \frac{5L - 3l}{8l - 5L} = 9.\]
| Верно изображены или описаны силы, действующие на плиту (включая их направления и точки приложения) | 5 баллов |
| Верно составлено первое условие равновесия | 2 балла |
| Верно составлено второе условие равновесия | 4 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 17 баллов |
В высотном здании установлена система автоматического пожаротушения. Согласно техническим требованиям ее насос должен поднимать воду из источника, расположенного у уровня земли, до форсунки, расположенной непосредственно под крышей здания, и обеспечивать ее истечение из этой форсунки с постоянной скоростью \(v = 15\textrm{\,м/с}\). Инженерные расчеты показали, что мощность насоса, требуемая для выполнения этих требований при отсутствии потерь, равна \(N\). Некоторое время спустя стандарты пожарной безопасности пересмотрели, подняв требуемую скорость истечения воды из форсунки до \(2v\), из-за чего требуемая полезная мощность насоса поднялась до \(2{,}5N\). Найдите высоту здания. Ускорение свободного падения \(g \approx 9{,}8\) м/с\(^2\).
Работа, совершаемая насосом, уходит на увеличение кинетической и потенциальной энергии воды. Поднимая порцию воды массой \(m\) на высоту здания \(h\) и разгоняя ее до скорости \(v\), насос совершает работу \[A = mgh + \frac{mv^2}{2}.\] При этом сама масса \(m\), проходящая через сечение трубы за время \(t\), прямо пропорциональна этой скорости: \[m = \rho S v t,\] где \(S\) — площадь поперечного сечения форсунки, \(\rho\) — плотность воды. Подставим эти выражения друг в друга и разделим на время \(t\), чтобы получить мощность: \[N = \frac{A}{t} = \rho v S\left(gh + \frac{v^2}{2}\right).\] Подставляя в это соотношения два случая, описанных в условиях, получим \[\frac{5}{2}\cancel{\rho v S} \left(gh + \frac{v^2}{2}\right) = 2\cancel{\rho v S}\left(gh + 2v^2\right) \Rightarrow \frac{gh}{2} = \frac{11}{4}v^2 \Rightarrow h = \frac{11v^2}{2g} \approx 126\textrm{\,м}.\]
126 м.
| Верно записана связь работы или мощности насоса с изменением механической энергии порции воды известной массы | 6 баллов |
| Указана прямая пропорциональность массового расхода воды скорости ее истечения | 3 балла |
| Верно составлено уравнение, связывающее два режима работы насоса | 3 балла |
| Получен правильный ответ | 5 баллов |
| Всего | 15 баллов |
Спортивный объект предполагается использовать только в дни проведения крупных мероприятий, поэтому, чтобы избежать замерзания воды в системе его отопления в периоды простоя, в качестве теплоносителя в ней используется состав на основе изопропилового спирта, имеющий плотность \(\rho_1 = 800\) кг/м\(^3\), удельную теплоемкость \(c_1 = 3000\) Дж/(кг\(\cdot\)К) и температуру кипения \(t_1 = 85~°\)C.
Однако ближайшая доступная котельная использует в качестве теплоносителя воду (плотность \(\rho_2 = 1000\) кг/м\(^3\), удельная теплоемкость \(c_2 = 4200\) Дж/(кг\(\cdot\)К)), и замена теплоносителя в любой из этих систем оказывается экономически нецелесообразной. Поэтому на стыке двух систем было решено установить теплообменник, обеспечивающий тепловой поток от одной жидкости к другой \(\Phi = \alpha \Delta t\), где \(\Delta t\) — разность температур между жидкостями на входе в теплообменник, а \(\alpha = 80\textrm{\,Вт/К}\). Но после долгого простоя объекта температура в котельной поднялась до \(t_2 = 90~°\)C.
Определите температуру \(t_0\), установившуюся к этому моменту на объекте, если для избежания закипания теплоносителя насосам его системы отопления необходимо прокачивать состав с объемным расходом не менее \(v = 2{,}1\textrm{\,л/мин}\).
Максимальную температуру спиртовой теплоноситель имеет на выходе из теплообменника, а минимальную — на входе в него. Первая не должна превышать \(t_1\), а последняя после долгого простоя должна установиться на уровне температуры помещения \(t_0\). Для нагревания объема \(V\) состава от температуры \(t_0\) до точки кипения \(t_1\) необходимо передать ему количество теплоты \[Q = c_1 \rho_1 V (t_1-t_0),\] на что теплообменнику необходимо время \[\tau = \frac{Q}{\Phi} = \frac{c_1 \rho_1 V (t_1-t_0)}{\alpha (t_2 -t_0)}.\] Прокачивая тот же объем за меньшее или равное \(\tau\) время, насосы не позволят ему закипеть. Перестановкой множителей получим \[\alpha (t_2 -t_0)= \frac{c_1 \rho_1 V (t_1-t_0)}{ \tau} = c_1\rho_1 v (t_1 - t_0),\] откуда выразим искомую температуру: \[t_0 = \frac{c_1 \rho_1 v t_1 - \alpha t_2}{c_1 \rho_1 v - \alpha} = -15~°\text{С}.\]
\[t_0 = \frac{c_1 \rho_1 v t_1 - \alpha t_2}{c_1 \rho_1 v - \alpha} = -15~°\text{С}.\]
| Верно записано уравнение теплового баланса | 4 балла |
| Продемонстрировано понимание смысла теплового потока — верно записана его связь с теплотой и временем или объемным расходом теплоносителя | 6 баллов |
| Продемонстрировано понимание того, что температура помещения совпадает с температурой теплоносителя на входе в теплообменник | 2 балла |
| Продемонстрировано понимание того, что температура закипания теплоносителя совпадает с максимальной допустимой температурой на выходе из теплообменника | 2 балла |
| Величина теплового потока выражена через правильные температуры и коэффициент \(\alpha\) | 2 балла |
| Получен правильный ответ | 7 баллов |
| Всего | 23 балла |
На большой строительной площадке имеется единственный надежный источник электроэнергии, представляющий собой электрический щиток, на клеммах которого поддерживается стабильное напряжение \(U_0\). На некотором этапе к щитку потребовалось подключить двух независимых потребителей с сопротивлением \(R=15\textrm{\,Ом}\) каждый, расположенных в дальних концах площадки так, что вместе со щитком они оказались в вершинах равностороннего треугольника со стороной \(a = 600\textrm{\,м}\).
К сожалению, единственный подходящий для этого провод, как оказалось, обладает настолько большим сопротивлением, что его отрезок длины \(a\) имеет сопротивление \(R/2\). Во сколько раз будут отличаться напряжения на потребителях в двух случаях:
- если подключить их к источнику последовательно, соединив минимальной достаточной для этого длиной провода,
- если подключить их к источнику параллельно, соединив минимальной длиной провода, достаточной для этого?
Указание: точка \(O\) такая, что сумма расстояний от нее до всех вершин правильного треугольника минимальна — есть центр этого треугольника.
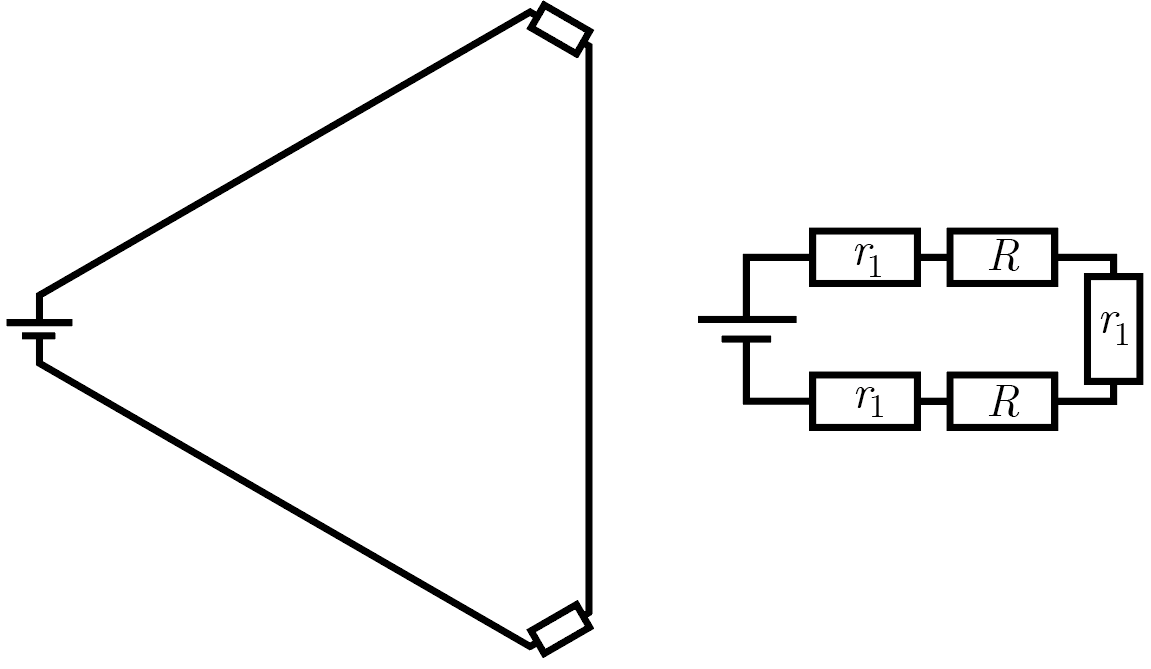
Кратчайшее последовательное соединение трех элементов обеспечивается прокладкой проводов вдоль сторон этого треугольника. Реалистичная схема такого подключения изображена в левой части рис. 1.4, а эквивалентная ей, более читаемая, — на правой. На эквивалентной схеме \(r_1\) — сопротивления отрезков провода, длина которых равна стороне треугольника.
Эффективное сопротивление такого соединения \[R_1 = 2R + 3r_1,\] следовательно, в нем протекает ток \[I_1 = \frac{U_0}{R_1} = \frac{U_0}{2R + 3r_1},\] а напряжение на каждом потребителе оказывается равно \[U_1 = I_1R = \frac{U_0 R}{2R + 3r_1} = \frac{2U_0}{7}.\]
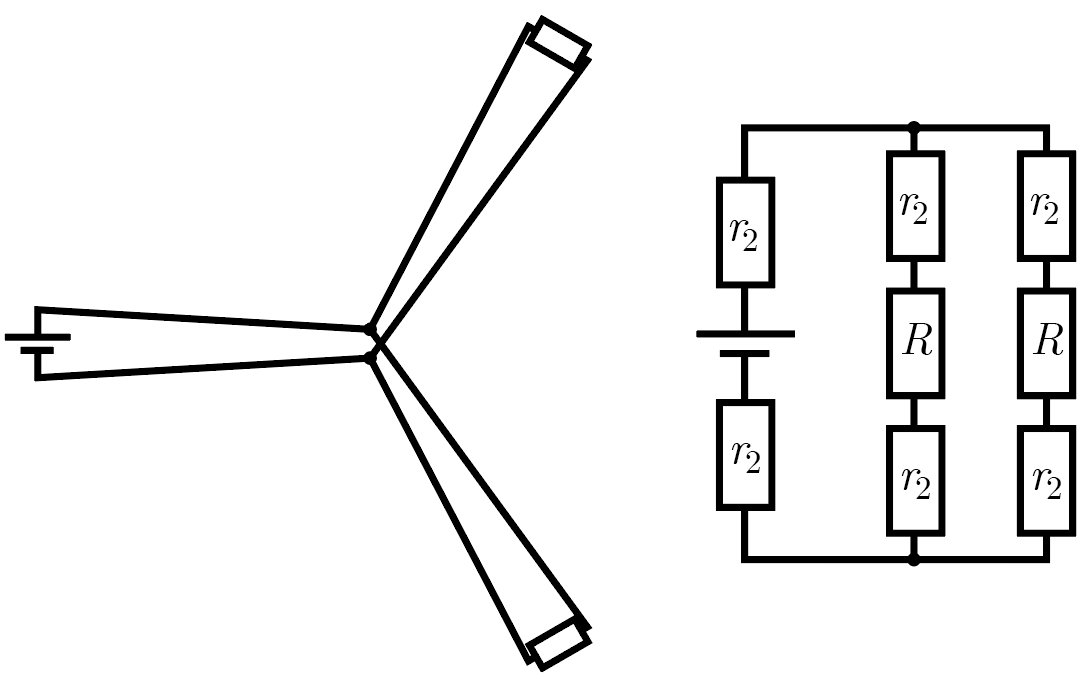
При параллельном соединении необходимо минимизировать сумму расстояний до потребителей и источника от точек ветвления цепи. Для этого, как было подсказано в условиях, точки ветвления должны находиться в центре треугольника. Соответствующие реалистичная и эквивалентная схемы также изображены на рис. 1.5. На последней \(r_2\) — сопротивление одного отрезка провода от вершины до центра треугольника.
Эффективное сопротивление \(R_2\) этого соединения равно \[R_2 = 2r_2 + \frac{2r_2 + R}{2} = 3r_2 + R/2,\] а напряжение на каждом из потребителей \[U_2 = I_2 R = \frac{U_0 R}{2R_2} = \frac{U_0 R}{6r_2 + R}.\]
Но так как сопротивление провода прямо пропорционально его длине, \(r_2 = \sqrt{3}r_1/3\) (из геометрии правильного треугольника), то есть \[U_2 = \frac{U_0 R}{2\sqrt{3}r_1 + R} = \frac{U_0}{\sqrt{3} + 1} \Rightarrow \frac{U_2}{U_1} = \frac{7}{2\sqrt{3} + 2}.\]
\[\frac{U_2}{U_1} = \frac{7}{2\sqrt{3} + 2} \approx 1{,}28.\]
| Верно изображена схема последовательного подключения | 2 балла |
| Верно найдено эквивалентное сопротивление этой схемы | 4 балла |
| Верно найдено напряжение на потребителях в этой схеме | 4 балла |
| Верно изображена схема параллельного подключения | 3 балла |
| Верно найдено эквивалентное сопротивление этой схемы | 4 балла |
| Верно найдено напряжение на потребителях в этой схеме | 4 балла |
| Верно найдена взаимосвязь между длиной отрезков провода на второй схеме и стороной треугольника | 4 балла |
| Получен правильный ответ | 5 баллов |
| Всего | 30 баллов |
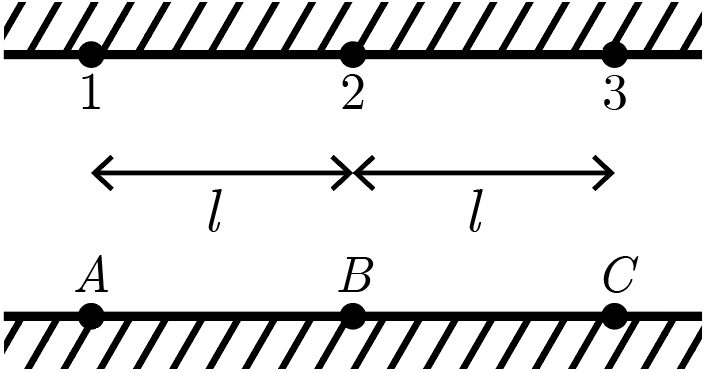
На фасаде здания было решено подвесить скульптуру сложной формы. Для этого, как изображено на рис. 2.1, используется прямолинейная стальная балка, которую можно считать абсолютно жесткой. К балке через равные расстояния \(l = 2\textrm{\,м}\) друг от друга, закреплены три троса одинаковой жесткости и одинаковой длины без нагрузки. Сама скульптура болтовыми соединениями закреплена на балке. Известно, что под весом скульптуры трос \(1\) растянулся на \(x_1 = 2\textrm{\,мм}\), а трос \(3\) — на \(x_3 = 5\textrm{\,мм}\). Найдите расстояние \(a\), на котором находится центр тяжести скульптуры с балкой от точки закрепления троса \(1\).
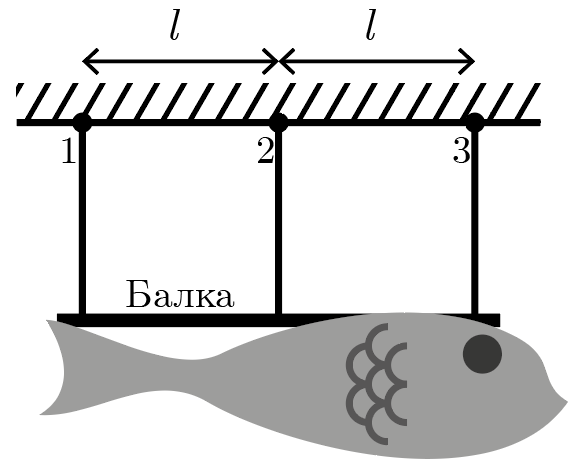
Балка считается прямолинейной и абсолютно жесткой, а это значит, что длина среднего троса, поддерживающего ее, должна быть равна среднему арифметическому длин правого и левого тросов, находящихся от него на одинаковых расстояниях. Поскольку по условиям длины этих тросов в покое и их коэффициенты жесткости равны, то такое же утверждение справедливо для удлинений и, следовательно, сил натяжения (обозначим их \(T_{1{,}2,3}\)): \[T_2 = \frac{T_1+T_3}{2}.\]
Эти силы направлены вертикально вверх и приложены в точках закрепления тросов. Единственная сила, противодействующая им — направленная вертикально вниз сила тяжести \(Mg\), приложенная к центру тяжести. Из первого условия равновесия (второго закона Ньютона) легко найти модуль этой силы: \[Mg = T_1 + T_2 + T_3 = \frac{3}{2}(T_1 + T_3).\]
Запишем второе условие равновесия балки (уравнение моментов) относительно точки закрепления троса \(1\): \[l T_2 + 2 l T_3 = Mg a \Rightarrow a = \frac{2(T_2 + 2T_3)}{3(T_1 + T_3)} = \frac{T_1 + 5T_3}{3(T_1 + T_3)},\] что, из закона Гука, равно \[a = l\frac{x_1 + 5x_3}{3(x_1 + x_3)} \approx 2{,}57\textrm{\,м}.\]
\[a = l\frac{x_1 + 5x_3}{3(x_1 + x_3)} \approx 2{,}57\textrm{\,м}\]
| Верно записано первое условие равновесия (сумма сил) | 3 балла |
| Верно записано второе условие равновесия (сумма моментов сил) | 4 балла |
| Верно записана связь между силами натяжения разных нитей, следующая из закона Гука | 3 балла |
| Получен правильный ответ | 5 баллов |
| Всего | 15 баллов |
В комнате с черными стенами и потолком в точках 1, 2 и 3 потолка, разделенных равными расстояниями \(l\), установлены три точечных светильника одинаковой яркости, равномерно испускающие свет во все стороны. В точках \(A\), \(B\) и \(C\), расположенных на полу комнаты строго под точками 1, 2, 3 соответственно, размещают фотометрические датчики, измеряющие суммарную плотность светового потока (Вт/м\(^2\)), достигающую их (равномерно со всех направлений).
Измерения при помощи этих датчиков показывают, что при включении только светильника 2 в точке \(B\) эта плотность оказывается точно такой же, как и при включении только светильников 1 и 3. Определите, во сколько раз будут отличаться плотности светового потока в точке \(A\) в тех же двух случаях.
Поскольку стены и потолок комнаты черные возможными переотражения света от них учитывать при расчете освещенности не нужно. Световой поток, испускаемый светильником через любую окружающую его сферу, одинаков. Площадь этой сферы прямо пропорциональна квадрату ее радиуса. Следовательно, плотность светового потока \(f\), представляющая собой отношение общей световой энергии, проходящей через некоторую площадку, к площади этой площадки, обратно пропорциональна квадрату расстояния \(r\) до источника освещения. Обозначим коэффициент в этой пропорциональности \(k\): \[f = \frac{k}{r^2}.\] Тогда, обозначив высоту потолка комнаты \(H\), получим, что плотности светового потока \(f^B_2\) и \(f^B_{13}\) в точке \(B\) в двух описанных в условиях случаях равны соответственно: \[f^B_2 = \frac{k}{H^2}; \quad f^B_{13} = 2\frac{k}{H^2 + l^2}.\] Но так как эти плотности дополнительно равны между собой, получим \[\frac{k}{H^2} = 2\frac{k}{H^2 + l^2} \Rightarrow 2H^2 = H^2 + l^2 \Rightarrow H = l.\] Тогда несложно найти плотности светового потока в точке \(A\) в тех же двух случаях: \[f^A_2 = \frac{k}{H^2 + l^2} = \frac{k}{2l^2}; \quad f^A_{13} = k \left(\frac{1}{H^2} + \frac{1}{H^2 + 2l^2}\right) = \frac{4k}{3l^2};\] и их отношение: \[\frac{f^A_{13}}{f^A_2} = \frac{8}{3}.\]
\[f^A_{13} : f^A_2 = 8:3 \approx 2{,}67.\]
| Продемонстрировано понимание роли цвета стен и потолка в задаче | 2 балла |
| Показано, что плотность светового потока обратно пропорциональна квадрату расстояния до источника | 4 балла |
| Верно найдены расстояния от светильников до датчиков | 3 балла |
| Найдено соотношение между высотой потолка и расстоянием между источниками | 3 балла |
| Получен правильный ответ | 6 баллов |
| Всего | 18 баллов |
Для здания крупного предприятия инженеры разработали лифт-патерностер с автоматизированной системой загрузки-выгрузки, позволяющей кабинкам двигаться безостановочно на высоких скоростях. В ходе испытаний этого лифта в его кабинках А, Б и В (см. рис. 2.3) разместили одинаковые многофункциональные датчики, после чего привели лифт в движение. В некоторый момент динамометр датчика в кабинке А показал, что он имеет вес \(P_\textrm{А} = 24\textrm{\,Н}\), в то время как динамометр датчика в кабинке Б точно в тот же момент времени показал, что его вес \(P_\textrm{Б} = 16\textrm{\,Н}\). Одновременно с этим спидометры тех же датчиков показали, что скорость их движения друг относительно друга \(v_\textrm{АБ} = 5\textrm{\,м/с}\). Акселерометр датчика в кабинке В передает в тот же момент показания о модуле его ускорения. Чему оно равно, если радиус ведущих валов лифта \(R = 4\textrm{\,м}\)? Ускорение свободного падения \(g \approx 9{,}8\) м/с\(^2\).
Лифт-патерностер — это лифт непрерывного движения, состоящий из множества кабинок, закрепленных на едином ведущем тросе, движущемся подобно конвеерной ленте, как это изображено на рис. 2.3. Такой лифт обычно не имеет дверей и не останавливается для посадки-высадки. В большинстве случаев лифты этого типа используются как грузовые, а не пассажирские. Движение кабинок лифта все время (включая прохождение скругленных участков) остается чисто поступательным.
Чтобы ведущий трос не рвался, относительно лифтовой шахты датчики в кабинках А и Б могут двигаться только с одинаковыми по модулю скоростями \(v\) в противоположных направлениях, поэтому \[v_\textrm{АБ} = 2v \Rightarrow v = \frac{v_\textrm{АБ}}{2}.\] То же самое справедливо для их ускорений. Записав относительно инерциальной системы отсчета второй закон Ньютона для этих датчиков в проекции на вертикальную ось, получим \[\left\{\begin{aligned} &m a = N_\textrm{А} - mg, \\ -&m a = N_\textrm{Б} - mg, \end{aligned}\right.\] где \(a\) — модули ускорения этих датчиков, \(N_\textrm{А,Б}\) — действующие на них силы нормальной реакции опоры, по модулю равные весам соответствующих датчиков, \(m\) — массы этих датчиков. Решая эту систему и подставляя равенства \(N_\textrm{АБ} = P_\textrm{АБ}\), получим \[a = g\frac{P_\textrm{A} - P_\textrm{Б}}{P_\textrm{A} + P_\textrm{Б}}.\]
Датчик в кабинке В движется с ускорением двух видов. Горизонтальная проекция его ускорения совпадает, исходя из требования неразрывности троса, с найденным выше ускорением \(a\). Вертикальная проекция его ускорения — центростремительная. Двигаясь с той же по модулю скоростью \(v\), что и две других рассмотренных кабинки, он поворачивает по радиусу \(R\): \[a_\textrm{цс} = \frac{v^2}{R} = \frac{v_\textrm{АБ}^2}{4R}.\]
Тогда модуль ускорения этого датчика можно найти по теореме Пифагора: \[a_\textrm{В} = \sqrt{a^2 + a_\textrm{цс}^2} = \sqrt{\left(g\frac{P_\textrm{A} - P_\textrm{Б}}{P_\textrm{A} + P_\textrm{Б}}\right)^2 + \frac{v_\textrm{АБ}^4}{16 R^2}} \approx 2{,}5\textrm{\,м/с}^2.\]
\[a_\textrm{В} = \sqrt{\left(g\frac{P_\textrm{A} - P_\textrm{Б}}{P_\textrm{A} + P_\textrm{Б}}\right)^2 + \frac{v_\textrm{АБ}^4}{16 R^2}} \approx 2{,}5\textrm{\,м/с}^2.\]
| Найдена скорость кабинок относительно лифтовой шахты | 2 балла |
| Верно записан второй закон Ньютона для датчиков | 4 балла |
| Верно найдено ускорение кабинок А и Б относительно ИСО | 3 балла |
| Понято, что кабинка В имеет ненулевые проекции ускорения на вертикальную и горизонтальную оси | 3 балла |
| Верно найдено центростремительное ускорение кабинки В | 3 балла |
| Получен правильный ответ | 5 баллов |
| Всего | 20 баллов |
На большой строительной площадке имеется единственный надежный источник электроэнергии, представляющий собой электрический щиток, на клеммах которого поддерживается стабильное напряжение \(U_0 = 220\textrm{\,В}\). На некотором этапе к щитку потребовалось подключить двух независимых потребителей с сопротивлением \(R\) каждый, расположенных в дальних концах площадки так, что вместе со щитком они оказались в вершинах равностороннего треугольника. К сожалению, единственный подходящий для этого провод, как оказалось, обладает настолько большим сопротивлением, что при подключении обоих потребителей к источнику последовательно и соединении их минимальной достаточной для этого длиной провода, напряжение на клеммах каждого потребителя оказалось равно \(U_0/4\). Каким будет напряжение на клеммах каждого потребителя, если подключить их к источнику параллельно минимальной достаточной для этого длиной провода?
Указание: известно, что точка \(O\) такая, что сумма расстояний от нее до всех вершин правильного треугольника минимальна — центр этого треугольника.
Кратчайшее последовательное соединение трех элементов обеспечивается прокладкой проводов вдоль сторон этого треугольника. Реалистичная схема такого подключения изображена на левой части рис. 2.4, а эквивалентная ей более читаемая — на правой. На эквивалентной схеме \(r_1\) — сопротивления отрезков провода, длина которых равна стороне треугольника.
Эффективное сопротивление такого соединения \[R_1 = 2R + 3r_1,\] следовательно, в нем протекает ток \[I_1 = \frac{U_0}{R_1} = \frac{U_0}{2R + 3r_1},\] а напряжение на каждом потребителе оказывается равно \[U_1 = I_1R = \frac{U_0 R}{2R + 3r_1}.\] Зная, что оно равно \(U_0/4\), легко установить, что \(r_1 = 2R/3\).
При параллельном соединении необходимо минимизировать сумму расстояний до потребителей и источника от точек ветвления цепи. Для этого, как было указано в условиях, точки ветвления должны находиться в центре треугольника. Соответствующие реалистичная и эквивалентная схемы также изображены на рис. 2.5. На последней \(r_2\) — сопротивление одного отрезка провода от вершины до центра треугольника.
Эффективное сопротивление \(R_2\) этого соединения равно \[R_2 = 2r_2 + \frac{2r_2 + R}{2} = 3r_2 + R/2,\] а напряжение на каждом из потребителей \[U_2 = I_2 R = \frac{U_0 R}{2R_2} = \frac{U_0 R}{6r_2 + R}.\]
Но так как сопротивление провода прямо пропорционально его длине, \(r_2 = \sqrt{3}r_1/3 = 2\sqrt{3}R/9\) (из геометрии правильного треугольника), то есть \[U_2 = \frac{U_0 R}{4\sqrt{3}R/3 + R} = \frac{3U_0}{4\sqrt{3} + 3} \approx 66{,}5\textrm{\,В}.\]
\[U_2 = \frac{3U_0}{4\sqrt{3} + 3} \approx 66{,}5\textrm{\,В}.\]
| Верно изображена схема последовательного подключения | 2 балла |
| Верно найдено эквивалентное сопротивление этой схемы | 3 балла |
| Верно найдено напряжение на потребителях в этой схеме | 3 балла |
| Верно изображена схема параллельного подключения | 3 балла |
| Верно найдено эквивалентное сопротивление этой схемы | 3 балла |
| Верно найдено напряжение на потребителях в этой схеме | 3 балла |
| Верно найдена взаимосвязь между длиной отрезков провода на второй схеме и стороной треугольника | 3 балла |
| Получен правильный ответ | 4 балла |
| Всего | 24 балла |
При проведении отделочных работ часто возникает необходимость установить в помещении осушитель, существенно уменьшающий время засыхания строительных растворов. Изготовленный для этих целей прибор состоит из сосуда для газа максимальным объемом \(V_0 = 5\textrm{\,л}\), снабженного подвижным поршнем и автоматизированными клапанами, а также подключенного к нему резервуара для конденсата объемом \(v = 2\textrm{\,л}\).
Рабочий цикл прибора состоит из следующих этапов: сначала сосуд имеет объем \(V_0\), его входной клапан (соединяющий сосуд с окружающим воздухом) открыт, а клапан, ведущий в емкость для конденсата, закрыт. При этом воздух внутри осушителя имеет ту же влажность, что и снаружи. Затем входной клапан закрывается, и электромотор приводит поршень в движение, сжимая сосуд до объема \(V_1 = V_0/2\). После этого открывается клапан, соединяющий сосуд с резервуаром для конденсата, и позволяет стечь образовавшейся воде в этот резервуар. На последнем этапе клапан для конденсата закрывается, открывается входной клапан, и электромотор вновь расширяет сосуд до изначального объема \(V_0\), впуская в него окружающий воздух, пока между окружающим и внутренним воздухом не установится равновесие.
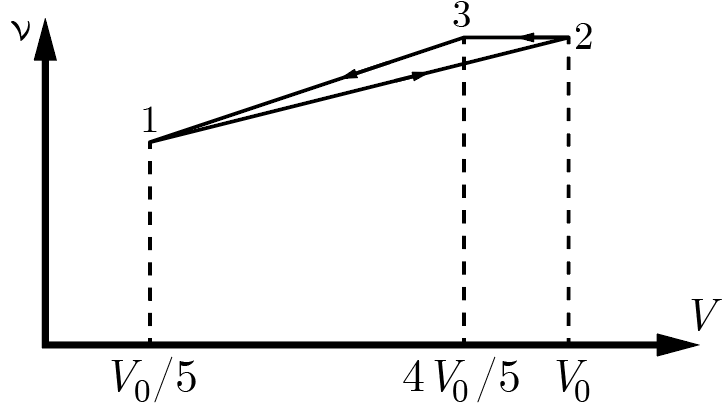
На рис. 2.6 приведена диаграмма этого цикла в координатах \(\nu V\), где \(\nu\) — общее количество газа в сосуде, \(V\) — объем этого сосуда.
Все процессы в цикле являются изотермическими. Рассмотрев ее, ответьте на следующие вопросы:
- Какой была относительная влажность воздуха в помещении в момент, в который построена эта диаграмма?
- До какой минимальной относительной влажности может осушить помещение данный прибор?
- Помещение какого максимального объема прибор может довести от изначальной влажности, найденной в первом вопросе, до минимальной, найденной во втором, без опустошения резервуара для конденсата, если начальная абсолютная влажность воздуха в помещении \(f = 16\) г/м\(^3\)?
В процессе 1–2 объем и количество газа синхронно увеличиваются, следовательно, этот процесс соответствует впуску воздуха в сосуд осушителя. Затем на процессе 2–3–1 воздух сжимается, но в течение какого-то времени (процесс 2–3) при постоянном количестве — как идеальный газ. Следовательно, на этом процессе давление пара еще не достигло точки насыщения. В процессе 3–1 уменьшение объема происходит совместно с уменьшением количества газа, что в закрытом сосуде можно объяснить только конденсацией.
Пускай в воздухе изначально содержится некоторая масса \(m\) воды. В процессе 2–3 эта масса не меняется, но, как было выяснено, точка 3 является началом процесса конденсации, а значит, абсолютная влажность в этой точке соответствует абсолютной влажности \(f_0\) насыщенного пара. Тогда массу \(m\) можно выразить как \[m = \frac{4V_0}{5} f_0 = V_0 \phi f_0,\] где \(\phi\) — относительная влажность окружающего воздуха: по условиям к началу сжатия воздух внутри осушителя имеет ту же влажность, что и снаружи. Из этого уравнения легко дать ответ на первый вопрос: \[\varphi = \frac{4}{5} = 80\%.\]
Минимальный объем газа в цикле равен \(V_0/5\), поэтому когда пар в этой точке (состояние \(1\)) насыщен, общая масса воды в сосуде составляет \[m_1 = f_0 \frac{V_0}{5}.\] Далее начинается фаза впуска, и больше воды не конденсируется ни при каких условиях. После расширения газа вновь до состояния \(2\) его объем возрастает в пять раз и та же масса влаги уже соответствует абсолютной влажности \(f_{min} = m_1/V_0\) или относительной \[\phi_{min} = \frac{f_{min}}{f_0} = \frac{1}{5} = 20\%.\]
Чтобы ответить на последний вопрос задачи, найдем \(f_0\). Установлено, что \(\phi = 4/5\), следовательно, \(f_0 = 5/4f\). Известно, что \(f_{min} = f_0/5 = f/4\). Следовательно, общая масса влаги, конденсирующейся из помещения с объемом \(V_{max}\) при его осушении от абсолютной влажности \(f\) до \(f_{min}\), задается выражением \[m_{max} = V_{max} (f - f_{min}) = \frac{3}{4} V_{max} f.\] Учитывая дополнительно, что \(m_{max} = \rho v\), где \(\rho = 1000\) кг/м\(^3\), получим последний ответ: \[\rho v = \frac{3}{4} V_{max} f \Rightarrow V_{max} = \frac{4 \rho v}{3 f} \approx 167\textrm{\,м}^3.\]
\[\phi = 80\%; \quad \phi_{min} = 20\%; \quad V_{max} = \frac{4 \rho v}{3 f} \approx 167\textrm{\,м}^3.\]
| Продемонстрировано понимание того, на каком участке цикла происходит конденсация пара | 6 баллов |
| Найден верный ответ на первый вопрос задачи | 5 баллов |
| Найден верный ответ на второй вопрос задачи | 5 баллов |
| Верно записана хотя бы одна связь между абсолютной и относительной влажностью воздуха | 3 балла |
| Найден верный ответ на последний вопрос задачи | 7 баллов |
| Всего | 26 баллов |