Предметный тур. Информатика. 3 этап
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 64 Мбайт.
Победил Иван Змея Горыныча и пришел за наградой. Свадьбу с Царевной сразу сыграли, а вот как полцарства в придачу выделить — стали думать.
Царство задано прямоугольной матрицей, в каждой ячейке которой указано количество сторожевых башен. Разделить царство можно только по прямой, при этом прямая должна быть строго вертикальной или горизонтальной.
Помогите разделить царство на две части так, чтобы количество сторожевых башен в каждой из частей было одинаковым, или сообщите, что это невозможно.
Формат входных данных
В первой строке содержатся два числа: \(N, M\) (\(1 \leqslant N, M \leqslant 1000\)) — ширина и высота царства.
В последующих \(N\) строках содержатся \(M\) чисел \(d_{ij}\) через пробел (\(0 \leqslant d_{ij} \leqslant 10^8\)) — количество башен в данной части царства.
Формат выходных данных
Если царство можно разделить горизонтально (независимо от того, можно ли его разделить вертикально), в ответ выведите символ \(h\) и число \(i\) — номер последней строки матрицы, принадлежащей верхнему полцарству (если подходящих \(i\) несколько — выведите минимальный).
Если царство нельзя разделить горизонтально, но можно разделить вертикально, в ответ выведите символ \(\nu\) и число \(j\) — номер последнего столбца матрицы, принадлежащей левому полцарству (если подходящих \(j\) несколько — выведите минимальный).
Если царство нельзя разделить поровну на два полцарства, в ответ выведите indivisible.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 4 1 1 1 3 1 1 1 2 1 1 1 4 |
v3 |
2 |
2 2 1 1 1 9 |
indivisible |
Примечания
В первом примере можно разделить царство вертикальной чертой после третьего столбца (суммы башен будут равны 9).
Во втором примере нет возможного разбиения.
Пример программы-решения
Ниже представлено решение на языке Python.
def solution(n, m, kingdom):
add_kingdom = []
for i in range(n):
add_kingdom.append([])
for j in range(m):
if i == 0:
if j == 0:
add_kingdom[i].append(kingdom[i][j])
else:
add_kingdom[i].append(add_kingdom[i][j - 1] + kingdom[i][j])
else:
if j == 0:
add_kingdom[i].append(add_kingdom[i - 1][j] + kingdom[i][j])
else:
add_kingdom[i].append(add_kingdom[i - 1][j] + add_kingdom[i][j - 1] -
add_kingdom[i - 1][j - 1] + kingdom[i][j])
for i in range(n):
if add_kingdom[i][m - 1] * 2 == add_kingdom[n - 1][m - 1]:
return 'h' + str(i + 1)
for j in range(m):
if add_kingdom[n - 1][j] * 2 == add_kingdom[n - 1][m - 1]:
return 'v' + str(j + 1)
return 'indivisible'
n, m = [int(x) for x in input().split()]
kingdom = []
for _ in range(n):
kingdom.append([int(x) for x in input().split()])
print(solution(n, m, kingdom))Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 64 Мбайт.
Представлена разновидность настольной игры «Змеи и лестницы».
Фишка начинает движение в клетке «старт» (номер клетки 0) и двигается в сторону клетки «финиш» (номер клетки \(N\)), где поле представляет собой \(N+1\) клеток, пронумерованных от 0 до \(N\) с шагом 1. Движение происходит по ходам, где ход — это бросок шестигранного кубика и перемещение фишки (в соответствии с тем, какая цифра выпадает на кубике — на столько клеток вперед продвигается фишка).
При этом на поле есть специальные пары клеток:
- лестницы — задаются форматом \(i\) \(j\), где \(i < j\); при попадании на клетку \(i\) фишка немедленно (не тратя хода) перемещается на клетку \(j\);
- змеи — задаются форматом \(i\) \(j\), где \(i > j\); при попадании на клетку \(i\) фишка немедленно (не тратя хода) перемещается на клетку \(j\).
Каждый тест в задаче представляет собой вопрос: можно ли при удачных1 бросках кубика пройти игру за указанное количество ходов или менее, и если можно — то за какое?
Формат входных данных
В первой строке через пробел заданы три целых числа \(N\) — порядковый номер клетки финиша (\(1 \leqslant N \leqslant 10^5\)), \(M\) — количество специальных пар клеток: лестниц или змей (\(0 \leqslant M \leqslant \dfrac{N}{2}\)), \(T\) — предел количества ходов, доступных в данной игре (\(1 \leqslant T \leqslant 10^6\)).
В дальнейших \(M\) строках через пробел содержатся по два числа \(i\) \(j\) — описание лестницы или змеи (\(1 \leqslant i, j \leqslant N-1\)).
Гарантируется, что если пара клеток \(i\) \(j\) — лестница или змея, то ни одной другой лестницы или змеи не начинается и не заканчивается в клетках \(i\) \(j\).
Формат выходных данных
Если есть возможность пройти из старта на финиш за менее, чем \(T\) ходов — выведите минимально возможное количество ходов, иначе выведите (\(-1\)).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
12 2 5 6 3 1 7 |
2 |
2 |
12 1 5 6 3 |
3 |
3 |
30 1 4 10 1 |
-1 |
Примечания
В примере 1 можно достигнуть финиша (клетки 12) за два хода: бросок 1 (из клетки 1 перемещаемся в клетку 7) + бросок 5 (\(7 + 5 = 12\)).
В примере 2 можно достигнуть финиша (клетки 12) за три хода, например, один из способов: бросок 1 + бросок 6 + бросок 5 (заметим, что за 2 хода — бросок 6 + бросок 6 — игру нельзя закончить, так как при первом броске 6 переместимся в клетку 3).
В примере 3 за четыре хода игру закончить нельзя.
Пример программы-решения
Ниже представлено решение на языке Python.
def can_move(step, finish):
if step <= finish:
return True
return False
def solution(finish, snakes, limit):
next_points = [[0, 1]]
counter = 0
moves = [0] + [limit + 1] * finish
while len(next_points) > counter:
p0 = next_points[counter][0]
iterate = next_points[counter][1]
turn = [0, 1, 1, 1, 1, 1, 1, 0]
for dice in range(6):
if can_move(p0 + dice + 1, finish):
if p0 + dice + 1 in snakes.keys():
turn[dice + 1] = 2
else:
turn[dice + 1] = 0
for dice in range(6):
if turn[dice + 1] == 2:
if moves[p0 + dice + 1] > iterate:
moves[p0 + dice + 1] = iterate
moves[snakes[p0 + dice + 1]] = iterate
next_points.append([snakes[p0 + dice + 1], iterate + 1])
elif turn[dice + 1] > 0:
if moves[p0 + dice + 1] > iterate:
moves[p0 + dice + 1] = iterate
next_points.append([p0 + dice + 1, iterate + 1])
counter += 1
if moves[-1] <= limit:
return moves[-1]
else:
return -1
finish, n_snakes, turn = [int(x) for x in input().split()]
card = {}
for _ in range(n_snakes):
p1, p2 = [int(x) for x in input().split()]
card[p1] = p2
print(solution(finish, card, turn))Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 64 Мбайт.
Знаменитый пират Джон Сильвер только что вручил участникам карту Острова сокровищ. Но где конкретно Джон зарыл клад — на карте не указано, и Джон предлагает это угадать!
Карта представляет собой квадратную матрицу размером \(N\times N\) клеток. По верхней и левой границе проставлена нумерация столбца и строки соответственно, начинающаяся с нуля (то есть верхняя левая клетка имеет координату 0, 0).
Клад зарыт в одной из клеток карты, и Джон дает участникам 15 попыток угадать, в какой именно!
На первом шаге сообщается \(N\) — размер карты.
Далее участники могут предположить координату, в которой зарыт клад, на что будут получены в ответ 2 символа:
- Первый символ: S — если клад строго южнее (больше) предположенной координаты (south), или N — если координата клада севернее (меньше) или равна предположенной (north).
- Второй символ: E — если клад строго восточнее (больше) предположенной координаты (east), или W — если координата клада западнее (меньше) или равна предположенной (west).
Если координата клада определена, необходимо дать окончательный ответ.
Формат входных данных
Используйте стандартный ввод для чтения размеров карты и ответов на предположения.
В первой строке содержится число \(N\) — размеры карты (\(1 \leqslant N \leqslant 10^4\)).
После отправки предположения в ответе будет содержаться строка из двух символов \(x_1x_2\), каждый из которых равен одной из заглавных букв: S, N, E, W.
После отправки окончательного ответа в ответ будет получена строка success — если координата клада угадана верно, или failed — в обратном случае.
Формат выходных данных
Используйте стандартный вывод для взаимодействия, при этом укажите параметр flush=True.
Для отправки предположения выведите через пробел второй координаты \(x\) и \(y\) — предполагаемую позицию клада.
Для отправки окончательного ответа выведите через пробел символ восклицательный знак ! и \(x\) и \(y\) — окончательные координаты клада.
Примечания
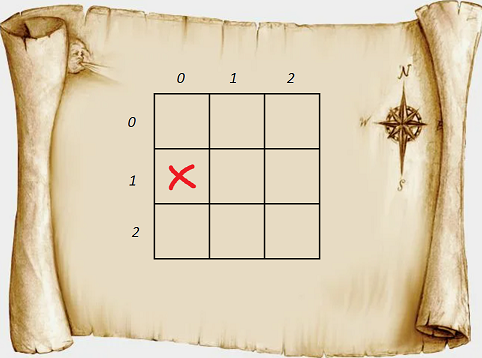
Рассмотрим пример взаимодействия для карты, изображенной на рис. 1.1:
- Ввод: 3
- Вывод: 0 0
- Ввод: SW
- Вывод: 1 0
- Ввод: NW
- Вывод: 2 0
- Ввод: NW
- Вывод: 0 1
- Ввод: SW
- Вывод: 1 1
- Ввод: NW
- Вывод: 2 1
- Ввод: NW
- Вывод: ! 1 0
- Ввод: success
Расшифровка:
- На первом шаге получаем размер карты: 3 на 3.
- Предполагаем, что клад в клетке 0, 0.
- Получаем ответ, что он на юго-западе.
- Предполагаем, что клад в клетке 1, 0.
- Получаем ответ, что он на северо-западе. и т. д.
- Даем окончательный ответ, что клад в клетке 1, 0.
- Получаем успешный ответ.
Пример программы-решения
Ниже представлено решение на языке Python.
def calculate(pa, a, fa):
res = ''
if fa == 0:
if pa[0] < a[1]:
res += 'S'
else:
res += 'N'
if pa[1] < a[2]:
res += 'E'
else:
res += 'W'
return res
map_size = int(input())
row_num = [0, map_size - 1]
col_num = [0, map_size - 1]
counter = 0
while row_num[0] != row_num[1] or col_num[0] != col_num[1]:
counter += 1
p1, p2 = (row_num[0] + row_num[1]) // 2, (col_num[0] + col_num[1]) // 2
print(p1, p2, flush=True)
direction = input()
if direction[0] == 'S':
row_num[0] = p1 + 1
else:
row_num[1] = p1
if direction[1] == 'E':
col_num[0] = p2 + 1
else:
col_num[1] = p2
print('!', row_num[0], col_num[0])Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 64 Мбайт.
Дано базовое число \(N\). На очередной итерации будет получено еще одно целое число \(m\), и можно сделать одну из трех операций:
- \(N + m\);
- \(N - m\);
- \(N \cdot m\).
После чего результат операции становится новым базовым числом (иными словами, операции между итерациями происходят последовательно, без учета приоритета умножения).
Рассчитайте, какое максимально возможное базовое число можно получить.
Формат входных данных
В первой строке через пробел заданы два целых числа \(M\) — количество чисел \(m\) (\(1 \leqslant M \leqslant 5\cdot 10^4\)), \(N\) — базовое число (\(-10 \leqslant N \leqslant 10\)).
В дальнейших \(M\) строках содержатся числа \(m\) (\(-10 \leqslant m \leqslant 10\)).
Формат выходных данных
В связи с тем, что максимально возможное базовое число будет большим, выведите только его остаток от деления на \(10^{10}\) (то есть если ответ — это число 123456789012345, выведите только 6789012345).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 1 1 2 3 |
12 |
2 |
3 7 0 -2 2 |
18 |
Примечания
В примере 1 максимально возможное базовое число получается так: \(1 + 1 = 2 + 2 = 4 \cdot 3 = 12\).
В примере 2: \(7- 0 = 7- (-2) = 9 \cdot 2 = 18\).
Пример программы-решения
Ниже представлено решение на языке Python.
def solution(n1, nums):
div = 10 ** 10
my_min = n1
my_max = n1
for x in nums:
new_min = min(my_min + x, my_min - x, my_min * x, my_max + x, my_max - x, my_max * x)
new_max = max(my_min + x, my_min - x, my_min * x, my_max + x, my_max - x, my_max * x)
my_min, my_max = new_min, new_max
return my_max % div
n, num1 = [int(x) for x in input().split()]
numbers = []
for i in range(n):
numbers.append(int(input()))
print(solution(num1, numbers))Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 64 Мбайт.
Добро пожаловать в Автобусное государство!
Оно названо так потому, что кататься на автобусах в нем можно совершенно бесплатно. При этом помимо автобусов, в государстве ходят поезда — они в два раза быстрее автобусов, но на поезд необходимо приобретать билет, стоимость которого зависит от расстояния.
Государство представляет собой неориентированный взвешенный граф, где города — это вершины графа, а существующие дороги заданы ребрами. Вес ребер — это длительность перемещения между двумя городами на автобусе (гарантируется, что вес — всегда четное число). Если существует ребро между городами \(I\) и \(J\) с весом \(w\), значит, между городами переместиться можно как бесплатно на автобусе за время \(w\), так и платно на поезде за время \(\displaystyle\frac{w}{2}\), потратив при этом \(w\) монет (при этом билет необходимо оплатить полностью).
Задача: добраться из города \(S\) в город \(F\) как можно быстрее, имея \(M\) монет.
Формат входных данных
В первой строке через пробел заданы три целых числа \(S\) — номер вершины стартового города (\(1 \leqslant S \leqslant 10^3\)), \(F\) — номер вершины конечного города (\(1 \leqslant F \leqslant 10^3\)), \(M\) — стартовое количество монет (\(0 \leqslant M \leqslant 10^3\)).
Во второй строке задано число \(N\) — количество дорог в государстве (\(1 \leqslant F \leqslant 5 \cdot 10^3\)).
В дальнейших \(N\) строках содержатся описания дорог в формате \(I\)–\(J\) \(w\) (\(1 \leqslant I, J \leqslant 10^3\), \(2 \leqslant w \leqslant 10^5\)).
Формат выходных данных
В ответ выведите единственное число — минимальную длительность перемещения из города \(S\) в город \(F\) (гарантируется, что путь существует).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1 7 18 8 1-2 2 1-3 2 2-4 20 3-5 12 3-6 22 4-7 2 5-6 12 6-7 2 |
20 |
2 |
1 7 0 8 1-2 2 1-3 2 2-4 20 3-5 12 3-6 22 4-7 2 5-6 12 6-7 2 |
24 |
Примечания
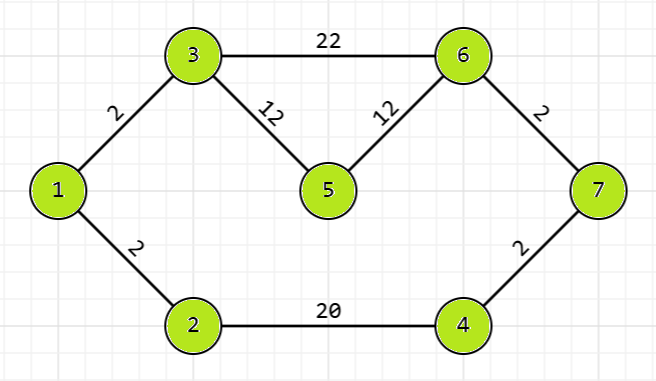
На рис. 1.2 указан граф из примеров №№ 1 и 2.
Очевидно, что при наличии 18 монет в примере № 1 наиболее выгодным маршрутом будет: \(1-3-5-6-7\) (где участки \(1-3\), \(3-5\), \(6-7\) проедем на поезде, потратив \(2+12+2=16\) монет и сократив время на 8). Тогда суммарное время будет равно: \(1+6+12+1=20\).
В примере № 2 у участников нет монет, поэтому все маршруты нужно проезжать на автобусах, следовательно, наиболее выгодным маршрутом будет: \(1-2-4-7\). Тогда суммарное время будет равно: \(2+20+2=24\).
Пример программы-решения
Ниже представлено решение на языке Python.
import heapq
def solution(s, f, m, r):
distances = {point: 10 ** 10 for point in r}
distances[s] = 0
cost_matrix = [[0] * (m + 1)]
drive = [(0, s, cost_matrix, 0)]
while drive:
current_distance, current_point, cost_matrix, points_in_road = heapq.heappop(drive)
# print(current_distance, current_point, cost_matrix, points_in_road)
if current_point == f:
return current_distance
if current_distance > distances[current_point]:
continue
for neighbor, road_len in r[current_point]:
current_cost = cost_matrix[:]
current_cost.append([])
time_win = road_len // 2
for j in range(m + 1):
if road_len > j:
current_cost[points_in_road + 1].append(current_cost[points_in_road][j])
else:
current_cost[points_in_road + 1].append(
max(current_cost[points_in_road][j], current_cost[points_in_road][j - road_len] + time_win))
new_discount = current_cost[points_in_road + 1][m] - current_cost[points_in_road][m]
distance = current_distance + road_len - new_discount
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(drive, (distance, neighbor, current_cost, points_in_road + 1))
return -1
start, finish, money = [int(x) for x in input().split()]
roads = int(input())
road_map = {}
for _ in range(roads):
road = input().split()
p1, p2 = [int(x) for x in road[0].split("-")]
cost = int(road[1])
if p1 not in road_map.keys():
road_map[p1] = [[p2, cost]]
else:
road_map[p1].append([p2, cost])
if p2 not in road_map.keys():
road_map[p2] = [[p1, cost]]
else:
road_map[p2].append([p1, cost])
print(solution(start, finish, money, road_map))- Считаем, что можно выбирать любую грань кубика для очередного хода вместо броска.↩︎