Предметный тур. Физика. 3 этап
В 1892 году российским ученым К. Э. Циолковским была предложена конструкция дирижабля объемом \(V = 500000\) м\(^3\). В 1931 году в Советском Союзе была построена модель этого дирижабля объемом \(V_\text{м} = 1000\) м\(^3\). Построить полномерный дирижабль не позволили как низкий технологический уровень, так и угроза взрыва водорода, которым наполняли большинство дирижаблей того времени. В настоящее время возрос интерес к дирижаблестроению как для военных, так и гражданских целей, а современный технологический уровень позволяет создавать большие дирижабли и заполнять их гелием.
Считая плотность воздуха равной \(\rho = 1{,}29\) кг/м\(^3\), а плотности водорода и гелия \(\rho_\text{в} = 0{,}09\) кг/м\(^3\) и \(\rho_\text{г} = 0{,}18\) кг/м\(^3\), определите:
- Груз какой массы \(m_1\) (включая корпус дирижабля) могла поднять построенная модель дирижабля при заполнении ее водородом?
- Во сколько раз возрастет масса поднимаемого груза (включая корпус дирижабля), если построить полномерный дирижабль и заполнить его более тяжелым, но безопасным гелием?
Будем считать внутренний и внешний объемы дирижаблей одинаковыми. Тогда на аппарат действуют: сила Архимеда, направленная вверх, сила тяжести со стороны корпуса и груза, направленная вниз, и сила тяжести, действующая на рабочий газ, также направленная вниз. Рассмотрим условие равновесия.
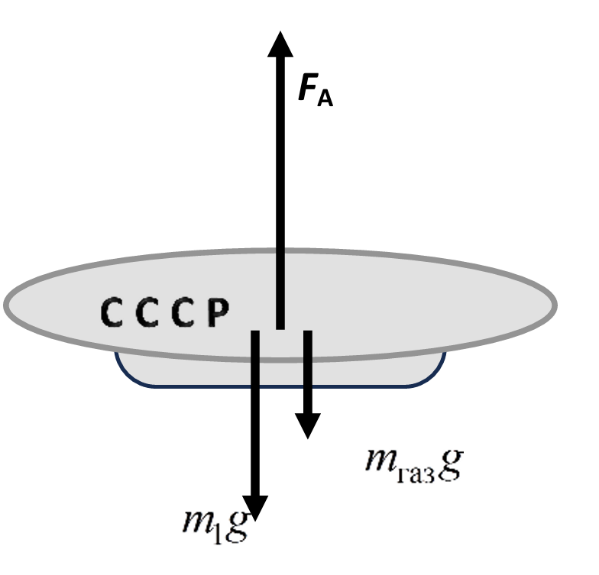
- Сила Архимеда, действующая на модель, равна \(F_A = \rho g V_\text{м}\). Дирижабль будет подниматься, если \(F_A = m_1 g + m_\text{газ} g\). Масса газа для модели равна \(m_\text{газ} = \rho_\text{в} V_\text{м}\). Таким образом: \[\rho g V_\text{м} \geqslant m_1 g + \rho_\text{в} V_\text{м} g.\] Отсюда: \[m_1 \leqslant (\rho - \rho_\text{в})V_\text{м}.\] Обратим внимание на равенство: \[m_1 = (\rho - \rho_\text{в}) V_\text{м} = 1{,}2 \cdot 10^3 \text{ кг}.\]
- Для полномерного дирижабля выполняются те же условия, что и для модели с поправкой на объем и плотность газа. Поэтому: \[\frac{M_1}{m_2} = \frac{(\rho - \rho_\text{г})V}{(\rho - \rho_\text{в}) V_\text{м}} = 462{,}5.\]
- \(m_1 = (\rho - \rho_\text{в}) V_\text{м} = 1{,}2 \cdot 10^3\) кг;
- \(\dfrac{M_1}{m_2} = \dfrac{(\rho - \rho_\text{г})V}{(\rho - \rho_\text{в}) V_\text{м}} = 462{,}5\).
- 10 баллов за правильный ответ на вопрос 1.
- 10 баллов за правильный ответ на вопрос 2.
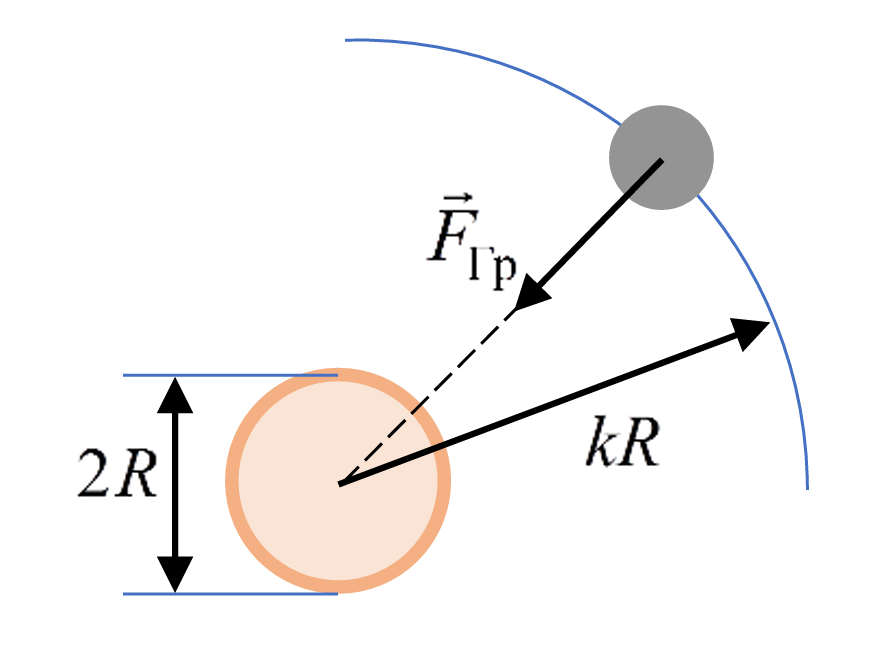
Период \(T\) обращения Деймоса, спутника Марса, 30 ч 18 мин, что составляет \(t = 109080\) с, а радиус его орбиты в \(k = 6{,}96\) больше радиуса Марса. Гравитационную постоянную примите равной \(G = 6{,}67 \cdot 10^{-11}\) Н\(\cdot\)м\(^2\cdot\)кг\(^{-2}\). По этим данным определите среднюю плотность Марса.
Со стороны Марса на спутник действует сила гравитации, равная \[F_{\text{гр}} = G \frac{Mm}{(k_R)^2},\] где \(M\) и \(m\) соответственно массы Марса и спутника, а \(k_R\) — радиус орбиты. Тогда второй закон Ньютона \(\vec{F_{\text{гр}}} = m\vec{a}\) в проекции на ось, направленную от спутника к центру Марса, примет вид: \[G \frac{Mm}{(k_R)^2} = m \frac{V^2}{k_R},\] где \(\dfrac{V^2}{k_R}\) — центростремительное ускорение, \(V\) — скорость спутника на орбите. Скорость спутника, радиус орбиты и период обращения связаны соотношением \(V = \dfrac{2\pi k_R}{T}\).
Массу Марса выразим через его объем и плотность: \(M = \rho \dfrac{4}{3}\pi R^3\). Подставляя эти выражения, получим: \[G \frac{\rho \frac{4}{3} \pi R^3 m}{(k_R)^2} = m \frac{\left(\frac{2\pi k_R}{T}\right)^2}{k_R}.\] После преобразований найдем плотность: \[\rho = \frac{3\pi k^3}{GT^2} = \frac{3 \cdot 3{,}14 \cdot 6{,}96^3}{6{,}67 \cdot 10^{-11} \cdot (30 \cdot 3600 + 18 \cdot 60)^2} \approx 4000 \text{ кг/м}^3 = 4 \text{ г/см}^3.\]
\(\rho \approx 4000\) кг/м\(^3\) \(= 4\) г/см\(^3\).
- 20 баллов за правильный ответ на вопрос.
Для демонстрации работы редуктора (устройства, понижающего частоту вращения) собрали систему, состоящую из набора \(N\) одинаковых блоков, скрепленных между собой двух шестеренок, причем количество зубьев большой шестеренки в \(n\) раз больше, чем у малой. Большая шестеренка каждого блока приведена в зацепление с малой шестеренкой предыдущего блока (рис. 1.3). Первый (левый) блок вращают дрелью с частотой \(\nu_0 = 500\) об/мин. Определите:
- Угол (в градусах), на который повернется блок с номером \(i = 3\), когда первый блок совершит один полный оборот вокруг оси, если \(n = 2\).
- Сколько времени \(T\) может вращаться первый блок с частотой \(\nu_0\), если при монтаже демонстрационной установки, состоящей из \(N = 13\) шестеренчатых блоков, у которых отношение количества зубьев \(n = 10\), ось последнего блока наглухо закрепили в стене так, что он вращаться не может, и для него допустим поворот, не превышающий одной угловой секунды (\(\alpha_N \leqslant 1^{\prime\prime}\))? В одном градусе 60 угловых минут, а в одной угловой минуте 60 угловых секунд (\(1° = 60^{\prime}\) и \(1^{\prime} = 60^{\prime\prime}\)). Ответ приведите в часах.
Угловая скорость каждого последующего блока шестеренок будет в \(n\) раз меньше скорости предыдущего блока, то есть \(\omega_i = \dfrac{\omega_{i-1}}{n}\). Угол поворота \(i\)-го блока за время \(t\) равен \[\alpha_i = \omega_i t = \frac{\omega_{i-1} t}{n} = \frac{\alpha_{i-1}}{n}.\] Получаем убывающую геометрическую прогрессию со знаменателем \(\dfrac{1}{n}\). Тогда \(i\)-й член будет равен \[\alpha_i = \alpha_1 \left(\frac{1}{n}\right)^{i-1} = \frac{\alpha_1}{n^{i-1}}.\] При заданных условиях \[\alpha_3 = \frac{360°}{2^{3-1}} = 90°.\]
Задачу также можно решить простой подстановкой, если есть понимание, что угловая скорость каждого последующего блока шестеренок будет в \(n\) раз меньше скорости предыдущего блока.
Задача аналогична первой, но задан угол последнего, 13-го блока, и нужно найти угол поворота первого, а через него — время вращения.
Из решения предыдущей задачи находим \(\alpha_1 = \alpha_N\cdot n^{N-1}\). Время найдем из условия \(T = \dfrac{\alpha_1}{\omega_1} = \dfrac{\alpha_N \cdot n^{N-1}}{360° \cdot \nu_0}\). Тогда \[T = \frac{1^{\prime\prime} \cdot 10^{13-1}}{360° \cdot 60 \cdot 60 \cdot 500} \approx 1543 \text{ мин} \approx 25{,}7 \text{ ч}.\]
- \(\alpha = \dfrac{360°}{n^{N-1}} \approx 90°\).
- \(T = \dfrac{\alpha_N \cdot n^{N-1}}{360° \cdot \nu_0} \approx 1543\) мин \(\approx 25{,}7\) ч.
- 10 баллов за правильный ответ на вопрос 1.
- 10 баллов за правильный ответ на вопрос 2.
На гидроаккумулирующих электростанциях в период низкого потребления электроэнергии воду с помощью электронасосов перекачивают из более низких резервуаров в более высокие, чтобы затем использовать накопленную потенциальную энергию воды. Определите увеличение потенциальной энергии воды объемом \(V = 10^7\) м\(^3\), если из резервуара с площадью дна \(S_1 = 1\) км\(^2\) ее перекачали в резервуар с площадью дна \(S_2 = 0{,}25\) км\(^2\). Резервуары цилиндрические, а их основания находятся на одной высоте. Плотность воды \(\rho = 1000\) кг/м\(^3\). Ускорение свободного падения примите равным \(g = 10\) м/с\(^2\).
Потенциальную энергию воды в резервуаре найдем с учетом того, что центр масс воды в цилиндрическом резервуаре находится на половине высоты уровня воды в нем: \(h_c = \dfrac{H}{2}\). Отсчет потенциальной энергии будем вести от дна сосуда. Учтем при этом, что масса воды \(m = \rho V\), а высоту уровня воды можно найти через объем и площадь основания резервуара \(H = \dfrac{V}{S}\). Отсюда: \[E_\text{п} = mgh_c = \rho V g \frac{H}{2} = \rho V g \frac{V}{2S} = \frac{\rho g V^2}{2S}.\] Отсюда разность потенциальных энергий для двух резервуаров: \[\begin{gather} \Delta E = E_{\text{п}2} - E_{\text{п}1} = \frac{\rho g V^2}{2S_2} - \frac{\rho g V^2}{2S_1} = \frac{\rho g V^2 (S_1 - S_2)}{2S_1 S_2} =\\= \frac{10^3 \cdot 10 \cdot (10^7)^2 \cdot (1 - 0,25) \cdot 10^6}{2 \cdot 1 \cdot 10^6 \cdot 0,25 \cdot 10^6} = 1,5 \cdot 10^{12} \text{ Дж} = 1500 \text{ ГДж}. \end{gather}\]
\(\Delta E = E_{\text{п}2} - E_{\text{п}1} = \dfrac{\rho g V^2 (S_1 - S_2)}{2S_1 S_2} = 1{,}5 \cdot 10^{12}\) Дж \(= 1500\) ГДж.
- 20 баллов за правильный ответ на вопрос.
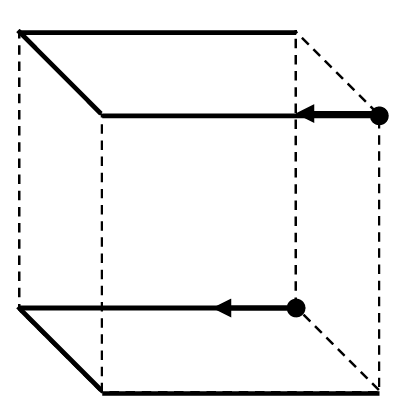
Два робота обследуют две одинаковые квадратные аудитории, расположенные на соседних этажах здания. Длина стены аудитории и расстояние между этажами одинаковые, и можно считать, что роботы движутся по граням куба. Роботы стартуют из углов одной стены, соединенных диагональю. Затем они начинают одновременно, с одинаковой скоростью, двигаться по ребрам аудитории так, что их траектория представляет собой трехзвенную ломаную (рис. 1.4) и завершается в углу, соседнем со стартовым, после чего роботы останавливаются. Минимальное расстояние между ними в процессе движения оказалось равным \(l = 20\) м. Определите:
- Максимальное расстояние между роботами в процессе движения \(l_{1\text{макс}}\).
- Максимальное расстояние между роботами \(l_{2\text{макс}}\) в интервале времени от одновременного старта до момента остановки первого (более быстрого) из них, если их скорости отличаются в три раза.
Мысленно соединим роботов прямой и рассмотрим проекцию их скоростей на эту прямую. Три участка пути вдоль каждого из ребер куба пронумеруем 1, 2 и 3 для каждого робота.
При движении с одинаковой скоростью вдоль первого участка проекции скоростей равны нулю, и расстояние между ними не меняется. При одновременном переходе на второй участок проекции скоростей направлены навстречу друг другу до середины участка, а затем — друг от друга, и расстояние сначала уменьшается, а затем увеличивается. Движение по третьему участку аналогично движению по первому. Поэтому минимальное расстояние между ними будет в момент нахождения в середине второго участка и равно ребру куба (расстоянию между этажами). Максимальное расстояние будет при движении по первому и третьему участкам и равно диагонали грани куба (стены): \(l_{1\text{макс}} = l\sqrt{2} \approx 28\) м.
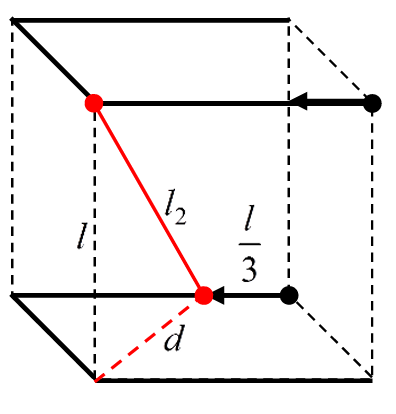 Рис. 1.5.
Рис. 1.5.При движении с разными скоростями по участку 1 углы между вектором скорости каждого робота и линией, их соединяющей, равны, поэтому более быстрый будет обгонять второго, и расстояние будет увеличиваться. Когда быстрый робот перейдет на второй участок, медленный пройдет \(\dfrac{1}{3}\) от первого участка. Проекции скоростей на линию, соединяющую роботов, будут иметь противоположные знаки, и расстояние между ними будет уменьшаться вплоть до момента перехода быстрого робота на третий участок и достижения медленным \(\dfrac{2}{3}\) своего первого участка. При движении быстрого робота по третьему участку расстояние между ними будет сначала уменьшаться, а затем увеличиваться. В момент остановки быстрого робота расстояние между ними будет равно длине диагонали стены \(l_{1\text{макс}} = l\sqrt{2} \approx 28\) м.
Таким образом, за время движения быстрого робота от старта до остановки расстояние между ними дважды достигало максимума (локального). Нужно выбрать наибольшее. Первый раз максимум был, когда быстрый робот прошел первый участок и оказался в соседнем углу, а медленный — \(\dfrac{1}{3}\) первого участка. Для определенности на рис. 1.5 верхний робот рассматривается как быстрый.
Из рис. 1.5 видно, что \(l_2 = \sqrt{l^2 + d^2} = \sqrt{l^2 + \left(\left(\dfrac{2}{3}l\right)^2 + l^2\right)}\).
Тогда \(l_2 = \dfrac{l\sqrt{22}}{3} = \dfrac{20\sqrt{22}}{3} \approx 31{,}3\) м. Так как это расстояние больше, чем \(l_{1\text{макс}} \approx 28\) м, то это и есть ответ \(l_2 = \dfrac{l\sqrt{22}}{3} \approx 31{,}3\) м.
Примечание
Приведем также другое решение. Расстояние между роботами в координатном пространстве \(XYZ\) определяется выражением \[l_2 = \sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2},\] но в процессе движения всегда выполняется условие \(\Delta z = l = \text{const}\). Поэтому на уменьшение или увеличение расстояния между ними влияет только движение в плоскости пола и изменение расстояния в этой плоскости (пунктир \(d\) на рис. 1.5).
Таким образом, если бы роботы двигались в одной горизонтальной плоскости, стартуя из соседних углов, или, что почти то же самое, за ними наблюдали бы сверху, строго вдоль оси \(Z\), то:
- в случае одинаковых скоростей максимальное расстояние между ними будет равно ребру куба \(l\);
- в случае разных скоростей: \[d = \sqrt{\left(\frac{2l}{3}\right)^2 + l^2}.\]
Учет расстояния между этажами и применение теоремы Пифагора даст для первого и второго вопросов ответы: \[\begin{aligned} l_{1\text{макс}} &= \sqrt{l^2 + l^2} = l\sqrt{2} \approx 28 \text{ м}, \\ l_{2\text{макс}} &= \sqrt{l^2 + d^2} = \sqrt{l^2 + \left(\left(\frac{2}{3}l\right)^2 + l^2\right)} = \frac{l\sqrt{22}}{3} \approx 31,3 \text{ м}. \end{aligned}\]
- \(l_{1\text{макс}} = \sqrt{l^2 + l^2} = l\sqrt{2} \approx 28\) м.
- \(l_{2\text{макс}} = \dfrac{l \sqrt{22}}{3} \approx 31{,}3\) м.
- 10 баллов за правильный ответ на вопрос 1.
- 10 баллов за правильный ответ на вопрос 2.
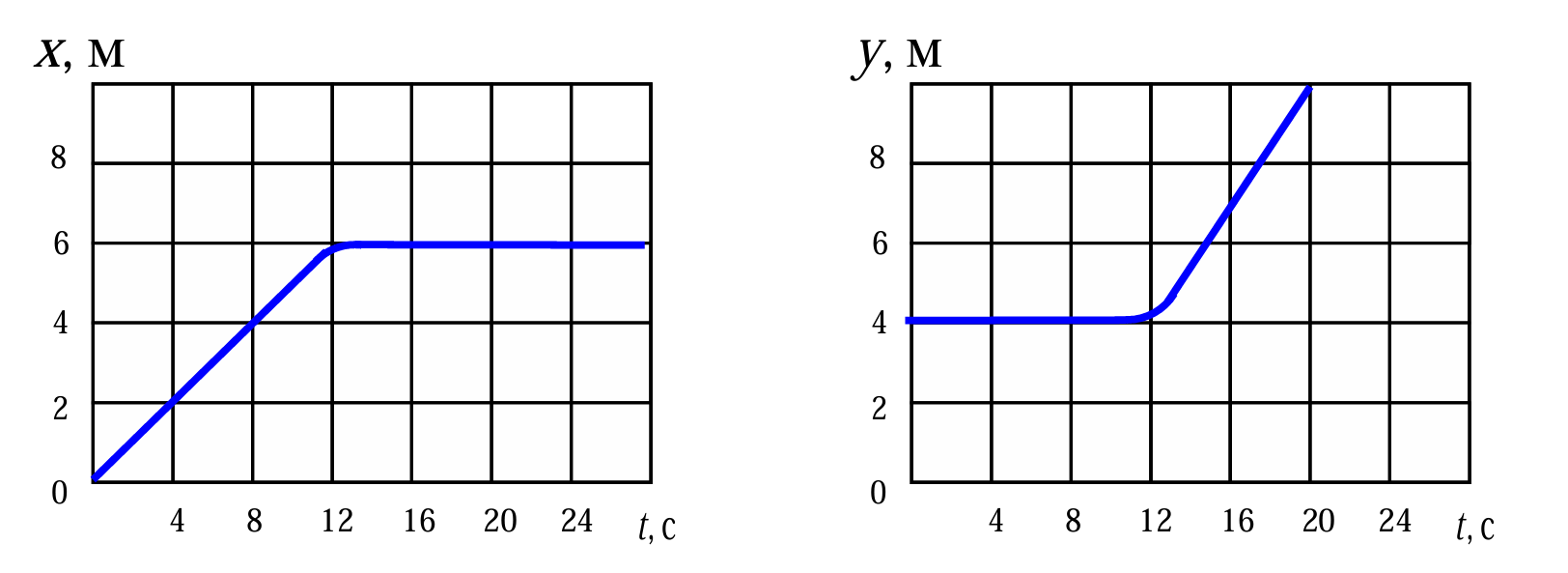
Гусеничная модель движется по горизонтальной поверхности. Датчики фиксируют декартовы координаты \(x\) и \(y\) модели в горизонтальной плоскости в зависимости от времени. По графикам \(x(t)\) и \(y(t)\) определите:
- максимальную скорость модели;
- модуль приращения вектора скорости модели за время от \(t = 4\) с до \(t = 20\) с.
- В соответствии с графиком первые 12 с модель движется в направлении оси \(x\) со скоростью \(|\vec{v}_1| = 0{,}5\) м/с, затем поворачивает и движется вдоль оси \(y\) со скоростью \(0{,}75\) м/с. Следовательно, максимальная скорость равна \(|\vec{v}_2| = 0{,}75\) м/с.
Приращение \(\Delta\vec{v} = \vec{v}_2 - \vec{v}_1\) вектора скорости найдем графически (рис. 2.2). Модуль этого вектора равен \(\Delta v = \sqrt{v_1^2 + v_2^2} \approx 0{,}90\) м/с.
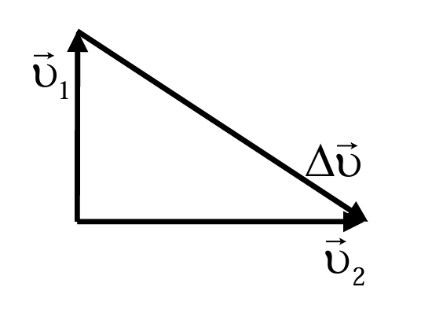 Рис. 2.2.
Рис. 2.2.
- \(0{,}75\) м/с.
- \(0{,}90\) м/с.
- 10 баллов за правильный ответ на вопрос 1.
- 10 баллов за правильный ответ на вопрос 2.
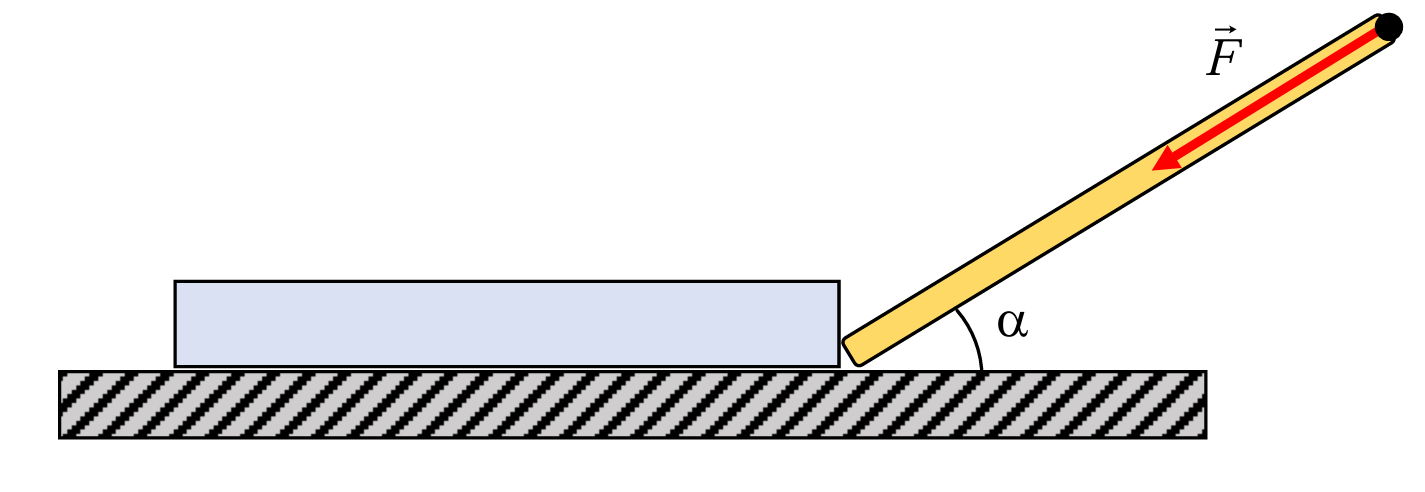
Кремниевую пластину массой \(m = 330\) г перемещают поступательно по горизонтальной поверхности стола с ускорением \(a = 1\) м/с\(^2\), толкая ее легкой стеклянной палочкой. Палочка составляет с горизонтом угол \(\alpha = 30^\circ\), а приложенная к палочке сила \(F\) направлена вдоль ее оси (рис. 2.3). Коэффициент трения между пластиной и поверхностью \(\mu = 0{,}4\), ускорение свободного падения \(g = 10\) м/с\(^2\). Определите величину силы \(F\), для случаев:
- палочка гладкая;
- коэффициент трения между палочкой и столом равен \(\mu/2\).
- Со стороны палочки на пластину действует горизонтально направленная сила \(F\cos\alpha\). Поэтому \(ma = F\cos\alpha - \mu mg\). Следовательно, \[F = \frac{m(a + \mu g)}{\cos\alpha} \approx 1{,}9 \text{ Н}.\]
- Так как палочка легкая, то сумма действующих на нее сил равна нулю. Поэтому \[\begin{aligned} N - F\sin\alpha &= 0, \\ F\cos\alpha - \frac{\mu}{2}N - f &= 0, \end{aligned}\] где \(N\) — сила реакции опоры, \(f\) — сила, действующая на палочку со стороны пластины. Учитывая третий закон Ньютона и записывая второй закон Ньютона для пластины \(ma = f - \mu mg\), после преобразований получим \[F = \frac{m(a + \mu g)}{\cos\alpha - \frac{\mu}{2}\sin\alpha} \approx 2{,}16 \text{ Н}.\]
- \(F = \dfrac{m(a + \mu g)}{\cos\alpha} \approx 1{,}9\) Н.
- \(F = \dfrac{m(a + \mu g)}{\cos\alpha - \frac{\mu}{2}\sin\alpha} \approx 2{,}16\) Н.
- 10 баллов за правильный ответ на вопрос 1.
- 10 баллов за правильный ответ на вопрос 2.
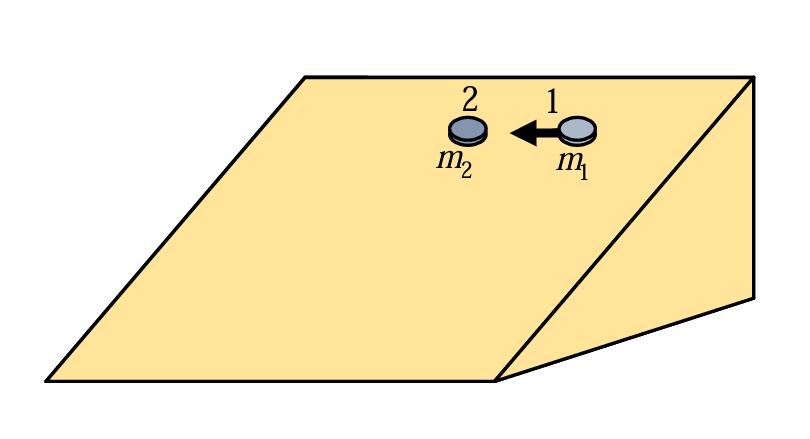
На гладкой наклонной плоскости сталкиваются две шайбы. Непосредственно перед ударом скорость первой шайбы направлена горизонтально и равна \(v_0 = 3\) м/с, а скорость второй шайбы равна нулю. Сразу после удара скорость первой шайбы изменив направление на противоположное, стала равной \(v_1 = 1\) м/с, а скорость второй шайбы \(v_2 = 2\) м/с. Удар центральный. Определите:
- отношение \(\dfrac{m_2}{m_1}\) массы второй шайбы к массе первой;
- скорость \(u_2\) второй шайбы в момент времени после удара, когда скорость первой шайбы стала равной \(u_1 = 4\) м/с.
- При центральном ударе скорости шайб \(v_1\) и \(v_2\) сразу после удара направлены горизонтально и удовлетворяют закону сохранения импульса: \[m_1 v_0 = m_2 v_2 - m_1 v_1.\] Из этого уравнения получим \[\frac{m_2}{m_1} = \frac{v_0 + v_1}{v_2} = 2.\] Заметим, что при этом сохраняется и механическая энергия: \[\frac{m_1 v_0^2}{2} = \frac{2m_1 v_2^2}{2} + \frac{m_1 v_1^2}{2}.\] Это означает, что рассматриваемый удар является упругим.
- Так как трения нет, то горизонтальная составляющая скорости первой шайбы в произвольный момент времени \(t\) после удара равна \(v_1\), а перпендикулярная ей составляющая, направленная вниз вдоль наклонной плоскости, равна \(u_y = (g\sin\alpha)t\), где \(\alpha\) — угол наклона плоскости к горизонту, \(g\) — ускорение свободного падения. Следовательно, \[u_1^2 = v_1^2 + (gt\sin\alpha)^2.\] Аналогично запишем для скорости второй шайбы в тот же момент времени: \[u_2^2 = v_2^2 + (gt\sin\alpha)^2.\] Из этих уравнений найдем \(u_2 = \sqrt{u_1^2 + v_2^2 - v_1^2} = \sqrt{19} \approx 4{,}4\) м/с.
- \(\dfrac{m_2}{m_1} = \dfrac{v_0 + v_1}{v_2} = 2\).
- \(u_2 = \sqrt{19} \approx 4{,}4\) м/с.
- 10 баллов за правильный ответ на вопрос 1.
- 10 баллов за правильный ответ на вопрос 2.
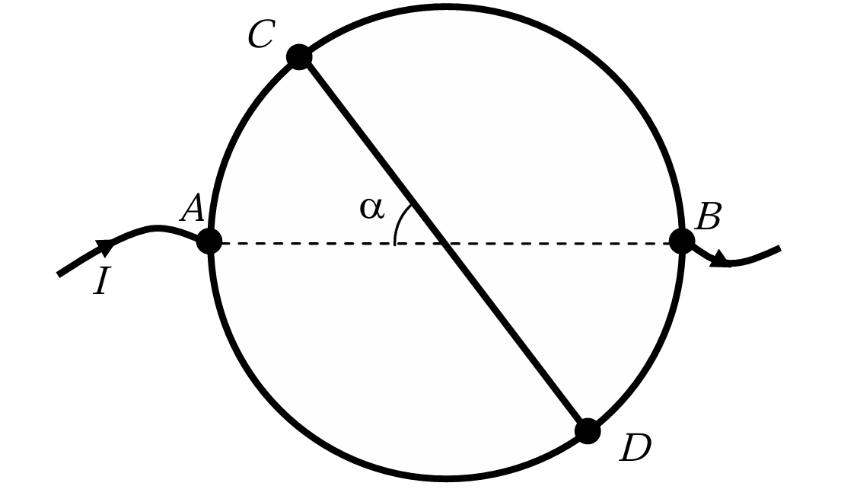
Из куска проволоки сопротивлением \(R_0 = 4{,}8\) Ом изготовлено кольцо. Перемычка сопротивлением \(R_1\) подключена к диаметрально противоположным точкам \(C\) и \(D\) кольца. Определите сопротивление \(R\) между точками кольца \(A\) и \(B\), расположенными на одном диаметре, если диаметры \(AB\) и \(CD\) составляют угол \(\alpha = \pi/4\). Рассмотрите случаи:
- \(R_1 = 0\).
- \(R_1 = \dfrac{R_0}{2}\).
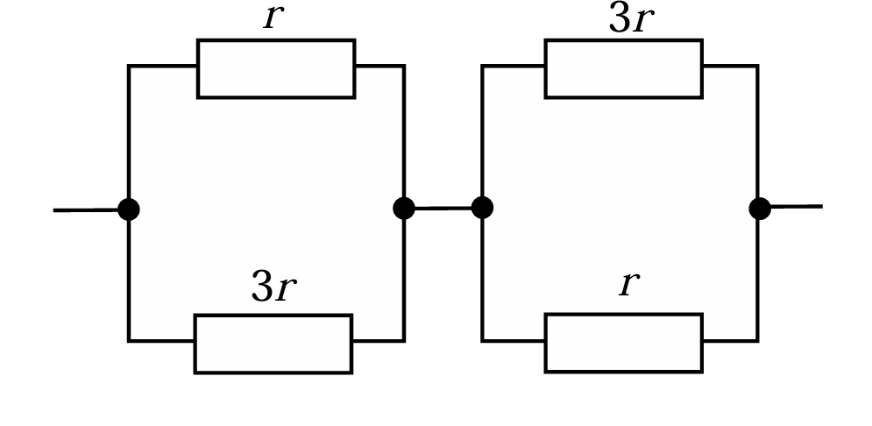
Сопротивление дуги \(AC\) равно \(r = \dfrac{R_0}{8} = 0{,}6\) Ом, сопротивление дуги \(AD\) равно \(3r\). Эквивалентная схема состоит из двух последовательно соединенных одинаковых резисторов сопротивлением (рис. 2.6) \[r_{12} = \frac{(3r)^2}{r + 3r} = \frac{3}{4}r\] каждый. Поэтому \[R = \frac{3}{2}r = \frac{3}{16}R_0 = 0{,}9 \text{ Ом}.\]
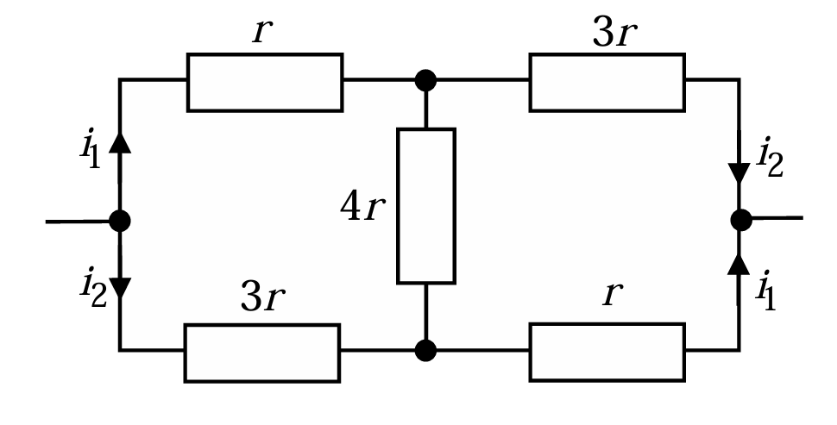
Рис. 2.6.В силу симметрии ток в дугах \(AC\) и \(DB\) одинаковый, обозначим его \(i_1\). Ток в дугах \(AD\) и \(CB\) обозначим \(i_2\). Ток, втекающий в кольцо \(I = i_1 + i_2\), приложенное к кольцу напряжение \(U = IR\), ток в перемычке \(i_1 - i_2\). Составим систему уравнений: \[\begin{cases} i_1 r + 3i_2 r = U, \\ i_1 r + (i_1 - i_2) R_1 = i_2 3r, \\ i_1 + i_2 = I = \dfrac{U}{R}. \end{cases}\] Из нее найдем \[R = \frac{r(3r + 2R_1)}{2r + R_1} = 1{,}1 \text{ Ом}.\]
Рис. 2.7.
- \(R = \dfrac{3}{16} R_0 = 0{,}9\) Ом.
- \(R = \dfrac{r(3r + 2R_1)}{2r + R_1} = 1{,}1\) Ом, где \(r = \dfrac{R_0}{8} = 0{,}6\) Ом.
- 10 баллов за правильный ответ на вопрос 1.
- 5 баллов за правильное обозначение токов п. 2 и выявленную симметрию токов.
- 5 баллов за полную систему уравнений в п. 2 и правильное ее решение.
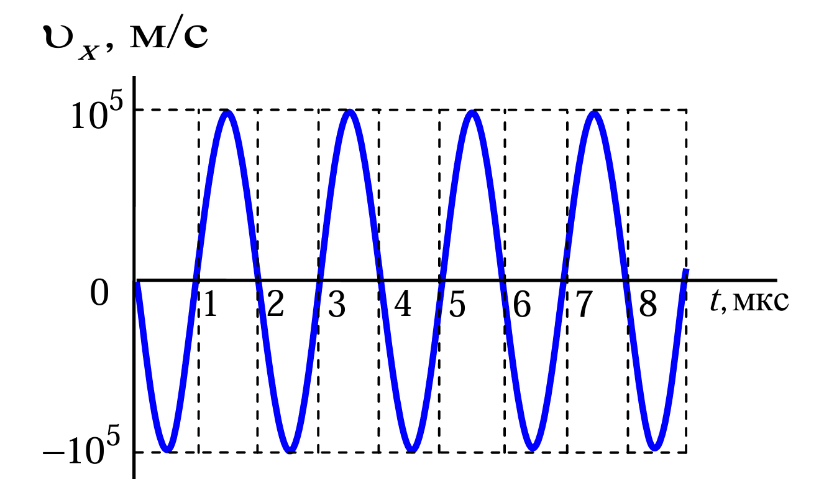
Заряженная частица движется в плоскости \(XY\) в однородном магнитном поле. На рис. 2.8 приведен график зависимости проекции скорости частицы на ось \(X\) от времени \(t\). Определите:
- радиус траектории частицы;
- модуль вектора индукции магнитного поля.
Отношение заряда частицы к ее массе \(\dfrac{q}{m} = 9{,}6 \cdot 10^7\) Кл/кг.
Магнитная сила работу не совершает, поэтому кинетическая энергия частицы и модуль ее скорости остаются постоянными. По условию траектория движения частицы лежит в одной плоскости, а магнитное поле однородное. Известно, что в этом случае частица движется по окружности. По графику находим период обращения частицы \(T = 2\) мкс, модуль ее скорости \(v = 10^5\) м/с и радиус окружности \[R = \frac{vT}{2\pi} \approx 32 \text{ мм}.\] Подставляя в выражение для \(R\) формулу \[\frac{mv^2}{R} = qvB,\] выражающую второй закон Ньютона, получим \[B = \frac{2\pi m}{qT} \approx 0{,}033 \text{ Тл}.\]
- \(R = \dfrac{vT}{2\pi} \approx 32\) мм.
- \(B = \dfrac{2\pi m}{qT} \approx 0{,}033\) Тл.
- 10 баллов за правильный ответ на вопрос 1.
- 10 баллов за правильный ответ на вопрос 2.