Инженерный тур. 1 этап
Задачи, представленные в первом отборочном этапе НТО инженерного тура по профилю Цифровые сенсорные системы, разделены на два блока: «Электрические цепи» и «Программирование», по семь задач в блоке. В рамках первого блока предлагаются задания по темам: электротехника, преобразования схем, закон Ома, конденсатор, переходный процесс, резонанс, реактивная нагрузка, электроника, диод, операционный усилитель, светодиод. В рамках блока «Программирование» задачи основываются на следующих темах: основы программирования, логические операции, ассемблер, язык Си, алгоритмы сортировки. Задачи имеют разную стоимость баллов в зависимости от сложности. В каждом блоке есть две задачи повышенной сложности.
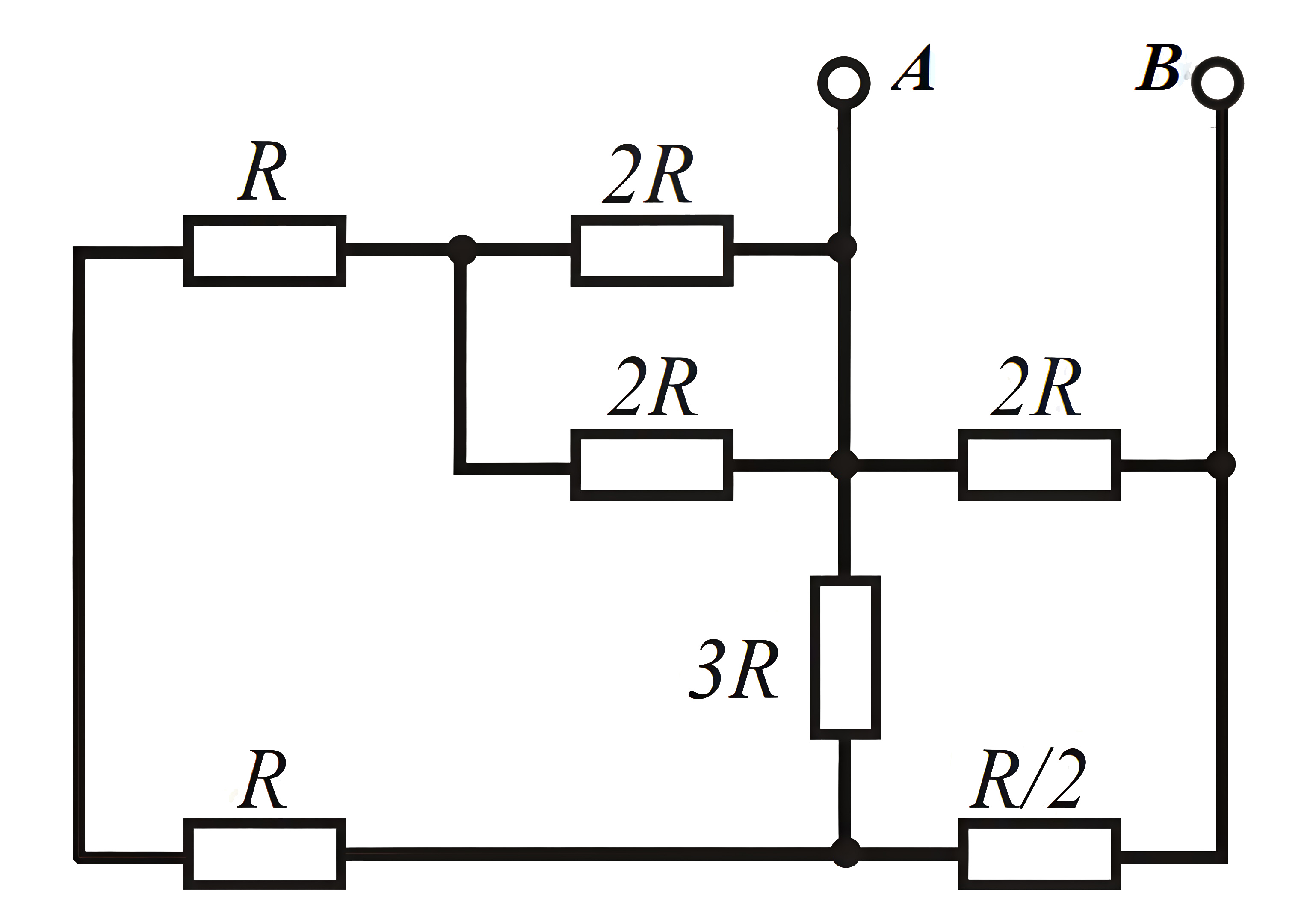
Найдите эквивалентное сопротивление схемы, показанной на рис. 1.1, измеренное между точками A и B. Примите сопротивление \(R = 100\) Ом. Если необходимо, ответ округлите до целых по правилам арифметического округления. Ответ дайте в омах.
Преобразуем схему в более удобную для решения (рис. 1.2).
Далее вычисляем общее сопротивление \(R_o\): \[R_0=\frac{2R(1{,}5R+0{,}5R)}{2R+1{,}5R+0{,}5R}=R=100 \text{~Ом}.\]
100.
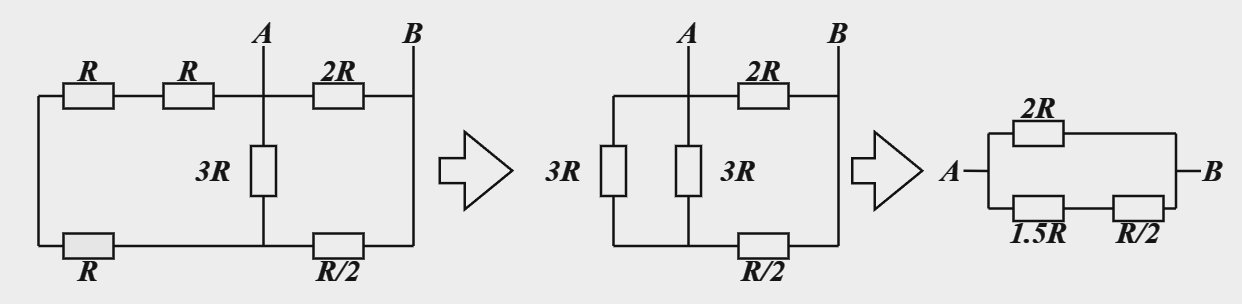
На рис. 1.3 представлена схема. Вычислите, чему равно сопротивление резистора \(R_2\) (в омах), если показание вольтметра, включенного параллельно ему, составляет 4,5 В. Все прочие номиналы приведены на рис. 1.3. В случае необходимости ответ округлите до десятых по правилам арифметического округления.
Соединение резисторов последовательное, значит, сила тока \(I\) на всех резисторах одинакова. \[U_{R_1}= U_\text{ИСТ} - U_\text{ВЫХ}= 7{,}5 \text{~В};\] \[R_2= \frac{U_\text{ВЫХ}}{\frac{U_{R_1}}{R_1}} = 600 \text{~Ом}.\]
600.
Пусть к телевизионному контуру последовательно подключены катушка индуктивности и конденсатор, как показано на рис. 1.4.
В любом из телевизионных каналов амплитуда переменного напряжения \(E\) составляет 100 мкВ. Индуктивность катушки \(L = 1{,}26\) мкГн, а ее сопротивление \(R\) (активное, присущее любому проводнику при нормальных условиях) составляет 20 Ом. Емкость конденсатора \(C = 0{,}567\) пФ.
Определите, чему равна амплитуда переменного напряжения на конденсаторе (в милливольтах) при резонансной частоте \(f_0 = 188\) МГц.
Подсказка: при последовательном включении активных и реактивных элементов при достижении особенной частоты, именуемой резонансной, наблюдается резонанс напряжений, при котором реактивные сопротивления (индуктивности и емкости) компенсируют друг друга, оставляя ТОЛЬКО активное сопротивление \(R\). Этот факт важно учесть при расчете тока в последовательном контуре.
Ответ округлите до десятых по правилам арифметического округления.
\[X_c= \frac{1}{2\pi f_0 C};\] \[I_\text{общ}= \frac{E}{R};\] \[U_c= \frac{E}{R} X_c= \frac{E}{2\pi f_0 CR} = 7{,}5 \text{~мВ}.\]
7,5.
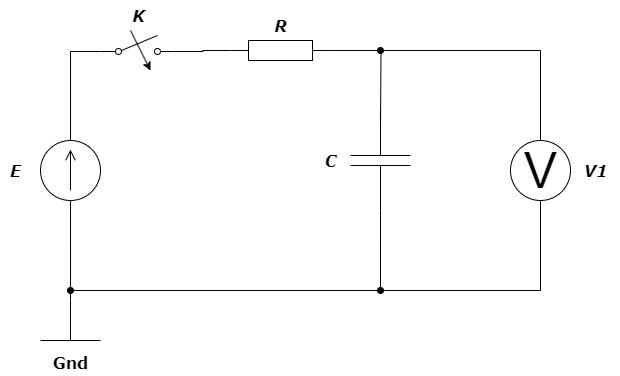
Ниже на рис. 1.5 приведена схема, содержащая \(RC\)-цепь, источник постоянного напряжения \(E\) и ключ \(K\). Изначально \(K\) разомкнут, а конденсатор \(C\) полностью разряжен. При замыкании \(K\) происходит заряд конденсатора \(C\). Определите, через какое время (в миллисекундах) после замыкания ключа \(K\) идеальный вольтметр \(V_1\) покажет значение 4,85 В, если известно, что источник \(E = 5\) В, сопротивление \(R = 10\) кОм, емкость \(C = 1\) мкФ. В случае необходимости ответ округлите до целых по правилам арифметического округления.
При заряде конденсатора через резистор напряжение на конденсаторе возрастает экспоненциально. Обычно используют постоянную времени \(RC\) цепи, равную \(\tau= R \cdot C\), определяющую время, за которое напряжение на конденсаторе станет \(\approx 63\),2% от приложенного к \(RC\) цепи. \[U(t)= E \cdot\left(1-e^{\frac{-t}{RC} }\right).\] В момент времени \(t\): \(U(t) = 4{,}85\) В. Тогда, подставив в уравнение значение напряжения на конденсаторе в момент \(t\), возьмем натуральный логарифм от обоих частей уравнения, получаем: \[\ln\left(e^{\frac{-t}{RC} } \right)= \ln\left(1-\frac{U(t)}{E}\right);\] \[-\frac{t}{10^{-2}} = \ln\left(1-\frac{4{,}85}{5}\right);\] \[t=-(10^{-2} ) \cdot (-3{,}5066)=35 \cdot 10^{-3} \text{~с}= 35 \text{~мс}.\]
35.
Одним из самых простых способов выпрямления переменного напряжения является применение диода.
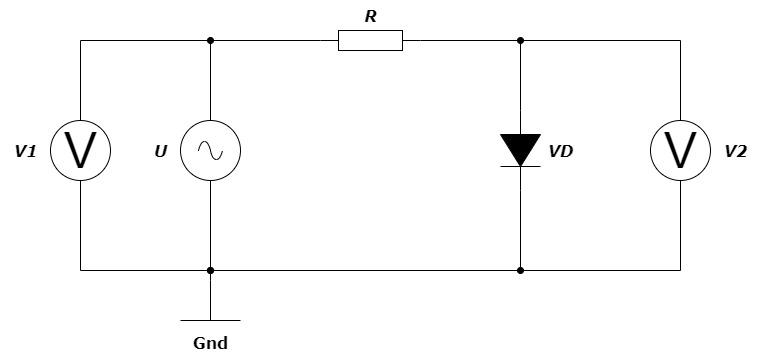
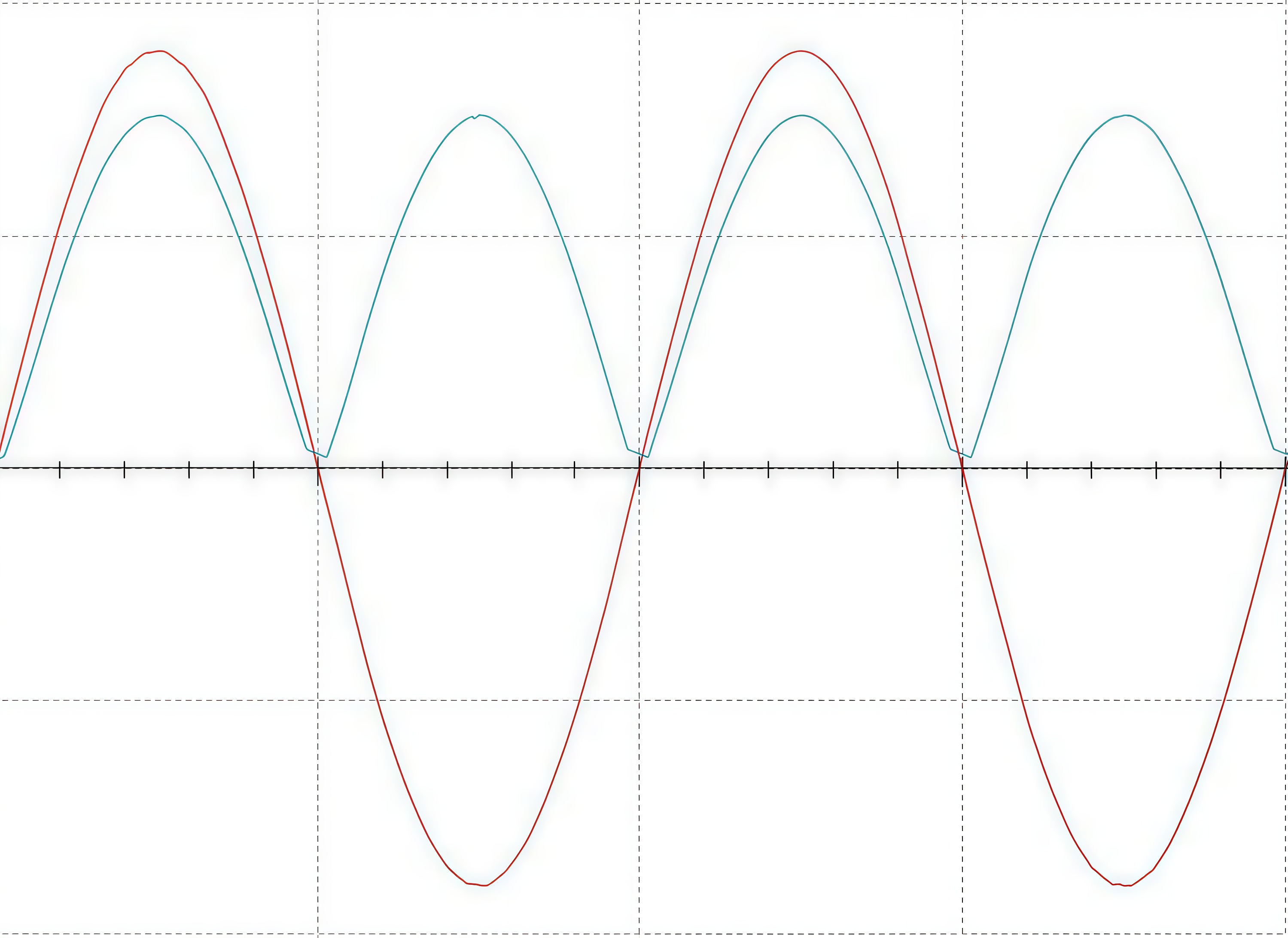
Рассмотрим схему на рис. 1.6. Изменение сигнала, порожденного источником синусоидального сигнала \(U\), фиксируется в виде осциллограммы, снимаемой с помощью щупа осциллографа \(V_1\) (на осциллограмме красная кривая). Пройденный через резистор сигнал снимается с диода с помощью щупа \(V_2\) (на осциллограмме синяя кривая).
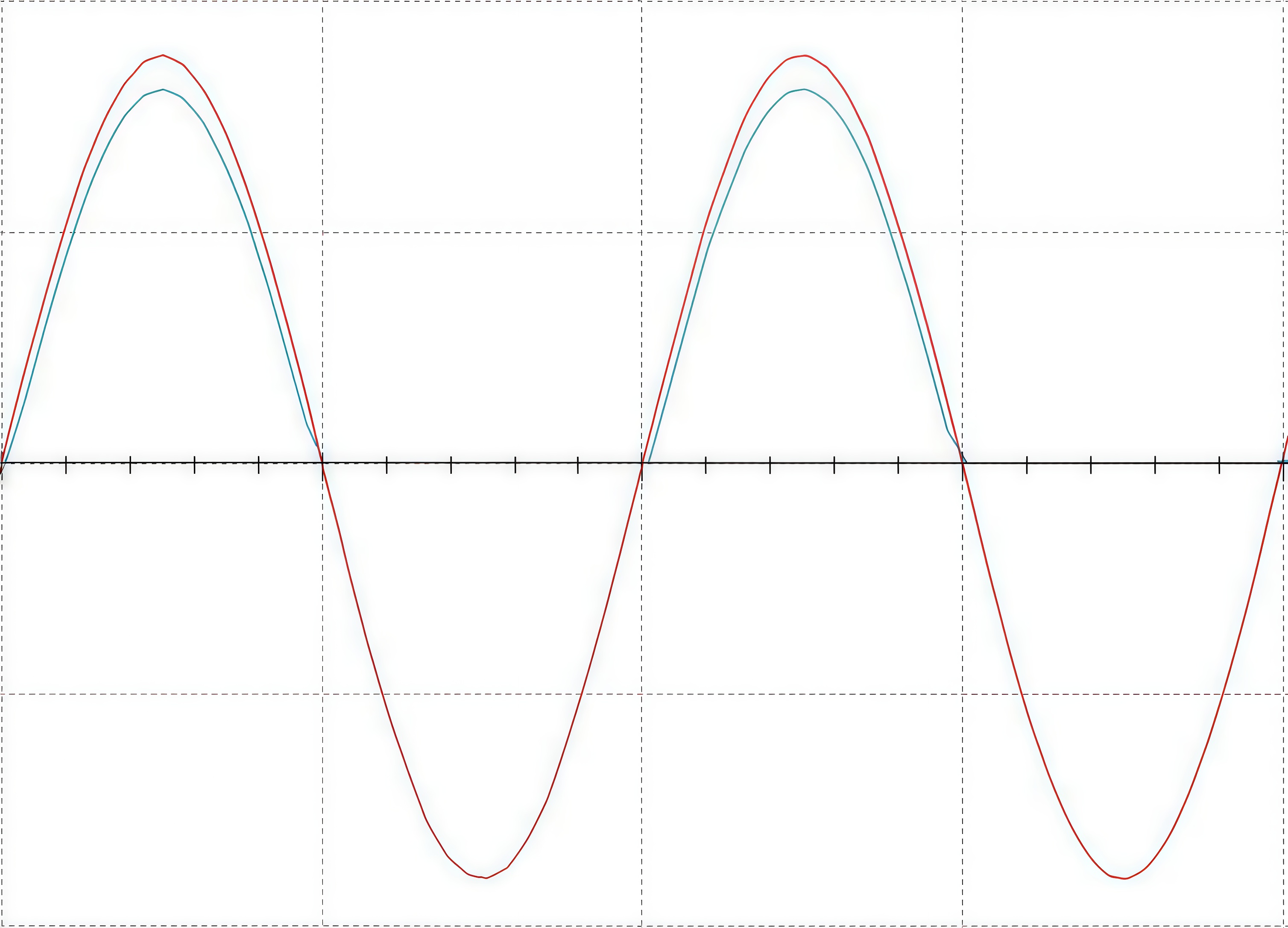
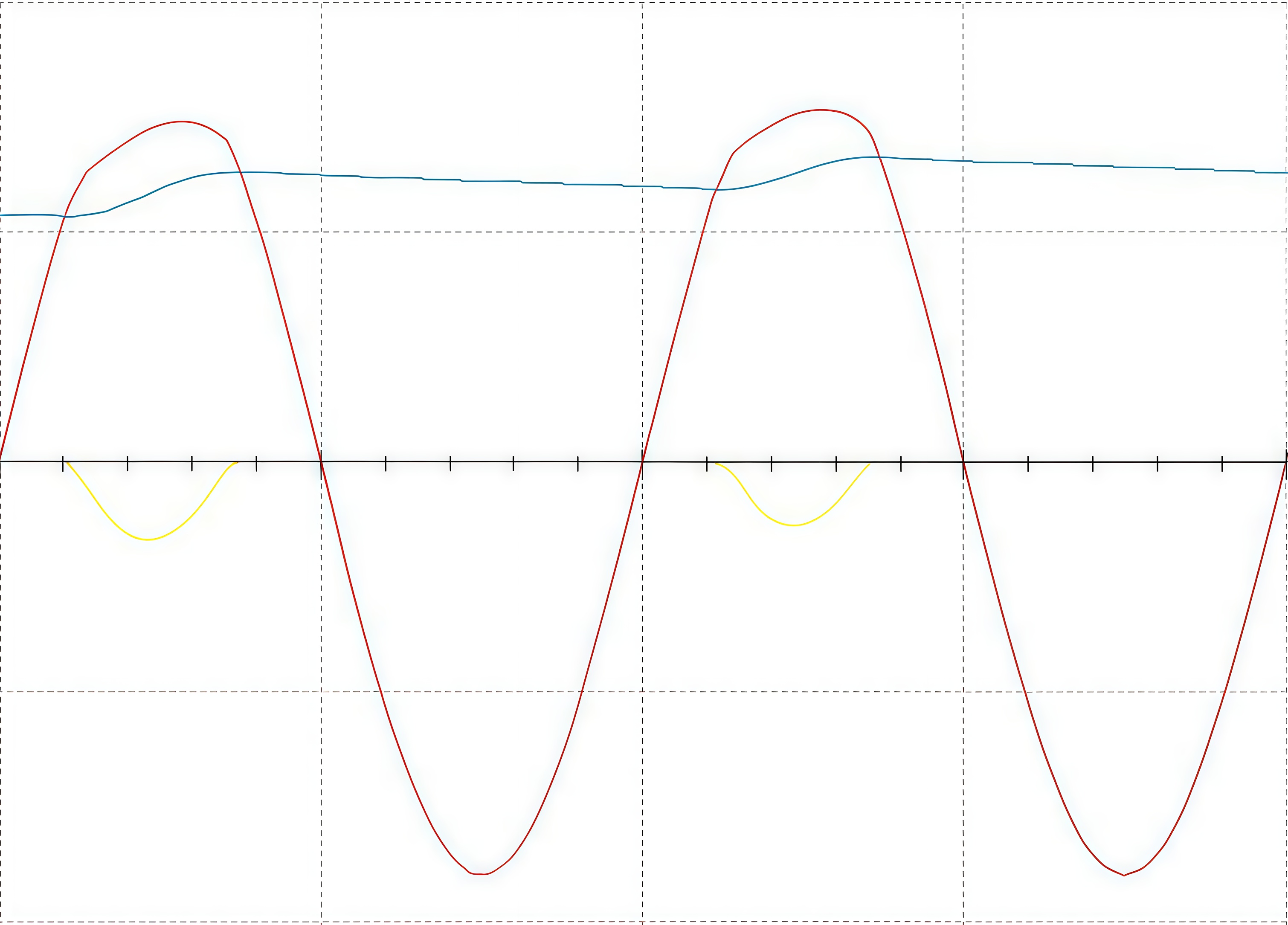
Определите, какая осциллограмма из приведенных соответствует данной схеме.
Осциллограммы.
Так как нет конденсатора, Б — не подходит.
То есть не мостовая схема, В — не подходит.
А.
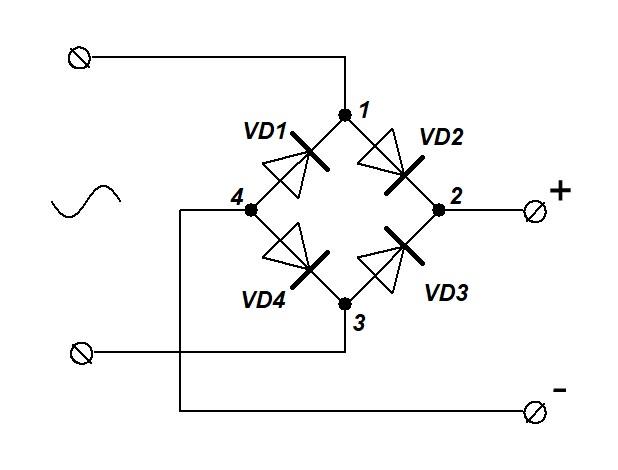
На схеме на рис. 1.7 представлен диодный мост. На вход диодного моста (между узлами 1 и 3) подается синусоидальное напряжение. На выходе (между узлами 2 и 4) получают монополюсный выпрямленный сигнал.
Укажите, какие диоды работают в прямом включении (то есть через них протекает прямой ток), когда входное мгновенное напряжение отрицательное — в этот момент потенциал в точке 3 больше, чем потенциал в точке 1 (такое возможно, например, на втором полупериоде синусоиды), при этом разность потенциалов достаточно высока для открытия нужных диодов в прямом смещении.
VD1иVD3.VD1иVD4.VD1,VD2иVD4.
Изначально в точках 2 и 4 потенциал равен нулю.
Так как рассматривается только отрицательный полупериод синусоиды, подаваемой от внешнего источника синусоидального напряжения, то в точке 1 потенциал ниже нуля, следовательно, VD1 открыт (прямое смещение), а VD2 закрыт (так как смещение обратное). В точке 3 потенциал выше нуля, следовательно, VD3 открыт (прямое смещение), а VD4 закрыт (обратное смещение).
1.
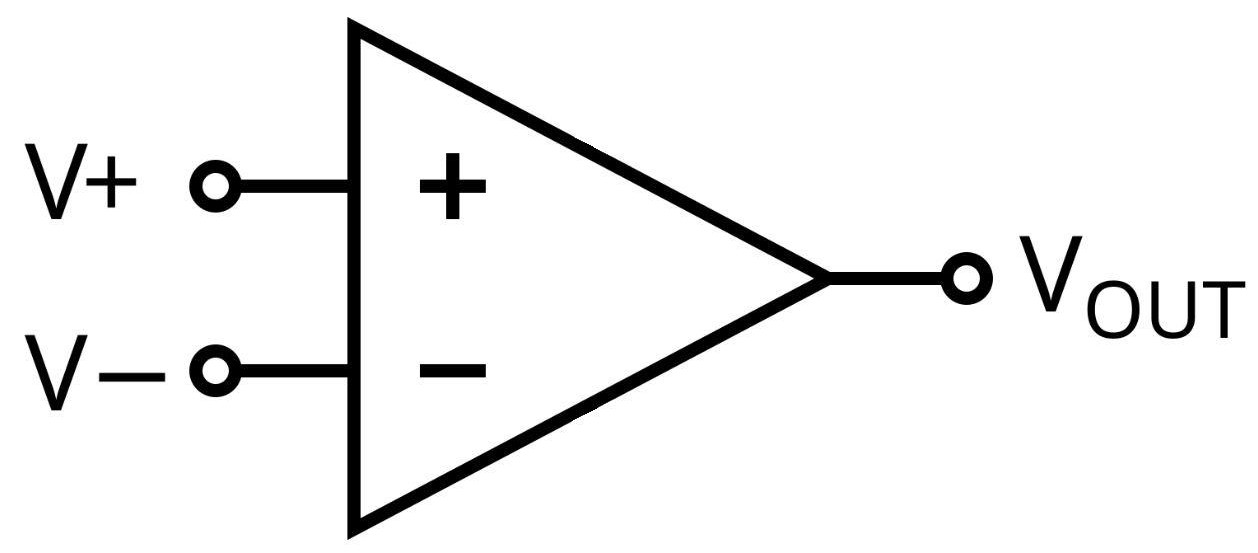
Во многих схемотехнических решениях аналоговой электроники применяют операционные усилители (далее ОУ). ОУ — усилитель постоянного тока с дифференциальным входом (то есть имеется два входа: инвертирующий, обозначен на схеме «\(-\)», и неинвертирующий, обозначен на схеме «\(+\)») и единственным выходом, имеющим высокий коэффициент усиления. Схематично ОУ обозначается так, как показано на рис. 1.8.
Использование таких устройств максимально эффективно в тех случаях, когда в схемах с ОУ используется отрицательная обратная связь, реализуемая с помощью резистивного соединения выхода с инвертирующим входом. Так, ОУ является «строительным» блоком аналоговой электроники, так как на его базе возможно построить множество схем, выполняющих аналоговые математические операции, помимо операции усиления. К таким схемам относятся: сумматор, дифференциатор и интегратор напряжения и многое другое.
Для упрощения расчетов существует модель идеального ОУ, построенная на двух правилах:
- На входы ОУ ток от внешнего источника сигнала не ответвляется, так как входное сопротивление велико: \(R_\text{ВХ}\rightarrow \infty\). Иначе говоря, ток во входы ОУ не течет.
- Напряжение между входами ОУ равно нулю, так как коэффициент усиления ОУ бесконечно большой: \(K_\text{ОУ}\rightarrow\infty\). Иначе говоря, если напряжение на одном входе задано (например, соединено с землей или подключено к источнику постоянного напряжения), то на втором входе будет тот же потенциал.
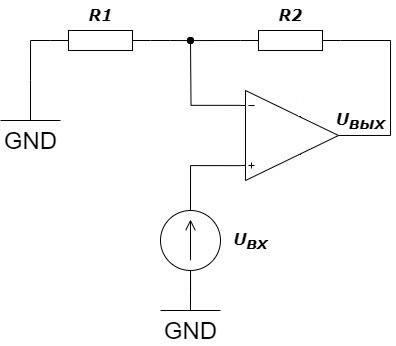
На рис. 1.9 дана типовая схема неинвертирующего усилителя на основе идеального ОУ.
Рассчитайте, чему равно напряжение на выходе \(U_\text{вых}\), если известны сопротивления: \(R_1 = 100\) кОм, \(R_2 = 150\) кОм, а также напряжение на входе: \(U_\text{вх} = 5\) В. В случае необходимости ответ округлите до десятых по правилам арифметического округления.
К неинвертирующему входу ОУ подключен источник постоянного напряжения. Так как ОУ — идеальный, на инвертирующем входе будет такой же потенциал. Так как ток через ветви \(R_1\) и \(R_2\) — это один и тот же ток, следовательно: \[\frac{U_\text{вых}-U_\text{вх}}{R_2} =\frac{U_\text{вх}}{R_1};\] \[U_\text{вых}=U_\text{вх} \cdot \left(1+\frac{R_2}{R_1}\right);\] \[5 \cdot \left(1+\frac{150}{100}\right)=12{,}5\text{~В}.\]
12,5.
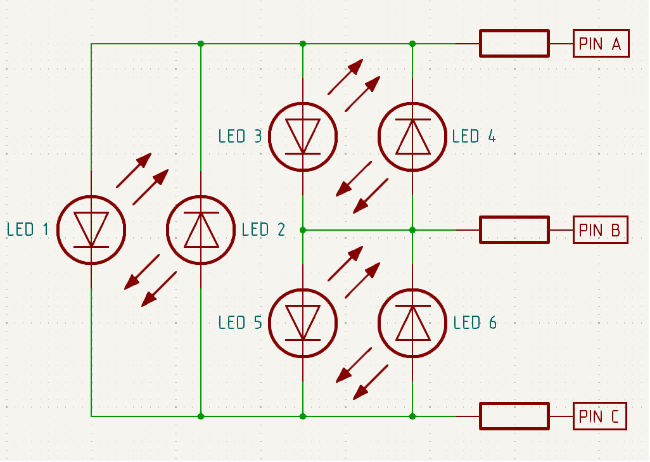
Светодиод — это электронный компонент, который пропускает ток только в одном направлении: от анода (\(+\)) к катоду (\(-\)) (по направлению стрелки). Если подключить его в обратном направлении, он не будет светиться.
Пины микроконтроллера могут находиться в двух состояниях:
1(высокий уровень) — на пине присутствует напряжение,0(низкий уровень) — пин подключен к земле (нулевое напряжение).
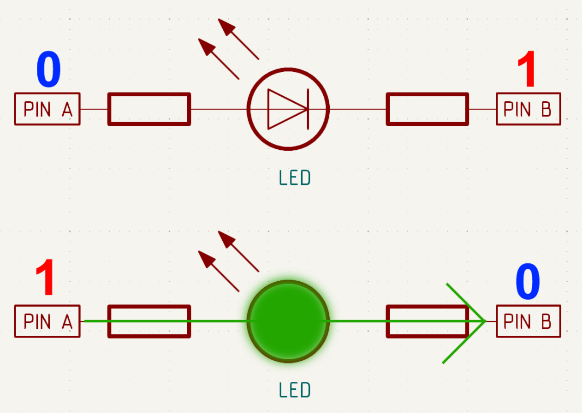
Какие светодиоды загорятся, если подать на пины комбинацию \(\text{А} = 1\), \(\text{В} = 0\), \(\text{С} = 1\)?
- LED 2 и LED 4.
- LED 3 и LED 6.
- LED 1 и LED 5.
- LED 3 и LED 4.
По условию задачи питание подано на пины A и C, а на В — нет. Следовательно, светодиоды 1 и 2 не будут гореть, так как обе ножки имеют при данных условиях одинаковые потенциалы, и прямой ток через диод не течет. Через светодиоды 5 и 4 ток так же не будет протекать, так как установлены они относительно поданного питания обратной полярностью. А через светодиоды 3 и 6 ток пойдет, так как имеется разность потенциалов и правильная полярность к питанию.
2.
Побитовая операция И (AND)
Операция И сравнивает соответствующие биты двух чисел и возвращает 1, если оба бита равны 1, иначе возвращает 0.
Число 1: 1010 (в двоичной системе).
Число 2: 1100.
Результат: 1000 (только там, где оба бита равны 1).
Побитовый сдвиг
Сдвиг перемещает биты числа влево или вправо на определенное количество позиций.
Левый сдвиг (
<<): все биты сдвигаются влево, а на место освободившихся битов справа ставятся нули. Это эквивалентно умножению числа на 2 в степени количества сдвигов.Число: 0010 (2 в десятичной системе).
Сдвиг на 1 (
<<): 0100 (4 в десятичной системе).Правый сдвиг (
>>): все биты сдвигаются вправо, а на место освободившихся битов слева ставятся нули. Это эквивалентно делению числа на 2 в степени количества сдвигов (для положительных чисел).Число: 0100 (4 в десятичной системе).
Сдвиг на 1 (
>>): 0010 (2 в десятичной системе).
Чему будет равна переменная i после выполнения следующих строк кода?
int i = 85;
i = i << 1;
i = i & 42;
i = i >> 2;
i = i & 7;i = 85.i = 170.i = 42.i = 10.i = 2.
2.
В практических задачах, выполняемых с помощью микроконтроллеров (далее — МК), зачастую необходимо использовать временную задержку. В тех задачах, где не требуется высокая точность временных интервалов задержек, не применяют таймеры, а используют программную задержку.
Работа программной задержки основана на том, что каждая команда, выполняемая на МК, требует определенного времени выполнения, зависящего от частоты тактирования.
Если частота тактирования 1 кГц, то период (промежуток времени между двумя тактами) составляет \[\frac {1} {1 \text{~кГц}} =\frac{ 1}{1000} = 0{,}001 \text{~с} = 1 \text{~мс}.\]
В ассемблере микроконтроллеров семейства AVR существует собственная система команд. Каждая команда может быть выполнена за определенное количество тактов.
| Инструкция | Описание | Операнды | Количество тактов |
|---|---|---|---|
| LDI | Загрузить константу в регистр | Rd, K | 1 |
| DEC | Декрементировать значение регистра | Rd | 1 |
| OUT | Запись значения регистра в порт | P, Rr | 1 |
| ADD | Суммирование без переноса | Rd, Rr | 1 |
| NOP | Нет операции (пустая операция) | Нет | 1 |
| CALL | Вызов подпрограммы | k | 4 |
| RET | Возврат подпрограммы | Нет | 4 |
| BRNE | Перейти на метку, если не равно 0 | k | 2/1: 2 — если произошел переход, 1 — если нет |
P — порт, k — метка (адрес команды),
K — 8-битная константа,
Rd — регистр (результирующий),
Rr — регистр (исходный).
Представлен код-листинг подпрограммы на языке Ассемблер для микроконтроллера AVR, реализующий программную задержку.
Учитывая, что частота тактирования МК составляет 10 МГц, определите в микросекундах (целое число) время полученной задержки, учитывая время, необходимое на вызов подпрограммы задержки и на выход из нее.
CALL DELAY
DELAY : LDI R16, 0xFF
AGAIN : NOP
NOP
NOP
DEC R16
BRNE AGAIN
RETКоманда — число тактов:
- CALL — 4,
- LDI — 1,
- NOP — 1 \(\times\) 3,
- DEC — 1,
- BRNE (переход) — 2,
- BRNE (нет перехода) — 1,
- RET — 4.
Время задержки: \[(4 + 1 + (1 \times 3 + 1 + 2) \times 255 + 1 + 4) = \frac{1540}{10} \text{~МГц} = 154 \text{~мкс}.\]
154.
| Инструкция | Операнды | Описание |
|---|---|---|
ADD |
Rd, Rr |
Суммирование без переноса |
RJMP |
k |
Относительный переход |
BRCS |
k |
Перейти, если перенос установлен |
BRNE |
k |
Перейти, если не равно |
LDI |
Rd, K8 |
Загрузить константу |
INC |
Rd |
Инкрементировать значение регистра |
DEC |
Rd |
Декрементировать значение регистра |
CALL |
k |
Вызов подпрограммы |
RET |
Нет | Возврат из подпрограммы |
Операнды:
- Rd — результирующий регистр,
- Rr — исходный регистр,
- K8 — константа (8 бит),
- K — метка.
Ниже приведен код-листинг на языке Ассемблер для МК из семейства AVR, реализующий некоторое арифметическое действие над двумя числами, записанными в регистры r16 и r17. Результатом этого действия является пара регистров: r19 — старший байт, r18 — младший байт. Числа, записанные в регистр, представлены в шестнадцатеричной системе счисления.
Каждый регистр хранит 8 бит информации.
Определите, какое число (в десятичной системе счисления), образованное парой регистров r19 и r18, будет получено в результате вызова подпрограммы sum.
start:
LDI r16, 0x61
LDI r17, 0x03
LDI r18, 0
LDI r19, 0
CALL sum
overflow:
INC r19
RJMP sumContinue
sum:
ADD r18, r16
BRCS overflow
sumContinue:
DEC r17
BRNE sum
RETПри первом вызове подпрограммы sum по ходу выполнения программы в регистре r18 образуется число 0x61, что соответствует в десятичной системе счисления 97. Так как в результате этой операции переполнения регистра не произошло, программа попадает на метку sumContuinue, в которой значение регистра r17 уменьшается на единицу. Далее происходит переход на метку sum, так как значение регистра r17 не равно нулю.
При добавлении в регистр r18 значение регистра r16 равно 97, происходит переполнение, что вызывает подпрограмму, в которой инкрементируется значение регистра r19. В регистре r18 остается часть сложения, оставшаяся без переноса.
Если проделать этот цикл до тех пор, пока r17 не станет равна 0, получится, что в регистр r19 будет записано число 0x01, а в регистр r18 — число 0x23, что в десятичной системе счисления равно 35. Так как r19 — старший регистр, применим сдвиг влево на 8 бит, что эквивалентно восьмикратному умножению на 2, и сложим со значением 35, получая таким образом число 291.
291.
include <stdio.h>
SIZE 10 // размер массива сортируемых элементов
// Функция сортировки прямыми включениями
void bubbleSort(int* num, int size)
{
// Для всех элементов
for (int i = 0; i <= size - 1; i++)
{
for (int j = (size); j > i; j++) // для всех элементов после i-ого
{
if (num[j - 1] > num[j]) // если текущий элемент меньше предыдущего
{
int temp = num[j - 1]; // меняем их местами
num[j - 1] = num[j];
num[j] = temp;
}
}
}
}
int main()
{
int a[SIZE]; // Объявляем массив из 10 элементов
// Вводим значения элементов массива
for (int i = 0; i < SIZE; i++)
{
printf("a[%d] = ", i);
scanf("%d", &a[i]);
}
bubbleSort(a, SIZE); // вызываем функцию сортировки
// Выводим отсортированные элементы массива
for (int i = 0; i < SIZE; i++) printf("%d ", a[i]);
return 0;
}Ниже представлено решение на языке C.
#include <stdio.h>
const int SIZE = 10; // размер массива сортируемых элементов
// Функция сортировки прямыми включениями
void bubbleSort(int* num, int size)
{
// Для всех элементов
for (int i = 0; i <= size - 1; i++)
{
for (int j = (size - 1); j > i; j--) // для всех элементов после i-ого
{
if (num[j - 1] > num[j]) // если текущий элемент меньше предыдущего
{
int temp = num[j - 1]; // меняем их местами
num[j - 1] = num[j];
num[j] = temp;
}
}
}
}
int main()
{
int a[SIZE]; // Объявляем массив из 10 элементов
// Вводим значения элементов массива
for (int i = 0; i < SIZE; i++)
{
printf("a[%d] = ", i);
scanf("%d", &a[i]);
}
bubbleSort(a, SIZE); // вызываем функцию сортировки
// Выводим отсортированные элементы массива
for (int i = 0; i < SIZE; i++) printf("%d ", a[i]);
return 0;
}Отсортированная в порядке возрастания последовательность 11 целых чисел, полученная из вводимых друг за другом 11 целых чисел.
На заводе изготавливают пластиковый конструктор, состоящий из различных строительных блоков, из которых можно собирать разнообразные конструкции. Одной из таких конструкций является лестница.
На этапе выходного контроля производства располагается конвейер, оборудованный датчиком контроля высоты блока. Датчик способен выявить наименьший блок, высотой 1, передавая на управляющее устройство значение, равное высоте блока. Если блок отсутствует, датчик возвращает 0. Максимальная высота блока не превышает 100.
Напишите программу, которая будет выявлять брак по условию, что из поступивших на конвейер деталей возможно собрать лестницу (то есть разница между отсортированными блоками не более одного, первый блок после сортировки обязательно должен быть равен 1).
В ответ передается строка YES или NO (без кавычек).
Решение необходимо реализовать на языке программирования C (C17(GCC14.2)).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
1 3 2 0 |
YES |
2 |
5 3 4 2 0 |
NO |
3 |
1 2 4 5 0 |
NO |
4 |
1 3 4 2 5 0 |
YES |
Ниже представлено решение на языке C.
#include <stdio.h>
#include <stdlib.h>
// Функция сортировки
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// Обмен значениями
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main() {
int heights[100]; // Массив для хранения высот блоков (до 100 элементов)
int count = 0;
int input;
// Ввод чисел, заканчивающийся нулем
while (1) {
scanf("%d", &input);
if (input == 0) break;
heights[count++] = input;
}
//лестница из одного символа тоже лестница
if (count == 2) {
printf("YES\n");
return 0;
}
// Сортировка массива высот
bubbleSort(heights, count);
for (int i = 1; i < count; i+=2) {
if ((heights[i] - heights[i - 1] != 1) || (heights[0] != 1)) {
printf("NO\n");
return 0;
}
}
// Если все условия выполнены, выводим YES
printf("YES\n");
return 0;
}Ниже представлен код-листинг на языке C, реализующий некоторое действие над массивом из пяти целочисленных элементов.
#include <stdio.h>
void specialFunc(int a[],int n)
{
for (int i =0;i <=(n-2);i++)
{
int min =i;
for (int j =i +1;j <=(n-1);j++)
{
if (a[j]<a[min]) min =j;
}
int tmp =a[i];
a[i]=a[min];
a[min]=tmp;
}
for (inti =0;i <n;i++) printf("%d ",a[i]);
}
int main()
{
int arr[5]={5,2,4,3,1};
specialFunc(arr,5);
return 0;
}Определите, что будет выведено в результате работы программы.
- 5 4 3 2 1
- 5 2 4 3 1
- 1 3 4 2 5
- 1 2 3 4 5
Алгоритм работы сортировки чисел по методу «пузырьковой сортировки» (или метод «сортировки bubble») работает на принципе сравнения каждого числа в ячейках массива с другими числами в ячейках этого массива и последующей перестановкой этих чисел местами. Таким образом, например, при упорядочивании чисел по возрастанию наибольшие «всплывают наверх», оказываясь в конце массива.
4.