Предметный тур. Математика. 3 этап
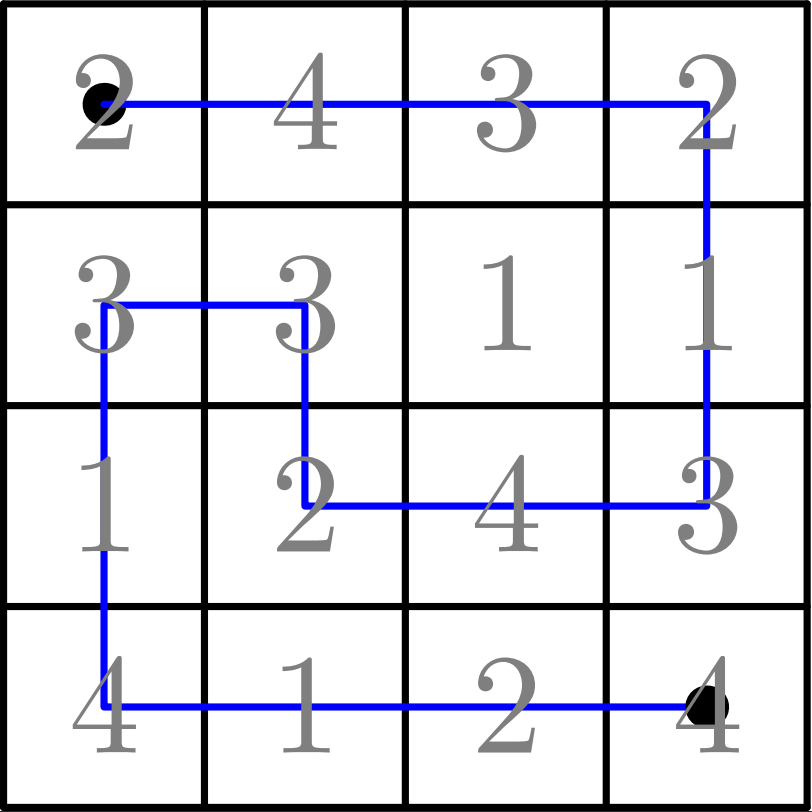
В левом верхнем углу квадратного клетчатого поля \(4 \times 4\) находится фишка. За один ход фишку можно перемещать по полю на одну клетку вправо, влево, вверх или вниз. При этом каждую клетку можно посетить не более одного раза. Фишку перемещают в правый нижний угол и подсчитывают сумму всех чисел в клетках, где побывала фишка. Какую наибольшую сумму можно получить?
\[\begin{array}{|c|c|c|c|} \hline 2 & 4 & 3 & 2\\ \hline 3 & 3 & 1 & 1\\ \hline 1 & 2 & 4 & 3\\ \hline 4 & 1 & 2 & 4\\ \hline \end{array}\]
Заметим, что сумма всех чисел на поле равна \[(1 + 2 + 3 + 4) \cdot 4 = 40.\]
Однако при соблюдении правил фишка не может побывать во всех клетках. Действительно, пусть фишку переместили \(r\) раз вправо, \(l\) раз влево, \(u\) раз вверх и \(d\) раз вниз. Тогда \[r - l = 3, \quad d - u = 3.\] Следовательно, количество клеток, в которых побывала фишка, равно \[1 + r + l + d + u = 1 + (l + 3) + l + (u + 3) + u = 2(l + u) + 7,\] то есть нечетному числу.
Значит, хотя бы одна клетка останется непосещенной. Поскольку наименьшее число на поле равно 1, то наибольшая сумма не превзойдет \(40 - 1 = 39\).
Сумму 39 можно набрать, проведя фишку, как показано на рис. 1.1.
39.
Чтобы лучше подготовиться к ОГЭ, Андрей смотрит обучающий видеоролик. В начале ролик был достаточно простой, поэтому Андрей увеличил скорость просмотра в 1,5 раза. Начиная с некоторого места начался разбор трудных задач. Тогда Андрей установил скорость, в 1,25 раза большую оригинальной, и так досмотрел ролик до конца. Известно, что продолжительность ролика и время, затраченное на его просмотр, относятся как \(7:5\). Сколько процентов от всего времени просмотра затратил Андрей на просмотр первых 75% ролика?
Пусть единица измерения времени такова, что на все видео приходится 7 единиц. Обозначим через \(t_{1}\) время просмотра ролика на скорости \(1{,}5\)x, а через \(t_{2}\) — на скорости \(1{,}25\)x. Тогда по условию задачи имеем систему \[\begin{cases} t_{1} + t_{2} = 5,\\ 1{,}5t_{1} + 1{,}25t_{2} = 7. \end{cases}\] Решая ее, находим \[t_{1} = 3, \quad t_{2} = 2.\]
На скорости \(1{,}5\)x школьник посмотрел \(1{,}5 t_{1} = 9/2\) единиц времени, то есть \(\dfrac{9/2}{7} = \dfrac{9}{14}\) от всего ролика. Так как \(\dfrac{9}{14} < \dfrac{3}{4}\), то школьник поменял скорость просмотра раньше, чем просмотрел 75% ролика. Значит, оставшиеся 25% были просмотрены на скорости \(1{,}25\)x. Таким образом, на оставшуюся четверть ролика было потрачено \[\frac{\frac{1}{4}\cdot 7}{1{,}25} = \frac{7}{5}\] единиц времени, то есть \(100 \cdot \dfrac{7/5}{5} = 28\%\) всего времени просмотра. Тогда на первые 75% приходится \(100 - 28 = 72\%\) всего времени просмотра.
72%.
Сколько существует различных пятизначных чисел, обладающих следующими свойствами:
- последние четыре цифры различны;
- число делится на 4.
На первое место можно поставить любую цифру, кроме 0 — всего 9 способов. На второе место можно поставить любую цифру, кроме тех, которые будут находиться на последних двух позициях — 8 способов. На третьем — так же, за исключением еще той, которая стоит на втором месте — 7 способов.
Число делится на 4, если делится на 4 число, образованное его двумя последними цифрами. Среди чисел \(0, 1, \ldots, 99\) имеется 25 делящихся на 4. Необходимо исключить 0, 44 и 88, поскольку в их записи одинаковые цифры. Таким образом, общее количество таких чисел равно \[9 \cdot 8 \cdot 7 \cdot (25 - 3) = 11088.\]
11088.
В треугольнике \(ABC\) с острым углом \(B\) проведена высота \(BD\), \(DE\) — биссектриса треугольника \(BDA\), а \(EF\) — медиана треугольника \(DEA\). Найти площадь четырехугольника \(FEBD\), если \(AB = 5\), \(BC = 8\), \(\sin \angle{ABC} = \frac{3}{5}\).
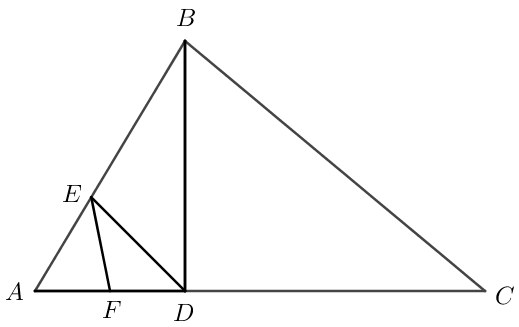
Площадь \(\triangle ABC\)
\[S_{ABC} = \frac{1}{2} AB \cdot BC \cdot \sin B = \frac{1}{2} \cdot 5 \cdot 8 \cdot \frac{3}{5} = 12.\] Так как \(\sin^{2}B + \cos^{2}B = 1\) и угол \(B\) по условию острый, то \(\cos B = \dfrac{4}{5}\). По теореме косинусов \[AC^{2} = AB^{2} + BC^{2} - 2 \cdot AB \cdot BC \cos B = 25 + 64 - 2 \cdot 5 \cdot 8 \cdot \frac{4}{5} = 25.\] То есть \(AC = 5\).
Так как \(S_{ABC} = \dfrac{1}{2} AC \cdot BD\) и \(S_{ABC} = 12\), то \(BD = \dfrac{2\cdot 12}{5} = \dfrac{24}{5}\). По теореме Пифагора \[AD^{2} = AB^{2} - BD^{2} = 25 - \frac{24^{2}}{25} = \frac{49}{25}.\] Тогда \(AD = \dfrac{7}{5}\). Далее \[S_{ABD} = \frac{1}{2}BD \cdot AD = \frac{1}{2}\cdot \frac{24}{5} \cdot \frac{7}{5} = \frac{84}{25}.\]
Рассмотрим \(\triangle ABD\). Так как \(DE\) — биссектриса, то \[\frac{AE}{EB} = \frac{AD}{BD} = \frac{7}{5}\cdot \frac{5}{24} = \frac{7}{24}.\] Треугольники \(AED\) и \(ABD\) имеют общую высоту, проведенную из точки \(D\). Следовательно, \[S_{AED} = \frac{AE}{AB}S_{ABD} = \frac{7}{31}\cdot \frac{84}{25}.\]
Так как \(EF\) — медиана в \(\triangle AED\), то \[S_{AEF} = \frac{S_{AED}}{2} = \frac{7}{31} \cdot \frac{42}{25}.\]
Искомая площадь \[S_{FEBD} = S_{ABD} - S_{AEF} = \frac{84}{25} - \frac{7\cdot 42}{31 \cdot 25} = \frac{462}{155}.\]
\(\dfrac{462}{155}\).
Определите, сколько целых решений имеет неравенство \[\sum\limits_{k=1}^{2025}\left(|x - k| - \frac{1012}{2025}k\right) \leqslant 1000000.\]
Преобразуем левую часть неравенства: \[\sum\limits_{k=1}^{2025}\left(|x - k| - \frac{1012}{2025}k\right) = \sum\limits_{k=1}^{2025}|x - k| - \frac{1012}{2025} \sum\limits_{k=1}^{2025}k.\] Сумма арифметической прогрессии \[\sum\limits_{k=1}^{2025}k = \frac{1 + 2025}{2}\cdot 2025 = 1013 \cdot 2025.\] Тогда \[\frac{1012}{2025}\sum\limits_{k=1}^{2025}k = 1012 \cdot 1013.\] Значит, исходное неравенство равносильно \[\sum\limits_{k=1}^{2025}|x - k| \leqslant 1012 \cdot 1013 + 10^{6}.\]
Если \(x \leqslant 0\) или \(x \geqslant 2026\), то \[\sum\limits_{k=1}^{2025}|x - k| \geqslant \sum\limits_{k=1}^{2025}k = \frac{1 + 2025}{2}\cdot 2025 = 1013 \cdot 2025.\] Имеем \[1013 \cdot 2025 = 1013\cdot(1012 + 1013) = 1013 \cdot 1012 + 1013^{2} > 1013 \cdot 1012 + 10^{6}.\] Поэтому числа \(x \leqslant 0\) и \(x \geqslant 2026\) не являются решениями.
Рассмотрим сумму \(S = \sum\limits_{k=1}^{2025}|x - k|\), когда \(x\) — целое число от 1 до 2025. Имеем: \[\begin{aligned} &x = 1: \quad S = 0 + 1 + 2 + 3 + \ldots + 2024,\\ &x = 2: \quad S = 1 + 0 + 1 + 2 + \ldots + 2023,\\ &x = 3: \quad S = 2 + 1 + 0 + 1 + \ldots + 2022,\\ & \ldots\\ &x = 2025: \quad S = 2024 + 2023 + 2022 + \ldots + 0. \end{aligned}\] То есть число \(S\) — сумма двух арифметических прогрессий, \[S = \frac{(x - 1) + 0}{2}\cdot x + \frac{1 + (2025 - x)}{2}\cdot (2025 - x) = x^{2} - 2026x + 1013 \cdot 2025.\]
Таким образом, требуется найти количество целых решений неравенства \[x^{2} - 2026x + 1013 \cdot 2025 \leqslant 1012 \cdot 1013 + 10^{6},\] которое равносильно \[x^{2} - 2026x + 1013^{2} - 10^{6} \leqslant 0.\]
Дискриминант, деленный на 4, трехчлена в левой части равен \[\frac{D}{4} = 1013^{2} - (1013^{2} - 10^{6}) = 10^{6}.\] Поэтому решения неравенства лежат в промежутке \([1013 - 10^{3}, 1013+10^{3}]\). На этом отрезке находится 2001 целое число.
2001.
Найдите все решения уравнения \[4^{\sin^{2}x} + 4^{\cos^{2}x} + \operatorname{tg} x + \operatorname{ctg} x = 6.\] на интервале \(\left(0, \dfrac{\pi}{2}\right)\).
Рассмотрим функцию \[f(x) = 4^{\sin^{2}x} + 4^{\cos^{2}x} = 4^{\sin^{2}x} + \frac{4}{4^{\sin^{2}x}} = t + \frac{4}{t},\] где \(t = 4^{\sin^{2}x}\). Функция \(f\) достигает наименьшего значения при \(t = 2\), то есть при \(x = \dfrac{\pi}{4}\): \(f\left(\dfrac{\pi}{4}\right) = 4\). Во всех остальных точках интервала \(\left(0, \dfrac{\pi}{2}\right)\) ее значения строго больше 4.
Рассмотрим функцию \[g(x) = \operatorname{tg} x + \operatorname{ctg} x = \operatorname{tg} x + \frac{1}{\operatorname{tg} x} = u + \frac{1}{u},\] где \(u = \operatorname{tg} x\). Функция \(g\) достигает наименьшего значения при \(u = 1\), то есть при \(x = \dfrac{\pi}{4}\): \(g\left(\dfrac{\pi}{4}\right) = 2\). Во всех остальных точках интервала \(\left(0, \dfrac{\pi}{2}\right)\) ее значения строго больше 2.
Таким образом, левая часть уравнения достигает значения \(6\) при \(x = \dfrac{\pi}{4}\), а во всех остальных точках интервала \(\left(0, \dfrac{\pi}{2}\right)\) ее значения строго больше 6. Следовательно, имеется единственный корень \(x = \dfrac{\pi}{4}\).
\(\dfrac{\pi}{4}\).
20 одинаковых роз надо расставить по 5 различным вазам. Сколькими способами это можно сделать, если могут оставаться пустые вазы?
Неважно, в каком порядке будем заполнять вазы цветами, важен только окончательный результат: сколько цветов будет в каждой из различных ваз. Поэтому речь идет о выборке без учета порядка, то есть о сочетаниях. Далее: цветы не выбираем, они одинаковые. Беря розу, выбираем вазу, в которую поставим эту розу. Одну и ту же вазу можно выбрать несколько раз, поэтому речь идет о схеме с повторениями. Таким образом, имеем сочетания с повторениями. Формула для числа сочетаний с повторениями имеет вид \[\overline{C_{n}^{m}} = C_{n+m - 1}^{m} = \frac{(n+m-1)!}{m!(n-1)!},\] где \(n\) — число различных объектов, а \(k\) — число их выбора. В нашем случае \(n = 5\), \(k = 20\), таким образом, будем иметь \[\overline{C_{5}^{20}} = C_{20+5-1}^{20} = \frac{24!}{20!4!} = \frac{24 \cdot 23 \cdot 22 \cdot 21}{4 \cdot 3 \cdot 2 \cdot 1} = 10626.\]
10626.
Найдите площадь фигуры, заданной системой неравенств
\[\begin{cases} x^2 + y^2 \leqslant 2(y-x) + 34, \\ x + \sqrt{3}|y - 1| \leqslant -1. \end{cases}\\ \]
Преобразуем систему следующим образом:
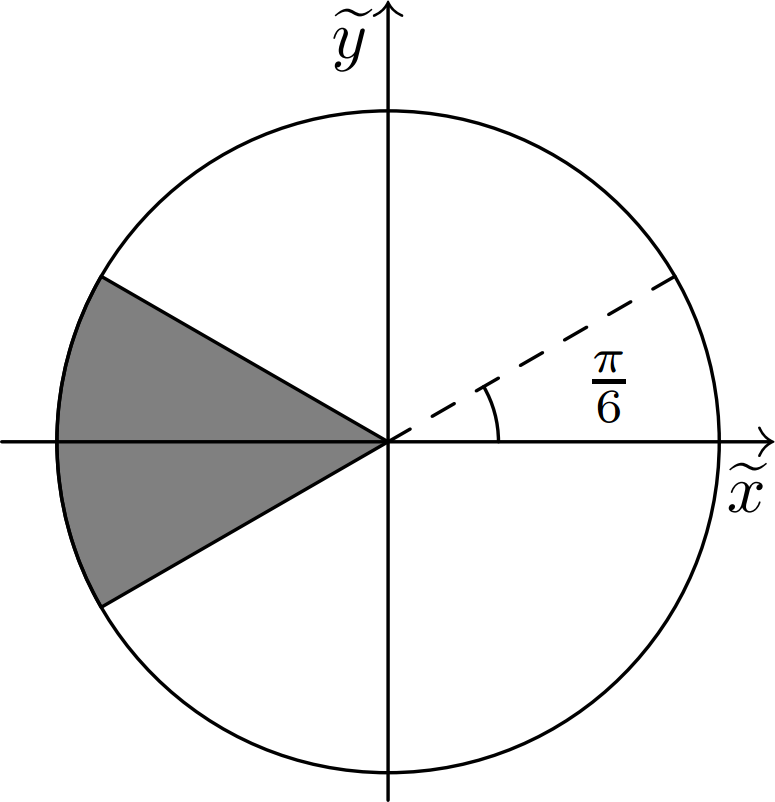
\[\begin{cases} (x + 1)^2 + (y - 1)^2 \leqslant 36, \\ x + 1 + \sqrt{3}|y - 1| \leqslant 0. \end{cases}\\ \] Введем замену \(\widetilde{x} = x + 1\), \(\widetilde{y} = y - 1\). Тогда система примет вид: \[\begin{cases} \widetilde{x}^2 + \widetilde{y}^2 \leqslant 36, \\ \widetilde{x} + \sqrt{3}|\widetilde{y}| \leqslant 0. \end{cases}\\ \] Система задает сектор круга радиуса \(R = 6\), заключенный между прямыми \(\widetilde{y} = \dfrac{1}{\sqrt{3}} \widetilde{x}\) и \(\widetilde{y} = -\dfrac{1}{\sqrt{3}} \widetilde{x}\) (при \(\widetilde{y} \geqslant \dfrac{1}{\sqrt{3}} \widetilde{x}\) и \(\widetilde{y} \leqslant -\dfrac{1}{\sqrt{3}} \widetilde{x}\)).
Угол сектора круга при этом равен \(\alpha = 2 \cdot \dfrac{\pi}{6} = \dfrac{\pi}{3}\) радиан (прямая \(\widetilde{y} = \dfrac{1}{\sqrt{3}}\widetilde{x}\) проходит под углом \(\operatorname{arctg} \dfrac{1}{\sqrt{3}} = \dfrac{\pi}{6}\) к оси \(\widetilde{x}\)), а значит, площадь кругового сектора \[S = \frac{1}{2}R^{2} \cdot \alpha = \frac{1}{2} \cdot 6^{2} \cdot \frac{\pi}{3} = 6 \pi.\]
\(6\pi\).
В правильной четырехугольной призме \(ABCDA_{1}B_{1}C_{1}D_{1}\) боковые ребра равны 8, а стороны основания — 4. Точка \(M\) делит ребро \(DD_{1}\) в отношении \(3:5\), считая от вершины \(D\). Найдите площадь сечения призмы плоскостью, проходящей через точку \(M\) перпендикулярно прямой \(DB_{1}\).
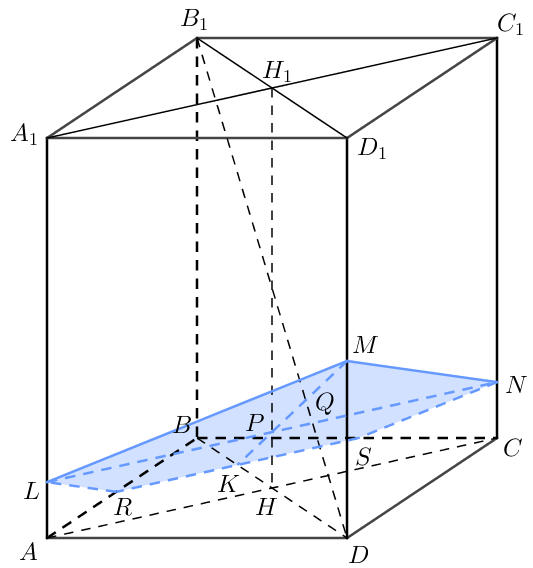
Построение сечения:
- В плоскости \(BB_{1}D_{1}\): \(MK \perp DB_{1}\), \(K = MK \cap BD\), \(P = MK \cap HH_{1}\), где \(H\) и \(H_{1}\) — центры оснований призмы.
- В плоскости \(ABC\): \(RS \parallel AC\), \(K \in RS\), \(R = RS \cap AB\), \(S = RS \cap BC\).
- В плоскости \(AA_{1}C_{1}\): \(LN \parallel AC\), \(P \in LN\), \(L = LN \cap AA_{1}\), \(N = LN \cap CC_{1}\).
- \(RLMNS\) — искомое сечение: \(MK \subset RLMNS\), \(MK \perp DB_{1}\) по построению, \(LN \subset RLMNS\), \(LN \parallel AC\), \(AC \perp DB_{1}\) по теореме о трех перпендикулярах.
Вычисление площади:
Найдем косинус угла между построенной плоскостью и плоскостью основания. Имеем: \(RS\) — ребро двугранного угла, \(BD \perp AC\) (диагонали квадрата), \(RS \parallel AC\), тогда \(BD \perp RS\), а \(MK \perp RS\) (теорема о трех перпендикулярах). Следовательно, \(\angle(RLM, ABC) = \angle(MK, BD) = \angle MKD = \alpha\).
Треугольник \(KMD\) — прямоугольный, \(DQ\) — его высота.
Значит, \(\triangle KMD \sim \triangle DMQ\) и \(\alpha = \angle MKD = \angle QDM\). Далее \[\begin{gather} B_{1}D = \sqrt{8^{2} + (4 \sqrt{2})^{2}} = 4 \sqrt{6},\\ \cos \alpha = \frac{DD_{1}}{B_{1}D} = \frac{8}{4 \sqrt{6}} = \frac{2}{\sqrt{6}},\\ \operatorname{tg} \alpha = \frac{1}{\sqrt{2}}. \end{gather}\]
- \(RSCDA\) — ортогональная проекция сечения \(RLMNS\) на плоскость основания. Имеем \[\begin{gather} BD = AC = 4 \sqrt{2},\\ KD = \frac{MD}{\operatorname{tg} \alpha} = 3 \sqrt{2},\\ KH = KD - DH = (3 - 2)\sqrt{2} = \sqrt{2}. \end{gather}\] Имеем \[\frac{RS}{AC} = \frac{BK}{HB} = \frac{2 \sqrt{2} - \sqrt{2}}{2 \sqrt{2}} = \frac{1}{2}.\] Тогда \(S_{RBS} = \frac{1}{4}S_{ABC} = 2\). Отсюда \[S_{RSCDA} = S_{ABCD} - S_{RBS} = 16-2 = 14.\] Окончательно находим \[S_{RLMNS} = \frac{S_{RSCDA}}{\cos \alpha} = \frac{14}{2 / \sqrt{6}} = 7 \sqrt{6}.\]
\(7 \sqrt{6}\).
Вычислите \[\sum\limits_{n=1}^{2025} \sqrt{\left(\sum\limits_{j=1}^{n} \sum\limits_{i=j}^{n}i^2\right)^{-1}}.\]
Рассмотрим выражение в скобках: \[\begin{aligned} \sum\limits_{j=1}^{n} \sum\limits_{i=j}^{n}i^2 = \sum\limits_{j=1}^{n}(j^2+(j+1)^2+\dots+&n^2)=\\ = 1^{2} + 2^{2} + 3^{2} + \ldots + &n^{2} +\\ 2^{2} + 3^{2} + \ldots + &n^{2}+\\ 3^{2} + \ldots + &n^{2} +\\ \ldots &\\ +&n^{2}=\\ =1\cdot 1^2+2\cdot 2^2+ 3 \cdot 3^{2} +\dots+&n\cdot n^2 = \sum\limits_{k=1}^{n}k^{3}. \end{aligned}\]
Воспользуемся формулой для суммы кубов: \[\sum\limits_{k=1}^{n}k^{3} = \frac{n^{2}(n+1)^{2}}{4}.\] Тогда \[\begin{aligned} &\sum\limits_{n=1}^{2025} \sqrt{\left(\sum\limits_{j=1}^{n} \sum\limits_{i=j}^{n}i^2\right)^{-1}} = \sum\limits_{n=1}^{2025} \sqrt{\dfrac{4}{n^2(n+1)^2}} = \sum\limits_{n=1}^{2025} \dfrac{2}{n(n+1)}=\\ &= 2\sum\limits_{n=1}^{2025}\left(\frac{1}{n} - \frac{1}{n+1}\right) = 2\left(1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \ldots + \frac{1}{2025} - \frac{1}{2026}\right)= \\ &=2\left(1-\dfrac{1}{2026}\right)=\dfrac{2025}{1013}. \end{aligned}\]
\(\dfrac{2025}{1013}\).