Предметный тур. Информатика. 3 этап
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 64 Мбайт.
Алиса пишет программу для шоу дронов. Одним из номеров будет совместный полет \(n\times m\) дронов, построенных в \(n\) рядов, по \(m\) дронов в каждом. Для создания большего эффекта Алиса хочет, чтобы расстояния между соседними дронами в одном ряду и между соседними рядами совпадали и были минимально допустимыми. Но она опасается допустить столкновение некоторых дронов, поэтому намерена распределить все дроны по \(4\) коридорам по высоте так, чтобы соседние дроны занимали разные коридоры.
Схематично можно представить расположение дронов в виде таблицы из \(n\) строк и \(m\) столбцов, где в каждой ячейке будет находиться число от \(1\) до \(4\), обозначающее номер коридора для конкретного дрона. Алиса хочет распределить коридоры так, чтобы соседние дроны по вертикали, горизонтали или диагонали занимали различные коридоры.
Напишите программу, которая найдет любое размещение дронов с заданным условием.
Формат входных данных
На вход поступает два целых числа \(n\), \(m\) — размеры таблицы, (\(1\leqslant n, m\leqslant 10)\).
Формат выходных данных
Программа должна вывести таблицу требуемого размера, состоящую из чисел от \(1\) до \(4\).
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 4 |
1 4 3 2 3 2 1 4 1 4 3 2 |
Эта задача допускает много возможных решений. Например, можно чередовать в строках с четными номерами числа \(1\) и \(2\), а в строках с нечетными номерами числа \(3\) и \(4\).
Пример программы-решения
Ниже представлено решение на языке Python.
n, m = map(int, input().split())
for i in range(n):
if i % 2 == 0:
print(*([1,2]*5)[:m])
else:
print(*([3,4]*5)[:m])Тест № 1 совпадает с тестом из условия задачи. Баллы за него не начисляются.
Успешное прохождение каждого теста №№ 2–9 оценивается в один балл.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 128 Мбайт.
В городе Энске есть большой парк прямоугольной формы. Некоторые деревья в нем нужно обработать от вредителей — горностаевой моли. Известны координаты на плоскости всех деревьев, нуждающихся в обработке. Специальный дрон будет двигаться от одного дерева к другому и обрабатывать их инсектицидными аэрозолями. Но для дрона необходимо составить маршрут движения, по возможности близкий к оптимальному.
Было решено использовать следующий алгоритм. Зададим координаты так, что левый нижний угол парка будет находиться в точке \((0,~0)\), а правый верхний — в точке \((w,~h)\). Разделим получившийся прямоугольник на вертикальные полосы шириной \(s\). Последняя полоса может иметь меньшую ширину. Пронумеруем все полосы числами от нуля. Будем считать, что точка принадлежит полосе с номером \(k\), если для ее координаты \(x\) выполняется неравенство \(ks\leqslant x< (k+1)s\). Сначала дрон обработает все деревья, попавшие в нулевую полосу, потом — в первую и так далее.
Двигаясь по полосам с четными номерами, дрон будет обрабатывать деревья в порядке возрастания их координаты \(y\). Если же номер полосы будет нечетным, то дрон будет двигаться в порядке убывания координаты \(y\). Если координаты \(y\) у двух деревьев в пределах одной полосы совпадут, то дрон будет обрабатывать их в порядке возрастания координаты \(x\) вне зависимости от четности номера полосы.
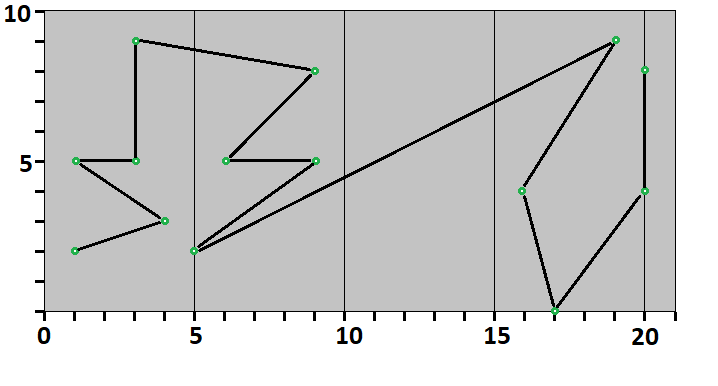
Обратите внимание, что алгоритм будет исполняться формально, то есть на его исполнение, например, не окажет влияние отсутствие деревьев в некоторых полосах или то, что последняя полоса будет иметь ширину \(1\). Для лучшего понимания алгоритма движения посмотрите на схему ниже. Здесь пять полос, в нулевую полосу попали все деревья с координатой \(x\) в полуоткрытом интервале \([0; 5)\). Они обходятся снизу вверх. В первую и третью полосу попали деревья с координатой \(x\) из полуоткрытых интервалов \([5; 10)\) и \([15; 20)\). Они обходятся сверху вниз. Последняя полоса содержит только деревья с координатой \(x=20\).
Напишите программу, которая по заданным координатам деревьев найдет длину пути дрона от первого обработанного дерева до последнего.
Формат входных данных
В первой строке на вход программы поступают три целых числа \(w, h, s\) — размеры парка по оси \(Ox\), по оси \(Oy\) и ширина полосы (\(1\leqslant w, h, s\leqslant 10000\)).
Во второй строке на вход программы поступает одно натуральное число \(n\) — количество деревьев в парке, \(2\leqslant n\leqslant 200000\).
Далее в \(n\) строках записаны по два числа \(x_i\) и \(y_i\) — координаты на плоскости каждого из \(n\) деревьев, \(0\leqslant x_i < w\), \(0\leqslant y_i < h\).
Формат выходных данных
Выведите одно вещественное число — расстояние, пройденное дроном от первого дерева в маршруте до последнего. Ответ засчитывается верным, если он будет отличаться от точного значения не более, чем на \(10^{-3}\).
Примечания
Маршрут для первого теста изображен на рис. 1.1.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
21 10 5 14 5 2 20 4 9 5 6 5 20 8 17 0 9 8 1 5 19 9 3 5 3 9 1 2 4 3 16 4 |
65.69976551601135 |
Для решения этой задачи требуется упорядочить координаты деревьев в заданной последовательности. В Python для этого можно использовать встроенный алгоритм сортировки с параметром key, задающим порядок. Сохраним координаты деревьев в список кортежей, где нулевой элемент кортежа будет задавать координату \(x\), а первый — \(y\).
Номер полосы можно вычислить по формуле \(\dfrac xs\). В момент сортировки координату \(y\) в полосах с нечетным номером можно умножить на (\(-1\)), чтобы обеспечить порядок по убыванию. Таким образом сформируем ключ сортировки в виде кортежа с тремя параметрами: номер полосы, координата \(y\), домноженная на (\(-1\)) в нечетных полосах, координата \(x\).
Два кортежа сравниваются по нулевому элементы, в случае равенства — по первому, в случае равенства первых элементов — по второму. Это обеспечивает требуемый порядок сортировки.
В конце программы требуется просто посчитать сумму расстояний между соседними деревьями.
Пример программы-решения
Ниже представлено решение на языке Python.
w, h, s = map(int,input().split())
n = int(input())
p = sorted([tuple(map(int,input().split())) for _ in range(n)],\
key = lambda p:(p[0]//s,p[1]*(-1 if (p[0]//s)%2==1 else 1),p[0]))
ans = 0.
for i in range(1,len(p)):
ans+=((p[i][0]-p[i-1][0])**2+(p[i][1]-p[i-1][1])**2)**0.5
print(ans)Тест № 1 совпадает с тестом из условия задачи. Баллы за него не начисляются.
Успешное прохождение каждого теста №№ 2–17 оценивается в один балл.
В тестах №№ 2–3 выполняется \(s=w\), то есть в этих тестах ровно одна полоса.
В тестах №№ 4–5 выполняется \(w/2\leqslant s < w\), то есть в этих тестах ровно две полосы.
В тестах №№ 2–9 все координаты \(y\) в пределах одной полосы различны.
В тестах №№ 2–13 количество деревьев не превосходит 10000.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 128 Мбайт.
Рассмотрим координатную плоскость. На оси \(Ox\) в точках с координатами \((1,~0)\), \((2,~0)\), …, \((n,~0)\) в воздухе на некоторой высоте неподвижно висит \(n\) дронов. Даны \(n\) целых чисел \(t_1, t_2, ..., t_n\), задающих некоторые моменты времени. Дрон, изначально находящийся в точке \((i, 0)\), стартует в момент времени \(t_i\) и двигается параллельно оси \(Oy\) в сторону увеличения координаты \(y\).
Аналогично на оси \(Oy\) в воздухе на другой высоте расположены еще \(m\) дронов в точках с координатами \((0, 1)\), \((0, 2)\), …, \((0, m)\). Для них также заданы моменты времени \(q_1, q_2, \ldots, q_m\). Дрон, изначально находящийся в точке с координатами \((0, j)\), стартует в момент времени \(q_j\) и двигается параллельно оси \(Ox\) в сторону увеличения координаты \(x\).
Все дроны летят с одинаковыми скоростями. Если единицу расстояния считать метром, а единицу времени — секундой, то все скорости будут равны \(1\) м/с.
Поскольку дроны летят на различных высотах, столкновений не произойдет, однако будем считать событием ситуацию, когда один дрон пролетит строго над другим в один и тот же момент времени.
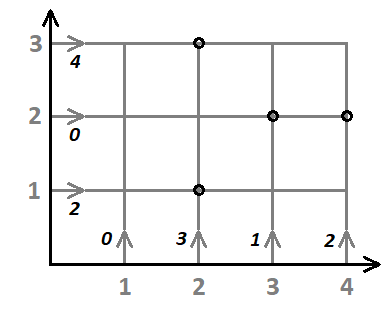
Рассмотрим пример на рис. 1.2. С оси \(Ox\) стартуют четыре дрона в моменты времени \(0, 3, 1, 2\). С оси \(Oy\) стартует три дрона в моменты времени \(2,~0,~4\).
Два дрона пролетят над точкой \((2, 1)\) в момент времени \(4\); над точкой \((3, 2)\) в момент времени \(3\); над точкой \((4, 2)\) в момент времени \(4\); над точкой \((2, 3)\) в момент времени \(6\). Ни в какой другой точке два дрона одновременно не окажутся.
Напишите программу, которая посчитает количество указанных событий.
Формат входных данных
В первой строке на вход поступают два натуральных числа \(n\) и \(m\) — количество дронов на оси \(Ox\) и на оси \(Oy\) соответственно, \(1\leqslant n, m\leqslant 100000\).
Во второй и в третьей строках на вход поступают целые числа \(t_1, \ldots, t_n\) и \(q_1, \ldots, q_m\) — моменты начала движения для дронов, ожидающих на оси \(Ox\) и на оси \(Oy\) соответственно, \(0\leqslant t_i, q_i\leqslant 10^9\).
Формат выходных данных
Выведите одно целое число — количество событий указанного вида.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
4 3 0 3 1 2 2 0 4 |
4 |
Примечания
Тест из условия задачи разобран в примере.
Из условия задачи следует, что два дрона, стартующих из точек \((i, 0)\) и \((0, j)\), могут оказаться одновременно в точке \((i, j)\). Первый дрон окажется там в момент времени \(t_i+j\), а второй — \(t_j+i\). Таким образом, требуется посчитать количество пар \((i, j)\), для которых выполняется равенство \(t_i+j=t_j+i\). Решение, перебирающее все пары двумя вложенными циклами, сможет набрать не более \(12\) баллов. Чтобы получить полное решение, перепишем равенство в виде \(t_i-i=t_j-j\). Найдем все значения \(k_i=t_i-i\) и составим словарь из пар \(k_i:c(k_i)\), где \(c(k_i)\) — количество найденных чисел \(k_i\).
Теперь переберем отдельным циклом все значения \(q_j\) и просуммируем все значения \(c(q_j-j)\) из словаря.
Пример программы-решения
Ниже представлено решение на языке Python.
n, m = map(int,input().split())
cnt = dict()
for i,t in enumerate(map(int,input().split())):
if not t-i in cnt.keys():
cnt[t-i]=0
cnt[t-i]+=1
ans = 0
for j,q in enumerate(map(int,input().split())):
if q-j in cnt.keys():
ans+=cnt[q-j]
print(ans)Тест № 1 совпадает с тестом из условия задачи. Баллы за него не начисляются.
Успешное прохождение каждого теста №№ 2–41 оценивается в 0,5 балла.
В тестах №№ 2–13 \(n\), \(m\) и все значения времени не превосходят 100.
В тестах №№ 14–25 \(n\), \(m\) и все значения времени не превосходят 2000.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 2 с.
Ограничение по памяти: 256 Мбайт.
Фермер Василий попал в очень неприятную ситуацию. Он доверил написать программу для обработки своего поля двумя сельскохозяйственными дронами одному болтливому попугаю, и тот все напутал.
Поле Василия имеет прямоугольную форму и условно разделено на квадратные клетки. Будем считать, что каждая клетка имеет размер 1 м, а поле имеет размер \(n\times m\). Можно сказать, что поле состоит из \(n\) горизонтальных и \(m\) вертикальных рядов. Все ряды пронумерованы, начиная с единицы, горизонтальные — снизу вверх, вертикальные — слева направо.
Программа, написанная болтливым попугаем, заключалась в следующем. Первый дрон двигался по горизонтальным рядам и обрабатывал клетки удобрениями, но из-за ошибки в программе он посетил не все клетки в каждом ряду. Более точно: в \(i\)-м ряду дрон обработал ровно \(a_i\) идущих подряд клеток, начиная с западного края поля. А второй дрон двигался по вертикальным рядам и в \(i\)-м ряду обработал ровно \(b_i\) идущих подряд клеток, начиная с южного края поля. В результате некоторые клетки были обработаны дважды, а некоторые — ни разу. Теперь Василий должен как-то исправить ситуацию, но для начала ему надо понять, сколько клеток всего осталось необработанными.
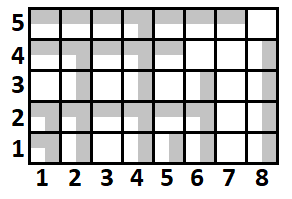
Для лучшего понимания проблемы посмотрите пример на рис. 1.3. Числа на схеме задают номера рядов. \(\tilde{a} = (1,~6,~0,~5,~7)\), \(\tilde{b}=(2,~4,~0,~5,~1,~3,~0,~4)\). Клетки, обработанные первым дроном, обозначены горизонтальными прямоугольниками, а вторым — вертикальными. Как видим, восемь клеток были обработаны дважды, а десять — ни разу.
Напишите программу, которая найдет количество клеток поля, которые не были обработаны ни одним из двух дронов.
Обратите внимание, что в этой задаче есть несколько групп тестов, для которых можно реализовать более простые алгоритмы решения, чем в общем случае.
Формат входных данных
В первой строке на вход поступают два натуральных числа \(n\) и \(m\) — размеры поля, \(1\leqslant n, m\leqslant 200000\).
Во второй строке записаны числа \(a_1, \ldots, a_n\) — количество обработанных клеток в каждом из горизонтальных рядов, \(0\leqslant a_i \leqslant m\).
В третьей строке записаны числа \(b_1, \ldots, b_m\) — количество обработанных клеток в каждом из вертикальных рядов, \(0\leqslant b_i\leqslant n\).
Формат выходных данных
Программа должна вывести одно целое число — количество необработанных клеток поля.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
5 8 1 6 0 5 7 2 4 0 5 1 3 0 4 |
10 |
Примечания
Тест из условия задачи разобран в примере.
Попробуем записать решение, связанное с перебором столбцов поля и подсчетом необработанных клеток в каждом столбце. Рассмотрим столбец с номером \(j\). Двигаясь по этому столбцу, дрон обработал клетки с номерами от \(1\) до \(b_j\). Таким образом, надо узнать, сколько клеток с номерами от \(b_j+1\) до \(n\) не были обработаны, когда дрон двигался по строкам. Формально это означает, что требуется определить, сколько из чисел \(a_{b_j+1}, \ldots, a_n\) удовлетворяют неравенству \(a_i < j\). Если размеры поля невелики, то это можно сделать перебором. Если числа \(a_i\) упорядочены, то можно использовать бинарный поиск. Для решения задачи в общем случае потребуются более сложные структуры данных, такие как деревья.
Будем перебирать пары \((j,b_j)\) в порядке убывания \(b_j\). Для этого их можно сначала отсортировать. В начале каждого шага цикла будем добавлять в дерево элементы списка \(a\) так, чтобы в нем находились все числа \(a_{b_j+1}, \ldots, a_n\). Из упорядоченности \(b_j\) следует, что потребуется не более \(n\) операций добавления. Теперь, поскольку рассматривается \(j\)-й столбец, надо найти и прибавить к ответу количество элементов дерева, которые строго меньше \(j\).
Для решения задачи можно использовать бинарное сбалансированное дерево с подсчетом числа узлов, дерево Фенвика или дерево отрезков. Дополнительную информацию об этих структурах данных можно найти по ссылке http://e-maxx.ru/algo/.
Пример программы-решения
Ниже представлено решение на языке Python.
n, m =map(int,input().split())
a = [int(t) for t in input().split()]
blst = sorted(list(enumerate(map(int,input().split()))),
key = lambda x:-x[1])
tree = [0]*(2*(m+1))
i = n
ans = 0
for b in blst:
while i>b[1]:
i-=1
pos = a[i]+m+1
while pos>0:
tree[pos]+=1
pos//=2
posr = m+1+b[0]+1
posl = m+1
while posr>posl:
if posr%2==1:
posr-=1
ans += tree[posr]
if posl%2==1:
ans += tree[posl]
posl+=1
posr//=2
posl//=2
print(ans)Тест № 1 совпадает с тестом из условия задачи. Баллы за него не начисляются.
Успешное прохождение каждого теста №№ 2–29 оценивается в 1 балл.
В тестах №№ 2–7 размеры поля не превышают 100 по каждому измерению.
В тестах №№ 8–14 для размеров поля выполняются неравенства \(1\leqslant n\leqslant 200000\), \(1\leqslant m\leqslant 10000\).
В тестах №№ 15–21 значения \(a_1, \ldots, a_n\) упорядочены по неубыванию.
Имя входного файла: стандартный ввод или input.txt.
Имя выходного файла: стандартный вывод или output.txt.
Ограничение по времени выполнения программы: 1 с.
Ограничение по памяти: 128 Мбайт.
Логические или булевы функции — это функции многих переменных, определенные на множестве \(\{0, 1\}\). Они широко используются при проектировании различных микросхем. Напишите программу для работы с такими функциями.
Наиболее распространенный способ задания булевых функций — через таблицу истинности, см. таблицу 1.1.
| \(x_1\) | \(x_2\) | \(x_3\) | \(f(x_1, x_2 ,x_3)\) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Если функция зависит от \(n\) переменных, то в левой части таблицы расположены все двоичные наборы длины \(n\), обычно упорядоченные в натуральном порядке. Поэтому булеву функцию можно задать вектором из правой части таблицы. Длина такого вектора будет равна \(2^n\). Для данного примера вектор будет равен \(f(x_1, x_2, x_3) = (00111010)\).
Функции также можно задавать при помощи формул. В этой задаче будем строить формулы с использованием заданного набора \(m\) функций \(n\) переменных \(f_1(x_1, \ldots, x_n), \ldots, f_m(x_1, \ldots, x_n)\) и бинарных операций \(\vee\) («или») и \(\wedge\) (И). Обратите внимание, что в формулах нет отрицаний, операции всегда применяются к двум функциям \(n\) переменных, а все заданные функции \(f_i(x_1, \ldots, x_n)\) всегда зависят от \(n\) переменных, записанных только в указанном порядке \(x_1, \ldots, x_n\).
Напомним, что результат операции \(\vee\) равен единице, если хотя бы один из аргументов равен единице. Результат операции \(\wedge\) равен единице, если оба аргумента равны единице.
Например, найдем функцию, заданную формулой \(g = (f_1\vee f_2) \wedge (f_3\vee f_2)\), где \(f_1, f_2, f_3\) — функции трех переменных, \(f_1=(00010111)\), \(f_2=(10000001)\), \(f_3=(10110100)\).
| \(f_1\) | \(f_2\) | \(f_3\) | \(f_1\vee\) \(f_2\) | \(f_3\vee\) \(f_2\) | \(g\) |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
Теперь можно сформулировать саму задачу. Пусть заданы два набора функций от \(n\) переменных \(f_1, \ldots, f_m\) и \(g_1, \ldots, g_k\). Напишите программу, которая для каждой из функций \(g_i\) определит, можно ли ее представить в виде формулы указанного вида, использующей только функции \(f_j\). Каждую функцию можно использовать несколько раз или не использовать вовсе. Формула может состоять из одного символа функции без операций, но не может быть пустой.
Формат входных данных
В первой строке на вход подается одно натуральное число \(n\) — количество переменных в функциях, \(1\leqslant n\leqslant 10\).
Во второй строке записано одно натуральное число \(m\) — количество функций \(f_1, \ldots, f_m\), используемых при построении формул, \(1\leqslant m\leqslant 2000\).
Далее в \(m\) строках записаны векторы, задающие функции \(f_1, \ldots, f_m\). Каждый вектор записан в виде строки длины \(2^n\) из нулей и единиц.
Далее в \((m+3)\)-й строке записано одно натуральное число \(k\) — количество функций \(g_1, \ldots, g_k\), для которых требуется найти формулу, \(1\leqslant k\leqslant 2000\).
Далее в \(k\) строках записаны векторы, задающие функции \(g_1, \ldots, g_k\) в том же формате, как и функции \(f_i\).
Формат выходных данных
Программа должна вывести через пробел последовательность из \(k\) нулей или единиц. Если функцию \(g_i\) можно представить формулой указанного вида, то \(i\)-й символ в последовательности должен быть единицей, иначе — нулем.
Тестовые данные
| Номер теста | Стандартный ввод | Стандартный вывод |
|---|---|---|
1 |
3 3 00010111 10000001 10110100 6 00000000 10000001 11111111 10010101 00010110 01000000 |
1 1 0 1 0 0 |
Примечания
Функцию с нулевым вектором можно получить по формуле \(f_1\wedge f_2\wedge f_3\).
Функция \(g_2\) совпадает с \(f_2\).
Построение функции \(g_4\) разобрано в примере.
Можно показать, что остальные функции нельзя получить в виде формул указанного вида.
Для булевых функций имеет место тождество \((x\vee y)\wedge z=(x\wedge z) \vee (y\wedge z)\). Используя это тождество, можно преобразовать любую формулу к виду \(K_1\vee K_2 \vee\cdots\vee K_s\), где \(K_j=f_{i_1}\wedge f_{i_2}\wedge\cdots\wedge f_{i_r}\). Поэтому будем искать представление произвольной функции \(g\) в виде формул такого вида. Обозначим за \(f(x)\) значение функции \(f\) на двоичном наборе \(x\). Заметим, что если \(f\) — это векторное представление функции в виде строки, то \(f(x)\) — это символ на позиции \(x\). Определим \(T_x\) как результат применения операции \(\wedge\) ко всем функциям \(f_i\), таким что \(f_i(x)=1\).
\[T_x=\bigwedge\limits_{f_i(x)=1} f_i.\]
Если не существует \(f_i\) таких, что \(f_i(x)=1\), то \(T_x=(0\ldots 0)\).
Заметим, что если \(K_j(x)=1\), то \(K_j\vee T_x=K_j\), так как в этом случае \(K_j\) состоит только из тех функций, которые входят в \(T_x\).
Рассмотрим представление \(g=K_1\vee K_2 \vee\cdots\vee K_s\). Если для некоторого \(x\) \(g(x)=1\), то найдется \(K_j\) такое, что \(K_j(x)=1\). Из этого, в частности, следует, что если некоторая функция \(g\) может быть представлена в виде формулы от \(f_1, \ldots, f_n\), и \(g(x)=1\), то \(g\vee T_x=g\).
Определим функцию \(g'\) по следующей формуле:
\[g'=\bigvee\limits_{g(x)=1} T_x.\]
Из построения \(g\vee g'=g'\). С другой стороны, если \(g\) может быть представлена в виде формулы от \(f_1, \ldots, f_n\), то \(g\vee g'=g\). Тогда, \(g=g'\). Отсюда следует алгоритм для решения задачи. Сначала найдем функции \(T(x)\) для всех \(x\) от нуля до \(2^k-1\).
Далее для каждой функции \(g_j\) найдем \(g'_j\). Если функции совпадут, то ответ существует, иначе — нет. Следует также отдельно рассмотреть случай \(g_j=(0\cdots 0)\).
При реализации следует обязательно использовать один из способов компактного хранения векторов. В языке Python каждый из двоичных векторов следует перевести в целое число, что упростит реализацию и существенно уменьшит время работы программы.
Пример программы-решения
Ниже представлено решение на языке Python.
from functools import reduce
k = 2**int(input())
n = int(input())
fbits = [input() for _ in range(n)]
fint = [int(t,2) for t in fbits]
fw = [0]*k
fwbits = ['']*k
for i in range(k):
b = 0
for j in range(n):
if fbits[j][i]=='1':
if b==0:
b = fint[j]
else:
b &= fint[j]
fw[i]=b
t = bin(b)[2:]
fwbits[i] = '0'*(k-len(t))+t
wed = reduce(lambda x,y:x&y,fint)
m = int(input())
for i in range(m):
g = input()
gint = int(g,2)
if gint==0:
print(int(wed==0),end=' ')
else:
b = 0
for j in range(k):
if g[j]=='1':
b |= fw[j]
print(int(b==gint),end=' ')Тест № 1 совпадает с тестом из условия задачи. Баллы за него не начисляются.
Успешное прохождение каждого теста №№ 2–29 оценивается в 1 балл.
В тестах №№ 2–7 количество переменных не превосходит \(3\). В качестве функций \(g_i\) используются все возможные функции от заданного числа переменных.
В тестах №№ 8–13 количество переменных не превосходит \(5\). При этом \(m\leqslant 50\), \(k\leqslant 100\).
В тестах №№ 14–21 количество переменных не превосходит \(8\). При этом \(m\leqslant 500\), \(k\leqslant 500\).