Инженерный тур. 2 этап
На втором отборочном этапе участники решают задачи по определению траектории полета, определению положения обнаруженного объекта, а также по обработке изображений. Задачи носят междисциплинарный характер и в упрощенной форме воссоздают элементы решения комплексной инженерной задачи заключительного этапа.
Командные задачи второго этапа инженерного тура открыты для решения. Соревнование доступно на платформе Яндекс.Контест: https://contest.yandex.ru/contest/69913/enter/.
Современные системы автоматического управления беспилотных летательных аппаратов (БЛА) самолетного типа преимущественно имеют следующие контуры управления:
- управление низкого уровня — выход на необходимые значения угловой ориентации (тангаж, крен, курс) и горизонтальной скорости полета БЛА;
- управление высокого уровня — формирование опорной траектории по полетному заданию, выданному оператором БЛА.
В рамках данной задачи необходимо разработать программу на языке программирования Python, которая по входному полетному заданию (ПЗ) — набору промежуточных пунктов маршрута (ППМ) в стартовой системе координат — рассчитывает оптимальную опорную траекторию по критерию кратчайшей траектории полета БЛА с учетом условий прохождения ППМ.
Считается, что БЛА передвигается на постоянной высоте \(H = const\) с постоянной крейсерской скоростью \(V_g=120\) км/ч, ограничение на максимальный угол крена \(-60° \leqslant \gamma \leqslant 60°\), ускорение свободного падения \(g=9{,}8 \text{~м/с}^2\), значение минимально допустимого радиуса разворота можно определить по формуле:
\[R=\frac{V_g^2}{g\cdot \operatorname{tg}(\gamma )}.\] Начальное положение БЛА — \(A(x_0,z_0)=(0{,}0)\) м.
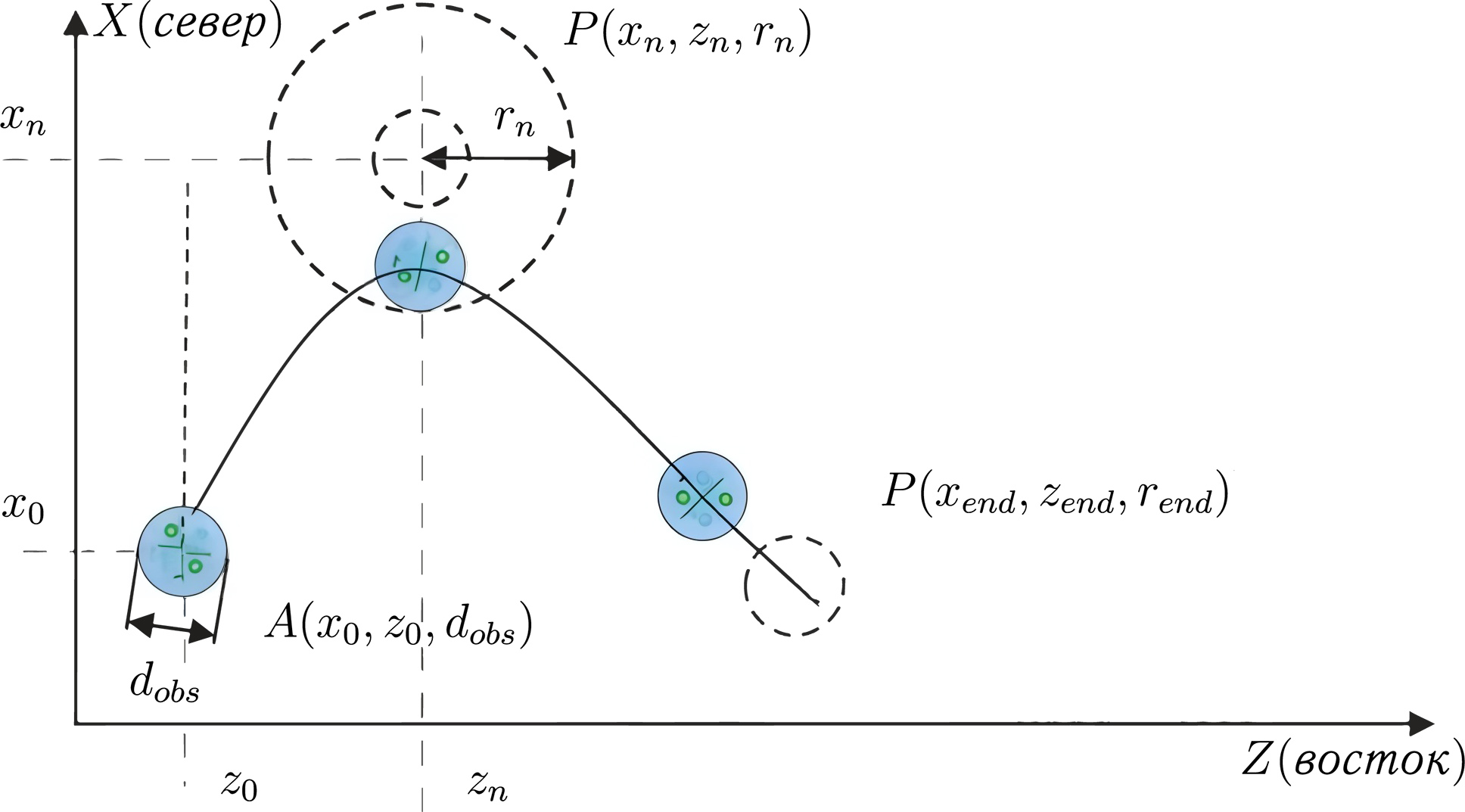
Входные данные на задачу ограничены тремя точками, СТ — точка старта, ППМ — промежуточный пункт маршрута с дополнительным критерием прохождения и КПМ — конечный пункт маршрута.
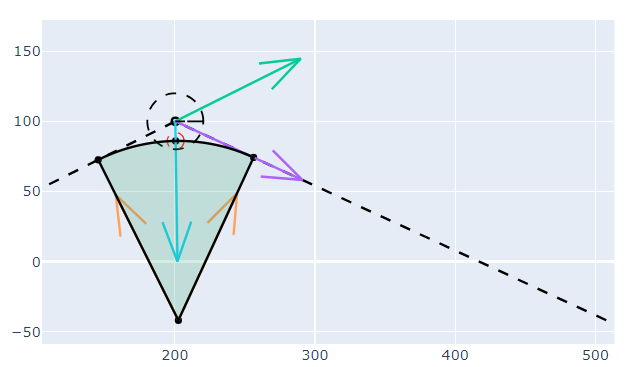
Критерием прохождения ППМ (точка 2) является попадание полного диаметра действия полезной нагрузки БЛА \(d_{obs}= 2r_{obs}\) в радиус ППМ \(r_n\). Рекомендуется использовать методы пролета точки с радиусом упреждения (Fillet Path).
Критерием прохождения КПМ (точка 3) является момент пересечения координат КПМ с опорной траекторией БЛА.
Формат входных данных
На вход программы поступает файл в формате CSV:
Z,X,r
0.0,0.0,9
1323.310446804855,741.2170326700434,35
3751.0326937190257,-425.39693527203053,0Данный файл можно легко прочитать, используя библиотеку Pandas, при помощи функции read_csv. На выходе данной функции вас будет ожидать DataFrame следующего вида, см. рис. 1.3.
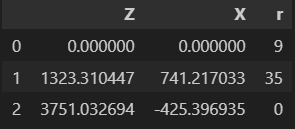
Нулевым индексом является исходное положение БЛА (СТ), в столбцах \(Z\) и \(X\) приведены соответствующие координаты (всегда равны нулю), в столбце с наименованием \(r\) приведен радиус действия полезной нагрузки \(d_{obs}= 2 r_{obs}\), значение \(r_{obs}\) отличается в каждом новом тесте.
Первым индексом является ППМ с условием прохождения, в столбцах \(Z\) и \(X\) приведены соответствующие координаты, значения которых отличаются в каждом новом тесте, в столбце с наименованием \(r\) приведен радиус зоны интереса ППМ \(r_{ppm}\), значение которого отличается в каждом новом тесте.
Вторым индексом является КПМ, в столбцах \(Z\) и \(X\) приведены соответствующие координаты, значения которых отличаются в каждом новом тесте, значение столбца с наименованием \(r\) на данном индексе всегда равно нулю ввиду условия задачи.
Формат выходных данных
На стандартный вывод программы требуется вывести одно число: суммарная длина полученной опорной траектории в метрах.
Пример:
4193.68Значение длины полученной опорной траектории всегда выводится с точностью до второго знака после запятой (даже если это нули).
Краткий алгоритм решения задачи:
- прочитать входные данные из файла;
- определить минимальный радиус разворота;
- определить угол между линиями пути треугольника точек;
- найти биссектрису угла между линиями пути;
- найти точку, при прохождении которой выполняются условия перемещения радиуса интереса ППМ с полным диаметром действия полезной нагрузки;
- найти радиус дуги и центр окружности, формирующей эту дугу, для построения траектории при пересечении этой точки;
- найти точки перехода с прямолинейной траектории на дугу окружности;
- найти длины всех участков траектории и сложить их, чтобы получить длину всей траектории.
import numpy as np
import pandas as pd
from math import cos,sin,hypot,tan,hypot,pi,pow
import math
# Матрица пересчета на ось Z
def rotz(theta=None):
# Rotation around z
R = np.array([ [cos(theta), -sin(theta), 0],
[sin(theta), cos(theta), 0],
[0, 0, 1] ])
return R
# Угол между векторами через библиотеку numpy
def angle_between_vectors_np(u, v):
u = np.array(u)
v = np.array(v)
cos_theta = np.dot(u, v) / (np.linalg.norm(u) * np.linalg.norm(v))
angle_rad = np.arccos(np.clip(cos_theta, -1.0, 1.0))
angle_deg = np.degrees(angle_rad)
return angle_rad, angle_deg
def solve(filename):
# минимальный радиус разворота
Vg = 120/3.6
gamma_max = math.radians(60)
g = 9.8
R_min = math.pow(Vg,2)/(g*math.tan(gamma_max))
# Загрузка ПЗ
df_input = pd.read_csv(filename)
# Объявим точки как массив
w_0 = np.array([df_input["Z"][0],df_input["X"][0],0]).T
w_1 = np.array([df_input["Z"][1],df_input["X"][1],0]).T
w_2 = np.array([df_input["Z"][2],df_input["X"][2],0]).T
# Загрузим радиус действия полезной нагрузки и радиус интереса ППМ
# Радиус обзора полезной нагрузки
R_obs = df_input["r"][0]
# Радиус интереса ППМ
R_wp = df_input["r"][1]
# Найдем единичные вектора между точками
q_s = (w_1 - w_0) / np.linalg.norm(w_1 - w_0,ord=2)
q_n = (w_2 - w_1) / np.linalg.norm(w_2 - w_1,ord=2)
# Найдем угол между линиями пути треугольника точек
theta,theta_degrees = angle_between_vectors_np(-q_s.T,q_n)
# Найдем вектор отражающий биссектрису найденного угла
q_R = q_n @ rotz(theta/2)
# Найдем точку при прохождении которой, выполняются условия прохождения радиуса интереса ППМ с полным диаметром действия полезной нагрузки
# point_org_global = w_1 - np.dot(-R_wp+R_obs,q_R)
# Найдем необходимый радиус дуги окружности для построения траектории при пересечении этой точки
R_calc = (abs(-R_wp+R_obs))/(1/sin(theta/2) -1)
R = R_calc if (R_calc > R_min) else R_min
# Найдем центр окружности формирующей дугу
center_circle = w_1 - (R/sin(theta/2))*(q_s - q_n) / np.linalg.norm(q_s - q_n,ord=2)
# Найдем точки перехода с прямолинейной траектории на дугу окружности
r1 = w_1 - np.dot(R/tan(theta/2),q_s)
r2 = w_1 + np.dot(R/tan(theta/2),q_n)
# Найдем угол сектора, чтобы рассчитать длину дуги
q_r1 = (r1 -center_circle) / np.linalg.norm(r1 -center_circle,ord=2)
q_r2 = (r2 -center_circle) / np.linalg.norm(r2 - center_circle,ord=2)
theta_R,theta_R_degrees = angle_between_vectors_np(q_r1,q_r2)
# Найдем длину первого прямолинейного участка до точки r1
L_0 = hypot(w_0[0]-r1[0],w_0[1]-r1[1])
# Найдем длину дуги окружности
L_R = theta_R * R
# Найдем длину второго участка траектории после точки r2
L_2 = hypot(r2[0]-w_2[0],r2[1]-w_2[1])
# Найдем общую длину траектории
L = L_0 + L_R + L_2
# Выведем длину участка, с точностью до 2 знака после запятой
print("%.2f" % L)
solve("input.txt")К задаче разработано пять автоматических тестов. За прохождение каждого из этих тестов решение участников набирает 5 баллов (максимум 25 баллов за задачу).
Ссылка на тестовые данные и материалы задачи: https://disk.yandex.ru/d/tF438BK2KnLDCg/1.
Задача поиска объектов является одной из основных задач, решаемых бортовой системой технического зрения.
При решении этой задачи требуется не только обрабатывать полученные изображения и распознавать на них искомые объекты, но и определять их координаты на основе информации о текущем местоположении БЛА, дальности и угломерной информации о визируемом объекте. Также может решаться обратная задача. При заранее известных координатах визируемых объектов определяются параметры движения самого БЛА. Для этого могут использоваться либо заведомо известные параметры искомых объектов, либо дополнительные датчики (например, лазерный дальномер).
Предположим, что БЛА совершает автоматический полет и его бортовая программа должна, на основе измерения системы технического зрения, определять количество искомых ориентиров в кадре. Кроме того, БЛА оснащен лазерным дальномером, оси которого жестко связаны со строительными осями БЛА. Измерение дальности происходит по оси \(Y_b\) в обратном направлении. Кватернион ориентации БЛА относительно нормальной земной системы координат известен.
Математически кватернион \(q(w, x, y, z)\) можно записать так: \[q = w + xi + yj + zk,\] где \(w, x, y, z\) — вещественные числа; \(i, j, k\) — мнимые единицы.
Параметры \(x, y, z\) характеризуют направление оси вращения (проекции орта оси вращения на оси \(i, j, k\)). Параметр \(w\) характеризует величину угла поворота.
Таким образом, кватернион описывает ориентацию объекта как кратчайший поворот вокруг произвольно направленной оси (в то время как при использовании углов Эйлера вращение всегда происходит вокруг одних и тех же осей). Кватернион обладает следующими свойствами:
- модуль кватерниона всегда должен быть равен единице;
- кватернион может быть использован как для представления ориентации объекта, так и для представления изменения ориентации (вращения);
- кватернион вращения всегда описывает кратчайший поворот.
Напишите программу, обрабатывающую входное изображение, определяющую количество контрастных ориентиров на этом изображении и реализующую расчет высоты полета БЛА по измерениям лазерного дальномера с учетом кватерниона ориентации БЛА.
Формат входных данных
На вход программы поступает файл в формате PGM (https://netpbm.sourceforge.net/doc/pgm.html):
P2
# 130.5 0.966 0.0 0.0 0.259
320 240 220 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 63 129 63 63 115 63 63 63 63 63 63 63Первое значение P2 — идентификатор формата pgm.
Вторая строка, отмеченная символом #, — это комментарий. Он не содержит данных, связанных с изображением, но содержит измерения лазерного дальномера и кватернион ориентации БЛА в момент получения изображения, записанные через пробел.
В рассматриваемом примере:
- значение 130.5 — расстояние в метрах, измеренное лазерным дальномером;
- 0.966 — значение \(W\) кватерниона ориентации;
- 0.0 0.0 0.259 — значения проекций вектора поворота на орты осей \(X_b\), \(Y_b\), \(Z_b\) соответственно.
Первые два числа третьей строки — разрешение изображения (количество пикселей по горизонтали и вертикали).
В примере изображение содержит 320 px (пикселей) по горизонтали и 240 px по вертикали.
Третье число третьей строки — максимальная яркость пикселя изображения в файле.
В примере максимальная яркость составляет 220 единиц.
Каждое следующее число — яркость 1 px (пикселя) изображения в интервале от 0 до указанного максимального значения (которое не может превышать 255). Яркость пикселей записывается в порядке слева направо и сверху вниз. В представленном примере первые 320 пикселей после значения максимальной яркости описывают первую (верхнюю) строку изображения.
Значение яркости 0 соответствует черному цвету на изображении. Значение 255 — белому цвету.
Формат выходных данных
На стандартный вывод программы требуется вывести два числа, записанные через пробел: высоту полета БЛА и число контрастных ориентиров в кадре.
Пример ответа:
90.57 8Значение высоты всегда выводится с точностью до второго знака после запятой (даже если это нули). Количество ориентиров в кадре всегда целое.
Примечания
Ориентирами считаются «светлые» области кадра, значение яркости которых превышает некоторое пороговое значение.
Гарантируется, что на вход программы поступает изображение в формате pgm.
Гарантируется, что вторая строка файла — комментарий, содержащий измерение лидара (лазерного дальномера) и кватернион ориентации.
Краткий алгоритм решения задачи:
- прочитать входные данные из файла;
- найти углы Эйлера, используя заданный кватернион;
- найти высоту полета БЛА, используя найденные углы Эйлера и заданное значение показаний дальномера;
- выполнить размытие изображения;
- подобрать значение пороговой яркости;
- выполнить поиск и подсчет контрастных ориентиров.
from math import sin, cos, sqrt, atan2, asin, pi
import sys
import copy
def normalize_quaternion(q):
w, x, y, z = q
norm = sqrt(w**2 + x**2 + y**2 + z**2)
if norm == 0:
raise ValueError("Cannot normalize a zero quaternion")
return (w / norm, x / norm, y / norm, z / norm)
def quaternion_to_euler(q):
# Normalize the quaternion
q = normalize_quaternion(q)
w, x, y, z = q
# Calculate roll (phi)
roll = atan2(2 * (y * z + w * x), 1 - 2 * (y**2 + x**2))
# Calculate pitch (theta)
pitch = asin(2 * (w * y - x * z))
# Calculate yaw (psi)
yaw = atan2(2 * (x * y + w * z), 1 - 2 * (z**2 + y**2))
return (roll, pitch, yaw)
def apply_simple_blur(image):
"""Apply a simple blur to a 2D list representing an image."""
height = len(image)
width = len(image[0])
blurred_image = [[0] * width for _ in range(height)]
# Define the blur radius
radius = 1 # Since we want to blur within 3 pixels area (1 on each side)
for i in range(height):
for j in range(width):
total = 0
count = 0
# Iterate over the neighborhood
for dx in range(-radius, radius + 1):
for dy in range(-radius, radius + 1):
nx, ny = i + dx, j + dy
# Check bounds
if 0 <= nx < height and 0 <= ny < width:
total += image[nx][ny]
count += 1
# Calculate the average and assign it to the blurred image
blurred_image[i][j] = total // count # Use integer division
return blurred_image
def numIslands(grid, weight) -> int:
# weight = 0.8
def dfs(row, col):
if grid[row][col] < weight:
return 0
grid[row][col] = 0.0
if (col + 1) < len(grid[0]):
dfs(row, col+1)
if col > 0:
dfs(row, col-1)
if (row + 1) < len(grid):
dfs(row+1, col)
if row > 0:
dfs(row - 1, col)
return 1
count = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] >= weight:
count += 1
dfs(i, j)
return count
def solve(filename):
f = open(filename, "r")
inp = f.read()
arr = inp.split(" ")
laser = float(arr[2])
quat = [float(x) for x in arr[3:7]]
quat_sum = sqrt(quat[0]**2 + quat[1]**2 + quat[2]**2 + quat[3]**2)
if not quat_sum == 1:
quat = [quat[0] / quat_sum, quat[1] /quat_sum, quat[2] / quat_sum, quat[3] / quat_sum]
width = int(arr[7])
height = int(arr[8])
max_brightness = int(arr[9])
pgm_image = [int(x) for x in arr[10:-1]]
rot = quaternion_to_euler([quat[0], quat[1], quat[3], quat[2]])
angles = rot
H = cos(angles[0] ) * cos(angles[1]) * laser
norm_image = [float(x) for x in pgm_image]
norm_image_arr = []
for i in range(int(len(norm_image) / width)):
norm_image_arr.append(norm_image[i*(width):(i+1)*width])
norm_image_arr = apply_simple_blur(norm_image_arr)
sys.setrecursionlimit(85000)
sacrefise = copy.deepcopy(norm_image_arr)
sol = numIslands(sacrefise, 0.8 * max_brightness)
bright_pixels = [x for x in norm_image if x > 0.8*max_brightness]
print(f'{H:.2f} {sol}')
solve('input.txt')
К задаче разработано 15 автоматических тестов. За прохождение каждого из этих тестов решение участников набирает 2 балла (максимум 30 баллов за задачу).
Ссылка на тестовые данные и материалы задачи: https://disk.yandex.ru/d/tF438BK2KnLDCg/2.
При поиске различных объектов при помощи БЛА чаще всего используются алгоритмы распознавания объектов на изображении. Однако после обнаружения объекта на изображении необходимо определить его координаты в реальном мире. При решении такой задачи необходимо учитывать множество факторов, в частности, рельеф обследуемой местности.
Напишите программу для определения долготы и широты обнаруженного объекта, который лежит на оптической оси камеры БЛА, летящего горизонтально вдоль поверхности земли.
Для решения известны координаты БЛА, кватернион ориентации и карта рельефа местности. Координаты БЛА задаются в географической системе координат: широта, долгота, истинная высота. Считается, что координаты БЛА совпадают с координатами камеры. Кватернион описывает ориентацию осей камеры относительно осей нормальной земной системы координат. Направление осей нормальной земной системы координат вводится следующим образом:
- ось \(XX\) направлена на восток,
- ось \(YY\) направлена на север,
- ось \(ZZ\) направлена вертикально вверх.
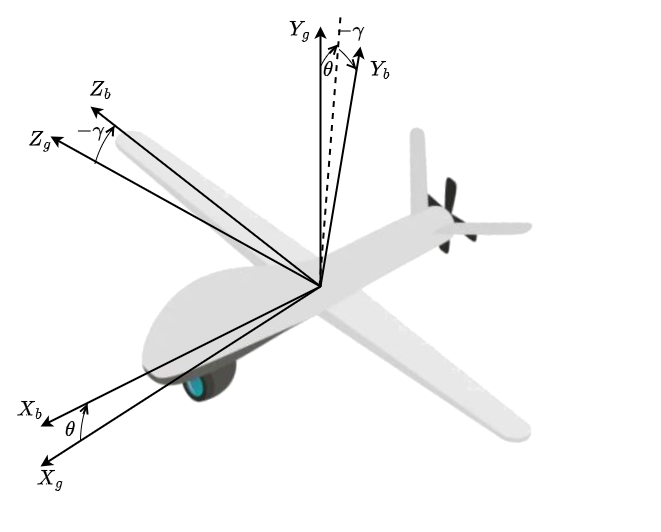
Направление осей камеры отображено на рис. 1.5.
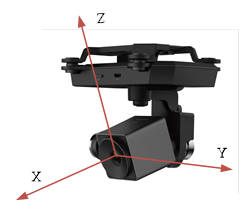
Сам рельеф задан в виде высот над общеземным эллипсоидом, записанных в виде матрицы, где каждое значение определяет фиксированную высоту в квадрате \(1\times 1\) м. Для позиционирования матрицы задаются координаты центра квадрата ее верхнего левого угла. Каждый ряд матрицы — это набор высот в положительном направлении оси \(x\), а каждый столбец — это набор высот в отрицательном направлении оси \(y\). Базовым направлением оптической оси камеры считается направление строго на восток.
В масштабах, рассматриваемых в задаче, местность считается плоской, то есть кривизну Земли учитывать не надо, однако изменения градуса долготы на разных широтах учитывать необходимо. Атмосферные искажения и другие внешние факторы, влияющие на распространение оптического сигнала, также учитывать не нужно. Считать, что одна угловая минута по широте равна одной морской миле. Угловое расстояние по долготе пересчитать с использованием сферической геометрии.
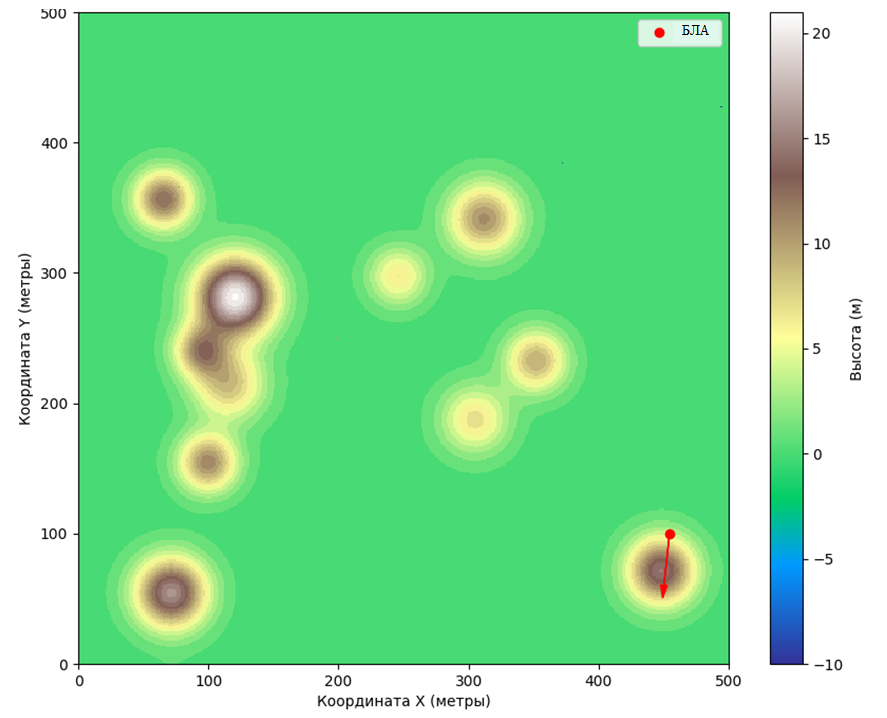
Теоретическую информацию по понятию «кватернион» можно получить из задачи [task:bas0103] инженерного тура первого этапа «Кватернион ориентации». На рис. 1.6 представлена визуализация примера исходных данных — изображен рельеф местности (используются данные матрицы абсолютных высот \(500 \times 500\)) с положением БЛА (координаты БЛА) и направлением камеры (кватернион ориентации камеры).
Формат входных данных
В реальных данных задачи рельеф задается матрицей \(500 \times 500\).
Пример
Координаты БЛА (широта, долгота) и истинная высота:
55.811539 37.499727 8Кватернион ориентации камеры в формате \(w~x~y~z\):
1 0 0 0Координаты верхнего левого угла матрицы абсолютных высот:
55.811539 37.499727Фрагмент матрицы абсолютных высот (\(500\times500\)), задающей рельеф местности:
22 17 16 20 30
23 17 15 18 27
22 17 14 19 25
20 17 10 19 23
18 17 10 12 20Формат выходных данных
На стандартный вывод программы требуется вывести два числа, записанные через пробел: долгота и широта обнаруженного объекта, лежащего на оптической оси камеры. В случае невозможности по любой причине определения координат обнаруженного объекта выведите координаты БЛА.
Пример ответа:
55.801453 37.471452Значение всегда выводится с точностью до шестого знака после запятой (даже если это нули).
Краткий алгоритм решения задачи:
- прочитать входные данные из файла;
- преобразовать градусы в метры;
- преобразовать координаты БЛА в его координаты в матрице рельефа;
- вычислить направление камеры;
- нормализовать вектор направления камеры;
- найти координаты точки пересечения вектора с матрицей рельефа;
- преобразовать координаты точки пересечения в географические координаты.
import numpy as np
def quaternion_rotate_vector(q, v):
# Поворот вектора v с помощью кватерниона q
qvec = np.array([q[0], q[1], q[2]])
uv = np.cross(qvec, v)
uuv = np.cross(qvec, uv)
uv *= (2.0 * q[3])
uuv *= 2.0
return v + uv + uuv
def get_terrain_height(terrain_matrix, x, y):
# Получение высоты рельефа в точке (x, y) без интерполяции
x0 = int(np.floor(x))
y0 = int(np.floor(y))
if x0 < 0 or x0 >= terrain_matrix.shape[1] or y0 < 0 or y0 >= terrain_matrix.shape[0]:
return None
return terrain_matrix[y0, x0]
def find_intersection(uav_pos, direction, terrain_matrix):
t = 0.0
delta_t = 0.5 # Шаг в метрах
max_distance = 10000 # Максимальное расстояние поиска (в метрах)
uav_x, uav_y, uav_z = uav_pos
dx, dy, dz = direction
terrain_size = terrain_matrix.shape[0]
while t < max_distance:
x = uav_x + t * dx
y = uav_y + t * dy
z = uav_z + t * dz
if x < 0 or x >= terrain_size - 1 or y < 0 or y >= terrain_size - 1:
# Луч вышел за пределы рельефа без пересечения
return None
terrain_height = get_terrain_height(terrain_matrix, x, y)
if terrain_height is None:
return None
if z <= terrain_height:
# Найдена точка пересечения
# Уточнение точки пересечения
# Возврат назад и использование меньших шагов
t_high = t
t_low = t - delta_t
for _ in range(100):
t_mid = (t_low + t_high) / 2.0
x_mid = uav_x + t_mid * dx
y_mid = uav_y + t_mid * dy
z_mid = uav_z + t_mid * dz
terrain_height_mid = get_terrain_height(terrain_matrix, x_mid, y_mid)
if terrain_height_mid is None:
return None
if z_mid <= terrain_height_mid:
t_high = t_mid
else:
t_low = t_mid
t = t_high
x = uav_x + t * dx
y = uav_y + t * dy
z = uav_z + t * dz
return x, y, z # Точка пересечения в координатах рельефа
t += delta_t
# Пересечение не найдено в пределах максимального расстояния
return None
def read_and_compute(filename):
with open(filename, 'r') as f:
lines = f.readlines()
# Чтение координат БЛА и высоты
uav_line = lines[0].strip()
uav_latitude, uav_longitude, uav_altitude = map(float, uav_line.split())
if uav_altitude < 0:
print(f"{uav_latitude:.6f} {uav_longitude:.6f}")
return
# Чтение кватерниона
quat_line = lines[1].strip()
qw, qx, qy, qz = map(float, quat_line.split())
# Чтение начальных координат рельефа
terrain_line = lines[2].strip()
terrain_latitude, terrain_longitude = map(float, terrain_line.split())
# Чтение матрицы рельефа
terrain_data = lines[3:]
terrain_matrix = np.array([list(map(int, line.strip().split())) for line in terrain_data])
terrain_matrix = np.flipud(terrain_matrix)
# Конвертация градусов в метры
latitude_rad = np.radians(terrain_latitude)
meters_per_degree_latitude = 111120 # Среднее количество метров на градус широты
meters_per_degree_longitude = 111120 * np.cos(latitude_rad) # Метров на градус долготы зависит от широты
# Преобразование координат БЛА в координаты матрицы рельефа
delta_lat_uav = uav_latitude - (terrain_latitude - terrain_matrix.shape[0]/meters_per_degree_latitude)
delta_lon_uav = uav_longitude - terrain_longitude
delta_x_meters = delta_lon_uav * meters_per_degree_longitude
delta_y_meters = delta_lat_uav * meters_per_degree_latitude
# Координаты БЛА в матрице рельефа
uav_x = delta_x_meters
uav_y = delta_y_meters
terrain_height_under_uav = get_terrain_height(terrain_matrix, uav_x, uav_y)
if terrain_height_under_uav is None:
print(f"{uav_latitude:.6f} {uav_longitude:.6f}")
return
uav_z = uav_altitude + terrain_height_under_uav
# Вычисление направления камеры
q = np.array([qx, qy, qz, qw])
camera_forward = np.array([1, 0, 0]) # Ось X в системе координат камеры (направление оптической оси)
direction_vector = quaternion_rotate_vector(q, camera_forward)
# Нормализация вектора направления
norm_dir = np.linalg.norm(direction_vector)
if norm_dir == 0:
print(f"{uav_latitude:.6f} {uav_longitude:.6f}")
return
direction = direction_vector / norm_dir
# Поиск точки пересечения
intersection = find_intersection((uav_x, uav_y, uav_z), direction, terrain_matrix)
if intersection is None:
print(f"{uav_latitude:.6f} {uav_longitude:.6f}")
return
intersect_x, intersect_y, intersect_z = intersection
# Преобразование координат точки пересечения обратно в географические координаты
delta_lat_intersect = intersect_y / meters_per_degree_latitude
delta_lon_intersect = intersect_x / meters_per_degree_longitude
object_latitude = (terrain_latitude - terrain_matrix.shape[0]/meters_per_degree_latitude) + delta_lat_intersect
object_longitude = terrain_longitude + delta_lon_intersect
print(f"{object_latitude:.6f} {object_longitude:.6f}")
read_and_compute('input.txt')К задаче разработано девять автоматических тестов. За прохождение каждого из этих тестов решение участников набирает 5 баллов (максимум 45 баллов за задачу).
Ссылка на тестовые данные и материалы задачи: https://disk.yandex.ru/d/tF438BK2KnLDCg/3.