Инженерный тур. 1 этап
Летательный аппарат (ЛА) совершает горизонтальной полет на высоте \(H = 13500\) м с постоянной скоростью \(V = 550\) км/ч. Масса ЛА \(m = 9980\) кг, площадь крыла \(S = 36{,}7\) \(\text{м}^2\), коэффициент лобового сопротивления \(Cx_a=0{,}025\). Плотность воздуха \(\rho = 0{,}2465~ \text{кг}/\text{м}^3\), ускорение свободного падения \(g = 9{,}81~ \text{м}/\text{с}^2\).
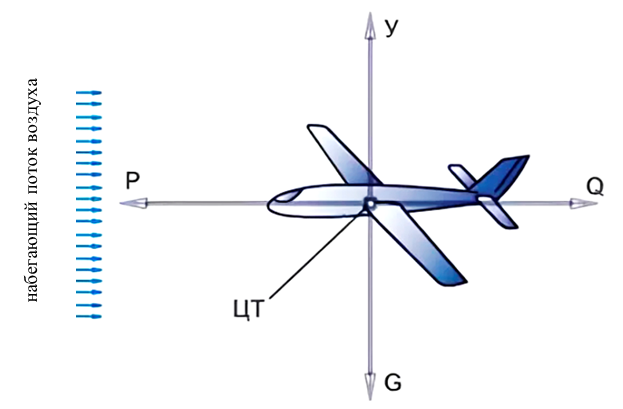
Горизонтальный полет — прямолинейный полет с постоянной скоростью на постоянной высоте. Схема сил, действующих на самолет, показана на рис. 1.1: \(\text{Y}\) — подъемная сила, \(\text{P}\) — тяга самолета, \(\text{Q}\) — сила лобового сопротивления, \(\text{ЦТ}\) — центр тяжести, \(\text{G}\) — сила тяжести.
\(Q = Cx_a \dfrac{\rho V^2}{2} S\) — лобовое сопротивление, H;
\(Y = Cy_a \dfrac{\rho V^2}{2} S\) — подъемная сила, H.
Аэродинамическое качество \(K\) в горизонтальном полете равно отношению подъемной силы к силе лобового сопротивления: \[K =\frac{Y}{Q}.\]
Определите аэродинамическое качество \(K\) в горизонтальном полете. Ответ округлите до целого числа.
Введем систему координат, связанную с летательным аппаратом. Начало координат совпадает с его центром тяжести; ось \(X\) направлена вдоль продольной оси в сторону носа ЛА; ось Y перпендикулярна оси \(X\), лежит в вертикальной плоскости симметрии ЛА и направлена вверх; ось \(Z\) перпендикулярна осям \(X\) и \(Y\) и направлена вдоль крыла вправо.
Воспользуемся вторым законом Ньютона и запишем уравнение для проекций на ось \(OY\) сил, действующих на летательный аппарат: \[Y-mg = 0.\]
Выразим коэффициент подъемной силы через силу тяжести: \[Cy_a=\dfrac{mg}{\dfrac{\rho V^2}{2} S}.\]
Найдем выражение для аэродинамического качества, используя формулы из условия: \[K=\dfrac{Y}{Q}= \dfrac{Cy_a \dfrac{\rho V^2}{2}}{Cx_a \dfrac{\rho V^2}{2}} =\dfrac{Cy_a}{Cx_a} = \dfrac{\dfrac{mg}{\dfrac{\rho V^2}{2} S}}{Cx_a} =\dfrac{2mg}{Cx_a \rho V^2 S}.\]
Подставим значения из условия и учтем перевод скорости из километров в час в метры в секунду: \[K=\dfrac{2\cdot 9980\cdot9{,}81}{0{,}025\cdot0{,}2465\cdot\left(\dfrac{550}{3{,}6}\right)^2\cdot36{,}7}\approx 37{,}0925.\]
По условию требуется округлить ответ до целого числа. Получаем 37.
37.
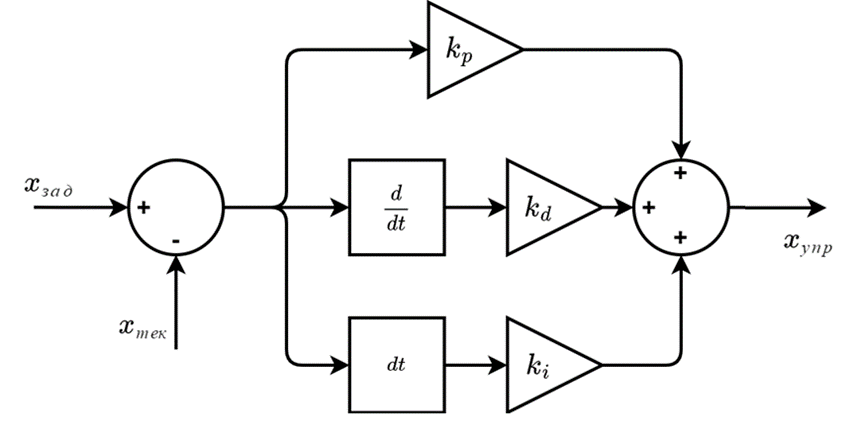
Одним из самых простых и эффективных подходов к управлению движением БВС является использование ПИД-регуляторов. Такие регуляторы включают в себя три звена: пропорциональное, интегральное и дифференциальное. Структура ПИД-регулятора представлена на рис. 1.2.
Как показано на рис. 1.2, на вход регулятора подается значение ошибки регулируемой величины (разница целевого значения \(x_{\text{зад}}\) и текущего значения \(x_{\text{тек}}\)). Эта ошибка поступает на вход трех звеньев: пропорционального, интегрального и дифференциального. Пропорциональное звено умножает (усиливает) значение ошибки на некоторый постоянный коэффициент \(k_p\), интегральное звено умножает интеграл ошибки на коэффициент \(k_i\), а дифференциальное звено умножает производную ошибки на коэффициент \(k_d\). На выходе ПИД-регулятора формируется управляющий сигнал \(x_{\text{упр}}\), размерность управляющего сигнала соответствует производной управляемой величины.
Математическое представление этой структуры имеет вид: \[\delta=x_{\text{зад}}-x_{\text{тек}};\] \[x_{\text{упр}}=k_p \delta+k_i \int_{\square}^{\square} \square \delta dt+k_d \dfrac{d}{dt} \delta.\]
Таким образом, для формирования управляющего сигнала необходимо знать только целевое значение регулируемой величины, ее текущее значение и значения трех постоянных коэффициентов.
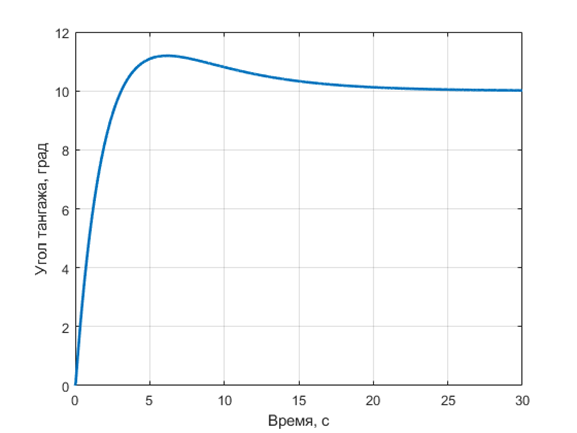
Естественным подходом к нахождению значений коэффициентов \(k_p\), \(k_i\), \(k_d\) является ручной перебор их значений с целью получения удовлетворительного переходного процесса. Пример такого процесса представлен на рис. 1.3.
При моделировании точные значения коэффициентов можно вычислить, если построить математическую модель всей системы в целом (БВС). Однако для реального БВС точной модели движения не существует, поэтому можно найти лишь приближенные значения коэффициентов. Для этого используют сложные математические методы оптимизации вроде метода градиентного спуска и других. Применение этих методов на практике довольно трудозатратно и не всегда возможно.
В то же время большинство современных полетных контроллеров обладают функцией автоматического определения параметров регулятора. Они тоже используют математический метод оптимизации, только упрощенный — метод Циглера – Никольса.
Этот метод достаточно прост и заключается в последовательном выполнении следующих операций:
- обнуляем все коэффициенты регулятора;
- задаем некоторое целевое значение регулируемой величины \(x_{\text{зад}}\);
- постепенно начинаем увеличивать пропорциональный коэффициент \(k_p\) и отслеживаем реакцию системы (БВС);
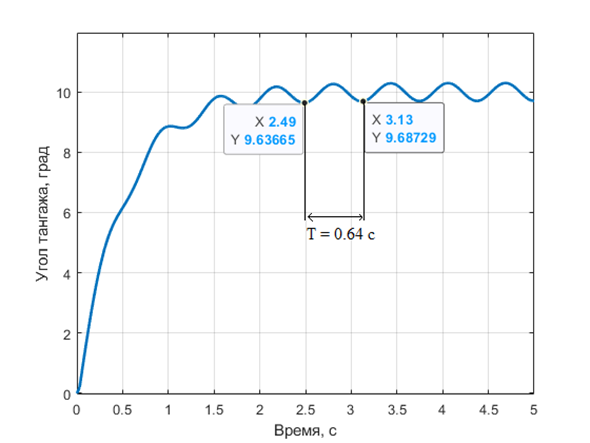
- при определенном значении коэффициента возникнут незатухающие колебания регулируемой величины (см. рис. 1.4);
- записываем значение пропорционального коэффициента, при котором возникают незатухающие колебания, как \(K\).
Из полученного значения \(K\) можно рассчитать значения всех коэффициентов ПИД-регулятора. Для этого воспользуемся соотношениями: \[\begin{gather} k_p=0,6\times K;\\ k_i=\dfrac{2k_p}{T};\\ k_d=\dfrac{k_p T}{8}, \end{gather}\] где \(T\) — период колебаний системы (см. рис. 1.4).
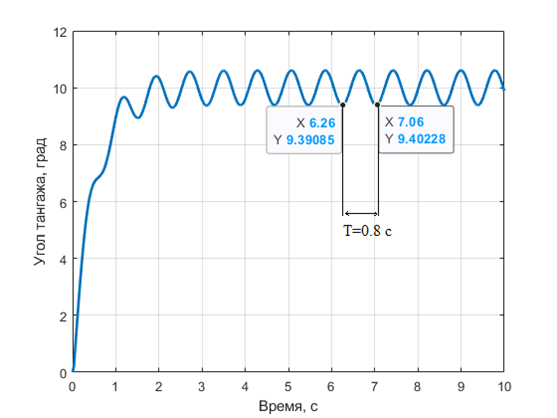
Рассчитайте значения всех трех коэффициентов \(k_p\), \(k_i\), \(k_d\) ПИД-регулятора управления углом тангажа БВС, если при формировании целевого значения угла тангажа \(x_{\text{зад}}=10°\), и значении пропорционального коэффициента \(k_p=1{,}4\) \(1/\text{с}\) был получен следующий отклик системы (переходный процесс) — рис. 1.5.
Варианты ответа:
- \(k_p=1{,}12\), \(k_i=2{,}8\), \(k_d=0{,}112\);
- \(k_p=1{,}4\), \(k_i=3{,}5\), \(k_d=0{,}14\);
- \(k_p=1{,}75\), \(k_i=4{,}375\), \(k_d=0{,}175\);
- \(k_p=0{,}84\), \(k_i=2{,}1\), \(k_d=0{,}084\);
- \(k_p=1{,}4\), \(k_i=2{,}5\), \(k_d=0{,}08\);
- \(k_p=0{,}84\), \(k_i=1{,}05\), \(k_d=0{,}084\).
Согласно методу Циглера – Никольса нужно значение \(K\). Из условия задачи получаем, что \(K=1{,}4\).
Для расчета коэффициентов ПИД-регулятора также требуется значение \(T\). Из представленного в условии графика получаем \(T=0{,}8\) с.
Подставим полученные значения в формулы коэффициентов из условия: \[\begin{gather} k_p=0,6\times K=0,84;\\ k_i=\dfrac{2k_p}{T}=2,1;\\ k_d=\dfrac{k_p T}{8}=0,084. \end{gather}\]
4.
Привычным способом представления ориентации объекта являются углы его поворота вокруг трех взаимоперпендикулярных осей — углы Эйлера. В бытовых задачах это действительно самый удобный и интуитивно понятный способ представления ориентации объекта, однако для представления ориентации подвижных объектов с шестью степенями свободы (например, БВС) углы Эйлера плохо подходят про двум основным причинам. Причина первая — при вращении БВС вокруг трех осей итоговая ориентация будет зависеть от порядка поворотов. Вторая причина — явление «складывания рамок» (gimbal lock), при котором одна из осей поворота фактически вырождается. Подробнее про этот эффект можно почитать по ссылке: https://ru.wikipedia.org/wiki/Складывание_рамок.
В этой связи в задачах навигации подвижных объектов для представления их ориентации используют кватернионы. С научной точки зрения кватернион — вектор из четырех гиперкомплексных чисел. С практической точки зрения — это вектор из четырех параметров, который позволяет однозначно представить ориентацию объекта в пространстве и не обладает недостатками углов Эйлера. Математически кватернион \(q(w, x, y, z)\) можно записать так: \[q=w+xi+yj+zk,\] где \(w\), \(x\), \(y\), \(z\) — вещественные числа; \(i\), \(j\), \(k\) — мнимые единицы.
Параметры \(x\), \(y\), \(z\) характеризуют направление оси вращения (проекции орта оси вращения на оси \(i\), \(j\), \(k\)). Параметр \(w\) характеризует величину угла поворота.
Таким образом, кватернион описывает ориентацию объекта как кратчайший поворот вокруг произвольно направленной оси (в то время как при использовании углов Эйлера вращение всегда происходит вокруг одних и тех же осей).
Кватернион обладает следующими свойствами:
- модуль кватерниона всегда равен единице;
- кватернион может быть использован как для представления ориентации объекта, так и для представления изменения ориентации (вращения);
- кватернион вращения всегда описывает кратчайший поворот.
Допустим, у нас есть кватернион ориентации объекта \(S\) и кватернион вращения \(R\). Тогда итоговую ориентацию объекта \(T\) после поворота из ориентации \(S\) на кватернион \(R\) можно получить путем векторного перемножения: \[\begin{gather} T=R\times S;\\ T_w=R_w\cdot S_w-R_x\cdot S_x-R_y\cdot S_y-R_z\cdot S_z;\\ T_x=R_x\cdot S_w+R_w\cdot S_x+R_z\cdot S_y-R_y\cdot S_z;\\ T_y=R_y\cdot S_w-R_z\cdot S_x+R_w\cdot S_y+R_x\cdot S_z;\\ T_z=R_z\cdot S_w+R_y\cdot S_x-R_x\cdot S_y+R_w\cdot S_z. \end{gather}\] Найдите итоговый кватернион ориентации БВС \(T\), если до осуществления поворота ориентация БВС была представлена кватернионом \(S = (0{,}707,~ 0,~ 0{,}707,~ 0)\), а кватернион поворота равен \(R = (0{,}95, 0{,}083, -0{,}026, 0{,}3)\).
Примечание: в силу округления до третьего знака после запятой и ошибок вычисления, модуль итогового кватерниона может незначительно отличаться от единицы.
Варианты ответа:
- \(T = (0{,}478, -0{,}002, -0{,}833, 0{,}278)\),
- \(T = (0{,}69, 0{,}293, 0{,}562, 0{,}349)\),
- \(T = (0{,}269, -0{,}39, 0{,}748, -0{,}465)\),
- \(T = (0{,}269, 0{,}691, 0{,}152, 0{,}654)\),
- \(T = (0{,}679, -0{,}297, 0{,}570, -0{,}354)\),
- \(T = (0{,}69, 0{,}2708, 0{,}6533, 0{,}1534)\).
Воспользуемся формулами для итогового кватерниона ориентации БВС \(T\), представленными в условии, и подставим из условия значения кватернионов \(R\) и \(S\): \[\begin{gather} T_w=R_w\cdot S_w-R_x\cdot S_x-R_y\cdot S_y-R_z\cdot S_z=0,69;\\ T_x=R_x\cdot S_w+R_w\cdot S_x+R_z\cdot S_y-R_y\cdot S_z=0,2708;\\ T_y=R_y\cdot S_w-R_z\cdot S_x+R_w\cdot S_y+R_x\cdot S_z=0,6533;\\ T_z=R_z\cdot S_w+R_y\cdot S_x-R_x\cdot S_y+R_w\cdot S_z=0,1534. \end{gather}\]
6.
При поиске различных объектов при помощи БВС чаще всего используются алгоритмы распознавания объектов на изображении, однако после обнаружения объекта на изображении необходимо определить его координаты в реальном мире. При решении такой задачи необходимо учитывать множество факторов, в частности, рельеф обследуемой местности.
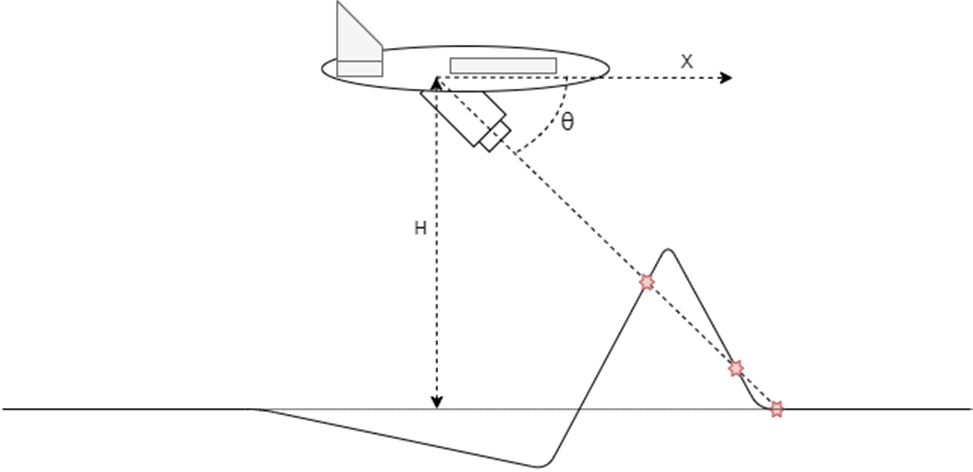
Определите координату \(X\) и высоту \(h\) точки на местности, которая лежит на оптической оси камеры БВС, летящего горизонтально вдоль оси \(X\) так, что его камера находится на высоте 30 м. При этом угол \(\theta\) отклонения оптической оси камеры от плоскости горизонта составляет 45°, по другим осям отклонений камеры от осей БВС нет. Координата \(X\) камеры БВС 3 м. Для определения высоты имеется карта высот с шагом 1 м. В промежутках между отметками высот высота определяется линейной аппроксимацией.
Карта высот необходимого участка приведена в таблице 1.
| Координата \(X\), м. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Высота \(h\), м. | 0 | 0 | 0 | 2 | 4 | 7 | 7 | 4 |
| Координата \(X\), м. | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Высота \(h\), м. | 3 | 2 | \(-1\) | \(-4\) | \(-4\) | \(-6\) | 0 | 5 |
| Координата \(X\), м. | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| Высота \(h\), м. | 18 | 16 | 6 | 7 | 7 | 5 | 4 | 3 |
| Координата \(X\), м. | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| Высота \(h\), м. | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 5 |
Точность ответа — до второго знака после запятой. Иллюстрация полета БВС и данных параметров приведены на рис. 1.6.
Координата \(X\) и координата \(h\), разделенные пробелом. Значения указываются с точностью ровно два знака после запятой. В качестве разделителя используйте точку.
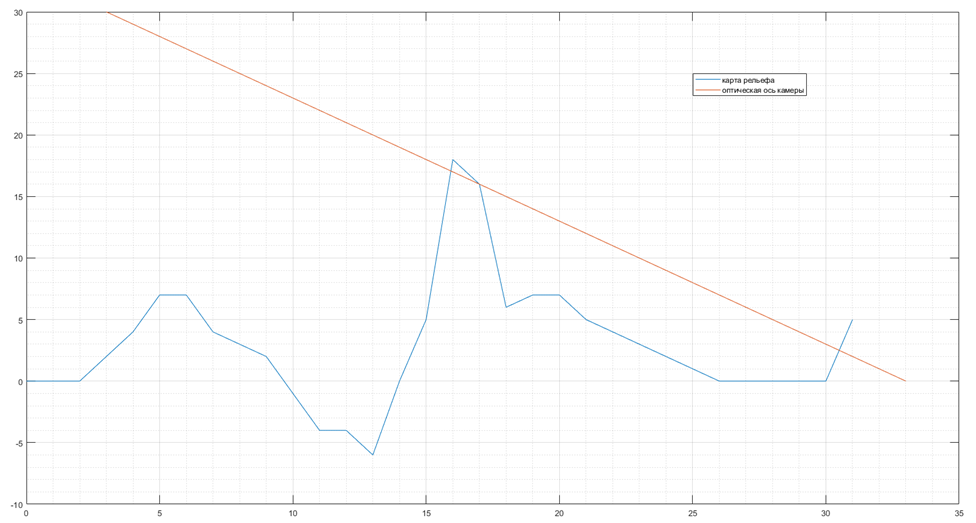
Для определения участка пересечения оптической оси с рельефом в первом приближении воспользуемся графическим методом. Построим график карты высот и линии оптической оси. Так как угол отклонения камеры равен 45°, то оптическую ось можно построить как гипотенузу равнобедренного прямоугольного треугольника, то есть в виде отрезка с двумя точками, положением камеры (3, 30) и точки с нулевой высотой на расстоянии 30 м от положения камеры (33, 0). Полученный график приведен на рис. 1.7.
Пересечение происходит между отметкам 15 м и 16 м, таким образом, правильным ответом является точка пересечения отрезка \([(3, 30); (33, 0)]\) и отрезка [(15, 5); (16, 18)].
Для поиска точки пересечения воспользуемся уравнением прямой на плоскости: \[\dfrac{x-x_a}{x_b-x_a}= \dfrac{y-y_a}{y_b-y_a}.\]
Прямые будут иметь следующие уравнения: \[y = -x + 33,\] \[y = 13x - 190.\]
Точка пересечения этих прямых определяется решением этих уравнений как системы.
Получаем ответ \[X = 15 \dfrac{13}{14}\approx 15.92857;\] \[h = 17 \dfrac{1}{14}\approx 17.07143.\]
15.93 17.07.
Что такое угол крена?
- Угол между продольной осью летательного аппарата и направлением его движения относительно земной поверхности.
- Угол между продольной осью летательного аппарата и направлением вектора скорости набегающего на летательный аппарат воздушного потока.
- Угол, который возникает при повороте корпуса летательного аппарата вокруг его продольной оси.
- Угол между продольной осью летательного аппарата и горизонтальной плоскостью.
ОтветC.
Что такое угол сноса?
- Угол между продольной осью летательного аппарата и направлением его движения относительно земной поверхности.
- Угол между продольной осью летательного аппарата и направлением вектора скорости набегающего на летательный аппарат воздушного потока.
- Угол, который возникает при повороте корпуса летательного аппарата вокруг его продольной оси.
- Угол между продольной осью летательного аппарата и горизонтальной плоскостью.
ОтветA.
Что измеряет гироскоп?
- Угловую скорость вращения тела, на котором он установлен, относительно одной, двух или трех осей в зависимости от его типа.
- Интенсивность одной или нескольких составляющих магнитного поля, позволяет определять углы между собственными осями сенсора \(X\), \(Y\), \(Z\) и силовыми линиями магнитного поля Земли.
- Расстояние, время и определяет местоположение во всемирной системе координат
WGS-84. - Ускорение (перегрузка), возникающее на летательных аппаратах, ракетах, самолетах и других движущихся объектах.
ОтветA.
Какое давление регистрируется с помощью трубки Пито?
- Статическое давление.
- Динамическое давление набегающего потока воздуха.
- Полное давление набегающего потока воздуха.
- Атмосферное давление.
ОтветC.
Где на летательном аппарате самолетного типа нормальной схемы находится руль направления?
- На крыле.
- На киле.
- На стабилизаторе высоты.
- На фюзеляже.
ОтветB.
Для чего предназначены винглеты на крыльях летательного аппарата самолетного типа?
- Для красоты.
- Для подвески дополнительных топливных баков.
- Для увеличения эффективного размаха крыла, снижения индуктивного сопротивления и увеличения подъемной силы на концах крыла.
- Для увеличения скорости.
ОтветC.
Какое устройство из приведенного ниже списка не относится к элементам механизации крыла летательного аппарата самолетного типа (не обязательно присутствие всех возможных элементов механизации крыла на конкретном самолете)?
- Спойлеры.
- Предкрылки.
- Надкрылья.
- Закрылки.
ОтветC.
Какая сила направлена противоположно вектору скорости полета летательного аппарата?
- Сила тяги.
- Подъемная сила.
- Вес.
- Сила лобового сопротивления.
ОтветD.
Какая высота полета летательного аппарата измеряется от его поверхности до точки на земной поверхности, над которой в данный момент он пролетает?
- Абсолютная.
- Относительная.
- Истинная.
- Приведенная.
ОтветC.
Центр давления крыла летательного аппарата самолетного типа...
- всегда совпадает с центром масс летательного аппарата;
- находится в условной точке приложения равнодействующей аэродинамических сил, действующих в полете на летательный аппарат;
- всегда находится в геометрическом центре летательного аппарата;
- всегда совпадает с аэродинамическим фокусом крыла летательного аппарата.
ОтветB.