Предметный тур. Информатика. 3 этап

Информатика. 8–11 классы

Задача 1.1.(10 баллов)

Новогодние каникулы на Плюке

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

На планете Плюк год длится \(N\) дней. При этом месяц на Плюке продолжается \(M\) дней, а неделя — \(K\) дней. Цикличность лет, месяцев и недель никак не зависит друг от друга и, например, окончание года вполне может прийтись на середину месяца.

Как и у всех нормальных людей, у жителей Плюка имеются новогодние каникулы, которые начинаются с первого дня нового года. Согласно плюкианскому закону, начало рабочего периода (и, соответственно, окончание новогодних каникул) должно приходиться либо на первый день первого месяца, либо на первый день первой недели, наступивший сразу после нового года. Так как в законе не уточняется, какой конкретно из этих двух вариантов нужно выбрать, легкомысленные плюкианцы выбирают начало рабочего года так, чтобы каникулы были как можно более длинными.

В текущем году им не повезло: первый день года стал первым днем недели и первым днем месяца, то есть каникул у них не было. Нужно определить, какую максимально разрешенную законом длительность новогодних каникул они могут позволить себе в следующем после текущего году.

Формат входных данных

На вход подаются три целых числа \(N\), \(M\) и \(K\) через пробел. Эти числа задают соответственно продолжительность года, месяца и недели на Плюке.

\(1 \leqslant M, K \leqslant N \leqslant 10^{18}\).

Формат выходных данных

Вывести одно число — максимально возможную длительность новогодних каникул при этих условиях.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	17 8 9	7
2	365 30 7	25

Примечания

В первом примере длительность года 17 дней, длительность месяца 8 дней и длительность недели 9 дней, то есть в текущем году в него вошло 2 месяца и 1 день, а значит, первый рабочий день (первый день следующего месяца) наступит на восьмой день после нового года, а 7 дней из предыдущего месяца могут быть выходными. С другой стороны, в текущем году была 1 неделя и еще 8 дней, то есть по этому параметру в новом году будет всего 1 выходной. Выбираем ответ — 7 дней.

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;

signed main(){
       ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, m, k;
    cin >> n >> m >> k;

    int a = m - n % m;
    if(a == m){
        a = 0;
    }
    int b = k - n % k;
    if(b == k){
        b = 0;
    }

    cout << max(a, b);
}

Задача 1.2.(15 баллов)

Правила перевозок пепелацем

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

Согласно правилам перевозок, на каждые \(n\) пацаков, перевозимых пепелацем, должен быть назначен один чатланин, который должен их сопровождать и находиться в этом же пепелаце. Если количество пацаков в пепелаце не делится нацело на \(n\), то для тех, кто в остатке, должен быть выделен еще один чатланин. При этом все находящиеся в пепелаце обязаны сидеть каждый на своем месте. Требуется перевезти \(k\) пацаков с Хануда на Плюк, и можно заказать любое количество пепелацев, каждый на \(m\) мест. Нужно узнать, какое минимальное количество пепелацев нужно заказать, чтобы вывезти всех \(k\) пацаков, не нарушая правила перевозок. Пацаков нужно вывезти за один раз, так как на планете Хануд долго жить нельзя. Можно считать, что всегда найдется необходимое количество чатлан, готовых прийти на помощь и поучаствовать в перевозке.

Формат входных данных

В единственной строке содержится три числа через пробел — \(n\), \(k\) и \(m\).

\(1 \leqslant n, k \leqslant 10^9\), \(2 \leqslant m \leqslant 10^9\).

Формат выходных данных

Вывести одно число — минимальное требуемое количество пепелацев.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	10 200 20	12

Примечания

Рассмотрим пример. На каждые 10 пацаков, находящихся в пепелаце, нужно выделить одного сопровождающего их чатланина. Требуется перевезти 200 пацаков, каждый доступный пепелац вмещает 20 человек. Тогда в одном пепелаце максимум можно перевезти 18 пацаков в сопровождении двух чатлан. Откуда получаем, что в 11 пепелацах можно перевезти 198 пацаков и потребуется заказать еще один для двух оставшихся пацаков.

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define int long long

using namespace std;
typedef pair<int, int> pii;


signed main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, t, m;
    cin >> n >> t >> m;
    int w = m / (n+1);
    int z = w * n + m % (n+1);
    if(m % (n+1) > 0) z--;
    int ans = t / z + ((t % z) > 0);
     cout << ans;
}

Задача 1.3.(20 баллов)

Пересыпание песка

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

Би и Уэф заняты важным делом — добыванием чатлов. Они нашли странную конструкцию, состоящую из \(n\) ржавых емкостей. Емкости стоят в один ряд и имеют объемы \(v_1, v_2, \ldots, v_n\). Изначально все емкости были пустыми.

Би нагребает песок в первую емкость объемом \(v_1\) до ее верха, а Уэф нажимает кнопку. После этого автоматически происходит пересыпание песка из емкости № \(1\) в емкость № \(2\), затем из емкости № \(2\) в емкость № \(3\) и т. д. На каждом этапе песок пересыпается либо до тех пор, пока не опустеет емкость № \(i\), либо пока до верху не наполнится емкость № \(i + 1\). Из последней емкости № \(n\) песок высыпается обратно на поверхность планеты.

После этого Би снова засыпает доверху емкость № \(1\), и Уэф снова нажимает кнопку.

После каждого такого набора пересыпаний Уэф находит в последней емкости ровно столько чатлов, какова разность между объемом засыпанного в первую емкость песка и высыпавшегося из \(n\)-й на этой стадии.

В какой-то момент они заметили, что чатлы перестали появляться, то есть объем засыпанного песка стал равен объему высыпавшегося. Осталось выяснить, сколько всего чатлов они добыли таким образом.

Формат входных данных

В первой строке находится целое число \(n\) — количество емкостей, \(1 \leqslant n \leqslant 10^5\).

Во второй строке через пробел находятся числа \(v_1, v_2, \ldots, v_n\) — объемы соответствующих емкостей, \(1 \leqslant v_i \leqslant 10^9\).

Формат выходных данных

Вывести одно число — максимальное количество чатлов, которое смогут добыть Би и Уэф.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	5 8 9 4 6 3	15

Примечания

На первой стадии в первую емкость Би насыплет 8 мер песка. Далее из первой во вторую пересыплется 8 мер, из второй в третью — 4, из третьей в четвертую — 4, из четвертой в пятую — 3, из пятой на поверхность планеты высыплется 3 меры песка. Таким образом, за первую стадию Би и Уэф получат \(8 - 3\), то есть 5 чатлов.

На второй стадии в первую емкость Би насыплет 8 мер песка. Далее из первой во вторую пересыплется 5 мер (так как во второй уже есть 4 меры), из второй в третью — 4, из третьей в четвертую — 4 (в ней окажется уже 5 мер, так как 1 осталась с прошлого раза), из четвертой в пятую — 3, из пятой на поверхность планеты высыплется 3 меры песка. Таким образом, за вторую стадию Би и Уэф получат \(8 - 3\), то есть 5 чатлов.

На третьей стадии в первую емкость Би насыплет 5 мер песка, так как с прошлой стадии в первой емкости осталось 3 меры. Далее из первой во вторую пересыплется 4 меры (так как во второй уже есть 5), из второй в третью — 4, из третьей в четвертую — 4 (в ней окажется уже 6 мер, так как 2 осталась с прошлых стадий), из четвертой в пятую — 3, из пятой на поверхность планеты высыплется 3 меры песка. Таким образом, за третью стадию Би и Уэф получат \(5 - 3\), то есть 2 чатла.

На четвертой стадии в первую емкость Би насыплет 4 меры песка, так как с прошлой стадии в первой емкости осталось 4 меры. Далее из первой во вторую пересыплется 4 меры (так как во второй уже есть 5), из второй в третью — 4, из третьей в четвертую — 3 (так как в четвертой уже есть 3 меры), из четвертой в пятую — 3, из пятой на поверхность планеты высыплется 3 меры песка. Таким образом, за четвертую стадию Би и Уэф получат \(4 - 3\), то есть 1 чатл.

На пятой стадии в первую емкость Би насыплет 4 меры песка. Далее из первой во вторую пересыплется 4 меры, из второй в третью — 3 (в ней осталась 1 мера с прошлой стадии), из третьей в четвертую — 3, из четвертой в пятую — 3, из пятой на поверхность планеты высыплется 3 меры песка. Таким образом, за пятую стадию Би и Уэф получат \(4 - 3\), то есть 1 чатл.

На шестой стадии в первую емкость Би насыплет 4 меры песка. Далее из первой во вторую пересыплется 3 меры, из второй в третью — 3, из третьей в четвертую — 3, из четвертой в пятую — 3, из пятой на поверхность планеты высыплется 3 меры песка. Таким образом, за шестую стадию Би и Уэф получат \(4 - 3\), то есть 1 чатл.

Далее в первую емкость можно засыпать только 3 меры, что в итоге окажется равно тому, что высыплется на поверхность.

Таким образом, во время этих действий, Би и Уэф добудут \(5 + 5 + 2 + 2 + 1 + 1 + 1 = 15\) чатлов.

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define int long long
using namespace std;
typedef vector<int> vi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;
signed main(){
      ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, mn = INF;
    cin >> n;
    vi v(n);
    for0(i, n){
        cin >> v[i];
        mn = min(mn, v[i]);
    }
    int ans = 0;
    for0(i, n){
        ans += v[i] - mn;
        if(v[i] == mn){
            break;
        }
    }
    cout << ans << endl;
}

Задача 1.4.(25 баллов)

Упорядочивание галактик в Тентуре

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

Немногие знают, что все звезды в Тентуре (обитаемой вселенной) находятся в одной плоскости. Более того, все звезды Тентуры совместно образуют прямоугольник \(n \times m\), и в каждой ячейке этого прямоугольника находится ровно одна звезда.

Когда-то давным-давно всеми звездами и планетами Тентуры управлял один правитель — далекий предок Господина ПЖ. Но время шло и, согласно закону Тентуры, управляющий должен разделить свою галактику на две (не обязательно равные) прямоугольные части и отдать их в наследство двум своим старшим потомкам. Делить свою галактику можно только по прямой линии между двумя рядами звезд от края до края галактики. Каждая из этих частей становилась отдельной галактикой. Так поступал каждый правитель, и в итоге все множество звезд Тентуры оказалось разделено на несколько прямоугольных областей. И, что удивительно, всегда выполнялось такое свойство: среди любых четырех звезд, образующих квадрат \(2 \times 2\) есть хотя бы две из одной галактики. Иными словами, границы галактик всегда образуют \(T\)-образные пересечения, и нет ни одного «перекрестка» в котором встречаются четыре галактики.

Для определенности введем направления в Тентуре «верх-низ» и «лево-право». Тогда любую границу можно характеризовать либо как горизонтальную, либо как вертикальную. Горизонтальная граница делит свою галактику на верхнюю и нижнюю части, а вертикальная — на левую и правую части.

В целях наведения порядка ученые Тентуры решили упорядочить все существующие галактики согласно следующему правилу: для любой разделенной галактики, если она разделена горизонтально, первыми перечисляются галактики сверху, потом галактики снизу; если она разделена вертикально — первыми перечисляются галактики слева, потом галактики справа. И так для каждой из разделенных когда-то галактик. Далее из таких перечислений для меньших галактик складываются по тому же правилу перечисления для старых больших галактик до тех пор, пока не получится перечисления всех галактик Тентуры. Требуется получить такое упорядочение галактик Тентуры по ее карте.

Формат входных данных

В первой строке вводятся через пробел два числа \(n\) и \(m\) — размеры прямоугольника, который образуют планеты Тентуры.

Далее в следующих \(n\) строках, каждая длиной по \(m\) символов, без пробелов между ними, указаны планеты. Карта ориентирована таким образом, что направления «верх-низ» и «лево-право» совпадают с теми, что определили ученые Тентуры. Каждая планета задается одной буквой от a до z. Если две планеты заданы одной буквой, значит, они находятся в одной галактике. Гарантируется, что все галактики удовлетворяют условиям задачи: любая галактика является прямоугольной областью, никакие четыре галактики не сходятся своими углами в одном «перекрестке». Весь набор галактик был получен пошагово, путем разделения на каждом шаге ровно одной галактики на два меньших прямоугольника.

Ограничения: \(1 \leqslant n, m \leqslant 50\).

Формат выходных данных

Вывести одну строку, в которой буква каждой галактики карты упомянута ровно один раз, причем все вместе они задают порядок на карте, согласно условию задачи.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	7 9 zzctooooo zzctooooo zzcdddhbb zzcaaaabb pppaaaaxx pppaaaaxx pppuuuuuu	zcptodhabxu

Пример программы-решения

Ниже представлено решение на языке C++.

C++

Авторское решение на С++
#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef pair<int, int> pii;
typedef pair<pii, pii> galact;
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;

pair<galact, galact> del(galact a, vector<string> &v){
    pair<galact, galact> res = {{{-1, -1},{-1, -1}}, {{-1, -1}, {-1, -1}} };
    int x1 = a.x.x;
    int x2 = a.y.x;
    int y1 = a.x.y;
    int y2 = a.y.y;
    for(int i = x1; i < x2; i++){
        bool ok = 1;
        for(int j = y1; j <= y2; j++){
            if(v[i][j] == v[i + 1][j]){
                ok = 0;
            }
        }
        if(ok){
            return {{{x1, y1}, {i, y2}}, {{i + 1, y1}, {x2, y2}}};
        }
    }
    for(int j = y1; j < y2; j++){
        bool ok = 1;
        for(int i = x1; i <= x2; i++){
            if(v[i][j] == v[i][j + 1]){
                ok = 0;
            }
        }
        if(ok){
            return {{{x1, y1}, {x2, j}}, {{x1, j + 1}, {x2, y2}}};
        }
    }
    return res;
}

string order(galact a, vector<string> &v){
    string res;
    pair<galact, galact> t = del(a, v);
    if(t.x.x.x == -1){
        res = v[a.x.x][a.x.y];
    }
    else{
        res = order(t.x, v) + order(t.y, v);
    }
    return res;
}

signed main(){
       ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, m;
    cin >> n >> m;
    vector<string> v(n);
    for0(i, n){
        cin >> v[i];
    }
    string ans = order({{0, 0}, {n - 1, m - 1}}, v);
    cout << ans << endl;
}

Задача 1.5.(30 баллов)

Пролетая мимо Плюка

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 11 с.

Ограничение по памяти: 64 Мбайт.

Условие

Автоматический зонд стартует из некоторой точки на координатной плоскости и бесконечно долго выполняет записанную в нем программу перемещений. Каждое перемещение — это сдвиг на одну позицию по координате \(X\) или по координате \(Y\). Более точно смещение в сторону увеличения координаты \(X\) обозначается символом \(R\) (вправо), смещение в сторону уменьшения координаты \(X\) обозначается символом \(L\) (влево), смещение в сторону увеличения координаты \(Y\) обозначается символом \(U\) (вверх), смещение в сторону уменьшения координаты \(Y\) обозначается символом \(D\) (вниз). Программа перемещений состоит не более, чем из \(10^5\) символов, и после того, как зонд ее выполнит, он начинает выполнять ее заново. Известно, что в процессе полета зонд как минимум один раз заканчивает и начинает заново свою программу в точке \((0, 0)\).

Известны координаты планеты Плюк — целые числа \(XP\) и \(YP\). Требуется определить минимальное расстояние до Плюка, на котором зонд окажется, находясь в какой-либо целочисленной точке плоскости в ходе своего полета.

Формат входных данных

В первой строке содержится одно натуральное число \(n\) — количество команд в программе перемещения зонда, \(1 \leqslant n \leqslant 10^5\).

Во второй строке содержится \(n\) символов из множества \(L, R, D, U\) — программа перемещения.

В третьей строке содержатся координаты планеты Плюк \(XP, YP\) — целые числа, по абсолютному значению не превосходящие \(10^6\). В данной задаче считать планету Плюк точкой плоскости.

Формат выходных данных

Вывести одно число — наименьшее расстояние, на котором окажется зонд в процессе бесконечного выполнения указанной программы перемещений. Ответ вывести с точностью не менее шести знаков после десятичной точки.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	7 RUURDDD 6 3	2.8284271

Примечания

Рис. 1.1.

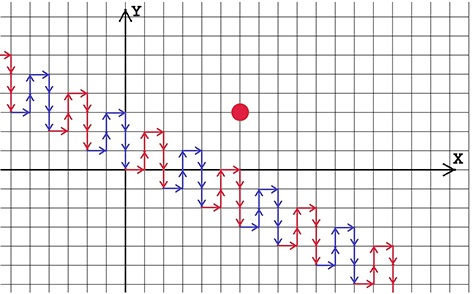
На рис. 1.1 представлен путь зонда для примера из условия. Чередующимся красным и синим показаны отдельные наборы выполненных команд из программы перемещений.

Видно, что зонд один раз закончил программу в точке (0, 0) и снова начал выполнять ее далее. Видно, что в точке (4, 1) зонд подлетает к Плюку на расстояние \(\sqrt{8})\).

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define all(a) a.begin(), a.end()
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 19;

int sqdist(pii a, pii b){
    return ((a.x - b.x)*(a.x - b.x) + (a.y - b.y)*(a.y - b.y));
}

pii pos(pii t, pii v, int M){
    return {t.x + v.x * M, t.y + v.y * M};
}

signed main(){
       ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);

    map<char, pii> dxy = {{'L',{-1, 0}}, {'R', {1, 0}}, {'U', {0, 1}}, {'D', {0, -1}}};
    int n;
    cin >> n;
    string s;
    cin >> s;
    pii P;
    cin >> P.x >> P.y;
    pii t = {0, 0};
    for(auto c : s){
        t.x += dxy[c].x;
        t.y += dxy[c].y;
    }
    int mn = INF;
    if(t.x == 0 && t.y == 0){
        t = {0, 0};
        for(auto c : s){
            t.x += dxy[c].x;
            t.y += dxy[c].y;
            mn = min(mn, sqdist(t, P));
        }
        cout.precision(7);
        double ans = mn;
        cout << fixed << sqrt(ans);
        return 0;
    }


    pii z = {0, 0};
    for(auto c : s){
        z.x += dxy[c].x;
        z.y += dxy[c].y;
        int L = -1, R = 1;
        pii tl = pos(z, t, L);
        while(abs(tl. x) < 1e7 && abs(tl.y) < 1e7){
            L *= 2;
            tl = pos(z, t, L);
        }
        pii tr = pos(z, t, R);
        while(abs(tr. x) < 1e7 && abs(tr.y) < 1e7){
            R *= 2;
            tr = pos(z, t, R);
        }

        while(R - L > 2){
            int M1 = (2 * L + R) / 3;
            int M2 = (L + 2 * R) / 3;
            pii p1 = pos(z, t, M1);
            pii p2 = pos(z, t, M2);
            if(sqdist(p1, P) < sqdist(p2, P)){
                R = M2;
            }
            else{
                L = M1;
            }
        }
        pii p1 = pos(z, t, L);
        pii p2 = pos(z, t, (R + L) / 2);
        pii p3 = pos(z, t, R);
        mn = min({mn, sqdist(p1, P), sqdist(p2, P), sqdist(p3, P)});
    }
    cout.precision(7);
    double ans = mn;
    cout << fixed << sqrt(ans);
}