Предметный тур. Физика. 3 этап
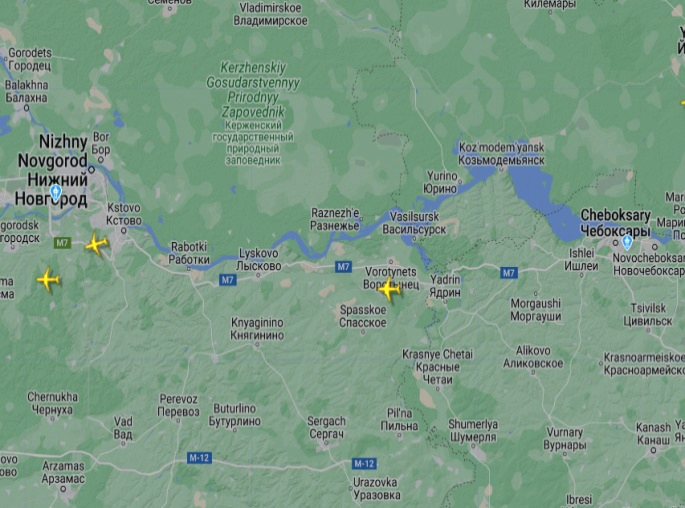
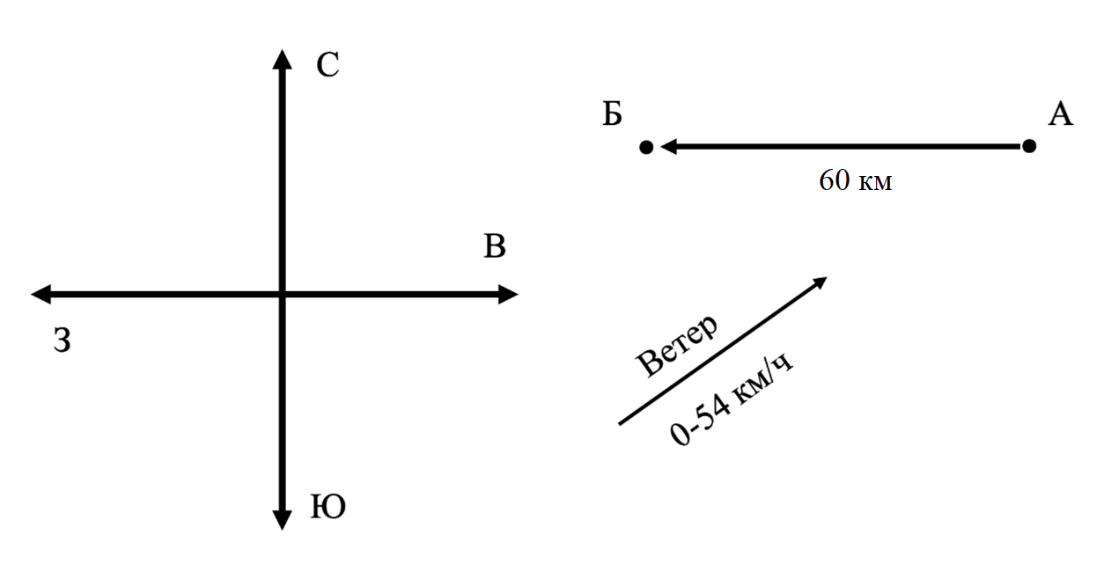
Согласно прогнозу погоды, в ближайшие несколько часов ожидается сильный ветер, дующий преимущественно в северо-восточном направлении. Ожидаемые порывы ветра будут достигать скорости до 54 км/ч. Поэтому запланированный перелет беспилотного транспортного средства вынужденно будет осуществляться в сложных метеоусловиях.
Неблагоприятные погодные условия могут потребовать существенного увеличения заряда аккумулятора для повышения запаса хода (длительности полета) беспилотника по сравнению с зарядом, способным обеспечить полет на ту же дистанцию в безветренную погоду.
На сколько полных минут полета необходимо увеличить заряд аккумулятора беспилотника, чтобы надежно гарантировать доставку груза (в ожидаемых неблагоприятных метеоусловиях) из пункта А в пункт Б, расположенный в 60 км западнее пункта А, если крейсерская скорость беспилотника в условиях полного штиля составляет 30 м/с?
Крейсерская скорость беспилотника (\(V_{\text{кр}} = 30\) м/с) в условиях полного штиля — это скорость его движения относительно воздушной среды. Относительно же поверхности Земли скорость беспилотника будет складываться из скоростей самого беспилотника и скорости движения воздушных масс (т. е. скорости ветра). При этом (согласно заданию) требуется, чтобы беспилотник двигался в строго западном направлении.
Рассмотрим самый негативный (из возможных) сценарий, когда сила (скорость) ветра \(V_{\text{в}}\) достигает максимальных значений (до 54 км/ч) на протяжении всего полета.
Скорость ветра, при переводе в метры в секунду, составит 15 м/с. \[V_{\text{в}} = 54\frac{\text{км}}{\text{ч}}=\frac{54~\text{км/ч}}{3{,}6~\text{км/м с/ч}} = 15~\text{м/с}.\]
При движении из А в Б беспилотник должен двигаться на запад, т. е. в направлении, строго противоположном оси X. Другими словами, скорость вдоль оси Y должна отсутствовать: \(V_y = 0\).
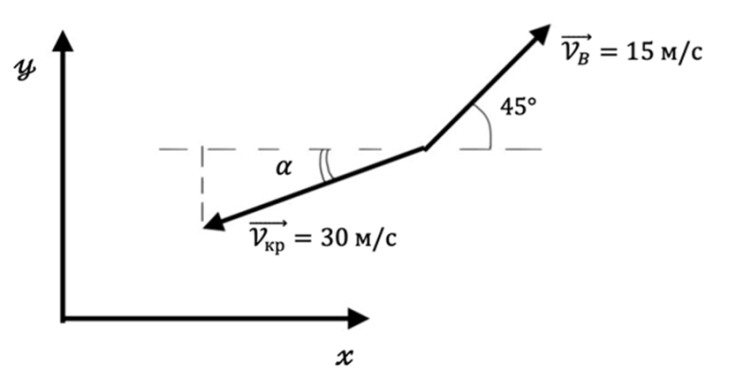
Из чего следует, что \(V_{\text{кр}} \cdot \sin \alpha = V_{\text{B}} \cdot \sin 45°\) (см. пояснительный рис. 1.3).
Согласно этому, угол \(\alpha\) — угол, под которым следует подержать ориентировку, можно получить из следующего соотношения: \[\sin \alpha = \frac{V_B}{V_{\text{кр}}} \cdot \sin 45° = \frac{15}{30} \cdot \frac{\sqrt{2}}{2} \approx 0{,}35355.\]
Тогда скорость вдоль оси \(X\) для беспилотника, сориентированного таким образом, составит: \[V_x = -V_{\text{кр}} \cdot \cos \alpha + V_B \cdot \cos 45°.\]
Учитывая прямое следствие из основного тригонометрического тождества, \[\cos \alpha = \sqrt{1 - \sin^2 \alpha} = \sqrt{1 - (0{,}35355)^2} = \sqrt{0{,}875} \approx 0{,}93541.\]
Получим итоговое значение для модуля скорости вдоль оси \(X\): \[\begin{aligned} |V_x| &= V_{\text{кр}} \cdot \sqrt{1 - \left(\frac{V_B}{V_{\text{кр}}} \cdot \sin 45°\right)^2} - V_B \cdot \cos 45°; \\ |V_x| &= 30~\text{м/с} \cdot \sqrt{1 - \left(\frac{15}{30} \cdot \frac{\sqrt{2}}{2}\right)^2} - 15~\text{м/с} \cdot \frac{\sqrt{2}}{2} \approx 17,456~\text{м/с}. \end{aligned}\]
Время движения из \(A\) в \(B\) при сильном ветре составит: \[t_{\text{В}} = \frac{S}{V_x} = \frac{60 \cdot 10^3~\text{м}}{17{,}456~\text{м/с}} \approx 3437{,}21~\text{с}.\]
При полете в безветренную погоду потребовалось бы: \[t_0 = \frac{S}{V_{\text{кр}}} = \frac{60 \cdot 10^3~\text{м}}{30~\text{м/с}} = 2000~\text{с}.\]
Таким образом, необходимо закладывать дополнительный запас хода (времени полета) в расчете на неблагоприятные погодные условия: \[\Delta t = t_{\text{В}} - t_0 \approx 3437{,}21 - 2000 = 1437{,21}~\text{с} \approx 23{,}95~\text{мин} \approx 24~\text{мин}.\]
Примечание
Так как речь в задаче шла о запасе хода, то округление в этом случае нужно делать не по правилам округления, а по логике происходящего, т. е. до целого значения и в большую сторону.
На 24 мин.
| Критерий | Баллы |
|---|---|
| Сформулирована мысль об относительности механического движения в условиях ветра | 2 |
| Сделаны пояснительные рисунки, отображающие влияние ветра на скорость полета беспилотника относительно Земли | 2 |
| Получено аналитическое выражение для вычисления скорости движения беспилотника относительно поверхности Земли с учетом действия ветра | 4 |
| Вычислено численное значение скорости беспилотника (при движении на запад из пункта А в пункт Б) с учетом ветра | 3 |
| Вычислено время движения из пункта А в пункт Б с учетом ветра | 2 |
| Вычислено время движения из пункта А в пункт Б в безветренную погоду | 1 |
| Определено, на сколько полных минут полета необходимо увеличить заряд аккумулятора по сравнению с полетом в безветренную погоду | 1 |
| Всего | 15 |
Для увеличения проходимости на сложном грунтово-каменистом участке дороги во всех четырех шинах транспортного средства снизили давление.
Автомобильного манометра с собой не было, поэтому совершая данную процедуру, приходилось ориентироваться на глаз. Внутренний голос опытного водителя подсказывал, что судить о величине остаточного давления в шинах можно было по возрастающему размеру пятна контакта шин с дорожным покрытием.
Стравливание давления в каждом из колес прекращали в тот момент, когда протяженность пятна контакта (A) для данного колеса достигала отметки в 40 см (разумеется, примерно). Пренебрегая жесткостью автомобильных шин и принимая ускорение свободного падения равным 10 м/c\(^2\), оцените абсолютную величину остаточного давления в шинах автомобиля, если снаряженная масса автомобиля составляла 2,4 т, а ширина (B) используемых покрышек была 25 см. Ответ выразите в единицах атмосферного давления с точностью до одной десятой. Примите, что давление в 100 кПа равно атмосферному.
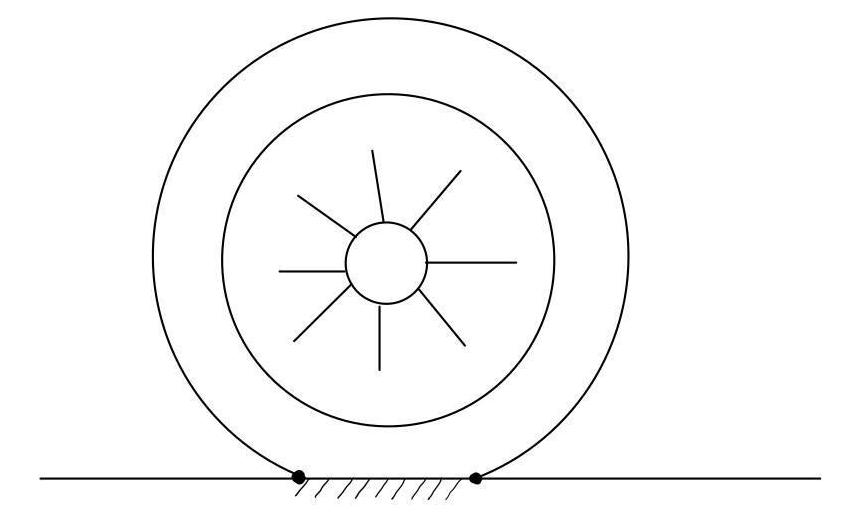
Пятно контакта возникает в результате деформации шины колеса (см. пояснительный рис. 1.5) под действием части веса автомобиля, приходящегося на данное колесо. На одно колесо (в среднем) приходится 1/4 веса автомобиля.
Эта нагрузка уравновешивается упругой реакцией, которая зависит от внутреннего давления в шинах, жесткости самих шин и той степени деформации, которую они испытывают. Если не учитывать жесткость материала шин, то можно считать, что деформацию шин ограничивает только избыточное внутреннее давление газа в шинах по сравнению с атмосферным давлением снаружи.
Учитывая все вышесказанное, можно записать уравнение баланса сил вдоль вертикальной оси: \[\frac{1}{4}N = \Delta P \cdot S,\] где \(N\) — вес автомобиля; \(\Delta P\) — избыточное давление (по сравнению с внешним (атмосферным)); \(S\) — площадь пятна контакта, приходящегося на каждое колесо (в среднем).
При известной величине пятна контакта избыточное давление в шинах составит: \[\Delta P =\frac{N}{4 \cdot S} = \frac{mg}{4 \cdot S} = \frac{2{,}4\cdot 10^3~\text{кг} \cdot 10~\text{м/с}^2}{4 \cdot 40\cdot 25 \cdot 10^{-4}~\text{м}^2} = 6\cdot 10^4~\text{Па} \approx 0{,}6~\text{атм}.\]
В итоге абсолютное давление в шинах составило: \[P_{\text{abs}} = \Delta P + P_{\text{атм}} = 0{,}6 + 1 = 1{,}6~\text{атм}.\]
1,6 атм.
| Критерий | Баллы |
|---|---|
| Сформулированы причины возникновения пятна контакта | 2 |
| Сделаны пояснительные рисунки | 2 |
| Упомянуто значение нагрузки, приходящейся на каждое колесо (в среднем) | 1 |
| Записано уравнение, связывающее избыток внутреннего давления, площадь пятна контакта и уровень нагрузки, приходящейся на колесо | 3 |
| Определено численное значение избыточного давления в шинах (переведены единицы измерения из паскалей в единицы атмосферного давления) | 2 |
| Вычислено абсолютное давление в шинах | 2 |
| Всего | 12 |
Провода, использованные в основных электрических узлах на борту квадрокоптера, изготовлены из технически чистой меди. Совокупная длина медных проводов (при температуре \(20~°\text{C}\)) составляла \(100\) м.
Про материал проводов известно, что:
Удельное электросопротивление чистой электротехнической меди имеет температурную зависимость вида: \[\rho_t = \rho_{20} \cdot \left[ 1 + \alpha(t - 20) \right],\] где
- \(\rho_t\) — удельное электросопротивления меди при некоторой температуре \(t\);
- \(\rho_{20}\) — удельное электросопротивление меди при температуре \(20~°\text{C}\) (равное \(0{,}0172\) Ом \(\cdot\) мм\(^2\)/м), принятое в качестве базового уровня;
- \(\alpha\) — температурный коэффициент, отражающий скорость изменения удельного электросопротивления, составляет \(0{,}004~°\text{C}^{-1}\);
- \(t\) — температура (\(°\text{C}\)).
Рис. 1.6.Тепловое расширение чистой электротехнической меди описывается уравнением вида: \[r_t = r_{20} \cdot \left[ 1 + \beta(t - 20) \right],\] где
- \(r_t\) — геометрический размер проводника при некоторой температуре \(t\);
- \(r_{20}\) — геометрический размер проводника при температуре \(20~°\text{C}\), принятой в качестве базового (опорного) значения;
- \(\beta\) — коэффициент теплового расширения, равный \(16{,}8 \cdot 10^{-6}~°\text{C}^{-1}\);
- \(t\) — температура (\(°\text{C}\)).
Вопрос: на сколько процентов будут различаться уровни электротепловых потерь, связанных с изменением омического сопротивления проводов в условиях тридцатиградусной жары, по сравнению с эксплуатацией квадрокоптера в тридцатиградусный мороз при неизменном значении силы тока, подаваемым с бортового источника питания?
Обозначим рассматриваемые температуры, при которых нужно сравнить уровни электротепловых потерь, следующим образом: \[t_1 = +30~°\text{C}, \quad t_2 = -30~°\text{C}.\]
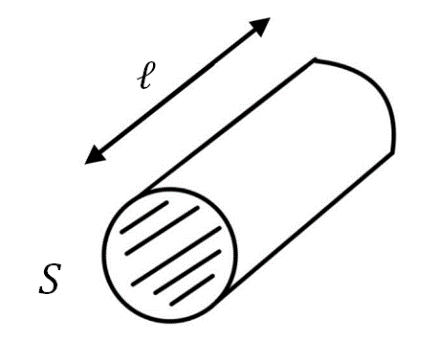
Общее изменение сопротивления медных электрических проводов при изменении эксплуатационной температуры происходит под влиянием не только изменения удельного электросопротивления, но также за счет изменения длины и площади сечения проводов. Это связано напрямую с тем, что общее сопротивление проводника связано с удельным сопротивлением формулой: \[R = \rho \cdot \frac{l}{S}.\]
За счет теплового расширения у медных проводов увеличится не только длина, но и возрастет площадь сечения, причем относительное изменение площади сечения будет пропорциональным квадрату отношения диаметров: \[\frac{S_2}{S_1} = \left(\frac{d_2}{d_1}\right)^2.\] Это связано с тем, что площадь сечения связана с диаметром формулой: \[S = \frac{\pi d^2}{4}.\]
При однородном тепловом расширении относительное изменение диаметра проводника происходит в той же мере, что и относительное изменение длины проводника. Поэтому относительное изменение сечения можно выразить иначе, а именно: \[\frac{S_2}{S_1} = \left(\frac{d_2}{d_1}\right)^2 = \left(\frac{l_2}{l_1}\right)^2.\]
В результате отношение электросопротивлений проводников можно выразить как: \[\frac{R_1}{R_2} = \frac{\rho_1 \cdot l_1 / S_1}{\rho_2 \cdot l_2 / S_2} = \frac{\rho_1}{\rho_2} \cdot \frac{l_1}{l_2} \cdot \frac{S_2}{S_1} = \frac{\rho_1}{\rho_2} \cdot \frac{l_1}{l_2} \cdot \left(\frac{l_2}{l_1}\right)^2 = \frac{\rho_1}{\rho_2} \cdot \frac{l_2}{l_1}.\]
Таким образом, чтобы найти отношение электросопротивлений проводников при температурах: \(t_1 = +30~°\text{C}\) и \(t_2 = -30~°\text{C}\), нужно вычислить отношения удельных электросопротивлений \(\dfrac{\rho_1}{\rho_2}\) и отношение линейных размеров \(\dfrac{l_2}{l_1}\) при соответствующих температурах.
Удельное электросопротивление чистой электротехнической меди имеет температурную зависимость вида: \[\rho_t = 0{,}0172 \cdot \left[1 + 0{,}004 \cdot (t - 20)\right].\] Следовательно: \[\frac{\rho_1}{\rho_2} = \frac{0{,}0172 \cdot \left[1 + 0{,}004 \cdot (+30 - 20)\right]}{0{,}0172 \cdot \left[1 + 0{,}004 \cdot (-30 - 20)\right]} = \frac{1 + 0{,}004 \cdot 10}{1 - 0{,}004 \cdot 50} = \frac{1{,}04}{0{,}8} = 1{,}3.\]
Тепловое расширение чистой электротехнической меди описывается уравнением вида: \[r_t = r_{20} \cdot \left[1 + \beta(t - 20)\right],\] где \(\beta\) — коэффициент теплового расширения, равный \(16{,}8 \cdot 10^{-6}~°\text{C}^{-1}\).
Здесь необходимо учесть, что \(r_{20}\) — исходный геометрический размер медного проводника при температуре, принятой в качестве базового (опорного) значения. Этот размер может иметь разные значения, в отличие от удельного сопротивления, имеющего вполне конкретную величину!
Следовательно, отношение линейных размеров \(\dfrac{l_2}{l_1}\) при соответствующих температурах будет равно: \[\begin{aligned} \frac{l_2}{l_1} = \frac{l_{20} \cdot \left[1 + \beta(t_2 - 20)\right]}{l_{20} \cdot \left[1 + \beta(t_1 - 20)\right]} = \frac{1 + 16,8 \cdot 10^{-6} \cdot (-30 - 20)}{1 + 16,8 \cdot 10^{-6} \cdot (30 - 20)}=\\ = \frac{1 - 16,8 \cdot 10^{-6} \cdot 50}{1 + 16,8 \cdot 10^{-6} \cdot 10} \approx \frac{0,99916}{1,000168} \approx 0,998992. \end{aligned}\] В результате отношение электросопротивлений проводников при изменении температуры составит: \[\frac{R_1}{R_2} = \frac{\rho_1}{\rho_2} \cdot \frac{l_2}{l_1} = 1{,}3 \cdot 0{,}998992 \approx 1{,}2987.\]
Согласно закону Джоуля – Ленца, мощность нагрева от электрического тока можно выразить через силу тока, напряжение и электросопротивление следующими способами: \[W = IU = \frac{U^2}{R} = I^2 R.\]
При неизменном значении тока удобнее всего пользоваться последним выражением для тепловой мощности. В итоге отношение тепловых потерь при разных температурах будет выражаться через соотношение сопротивлений: \[\frac{W_1}{W_2} = \frac{I_1^2 R_1}{I_2^2 R_2} = \frac{R_1}{R_2} = \frac{\rho_1}{\rho_2} \cdot \frac{l_2}{l_1} = 1{,}3 \cdot 0{,}998992 \approx 1{,}2987.\]
Данное относительное изменение эквивалентно относительному приросту величины теплопотерь на \(29{,}87\%\).
Увеличится на 29,87%.
| Критерий | Баллы |
|---|---|
| Сформулирована мысль о причинах возникновения потерь (закон Джоуля – Ленца) | 2 |
| Показана роль и характер влияния факторов, отвечающих за изменение величины электросопротивления | 3 |
| Вычислено значение удельного электросопротивления при разных температурах | 4 |
| Вычислено или учтено относительное изменение длины проводов в результате теплового расширения | 4 |
| Вычислено или учтено относительное изменение сечения проводов в результате теплового расширения | 4 |
| Определено относительное изменение общего омического электросопротивления с ростом температуры с учетом изменения удельного электросопротивления и теплового расширения | 4 |
| Вычислено относительное изменение величины тепловых потерь (с учетом закона Джоуля – Ленца при неизменной величине тока) | 3 |
| Выражено в процентах относительное изменение тепловых потерь | 1 |
| Всего | 25 |
Грунтозацепы гусеничных траков вездехода обеспечивают такой уровень сцепления с грунтом, что вездеход способен тянуть буксировочный трос с усилием, в три раза превышающим его собственный вес. Максимальный крутящий момент, передаваемый от силовой установки на ведущие колеса (при включенной нижней передаче), таков, что соответствующее суммарное сдвиговое усилие, передаваемое от ведущих колес на гусеницы, в пять раз превышает вес вездехода, находящегося в состоянии покоя. Все четыре колесные оси вездехода, когда он стоит на ровной горизонтальной поверхности, нагружены равномерно. Оси расположены на расстоянии 1 м друг от друга (см. фотографию рис. 1.8).
Определите предельно допустимую высоту в расположении центра тяжести вездехода для предотвращения его возможного опрокидывания при преодолении максимально крутых подъемов, на которые он гипотетически способен взбираться. Грунт считайте всюду однородным, одинаково плотным и достаточно жестким (т. е. вездеход не вязнет и не закапывается в нем).
Согласно условию задачи и данному в нем описанию вездехода, можно сделать следующие логически непротиворечивые выводы:
- Центр тяжести вездехода (в продольном направлении) располагается между второй и третьей осями и строго посередине вездехода (см. пояснительный рис.), т. е. на расстоянии по \(1{,}5\) м от переднего и заднего краев пятна контакта. Это следует из того, что у вездехода, стоящего на месте и в горизонтальном положении, оси нагружены равномерно, а расстояния между осями равны \(1\) м, при том, что межосевых пролетов всего три, а это означает, что \(l\) — длина пятна контакта гусеницы с грунтом — составляет \(3\) м.
Коэффициент трения (эффективное значение) между гусеницами и грунтом достигает значения \(\mu = 3\). Это прямое следствие из того, что максимальное усилие, с которым вездеход может тянуть буксировочный трос, составляет три его веса: \[F_{\text{тяги (буксир)}} = F_{\text{трения}} = \mu N = \mu mg.\] Так как \(F_{\text{тяги (буксир)}} = 3mg \implies \mu = 3\).
Рис. 1.9.- Ограничение по тяге определяется исключительно трением (сцеплением с грунтом), т. к. запас по крутящему моменту в \(5\) раз превышает вес вездехода. При неограниченном уровне сцепления \(F_{\text{тяги}}\) была бы равна \(5mg\). Но в условиях имеющегося уровня сцепления реально воплощаемая сила тяги \(F_{\text{тяги}}\) будет ограничена значением, равным \(\mu N\), а не \(5mg\).
Максимально возможный угол подъема определяется через соотношение: \[\operatorname{tg} \alpha = \mu = 3.\] Это непосредственно следует из того, что при движении под углом \(\alpha\) к горизонту сила реакции опоры \(N\) определяется из соотношения: \[N = mg \cos \alpha.\] При этом сила тяги \(F_{\text{тяги}}\), реализуемая вездеходом, должна быть не меньше, чем \(mg \sin \alpha\) (проекция силы тяжести на наклонную плоскость), иначе вездеход не сможет двигаться вверх. Из этого следует, что максимально возможный угол подъема определяется через соотношение: \[\mu \cdot mg \cdot \cos \alpha = mg \cdot \sin \alpha.\] В результате тангенс предельного угла атаки (максимально возможный угол подъема) составляет: \(\operatorname{tg} \alpha = \mu = 3\).
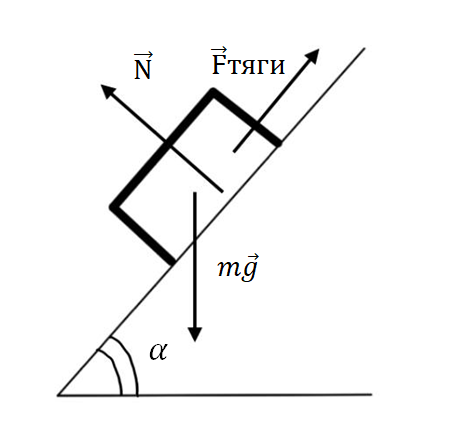 Рис. 1.10.
Рис. 1.10.При подъеме вездеход сохраняет устойчивость (не опрокидывается), если вектор силы тяжести пересекает пятно контакта гусениц с грунтом, а не выходит за его рамки.
В предельном случае вектор силы тяжести может проходить через крайнюю точку (нижнюю границу) пятна контакта (см. точку \(A\) на пояснительном рис. 1.11).
В результате при подъеме с максимально возможным углом атаки положение центра тяжести вездехода должно быть не выше точки \(O\), т. е. располагаться на высоте, относительно поверхности грунта, не большей, чем величина отрезка \(OH\).
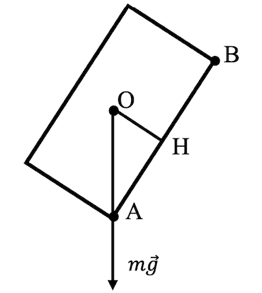 Рис. 1.11.
Рис. 1.11.Значение \(OH\) легко найти из прямоугольного треугольника \(AOH\): \[OH = \frac{AH}{\operatorname{tg} \alpha} = \frac{AB/2}{\operatorname{tg} \alpha} = \frac{3\,\text{м}/2}{3} = 0{,}5\,\text{м}.\]
Не более 0,5 м от поверхности.
| Критерий | Баллы |
|---|---|
| Сделан вывод о том, где находится центр тяжести в продольном направлении | 3 |
| Определено значение для протяженности пятна контакта гусениц вездехода | 3 |
| Вычислено значение эффективного коэффициента трения | 5 |
| Показано (объяснено), что именно является лимитирующим (сила трения или мощность (крутящий момент) двигателя на способности вездехода преодолевать крутые подъемы | 5 |
| Вычислен тангенс (или сам угол) предельно крутого подъема для данного вездехода | 4 |
| Сформулировано условие равновесия (или условия опрокидывания) вездехода при движении по наклонной плоскости | 5 |
| Вычислено предельное значение для высоты, определяющей точку расположения центра тяжести вездехода | 3 |
| Всего | 28 |
Адаптивный круиз-контроль (далее АКК) автоматически поддерживает заданную водителем скорость и варьирует ее в зависимости от текущей дистанции до попутного транспортного средства. Специальный сенсор периодически подает сигнал, который, отразившись от впереди идущего транспорта, возвращается обратно. Исходя из полученных данных, процессор АКК оценивает текущее расстояние, рассчитывает динамику его изменения, после чего принимает решение, нужно ли автомобилю ускориться или притормозить. Для оценки ситуации на дороге и принятия соответствующего решения системе АКК требуется промежуток времени (не менее 0,2 с). Еще около 0,3 с потребуется на приведение тормозной системы в режим интенсивного (аварийного) торможения (время на нагнетание и передачу давления к тормозным цилиндрам, осуществляющим прижим тормозных колодок к тормозным дискам колес).
Определите, какую минимально безопасную дистанцию между автомобилями должен поддерживать АКК, если движение автомобиля с системой АКК происходит в потоке, имеющем скорость 90 км/ч. Примите уровень сцепления шин автомобилей с дорогой таковым, что эффективный коэффициент трения (в зависимости от качества используемых шин) находится в диапазоне от 0,6 до 0,8. Считайте что движение происходит на горизонтальном ровном участке, а ускорение свободного падения равно 10 м/с\(^2\). Ответ выразите в метрах (округлив до целых значений).
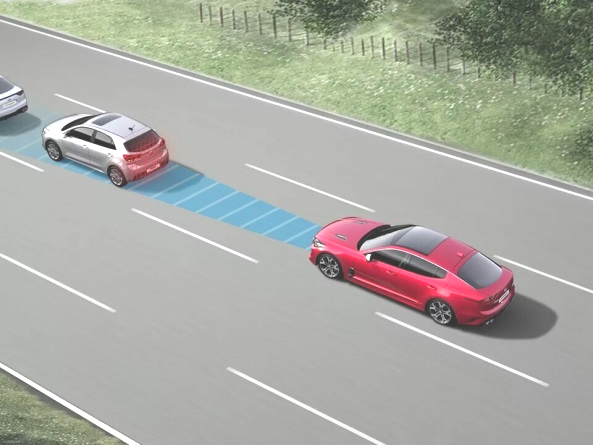
Согласно данным о скорости работы АКК и срабатывания тормозной системы, автомобиль, движущийся следом за впереди идущим автомобилем, совершающим экстренное торможение, начнет совершать торможение в полную силу спустя 0,5 с.
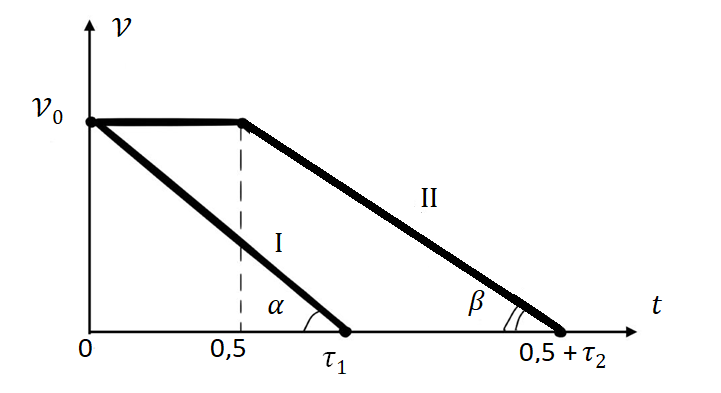
Наиболее неблагоприятная ситуация может реализоваться в том случае, если первый автомобиль оттормаживается лучше, чем следующий за ним (т. е. коэффициент трения у шин первого автомобиля достигает значения 0,8, а у второго — только 0,6). Следовательно, угол наклона (\(\beta\)) на графике изменения скорости от времени будет заметно меньше \(\angle\alpha\), т. к. тангенсы этих углов наклона на этих участках графиков численно равны соответствующим величинам ускорений при торможении.
В момент времени \(t = 0\) оба автомобиля двигались со скоростью 90 км/ч, что соответствует 25 м/с (\(90/3{,}6 = 25\)).
Ускорения, развиваемые при активной фазе торможения, определяются уровнем сцепления шин с дорожным полотном и величиной ускорения свободного падения:
\[a_i = \frac{F_{\text{тр}}}{m} = \frac{\mu_i N}{m} = \frac{\mu_i mg}{m} = \mu_i g.\]
Длительность фазы активного торможения (до полной остановки) зависит от скорости потока (т. е. от скорости на момент начала торможения) и от величины развиваемого ускорения при торможении: \[\tau_i = \frac{\Delta V}{a_i} = \frac{V_0 - 0}{a_i} = \frac{V_0}{a_i}.\]
Тормозной путь, включающий временную задержку до начала активной фазы торможения, определяется площадью под соответствующими графиками. Соответственно, для впереди идущего (первого) автомобиля: \[S_1 = V_0 \cdot \frac{\tau_1}{2} = \frac{V_0^2}{2\mu_1 g} = \frac{25^2}{2 \cdot 0{,}8 \cdot 10} \approx 39{,}0625\,\text{м}.\]
Для автомобиля (II), движущегося сзади: \[\begin{aligned} S_2 = V_0 \cdot 0{,}5 + \frac{V_0 \cdot \tau_2}{2} \nonumber = V_0 \cdot 0{,}5 + \frac{V_0^2}{2\mu_2 g} \nonumber =\\ = 25 \cdot 0{,}5 + \frac{25^2}{2 \cdot 0{,}6 \cdot 10} \nonumber \approx 64{,}5833\,\text{м}. \end{aligned}\]
Разность тормозных путей определяет тот необходимый минимум безопасной дистанции между автомобилями, который необходимо поддерживать системе АКК во избежание столкновения.
Т. е. необходимая (безопасная) дистанция при движении в потоке (со скоростью \(90\) км/ч) должна составлять не менее: \[S_{\text{мин}} \geqslant \Delta S = S_2 - S_1 \approx 64{,}5833\,\text{м} - 39{,}0625\,\text{м} \approx 25{,}5\,\text{м}.\]
При округлении полученного значения до целого значения необходимо округлять непременно в бОльшую сторону (без оглядки на правила округления!), т. к. здесь речь идет о минимально необходимой (безопасной) дистанции. Она однозначно должна быть не меньше найденного значения!
\(S_{\text{min}} \geqslant 26~\text{м}\).
| Критерий | Баллы |
|---|---|
| Разъяснена суть и причина для необходимости поддерживать дистанцию между машинами | 3 |
| Сформулирована мысль о том, что является благоприятным и неблагоприятным сценарием развития аварийной ситуации | 2 |
| Построен график или сделано текстовое пояснение, отражающие характер изменения скоростей автомобилей | 4 |
| Определены достижимые уровнем сцепления значения ускорений при торможении | 3 |
| Вычислены времена ускоренного движения, необходимые для подавления скорости до полной остановки | 2 |
| Вычислен тормозной путь для движущейся впереди машины | 2 |
| Вычислен тормозной путь автомобиля, идущего сзади и снабженного системой АКК | 3 |
| Определено значение безопасной дистанции по разности тормозных путей при неблагоприятном сценарии развития аварийной ситуации на дороге | 1 |
| Всего | 20 |
Колесная база (межосевое расстояние) автомобиля составляет 2,5 м. Центр тяжести автомобиля находится на высоте 50 см от поверхности дорожного полотна и немного смещен в сторону передней оси. В результате такого смещения 60% веса автомобиля приходится на переднюю ось и только 40% — на заднюю.
Все четыре колеса автомобиля «обуты» в шины одного типа и размера и имеют одну и ту же степень износа. Автомобиль снабжен дисковыми тормозами (вентилируемыми спереди и обычными сзади). Диаметр тормозных дисков при этом одинаков. Тормозные колодки также ничем не отличаются. Так как при торможении на долю передних тормозов обычно приходится существенно более высокая нагрузка, дополнительная вентиляция передних дисков сделана исключительно для предотвращения их преждевременного перегрева.
В попытке реализовать максимально эффективное торможение инженер-механик занимался настройкой баланса тормозов. Наилучший результат был достигнут при некотором (вполне конкретном) соотношении усилий, которые создавали тормозные цилиндры, обеспечивая соответствующий прижим тормозных колодок к передним и задним тормозным дискам. При этом полная остановка автомобиля, изначально движущегося со скоростью 108 км/ч, была осуществлена за 45 м пути.
Вопрос: какое соотношение прижимных усилий, переданных на передние и задние тормозные диски, позволило осуществить автомобилю максимально эффективное торможение?
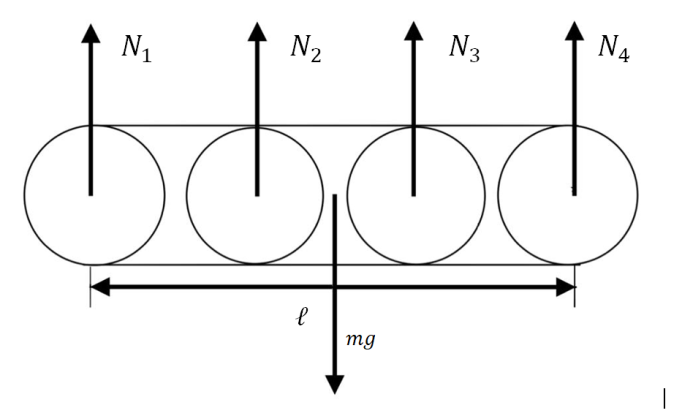
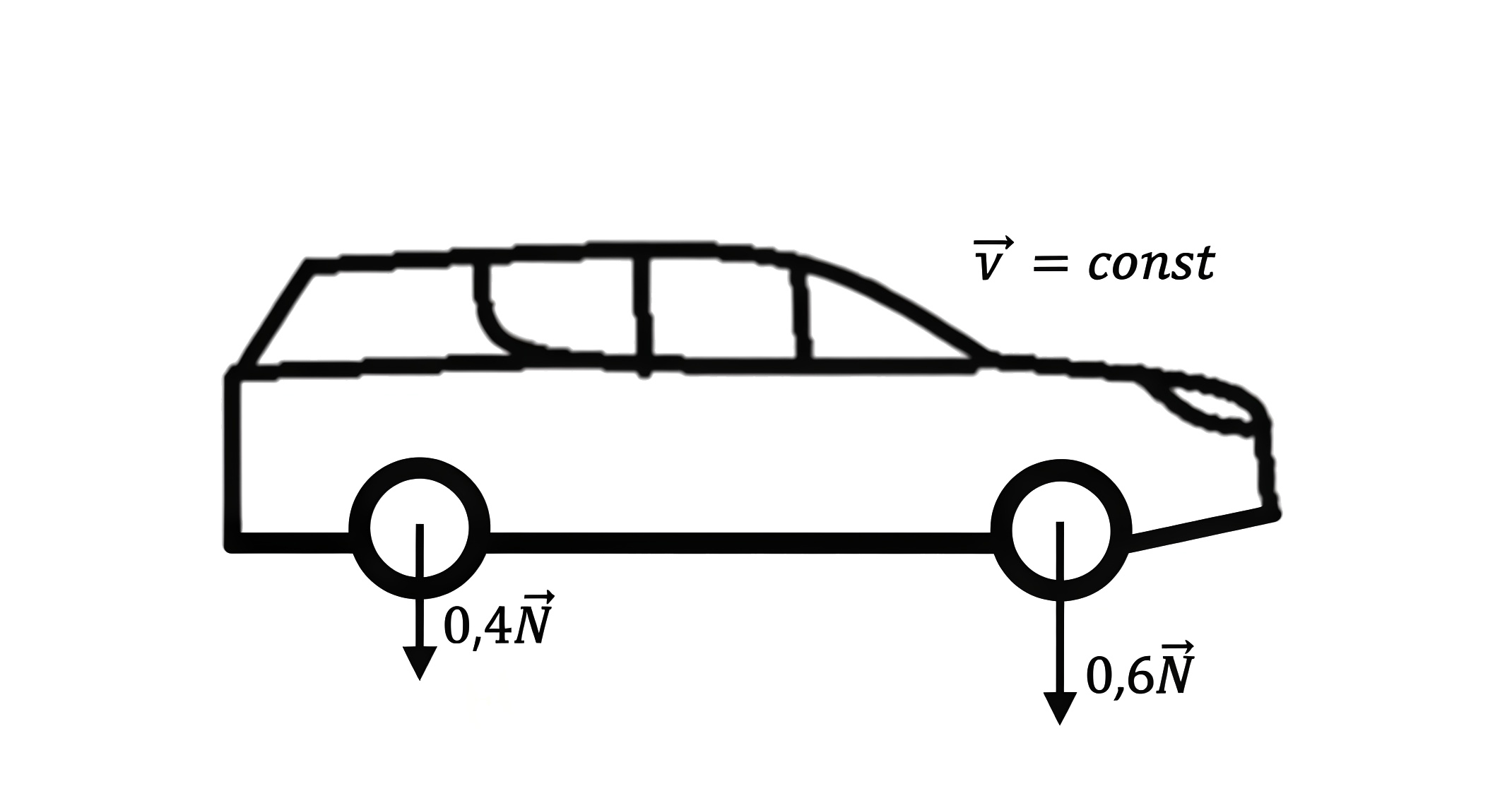
Когда автомобиль покоится или движется равномерно по горизонтальной поверхности, его оси нагружены соответственно с силой \(0{,}6N\) и \(0{,}4N\) (где \(N\) — вес автомобиля).
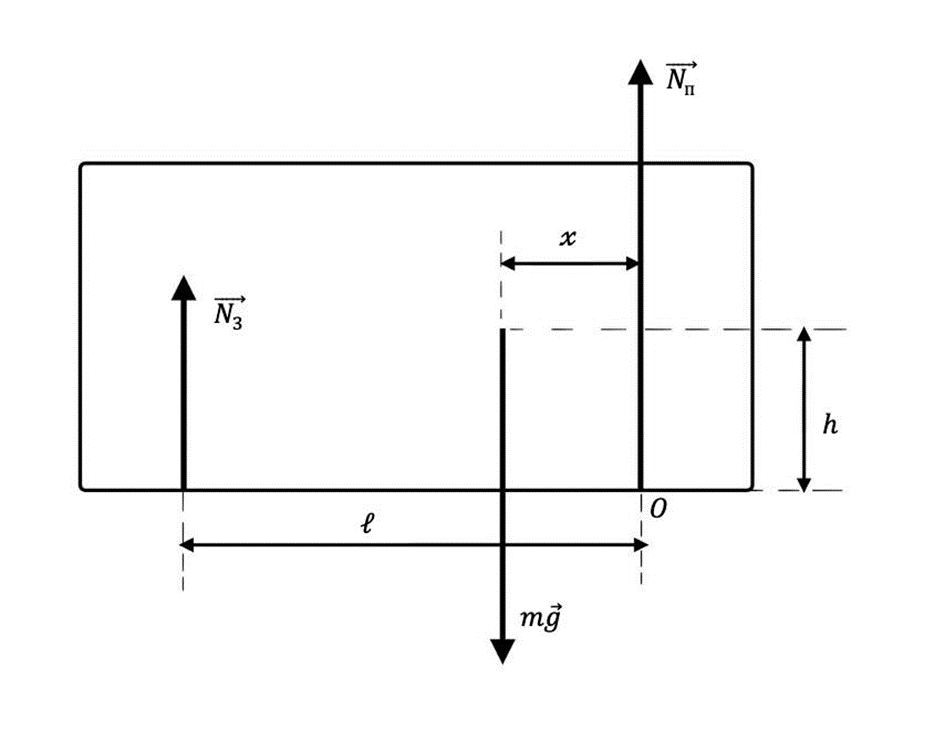
При торможении передняя ось автомобиля будет дополнительно перегружена (за счет перераспределения веса). При этом вес, приходящийся на переднюю ось \(N_{\text{п}}\), увеличится ровно на столько, на сколько снизится нагрузка \(N_{\text{з}}\), приходящаяся на заднюю ось. В сумме эти две силы остаются равными весу автомобиля.
Рассмотрим динамику торможения автомобиля, которому нужно погасить скорость 108 км/ч (\(\approx30\) м/с) за 45 м тормозного пути. Работа сил трения численно равна изменению кинетической энергии автомобиля: \[F_{\text{тр}} \cdot S = \frac{m\Delta V^2}{2} \Rightarrow F_{\text{тр}} = \frac{m\cdot(\Delta V^2)}{2S}.\]
При этом ускорение, с которым будет замедляться автомобиль, согласно второму закону Ньютона: \[a = \frac{F_{\text{тр}}}{m} = \frac{(\Delta V^2)}{2S} = \frac{30^2}{2\cdot45} = 10~\text{м/c}^2.\]
Из этого следует, что эффективное значение коэффициента трения (точнее сцепления шин с дорожным полотном) в данном случае составит \(\mu=1\) (т. к. \(a=g=10~\text{м/c}^2\)), т. е. сила трения численно равна весу автомобиля. Реальный коэффициент трения может быть и большим, т. к. ограничение по степени торможения регламентируется либо силой сцепления шин с дорожным полотном, либо величиной суммарного момента сил трения, создаваемым тормозной системой. Формулировка задачи подразумевает, что за эффективность торможения отвечает именно тормозная система. Она должна быть сбалансирована таким образом, чтобы максимально использовать силы трения, возникающие на контактных поверхностях каждого колеса (по всем осям). Т. е. подразумевается, что при этом фактическое значение коэффициента трения может иметь и большее значение, чем реализуемое при данном торможении.
Далее рассмотрим автомобиль схематично (как твердое тело прямоугольной формы) и покажем силы, создающие моменты сил, пытающиеся перевернуть и удержать автомобиль относительно выбранной оси, проходящей через две условные точки в месте контакта двух передних колес с асфальтом.
При \(a=0\). Согласно условию задачи, размерные величины на вспомогательном рисунке 2.5 имеют следующие значения: \(h=0{,}5\) м; \(l=2{,}5\) м.
Так как автомобиль не опрокидывается (не вращается) \(\Rightarrow\) относительно точки \(O\): \[\sum\vec{M}=0,\] что равносильно тому, что: \[N_3\cdot l - mgx=0;\] \[x=\frac{N_3\cdot l}{mg}=\frac{0{,}4N\cdot l}{N}=0{,}4l.\]
В результате: \[x=0{,}4\cdot2{,}5~\text{м}=1~\text{м}.\]
Таким образом, установлено, что центр тяжести автомобиля расположен на расстоянии 1 м от передней оси и в 1,5 м от задней, если отсчет вести в горизонтальной плоскости. Дополнительного известно (из условия), что центр тяжести смещен вверх на 0,5 м.
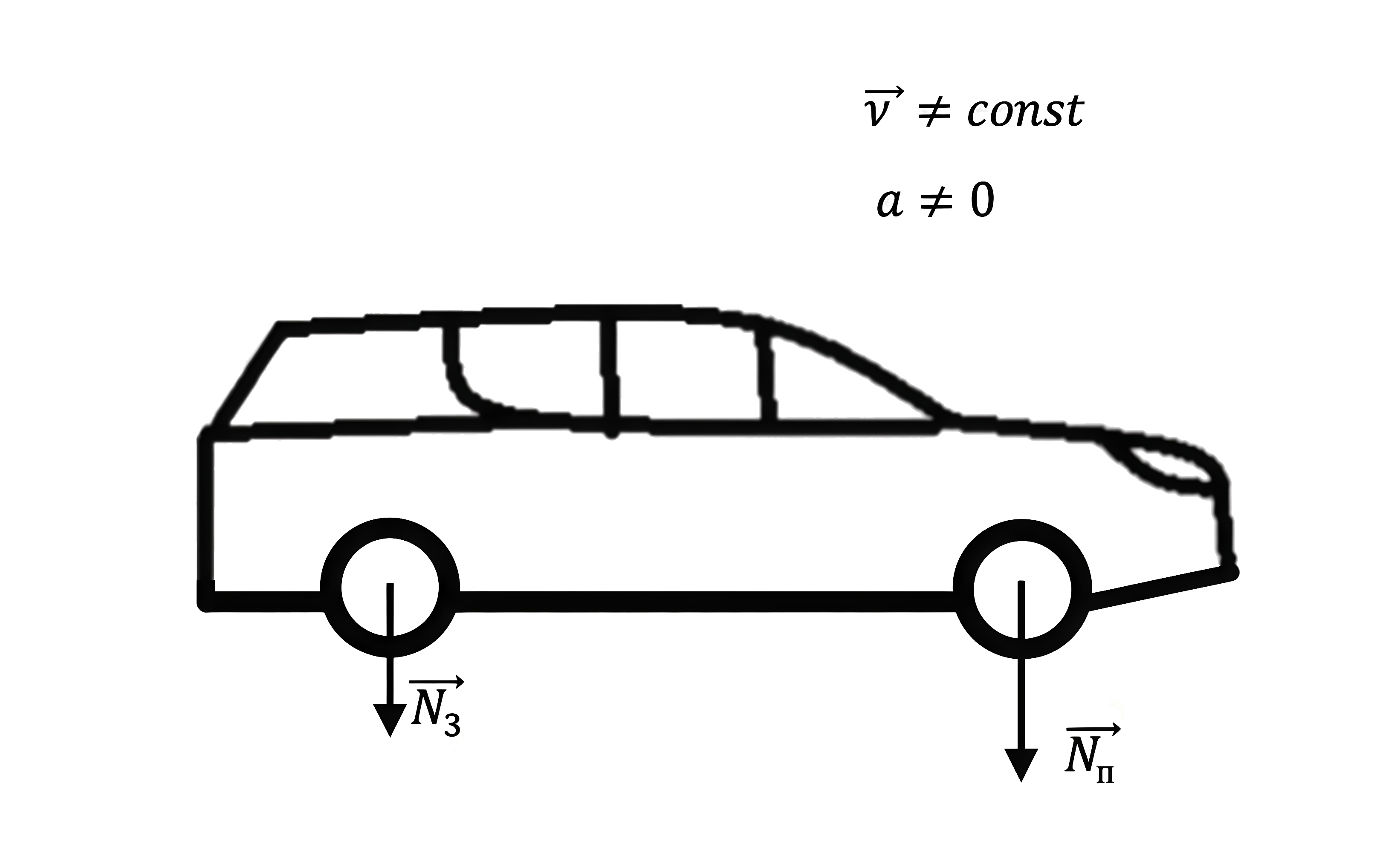
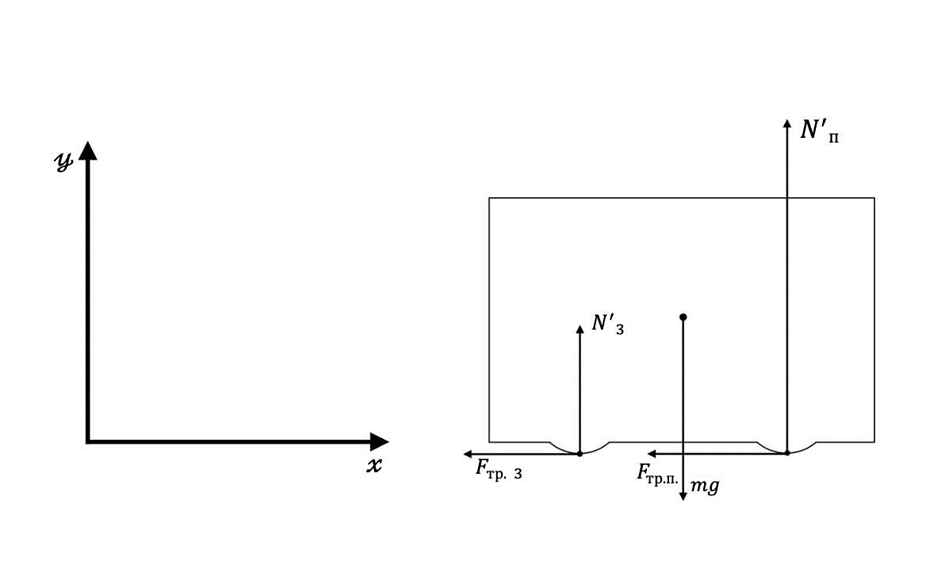
При торможении, когда \(a\neq0\) (\(a<0\)), возникают дополнительные силы, действующие на автомобиль (силы трения).
Рассмотрим моменты сил относительно центра тяжести (Ц. Т.) автомобиля, местоположение которого мы ранее определили.
Относительно Ц. Т.: \[\sum\vec{M}=0,\] что равносильно тому, что: \[N_3^\prime\cdot(l-x)+F_{\text{тр.3}}\cdot h+F_{\text{тр.п}}\cdot h-N_{\text{п}}^\prime\cdot x=0.\]
При этом сумма сил по вдоль оси \(Y\) равна нулю (автомобиль не взлетает и не проваливается). Следовательно: \[N_3^\prime+N_{\text{п}}^\prime=mg.\] Откуда: \[N_3^\prime=mg-N_{\text{п}}^\prime.\]
Таким образом: \[(mg-N_{\text{п}}^\prime)\cdot(l-x)+\mu N_3^\prime\cdot h+\mu N_{\text{п}}^\prime\cdot h-N_{\text{п}}^\prime\cdot x=0.\] \[(mg-N_{\text{п}}^\prime)\cdot(l-x)+\mu(mg-N_{\text{п}}^\prime)\cdot h+\mu N_{\text{п}}^\prime\cdot h-N_{\text{п}}^\prime\cdot x=0.\]
Учитывая, что: \(x=1\) м, \(h=0{,}5\) м; \(l=2{,}5\) м, \(\mu=1\), получаем: \[1{,}5mg-1{,}5N_{\text{п}}^\prime+0{,}5mg-0{,}5N_{\text{п}}^\prime+0{,}5N_{\text{п}}^\prime-N_{\text{п}}^\prime=0;\] \[2mg-2{,}5N_{\text{п}}^\prime=0.\]
Откуда: \[N_{\text{п}}^\prime=0{,}8mg;\] \[N_3^\prime=mg-N_{\text{п}}^\prime=0{,}2mg.\]
Получается, что силы реакции опоры при данном торможении соотносятся как \(\dfrac{N_{\text{п}}^\prime}{N_3^\prime}=4\).
Требуемое соотношение тормозных усилий со стороны тормозных колодок для создания соответствующих моментов сил трения (из-за равенства диаметров тормозных дисков) будет тем же: \(4:1\). При таком соотношении тормозные усилия будут максимально эффективно задействованы, обеспечивая равновероятный срыв колес в скольжение, если фактический уровень сцепления с дорогой окажется недостаточным для достижения требуемого замедления при торможении.
Таким образом, баланс тормозов (соотношение тормозных усилий, создаваемых тормозными цилиндрами) на передние и задние тормозные диски составляет \(4:1\), что обеспечит максимально эффективное и полное торможение автомобиля со 108 км/ч за 45 м пути, разумеется, при том условии, что уровень сцепление шин с дорогой достаточен (\(\mu\geqslant1\)) для фактической реализации такого торможения.
\(4:1\).
| Критерий | Баллы |
|---|---|
| Найдено положение центра тяжести вдоль горизонтальной оси | 3 |
| Определено значение ускорения при торможении | 3 |
| Найдено эффективное значение коэффициента трения (сцепления) шин об асфальт | 2 |
| Сделаны пояснительные рисунки (схемы) с указанием сил, действующих в период торможения | 4 |
| Записан баланс моментов сил при торможении | 5 |
| Найдены значения вертикальных сил, действующие на переднюю и заднюю оси при торможении | 3 |
| Определены соотношения тормозных усилий (найден баланс тормозов) | 3 |
| Всего | 23 |
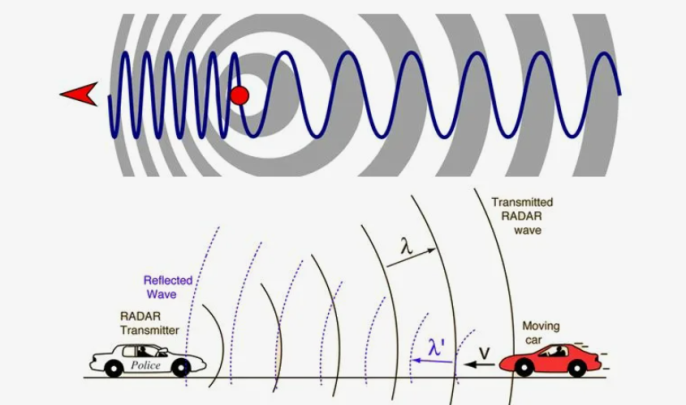
Эффект, связанный с изменением частоты и, соответственно, длины волны излучения, которую воспринимает наблюдатель (приемник), вследствие движения источника излучения относительно наблюдателя, назван в честь австрийского физика Кристиана Доплера. Причина данного эффекта заключается в том, что, когда источник волн движется в направлении наблюдателя, каждый последующий гребень волны выходит из положения более близкого к наблюдателю, чем гребень предыдущей волны. Таким образом, каждой последующей волне необходимо немного меньше времени, чтобы добраться до наблюдателя, чем предыдущей волне, что воспринимается наблюдателем как увеличение частоты.
Стационарный полицейский радар, работающий на эффекте Доплера, излучает радиосигнал с частотой 24 кГц (являясь первоисточником излучения). Это излучение, достигнув металлических деталей автомобиля, воспринимается в искаженном виде (вследствие сближения автомобиля с источником). Далее происходит переизлучение радиосигнала в обратном направлении с уже искаженной частотой (с частотой, которую воспринял автомобиль).
В результате радиосигнал, который будет зарегистрирован радаром, получит дополнительное изменение частоты, которое также будет зависеть от скорости движения этого автомобиля и скорости распространения электромагнитных волн.
Фиксируя отраженный сигнал и определяя его частоту (и/или длину волны), прибор сопоставляет эти искаженные значения с исходными характеристиками излучения и по величине этих изменений (например, по изменению длины волны) вычисляет скорость движения автомобиля.
Вопрос: с какой допустимой ошибкой полицейский радар должен зафиксировать изменение длины электромагнитной волны, чтобы обеспечить определение скорости автомобиля, движущегося со скоростью 100 км/ч, с погрешностью, не превышающей 1%, предполагая, что прибор идеально отъюстирован и ведет регистрацию в прекрасных условиях видимости на ровном и прямом участке автодороги?
Эффект Доплера связан с изменением частоты и, соответственно, длины волны излучения, которое воспринимает наблюдатель (прибор) вследствие движения источника (источника и/или наблюдателя). Когда источник волн движется к наблюдателю, каждый последующий гребень волны выходит из положения, более близкого к наблюдателю, чем гребень предыдущей волны. Таким образом, каждой последующей волне необходимо немного меньше времени, чтобы добраться до наблюдателя, чем предыдущей волне, что воспринимается наблюдателем как увеличение частоты.
Если наблюдатель (радар) неподвижен, а движется только источник (в нашем случае автомобиль), то нетрудно показать, что каждый последующий гребень волны отражаемого от автомобиля излучения выходит из положения, более близкого к наблюдателю (к радару), чем гребень предыдущей волны. Если математически формализовать это утверждение, то получим следующее соотношение:
\[V\cdot f_s^\prime = f\cdot(V-V_s),\] где
- \(V\) — скорость распространения волн; в нашем случае \(V = c \approx 3\cdot10^8\) м/c (равно скорости света);
- \(V_s\) — скорость сближения источника (автомобиля) к наблюдателю (к радару);
- \(f_s^\prime\) — частота испущенного от автомобиля сигнала;
- \(f\) — частота, воспринимаемая прибором.
Следовательно, частота, воспринимаемая прибором (\(f\)), будет связана с частотой отраженного от автомобиля сигнала \(f_s^\prime\) следующим образом: \[f = \frac{V}{V-V_s}\cdot f_s^\prime.\]
Однако в рассматриваемом случае прибор регистрирует отраженное излучение, которое уже было искажено по сравнению с исходным сигналом, испущенным с частотой \(f_0=24\) кГц: \[f_S^\prime = \frac{V}{V-V_s}\cdot f_0,\] где \(V=c\) — скорость света.
Таким образом: \[f = \left(\frac{c}{c-V_s}\right)^2\cdot f_0 \Rightarrow \frac{f_0}{f} = \left(1-\frac{V_s}{c}\right)^2.\]
Длина волны \(\lambda\) связана с частотой \(f\) и скоростью \(c\) как: \[\lambda = \frac{c}{f} \Rightarrow \frac{\lambda_1}{\lambda_2} = \frac{f_2}{f_1}.\]
Следовательно, для нашего случая: \[\frac{\lambda}{\lambda_0} = \frac{f_0}{f} = \left(1-\frac{V_S}{c}\right)^2 = 1 - 2\left(\frac{V_S}{c}\right) + \left(\frac{V_S}{c}\right)^2.\]
В силу того, что скорость света на много порядков больше скорости сближения источника (автомобиля) к наблюдателю (к радару), последним членом выражения \(\left(\frac{V_S}{c}\right)^2\) можно пренебречь по причине его чрезвычайной малости при \(V_S \ll c\).
В результате отношение длин волн и частот можно рассчитывать по формуле: \[\frac{\lambda}{\lambda_0} = \frac{f_0}{f} \approx 1 - 2\left(\frac{V_S}{c}\right).\]
Тогда абсолютное изменение длины волны, зарегистрированное прибором, должно иметь следующее значение: \[|\Delta\lambda| = |\lambda-\lambda_0| = 2\left(\frac{V_S}{c}\right)\cdot\lambda_0 = 2\frac{V_s}{c}\cdot\frac{c}{f_0} = 2\left(\frac{V_s}{f_0}\right) \approx 2\cdot\frac{(100/3{,}6)~\text{м/с}}{24\cdot10^3~\text{Гц}} \approx 2{,}315\cdot10^{-3}~\text{м}.\]
Прибор должен зафиксировать скорость автомобиля с погрешностью не более 1%, поэтому он должен обладать достаточной точностью и чувствительностью, при которой он будет способен надежно фиксировать изменения длин волн, не превышающих одной сотой доли от найденной нами величины абсолютного изменения, возникшего при движении автомобиля со скоростью 100 км/ч, что соответствует: \(2{,}3\cdot10^{-5}\) м.
\(2{,}3\cdot10^{-5}~\text{м}\).
| Критерий | Баллы |
|---|---|
| Записано (выведено) выражение для изменения частоты (и/или длины волны) излучения, воспринимаемое наблюдателем в зависимости от скорости источника и скорости распространения сигнала | 7 |
| Сделан учет того, что исходным источником излучения является не автомобиль, а радар | 5 |
| Записана взаимосвязь длины волны со скоростью распространения и частотой излучения | 5 |
| Определено изменение длины волны, возникающее при регистрации отраженного сигнала от движущегося со скоростью 100 км/ч автомобиля | 3 |
| Вычислена необходимая точность прибора (его разрешающая способность) для погрешности измерения скорости не более 1% | 2 |
| Всего | 22 |
Фары автомобиля, использующие лампы накаливания (с температурой нагрева нити 2127 °С), обеспечивают необходимый уровень освещенности только на ближайшие 10 м дорожного полотна, что часто является недостаточным, повышая риск ДТП по причине позднего визуального обнаружения другого транспортного средства, пешехода, велосипедиста, животного или иного вида препятствия или помехи.
Энергетическая светимость (\(W\)) нагретого серого тела, коим является нить накала, подчиняется закону Стефана – Больцмана, согласно которому \(W=\varepsilon\cdot\sigma\cdot T^4\), где \(\varepsilon\) — степень черноты тела, \(\sigma\) — постоянная Стефана – Больцмана, \(T\) — абсолютная температура.
Определите, на сколько градусов по шкале Цельсия необходимо повысить температуру накала нити, чтобы, не внося изменений в конструкцию фар и ламп, обеспечить надлежащий уровень освещенности на дистанции в 15 м. Интенсивность светового потока, проходящего через основание конуса условно примите распределенным равномерно. Учтите, что распространение света от фары можно считать происходящим внутри некоторого конуса, сохраняющего самоподобие.
Исходная рабочая температура накала нити лампы составляет: \(t_1 = 2127~°\)С, что эквивалентно 2400 К (по абсолютной шкале температур).
Энергетическая светимость серого тела \(W\sim T^4\) (\(W=\varepsilon\cdot\sigma\cdot T^4\)), где
- \(\varepsilon\) — степень черноты тела,
- \(\sigma\) — постоянная Стефана – Больцмана,
- \(T\) — абсолютная температура.
Так как конструктивных изменений в устройство не вносилось, отношение светимостей будет связано исключительно с изменением температуры накала нити: \[\frac{W_2}{W_1} = \left(\frac{T_2}{T_1}\right)^4.\]
Световой поток \(\Phi\), создаваемый лампой, пропорционален энергетической светимости лампы, следовательно, \[\frac{\Phi_2}{\Phi_1} = \left(\frac{T_2}{T_1}\right)^4.\]
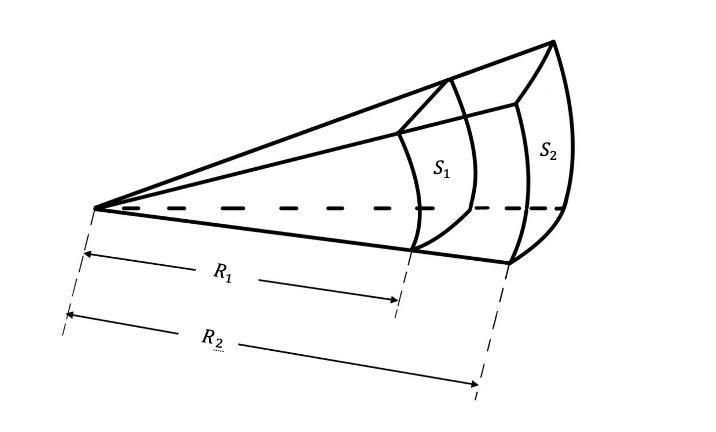
На расстояниях в 10–15 м нить накала лампы можно смело считать точечным источником света. Следовательно, освещенность (\(E\)) будет убывать обратно пропорционально площади поверхности той части сферы, находящейся в пределах телесного угла, в котором распространяется световой поток, испускаемый источником света (фарой): \[E = \frac{\Phi}{S_{\text{пов.}}}.\]
Площадь части сферы \(S_{\text{пов.}}\) внутри телесного угла \(\omega\) численно равна: \[S_{\text{пов.}} = 4\pi R^2 \frac{\omega}{4\pi} = \omega R^2,\] где \(\omega\) — телесный угол, \(R\) — радиус сферы.
В результате отношение освещенностей, создаваемых лампами, разогретыми до разных температур на разных расстояниях, определяются из соотношения: \[\frac{E_2}{E_1} = \frac{\Phi_2}{\Phi_1}\cdot\left(\frac{R_1}{R_2}\right)^2 = \left(\frac{T_2}{T_1}\right)^4\cdot\left(\frac{R_1}{R_2}\right)^2.\]
Из чего следует, что: \[T_2 = T_1 \sqrt{\frac{R_1}{R_2}}\cdot \sqrt[4]{\frac{E_2}{E_1}}.\]
Так как в задаче требуется, чтобы уровень освещенности на дистанции 15 м для более разогретой лампы был тем же, что и на 10 м для исходной лампы, т. е.: \[E_2 = E_1;\] \[T_2 = T_1 \sqrt{\frac{R_2}{R_1}} = 2400~\text{К}\sqrt{\frac{15~\text{м}}{10~\text{м}}} \approx 2939~\text{К};\] \[\Delta T = T_2 - T_1 = (2939 - 2400)~\text{К} = 539~\text{К} = 539~°\text{С}.\]
На 539 °С.
| Критерий | Баллы |
|---|---|
| Осуществлен перевод температуры накала в абсолютную шкалу температур (из градусов Цельсия в градусы Кельвина) | 2 |
| Записано выражение о связи температуры с энергетической светимостью в привязке к выражению светового потока, формируемому фарой | 4 |
| Показано, что отношение световых потоков, формируемых серым телом, при неизменности прочих факторов, будет определяться по соотношению абсолютных температур, возведенных в четвертую степень | 4 |
| Сделан пояснительный рисунок, показано, что уровень освещенности убывает с квадратом расстояния (объяснено через отношение площадей оснований у подобных конусов или через телесный угол и площадь части сферы) | 5 |
| Вычислена температура накала нити, необходимая для создания требуемой освещенности на дистанции в 15 м | 4 |
| Получено значение необходимого изменения температуры накала нити | 1 |
| Всего | 20 |
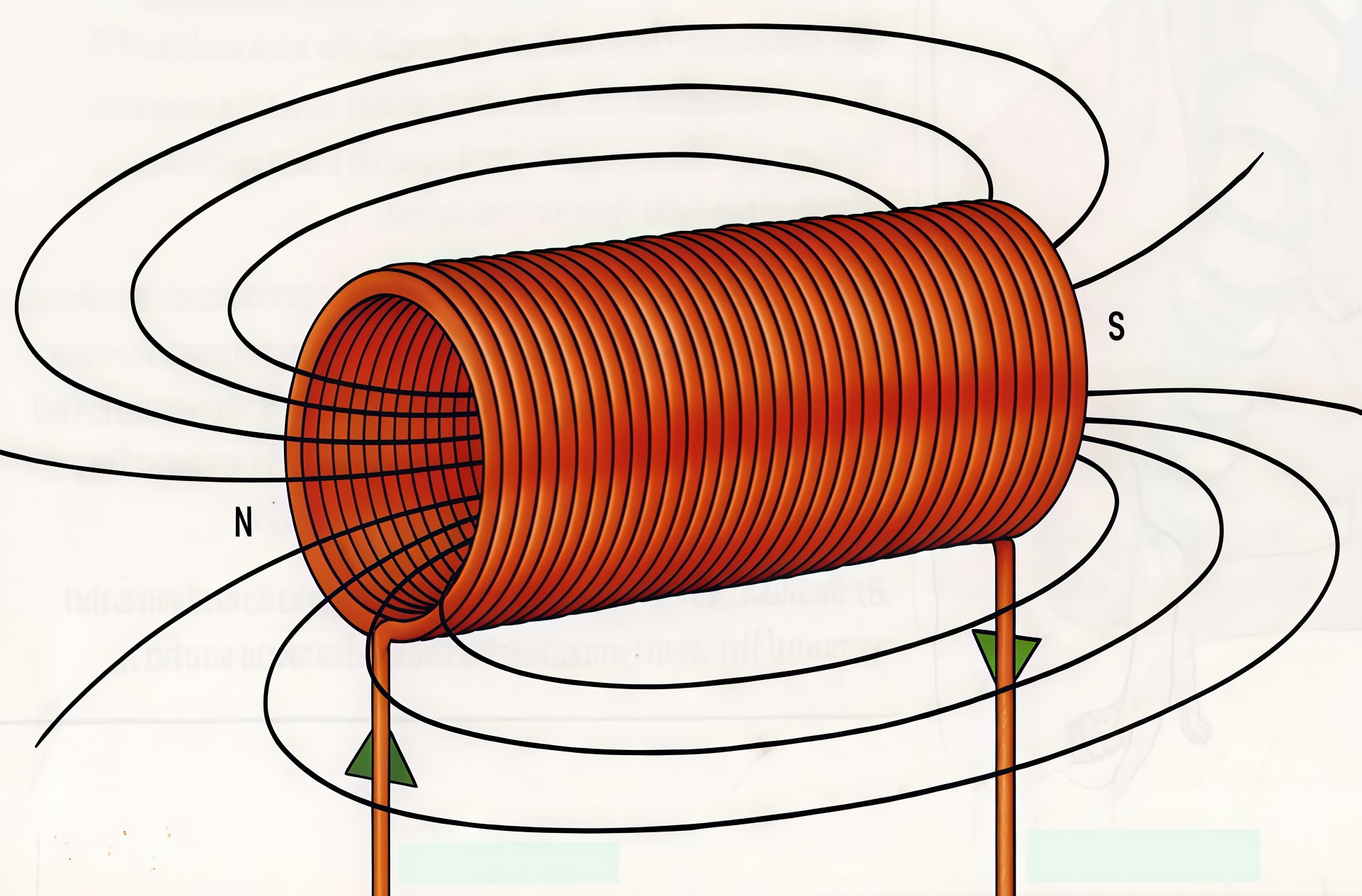
Индуктивность соленоида (\(L\)) зависит от числа витков соленоида (\(n\)), его длины (\(l\)), площади витков с током (\(S\)), магнитной проницаемости (\(\mu\)) и некоторого коэффициента (\(k\)), зависящего от формы соленоида: \[L = k\cdot \mu_0\cdot\mu\cdot\frac{n^2 \cdot S}{l}.\]
В результате небольшой технической аварии была случайно повреждена медная катушка, использованная в качестве соленоида (с индуктивностью \(L\)), входящего как один из основных элементов колебательного контура в антенне радиоприемника квадрокоптера.
После анализа состояния пострадавшей катушки и обнаружения мест повреждения выяснилось, что проволока была намотана на цилиндрическую оправку плотно в один слой, и что повторно можно будет использовать не всю проволоку, а только основной ее фрагмент, составляющий 85% от первоначальной длины проволоки. Ремонт катушки заключался в повторной намотке неповрежденной части проволоки на оправку того же диаметра с тем же шагом.
Во сколько раз необходимо будет изменить емкость конденсатора, чтобы после ремонта катушки частота приема сигнала осталась прежней?
Индуктивность соленоида (\(L\)) зависит от числа витков соленоида (\(n\)), его длины (\(l\)), площади витков с током (\(S\)), магнитной проницаемости (\(\mu\)) и некоторого коэффициента (\(k\)), зависящего от формы соленоида: \[L = k\cdot \mu_0\cdot\mu\cdot\frac{n^2 \cdot S}{l}.\]
Из-за того что катушка индуктивности частично пострадала, длина проволоки, которую можно было использовать повторно, уменьшилась и составила 85% от первоначальной длины. Если осуществлять повторную намотку с тем же шагом и на том же диаметре оправки, то: \[n^\prime = 0{,}85\cdot n_0;\] \[l^\prime = 0{,}85\cdot l_0;\] \[S^\prime = S_0.\]
При этом индуктивности «после» и «до», будут соотносится как: \[\frac{L^\prime}{L_0} = \frac{0{,}85^2}{0{,}85} = 0{,}85.\]
Электрическую схему приемника радиосигнала можно изобразить в виде трех составных элементов, имеющих соответствующее омическое, емкостное и индуктивное сопротивление.
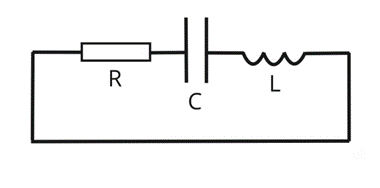
Условие резонанса в такой цепи будет удовлетворять циклическая частота \(\omega_0 = \frac{1}{\sqrt{LC}}\), при которой полное сопротивление достигает минимума (постепенно достигая величины омического сопротивления), т. е. когда \(\omega_0 L = \frac{1}{\omega_0 C}\) (когда индуктивное равно емкостному сопротивлению), при этом: \[C = \frac{1}{L\cdot\omega_0^2}.\]
Так как по условию задачи требуется сохранить резонансную частоту (частоту приема), то: \[\frac{C^\prime}{C_0} = \frac{L_0}{L^\prime} = \frac{L_0}{0{,}85\cdot L_0} \approx 1{,}17647 \approx 1{,}18.\]
Необходимо увеличить примерно в 1,18 раза.
| Критерий | Баллы |
|---|---|
| С учетом формулы для вычисления индуктивности соленоида показано, какие параметры, влияющие на индуктивность соленоида, изменились и насколько сильно они изменились при сокращении длины проволоки | 3 |
| Численно оценено изменение индуктивности после ремонта по сравнению со значением индуктивности до аварии | 3 |
| Сформулировано условие резонанса в цепи колебательного контура | 4 |
| Записано аналитическое выражение для резонансной частоты | 3 |
| Получено численное значение, отражающее степень требуемого изменения емкости конденсатора для сохранения резонансной частоты (частоты приема сигнала) при измененном значении индуктивности соленоида | 2 |
| Всего | 15 |
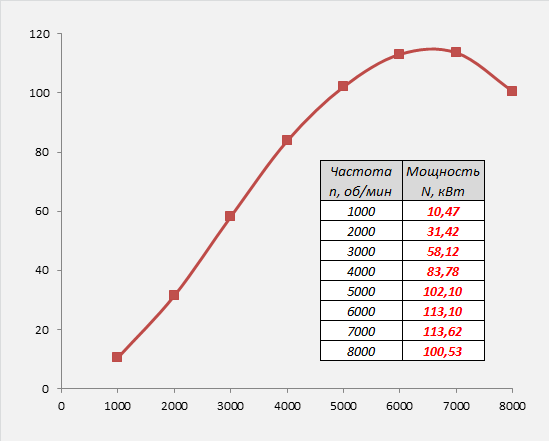
На испытательном стенде при проверке и обкатке двигателя была получена зависимость развиваемой им мощности от частоты оборотов двигателя (см. соответствующий график и таблицу на рис. 2.12).
На основании полученных экспериментальных данных оцените, при какой частоте вращения (из числа приведенных в таблице) испытуемый двигатель выдал максимальный крутящий момент и какова при этом была его величина?
Момент силы — векторная величина, которая характеризует силовое воздействие, вызывающее вращательное движение.
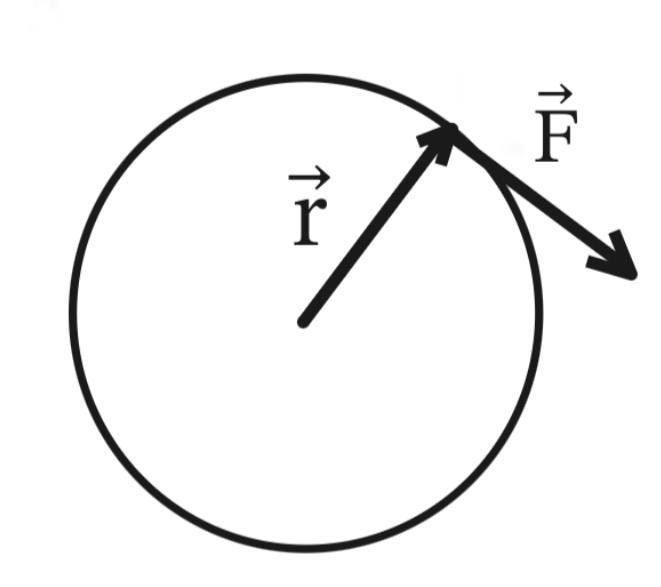
Крутящий момент двигателя можно выразить как векторное произведение радиус-вектора \(\vec{r}\) — вектора, проведенного от оси вращения до точки приложения (генерации) силы \(\vec{F}\), на вектор силы \(\vec{F}\): \[\vec{M} = [\vec{r} \times \vec{F}].\]
Мощность двигателя можно воспринять как некий объем работы, который может выполнять двигатель за рассматриваемый промежуток времени и отнесенный к длительности этого промежутка времени.
Мощность связана с действием силы, совершаемом на некотором преодолеваемом расстоянии: \[N = \frac{\Delta A}{\Delta t} = \frac{F\cdot \Delta S\cdot\cos\alpha}{\Delta t} = F\cdot V\cdot\cos\alpha,\] где \(\alpha\) — угол между векторами \(\vec{F}\) и \(\vec{V}\); \(\vec{V}\) — скорость материальной точки.
В случае воздействия момента силы совершаемое действие выражается через «угловое расстояние» \(\Delta\varphi\) (изменение угла): \[N = \frac{\Delta A}{\Delta t} = \frac{M\cdot \Delta\varphi}{\Delta t} = M\cdot\omega,\] где \(\omega\) — угловая скорость (рад/сек): \(\omega = 2\pi n\); \(n\) — частота вращения (об/с).
В результате: \[N = \frac{2\pi M n^*}{60},\] где \(n^*\) — частота оборотов двигателя, выраженная в (об/мин).
В итоге для выражения крутящего момента можно получить выражение, связывающее его с мгновенной мощностью и частотой оборотов: \[M = \frac{30\cdot N}{\pi\cdot n^*}.\]
Согласно данным, приведенным в таблице, и сделанным соответствующим вычислениям момента, можно сделать вывод о том, что максимальное значение момента \(M_{\text{мах}} \approx 200\) Н\(\cdot\)м было достигнуто при частоте \(n^* = 4000\) об/мин.
| Частота, об/мин | Мощность, кВт | Крутящий момент, Н\(\cdot\)м |
|---|---|---|
| 1000 | 10,47 | 100 |
| 2000 | 31,42 | 150 |
| 3000 | 58,12 | 185 |
| 4000 | 83,78 | 200 |
| 5000 | 102,1 | 195 |
| 6000 | 113,1 | 180 |
| 7000 | 113,62 | 155 |
| 8000 | 100,53 | 120 |
200 Н\(\cdot\)м при 4000 об/мин.
| Критерий | Баллы |
|---|---|
| Дано определение, что такое крутящий момент | 1 |
| Приведена формула, выражающая значение крутящего момента через приложенную силу и плечо (сделан поясняющий рисунок) | 2 |
| Дано определение мощности | 2 |
| Показана взаимосвязь между воздействием момента силы и совершаемым действием с определенной циклической частотой, которое можно выразить как мощность | 5 |
| Получено итоговое выражение для вычисления крутящего момента, связывающее его с мгновенной мощностью и частотой оборотов двигателя | 4 |
| Согласно данным, приведенным в таблице, сделаны соответствующие вычисления крутящего момента | 4 |
| Согласно вычислениям момента сделан вывод о том, что максимальное значение момента \(M_{\text{мах}} \approx 200\) Н\(\cdot\)м было достигнуто при частоте \(n^* = 4000\) об/мин. | 2 |
| Всего | 20 |