Предметный тур. Информатика. 3 этап

Информатика. 8–11 классы

Задача 1.1.(10 баллов)

Тренировка многоборца

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

В качестве тренировки один спортсмен по многоборью дважды проводит забег-заезд из пункта \(A\) в пункт \(C\).

В первый раз он пробегает часть этой дистанции от пункта \(A\) до некоторого промежуточного пункта \(B\) на маршруте бегом, в пункте \(B\) садится на велосипед и проезжает оставшуюся часть пути до пункта \(C\) на нем. В итоге он тратит на это \(X\) часов.

В следующий раз он, наоборот, из пункта \(A\) до пункта \(B\) проезжает на велосипеде, а из пункта \(B\) до пункта \(C\) бежит бегом. В этот раз он тратит на весь маршрут \(Y\) часов.

Требуется узнать, за какое время он может пробежать всю дистанцию от \(A\) до \(C\), если его скорость на велосипеде в \(k\) раз выше скорости его бега. Можно считать, что скорость его бега и скорость его езды на велосипеде всегда постоянные.

Формат входных данных

В одной строке через пробел заданы три целых числа \(X\), \(Y\) и \(k\) — время первого прохождения маршрута, время второго прохождения маршрута и величина, показывающая, во сколько раз быстрее он передвигается на велосипеде, чем бегом. \(1 \leqslant X, Y, k \leqslant 1000\).

Формат выходных данных

Вывести одно число — время, за которое спортсмен пробежит весь маршрут от \(A\) до \(C\).

Тесты, на которых будет проверяться ваше решение, сгенерированы таким образом, что ответ всегда является целым числом.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	3 5 3	6

Примечания

В примере из условия для объяснения теста приведем полное рассуждение с построением расстояний \(AB\) и \(BC\), хотя эти расстояния находить не обязательно. Дано, что в первый раз спортсмен затратил три часа, а во второй — пять часов, при этом на велосипеде он едет в три раза быстрее, чем бежит бегом.

После некоторых рассуждений можно получить, что если взять длину \(AB\) равной 15 км, длину \(BC\) равной 45 км, скорость бега равной 10 км/ч, а скорость на велосипеде равной 30 км/ч, то получим требуемые результаты: \(\displaystyle \frac{15}{10} + \frac{45}{30} = 3\), \(\displaystyle\frac{15}{30} + \frac{45}{10} = 5\). Общее расстояние \(AB\) равно \(15 + 45\) и равно 60 км. Тогда спортсмен, имея скорость бега равную 10 км/ч, пробежит 60 км за шесть часов.

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
using namespace std;
signed main()
{
    int x, y, k;
    cin >> x >> y >> k;
    int v = (x + y) / (k + 1);
    int b = x + y - v;
    cout << b << endl;
}

Задача 1.2.(15 баллов)

Пространственная решетка

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

После открытия так называемых точек сингулярности пространства и формирования теории пространственной решетки всей Вселенной пришла пора практического освоения космоса. Если кратко, то у каждой точки сингулярности \(A\) есть своя уникальная характеристика \(P(A)\) — натуральное число от \(1\) до \(10^{12}\). Между некоторыми точками есть силовые линии, вдоль которых возможно движение со сверхсветовыми скоростями. Из одной точки \(A\) можно попасть таким образом в другую точку \(B\), если характеристика \(P(A)\) получается из \(P(B)\) либо делением на простое число, либо умножением на простое число. Независимо от размеров характеристик, движение вдоль одной такой линии занимает одинаковое время, называемое константой Диогена. По этой причине все космические межзвездные перелеты измеряются этими константами.

Предлагаемая задача входит в базовый курс звездной навигации, изучаемой курсантами на первом цикле. Даны две точки сингулярности \(A\) и \(B\), причем \(P(A)\) делит \(P(B)\). Необходимо перечислить все точки сингулярности, которые находятся на кратчайших путях из \(A\) в \(B\).

Формат входных данных

Заданы два натуральных числа \(P(A)\) и \(P(B)\) — характеристики точек \(A\) и \(B\). Гарантируется, что \(P(B)\) нацело делится на \(P(A)\). Обе характеристики находятся в пределах от \(1\) до \(10^{12}\).

Формат выходных данных

В первой строке вывести количество искомых точек. Во второй строке вывести через пробел в порядке возрастания все характеристики точек сингулярности, которые находятся на всех кратчайших расстояниях из точки \(A\) в точку \(B\).

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	6 120	6 6 12 24 30 60 120

Примечания

Приведем несколько примеров кратчайших путей из точки 6 в точку 120 (точки представлены своими характеристиками):

6 – 12 – 24 – 120;
6 – 30 – 60 – 120;
6 – 12 – 60 – 120.

Можно видеть, что других чисел, кроме представленных в ответе на этих и других кратчайших путях из 6 в 120, также нет.

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define int long long
using namespace std;
signed main(){
    int a, b;
    cin >> a >> b;
    int c = b / a;
    set<int> S;
    for(int i = 1; i * i <= c; i++){
        if(c % i == 0){
            S.insert(i);
            S.insert(c / i);
        }
    }
    cout << sz(S)<< endl;
    for(auto el : S){
        cout << el * a <<' ';
    }
    cout << endl;
}

Задача 1.3.(20 баллов)

Ключ и замок

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

Замок представляет собой конструкцию размера \(h\) единиц в высоту и \(n\) единиц в длину. Внутри замка содержатся \(n\) вертикальных цилиндров, каждый имеет ширину \(1\) и высоту \(a_i\). Эти цилиндры расположены внутри замка в порядке неубывания, то есть \(a_{i - 1} \geqslant a_i\) для всех \(i\) от \(2\) до \(n\). Все \(a_i\) строго меньше высоты замка \(h\). Цилиндры внутри замка закреплены неподвижно.

Ключ представляет собой также объект длиной \(n\) единиц и состоит из \(n\) прямоугольников, каждый имеет ширину \(1\) и высоту \(b_i\). В ключе, наоборот, высоты прямоугольников не возрастают, то есть \(b_{i - 1} \leqslant b_i\) для всех \(i\) от \(2\) до \(n\). Все \(b_i\) также строго меньше высоты замка \(h\).

Ключ и замок не обязательно подходят друг к другу. Ключ пытаются вставить как можно дальше в замок и фиксируют длину, на которую это получится сделать. Изначально самый маленький (допустим, левый) прямоугольник ключа находится на позиции (\(n + 1\)), и все остальные его прямоугольники — на последующих еще больших позициях. Далее, до тех пор пока можно сдвинуть ключ на одну позицию левее, ключ сдвигают. В какой-то момент либо прямоугольники ключа и цилиндры замка начинают мешать дальнейшему движению, либо ключ вставляется до конца. В этот момент процесс прекращается и измеряется количество позиций, на которые был сдвинут ключ влево. Это и является ответом.

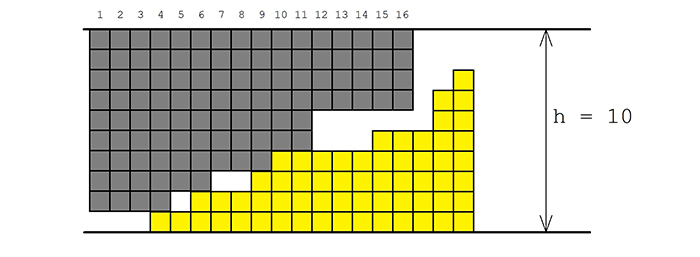
Для понимания условия рассмотрим первый тест. Схематичное его изображение приведено на рис.1.1. Замок обозначен серым, ключ — желтым. Можно видеть, что ключ можно вставить внутрь замка на \(13\) позиций, после чего прямоугольник ключа высотой \(4\) упрется в цилиндр замка высотой \(7\), и дальнейшее движение влево станет невозможным.

Рис. 1.1.

Формат входных данных

В первой строке содержится два числа \(n\) и \(h\) через пробел — длина замка и ключа и высота замка, \(1 \leqslant n, h \leqslant 3 \cdot 10^5\).

Во второй строке находится набор чисел \(a_i\) через пробел — высоты цилиндров замка в порядке их расположения внутри замка. \(a_{i - 1} \geqslant a_i\) для всех \(i\) от \(2\) до \(n\), \(1 \leqslant a_i < h\).

В третьей строке находится набор чисел \(b_i\) через пробел — высоты прямоугольников ключа в порядке их расположения внутри ключа. \(b_{i - 1} \leqslant b_i\) для всех \(i\) от \(2\) до \(n\), \(1 \leqslant b_i < h\).

Формат выходных данных

Вывести одно число — наибольшее число позиций, на которое можно вставить ключ внутрь замка.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	16 10 9 9 9 9 8 8 7 7 7 6 6 4 4 4 4 4 1 1 2 2 2 3 4 4 4 4 4 5 5 5 7 8	13
2	16 10 9 9 9 9 8 8 7 7 7 6 6 4 4 4 4 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	16
3	16 10 9 9 9 9 8 8 7 7 7 6 6 4 4 4 4 4 7 7 7 8 8 8 9 9 9 9 9 9 9 9 9 9	0

Номер теста

Стандартный ввод

Стандартный вывод

16 10
9 9 9 9 8 8 7 7 7 6 6 4 4 4 4 4
1 1 2 2 2 3 4 4 4 4 4 5 5 5 7 8

16 10
9 9 9 9 8 8 7 7 7 6 6 4 4 4 4 4
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

16 10
9 9 9 9 8 8 7 7 7 6 6 4 4 4 4 4
7 7 7 8 8 8 9 9 9 9 9 9 9 9 9 9

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define for0(i, n) for(int i = 0; i < n; i++)
#define int long long
using namespace std;
typedef vector<int> vi;
const int INF = 1e18;
signed main(){
    int n, h;
    cin >> n >> h;
    vi a(n), b(n);
    for0(i, n){
        cin >> a[i];
    }
    for0(i, n){
        cin >> b[i];
    }
    int tb = 0;
    int mx = -INF;
    for0(i, n){
        while(tb < n && b[tb] + a[i] <= h){
            tb++;
        }
        mx = max(mx, i + n - tb + 1);
    }
    cout << 2 * n - mx << endl;
}

Задача 1.4.(25 баллов)

Фрактальная федерация

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 64 Мбайт.

Условие

Фрактальная федерация имеет форму клетчатого прямоугольника. При ее основании было выбрано натуральное число \(z\), большее \(1\), и основание \(k\), большее \(0\). Далее на местности выделили клетчатый прямоугольник \(z^k \times z^{k - 1}\).

Рис. 1.2.

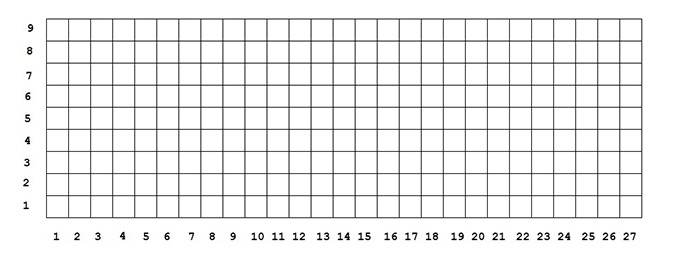
На рис. 1.2 приведен пример для \(z = 3\) и \(k = 3\), то есть федерация в этом примере имеет вид прямоугольника \(27 \times 9\).

Далее, если \(k > 1\), федерацию разделили на \(z^2\) федеральных территорий. Каждая такая территория подобна исходной федерации и имеет также форму прямоугольника, но размера \(z^{k - 1} \times z^{k - 2}\). Федеральные территории расположены в один ряд, границы между ними имеют уровень \(k - 1\).

Рис. 1.3.

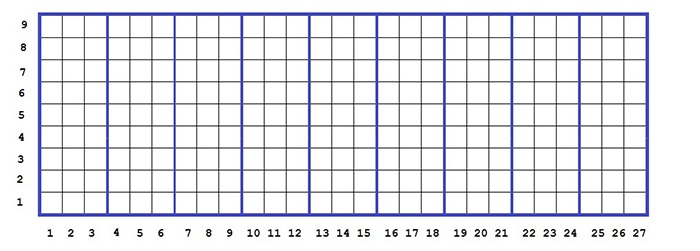
\(9\) синих прямоугольников обозначают \(9\) федеральных территорий \(9 \times 3\) каждая, границы между ними имеют уровень \(2\) (рис. 1.3).

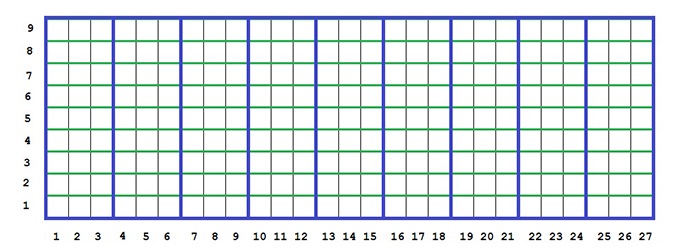
Далее, если \(k > 2\), каждую федеральную территорию снова разделили на \(z^2\) регионов. Каждый такой регион снова подобен исходной федерации и имеет также форму прямоугольника, но размера \(z^{k - 2} \times z^{k - 3}\). Регионы снова расположены внутри федеральных территорий в один ряд, границы между ними имеют уровень \(k - 2\) (рис. 1.4).

Рис. 1.4.

Внутри каждой из \(9\) федеральных территорий зеленым выделены по \(9\) регионов \(3 \times 1\). Зеленые границы имеют уровень \(1\).

Такое фрактальное деление производилось, и границы соответствующего уровня проводились и далее до тех пор, пока очередная область разбиения не стала иметь размеры \(z \times 1\). На этом этапе решено было остановиться. Оставшиеся никак не затронутыми границы между единичными клетками получили уровень \(0\).

Клетки, из которых состоит федерация, пронумеровали от \(1\) до \(z^k\) по первой координате и от \(1\) до \(z^{k - 1}\) по второй координате. Внутри федерации можно перемещаться из клетки в любую соседнюю с ней по стороне. При этом если между этими клетками проходит граница уровня \(t\), то за это перемещение требуется заплатить \(z^t\) единиц.

На территории федерации находится \(n\) городов, каждый занимает ровно одну клетку. По заданным координатам этих городов требуется составить матрицу минимальных стоимостей для перемещения между двумя любыми городами. Более точно, на пересечении строки номер \(i\) и столбца номер \(j\) в матрице должна содержаться минимальная стоимость, за которую можно добраться из города номер \(i\) в город номер \(j\) с учетом пересечения всех границ между ними. На главной диагонали матрицы должны содержаться нули.

Рис. 1.5.

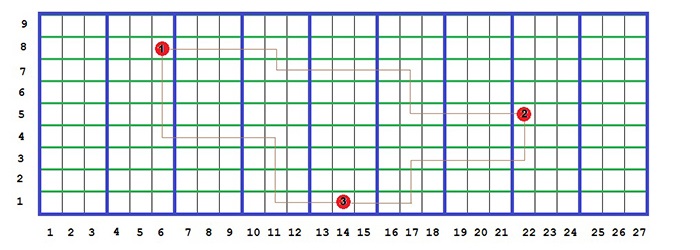
В предложенном примере за пересечение любой черной границы требуется заплатить \(1\) единицу, за пересечение любой зеленой границы — \(3\) единицы, за пересечение любой синей границы — \(9\) единиц. На рис. 1.5 представлены три города и некоторые кратчайшие по стоимости пути между ними. Например, при движении от города № 1 до города № 2 по указанному на рисунке пути между ними, затраты составят: \(9 + 1 + 1 + 9 + 1 + 3 + 1 + 9 + 1 + 1 + 9 + 1 + 3 + 3 + 1 + 9 + 1 + 1 + 9 = 73\).

Формат входных данных

В первой строке через пробел приведены два целых числа \(z\) и \(k\), лежащие в основе федерации, \(2 \leqslant z \leqslant 10\). Число \(k > 0\) и таково, что \(z^k \leqslant 10^{17}\).

Во второй строке содержится число городов \(n\), \(2 \leqslant n \leqslant min(z^{2k-1}, 1000)\).

В следующих \(n\) строках содержится по два целых числа \(x_i\) и \(y_i\) через пробел — координаты очередного города. \(1 \leqslant x_i \leqslant z^k\), \(1 \leqslant y_i \leqslant z^{k - 1}\), все города находятся в попарно различных клетках.

Формат выходных данных

В ответ вывести матрицу \(n \times n\). На пересечении строки номер \(i\) и столбца номер \(j\) в этой матрице должна содержаться минимальная стоимость, за которую можно добраться из города номер \(i\) в город номер \(j\) с учетом пересечения всех границ между ними. Если на пути между двумя городами находится третий город, это никак не влияет на стоимость перемещения. Числа внутри каждой строки матрицы разделять одним пробелом.

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	3 3 3 6 8 22 5 14 1	0 73 53 73 0 44 53 44 0

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define sz(a) (int)a.size()
#define pb push_back
#define for0(i, n) for(int i = 0; i < n; i++)
#define x first
#define y second
#define int long long
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
signed main(){
    int z, k;
    cin >> z >> k;
    int n;
    cin >> n;
    vector<pii> v(n);
    for0(i, n){
        cin >> v[i].x >> v[i].y;
        v[i].x--;
        v[i].y--;
    }
    vector<pii> V, H;
    V.pb({1, 1});
    int d =  1;
    for0(i, k - 1){
        if(i % 2 == 0){
            H.pb({d, d * z});
        }
        else{
            V.pb({d, d * z});
        }
        d *= z;
    }
    if(k % 2 == 0){
        swap(V, H);
    }
    vvi ans(n, vi(n, 0));
    for0(i, n){
        for(int j = i + 1; j < n; j++){
            int dxans = 0;
            int dxk = 0;
            for(int t = sz(V) - 1; t >= 0; t--){
                int di = v[i].x / V[t].x;
                int dj = v[j].x / V[t].x;
                dxans += (abs(di - dj) - dxk) * V[t].y;
                dxk += (abs(di - dj) - dxk);
            }
            int dyans = 0;
            int dyk = 0;
            for(int t = sz(H) - 1; t >= 0; t--){
                int di = v[i].y / H[t].x;
                int dj = v[j].y / H[t].x;
                dyans += (abs(di - dj) - dyk) * H[t].y;
                dyk += (abs(di - dj) - dyk);
            }
            ans[i][j] = dxans + dyans;
            ans[j][i] = ans[i][j];
        }
    }
for0(i, n){
    for0(j, n){
        cout << ans[i][j]<<' ';
    }
    cout << endl;
}
}

Задача 1.5.(30 баллов)

Рейтинг проекта

Имя входного файла: стандартный ввод или input.txt.

Имя выходного файла: стандартный вывод или output.txt.

Ограничение по времени выполнения программы: 1 с.

Ограничение по памяти: 128 Мбайт.

Условие

Директор института Эдуард Леонидович составляет итоговый отчет о проделанной работе. Каждый день в подведомственном ему заведении либо стартует ровно один новый проект, либо завершается ровно один из уже начатых. Каждый проект имеет свой уникальный номер, но порядок, в котором они стартуют, никак не связан с их нумерацией.

Перед Эдуардом Леонидовичем лежит список, в котором содержится очередность произведенных институтом действий в хронологическом порядке. В нем для каждого дня указан номер начатого или законченного в этот день проекта. Например, если порядок такой: 2, 4, 5, 6, 6, 5, 3, 2, 1, 4, 1, 3, то это значит, что проект № \(2\) стартовал в первый день, а завершился в восьмой, проект № \(3\) стартовал в седьмой день, а завершился в двенадцатый, и т. д.

Нужно заметить, что в министерстве, к которому принадлежит институт, важное значение имеет преемственность. Считается, что проект \(B\) является продолжением проекта \(A\), если проект \(B\) начался между датами начала и окончания проекта \(A\) и закончился строго после окончания проекта \(A\). Если проследить это в хронологическом списке, то указанные проекты должны в нем располагаться так: \(\ldots A \ldots B \ldots A \ldots B \ldots\)

Исходя из этого вычисляется рейтинг для каждого проекта. Для некоторого проекта \(A\) его рейтинг равен числу всех проектов, которые либо являются его продолжением, либо для которых проект \(A\) является продолжением.

В рассмотренном примере у проекта № 5 рейтинг равен \(0\), у проекта № 1 рейтинг равен \(1\) (он продолжает проект № 4), а у проекта № 4 рейтинг уже равен 3, так как он продолжает проект № 2, и его в свою очередь продолжают проекты \(1\) и \(3\).

Теперь нужно помочь Эдуарду Леонидовичу с отчетностью и для каждого проекта найти его рейтинг.

Формат входных данных

В первой строке задается количество проектов \(n\), выполненных институтом за отчетный период, \(1 \leqslant n \leqslant 3 \cdot 10^5\).

Во второй строке задана последовательность выполнения проектов. Она состоит из \(2 \cdot n\) чисел через пробел. Каждое из этих чисел от \(1\) до \(n\), и каждое встречается в последовательности ровно два раза. Первое вхождение соответствует началу проекта с этим номером, второе вхождение — окончанию.

Формат выходных данных

Вывести в одну строку через пробел рейтинги всех проектов. На первом месте должен быть рейтинг проекта № \(1\), но втором — рейтинг проекта № \(2\) и т. д. до рейтинга проекта № \(n\).

Тестовые данные

Номер теста	Стандартный ввод	Стандартный вывод
1	6 2 4 5 6 6 5 3 2 1 4 1 3	1 2 2 3 0 0

Пример программы-решения

Ниже представлено решение на языке C++.

C++

#include<bits/stdc++.h>
#define for0(i, n) for(int i = 0; i < n; i++)
#define for1(i, n) for(int i = 1; i <= n; i++)
#define int long long
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> vi;
typedef vector<vector<int> > vvi;
const int INF = 1e18;
const int MOD = 1e9 + 7;
const int LG = 20;
const int N = (1LL << LG);
vi tr(2 * N, 0);
void upd(int pos, int d){
    pos += N;

    tr[pos] += d;
    pos /= 2;
    while(pos){
        tr[pos] = tr[2 * pos] + tr[2 * pos + 1];
        pos /= 2;
    }
}
int get(int l, int r){
    l += N;
    r += N;
    int res = 0;
    while(l <= r){
        if(l % 2 == 1){
            res += tr[l];
        }
        if(r % 2 == 0){
            res += tr[r];
        }
        l = (l + 1) / 2;
        r = (r - 1) / 2;
    }
    return res;
}
signed main(){
    int n;
    cin >> n;
    vi frst(n + 1, -1);
    vi ans(n + 1, -1);
    for0(i, 2 * n){
        int a;
        cin >> a;
        if(frst[a] == -1){
            frst[a] = i;
            upd(i, 1);
            continue;
        }
        int diff = get(frst[a] + 1, i - 1);
        int all = i - frst[a] - 1;
        int rep = all - diff;
        ans[a] = all - 2 * rep;
        upd(frst[a], -1);
        upd(i, 1);
    }
    for1(i, n){
        cout << ans[i] <<' ';
    }
    cout << endl;
}