Предметный тур. Математика. 3 этап

Будем считать, что Иван поехал по часовой стрелке, а Сергей поехал против часовой стрелки. Тогда он остановился, учитывая цикличность, на расстоянии 5 км (по часовой стрелке) от начальной точки, то есть на расстоянии 2 км против часовой стрелки от начала. Сергей же остановился на расстоянии 1 км против часовой стрелки. То есть после остановки между ними расстояние равно 1 км.

Исходя из данных задачи, имеем, что \(x^2 + x = 1980\), откуда \(x = 44\). До 2025 года прошло еще 45 лет, то есть суммарный возраст компании стал \(89\) лет.

• Пусть некоторый поставщик, удовлетворяющий всем требованиям, предлагает гибкость и надежность. Тогда, согласно второму пункту и комментарию к условию, поставщик не будет обладать скоростными качествами. Однако, согласно третьему правилу, так как поставщик надежен, он должен обеспечивать и оперативную доставку — противоречие.

• Тогда во втором условии первая часть не выполнена (то есть неверно, что компания предлагает гибкость и надежность), а вторая — выполнена, то есть поставщик предлагает скорость доставки. Так как первая часть условия должна быть не выполнена, то такая компания не может обладать одновременно и гибкостью, и надежностью (а, быть может, не обладает и ни одним из этих качеств).

  1. Если поставщик обладает надежностью, то так как также обладает скоростью, то не обладает гибкостью. Тогда легко видеть, что первое условие также выполнено (есть скорость и есть негибкость, есть надежность). Также и третье условие также выполнено. То есть такая комбинация характеристик подходит (скорость, надежность, негибкость).
  2. Если поставщик обладает гибкостью, то не обладает надежностью (и обладает скоростью). В этой ситуации первое и третье правило не применимы, так как предварительные условия (предпосылки) не выполнены. Значит, все релевантные условия выполнены, конфигурация «скорость, гибкость, ненадежность» также подходит.
  3. Если поставщик не обладает ни надежностью, ни гибкостью, то третье условие не выполнено.

Заметим, что любое трехзначное число больше суммарных 72, потому на листочке ни одно из записанных чисел не было трехзначным или более. Также отметим, что если бы все числа были однозначны, то сумма была бы \(9\cdot 10/2 = 45 < 72\). То есть двузначные числа должны были в записи присутствовать.

Легко видеть, что двузначное число в записи не могло начинаться с 8 или 7, иначе сумма заведомо больше 72 получается (сразу у одного того двузначного числа). На 6 также не может начинаться, так как \(67+8+9\) больше 72. Аналогично двузначное число из записи не может начинаться на 5 (так как \(56 + 7 + 8 + 9 = 80 > 72\)). Аналогично двузначное из этой записи (ни одно из, если их более одного) не может начинаться на 4: \(45+6+7+8+9 = 75 > 72\).

Заметим, что если было записано двузначное число 34, то если все остальные цифры были записаны как разные числа, получаем выражение \(1 + 2 + 34 + 5 + 6 + 7 + 8 + 9 = 72\), что подходит. Значит, если было в записи двузначное число 34, то единственный вариант, что все остальные числа однозначны.

Допустим, есть еще какие-то решения. Тогда значит, что все числа от 3 до 9 включительно были записаны как отдельные. Но тогда единственный вариант иметь хотя бы одно двузначное число — это если будет присутствовать число \(12\). Но этот вариант дает меньшую сумму.

Сначала приведем пример расстановки четырех таких фигур (на рисунке слева).

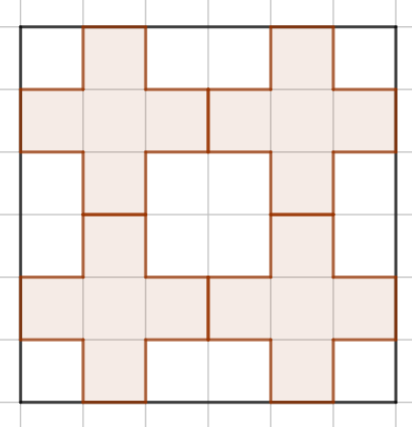
Рис. 1.1. Оценка

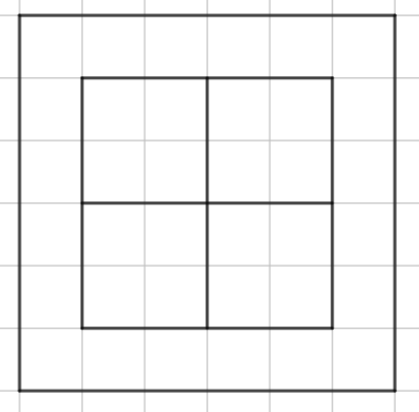
Рис. 1.2. Пример

Докажем, что больше четырех таких фигур расположить в квадрате не получится. Для этого отметим в квадрате \(6 \times 6\) внутренний квадрат \(4 \times 4\). Центральной клеткой рассматриваемой фигуры «крест» будем называть клетку, соседнюю с другими. Тогда легко видеть, что если крест расположен в большом квадрате, то центр этого креста находится во внутреннем квадрате \(4 \times 4\). Больше того, легко видеть, что если центры двух крестов попали в один и тот же квадрат \(2 \times 2\), то такие два креста обязательно пересекаются. Значит, такого не должно происходить в правильной расстановке. Но тогда во внутреннем квадрате \(4 \times 4\) можно расположить не более четырех центральных клеток от крестов, так как этот квадрат можно разбить на 4 квадрата \(2 \times 2\), в каждом — не более одного центра креста.

Заметим: чтобы составить круговой маршрут из данных шести возможных сегментов пути, необходимо выбрать два сегмента, которые затрагивают в совокупности все четыре города. Это можно сделать тремя возможными способами:

1. Москва — Санкт-Петербург и Казань — Нижний Новгород (сумма 6300 руб.);
2. Москва — Казань и Санкт-Петербург — Нижний Новгород (сумма 6700 руб.);
3. Москва — Нижний Новгород и Санкт-Петербург — Казань (сумма 6500 руб.).

Как видно, максимальная стоимость таких двух сегментов в сумме — это 6700 руб. во втором варианте. Тогда суммарная стоимость остальных четырех сегментов будет минимальна из циклических маршрутов, так как равна сумме всех (19500 руб.) минус 6700 руб. То есть искомая минимальная стоимость составляет 12800 руб.

Вычислим площадь листа (в квадратных миллиметрах) каждого из форматов: для А4 площадь равна 62370, для формата Letter площадь равна 60322,46. То есть площадь одного листа A4 превышает площадь одного листа формата Letter на 2047,54. Отношение площади Letter к такой площади «превышения» (первые цифры при делении столбиком) равно 29,4 (следующие цифры уже не интересуют, так как это отношение получается меньше 29,5). Значит, таких превышений с 29 листов А4 не хватит, чтобы набрать на площадь дополнительного листа формата Letter. На тридцати же листах А4 дополнительной площади уже будет достаточно. Остается заметить, что «грубого» способа, когда 30 листов А4 разрезаются на квадраты \(0{,}1 \times 0{,}1\) мм, а далее из этих квадратов перескладываются листы формата Letter, достаточно, чтобы предъявить какой-то способ перекраивания, очевидно, абсолютно неоптимальный, например, по количеству разрезанных частей.

Вспомним полезное вспомогательное утверждение:

Если два треугольника \(XYZ\) и \(NMZ\) имеют общую высоту, проведенную из общей вершины \(Z\), то отношение площадей этих треугольников равно отношению длин их сторон \(XY\) и \(NM\).

Утверждение довольно известно, доказывается выписыванием упомянутых двух площадей по формуле «высота на сторону пополам».

Заметим, что точка \(T\) лежит на диагонали \(BD\). Действительно: если точка \(O\) — центр данного прямоугольника, то \(SORD\) также прямоугольник, причем \(SR\) будет его диагональю, а точка \(T\) тогда будет его центром. В частности, тогда \(T\) является серединой диагонали \(DO\). Но, с другой стороны, аналогично \(O\) — середина диагонали \(BD\) прямоугольника \(ABCD\), поэтому точки отрезка \(DO\), в частности, точка \(T\), лежат на отрезке \(BD\).

Тогда по указанному в начале свойству отношение площадей треугольников \(TQD\) и \(BQD\), у которых высота из вершины \(Q\) общая (а основания лежат на прямой \(BD\)), относятся как \(TD / BD\). При этом \(TD\) — половина \(OD\), а \(OD\) — половина \(BD\).

Таким образом, площадь \(TQD\) в 4 раза меньше площади \(BDQ\). Но аналогично площадь треугольника \(BDQ\) в 2 раза меньше площади треугольника \(BDC\). А площадь \(BDC\), очевидно, равна половине площади прямоугольника \(ABCD\), которая равна 80 см\(^2\). Откуда легко вычислить, что площадь треугольника \(TQD\) составляет \(80 / 16 = 5\) см\(^2\).

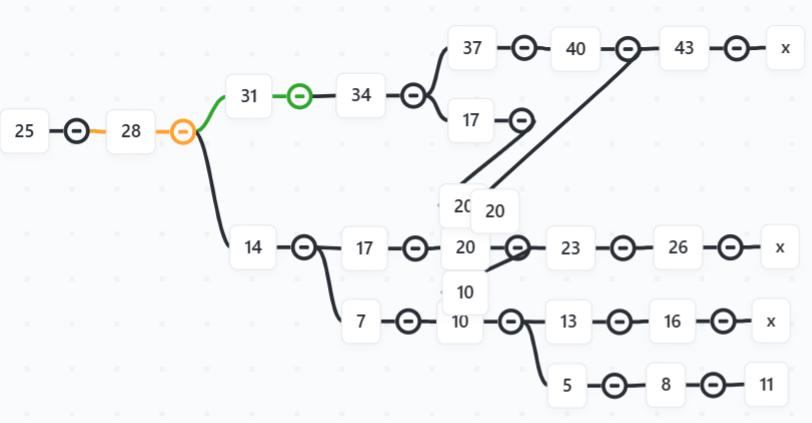
Построим диаграмму возможных значений плана «обратным ходом», то есть от числа 25 (предполагая, что варианты получить такое значение вообще есть) переходя к другим, предшествующим, значениям при помощи операций \(+3\) и \(/2\), предполагая деление на 2 целочисленным и возможным только в той ситуации, когда рассматриваемое значение делится на 2 без остатка. В частности, это означает, что если рассматриваемое число нечетное, то «после него» (при продвижении обратным ходом) будет следовать только одно значение (полученное как \(+3\)). Если же рассматриваемое число четное, то «после него» следуют два значения.

Отметим, что по ходу построения такой диаграммы (графа или MindMap) естественным образом находится вариант цепочки из семи ходов: \(11 \to 8 \to 5 \to 10 \to 7 \to 14 \to 28 \to 25\). Поэтому построение диаграммы логично ограничить глубиной 7, что позволит проверить, есть ли более короткие способы (нет) и обосновать, что все возможности рассмотрены. Поэтому если какая-то ветка диаграммы продлевается до длины 7 и на этом уровне нет возможности закончить ветку числом 11, в соответствующей ячейке будем ставить знак \(X\), обозначающий конец рассматриваемой ветки.

Также отметим, что некоторые значения (20, 10 и другие) можно получить не одним способом. Поэтому на диаграмме такие повторяющиеся значения, полученные на более позднем уровне, собраны вокруг такого же значения на более раннем уровне (так его использование позволит быстрее добраться до последующих позиций).

На рис. 2.1 получаемая диаграмма, которая показывает, что быстрее, чем за 7 шагов не справиться.

Обозначим: \(v_k\) — скорость контролера, \(v_l\) — скорость конвейерной ленты, \(t\) — время, за которое контролер проходит путь от последнего изделия до первого и обратно.

При движении контролера вперед его относительная скорость относительно ленты равна \(v_k + v_l\). Расстояние, которое ему требуется преодолеть при движении относительно ленты до первого изделия, равно \(12\) м. То есть время движения вперед равно \(t_1 = \frac{12}{v_k + v_l}\). Аналогично время его движения назад, посчитанное относительно ленты, равно \(t_2 = \frac{12}{v_k - v_l}\). Итого \[t = t_1 + t_2 = \frac{12}{v_k + v_l} + \frac{12}{v_k - v_l}.\]

За это время \(t\) конвейерная лента продвинулась на 5 м, то есть \(v_l \cdot t = 5\). Объединяя с предыдущим результатом, имеем \[v_l \left( \frac{12}{v_k + v_l} + \frac{12}{v_k - v_l} \right) = 5.\]

Упростим: \[\frac{12 v_l}{v_k + v_l} + \frac{12 v_l}{v_k - v_l} = 5;\] \[12 v_l \left( \frac{1}{v_k + v_l} + \frac{1}{v_k - v_l} \right) = 5;\] \[\begin{gather} 12 v_l \left( \frac{v_k - v_l + v_k + v_l}{(v_k + v_l)(v_k - v_l)} \right) = 5;\\ 12 v_l \left( \frac{2 v_k}{v_k^2 - v_l^2} \right) = 5;\\ \frac{24 v_k v_l}{v_k^2 - v_l^2} = 5. \end{gather}\] Решаем уравнение относительно \(v_k\): \[\begin{gather} 24 v_k v_l = 5 (v_k^2 - v_l^2);\\ 24 v_k v_l = 5 v_k^2 - 5 v_l^2;\\ 5 v_k^2 - 24 v_k v_l - 5 v_l^2 = 0. \end{gather}\] Это квадратное уравнение относительно \(v_k\). Решим его: \[\begin{gather} v_k = \frac{24 v_l \pm \sqrt{(24 v_l)^2 + 4 \cdot 5 \cdot 5 v_l^2}}{2 \cdot 5};\\ v_k = \frac{24 v_l \pm \sqrt{576 v_l^2 + 100 v_l^2}}{10};\\ v_k = \frac{24 v_l \pm \sqrt{676 v_l^2}}{10};\\ v_k = \frac{24 v_l \pm 26 v_l}{10}. \end{gather}\]

Получаем два решения: \(v_k = 5 v_l \text{ или } v_k = -\frac{v_l}{5}\). Поскольку скорость не может быть отрицательной, имеем \(v_k = 5 v_l\).

Тогда общее расстояние, которое преодолел контролер, равно \[v_k \cdot t = 5 v_l \cdot \left( \frac{12}{5 v_l + v_l} + \frac{12}{5 v_l - v_l} \right) = 5 v_l \cdot \left( \frac{12}{6 v_l} + \frac{12}{4 v_l} \right) = 5 v_l \cdot \dfrac{2 + 3}{v_l} = 5 \cdot 5 = 25 \text{ м}.\]